Página 195
UNIDADE
10
Polígonos e circunferência

Agora vamos estudar...
- polígonos e seus elementos;
- diagonais de um polígono convexo;
- figuras congruentes;
- pontos notáveis de um triângulo;
- quadriláteros;
- circunferência, círculo e seus elementos;
- polígonos inscritos e circunscritos na circunferência;
- medida do comprimento da circunferência.
Página 196
Diagonais de um polígono
Em anos anteriores, apresentamos o conceito de polígono, que é toda linha fechada no plano, formada por segmentos de reta que não se cruzam, de maneira que dois segmentos consecutivos não são parte de uma mesma reta. Cada segmento de reta é um lado do polígono. Exceto quando dito o contrário, nesta coleção apresentaremos os polígonos com suas regiões internas coloridas, conforme as imagens desta página.
Com base em algumas características, podemos classificar os polígonos em convexos ou não convexos.
Polígono convexo: quando qualquer reta que passa por seu interior corta seus lados em somente dois pontos. Analise os exemplos.
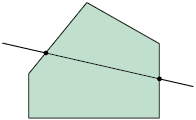
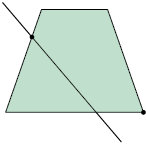
Polígono não convexo: quando existe pelo menos uma reta que passa por seu interior cortando seus lados em mais de dois pontos. Analise os exemplos.


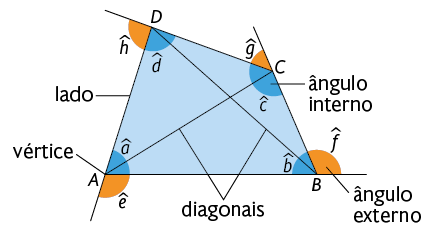
As diagonais de um polígono convexo são os segmentos de reta que ligam dois vértices e não são lados desse polígono. No polígono convexo , temos os seguintes elementos.
- Vértices: A, B, C e D.
- Lados: , , e .
- Diagonais: e .
- Medida dos ângulos internos: , , e .
- Medida dos ângulos externos: , , e .
Analise nas figuras a seguir a quantidade de diagonais que partem de um único vértice em alguns polígonos convexos.
4 lados
1 diagonal
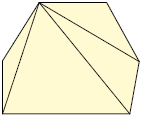
6 lados
3 diagonais
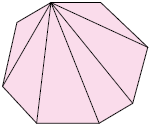
8 lados
5 diagonais
Questão 1. Com base nos polígonos
anteriores, quantas diagonais partem de
um único vértice de um polígono convexo de 10 lados?
Questão 2. O que você pode perceber em
relação à quantidade de diagonais
que partem de um único vértice de cada um desses
polígonos?
Página 197
Ao analisar os polígonos convexos ao final da página anterior, percebemos que a quantidade de diagonais que partem de um único vértice de cada um deles é igual à quantidade de lados ou vértices do polígono menos 3.
- Quadrilátero:
- Hexágono:
- Octógono:
Utilizando o mesmo raciocínio em um heptágono convexo, temos:
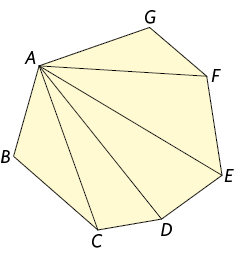
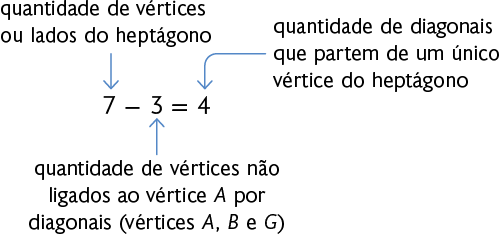
Analise todas as diagonais do heptágono convexo apresentado na imagem a seguir.
Podemos calcular a quantidade total de diagonais desse polígono da seguinte maneira.
Inicialmente, multiplicamos a quantidade de diagonais que partem de um único vértice pela quantidade de vértices ou lados desse polígono.
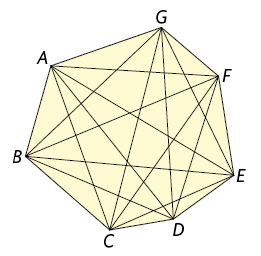

Os segmentos de reta e , por exemplo, representam uma mesma diagonal, e isso acontece com todos os segmentos de reta que ligam vértices não consecutivos do heptágono. Para que cada diagonal não seja contada duas vezes, dividimos o resultado anterior por 2.
Assim, o heptágono convexo tem 14 diagonais ao todo.
Em um polígono convexo de n lados ou vértices, a quantidade D de diagonais é calculada por:
Questão 3. Qual polígono convexo não tem
diagonal? Justifique sua
resposta.
Página 198
Atividades
Faça as atividades no caderno.
1. Classifique cada figura em polígono convexo, polígono não convexo ou não polígono.




2. Determine a palavra ou o número que substitui cada adequadamente.
a) Um polígono que tem 6 lados tem vértices.
b) Um polígono tem no mínimo lados.
c) Um polígono convexo de 12 lados tem diagonais.
d) O convexo tem diagonais.
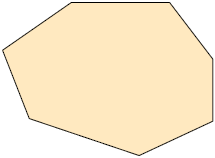
3. Determine quantas diagonais partem de um único vértice de cada polígono convexo a seguir.

4. Determine a quantidade de diagonais de um polígono convexo que tem:
a) 5 lados;
b) 13 lados;
c) 20 lados;
d) 15 lados.
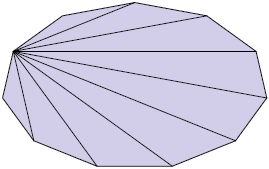
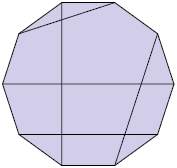
5. Quantas diagonais faltam em cada polígono a seguir para que sejam traçadas todas as diagonais?
6. Certa figura geométrica espacial é formada por 12 faces com formato de pentágono e 20 faces com formato de hexágono.
Ao traçar todas as diagonais de cada face, quantas diagonais traçaremos ao todo?
7. No
interior do polígono amarelo foi desenhado um polígono rosa. Sabendo que os
segmentos destacados em vermelho representam diagonais desses
polígonos, responda os itens.
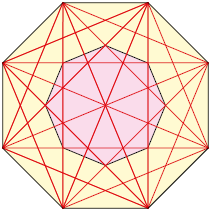
a) Quantas diagonais do polígono amarelo não representam diagonais do polígono rosa?
b) Quantas diagonais faltam no polígono rosa para que sejam traçadas todas as diagonais?
Página 199
Ângulos em um polígono convexo
Analise como podemos calcular a soma das medidas dos ângulos internos dos polígonos convexos a seguir.

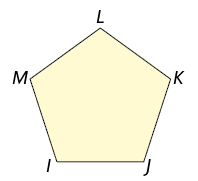
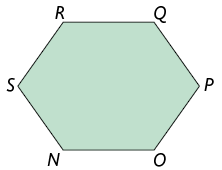
Decompomos cada polígono em triângulos traçando todas as diagonais a partir de um único vértice.
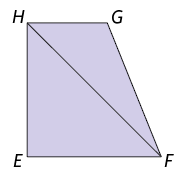
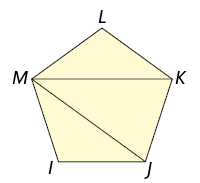
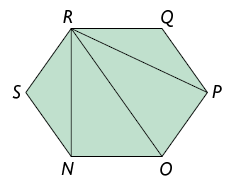
Atenção!
Note que cada triângulo obtido é formado por exatamente 3 vértices do polígono.
Como a soma das medidas dos ângulos internos de um triângulo é , multiplicamos pela quantidade de triângulos obtida em cada polígono para obter a soma das medidas dos ângulos internos de cada um deles.
- Quadrilátero:
- Pentágono:
- Hexágono:
O quadro a seguir apresenta a quantidade de lados e de triângulos obtidos em cada polígono, bem como a soma das medidas dos ângulos internos deles.
|
Nome do polígono convexo |
Quantidade de lados |
Quantidade de triângulos obtidos |
Soma das medidas dos ângulos internos |
|---|---|---|---|
|
Quadrilátero |
4 |
2 |
|
|
Pentágono |
5 |
3 |
|
|
Hexágono |
6 |
4 |
Note que a quantidade de triângulos obtidos em cada polígono é igual à quantidade de lados menos 2, ou seja, em um polígono convexo de n lados são obtidos triângulos, traçando todas as diagonais partindo de um único vértice.
A soma das medidas dos ângulos internos de um polígono de n lados é calculada por:
Questão 4. Qual é a soma das medidas dos
ângulos internos de um
retângulo?
Página 200
Agora, analise de maneira experimental como podemos obter a soma das medidas dos ângulos externos de um polígono convexo por meio de recortes.
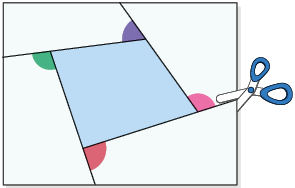
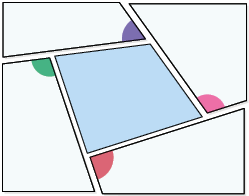
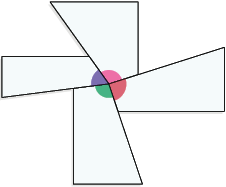
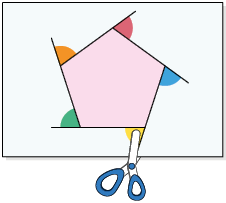
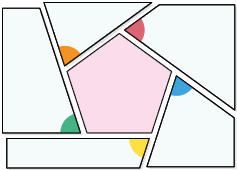
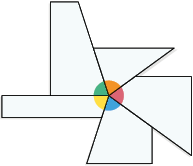
Com base nas imagens, notamos que a soma das medidas dos ângulos externos de um quadrilátero e de um pentágono convexos é .
A seguir, vamos demonstrar que a soma das medidas dos ângulos externos de um polígono convexo de n lados é igual a .
Podemos obter a soma das medidas de todos os ângulos internos () e todos os ângulos externos () de um polígono convexo multiplicando a quantidade de lados n por . Nesse caso, podemos escrever .
Atenção!
Os ângulos interno e externo de cada vértice de um polígono convexo são suplementares.
Como , temos:
A soma das medidas dos ângulos externos de um polígono convexo de n lados é .
Página 201
Analise agora o polígono convexo a seguir, que tem ângulos internos de mesma medida e lados de mesma medida de comprimento. Um polígono com essas características é chamado polígono regular.
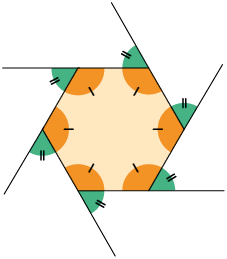
As medidas dos ângulos externos de um polígono regular também são iguais.
Atenção!
Quando dois ângulos têm medidas iguais, dizemos que eles são congruentes. No polígono apresentado, os ângulos congruentes estão indicados com a mesma quantidade de "tracinhos". Nas próximas páginas deste capítulo, os "tracinhos" também serão utilizados para indicar a congruência dos lados.
Atividades
Faça as atividades no caderno.
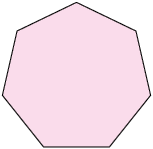
8. Calcule a soma das medidas dos ângulos internos de cada polígono.



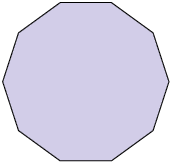
9. Determine a medida de cada ângulo interno dos polígonos regulares a seguir.



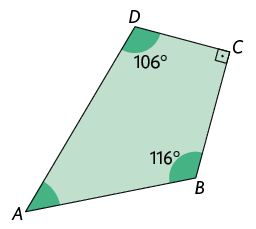
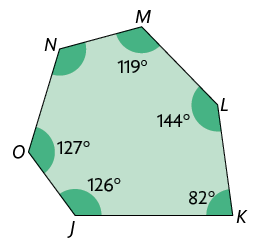
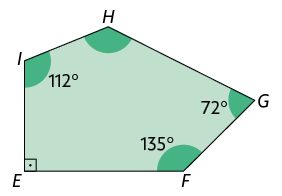
10. Determine a medida do ângulo interno desconhecida em cada polígono.
11. Calcule a soma das medidas dos ângulos internos de um polígono convexo que tenha:
a) 2 diagonais.
b) 5 diagonais.
c) nenhuma diagonal.
Página 202
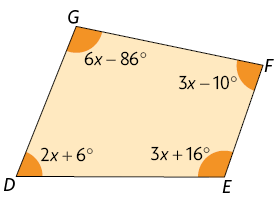
12. Efetue os cálculos e determine o valor de x e a medida de cada ângulo interno do polígono.
13. Existem vários tipos de piso para revestimento utilizados na construção ou reforma de um imóvel, entre eles pisos de borracha, de porcelana, de cerâmica e de concreto.

a) Quais são os nomes dos polígonos que lembram o formato dos pisos indicados na imagem?
b) Qual é a soma das medidas dos ângulos internos de cada um dos polígonos que você citou no item anterior? E a soma das medidas dos ângulos externos?
c) Sabendo que esses polígonos são regulares, qual é a medida de cada ângulo interno deles?
d) Quantas diagonais cada um desses polígonos tem?
14. Determine a quantidade de lados de um polígono regular cuja soma das medidas dos ângulos internos seja:
a) .
b) .
c) .
d) .
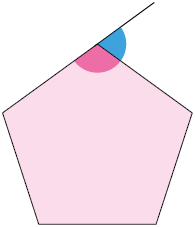
15. Sem realizar medições, determine a medida do ângulo externo de cada polígono regular.
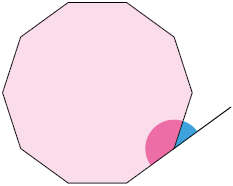
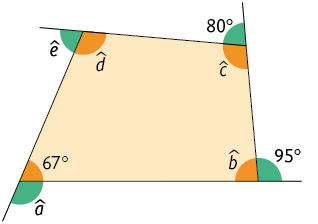
16. Calcule a medida de cada ângulo indicada por letras no quadrilátero.
17. Escreva no caderno o nome do polígono correspondente às informações de cada quadro.
A.A soma das medidas dos ângulos internos é .
Todos os ângulos internos têm medidas iguais.
B.Tem 12 vértices.
A medida de cada ângulo externo é .
Página 203
Triângulos
O triângulo é um polígono de três lados. Em um triângulo temos os seguintes elementos.
- Nome: triângulo ou .
- Lados: , e .
- Vértices: A, B e C.
- Medidas dos ângulos internos: , e .
- Medidas dos ângulos externos: , e .
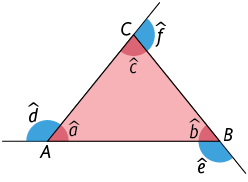
Atenção!
No triângulo , o lado é oposto ao ângulo e, do mesmo modo, o ângulo é oposto ao lado .
Podemos classificar os triângulos de acordo com:
as medidas dos comprimentos dos lados.
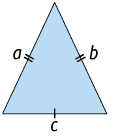
Isósceles
Triângulo que tem pelo menos 2 lados com medidas de comprimento iguais.
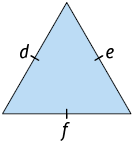
Equilátero
Triângulo que tem todos os lados com medidas de comprimento iguais.
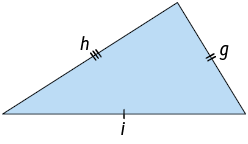
Escaleno
Triângulo que tem os 3 lados com medidas de comprimento diferentes.
, e
as medidas dos ângulos internos.
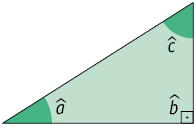
Retângulo
Triângulo que tem um ângulo interno reto.
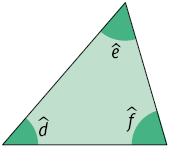
Acutângulo
Triângulo que tem os 3 ângulos internos agudos.
, e
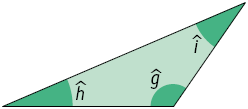
Obtusângulo
Triângulo que tem um ângulo interno obtuso.
Página 204
Ângulos nos triângulos
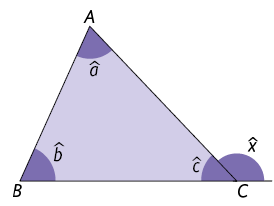
Considere um triângulo ABC qualquer, cujos ângulos internos medem , e . Ao prolongar o lado , determinamos um ângulo externo, adjacente ao ângulo de medida .
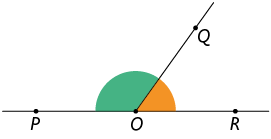
Atenção!
Dois ângulos que têm um lado comum e determinam duas regiões que não têm pontos em comum são chamados adjacentes. Na imagem a seguir, os ângulos e são adjacentes.
Por construção, os ângulos de medida e são suplementares, ou seja:
Consequentemente:
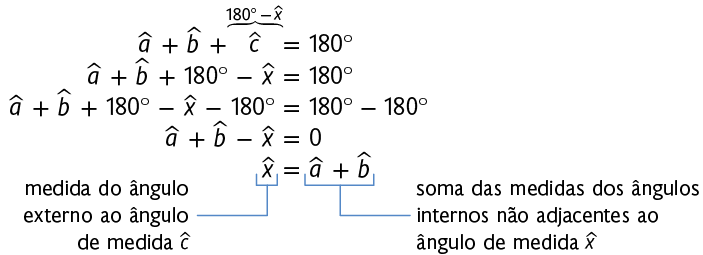
Se realizarmos esse procedimento com os outros vértices do triângulo, chegaremos à mesma relação entre as medidas dos ângulos. Nesse caso, temos a seguinte propriedade.
Em um triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele.
Questão 5. Em seu caderno, verifique, de maneira semelhante, a propriedade apresentada usando outro vértice do triângulo.
Atividades
Faça as atividades no caderno.
18. De acordo com as indicações no , responda às questões a seguir.
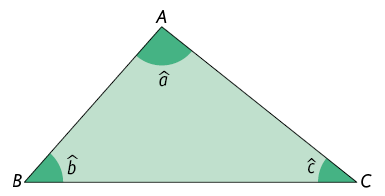
a) Qual é o lado oposto ao ângulo de medida ?
b) Qual é a medida do ângulo oposto ao lado ?
Página 205
19. Sabendo que os triângulos a seguir são equiláteros, determine o valor de x em cada um deles.


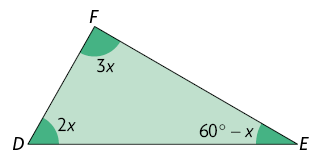
20. Calcule o valor de x e a medida de cada ângulo interno do triângulo . Em seguida, classifique o triângulo de acordo com as medidas obtidas para os ângulos internos.
21. No
triângulo , e . Determine a
medida do ângulo .
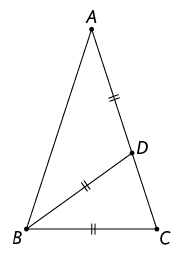
Atenção!
Os ângulos adjacentes à base de um triângulo isósceles são congruentes.
22. Sabendo que o triângulo a seguir é isósceles, indique a afirmação falsa.
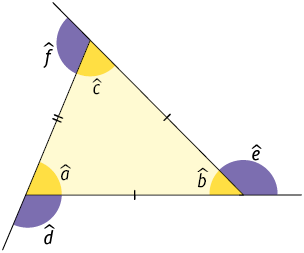
a)
b)
c)
d)
e)
23. Calcule x e y na figura a seguir, sabendo que .
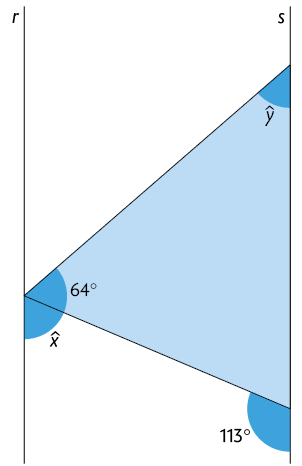
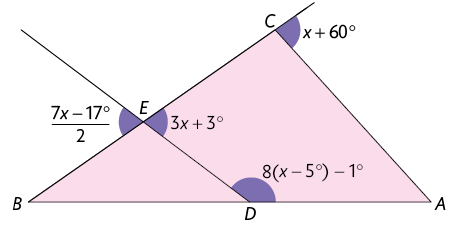
24. Determine a medida de cada ângulo interno do triângulo . Depois, classifique-o em relação à medida dos ângulos internos.
Página 206
Congruência de figuras
Certo programa de computador permite mover e fazer rotações das peças do tangram, cujo formato lembra polígonos. Utilizando esse programa, Heitor organizou esses polígonos e, ao sobrepor alguns deles, percebeu que há polígonos que coincidiram. Analise algumas sobreposições que ele fez.
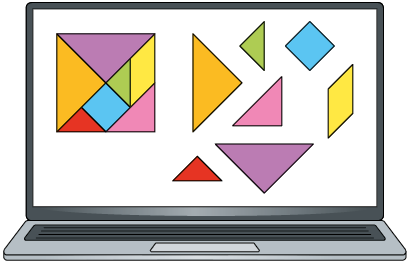
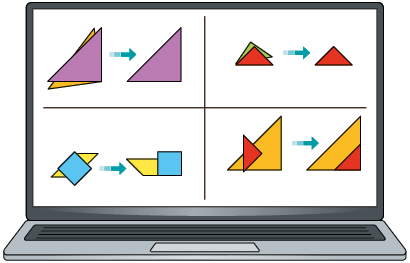
Os polígonos que coincidiram são chamados congruentes e, nesse caso, dizemos que os triângulos verde e vermelho, por exemplo, são congruentes.
Também podemos estabelecer outras congruências: dois segmentos de reta são congruentes quando têm a mesma medida de comprimento; dois ângulos são congruentes quando têm a mesma medida.
Dois ou mais polígonos são congruentes quando seus respectivos lados são congruentes e quando seus respectivos ângulos internos também são congruentes.
Por exemplo, os polígonos e a seguir são congruentes.


- Congruência dos lados: ; ; ; .
- Congruência dos ângulos internos: ; ; ; .
Atenção!
Utilizamos o símbolo para indicar congruência.
Questão 6. Junte-se a um colega e realizem uma pesquisa para verificar qual é a origem do tangram. Depois, registrem os resultados no caderno.
Questão 7. É possível afirmar que dois
hexágonos nos quais os respectivos
lados têm medidas de comprimento iguais são congruentes? Justifique sua
resposta.
Página 207
Triângulos congruentes
Para determinar se dois triângulos são congruentes, não é necessário medir o comprimento de todos os lados e todos os ângulos internos deles. Medindo o comprimento de lados e ângulos internos específicos, podemos garantir a congruência dos triângulos.
Atenção!
Os lados e os ângulos dos triângulos indicados com a mesma quantidade de "tracinhos" são congruentes.
Quando dois triângulos têm os 3 lados respectivamente congruentes, esses triângulos são congruentes.

Lado: .
Lado: .
Lado: .
Esse é o caso de congruência lado, lado e lado ().
Quando dois triângulos têm 2 lados respectivamente congruentes e o ângulo interno compreendido entre esses lados também respectivamente congruentes, esses triângulos são congruentes.
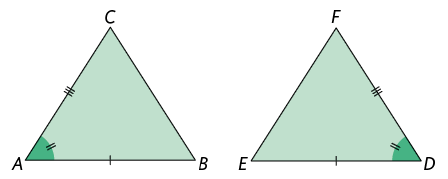
Lado: .
Ângulo: .
Lado: .
Esse é o caso de congruência lado, ângulo e lado ().
Quando dois triângulos têm 1 lado respectivamente congruente e os 2 ângulos adjacentes a esse lado também respectivamente congruentes, esses triângulos são congruentes.

Ângulo: .
Lado: .
Ângulo: .
Esse é o caso de congruência ângulo, lado e ângulo ().
Atenção!
Dois ângulos adjacentes a um lado significa que os vértices desses ângulos são as extremidades desse lado.
Página 208
Quando dois triângulos têm 1 lado respectivamente congruente, 1 ângulo adjacente a esse lado respectivamente congruente e o ângulo oposto a esse lado também respectivamente congruente, esses triângulos são congruentes.
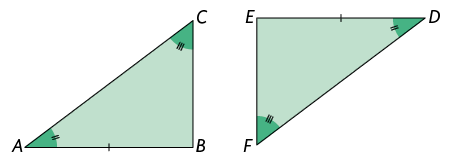
Lado: .
Ângulo adjacente: .
Ângulo oposto: .
Esse é o caso de congruência lado, ângulo e ângulo oposto .
Atividades
Faça as atividades no caderno.
25. Realize as medições necessárias e verifique se os triângulos apresentados em cada item são congruentes.

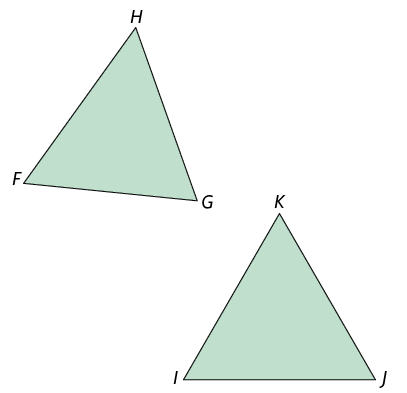
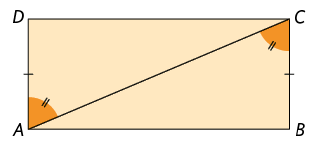
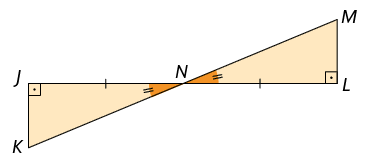
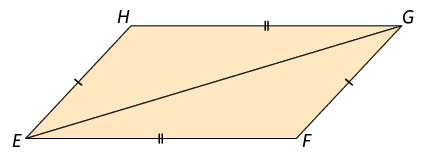
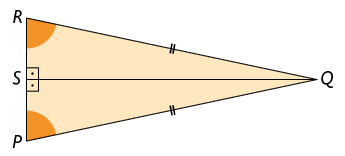
26. Em cada figura, é possível destacar 2 triângulos. Analise se eles são congruentes e determine qual caso pode ser utilizado para verificar essa congruência.
Página 209
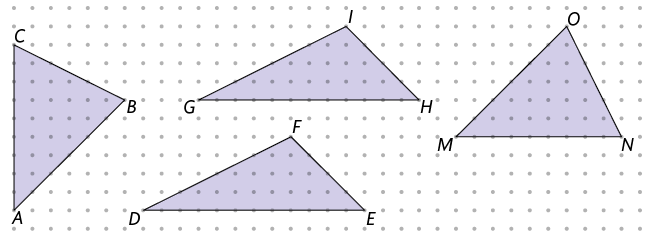
27. Quais dos triângulos representados na malha pontilhada são congruentes?
28. No triângulo , e .
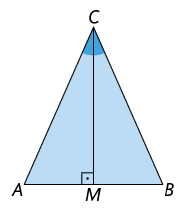
Atenção!
Note que é o lado comum aos triângulos e .
De acordo com a imagem, mostre no caderno que e .
29. Considere os triângulos cujas medidas estão indicadas nos quadros a seguir.
A.
B.
C.
D.
E.
F.
Quais pares de triângulos são congruentes?
30. Considere
os triângulos representados a seguir e o triângulo , cujas medidas estão indicadas no quadro.
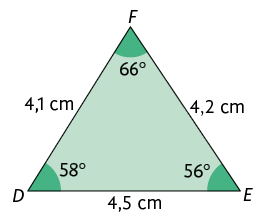
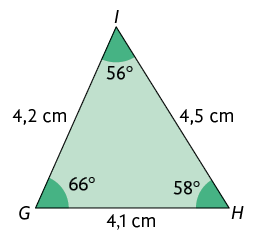
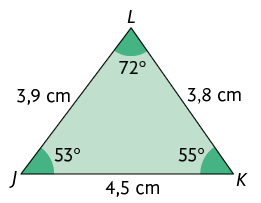
a) Quais desses triângulos são congruentes ao triângulo ?
b) Qual é a medida de comprimento do lado do ?
c) Qual é a medida do ângulo e do comprimento lado do ?
Página 210
Pontos notáveis de um triângulo
Agora, vamos estudar alguns pontos associados aos triângulos. Esses pontos, que têm características particulares, são chamados pontos notáveis. Para determiná-los, vamos traçar medianas, bissetrizes, alturas e mediatrizes nos triângulos.
Mediana
A mediana de um triângulo é o segmento de reta que tem uma extremidade em um vértice do triângulo e a outra extremidade no ponto médio do lado oposto a esse vértice. O ponto médio do lado do triângulo divide esse lado em dois segmentos de reta congruentes.
Analise as medianas do triângulo .
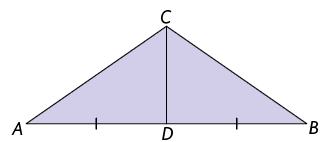
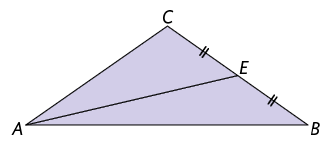
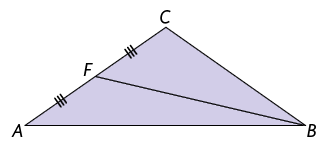
No triângulo a seguir, foram traçadas as medianas relativas a todos os lados. Todo triângulo tem 3 medianas, que se cruzam em um mesmo ponto. Esse ponto notável é chamado baricentro do triângulo.
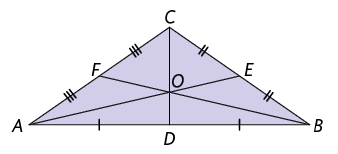
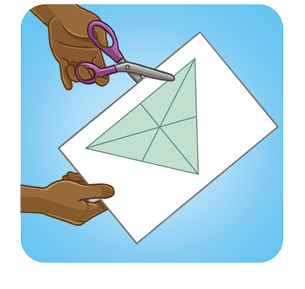
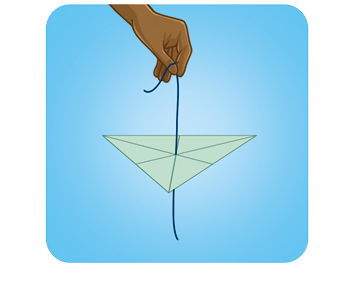
O baricentro é o centro de equilíbrio de um triângulo. Podemos verificar isso desenhando um triângulo qualquer em um papel grosso. Ao suspender o triângulo preso por um barbante fixado ao baricentro, ele se mantém em equilíbrio.

Página 211
Bissetriz
A bissetriz de um ângulo é a semirreta com origem no vértice desse ângulo que o divide em 2 ângulos congruentes. Analise na imagem a bissetriz do ângulo .

Demonstraremos que, dado um ponto qualquer sobre a bissetriz de um ângulo, esse ponto é equidistante dos lados desse ângulo.
Atenção!
A distância de um ponto M a uma reta r é o comprimento do segmento perpendicular a r que tem extremidades em M e em um ponto de r.
Vamos considerar um ponto M qualquer sobre a bissetriz de e os segmentos e , perpendiculares aos lados e , respectivamente.
Os triângulos e obtidos são congruentes pelo caso de congruência , pois (lado comum dos triângulos), ( é bissetriz do ângulo ) e (ângulos retos). Dessa forma, e o ponto M é equidistante dos lados do ângulo .

Portanto, qualquer ponto sobre a bissetriz de um ângulo é equidistante dos lados desse ângulo, e nenhum outro ponto do plano apresenta essa propriedade.
Atenção!
O conjunto de todos os pontos do plano que têm determinada propriedade é chamado lugar geométrico dessa propriedade.
O lugar geométrico dos pontos do plano equidistantes de duas semirretas FE e FG de mesma origem é a bissetriz do ângulo .
Página 212
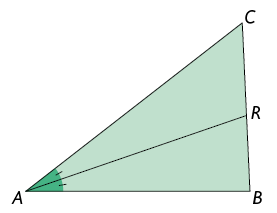
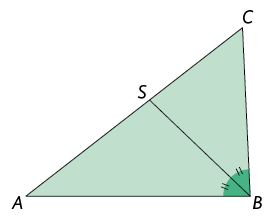
A bissetriz de um triângulo é o segmento de reta que tem uma extremidade em um vértice do triângulo – dividindo o ângulo interno desse vértice em 2 ângulos congruentes – e a outra extremidade no lado oposto a esse vértice.
Analise as bissetrizes do triângulo .
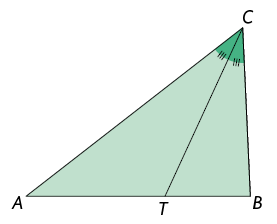
No triângulo a seguir, foram traçadas as bissetrizes relativas a todos os ângulos internos. Todo triângulo tem 3 bissetrizes, que se cruzam em um ponto. Esse ponto notável é chamado incentro do triângulo.
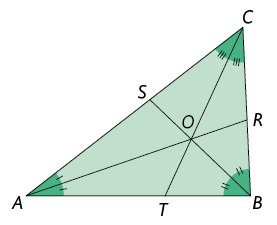
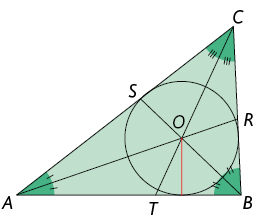
Em um triângulo, o incentro é equidistante de seus lados. Assim, podemos traçar uma circunferência com centro no incentro cuja medida de comprimento do raio é igual à medida da distância entre o incentro e qualquer um dos lados do triângulo. Com isso, obtemos uma circunferência inscrita no triângulo.
Altura
No dia a dia, é comum utilizar a palavra "altura" para indicar um comprimento vertical, como a altura de uma pessoa ou de um prédio.
No entanto, a altura de um triângulo é o segmento de reta que tem uma extremidade em um vértice do triângulo e é perpendicular ao lado oposto a esse vértice ou a seu prolongamento. A outra extremidade intersecta o lado oposto ao vértice ou seu prolongamento.
Página 213
Analise as alturas do triângulo .
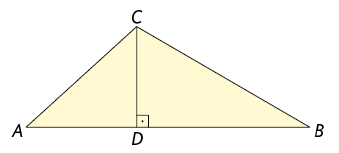


No triângulo a seguir, foram traçadas as alturas relativas a todos os lados. Todo triângulo tem 3 alturas. Essas alturas ou seus prolongamentos cruzam-se em um ponto. Esse ponto notável é chamado ortocentro do triângulo.
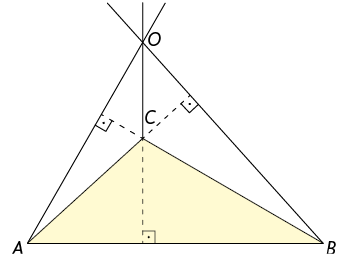
Analise cada triângulo a seguir e seu ortocentro, indicado pela letra .
Em um triângulo acutângulo, o ortocentro é um ponto no interior do triângulo.
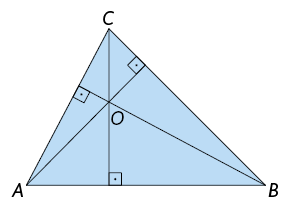
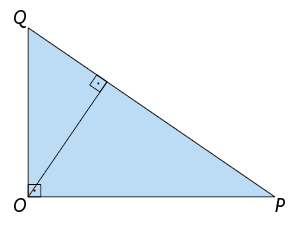
Em um triângulo retângulo, o ortocentro coincide com o vértice do ângulo reto.
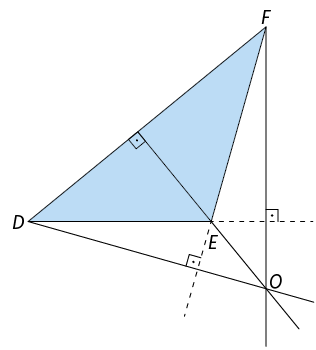
Em um triângulo obtusângulo, o ortocentro é um ponto exterior ao triângulo.
Página 214
Mediatriz
Na imagem, estão representados o segmento de reta e a reta , perpendicular a esse segmento de reta em seu ponto médio. Essa reta é chamada mediatriz do segmento de reta .
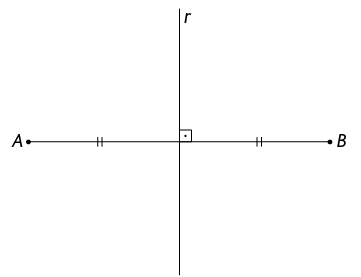
Atenção!
A distância entre dois pontos é o comprimento do segmento de reta que os une.
Demonstraremos agora que qualquer ponto da mediatriz de um segmento de reta é equidistante dos extremos desse segmento.
Vamos considerar um ponto P sobre a mediatriz de e analisar dois casos.
- Se P for o ponto médio de , temos que e P é equidistante dos extremos de .
- Se P não for o ponto médio de , ao traçarmos os segmentos e , obtemos dois triângulos congruentes e pelo caso de congruência , pois (O é o ponto médio de ), (lado comum dos triângulos) e (ângulos retos). Dessa forma, e o ponto P é equidistante dos extremos de .
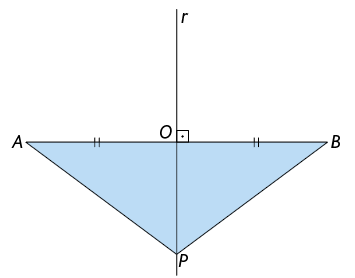
Portanto, qualquer ponto sobre a mediatriz de um segmento é equidistante dos extremos do segmento e nenhum outro ponto do plano tem essa propriedade.
O lugar geométrico dos pontos do plano equidistantes de dois pontos A e B dados é a mediatriz de .
Página 215
A mediatriz de um triângulo é a reta perpendicular a um lado do triângulo em seu ponto médio. O ponto médio do lado do triângulo divide esse lado em dois segmentos de reta congruentes.
Analise as mediatrizes do triângulo .
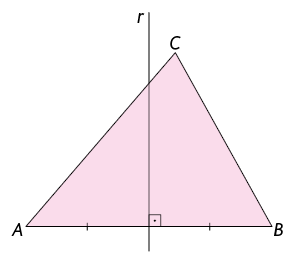
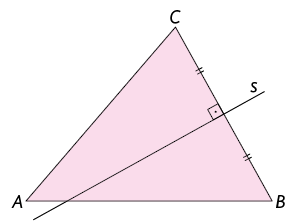
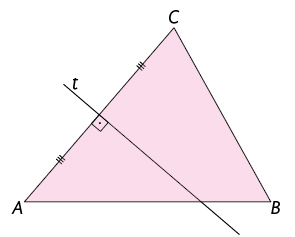
No triângulo a seguir, foram traçadas as mediatrizes relativas a todos os lados. Todo triângulo tem 3 mediatrizes, que se cruzam em um ponto. Esse ponto notável é chamado circuncentro do triângulo.
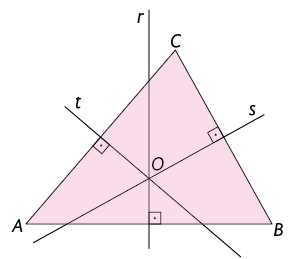
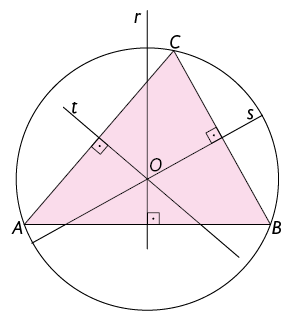
Em um triângulo, o circuncentro é equidistante de seus vértices. Assim, podemos traçar uma circunferência que passa pelos três vértices do triângulo, cujo centro é o circuncentro e a medida de comprimento do raio é igual à medida da distância entre o circuncentro e qualquer um dos vértices do triângulo. Com isso, obtemos a circunferência circunscrita ao triângulo.
Página 216
Instrumentos e softwares
Mediatrizes de um triângulo com régua e compasso
Siga as orientações do professor e o passo a passo para obter as mediatrizes de um triângulo usando régua e compasso.
1º. Com a ponta-seca do compasso em um dos vértices do triângulo e abertura maior do que a metade da medida do comprimento do lado, trace dois arcos.
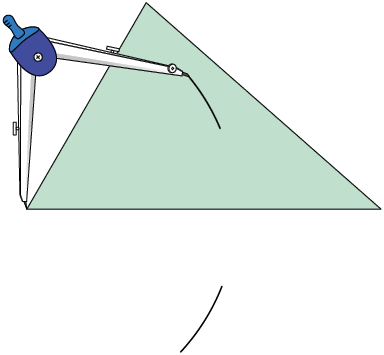
2º. Com a mesma abertura do compasso, posicione a ponta-seca no outro vértice do triângulo e trace novamente dois arcos que cruzam os anteriores.
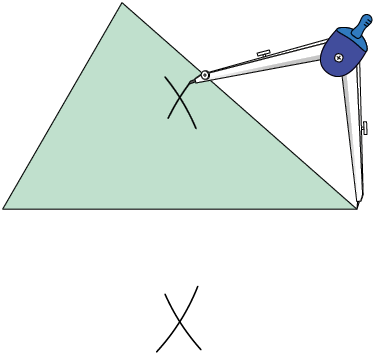
3º. Utilizando uma régua, trace uma reta perpendicular ao lado do triângulo, passando pelos pontos determinados pelos cruzamentos dos arcos e obtendo a mediatriz relativa ao lado que contém os dois vértices utilizados.
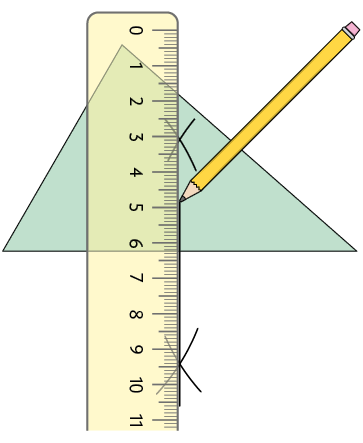
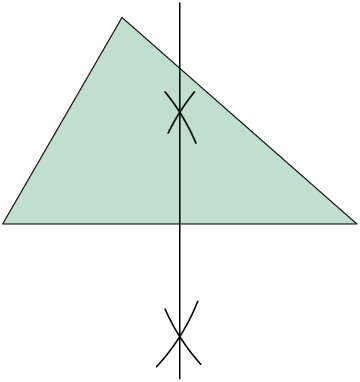
Repita os mesmos procedimentos para os demais lados do triângulo para obter as outras mediatrizes.
Página 217
Instrumentos e softwares
Bissetrizes e incentro de um triângulo com o GeoGebra
Siga as orientações do professor e o passo a passo para obter as bissetrizes e o incentro de um triângulo utilizando o GeoGebra.
1º. Com a ferramenta Ponto, marque três pontos não alinhados A, B e C. Depois, com a ferramenta Polígono construa o triângulo ABC. Para isso, clique sobre os pontos A, B, C e A, nessa ordem.
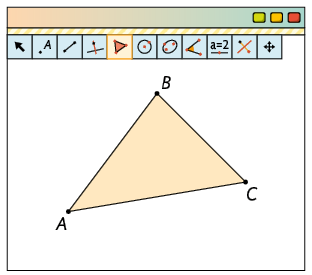
2º. Com a ferramenta Bissetriz, construa as bissetrizes do triângulo ABC. Para isso, sempre respeitando a ordem indicada, clique sobre os pontos B, A, C, sobre os pontos C, B, A e, por fim, sobre os pontos A, C, B.
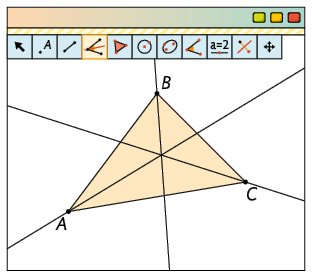
3º. Com a ferramenta Interseção de Dois Objetos, clique em duas das bissetrizes construídas. O ponto obtido é o incentro do triângulo.
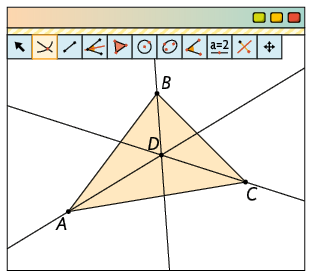
Com a ferramenta Mover, mude a posição dos vértices do triângulo e verifique o que acontece com as bissetrizes e o incentro.
Página 218
Atividades
Faça as atividades no caderno.
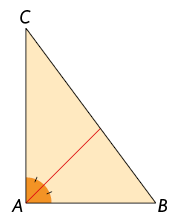
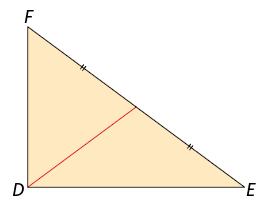
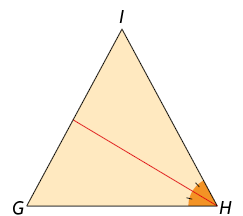
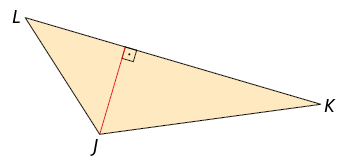
31. De acordo com as indicações em cada triângulo, classifique o segmento de reta vermelho em mediana, bissetriz ou altura.
32. No triângulo a seguir, os segmentos de reta em verde são medianas. Calcule a medida do perímetro desse triângulo.

33. Analise o triângulo e escreva em seu caderno como você faria para obter um ponto sobre o lado que seja equidistante dos vértices A e B desse triângulo.

34. Em cada item determine, entre as palavras a seguir, quais substituem cada corretamente.
-
circuncentro
-
alturas
-
mediatrizes
-
ortocentro
-
baricentro
-
medianas
a) O centro da circunferência circunscrita em um triângulo é obtido pelo cruzamento de suas .
b) é o centro de equilíbrio de um triângulo.
c) Nos triângulos obtusângulos, o ponto de encontro das é sempre externo ao triângulo.
d) O ponto comum das mediatrizes de um triângulo é chamado .
e) é o nome dado ao ponto de encontro das alturas de um triângulo, e o baricentro de um triângulo é obtido pelo cruzamento de suas .
Página 219
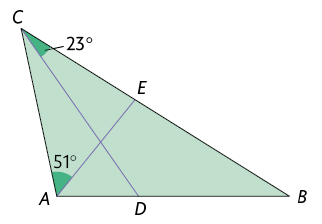
35. Sabendo que os segmentos de reta traçados em roxo são bissetrizes do triângulo, determine a medida de cada ângulo interno do triângulo.
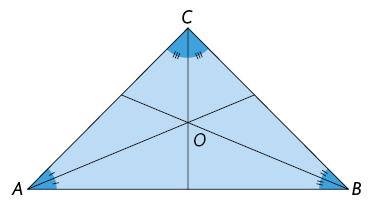
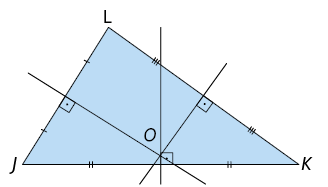
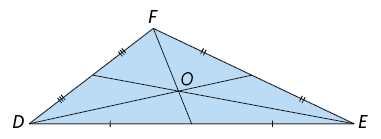
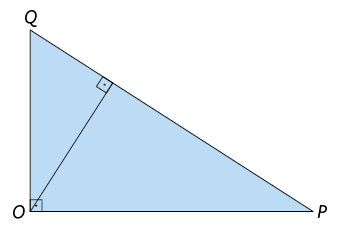
36. O que as retas ou os segmentos de reta traçados em cada triângulo representam? E o que o ponto O representa?
37. Uma professora de Matemática do 8º ano pediu aos estudantes que desenhassem um triângulo qualquer e determinassem seu circuncentro. Acompanhe os triângulos desenhados por três estudantes.
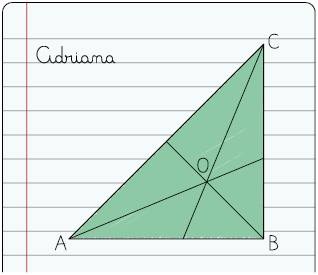
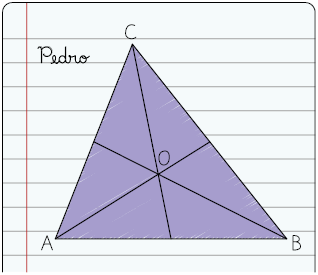
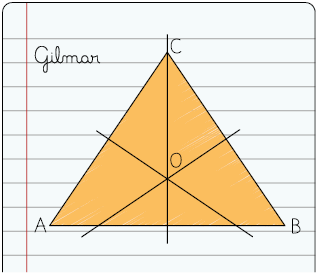
a) Realizando as medições necessárias, escreva no caderno qual dos estudantes obteve o circuncentro do triângulo.
b) Os pontos obtidos pelos outros dois estudantes nos triângulos desenhados por eles representam quais pontos notáveis?
Página 220
38. Identifique e copie no caderno as frases que apresentam as informações incorretas, corrigindo-as.
a) O incentro de um triângulo é o ponto de encontro de suas medianas.
b) Em um triângulo é possível traçar 3 bissetrizes.
c) Em um triângulo, o segmento de reta que liga um vértice do triângulo ao ponto médio de seu lado oposto é denominado altura.
d) O ortocentro de um triângulo é o ponto de encontro de suas alturas.
e) O encontro das mediatrizes de um triângulo é denominado circuncentro.
39. Realize as medições necessárias e escreva no caderno qual ponto notável está representado pelo ponto O em cada triângulo retângulo a seguir.
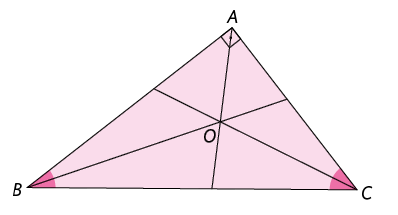
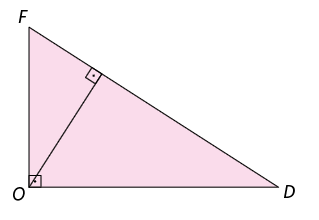
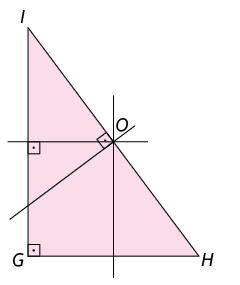
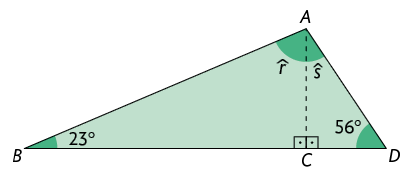
40. No triângulo a seguir, determine e , sabendo que é uma altura do triângulo.
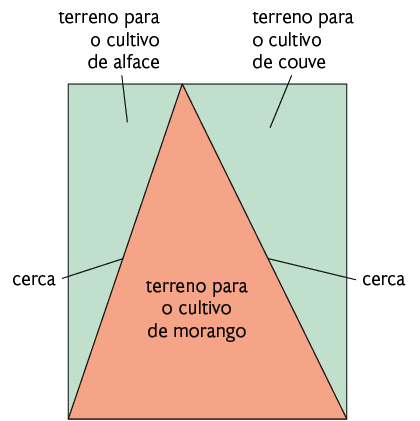
41. A figura a seguir representa um terreno no qual Juliana cultiva alface, couve e morangos. No interior do terreno do cultivo de morangos, ela pretende instalar um aspersor para auxiliar na irrigação, de modo que ele fique instalado a uma mesma medida de distância entre as cercas que dividem o terreno com o cultivo de alface e couve. No caderno, escreva como Juliana deve proceder para colocar esse aspersor considerando a condição estipulada.
42. Construa
no caderno um triângulo qualquer e, utilizando régua e compasso, trace as três
mediatrizes.
Versão adaptada acessível
42. Junte-se a um colega e construam um triângulo qualquer. Depois, utilizando régua e compasso, tracem as três mediatrizes desse triângulo.
43. Utilizando
o GeoGebra, construa um
triângulo qualquer e, em seguida, obtenha seu incentro
e a circunferência inscrita nele.
Página 221
44. Napoleão Bonaparte (1769-1821), um dos mais famosos generais dos tempos contemporâneos, nasceu em Ajácio, na Córsega, na França. De família pobre, mas dona de um título de nobreza da República de Gênova, aderiu à Revolução Francesa e ficou conhecido por suas brilhantes estratégias de guerra. Em 1793, com apenas 24 anos, tornou-se o mais jovem general do Exército francês. Napoleão Bonaparte era amigo de grandes matemáticos franceses de sua época. Influenciado pelo matemático Lorenzo Mascheroni, realizou alguns estudos relacionados a construções geométricas. A mais famosa das contribuições que Napoleão trouxe à área da Geometria está citada no teorema a seguir.

Teorema de Napoleão: os baricentros de 3 triângulos equiláteros, que têm como bases os lados de um triângulo qualquer, são vértices de outro triângulo equilátero.
Para aplicar o teorema de Napoleão, executamos os seguintes passos.
1º. Desenhamos um triângulo qualquer.

2º. A partir dos lados do triângulo anterior, desenhamos 3 triângulos equiláteros.
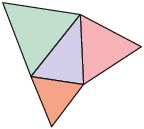
3º. Em seguida, determinamos os baricentros dos 3 triângulos equiláteros.
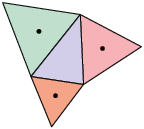
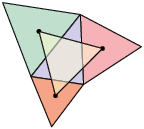
4º. Por último, traçamos segmentos de reta unindo os baricentros e obtemos outro triângulo equilátero.
Fontes de pesquisa: EVES, Howard. Introdução à história da matemática. Tradução: Hygino H. Domingues. Campinas: Ed. da Unicamp, 2004. p. 460, 485, 587, 589; REVISTA do professor de matemática (RPM). São Paulo: SBM, 1989. p. 47.
a) Quem foi Napoleão Bonaparte?
b) Cite, de acordo com o texto, dois fatos importantes na vida de Napoleão Bonaparte. Depois, compare com os colegas e verifique se vocês destacaram os mesmos fatos.
c) Em sua opinião, o interesse de Napoleão pela Matemática contribuiu para que ele se tornasse um estrategista de guerra?
d) O que você sabe sobre a Revolução Francesa? Faça uma pesquisa a esse respeito.
e) Realize uma pesquisa e verifique se existem outros teoremas relacionados aos pontos notáveis de um triângulo.
Página 222
Quadriláteros
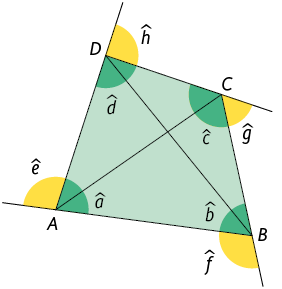
O quadrilátero é um polígono de quatro lados e, consequentemente, 4 vértices, 4 ângulos internos, 4 ângulos externos e 2 diagonais, quando convexos. Analise os elementos do quadrilátero a seguir.
- Nome: quadrilátero .
- Lados: , , e .
- Vértices: , , e .
- Diagonais: e .
- Medidas dos ângulos internos: , , e .
- Medidas dos ângulos externos: , , e .
Podemos classificar alguns quadriláteros em paralelogramos ou trapézios.
Paralelogramo é um quadrilátero que tem os lados opostos paralelos.
No paralelogramo :
- o lado é paralelo ao lado (indicamos assim: );
- o lado é paralelo ao lado .

Trapézio é um quadrilátero que tem somente 2 lados paralelos.
No trapézio :
- o lado é paralelo ao lado ;
- o lado não é paralelo ao lado .
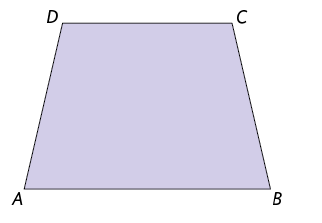
Em um trapézio, os lados paralelos são chamados bases. Nesse trapézio, é a base maior, e , a base menor.
Questão 8. Existem quadriláteros
que não são paralelogramos nem
trapézios. Com o auxílio de uma régua, construa no caderno dois quadriláteros
que não sejam paralelogramos nem trapézios e mostre para um colega. Depois,
explique para ele por que o quadrilátero que
você construiu não caracteriza um paralelogramo nem um trapézio.
Página 223
Atividades
Faça as atividades no caderno.
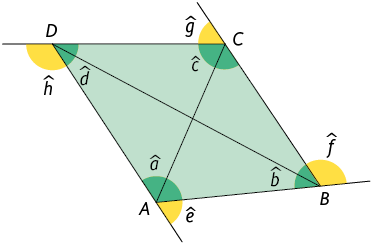
45. No caderno, nomeie os lados, os vértices, as diagonais, as medidas dos ângulos internos e as medidas dos ângulos externos do quadrilátero.
46. Indique somente as frases relacionadas a quadriláteros convexos.
A.Polígono que tem 2 diagonais.
B.De cada um de seus vértices partem 2 diagonais.
C.A soma das medidas dos ângulos internos é igual à dos ângulos externos.
D.Traçando uma de suas diagonais, é possível dividir esse polígono em 2 triângulos.
47. Considere os ângulos internos de um quadrilátero convexo cujas medidas são , , e .
Determine .
a)
b)
c)
d)
e)
48. A figura representa parte de um quadrilátero , no qual estão indicadas a medida de um ângulo interno e a medida de um ângulo externo.
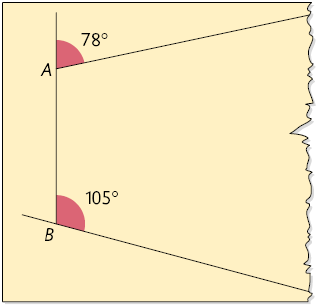
a) Quantas diagonais é possível traçar partindo do vértice ? E do vértice ?
b) Escreva no caderno as medidas dos ângulos internos e dos ângulos externos relacionados aos vértices e .
c) Escreva no caderno uma possível medida para cada ângulo interno e ângulo externo relacionados aos vértices C e D.
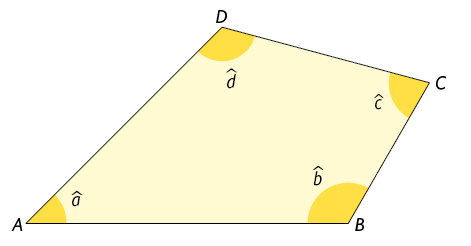
49. Determine as medidas dos ângulos internos do quadrilátero de acordo com as dicas a seguir.
O menor ângulo interno mede .
Página 224
Paralelogramos
Estudamos anteriormente que os paralelogramos têm os lados opostos paralelos. Agora, vamos aprofundar o estudo e verificar as seguintes propriedades dos paralelogramos.
1ª propriedade: em um paralelogramo, os lados opostos são congruentes.
Para verificar essa propriedade, vamos considerar o paralelogramo e traçar a diagonal , obtendo os triângulos e .
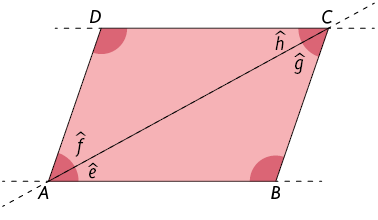
Temos e , pois essas são as medidas de pares de ângulos alternos internos. Além disso, é o lado comum dos triângulos e .
Assim, pelo caso de congruência de triângulos, temos .
Portanto, e , isto é, os lados opostos do paralelogramo são congruentes.
2ª propriedade: em um paralelogramo, os ângulos internos opostos são congruentes.
Para verificar essa propriedade, vamos considerar o paralelogramo apresentado na 1ª propriedade.
Vimos que . Então, .
De maneira semelhante, traçando a diagonal do paralelogramo, obtemos os triângulos e e verificamos que . Então, .
Portanto, os ângulos internos opostos do paralelogramo são congruentes.
3ª propriedade: em um paralelogramo, as diagonais se cruzam em seus pontos médios.
Para verificar essa propriedade, vamos traçar as diagonais do mesmo paralelogramo e analisar os triângulos e obtidos.
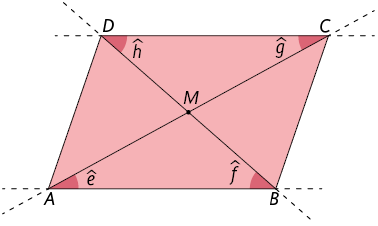
Temos e , pois são as medidas de pares de ângulos alternos internos. Além disso, , pois são lados opostos do paralelogramo.
Assim, pelo caso de congruência de triângulos, temos .
Portanto, e , isto é, o ponto M em que as diagonais se cruzam é o ponto médio de cada diagonal.
Página 225
Alguns paralelogramos podem ser classificados em retângulo, losango ou quadrado.
Retângulo é o paralelogramo que tem todos os ângulos internos retos.
Considere o retângulo a seguir.
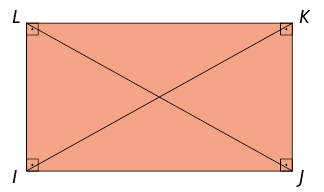
Propriedade: em um retângulo, as diagonais são congruentes.
Para verificar essa propriedade, vamos considerar os triângulos e do paralelogramo anterior, obtidos ao traçar as diagonais desse retângulo.
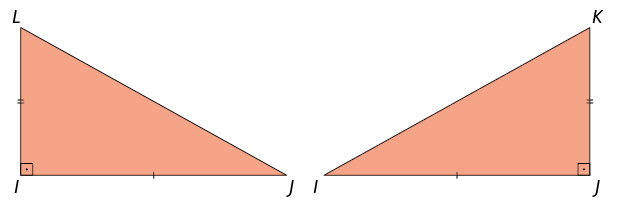
Note que e são ângulos retos e é o lado comum dos triângulos.
Além disso, , pois são lados opostos do retângulo.
Assim, pelo caso de congruência de triângulos, temos .
Portanto, , isto é, as diagonais do retângulo são congruentes.
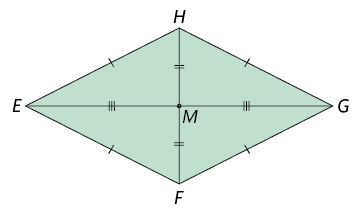
Losango é o paralelogramo que tem todos os lados com medidas iguais.
Considere o losango a seguir.
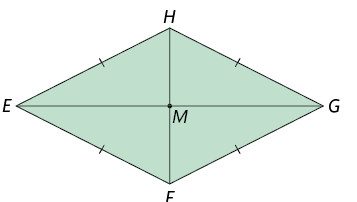
Propriedade: em um losango, as diagonais são perpendiculares entre si e correspondem às bissetrizes dos ângulos internos.
Para verificar essa propriedade, considere os triângulos , , e , obtidos ao traçar as diagonais do losango . Como (lados do losango são congruentes), ( é ponto médio do segmento ) e ( é ponto médio do segmento ), segue que os quatro triângulos são congruentes pelo caso LLL.
Página 226
Assim, os 4 ângulos correspondentes com vértices nas extremidades do segmento são congruentes. O mesmo ocorre com os 4 ângulos com vértices nas extremidades do segmento . Além disso, ainda da congruência dos quatro triângulos, os quatro ângulos com vértices em são congruentes. Como a soma das medidas desses ângulos é , segue que cada um deles mede .
Portanto, as diagonais do losango são perpendiculares entre si e correspondem às bissetrizes dos ângulos internos.
Quadrado é o paralelogramo que tem todos os lados com medidas iguais e todos os ângulos internos retos. Por isso, o quadrado é um caso particular de losango e de retângulo.
Considere o quadrado a seguir.
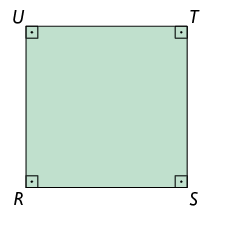
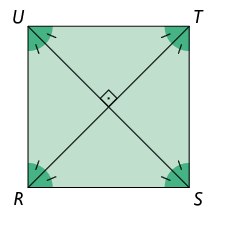
Propriedade: as diagonais de um quadrado são congruentes, perpendiculares entre si e correspondem às bissetrizes dos ângulos internos.
Para verificar essas propriedades, basta saber que o quadrado é um caso particular de losango e de retângulo e, então, que ele apresenta as propriedades de ambos.
- ;
- é perpendicular a ;
- é a bissetriz relativa ao ângulo ou ;
- é a bissetriz relativa ao ângulo ou .
Questão 9. Vimos que para verificar a propriedade do quadrado apresentada nesta página basta considerá-lo como um caso particular de losango e de retângulo. Agora, em seu caderno, demonstre essa propriedade utilizando a congruência de triângulos.
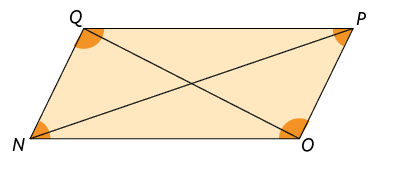
Há paralelogramos que não podem ser classificados como retângulo, losango ou quadrado. O paralelogramo a seguir, por exemplo, é um deles.
- ;
- não é a bissetriz relativa ao ângulo ou ;
- não é a bissetriz relativa ao ângulo ou .
Página 227
Resumindo as propriedades estudadas, obtemos o seguinte quadro.
|
Paralelogramos |
Retângulos |
Losangos |
Quadrados |
|---|---|---|---|
|
Os lados opostos são congruentes. Os ângulos internos opostos são congruentes. As diagonais se cruzam nos respectivos pontos médios. |
Têm as propriedades dos paralelogramos. As diagonais são congruentes. |
Têm as propriedades dos paralelogramos. As diagonais são perpendiculares entre si. As diagonais correspondem às bissetrizes dos ângulos internos. |
Como o quadrado é um caso particular de losango e de retângulo, ele tem todas as propriedades de ambos. |
Instrumentos e softwares
Construindo paralelogramos com régua, compasso e transferidor
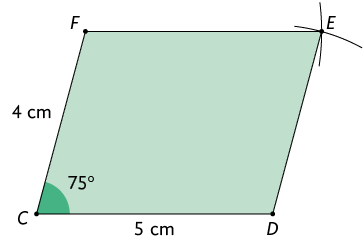
Nesta seção, com régua, compasso e transferidor, vamos construir um paralelogramo , tal que , e . Para isso, siga as orientações do professor e os passos apresentados.
1º. Com régua e transferidor, construa , e .

2º. Com a ponta-seca do compasso em D e abertura igual à medida do comprimento de , trace um arco como indicado a seguir.

Página 228
3º. Com a ponta-seca do compasso em F e abertura igual à medida do comprimento de , trace um arco cruzando o anterior.

4º. A interseção dos arcos é o vértice E do paralelogramo. Por fim, trace e para obter o paralelogramo.
Atividades
Faça as atividades no caderno.
50. Theo van Doesburg (1883-1931) foi um importante pintor holandês que iniciou sua carreira influenciado pelos estilos do Pós-Impressionismo e do Fauvismo. Destacou-se com obras abstratas, principalmente trabalhando com figuras geométricas. A seguir, veja uma de suas obras.

a) Quais quadriláteros você identifica nessa tela?
b) As medidas dos ângulos internos desses quadriláteros são iguais? Quais são as medidas desses ângulos internos?
Página 229
51. Considere o paralelogramo a seguir.
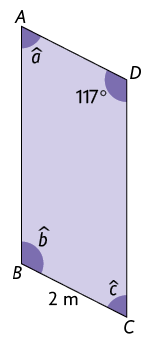
Escreva no caderno:
a) a medida do comprimento do lado .
b) as medidas e .
c) a medida do comprimento do lado , sabendo que o perímetro desse paralelogramo mede .
52. De acordo com as medidas indicadas, determine qual quadrilátero a seguir é um paralelogramo.



53. Considere o tangram representado a seguir.
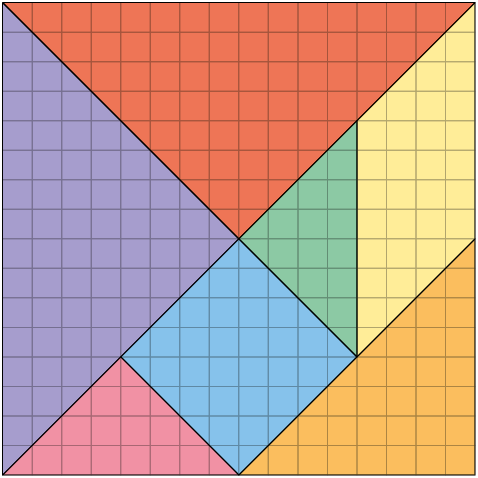
a) As peças que compõem o tangram têm formato de quais polígonos?
b) Qual desses quadriláteros tem ângulos internos retos?
c) Determine as medidas dos ângulos internos do quadrilátero que não têm ângulos retos.
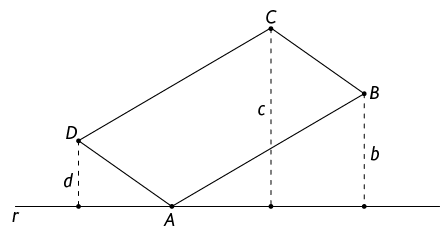
54. Na
figura a seguir,
é um paralelogramo e o vértice A pertence à
reta r. Sabendo que b, c e d são as medidas das distâncias dos
vértices B, C e D à reta r,
respectivamente, explique por que .
Página 230
55. Junte-se a um colega e construam no caderno os paralelogramos cujas medidas estão indicadas nos quadros. Depois verifiquem, entre os paralelogramos que vocês construíram, se há algum retângulo, losango ou quadrado.
A.Paralelogramo
B.Paralelogramo
C.Paralelogramo
56. Classifique, se possível, cada paralelogramo desenhado na malha quadriculada em quadrado, retângulo ou losango.
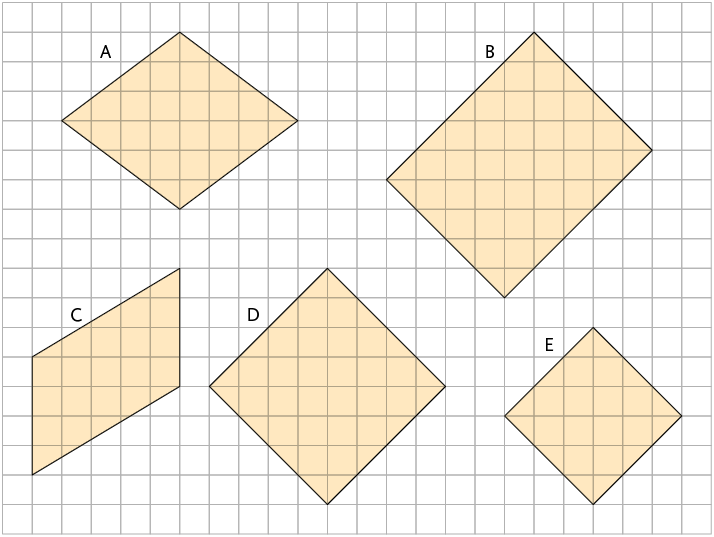
57. Calcule o valor de em cada paralelogramo.
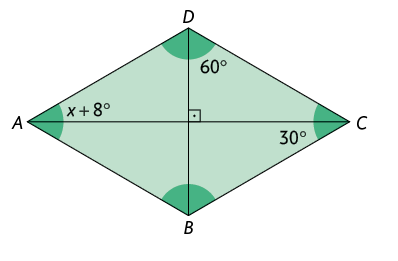
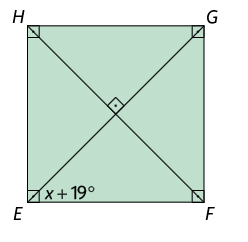
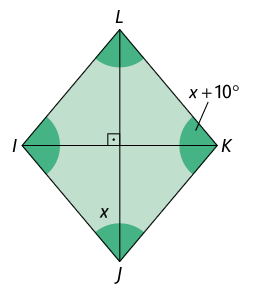
Página 231
58. Determine as medidas dos ângulos internos de cada paralelogramo.
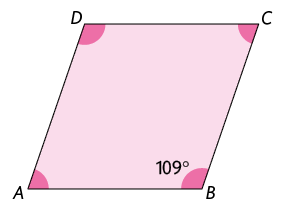
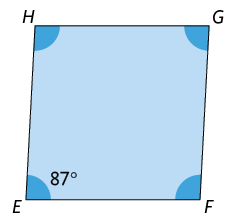

Trapézio
Estudamos anteriormente que os trapézios têm somente dois lados opostos paralelos, chamados bases.


Um trapézio pode ser classificado em isósceles, retângulo ou escaleno.
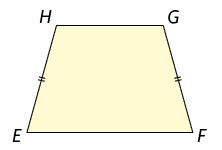
Trapézio isósceles é aquele que tem os lados não paralelos com medidas de comprimento iguais.
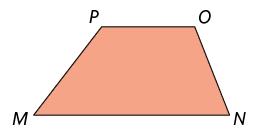
Trapézio escaleno é aquele que tem os lados não paralelos com medidas de comprimento diferentes.
Trapézio retângulo é um trapézio escaleno que tem um dos lados não paralelos perpendicular às bases.

Questão 10. Utilizando a congruência de triângulos, mostre, em seu caderno, que no trapézio isósceles, os ângulos internos da mesma base são congruentes e as diagonais são congruentes.
Página 232
Atividades
Faça as atividades no caderno.
59. Identifique e nomeie no caderno a base maior e a base menor de cada trapézio.


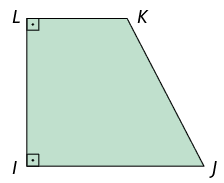
60. Classifique cada trapézio da malha quadriculada em isósceles, retângulo ou escaleno.

61. Determine o valor de x nos trapézios a seguir. Em seguida, calcule a medida de cada ângulo interno dos trapézios.
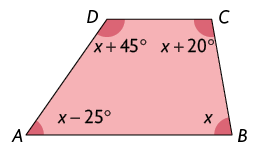
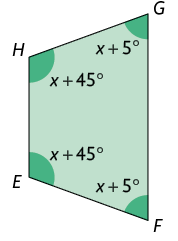

62. De acordo com as informações, determine a medida de cada ângulo interno dos trapézios a seguir.
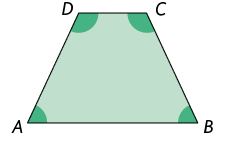
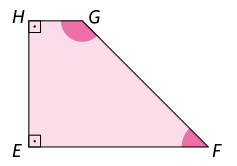
63. Determine as medidas do comprimento de e , sabendo que o trapézio é isósceles e que a medida de seu perímetro é .

Página 233
Círculo e circunferência
As formas circulares já eram conhecidas e utilizadas pelos povos antigos em várias situações. Temos alguns exemplos a seguir.


- Inuítes:
- povos nativos da região do Ártico americano.↰



Questão 11. Em sua opinião, quais seriam as
propriedades de uma figura
circular que propiciaram seu uso desde a Antiguidade?
Nessas imagens, podemos identificar formas que podem ser associadas a circunferências e círculos.
Uma linha fechada em um plano, formada por pontos equidistantes de um ponto fixo (centro) é chamada circunferência.
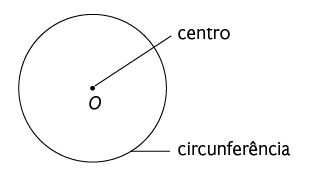
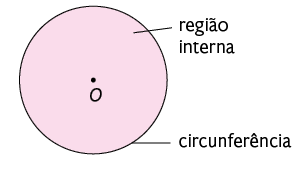
A união da circunferência com todos os pontos em seu interior é chamada círculo.
Página 234
Na circunferência apresentada na imagem, podemos destacar os seguintes elementos.
- O centro O.
- Os pontos A, B, C, D, E, F e G são pontos da circunferência.
- O raio da circunferência é qualquer segmento de reta que une o centro da circunferência a um de seus pontos. Na imagem, os segmentos , e são exemplos de raio.
- A corda da circunferência é qualquer segmento de reta que une dois pontos distintos dela. Na imagem, os segmentos , e são exemplos de corda.
- O diâmetro da circunferência é qualquer corda que passa pelo centro da circunferência. Na imagem, é exemplo de um diâmetro.
- O ângulo central da circunferência é qualquer ângulo com vértice no centro e lados passando por pontos dessa circunferência. Na imagem, o ângulo é um exemplo de ângulo central.

Atenção!
A medida do comprimento do diâmetro é o dobro da medida do comprimento do raio.
Atividades
Faça as atividades no caderno.
64. Tales usou uma lata como a apresentada a seguir para desenhar um círculo no caderno. Assim como a lata usada por Tales, outros objetos têm partes circulares que podem ser usadas para desenhar círculos. Escreva no caderno alguns objetos que também apresentam essa característica.

65. Sabendo que o comprimento do diâmetro de uma circunferência mede , qual é a medida do comprimento de seu raio?
Página 235
66. As circunferências a seguir têm centro B e C.
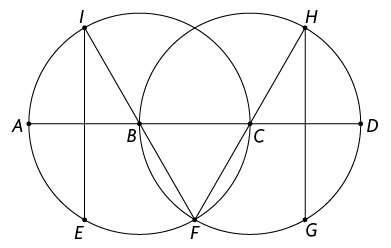
a) Classifique os segmentos de reta traçados em raio, diâmetro ou corda da circunferência de centro .
b) Classifique os segmentos de reta traçados em raio, diâmetro ou corda da circunferência de centro .
c) Identifique e nomeie dois ângulos centrais.
67. Responda a cada um dos itens a seguir.
a) Qual é a medida do comprimento do raio de uma circunferência cujo comprimento do diâmetro mede ?
b) Qual é a medida de comprimento do diâmetro de uma circunferência cujo comprimento do raio mede ?
68. O comprimento da diagonal do retângulo mede .
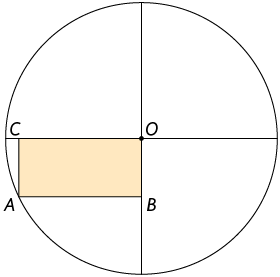
Qual é a medida de comprimento do diâmetro da circunferência de centro ?
69. Jade desenhou a maior circunferência possível em uma cartolina retangular de 27,4 cm por 15,3 cm. Qual é, em centímetros, a medida de comprimento do raio da circunferência desenhada por ela?
70. Félix pretende construir uma bicicleta semelhante à apresentada na foto a seguir. Para isso, ele planejou que a medida do comprimento do raio da roda maior será o dobro da medida do comprimento do diâmetro da roda menor.

a) Sabendo que o comprimento do raio da roda menor medirá , determine a medida de comprimento do diâmetro da roda maior.
b) Realize uma pesquisa e verifique quais outros tipos diferentes de bicicleta existem e quais benefícios o uso da bicicleta traz para a saúde e o bem-estar.
Página 236
Polígonos inscritos e circunscritos
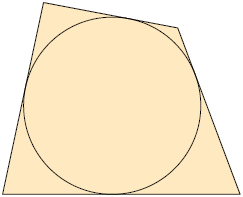
Considere as figuras a seguir.
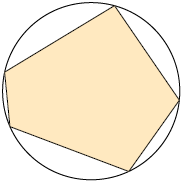
Note que, na figura A, todos os vértices do polígono pertencem à circunferência. Nesse caso, dizemos que esse polígono está inscrito na circunferência.
Na figura B, pode-se notar que todos os lados do polígono são tangentes à circunferência. Nesse caso, dizemos que o polígono está circunscrito à circunferência.
Se uma figura está inscrita em outra, dizemos que essa outra figura está circunscrita à primeira. Se um pentágono está inscrito em uma circunferência, por exemplo, a circunferência circunscreve ou está circunscrita ao pentágono. Em outro exemplo, se um hexágono está circunscrito a uma circunferência, a circunferência inscreve ou está inscrita no hexágono.
Atenção!
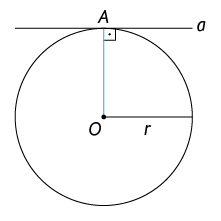
Quando uma reta qualquer tem um único ponto em comum com a circunferência, dizemos que essa reta é tangente à circunferência. Na imagem, a reta a é tangente à circunferência de centro O e raio cujo comprimento mede r.
A menor distância do centro O à reta a é o comprimento do segmento , perpendicular à reta a. Como o ponto A pertence à circunferência, representa um de seus raios.
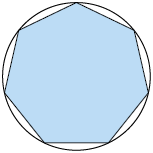
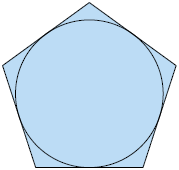
Quando consideramos um polígono regular, é sempre possível traçar uma circunferência:
- que contenha todos os seus vértices. Com isso, dizemos que todo polígono regular pode ser inscrito em uma circunferência.
- tangenciando todos os seus lados. Sendo assim, dizemos que todo polígono regular pode ser circunscrito a uma circunferência.
A seguir, temos alguns exemplos.


Página 237
Atividades
Faça as atividades no caderno.
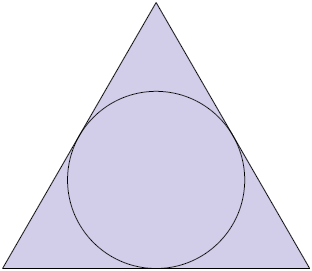
71. A seguir, identifique a figura com o polígono inscrito em uma circunferência.


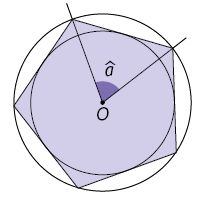
72. Em um polígono regular, podemos destacar o centro do polígono, que é o centro comum da circunferência inscrita e da circunferência circunscrita ao polígono. Além disso, podemos destacar o ângulo central, que é o ângulo cujo vértice é o centro do polígono e cujos lados contêm vértices consecutivos do polígono. Na imagem, esses elementos estão destacados em um pentágono regular.
a) Calcule mentalmente e escreva em seu caderno a medida do ângulo central, em graus, de cada polígono regular a seguir.
-
Triângulo
-
Quadrado
-
Hexágono
-
Decágono
b) Escreva no caderno como você calculou a medida do ângulo central dos polígonos do item anterior.
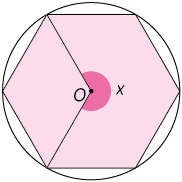
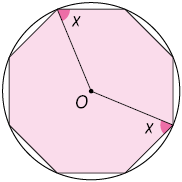
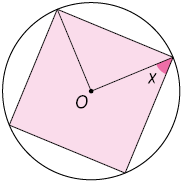
73. Os polígonos inscritos nas circunferências são regulares e o centro de cada um é O. Calcule o valor de x em cada item.
74. Yuri vai construir um quadrado utilizando compasso e esquadro.
a) Qual deverá ser a medida do ângulo central do quadrado?
b) Construa
um fluxograma descrevendo passo a passo como construir um quadrado usando
compasso e esquadro.
c) Usando o fluxograma do item anterior, construa um quadrado.
Versão adaptada acessível
c) Junte-se a um colega e, usando o fluxograma do item anterior, construam um quadrado.
Página 238
75. Usando régua e compasso, Antônia construiu um hexágono regular cujo comprimento do lado mede da seguinte maneira.
1º. Com régua e compasso, Antônia construiu um ângulo com medida igual à do ângulo central de um hexágono regular, que é . Depois, abriu o compasso com abertura medindo , fixou a ponta-seca no vértice do ângulo e girou, dando uma volta completa para traçar a circunferência de centro O. Na interseção entre as semirretas e a circunferência, marcou os pontos A e B.

2º. Com a ponta-seca do compasso em B e abertura igual a , marcou sobre a circunferência o ponto C.

3º. Com a mesma abertura e a ponta-seca em C, determinou o ponto D. Seguindo procedimento semelhante, obteve os pontos E e F na circunferência, determinando dessa forma todos os pontos correspondentes aos vértices do hexágono.

4º. Para finalizar a construção, traçou os lados , , , , e , obtendo, assim, o hexágono regular .
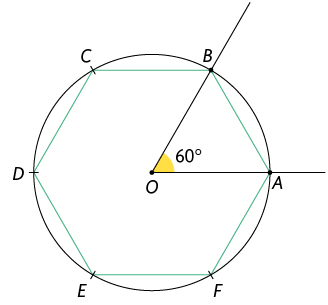
a) Em sua opinião, por que os procedimentos executados por Antônia garantem que ela construiu um hexágono regular?
b) Construa um fluxograma descrevendo, passo a passo, como construir um hexágono regular usando compasso e esquadro.
Página 239
Comprimento da circunferência
Para realizar um experimento, Natália utilizou uma fita métrica e mediu os comprimentos aproximados da circunferência e do diâmetro da circunferência de alguns objetos circulares. Depois, ela dividiu a medida do comprimento da circunferência (C) de cada objeto pela medida do comprimento de seu respectivo diâmetro (d) e verificou que o resultado é um número próximo de 3,14. Para organizar os dados, ela registrou as informações obtidas.


A razão entre a medida do comprimento de uma circunferência e a medida do comprimento de seu diâmetro é um número irracional que indicamos pela letra grega (lê-se pi), e isso ocorre em todas as circunferências. Assim, escrevemos a seguinte relação:
Atenção!
O número irracional é dado por No entanto, caso não seja dito o contrário, vamos usar neste livro uma aproximação de com duas casas decimais, isto é, .
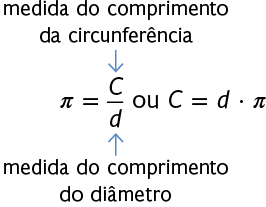
Como a medida do comprimento do diâmetro é o dobro da medida do comprimento do raio (), temos:
ou
Com essa fórmula, é possível obter a medida aproximada do comprimento de uma circunferência cujo comprimento do raio mede . Considerando , temos:
Portanto, a medida do comprimento dessa circunferência é, aproximadamente, .
Questão 12. Determine em seu caderno a medida aproximada do comprimento de uma circunferência cujo comprimento do diâmetro mede .
Página 240
Atividades
Faça as atividades no caderno.
76. Em cada item, determine a medida do comprimento da circunferência de centro O.
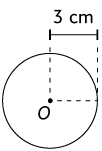
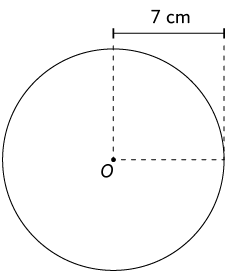
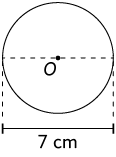
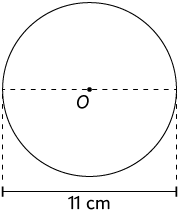
77. Rafael mediu o comprimento do diâmetro da roda do carro de seu pai para um experimento na aula de Ciências e encontrou .
a) Qual é, em metro, a medida da distância aproximada percorrida pelo carro quando a roda dá 1 volta completa?
b) Quantas voltas aproximadamente dá a roda do carro em um percurso de ?
78. Determine a medida do comprimento do raio de uma circunferência cuja medida do comprimento é .
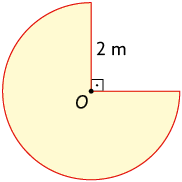
79. Qual é a medida do comprimento aproximado da linha vermelha da figura a seguir?
80. (Enem-2015) A figura é uma representação simplificada do carrossel de um parque de diversões, visto de cima. Nessa representação, os cavalos estão identificados pelos pontos escuros, e ocupam circunferências de raios e , respectivamente, ambas centradas no ponto O. Em cada sessão de funcionamento, o carrossel efetua 10 voltas.
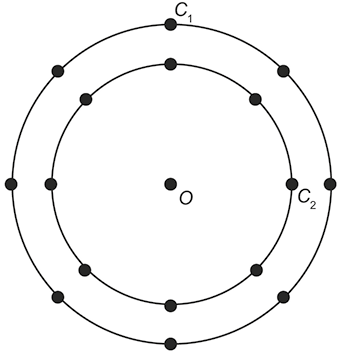
Quantos metros uma criança sentada no cavalo percorrerá a mais do que uma criança no cavalo , em uma sessão? Use 3,0 como aproximação para .
a) 55,5
b) 60,0
c) 175,5
d) 235,5
e) 240,0
Página 241
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Desenhe em uma folha de papel avulsa um polígono convexo que tenha as quantidades de diagonais a seguir. Depois, classifique-o de acordo com a quantidade de lados.
a) 9 diagonais.
b) 20 diagonais.
c) 5 diagonais.
2. Calcule a soma das medidas dos ângulos internos de um polígono convexo de:
a) 7 lados.
b) 10 lados.
c) 12 lados.
d) 8 lados.
3. Qual é a medida de cada ângulo interno de um:
a) pentágono regular?
b) octógono regular?
c) decágono regular?
d) dodecágono regular?
4. Quantos lados tem o polígono convexo em que de cada vértice partem 7 diagonais?
5. Quantas diagonais ao todo partem do vértice comum aos três hexágonos a seguir?
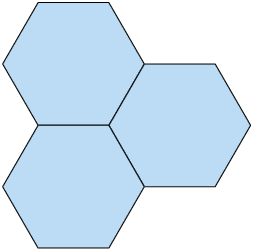
6. Qual é o
polígono regular cuja medida de cada ângulo interno é:
a) ?
b) ?
c) ?
7. Entre os polígonos regulares a seguir, escreva em uma folha de papel avulsa quais têm a soma das medidas dos ângulos internos maior do que .


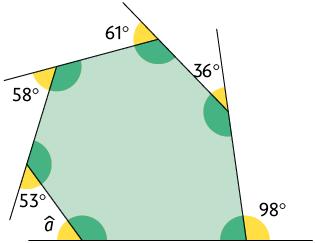
8. Determine .
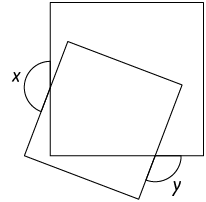
9. (OBM-2007) A figura mostra dois quadrados
sobrepostos. Qual é o valor de , em graus?
a) 270
b) 300
c) 330
d) 360
e) 390
Atenção!
Para resolver esta atividade, utilize o conceito de ângulos opostos pelo vértice.
Página 242
10. (Obmep-2005) O triângulo é isósceles de base e o ângulo mede . O triângulo é isósceles de base .
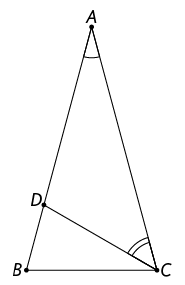
Determine a medida do ângulo .
a)
b)
c)
d)
e)
11. Considere o losango e suas diagonais.
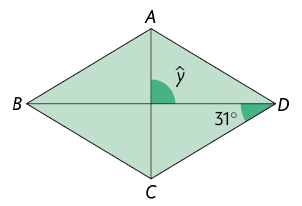
a) Qual é o valor de , em grau?
b) Qual é a medida de cada ângulo interno desse losango?
12. (Obmep-2007) Juliana tem 8 cartões de papelão, retangulares e iguais. Se ela enfileirar todos os cartões juntando apenas lados de mesma medida, a maior fila que ela poderá obter terá comprimento e a menor terá comprimento .
Qual é o perímetro de cada cartão?
a)
b)
c)
d)
e)
13. (Obmep-2006) Uma tira de papel retangular é dobrada ao longo da linha tracejada, conforme indicado, formando a figura plana da direita. Qual a medida do ângulo ?
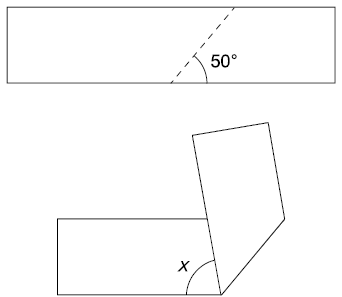
a)
b)
c)
d)
e)
14. Como se chama qualquer corda que passa pelo centro de uma circunferência?
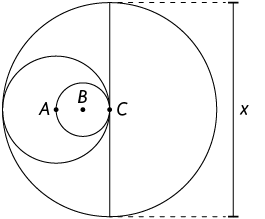
15. Determine o valor de indicado na figura, sabendo que e que , e são os centros das circunferências.
16. A medida do comprimento do raio de uma roda-gigante é . Uma pessoa que deu 8 voltas completas percorreu quantos metros, aproximadamente?