Página XLII
Resoluções
O que eu já sei?
1. a) O mosaico é formado por triângulos de cor verde e hexágonos de cor rosa.
b) Comparando a imagem apresentada com o mosaico, podemos identificar que o ângulo destacado em verde tem a mesma medida do ângulo interno de um triângulo equilátero, que mede .
c) Sugestão de resposta:
Como podemos verificar no mosaico, o ângulo externo do polígono de cor rosa coincide com o ângulo interno do polígono de cor verde. Portanto, os ângulos têm mesma medida.
2. Para construir um triângulo, é necessário que a medida de qualquer lado seja menor do que a medida da soma dos outros dois.
a) Não é possível construir um triângulo com as medidas indicadas, pois .
b) É possível construir um triângulo com as medidas indicadas, pois , e .
c) É possível construir um triângulo com as medidas indicadas, pois , e .
d) Não é possível construir um triângulo com as medidas indicadas, pois .
3. Resposta no final da seção Resoluções.
4. a) Como dos 60 lápis são em tons de verde, calculamos de 60, ou seja, . Portanto, Eduarda tem 12 lápis em tons de verde.
b) Como metade de dos 60 lápis são de tons claros de verde, a fração do total que representa a quantidade de lápis de tons claros de verde é dada por . Calculando de 60, obtemos . Portanto, há 6 lápis de tons claros de verde.
5. Resposta no final da seção Resoluções.
6. De acordo com os dados, temos:
|
Produção de tinta (em ) |
Quantidade de água (em ) |
|---|---|
|
2 |
60 |
|
4,5 |
x |
Como as grandezas são diretamente proporcionais, de maneira prática, podemos multiplicar o numerador de uma fração pelo denominador da outra.
Assim, para preparar 4,5 litros de tinta, são necessários 135 mililitros de água.
7. De acordo com as informações do enunciado, o carro custava R$ 32.500,00 no mês de janeiro. Para determinar o valor do carro em fevereiro, devemos calcular qual foi o desconto, em reais, correspondente a 5%. Sendo , calculamos:
Portanto, o carro passou a custar R$ 30.875,00 no mês de fevereiro.
Com o acréscimo de 10% sobre o preço de fevereiro, o carro teve um aumento de 10% sobre R$ 30.875,00. Sabendo que e realizando os cálculos, obtemos:
Portanto, o carro passou a custar R$ 33.962,50 no mês de março.
8. a) Usando a fórmula referente à medida do volume do cubo, devemos calcular a medida do volume interno de cada modelo de caixa.
A: , ou seja, .
B: , ou seja, .
C: , ou seja, .
D: , ou seja, .
E: , ou seja, .
b) Sim, os modelos C e E têm medida de volume interno maior do que .
9. O triângulo A é escaleno, pois as medidas de comprimento dos seus lados são diferentes. Calculando a medida da área do triângulo, obtemos:
Portanto, a área do triângulo A mede .
O triângulo B é isósceles, pois dois de seus lados têm mesma medida de comprimento. Calculando a medida da área do triângulo, obtemos:
Portanto, a área do triângulo B mede .
10. A. . Portanto, a área do quadrilátero A mede .
B. . Portanto, a área do quadrilátero B mede .
C. . Portanto, a área do quadrilátero C mede .
D. . Portanto, a área do quadrilátero D mede .
11. a) Acrescentando um palito a mais em cada lado do quadrado da 3ª figura, a 4ª figura será um quadrado com 4 palitos em cada lado, pois . Portanto, essa figura terá 16 palitos ao todo.
Página XLIII
b) Cada figura tem quatro lados e a mesma quantidade de palitos em cada lado. Assim, a quantidade total de palitos em cada uma delas é dada pelo produto obtido da multiplicação entre a quantidade de lados e a quantidade de palitos de cada lado.
1ª figura: , ou seja, 4 palitos;
2ª figura: , ou seja, 8 palitos;
3ª figura: , ou seja, 12 palitos;
4ª figura: , ou seja, 16 palitos;
n-ésima figura: , ou seja, palitos.
c) A sétima figura terá 28 palitos, pois , e a décima quinta figura terá 60 palitos, pois .
12. a) Calculando a média das medidas de altura dos sete jogadores, obtemos:
Portanto, a média é aproximadamente .
b) A amplitude é dada pela diferença entre a maior e a menor medida de altura. Assim:
Portanto, a amplitude do conjunto de dados é .
13. Como as balanças estão em equilíbrio, a medida de massa em cada prato é a mesma.
Considerando A a medida de massa da caixa A, temos:
Portanto, a massa da caixa A mede .
Considerando B a medida de massa da caixa B, temos:
Portanto, a massa da caixa B mede .
14. Utilizando o módulo, vamos calcular a diferença entre as medidas de temperatura.
Portanto, a diferença entre as medidas de temperatura é .
15. a) As chances de Sofia não são iguais, pois há mais fichas azuis do que fichas roxas. Por esse motivo, a chance de sair uma ficha azul é maior.
b) Das 20 fichas, há 10 com números pares. Então, a probabilidade de retirar uma ficha com um número par é , ou seja, 50%.
Das 20 fichas, há 15 que apresentam números menores do que 22. Então, a probabilidade de retirar uma ficha com número menor do que 22 é , ou seja, 75%.
Unidade 1
Potenciação e radiciação
Questão 1. Escrevendo cada um dos termos da sequência como potências de base , obtemos:
Atividades
1. a) A potência quatro elevado ao quadrado escrita com algarismos é . Efetuando os cálculos, obtemos .
b) A potência dez elevado ao cubo escrita com algarismos é . Efetuando os cálculos, obtemos .
c) A potência seis elevado à quarta potência escrita com algarismos é . Efetuando os cálculos, obtemos .
d) A potência três elevado ao cubo escrita com algarismos é . Efetuando os cálculos, obtemos .
e) A potência cinco elevado ao quadrado escrita com algarismos é . Efetuando os cálculos, obtemos .
f) A potência dois elevado à quarta potência escrita com algarismos é . Efetuando os cálculos, obtemos .
2. a)
b)
c) Como todo número diferente de zero elevado a zero é igual a 1, segue que .
d)
e)
f)
g)
h)
i)
j) Como todo número diferente de zero elevado a zero é igual a 1, segue que .
k)
l)
Página XLIV
m) Como todo número diferente de zero elevado a zero é igual a 1, segue que .
n)
o)
p) Como todo número diferente de zero elevado a zero é igual a 1, segue que .
3. A. Considerando a quantidade de cubos em cada dimensão da pilha, temos:

Portanto, a pilha tem 8 cubos.
B. Considerando a quantidade de cubos em cada dimensão da pilha, temos:

Portanto, a pilha tem 27 cubos.
C. Considerando a quantidade de cubos em cada dimensão da pilha, temos:

Portanto, a pilha tem 64 cubos.
4. As respostas dos itens A, B e C da atividade anterior foram, respectivamente:
, , .
Continuando essa sequência de potências de mesmo expoente com os quatro próximos termos, teremos:
, , , .
Desse modo, a pilha com 5 cubinhos em cada dimensão terá 125 cubinhos no total, pois .
A pilha com 6 cubinhos em cada dimensão terá 216 cubinhos no total, pois .
A pilha com 7 cubinhos em cada dimensão terá 343 cubinhos no total, pois .
A pilha com 8 cubinhos em cada dimensão terá 512 cubinhos no total, pois .
5. Efetuando os cálculos, obtemos:
a)
b)
c)
d)
e)
f)
g)
h)
6. a)
b) Nesse item, podemos, primeiro, simplificar a fração que está na base da potência e, depois, efetuar os cálculos.
Outra maneira de resolver esse item é calcular primeiro a potência e, depois, simplificar o resultado.
c)
d)
7. Substituindo por e por em cada item e efetuando os cálculos, temos:
a)
b)
c)
d)
e)
8. a) Como e , substituímos o pelo símbolo , obtendo .
b) Como , e , substituímos o pelo símbolo , obtendo .
c) Como , e , substituímos o pelo símbolo , obtendo .
Página XLV
d) Como , e , substituímos o pelo símbolo , obtendo .
e) Como , e , substituímos o pelo símbolo , obtendo .
f) Como e , substituímos o pelo símbolo , obtendo .
9. Como , verificamos que os itens A e 2 são potências equivalentes.
Como , verificamos que os itens B e 1 são potências equivalentes.
Como , verificamos que os itens C e 4 são potências equivalentes.
Como , verificamos que os itens D e 3 são potências equivalentes.
Portanto, a correspondência correta é A-2; B-1; C-4; D-3.
10. Resposta pessoal. Sugestão de resposta:
As caixas de determinado produto eram armazenadas no depósito de uma empresa em pilhas com 10 unidades nas suas três dimensões. Para melhor armazenamento dessas caixas, um funcionário dividiu essa pilha de caixas em pilhas menores, com 5 caixas nas suas 3 dimensões. Quantas pilhas com 5 caixas nas suas três dimensões foram feitas?
Resposta: 8 pilhas de caixas.
11. a)
b)
c)
d)
e)
f)
g)
h)
12. a)
b)
c)
d)
e)
f)
13. O esquema apresentado na atividade é um quadrado mágico, cuja constante mágica foi informada no enunciado. Desse modo, para obter o valor de cada letra, devemos igualar o produto das linhas, colunas ou diagonais à constante mágica correspondente.
Para o cálculo da letra A, efetuamos:
Para o cálculo da letra B, efetuamos:
Para o cálculo da letra C, vamos usar o resultado anterior, pois . Assim, efetuamos:
Para o cálculo da letra D, vamos usar o resultado obtido no primeiro cálculo, pois . Assim, efetuamos:
Como , concluímos que .
Para o cálculo da letra E, efetuamos:
Portanto, o esquema completo ficará da seguinte maneira.
Página XLVI
14. Efetuando os cálculos, temos:
a)
b)
c)
d)
e)
f)
15. Resposta pessoal. Sugestão de resposta:
Resolva a expressão numérica .
Resposta: .
16. a)
b)
c)
d)
e)
f)
g)
h)
17. No produto de duas potências de mesma base, adicionam-se os expoentes e mantém-se a base. Desse modo, obtemos . Portanto, o produto equivale ao item C.
18. Ao efetuarmos o produto de duas potências de mesma base, adicionamos os expoentes e mantemos a base. Desse modo, temos:
19. a)
b)
c)
d)
e)
f)
20. a)
b)
c)
d)
e)
f)
g)
h)
i)
21. Para calcular a população aproximada da Região Sul do Brasil em 2021, basta adicionarmos a população aproximada de cada estado dessa região.
Com isso, verificamos que em 2021 havia aproximadamente 30.401.000 habitantes na Região Sul. Sendo assim, em notação científica, temos:
Portanto, havia aproximadamente habitantes na Região Sul em 2021.
22. a) Resposta no final da seção Resoluções.
b)
Portanto, em notação científica, alguns vírus têm espessura aproximada de .
c)
Portanto, um homem tem cerca de glóbulos vermelhos em de sangue e uma mulher tem cerca de glóbulos vermelhos nessa mesma quantidade de sangue.
d)
Portanto, no vácuo, a luz viaja a uma velocidade de .
Questão 2. Observe que e . Como 5.184 é maior do que 4.900 e menor do que 6.400, sua raiz quadrada está entre 60 e 70. Assim, vamos calcular os quadrados dos números naturais entre 60 e 70 até obtermos 5.184 como resultado.
Portanto, concluímos que .
Questão 3. Usando a decomposição em fatores primos, temos:
Assim:
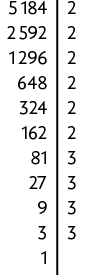
Logo, , que é o mesmo resultado obtido na questão 2.
Atividades
23. a) Decompondo o número 121 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 2, obtemos:
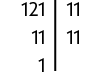
Portanto, .
Página XLVII
b) Decompondo o número 512 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 2, obtemos:
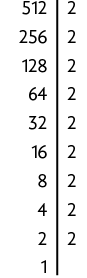
Portanto, .
c) De acordo com as propriedades de radiciação, podemos escrever . Pelo item a, sabemos que . Sendo assim, precisamos calcular . Para isso, vamos decompor o número 144 em fatores primos e reescrevê-lo como potência de expoente 2.
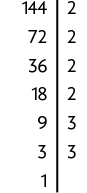
Então, . Portanto, .
d) Decompondo o número 729 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 2, obtemos:
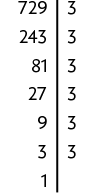
Portanto, .
e) De acordo com as propriedades de radiciação, podemos escrever . Além disso, , pois . Sendo assim, precisamos calcular . Para isso, vamos decompor o número 625 em fatores primos e reescrevê-lo como potência de expoente 2.
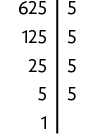
Então, . Portanto, .
f) Decompondo o número 216 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 2, obtemos:
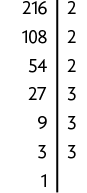
Portanto, .
24. A medida de área de um quadrado cujos lados têm medida de comprimento é dada por . Assim, conhecendo a medida de área , o comprimento dos lados mede . Desse modo, em cada item, temos:
A. Um quadrado com medida de área igual a tem lados com medida de comprimento igual a , pois .
B. Um quadrado com medida de área igual a tem lados com medida de comprimento igual a , pois .
C. Um quadrado com medida de área igual a tem lados com medida de comprimento igual a , pois .
D. Um quadrado com medida de área igual a tem lados com medida de comprimento igual a , pois .
25. A medida do volume de um cubo cujas arestas têm medida de comprimento é dada por . Assim, conhecendo a medida do volume , a medida de comprimento das arestas será . Desse modo, em cada item, temos:
a) Um cubo com medida de volume igual a tem arestas com medida de comprimento igual a , pois .
b) Um cubo com medida de volume igual a tem arestas com medida de comprimento igual a , pois .
c) Um cubo com medida de volume igual a tem arestas com medida de comprimento igual a , pois .
d) Um cubo com medida de volume igual a tem arestas com medida de comprimento igual a , pois .
Página XLVIII
e) Um cubo com medida de volume igual a tem arestas com medida de comprimento igual a , pois .
f) Um cubo com medida de volume igual a tem arestas com medida de comprimento igual a , pois .
26. Um tampo de mesa em formato quadrado com de medida de área tem lados com medida de comprimento igual a , pois .
Um tampo de mesa em formato quadrado com de medida de área tem lados com medida de comprimento igual a , pois .
Assim, a alternativa correta é a d, pois é a única que apresenta uma medida do comprimento compreendida entre e .
27. a) O resultado de com aproximação até os centésimos é 17,02. Portanto, o número 17,03 está entre 17 e 18.
b) O resultado de com aproximação até os centésimos é 30,98. Portanto, o número 30,98 está entre 30 e 31.
28. a) Decompondo o número 4.096 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 3, obtemos:
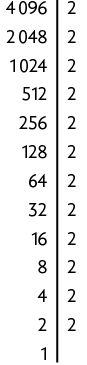
Portanto, .
b) Decompondo 39.304 em fatores primos e reescrevendo-o como potência de expoente 3, obtemos:

Portanto, .
c) Decompondo o número 15.625 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 3, obtemos:
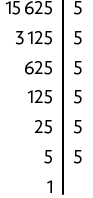
Portanto, .
d) Decompondo o número 4.913 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 3, obtemos:
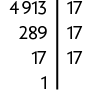
Portanto, .
e) Decompondo o número 64.000 em fatores primos e reescrevendo-o como potência de expoente 3, obtemos:

Portanto, .
f) Decompondo o número 8.000 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 3, obtemos:

Portanto, .
Página XLIX
g) Decompondo o número 59.319 em fatores primos e, em seguida, reescrevendo-o como potência de expoente 3, obtemos:

Portanto, .
h) Decompondo o número 46.656 em fatores primos e reescrevendo-o como potência de expoente 3, obtemos:

Portanto, .
i) Decompondo o número 125.000 em fatores primos e reescrevendo-o como potência de expoente 3, obtemos:
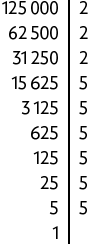
Portanto, .
29. a)
b)
c)
d)
30. a) O número 3 está entre 1 e 4, ou seja, entre e . Assim, está entre 1 e 2. Vamos calcular os quadrados dos números entre 1 e 2 que têm uma casa decimal até obter um número maior do que 3.
Como 2,89 está mais próximo de 3, verificamos que .
b) O número 12 está entre 9 e 16, ou seja, entre e . Assim, está entre 3 e 4. Vamos calcular os quadrados dos números entre 3 e 4 que têm uma casa decimal até obter um número maior do que 12.
Como 12,25 está mais próximo de 12, verificamos que .
c) O número 19 está entre 16 e 25, ou seja, entre e . Assim, está entre 4 e 5. Vamos calcular os quadrados dos números entre 4 e 5 que têm uma casa decimal até obter um número maior do que 19.
Como 19,36 está mais próximo de 19, verificamos que .
d) O número 23 está entre 16 e 25, ou seja, entre e . Assim, está entre 4 e 5. Vamos calcular os quadrados dos números entre 4 e 5 que têm uma casa decimal até obter um número maior do que 23. Como, no item anterior, já calculamos até 4,4, calcularemos de 4,5 em diante.
Como 23,04 está mais próximo de 23, verificamos que .
e) O número 31 está entre 25 e 36, ou seja, entre e . Assim, está entre 5 e 6. Vamos calcular os quadrados dos números entre 5 e 6 que têm uma casa decimal até obter um número maior do que 31.
Como 31,36 está mais próximo de 31, verificamos que .
Página L
31. a) O número 18 está entre 16 e 25, ou seja, entre e . Assim, está entre 4 e 5. Usando os cálculos feitos no item c da atividade anterior, verificamos que a raiz quadrada de 18 está entre 4,2 e 4,3. Então, vamos calcular os quadrados dos números entre 4,2 e 4,3 que têm duas casas decimais até obter um número maior do que 18.
Como 17,9776 está mais próximo de 18, verificamos que .
b) O número 21 está entre 16 e 25, ou seja, entre e . Assim, está entre 4 e 5. Usando os cálculos feitos no item d da atividade anterior, verificamos que a raiz quadrada de 21 está entre 4,5 e 4,6. Então, vamos calcular os quadrados dos números entre 4,5 e 4,6 que têm duas casas decimais até obter um número maior do que 21.
Como 20,9764 está mais próximo de 21, verificamos que .
c) O número 29 está entre 25 e 36, ou seja, entre e . Assim, está entre 5 e 6. Pelo item e da atividade anterior, verificamos que a raiz quadrada de 29 está entre 5,3 e 5,4. Então, vamos calcular os quadrados dos números entre 5,3 e 5,4 que têm duas casas decimais até obter um número maior do que 29.
Como 29,0521 está mais próximo de 29, verificamos que .
d) O número 32 está entre 25 e 36, ou seja, entre e . Assim, está entre 5 e 6. Usando os cálculos feitos no item e da atividade anterior, verificamos que . Continuando os cálculos, obtemos . Logo, a raiz quadrada de 32 está entre 5,6 e 5,7. Então, vamos calcular os quadrados dos números entre 5,6 e 5,7 que têm duas casas decimais até obter um número maior do que 32.
Como 32,0356 está mais próximo de 32, verificamos que .
e) O número 35 está entre 25 e 36, ou seja, entre e . Assim, está entre 5 e 6. Usando os cálculos feitos no item d desta atividade, obtemos . Continuando os cálculos, obtemos e . Logo, a raiz quadrada de 35 está entre 5,9 e 6. Então, vamos calcular os quadrados dos números entre 5,9 e 6 que têm duas casas decimais até obter um número maior do que 35.
Como 35,0464 está mais próximo de 35, verificamos que .
32. a) O número 5 está entre os quadrados perfeitos 4 e 9 e está mais próximo de 4 do que de 9. Assim, está mais próximo de e .
b) O número 23 está entre os quadrados perfeitos 16 e 25 e está mais próximo de 25 do que de 16. Assim, está mais próximo de e .
c) O número 50 está entre os quadrados perfeitos 49 e 64 e está mais próximo de 49 do que de 64. Assim, está mais próximo de e .
d) O número 95 está entre os quadrados perfeitos 81 e 100 e está mais próximo de 100 do que de 81. Assim, está mais próximo de e .
33. a) O número 8 está entre os quadrados perfeitos 4 e 9. Desse modo, está entre e . Portanto, está entre 2 e 3.
b) O número 50 está entre os quadrados perfeitos 49 e 64. Desse modo, está entre e . Portanto, está entre 7 e 8.
c) O número 90 está entre os quadrados perfeitos 81 e 100. Desse modo, está entre e . Portanto, está entre 9 e 10.
d) O número 200 está entre os quadrados perfeitos 196 e 225. Desse modo, está entre e . Portanto, está entre 14 e 15.
34. a)
b)
c)
d)
35. Escrevendo as raízes na forma de potências com expoente fracionário, temos:
A.
B.
C.
D.
E.
F.
G.
H.
Portanto, podemos relacionar 1-H; 2-E; 3-A; 4-B; 5-G; 6-C; 7-F; 8-D.
36. a)
b)
c)
d)
e)
Página LI
f)
g)
h)
37. Resposta pessoal. Sugestão de resposta:
Um terreno retangular tem medida de área igual a . Sabendo que a medida de comprimento de um de seus lados é o dobro da medida de comprimento do lado adjacente, quais são as medidas de comprimento dos lados desse terreno?
Resposta: e .
O que eu estudei?
1. a) O valor da potência de base 7 e expoente 3 é .
b) Como , para que a potência seja igual a 216 e a base seja 6, o expoente deve ser igual a 3.
c) Como , para que a potência seja igual a 32 e o expoente seja 5, a base dever ser igual a 2.
2. a)
b)
c)
d)
e)
f)
3. a)
b)
c)
d)
e)
f)
g)
h)
4. a) Como , segue que . Portanto, .
b) Como , segue que , ou seja, .
c) Todo número elevado a 1 é igual a ele próprio. Assim, . Portanto, .
d) Como , segue que , ou seja, .
e) Todo número diferente de zero elevado a zero é igual a 1. Assim, . Portanto, .
f) O número 1 elevado a qualquer número é igual a 1. Assim, . Portanto, .
g) Como , segue que . Portanto, .
5. Usando a propriedade comutativa da multiplicação e as propriedades de potências, efetuamos os cálculos a seguir.
Logo, a alternativa correta é a B.
6. a) O produto da raiz quadrada de 49 pela raiz quadrada de 64 é dado por:
b) Vamos calcular a raiz quadrada de 3.136 decompondo-o em um produto de fatores primos. Depois, vamos reescrevê-lo como potência de expoente 2.

Portanto, .
c) O produto da raiz cúbica de 125 pela raiz cúbica de 216 é dado por:
d) Podemos calcular a raiz cúbica de 27.000 da seguinte maneira.
e) O produto da raiz quadrada de 26 pela raiz cúbica de 27 é dado por:
f) Vamos calcular a raiz cúbica de 1.331 decompondo-o em um produto de fatores primos e reescrevendo-o como potência de expoente 3.
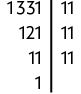
Portanto, .
Página LII
7. a) O número 43 está entre 36 e 49, ou seja, entre e . Assim, está entre 6 e 7. Vamos calcular os quadrados dos números entre 6 e 7 que têm uma casa decimal até obter um número maior do que 43.
Assim, verificamos que a raiz quadrada aproximada de 43 com duas casas decimais está entre 6,5 e 6,6. Então, vamos calcular os quadrados dos números entre 6,5 e 6,6 que têm duas casas decimais até obter um número maior do que 43.
Como 43,0336 está mais próximo de 43, verificamos que .
b) O número 54 está entre 49 e 64, ou seja, entre e . Assim, está entre 7 e 8. Vamos calcular os quadrados dos números entre 7 e 8 que têm uma casa decimal até obter um número maior do que 54.
Assim, verificamos que a raiz quadrada aproximada de 54 com duas casas decimais está entre 7,3 e 7,4. Então, vamos calcular os quadrados dos números entre 7,3 e 7,4, que têm duas casas decimais, até obter um número maior do que 54.
Como 54,0225 está mais próximo de 54, verificamos que .
c) O número 72 está entre 64 e 81, ou seja, entre e . Assim, está entre 8 e 9. Vamos calcular os quadrados dos números entre 8 e 9 que têm uma casa decimal até obter um número maior do que 72.
Assim, verificamos que a raiz quadrada aproximada de 72 com duas casas decimais está entre 8,4 e 8,5. Então, vamos calcular os quadrados dos números entre 8,4 e 8,5 que têm duas casas decimais até obter um número maior do que 72.
Como 72,0801 está mais próximo de 72, verificamos que .
d) O número 87 está entre 81 e 100, ou seja, entre e . Assim, está entre 9 e 10. Vamos calcular os quadrados dos números entre 9 e 10 que têm uma casa decimal até obter um número maior do que 87.
Assim, verificamos que a raiz quadrada aproximada de 87 com duas casas decimais está entre 9,3 e 9,4. Então, vamos calcular os quadrados dos números entre 9,3 e 9,4 que têm duas casas decimais até obter um número maior do que 87.
Como 87,0489 está mais próximo de 87, verificamos que .
e) O número 95 está entre 81 e 100, ou seja, entre e . Assim, está entre 9 e 10. Pelo item anterior, verificamos que é maior do que 9,4. Então, vamos calcular os quadrados dos números entre 9 e 10 que têm uma casa decimal, maiores que 9,4, até obter um número maior do que 95.
Assim, verificamos que a raiz quadrada aproximada de 95 com duas casas decimais está entre 9,7 e 9,8. Então, vamos calcular os quadrados dos números entre 9,7 e 9,8 que têm duas casas decimais até obter um número maior do que 95.
Como 95,0625 está mais próximo de 95, verificamos que .
f) O número 106 está entre 100 e 121, ou seja, entre e . Assim, está entre 10 e 11. Vamos calcular os quadrados dos números entre 10 e 11 que têm uma casa decimal até obter um número maior do que 106.
Assim, verificamos que a raiz quadrada aproximada de 106 com duas casas decimais está entre 10,2 e 10,3. Então, vamos calcular os quadrados dos números entre 10,2 e 10,3 que têm duas casas decimais até obter um número maior do que 106.
Como 106,09 está mais próximo de 106, verificamos que .
8. a) O número 85 está entre os quadrados perfeitos 81 e 100. Desse modo, está entre e . Portanto, está entre 9 e 10.
Página LIII
b) O número 10 está entre os quadrados perfeitos 9 e 16. Desse modo, está entre e . Portanto, está entre 3 e 4.
c) O número 120 está entre os quadrados perfeitos 100 e 121. Desse modo, está entre e . Portanto, está entre 10 e 11.
d) O número 250 está entre os quadrados perfeitos 225 e 256. Desse modo, está entre e . Portanto, está entre 15 e 16.
9. a)
b)
c)
d)
Unidade 2
Conjuntos
Questão 1. Considerando todos os elementos de B e todos os elementos de C, temos:
Atividades
1. Sugestão de resposta:
Conjunto dos objetos de papel:
Total: 2 elementos.
Conjunto dos objetos de higiene:
Total: 3 elementos.
Conjunto dos objetos de plástico:
Total: 4 elementos.
2. a) Conjunto dos múltiplos positivos de 3 menores do que 40:
.
b) Os divisores positivos de 55 são 1, 5, 11 e 55. Desses números, o 11 e o 55 são maiores do que 10. Portanto, o conjunto dos divisores positivos de 55 maiores do que 10 é:
c) Múltiplos positivos de 7 maiores do que 20 e menores do que 38:
d) Os divisores positivos de 80 são 1, 2, 4, 5, 8, 10, 16, 20, 40 e 80. Considerando apenas os divisores de 80 que são menores do que 60, obtemos o seguinte conjunto:
3. a)
b)
c)
d)
e)
f)
g)
h)
4. a) é falsa, pois existe pelo menos um elemento de A que não pertence a B.
b) é verdadeira.
c) é falsa, pois existe pelo menos um elemento de C que não pertence a A.
d) é verdadeira.
e) é falsa, pois existe pelo menos um elemento de D que não pertence a B.
f) é verdadeira.
5. a)
b)
c)
d)
e)
f) ou
g)
h)
i)
6. a)
b)
c) ou
7. a)
b) Como , então .
c)
d) Como e , então .
e)
f) , pois existe pelo menos um elemento de D que não pertence a A.
8. a) A quantidade de entrevistados que leem pelo menos um dos jornais é dada por . Portanto, 52 entrevistados leem pelo menos um dos jornais.
b) 14 entrevistados não leem nenhum dos jornais.
c) 25 entrevistados leem apenas o jornal A e 19 entrevistados leem apenas o jornal B.
d) 8 entrevistados leem ambos os jornais.
e) A quantidade de pessoas entrevistadas é dada por .
Portanto, foram entrevistadas 66 pessoas.
Questão 2. Devemos subtrair 1 unidade para encontrar o antecessor de um número e adicionar 1 unidade para encontrar o sucessor de um número.
a) , , ;
b) , , ;
c) , , .
Questão 3. Existem várias respostas para esta atividade. Sugestões de resposta:
; ; ; .
Página LIV
Atividades
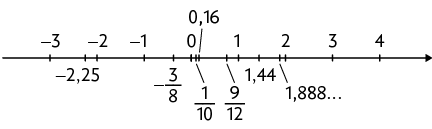
9. Os números das figuras B e C representam números naturais. Os números das figuras B, C e D representam números inteiros. Os números das figuras A, B, C e D representam números racionais.
10. a) Os números 11 e 29 pertencem ao conjunto dos números naturais.
b) Os números , , 11 e 29 pertencem ao conjunto dos números inteiros.
c) Os números , , , 0,38, , 11 e 29 pertencem ao conjunto dos números racionais.
11. a)
b)
c)
d)
e)
f)
g)
h)
12. a) Afirmação correta.
b) Afirmação incorreta. Sugestão de correção:
O conjunto dos números naturais está contido no conjunto dos números inteiros.
c) Afirmação correta.
d) Afirmação incorreta. Sugestão de correção:
Alguns números inteiros pertencem ao conjunto dos números naturais.
e) Afirmação correta.
13. a) Sugestão de respostas: 30, 40.
b) Sugestão de respostas: , e .
c) Sugestão de respostas: e .
d) Sugestão de respostas: , , e .
14. a) Falsa, pois .
b) Falsa, pois .
c) Verdadeira.
d) Falsa, pois .
e) Verdadeira.
f) Verdadeira.
g) Verdadeira.
h) Falsa, pois .
15. Os números que têm o mesmo valor são 0,375 e ; e ; e ; e .
16. a)
b)
c)
d)
e)
f)
17. a)
b)
c)
d)
18. Resposta no final da seção Resoluções.
19. a)
b)
c)
d)
20. a) Seja x a parte decimal da dízima periódica , ou seja, . Assim:
Portanto, a fração geratriz será .
b) Seja x a parte decimal da dízima periódica , ou seja, . Assim:
Portanto, a fração geratriz será .
c) Considere x a parte decimal da dízima periódica , ou seja, . Assim:
Adicionando a parte inteira, temos:
Portanto, a fração geratriz será .
d) Considere x a parte decimal da dízima periódica , ou seja, . Assim:
Adicionando a parte inteira, temos:
Portanto, a fração geratriz será .
Página LV
21. a) Considere . Assim:
Portanto, a fração geratriz será .
b) Considere . Assim:
Portanto, a fração geratriz será .
c) Considere . Assim:
Portanto, a fração geratriz será .
d) Considere . Assim:
Portanto, a fração geratriz será .
22. Há várias respostas para os itens dessa atividade. Apresentamos a seguir algumas delas.
a) e 5
b) e
c) , 0,58, e 15
d) , , , e
e) , e
f) 0,58 e
23. a)
b)
c)
d)
e)
f)
g)
h)
i)
24. a) pertence aos conjuntos e
b) pertence aos conjuntos e
c) 47 pertence aos conjuntos , , e
d) pertence aos conjuntos e
e) pertence aos conjuntos e
f) pertence aos conjuntos , , e
25. Resposta no final da seção Resoluções.
26. a) Os números que pertencem ao conjunto dos números naturais são 0 e 20.
b) Os números que pertencem ao conjunto dos números inteiros são 0, 20, e .
c) Os números que pertencem ao conjunto dos números racionais são 0, 20, , , , e .
d) Os números que pertencem ao conjunto dos números irracionais são , e .
e) Todos os números apresentados pertencem ao conjunto dos números reais.
27. •
28.
O que eu estudei?
1. a)
b)
c)
d)
e)
f)
2. Os elementos do conjunto A são .
3. Os números naturais são 2, 5, 7 e 8.
4. Escrevendo os números em ordem crescente, temos:
; ; ; ; 0; ; 1; ; 16;
5. a) Sugestão de resposta: 0,61.
b) Sugestão de resposta: 0,521 e 0,522.
c) Sugestão de resposta: 1,7311; 1,7312 e 1,7313.
Página LVI
6. a) Sugestão de resposta:
b) Sugestão de resposta:
c) Sugestão de resposta:
d) Sugestão de resposta:
7. a) Verdadeira.
b) Falsa, pois todo número racional é real, mas nem todo número real é racional.
c) Verdadeira.
d) Falsa, pois é um número irracional.
8. Como não há repetição o número é irracional, além disso, ele é positivo. Portanto, a alternativa d está correta.
9. As sentenças verdadeiras são: , , e .
10. Sugestão de resposta:
Unidade 3
Ângulos
Questão 1. Resposta pessoal. Sugestões de resposta: Ponteiros do relógio; abertura de uma porta.
Atividades
1. De acordo com as imagens, o ângulo A mede , o ângulo B mede , o ângulo C mede e o ângulo D mede . Sendo assim:
O ângulo da figura A é agudo, pois é menor do que .
O ângulo da figura B é reto.
O ângulo da figura C é obtuso, pois é maior do que .
O ângulo da figura D é raso.
2. Como o ângulo da figura A mede , calculamos:
Portanto, o complementar do ângulo da figura A mede e o seu suplementar mede .
Como o ângulo da figura B mede , calculamos:
Portanto, o complementar do ângulo da figura B mede e o seu suplementar mede .
Como o ângulo da figura C mede , calculamos:
Portanto, o complementar do ângulo da figura C mede e o seu suplementar mede .
Como o ângulo da figura D mede , calculamos:
Portanto, o complementar do ângulo da figura D mede e o seu suplementar mede .
3. a) Os pares de ângulos complementares são os que estão representados nas figuras:
B e F, pois ;
E e G, pois .
b) Os pares de ângulos suplementares são os que estão representados nas figuras:
A e D, pois ;
C e H, pois .
4. Os ângulos destacados são suplementares, pois, juntos, somam . Então, para determinar o valor de x na imagem A, resolvemos a seguinte equação:
Sendo assim, substituindo o valor de x nas expressões que representam cada ângulo, temos:
:
:
Como os ângulos destacados são complementares, pois, juntos, somam , para determinar o valor de x na imagem B, resolvemos a seguinte equação:
Sendo assim, substituindo o valor de x nas expressões que representam cada ângulo, temos:
:
Página LVII
:
Como os ângulos destacados, adicionados ao ângulo reto, resultam em , para determinar o valor de x na imagem C, resolvemos a equação:
Sendo assim, substituindo o valor de x nas expressões que representam cada ângulo, temos:
:
:
5. De acordo com a figura A e as características dos ângulos apresentados, efetuamos os seguintes cálculos:
Como e são suplementares e , temos:
De acordo com a figura B e as características dos ângulos apresentados, efetuamos os seguintes cálculos:
Na imagem, verificamos que e são congruentes, pois são opostos pelo vértice. Assim, .
Como e são complementares, obtemos:
De acordo com a figura C e as características dos ângulos apresentados, efetuamos os seguintes cálculos:
Como e são opostos pelo vértice, então .
6. Como os ângulos destacados na figura A são opostos pelo vértice, temos:
Para obter a medida dos ângulos destacados, substituímos o valor de x em qualquer um deles. Assim:
Portanto, cada um desses ângulos mede .
Como os ângulos destacados na figura B são opostos pelo vértice, temos:
Para obter a medida dos ângulos destacados, substituímos o valor de x em qualquer um deles. Assim:
Portanto, cada um desses ângulos mede .
7. Como os ângulos e são suplementares, então:
(I).
Como é o dobro da medida de , verificamos que (II).
Substituindo II em I, temos:
Assim,
Portanto, a medida do complementar de é .
8. a) Resposta pessoal. Sugestão de resposta:
1º. Com o auxílio de uma régua, trace uma reta e marque um ponto O sobre ela.
2º. Posicione o compasso com a linha de fé sobre o ponto O e marque o ângulo medindo .
3º. Em seguida, posicione o compasso sobre com a linha de fé em O e marque um ângulo medindo .
b) Resposta pessoal. Sugestão de resposta:
1º. Com o auxílio de uma régua, trace uma reta e marque um ponto O sobre ela.
2º. Posicione o compasso com a linha de fé sobre o ponto O e marque o ângulo medindo .
3º. Em seguida, posicione o compasso sobre com a linha de fé em O e marque um ângulo medindo .
Página LVIII
9. Resposta pessoal. Sugestão de resposta:
Determine a medida dos ângulos e , sabendo que e .
Resposta: e .
10. Como e são suplementares, então:
(I).
Além disso, como a diferença entre suas medidas é , obtemos:
(II).
Isolando em (II), temos .
Substituindo em (I), temos:
Portanto, .
11. a)
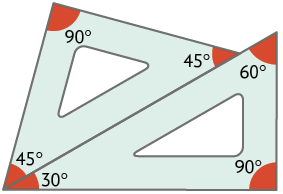
b)
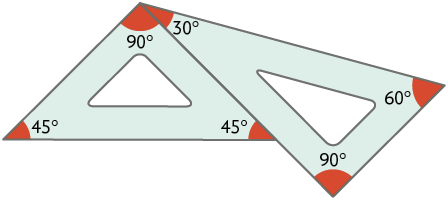
c)
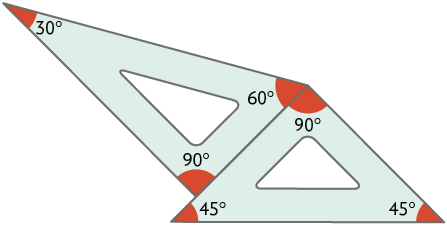
d)
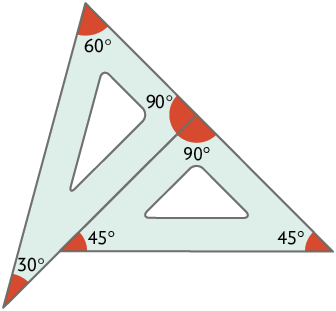
12. a) Como a bissetriz divide um ângulo em dois ângulos iguais, temos . Então, .
b) Como , verificamos que .
Além disso, .
Sendo assim, .
c) Como a bissetriz divide um ângulo em dois ângulos iguais, temos . Então, .
d) Como , então:
13. a)
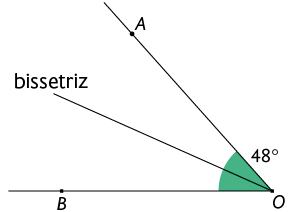
b)
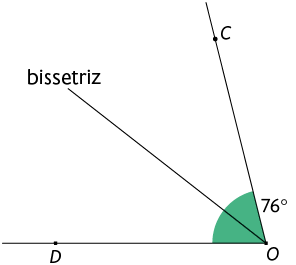
c)

14. Como a bissetriz divide um ângulo em dois ângulos de mesma medida, temos:
A. . Portanto, .
B. . Portanto, .
C. . Portanto, .
D. . Portanto, .
Página LIX
15. a) Resposta pessoal. Espera-se que os estudantes respondam que, nesse posicionamento, o goleiro tem maior alcance em toda a extensão do gol e, consequentemente, a chance de defesa aumenta.
b) Como a bissetriz divide o ângulo em dois ângulos de mesma medida, se o ângulo indicado em vermelho medir , o ângulo indicado em azul terá a mesma medida, ou seja, .
16. a) Márcia representou um ângulo simétrico em relação à linha verde, ou seja, ela representou um ângulo de .
b) Como os dois ângulos têm medidas iguais, a soma de suas medidas é .
c) Sim, a linha verde é a bissetriz do ângulo formado porque ela o divide ao meio, formando dois ângulos simétricos.
17. Como é bissetriz do ângulo , temos:
18. As bissetrizes dos ângulos e , quando se encontram, formam dois ângulos, um agudo e um obtuso.
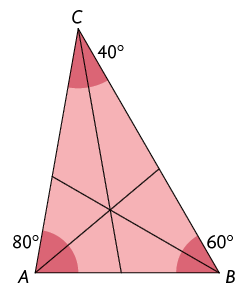
O ângulo obtuso formado pelas bissetrizes também é o ângulo interno do triângulo formado por elas. Como os ângulos da base desse triângulo medem, respectivamente, e , a medida do ângulo obtuso é dada por:
Desse modo, o ângulo agudo formado pelas bissetrizes é dado por .
Portanto, a alternativa correta é a c.
19. Como a semirreta é bissetriz de , temos:
Em seguida, para determinar o valor de um dos ângulos, substituímos o valor de x em uma das duas medidas expressas.
Assim:
Portanto, .
20. Como a semirreta é bissetriz de , temos:
Então, a medida de um dos ângulos formados pela bissetriz de é dada por:
Portanto, e .
21. Como a semirreta é bissetriz de , temos:
. Assim:
Como a semirreta é bissetriz de , temos:
. Assim:
Por fim, como , obtemos:
22. a) A bissetriz divide o ângulo ao meio. Então, . Além disso, a bissetriz divide o ângulo ao meio. Então, .
Em decorrência dessas duas afirmações, verificamos que .
b) Como o ângulo foi dividido em três ângulos de mesma medida, então podemos verificar que .
c) Como o ângulo foi dividido em três ângulos de mesma medida, então podemos verificar que .
23. O ângulo mede , pois . Assim, o ângulo mede , pois é bissetriz de . Portanto, o ângulo mede .
24. Considere e as bissetrizes dos ângulos e , respectivamente. Assim, e medem . Além disso, e medem .
Assim, a medida do menor ângulo formado entre as bissetrizes dos ângulos e é dada por:
25. De acordo com o enunciado, , está entre e e está entre e . Como , concluímos que estará entre e . Portanto, a alternativa b está correta.
26. a) Na página 47, é apresentada a construção de um ângulo de com régua e compasso. Para construir o ângulo de , deve-se repetir os mesmos procedimentos.
Página LX
Em seguida, com a ponta-seca do compasso em B e abertura maior do que a metade do arco , trace um arco. Repita esse processo com a ponta-seca do compasso em C e marque um ponto D na interseção dos arcos. Por fim, com a régua, trace a semirreta , obtendo , cuja medida é .
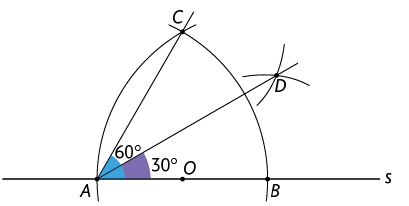
b) Para construir o ângulo de , repita os procedimentos da página 46, na qual é apresentada a construção de um ângulo de com régua e compasso.
Após finalizar esses procedimentos, com a abertura do compasso igual a , trace sobre a reta . Com a ponta-seca do compasso em B e abertura maior do que a metade da medida da distância entre e , trace um arco. Em seguida, repita esse processo, agora com a ponta-seca do compasso em , e marque um ponto E na interseção dos arcos. Por fim, com a régua, trace uma semirreta , obtendo , cuja medida é .

27. Como os dois triângulos são isósceles e congruentes, verificamos que mede , mede e mede . Pelas mesmas conclusões, também mede . Portanto, mede , pois .
O que eu estudei?
1. A. Complementar de :
Suplementar de :
B. Complementar de :
Suplementar de :
C. Complementar de :
Suplementar de :
D. Complementar de :
Suplementar de :
2. a)
b)
3. Para determinar a medida dos ângulos indicados, primeiro precisamos calcular o valor de x em cada item.
A. Os ângulos indicados somam . Assim:
Substituindo o valor de x em cada ângulo, temos:
B. Como e os ângulos indicados somam , obtemos:
Substituindo o valor de x em cada ângulo, temos:
4. Os ângulos indicados nos dois itens são opostos pelo vértice. Por esse motivo, são congruentes. Assim, podemos obter o valor de x igualando as duas sentenças em cada item.
A.
Por serem congruentes, podemos escolher qualquer um dos ângulos para substituir o valor de x encontrado.
Portanto, os ângulos em destaque medem .
B.
Por serem congruentes, podemos escolher qualquer um dos ângulos para substituir o valor de x encontrado.
Portanto, os ângulos em destaque medem .
Unidade 4
Proporcionalidade
Atividades
1. a) A razão entre a quantidade de partidas perdidas e a quantidade de partidas vencidas pode ser representada pela fração .
b) A razão entre a quantidade de pessoas que pagaram meia-entrada e a de pessoas que pagaram a entrada inteira pode ser representada pela fração .
c) A razão entre a quantidade de pessoas que preferem o ar-condicionado desligado e a quantidade de pessoas que preferem ele ligado pode ser representada pela fração .
Página LXI
d) A razão entre a quantidade de fotos de animais invertebrados e a quantidade de fotos de animais vertebrados pode ser representada por .
2. a) A razão entre a quantidade de questões de Português e de Matemática resolvidas por Rafael é dada pela fração .
b) A razão do item a significa que, a cada 3 questões resolvidas de Português, 4 questões de Matemática foram solucionadas.
3. Usando a propriedade fundamental das proporções, temos as seguintes considerações.
a) As frações não formam uma proporção, pois .
b) As frações formam uma proporção, pois .
c) As frações não formam uma proporção, pois .
d) As frações formam uma proporção, pois .
e) As frações formam uma proporção, pois .
f) As frações não formam uma proporção, pois .
g) As frações não formam uma proporção, pois .
h) As frações formam uma proporção, pois .
4. a) A razão entre a quantidade de pessoas idosas e a de não idosas é dada pela fração .
b) Como a razão entre a quantidade de pessoas idosas e a de não idosas nessa excursão é , e sabendo que, ao todo, são 45 pessoas nessa excursão, podemos representar por x a quantidade de pessoas idosas e calcular a seguinte proporção:
Portanto, há 18 pessoas idosas nessa excursão.
5. Calculando os produtos entre o numerador de uma fração e denominador de outra na proporção, obtemos:
a)
b)
c)
d)
e)
f)
g)
h)
6. a) Registre o número 50 em A1. Na célula B1, digite a fórmula e pressione Enter. A porcentagem desejada será exibida. Portanto, 18% de R$ 50,00 correspondem a R$ 9,00.
b) Registre o número 75 em A2. Na célula B2, digite a fórmula e pressione Enter. A porcentagem desejada será exibida. Portanto, 22% de R$ 75,00 correspondem a R$ 16,50.
c) Registre o número 55 em A3. Na célula B3, digite a fórmula e pressione Enter. A porcentagem desejada será exibida. Portanto, 38% de R$ 55,00 correspondem a R$ 20,90.
d) Registre o número 40 em A4. Na célula B4, digite a fórmula e pressione Enter. A porcentagem desejada será exibida. Portanto, 55% de R$ 40,00 correspondem a R$ 22,00.
Página LXII
e) Registre o número 30 em A5. Na célula B5, digite a fórmula e pressione Enter. A porcentagem desejada será exibida. Portanto, 80% de R$ 30,00 correspondem a R$ 24,00.
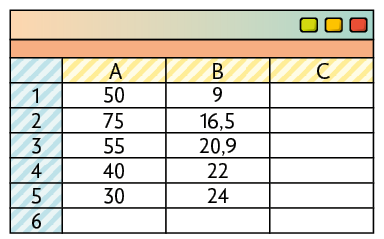
7. Sugestão de resposta: , pois .
Questão 1. Para determinar o consumo mensal do forno elétrico com tempo de uso diário medindo , basta substituir x por 8 em . Assim:
Portanto, o consumo mensal do forno elétrico com uso de por dia é .
Atividades
8. a) As grandezas são proporcionais, pois .
b) As grandezas não são proporcionais, pois .
c) As grandezas não são proporcionais, pois .
d) As grandezas são inversamente proporcionais, pois .
9. a) As grandezas apresentadas não são proporcionais, pois a quantidade de gols marcados não depende do tempo da partida de futebol.
b) As grandezas apresentadas são inversamente proporcionais, pois, quanto mais pintores para pintar a casa, menor será o tempo gasto.
c) As grandezas apresentadas são inversamente proporcionais, pois, quanto maior a velocidade média, menor será o tempo gasto na viagem.
d) As grandezas apresentadas são diretamente proporcionais, pois, quanto maior for a massa da carne a ser comprada, maior será o preço.
e) As grandezas apresentadas não são proporcionais, pois a duração de um filme não depende das dimensões de um DVD.
10. a) Verdadeira.
b) Falsa. A quantidade de comprimidos e a quantidade de dias são grandezas diretamente proporcionais.
c) Falsa. As grandezas são diretamente proporcionais. Assim, se 1 copo enche em 25 segundos, 3 copos encherão em 75 segundos, ou seja, mais do que 1 minuto.
d) Verdadeira.
e) Falsa. A duração de 10 episódios será de 450 minutos. Fazendo a conversão para horas, obtemos , ou seja, .
11. a) De acordo com as informações do quadro, são necessárias 3 colheitadeiras de mesmo modelo para colher a soja em 8 dias.
b) São inversamente proporcionais, pois, se aumentar a quantidade de colheitadeiras, a quantidade de dias vai diminuir.
12. a) De acordo com os valores apresentados, fazemos:
Portanto, e .
b) Podemos concluir que as grandezas são diretamente proporcionais, pois, à medida que uma grandeza aumenta, a outra grandeza aumenta proporcionalmente.
13. a) De acordo com as informações apresentadas, podemos construir o quadro a seguir.
|
Medida de massa em quilogramas (x) |
Preço total a pagar por de limões (y) |
|---|---|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
Portanto, a fórmula que representa a relação entre o preço pago por kg de limões e a medida da massa de limão, em quilograma, é dado por .
b) Analisando os valores do quadro do item a, temos as seguintes coordenadas:
, , , .
Portanto, o gráfico que representa essa fórmula é o B.
c) Usando a fórmula, obtemos , ou seja, de limão custa R$ 6,00.
14. a) Denominando x a quantidade de máquinas e y a quantidade de produtos embalados, temos:
|
x |
y |
|
|---|---|---|
|
1 |
600 |
|
|
2 |
1.200 |
|
|
3 |
1.800 |
|
|
4 |
2.400 |
Portanto, a quantidade de produtos embalados em relação à quantidade de máquinas é dada por .
Página LXIII
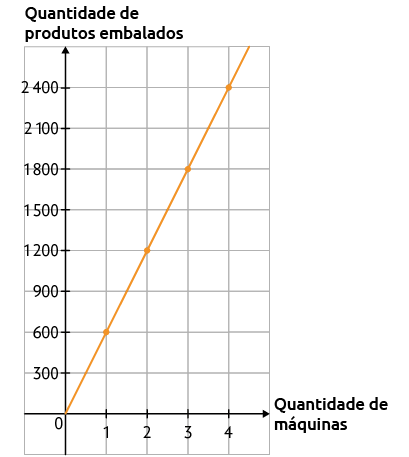
b) Indicando por x a quantidade de páginas e por y a quantidade de palavras, temos:
|
x |
y |
|
|---|---|---|
|
1 |
500 |
|
|
2 |
1.000 |
|
|
3 |
1.500 |
|
|
4 |
2.000 |
Portanto, a quantidade de palavras em relação à quantidade de páginas é dada por .
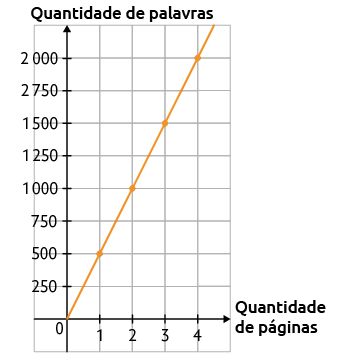
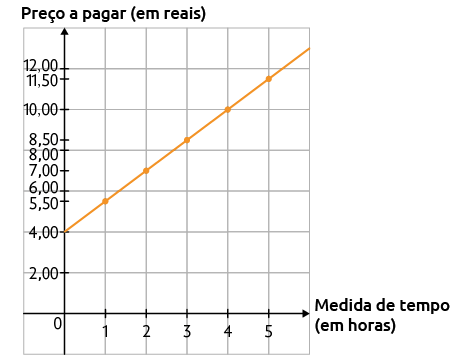
15. a) As grandezas apresentadas não são proporcionais, pois o valor a ser pago não aumenta proporcionalmente à quantidade de horas, devido ao valor fixo cobrado.
b) De acordo com o quadro a seguir, temos:
|
Medida de tempo (em horas) |
Preço total a pagar (R$) |
|---|---|
|
1 |
|
|
2 |
|
|
3 |
|
|
x |
Portanto, a fórmula é dada por .
c) Usando a fórmula, para , temos: , ou seja, R$ 11,50.
d)
16. Resposta pessoal. Sugestão de resposta: Quantos tomates serão colhidos em 30 minutos?
Resposta: Como as grandezas são diretamente proporcionais, em 30 minutos serão colhidos 210 tomates.
17. Como as grandezas são diretamente proporcionais, para determinar o valor de cada figura, fazemos:
18. a) Como as grandezas são diretamente proporcionais, temos:
b) Invertendo uma das razões, por serem inversamente proporcionais, temos:
c) Como as grandezas são diretamente proporcionais, temos:
Página LXIV
d) Invertendo uma das razões, por serem inversamente proporcionais, temos:
e) Invertendo uma das razões, por serem inversamente proporcionais, temos:
19. a) Considerando o consumo de energia do televisor, temos:
|
Medida de tempo (em horas) |
Consumo |
|---|---|
|
5 |
12 |
|
3 |
x |
, ou seja, aproximadamente .
b) Considerando o consumo de energia do ar-condicionado, temos:
|
Medida de tempo (em horas) |
Consumo |
|---|---|
|
8 |
129 |
|
6 |
x |
, ou seja, aproximadamente .
c) Considerando o consumo de energia do micro-ondas e sendo , temos:
|
Medida de tempo (em horas) |
Consumo |
|---|---|
|
14 |
|
|
1 |
x |
, ou seja, aproximadamente, .
d) Considerando o consumo de energia do chuveiro e sendo , temos:
|
Medida de tempo (em horas) |
Consumo |
|---|---|
|
0,5 |
72 |
|
1,5 |
x |
, ou seja, aproximadamente, .
20. a) Como deve ser aplicado de medicamento a cada , temos:
|
Medicamento () |
Medida de massa () |
|---|---|
|
1 |
50 |
|
x |
450 |
Portanto, devem ser aplicados de medicamento nesse animal.
b) De acordo com as informações do problema, consideramos o quadro a seguir.
|
Medicamento () |
Medida de massa () |
|---|---|
|
1 |
50 |
|
5,5 |
x |
Portanto, esse animal tem de medida de massa.
Página LXV
21. Segundo o enunciado, um saquinho com 6 balas tem, em média, . Então, cada bala tem, em média, . Considerando , temos:
|
Quantidade de balas |
Medida de massa (em ) |
|---|---|
|
6 |
55 |
|
x |
1.000 |
Portanto, em um saco de de medida de massa, há aproximadamente 109 balas.
22. a) Como as grandezas são diretamente proporcionais, temos:
|
Quantidade de cana-de-açúcar (em ) |
Etanol () |
|---|---|
|
1.000 |
70 |
|
2.500 |
x |
Portanto, com de cana-de-açúcar, podem ser produzidos, aproximadamente, de etanol.
b) De acordo com as informações do problema, temos:
|
Quantidade de cana-de-açúcar (em ) |
Etanol () |
|---|---|
|
1.000 |
70 |
|
x |
35 |
Portanto, para produzir de etanol, são necessários, aproximadamente, de cana-de-açúcar.
23. A quantidade de pessoas é inversamente proporcional à medida de tempo necessária para limpar o salão. Assim:
|
Quantidade de pessoas |
Medida de tempo (em horas) |
|---|---|
|
3 |
6 |
|
4 |
x |
Portanto, 4 pessoas levariam para limpar o salão de festas.
24. Como a quantidade de pessoas é inversamente proporcional à medida de tempo necessária para colher as frutas, temos:
|
Quantidade de pessoas |
Medida de tempo (em dias) |
|---|---|
|
15 |
7 |
|
x |
5 |
Portanto, seriam necessárias 21 pessoas trabalhando no mesmo ritmo para colher essas frutas em 5 dias.
25. a) A quantidade de funcionários é inversamente proporcional à medida de tempo necessária para terminar a encomenda. Sendo assim:
|
Quantidade de funcionários |
Medida de tempo (em dias) |
|---|---|
|
4 |
3 |
|
x |
1 |
, ou seja, 12 funcionários prepararam a encomenda em um dia.
Portanto, se considerarmos que Marilda e mais 3 funcionários já estão trabalhando, ela deveria contratar mais 8 funcionários para terminar a encomenda em 1 dia.
b)
|
Quantidade de pessoas |
Medida de tempo (em dias) |
|---|---|
|
6 |
x |
|
4 |
3 |
Página LXVI
Portanto, se Marilda contratasse mais 2 funcionários, considerando o mesmo ritmo de trabalho, finalizaria a encomenda em 2 dias.
26. Com a contratação de mais 6 digitadores, o material seria produzido por 15 pessoas. Como a quantidade de pessoas é inversamente proporcional à medida de tempo necessária para digitar o material, temos:
|
Quantidade de pessoas |
Medida de tempo (em dias) |
|---|---|
|
9 |
20 |
|
15 |
x |
Portanto, considerando o mesmo ritmo de trabalho, contratando mais 6 digitadores, todos terminariam o material em 12 dias.
27. As grandezas são diretamente proporcionais, pois o total de água desperdiçado aumenta de acordo com a medida de tempo. Como , temos:
|
Quantidade de gotas |
Medida de tempo (em segundos) |
|---|---|
|
1 |
3 |
|
x |
21.600 |
, ou seja, 7.200 gotas.
Cada gota tem de medida de volume. Então, o total de água desperdiçada é , ou seja, serão desperdiçados ou, aproximadamente, nesse período.
Portanto, a alternativa c está correta.
28. a) As grandezas são diretamente proporcionais. Sendo assim:
|
Medida de volume (em litros) |
Medida de tempo (em segundos) |
|---|---|
|
35 |
45 |
|
980 |
x |
, ou seja, 1.260 segundos.
Fazendo a conversão em minutos, obtemos 21 minutos. Portanto, vai levar 21 minutos para encher totalmente a caixa.
b) Fazendo a conversão de 18 minutos em segundos, obtemos , ou seja, 1.080 segundos. Assim:
|
Medida de volume (em litros) |
Medida de tempo (em segundos) |
|---|---|
|
35 |
45 |
|
x |
1.080 |
Portanto, ele vai bombear .
29. Como há 54 caixas cúbicas com dimensões medindo , a área total ocupada por elas mede . Calculando a área ocupada pelas caixas cujas dimensões medem , obtemos .
Como as grandezas são inversamente proporcionais, quanto maior forem as dimensões da caixa, menor será a quantidade de caixas que caberão no depósito.
|
Quantidade de caixas |
Medida de área (em metros) |
|---|---|
|
54 |
1 |
|
x |
2,25 |
Portanto, cabem 24 caixas com dimensões de nesse depósito.
30. As grandezas são diretamente proporcionais. Então:
|
Porcentagem |
Preço (R$) |
|---|---|
|
15 |
9,90 |
|
100 |
x |
Página LXVII
Assim:
Portanto, o preço do jogo sem o desconto é R$ 66,00 e Fábio pagou R$ 56,10.
31. As grandezas são diretamente proporcionais. Então:
|
Porcentagem |
Preço (R$) |
|---|---|
|
107 |
185,11 |
|
100 |
x |
Portanto, Eduardo pagaria R$ 173,00 sem o acréscimo.
32. Resposta pessoal. Sugestão de resposta:
Determinado veículo percorre de medida de distância com 7 litros de gasolina. Qual medida de distância ele percorrerá com 15 litros?
Resposta:
33. Para resolver essa atividade, devemos inicialmente contar a quantidade de "dentes" em cada engrenagem, pois essa informação é importante nos cálculos.
Engrenagem 1: 24 "dentes".
Engrenagem 2: 16 "dentes".
Engrenagem 3: 12 "dentes".
Na situação apresentada, as grandezas são inversamente proporcionais, pois, quanto maior for a quantidade de "dentes", menor será a quantidade de voltas.
a) Organizando essas grandezas em um quadro, temos:
|
Quantidade de voltas |
Quantidade de "dentes" |
|---|---|
|
8 |
24 |
|
x |
16 |
Portanto, se a engrenagem 1 der 8 voltas, a engrenagem 2 dará 12 voltas.
b) Realizando os cálculos da engrenagem 3 em relação à engrenagem 2, temos:
|
Quantidade de voltas |
Quantidade de "dentes" |
|---|---|
|
28 |
12 |
|
x |
16 |
Portanto, se a engrenagem 3 der 28 voltas, a engrenagem 2 dará 21 voltas.
Realizando os cálculos da engrenagem 3 em relação à engrenagem 1, temos:
|
Quantidade de voltas |
Quantidade de "dentes" |
|---|---|
|
28 |
12 |
|
x |
24 |
Portanto, se a engrenagem 1 der 14 voltas, a engrenagem 3 dará 28 voltas.
34. a) As grandezas apresentadas são inversamente proporcionais, pois, quanto maior for a vazão, menor será a medida de tempo para encher o reservatório.
• Considerando que , temos o seguinte quadro:
|
Litros de água por minuto |
Medida de tempo (em ) |
|---|---|
|
16 |
420 |
|
14 |
x |
Portanto, despejando por minuto, essa torneira levaria para encher o mesmo reservatório.
• Para que o reservatório fique cheio em ou , temos o seguinte quadro:
|
Litros de água por minuto |
Medida de tempo (em minuto) |
|---|---|
|
16 |
420 |
|
x |
240 |
Página LXVIII
, ou seja, 28 litros por minuto.
b) Espera-se que os estudantes citem atitudes como tomar banhos em menor tempo, não escovar os dentes com a torneira aberta, preferir varrer a calçada em vez de lavá-la e usar baldes para lavar automóveis em vez da mangueira, entre outras atitudes.
c) Resposta pessoal. Espera-se que os estudantes compartilhem as atitudes tomadas por seus familiares com a turma.
35. a) Resposta pessoal. Sugestão de resposta:
Em uma empresa de construção, 3 funcionários realizam determinado serviço em 12 dias. Para que esse mesmo serviço seja feito em 4 dias, mantendo o mesmo ritmo de trabalho, essa empresa deverá dispor de quantos funcionários?
Resposta: 9 funcionários.
b) Resposta pessoal. Sugestão de resposta:
Um automóvel a uma velocidade constante de faz uma viagem em 10 horas. Qual é a medida da velocidade que esse automóvel deve permanecer para que essa viagem seja feita em 8 horas?
Resposta: .
O que eu estudei?
1. a) A razão entre a quantidade de esfirras de carne e a de queijo é dada por .
b) A razão escrita no item a significa que, a cada 3 esfirras de carne, 2 eram de queijo.
2. a) Como as grandezas são diretamente proporcionais, temos:
|
Preço (R$) |
Quantidade de fichas |
|---|---|
|
50 |
3 |
|
450 |
x |
Portanto, Guilherme ganhou 27 fichas.
b) A razão que representa a quantidade de fichas para o sorteio e a quantia gasta é .
c) Para determinar o mínimo que uma pessoa deve gastar a fim de ganhar 18 fichas, calculamos:
|
Preço (R$) |
Quantidade de fichas |
|---|---|
|
50 |
3 |
|
x |
18 |
Portanto, uma pessoa deve gastar, no mínimo, R$ 300,00.
3. a) As grandezas não são proporcionais.
b) As grandezas são diretamente proporcionais, pois, quanto maior for a medida da área, maior será a quantidade de pisos.
c) As grandezas são inversamente proporcionais, pois, quanto maior for a quantidade de funcionários, menor será a medida de tempo.
4. a) A sentença matemática que relaciona corretamente essas grandezas é , pois, para cada bolo, o confeiteiro usa 3 ovos.
b) Considere o quadro a seguir.
|
x |
y |
(x, y) |
|---|---|---|
|
1 |
3 |
|
|
2 |
6 |
|
|
3 |
9 |
|
|
4 |
12 |
|
|
5 |
15 |
Comparando essas informações, verificamos que o gráfico D representa a reta dada pela expressão . Portanto, esse é o gráfico correspondente à formula correta determinada no item a.
c) Calculando primeiro a quantidade de ovos, quatro caixas com uma dúzia de ovos totalizam 48 ovos, pois . Substituindo em , temos:
Portanto, ele fez 16 bolos.
5. a) As grandezas envolvidas são quantidade de fotos e quantidade de postagens.
b) Se a porcentagem se mantiver, essas grandezas serão diretamente proporcionais.
c) Organizando as informações em um quadro, temos:
|
Quantidade de fotos |
Quantidade de postagens |
|---|---|
|
75 |
100 |
|
x |
228 |
, ou seja, Fernanda postou 171 fotos.
Página LXIX
6. As grandezas são diretamente proporcionais, pois, quanto mais combustível disponível houver, maior será a distância percorrida.
a) Antes de abastecer, havia no tanque de combustível. Sendo assim, depois de colocar mais , terá no tanque.
|
Quantidade de combustível () |
Medida da distância percorrida () |
|---|---|
|
8 |
100 |
|
37,8 |
x |
Portanto, Vera poderá percorrer aproximadamente .
b) Para determinar o consumo do carro de Vera no percurso de , montamos o seguinte quadro.
|
Quantidade de combustível () |
Medida da distância percorrida () |
|---|---|
|
8 |
100 |
|
x |
125 |
Portanto, o carro vai consumir aproximadamente de combustível nesse percurso.
7. Como as grandezas são diretamente proporcionais, temos:
|
Medida de tempo () |
Quantidade de clientes atendidos |
|---|---|
|
7 |
4 |
|
x |
32 |
Portanto, mantendo o mesmo ritmo, o funcionário levará, em média, 56 minutos para atender 32 clientes.
8. Essas grandezas são inversamente proporcionais, pois, quanto mais cães houver para alimentar, menos dias vai durar a ração. Assim:
|
Medida de tempo (em dias) |
Quantidade de cães |
|---|---|
|
30 |
2 |
|
x |
5 |
Portanto, Juliana poderá alimentar 5 cães por 12 dias com a mesma quantidade de ração.
9. Reescrevendo o enunciado do problema com os números adequados, temos o seguinte enunciado.
Para construir sua casa, Anselmo contratou 4 operários. Com essa quantidade de trabalhadores, a casa ficou pronta em 9 meses. Para que a construção fosse finalizada em 6 meses, quantos operários Anselmo deveria ter contratado?
Como as grandezas são inversamente proporcionais, temos:
Portanto, Anselmo deveria ter contratado 6 operários.
10. Como as grandezas são diretamente proporcionais, vamos montar o seguinte quadro.
|
Preço (R$) |
Percentual (%) |
|---|---|
|
217,70 |
70 |
|
x |
100 |
Portanto, se os produtos não estivessem na promoção, o preço pago seria R$ 311,00.
Unidade 5
Estatística, contagem e probabilidade
Atividades
1. a) A quantidade de veículos que circulam por dia em uma avenida é uma variável quantitativa discreta, pois é obtida por meio de contagem e assume valores inteiros positivos.
Página LXX
b) O esporte preferido dos estudantes do 8º ano é uma variável qualitativa nominal, pois descreve um atributo e não apresenta ordenação.
c) A medida de massa é uma variável quantitativa contínua, pois é obtida por meio de uma mensuração e assume qualquer valor em um intervalo de variação.
d) O estágio de uma doença é uma variável qualitativa ordinal, pois descreve uma qualidade e apresenta uma certa ordenação.
e) A quantidade de livros em uma biblioteca é uma variável quantitativa discreta, pois é obtida por meio de uma contagem e assume valores inteiros positivos.
f) O tipo sanguíneo é uma variável qualitativa nominal, pois descreve uma qualidade e não apresenta ordenação.
g) O salário dos funcionários de uma empresa é uma variável quantitativa contínua, pois é obtida por meio de contagem e pode assumir qualquer valor em um intervalo de variação.
h) A classe social é uma variável qualitativa ordinal, pois descreve uma qualidade e apresenta certa ordenação.
2. As variáveis presentes nesse gráfico são "produção brasileira" e "frutas cítricas". A variável "produção brasileira" é quantitativa, pois pode ser obtida por meio de contagem, e "frutas cítricas" é uma variável qualitativa, pois descreve uma qualidade.
3. a) De acordo com as informações, temos:
Portanto, foram entrevistados 400 clientes.
b) Como a quantidade de resposta para cada cor é a frequência absoluta de cada uma delas, temos:
Branco:
Preto:
Prata:
Vermelho:
Cinza:
|
Cor |
Frequência (f) |
Frequência relativa (fr) |
|---|---|---|
|
Branco |
56 |
14% |
|
Preto |
96 |
24% |
|
Prata |
120 |
30% |
|
Vermelho |
24 |
6% |
|
Cinza |
104 |
26% |
|
Total |
400 |
100% |
Fonte de pesquisa: administração da montadora de automóveis em 2023.
c) A cor com menor preferência é a vermelha.
4. a) De acordo com os dados, 8 estudantes obtiveram notas maiores do que 7,0.
b) A menor nota obtida foi 2,0 e a maior foi 10,0.
c) Resposta no final da seção Resoluções.
Questão 1. Contando a quantidade de idades no quadro, é possível verificar que 50 funcionários participaram da pesquisa.
Questão 2. De acordo com a tabela, a frequência dos funcionários nessa faixa etária é 12 e a frequência relativa é 24%.
Atividades
5. a) A quantidade de funcionários com menos de 41 anos representa a frequência acumulada da faixa etária de . Portanto, há 26 funcionários com menos de 41 anos.
b) O percentual de funcionários com idade na faixa etária de 46 a 50 anos é 12%.
c) A faixa etária com a maior quantidade de funcionários é a faixa etária de .
6. a) As pessoas que ganham menos do que 7 salários mínimos estão nas faixas salariais de e de . Assim, temos .
Portanto, 33 pessoas recebem menos do que 7 salários mínimos.
b) A amplitude de cada intervalo é igual a 3.
c) Resposta no final da seção Resoluções.
7. a) Resposta no final da seção Resoluções.
b) A classe com a maior frequência é .
8. a) Foi pesquisado o IMC de 40 pessoas.
b) A maior frequência ocorreu no intervalo de .
c) Não é possível determinar precisamente o IMC nesse caso. Espera-se que os estudantes respondam que a tabela apresenta apenas a frequência por intervalo.
d) Resposta pessoal.
9. a) A amplitude de cada intervalo é 4.
b) A maior frequência ocorreu no intervalo de .
c) Calculando primeiro a quantidade de atletas inscritos, temos: , ou seja, 250 atletas.
A quantidade de atletas com idade menor do que 22 anos é igual a 20 e .
Portanto, 8% dos atletas têm idade menor do que 22 anos.
10. a) A porcentagem de estudantes que realizaram a atividade física em pelo menos 3 minutos é dada por:
b) No histograma, há 4 intervalos de classes e a amplitude de cada intervalo é igual a 1.
c) A porcentagem de estudantes que gastaram menos de 2 minutos é igual a 12,5%. Como há 40 estudantes nessa turma, temos:
Portanto, 5 estudantes gastaram menos de 2 minutos para realizar a atividade física.
Página LXXI
11. a) Calculando a média entre os valores consumidos em cada mês, temos:
Portanto, houve um consumo médio de de água.
b) O consumo ficou abaixo da média nos meses de maio, julho, setembro, outubro e novembro.
12. a) Resposta no final da seção Resoluções.
b) A menor nota apresentada no quadro é 4,0 e a maior nota é 10. Assim, a amplitude total é 6, pois .
13. a) Como todos os candidatos obtiveram nota 9,0 no currículo, temos as seguintes médias para cada candidato:
Cecília:
Júlio:
Mariana:
Roberto:
Portanto, Mariana ficará em 1º lugar.
b) Para que Júlio tenha a maior média possível, sua nota na etapa do currículo deve ser 10,0, ou seja, ele precisa obter a maior nota possível. Desse modo:
Portanto, a maior média que Júlio poderá obter ao final das quatro etapas é 8,75.
14. Calculando a média, a moda e a mediana da medida da altura dos tenistas para cada país, obtemos:
a) • Brasil:
Portanto, a média aritmética é .
Como temos duas medidas iguais a e duas medidas iguais a , o conjunto de valores é bimodal e as modas são e .
Organizando os dados em ordem crescente, temos: 183, 183, 185, 185.
Como há 4 valores, a mediana é dada pela média aritmética dos valores centrais:
Portanto, a mediana das medidas de altura é .
Espanha:
Portanto, a média aritmética das medidas é igual .
A medida de altura que ocorre com maior frequência é . Logo, a moda é igual a .
Organizando os dados em ordem crescente, temos: 183, 185, 185, 188.
Nesse caso, como há 4 valores, a mediana é dada pela média aritmética dos valores centrais:
Portanto, a mediana das medidas de altura é igual a .
Estados Unidos:
Portanto, a média das medidas de altura é igual a .
Como nesse conjunto de dados não há valores que se repetem, o conjunto é amodal, ou seja, não tem moda.
Organizando os dados em ordem crescente, temos: 188, 196, 208, 211.
Como há 4 valores, a mediana é dada pela média aritmética dos valores centrais:
Portanto, a mediana é .
França:
Assim, a média das medidas é igual .
Nesse conjunto, não há medidas que se repetem, portanto o conjunto de dados é amodal.
Organizando os dados em ordem crescente, temos: 183, 188, 193, 196.
Como há 4 valores, a mediana é dada pela média aritmética dos valores centrais:
Portanto, a mediana é .
b) • Brasil:
Espanha:
Estados Unidos:
França:
Portanto, o país que apresenta a menor amplitude total é o Brasil.
15. Resposta no final da seção Resoluções.
16. Empresa A: , ou seja, 99 milhões de reais.
Empresa B: , ou seja, 102 milhões de reais.
Empresa C: , ou seja, 101 milhões de reais.
Empresa D: , ou seja, 100 milhões de reais.
Portanto, em média, quem mais investiu foi a empresa B.
17. O menor e o maior índice da Ibovespa nesse período foram 11.268 e 63.886, respectivamente.
Considerando o menor e o maior valor assumido por esse índice no período apresentado, ocorreu um aumento de 52.615 no índice, pois . Assim:
Portanto, houve um aumento percentual de, aproximadamente, 470%.
Página LXXII
Questão 3. O título da tabela é "Quantidade de pessoas imunizadas com a 1ª dose ou dose única da vacina contra COVID-19 por região no Brasil, até 7 de abril de 2022", e a fonte de pesquisa é "BRASIL. Ministério da Saúde. Vacinômetro - COVID-19. Disponível em: https://oeds.link/7FZ8v9. Acesso em: 7 abr. 2022.".
Questão 4. O título do eixo horizontal é "Tipo de dose" e o título do eixo vertical é "Quantidade de doses aplicadas".
Atividades
18. a) O alimento mais calórico é o amendoim torrado salgado.
b) Sabendo que de cada um desses alimentos têm , e , respectivamente, calculamos:
, ou seja, .
Portanto, essa pessoa vai ingerir .
c) O alimento mais calórico é a lentilha cozida, pois em de lentilha cozida há e em de iogurte natural há .
d) Resposta pessoal. Espera-se que os estudantes concluam que consumir menos calorias do que precisamos pode ocasionar, entre outros sintomas, fraqueza, fadiga, perda de cabelo, intolerância ao frio e desnutrição. Já a ação de consumir mais calorias do que precisamos pode levar a acúmulo de gordura, obesidade, hipertensão, colesterol alto e doenças cardíacas, entre outras consequências.
e) Resposta pessoal. Espera-se que os estudantes utilizem dados confiáveis, validem as informações com mais de uma fonte e compartilhem o resultado de sua pesquisa com os colegas, contribuindo assim para enriquecer o conhecimento de todos.
19. a) Sugestão de resposta: Faturamento mensal de um supermercado durante 1 ano.
b) Sugestão de resposta: Quantidade de desempregados por sexo em 2022 e em 2023.
c) Sugestão de resposta: Variação da medida da temperatura máxima de uma cidade ao longo de 1 mês.
d) Sugestão de resposta: Preferência dos estudantes do 8º ano por um esporte.
20. a) Sugestão de resposta: Gráfico de colunas, pois facilita a comparação da quantidade de habitantes por região.
b) Sugestão de resposta: Gráfico de linhas, pois facilita a visualização da variação da inflação em determinado período.
c) Sugestão de resposta: Gráfico de setores, por facilitar a comparação dos votos de cada candidato em relação a um total de votos.
21. A. A coluna referente à Região Norte está com a medida de largura diferente das colunas referentes às demais regiões. A medida da altura da coluna referente à Região Sul está maior do que a medida da altura da coluna referente à Região Centro-Oeste, mas esta última apresenta maior taxa de desocupação do que a Região Sul. A medida da altura da coluna referente à Região Nordeste está acima de 15%, porém sua taxa de desocupação é 14,7%.
B. Ausência da fonte de pesquisa e da medida da área referente ao setor ferroviário visivelmente igual à do setor aquaviário. Porém, este último tem um percentual significativamente menor do que o ferroviário.
C. Há espaçamentos diferentes no eixo horizontal entre 2018, 2019 e 2020. Além disso, a produção referente a 2020 está acima da produção referente a 2019, mas ela foi menor.
22. Calculando a quantidade total de bactérias em cada dia da semana das espécies I e II, temos:
Segunda-feira: , ou seja, 1.600 bactérias.
Terça-feira: , ou seja, 1.900 bactérias.
Quarta-feira: , ou seja, 1.750 bactérias.
Quinta-feira: , ou seja, 1.500 bactérias.
Sexta-feira: , ou seja, 1.700 bactérias.
Sábado: , ou seja, 1.290 bactérias.
Domingo: , ou seja, 1.350 bactérias.
Logo, a quantidade de bactérias foi máxima na terça-feira. Portanto, a alternativa a é a correta.
23. a) A porcentagem de estudantes sem acesso à educação foi maior na faixa etária de 6 a 10 anos.
b) A diferença das porcentagens é 3,4%, pois .
c) Resposta pessoal. Espera-se que os estudantes compreendam a importância de assegurar o direito à educação para crianças e adolescentes, contribuindo assim para uma sociedade mais justa, solidária e responsável.
d) Resposta pessoal. Espera-se que os estudantes encontrem, na pesquisa, que as possíveis consequências são a baixa autoestima, a falta de oportunidades empregatícias ou empregos com baixos salários e uma sociedade com mais desigualdade social.
e) Resposta pessoal. Espera-se que os estudantes exercitem o senso crítico e a argumentação, defendendo suas ideias e respeitando o modo de pensar dos colegas.
24. a) A primeira deputada indígena eleita foi Joenia Wapichana. Ela representa o estado de Roraima.
b) Em 2014, a população residente no Brasil da etnia Wapichana era 9.441 indivíduos. Os povos Wapichana também habitam a Guiana e a Venezuela.
c) Em 2020, a região que elegeu a maior quantidade de candidatos indígenas foi a Região Norte.
Página LXXIII
25. a) Vamos construir um gráfico de colunas. No eixo horizontal, representamos o Brasil e suas regiões e, no eixo vertical, a taxa de mortalidade por 100 mil habitantes, considerando uma escala tal que corresponde a 50 unidades da taxa de mortalidade. Em seguida, construímos as colunas relacionadas a cada região do Brasil, de mesma largura e com a medida de altura proporcional à taxa de mortalidade por 100 mil habitantes, de acordo com a escala escolhida. Por fim, inserimos o título e a fonte de pesquisa.
Taxa de mortalidade por 100 mil habitantes para COVID-19 registrada até 30 de abril de 2022
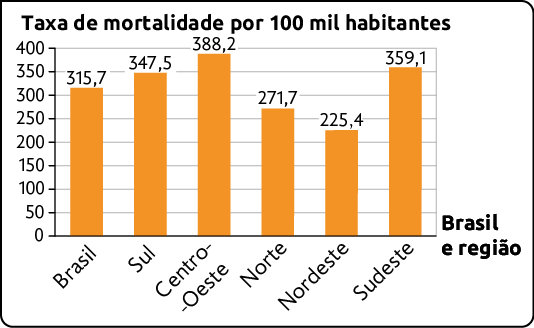
Fonte de pesquisa: BRASIL. Ministério da Saúde. Coronavírus Brasil. Disponível em: https://oeds.link/mH7eJZ. Acesso em: 30 abr. 2022.
b) Resposta pessoal. Espera-se que os estudantes respondam que o gráfico de colunas é o mais adequado para representar esses dados.
c) A região que apresentou a maior taxa de mortalidade por 100 mil habitantes foi a Região Centro-Oeste.
d) Como a taxa nacional é 315,7, as regiões que apresentam a taxa de mortalidade por 100 mil habitantes superior à taxa nacional são a Região Sul, a Região Centro-Oeste e a Região Sudeste.
26. Inicialmente, calculamos a medida do ângulo central, em grau, correspondente a cada setor do gráfico que representa uma disciplina. Adicionando a quantidade de votos em cada componente curricular, temos , isto é, 42 estudantes participaram da pesquisa. Com isso, obtemos os seguintes percentuais, indicados em cada item pela letra x.
Educação física
|
Quantidade de estudantes |
Medida do ângulo (em graus) |
|---|---|
|
42 |
360 |
|
12 |
x |
, ou seja, .
Ciências
|
Quantidade de estudantes |
Medida do ângulo (em graus) |
|---|---|
|
42 |
360 |
|
9 |
x |
, ou seja, .
Língua Portuguesa
|
Quantidade de estudantes |
Medida do ângulo (em graus) |
|---|---|
|
42 |
360 |
|
8 |
x |
, ou seja, .
Matemática
|
Quantidade de estudantes |
Medida do ângulo (em graus) |
|---|---|
|
42 |
360 |
|
6 |
x |
, ou seja, .
Arte
|
Quantidade de estudantes |
Medida do ângulo (em graus) |
|---|---|
|
42 |
360 |
|
5 |
x |
, ou seja, .
Outras
|
Quantidade de estudantes |
Medida do ângulo (em graus) |
|---|---|
|
42 |
360 |
|
2 |
x |
Página LXXIV
, ou seja, .
De acordo com esses resultados, traçamos uma circunferência e marcamos a medida de cada ângulo central que vai representar um setor circular e, em seguida, pintamos cada setor do gráfico de uma cor diferente, indicando sua legenda. Por fim, colocamos o título e a fonte de pesquisa.
Componente curricular preferido pelos estudantes do 8º ano em 2024
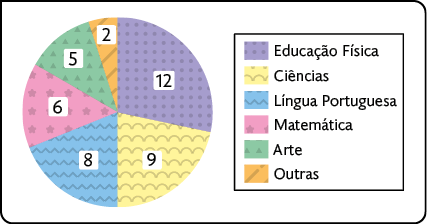
Fonte de pesquisa: setor pedagógico da escola.
27. a) No eixo horizontal, representamos as empresas e, no eixo vertical, os preços das assinaturas, em reais. No eixo vertical, usaremos uma escala tal que corresponderá a 5 reais. Construímos as colunas duplas relacionadas a cada tipo de assinatura de TV, de mesma largura e com medida de altura proporcional ao preço. Em seguida, colocamos o título e a fonte de pesquisa no gráfico construído.
Preço de assinatura de TV na modalidade streaming em 2024
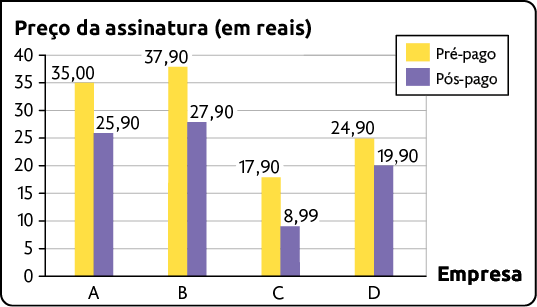
Fonte de pesquisa: catálogo de serviços de streaming.
b) Não é possível representar esses dados utilizando outro tipo de gráfico. Espera-se que os estudantes respondam que o gráfico de colunas agrupadas é o único modelo indicado para esses tipos de dados, pois apresenta mais de uma informação para uma mesma variável.
28. a) O IPCA apresentou a maior taxa no mês de outubro. Essa taxa foi de 1,25%.
b) Indicamos, no eixo horizontal, os meses do segundo semestre de 2021 e, no eixo horizontal, o IPCA, usamos uma escala no eixo vertical, onde corresponde a 0,2% do IPCA. Por fim, colocamos o título e a fonte de pesquisa.
IPCA no segundo semestre de 2021
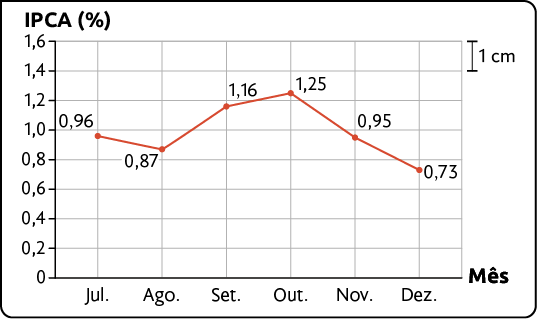
Fonte de pesquisa: IPCA: Índice Nacional de Preços ao Consumidor Amplo. IBGE. Disponível em: https://oeds.link/5tBdV1. Acesso em: 30 abr. 2022.
c) Resposta pessoal. Espera-se que os estudantes realizem a pesquisa sobre o IPCA utilizando fontes confiáveis.
d) Resposta pessoal. A resposta depende dos dados do IPCA de 2023 pesquisados pelos estudantes.
29. a) O gráfico a ser construído será o de colunas. No eixo horizontal, representamos as regiões do Brasil e, no eixo vertical, o Índice de Gini. No eixo vertical, usamos uma escala tal que corresponde a 0,5 do Índice de Gini. Construímos as colunas relacionadas a cada região do Brasil, de mesma largura e com medida de altura proporcional ao Índice de Gini. Por fim, colocamos o título e a fonte de pesquisa.
Índice de Gini do PIB das grandes regiões brasileiras em 2019
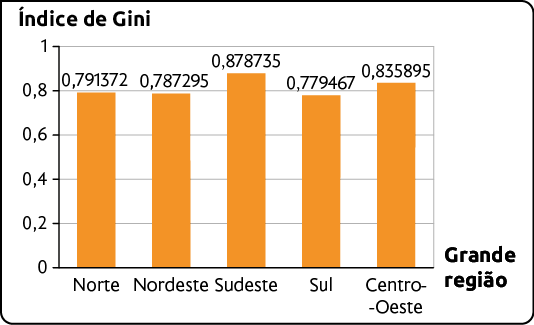
Fonte de pesquisa: IBGE. Disponível em: https://oeds.link/k3UxIu. Acesso em: 30 abr. 2022.
b) Resposta pessoal. Sugestão de questão: Qual das regiões brasileiras apresentadas na tabela teve a maior desigualdade do PIB?
Resposta: Sudeste.
Página LXXV
30. a) O tipo de pesquisa mais adequada é a amostral, devido à inviabilidade de analisar toda a produção.
b) O tipo de pesquisa mais adequada é a censitária, pois, para saber a área de conhecimento de interesse dos estudantes do 3º ano do Ensino Médio, é preciso pesquisar o interesse de todos.
c) O tipo de pesquisa mais adequada é a censitária, pois se trata de uma contagem para saber a quantidade exata de pessoas que residem na zona rural.
d) O tipo de pesquisa mais adequada é a amostral, devido à inviabilidade de pesquisar toda a população do país.
31. a) Essa é uma pesquisa censitária, pois todos os estudantes foram entrevistados.
b) A população entrevistada são todos os estudantes da escola.
c) Os dados obtidos serão a turma, a idade e o sabor do suco preferido de cada estudante.
32. a) Média:
Portanto, foram realizados, em média, 63 atendimentos por dia.
Mediana: Organizando os dados em ordem crescente, temos: 59, 61, 61, 66 e 68.
Portanto, a mediana da quantidade de atendimentos é 61 (valor central).
Moda: 61, pois aparece com mais frequência.
A amplitude total é 9, pois .
b) Sugestão de resposta: O melhor tipo de gráfico é o de colunas, pois permite comparar facilmente a quantidade de atendimentos por dia.
c) Resposta pessoal. Espera-se que os estudantes utilizem os dados da atividade, identifiquem o tema da pesquisa, escolham o melhor tipo de gráfico para representar os dados e elaborem uma conclusão utilizando as medidas de tendência central e a amplitude total dos dados.
33. a) Calculando a média geral do 1º bimestre de Rafael, temos:
Portanto, a média geral do 1º bimestre de Rafael foi 8,1.
b) Mediana: Organizando as médias em ordem crescente, temos: 6,0; 7,3; 7,4; 8,2; 9,0; 9,0 e 9,8.
Como a quantidade de médias é igual a 7, a mediana é o valor central, ou seja, 8,2.
Moda: A média que ocorre com mais frequência é 9,0.
Amplitude total:
Portanto, a amplitude total é 3,8.
c) Resposta no final da seção Resoluções.
d) Resposta pessoal. Espera-se que os estudantes elaborem uma conclusão utilizando as medidas de tendência central e a amplitude total dos dados apresentados na atividade.
34. Resposta pessoal. Espera-se que os estudantes planejem a pesquisa, definindo um tema de interesse e decidindo qual tipo de pesquisa será realizada. Em seguida, eles devem iniciar a coleta dos dados e organizá-los em tabelas ou gráficos. Por fim, devem analisar e interpretar os dados para escrever suas conclusões.
Questão 5. Se fossem 4 opções de cores, a quantidade de possibilidades diferentes que Daniel teria seria dada por , ou seja, 8 possibilidades.
Questão 6. Resposta no final da seção Resoluções.
Atividades
35. a) O diagrama de árvore que representa essa situação é:
O quadro de possibilidades que representa essa situação é:
|
Camiseta |
Bermuda |
|
|---|---|---|
|
Azul |
Verde |
|
|
Verde |
Verde, azul |
Verde, verde |
|
Azul |
Azul, azul |
Azul, verde |
|
Amarela |
Amarela, azul |
Amarela, verde |
|
Laranja |
Laranja, azul |
Laranja, verde |
b) Como são 4 possibilidades de camisetas e 2 de bermudas, o time pode compor o uniforme de 8 maneiras diferentes, pois .
36. Como são 3 possibilidades de cadernos e 4 de lapiseiras, a quantidade de possibilidades que Henrique tem para realizar sua compra é 12, pois .
37. a) Na caixa, há somente uma bola verde. Assim, se a primeira bola que Rogério retirar for verde, sobrarão apenas bolas nas cores azul, vermelha e amarela. Portanto, ele terá 3 possibilidades de cores ao retirar a segunda bola.
b) Resposta no final da seção Resoluções.
c) De acordo com o diagrama de árvore do item anterior, o total de possibilidades de cores é 15.
38. a) Com 4 opções de cor, 3 de tamanho e 2 de banco, Isadora pode compor a bicicleta de 24 maneiras diferentes, pois . Assim os devem ser substituídos por 2 e 24, respectivamente.
b) Se Isadora tivesse 5 opções de cor, 2 opções de tamanho e 4 opções de banco, o total de possibilidades para ela compor a bicicleta seria 40, pois .
Página LXXVI
39. a) Como são 4 opções de prato principal e 2 de bebida, podem ser formados 8 pedidos com 1 prato principal e 1 bebida, pois .
b) Sendo 4 opções de prato principal, 2 de bebida e 4 de sobremesa, podem ser formados 32 pedidos com 1 prato principal, 1 bebida e 1 sobremesa, pois .
40. Na formação de um número com as características solicitadas, temos 4 possibilidades de algarismos para a ordem das unidades de milhar, 3 para a ordem das centenas, 2 para a ordem das dezenas e 1 para a ordem das unidades.
Portanto, nesse caso, podem ser formados 24 números de quatro ordens, pois .
41. a) Para formar os números, Jade dispõe de 10 algarismos.
Primeiro, vamos contar a quantidade de cartões amarelos.
Para formar números com 3 algarismos, ela não colocou o 0 na posição da centena. Sendo assim, nessa posição, temos 9 possibilidades de algarismos. Já nas posições da dezena e da unidade, temos 10 possibilidades de algarismos para cada uma delas.
Portanto, Jade utilizou , ou seja, 900 cartões amarelos.
Em seguida, contamos a quantidade de cartões azuis.
Para formar números com 4 algarismos, Jade não colocou o 0 na posição da unidade de milhar. Sendo assim, nessa posição, temos 9 possibilidades de algarismos. Já nas posições da centena, da dezena e da unidade, temos 10 possibilidades de algarismos em cada uma delas.
Desse modo, Jade utilizou 9.000 cartões azuis, pois .
Portanto, Jade utilizou 9.900 cartões, pois .
b) De acordo com o item anterior, há 900 cartões amarelos na urna. Para que Jade tenha certeza de que há 2 cartões azuis entre os retirados, ela deve retirar 902 cartões.
42. Há 6 opções de saia. Nesse caso, indicando por x o total de opções de blusa, temos:
Portanto, são 7 opções de blusa.
43. Resposta pessoal: Sugestão de resposta:
Se Rafael optar pelo terno slim, quantas combinações de cores de terno e de sapato ele poderá escolher?
Resposta: Ele terá 6 combinações diferentes para escolher.
Questão 7. Esse espaço amostral tem 20 elementos e a probabilidade da ocorrência de cada um deles é . Sendo assim, temos . Portanto, a soma é igual a 1.
Questão 8. Entre os 36 resultados possíveis, em 6 deles o algarismo das dezenas é 3. Portanto, a probabilidade de Geraldo formar um número cujo algarismo das dezenas seja igual a 3 é ou .
Atividades
44. a) Foram colocadas no saco 24 bolinhas vermelhas, 18 azuis, 15 verdes e 31 laranjas. Portanto, ao todo, foram colocadas 88 bolinhas, pois .
b) A cor que tem a maior chance de ser retirada é a cor laranja, pois é a cor que há em maior quantidade.
c) Como são 88 bolinhas no saco, das quais 18 delas são azuis, a probabilidade de uma bolinha azul ser retirada é ou . Além disso, como há 15 bolinhas verdes, a probabilidade de uma bolinha verde ser retirada é .
45. a) Há 3 números terminados em zero, que são: 180, 190 e 30.
Logo, a probabilidade de retirar uma ficha com um número terminado em zero é ou .
b) Há 8 números pares, que são: 192, 180, 152, 136, 72, 190, 30 e 108.
Portanto, a probabilidade de retirar uma ficha com um número par é .
c) Há 10 números maiores do que 100, os quais são: 192, 205, 180, 152, 136, 117, 241, 190, 147 e 108.
Logo, a probabilidade de retirar uma ficha com um número maior do que 100 é ou .
d) Há 7 números menores do que 125, os quais são: 117, 72, 51, 30, 85, 67 e 108.
Logo, a probabilidade de retirar uma ficha com um número menor do que 125 é .
e) Há 7 números ímpares, que são: 205, 117, 241, 51, 85, 147 e 67.
Logo, a probabilidade de retirar uma ficha com um número ímpar é .
f) Há 5 números maiores do que 77 e menores do que 151, os quais são: 136, 117, 85, 147 e 108.
Logo, a probabilidade de retirar uma ficha com um número maior do que 77 e menor do que 151 é ou .
46. Do total de 21 balões, sabemos que:
a) 8 valem 20 pontos. Logo, a probabilidade de o 1º balão que Flávia estourar valer 8 pontos é .
b) 2 valem 50 pontos e 6 valem 70 pontos. Desse modo, 8 balões que valem mais do que 20 pontos. Logo, a probabilidade é .
c) se Flávia já estourou um balão que vale 10 pontos, sobraram 20 balões, dos quais 6 valem 70 pontos. Logo, a probabilidade de o 2º balão que Flávia estourar valer 70 pontos é ou .
47. Há 9 possibilidades de sorteio de um cartão branco e um preto, pois . As possíveis adições com resultado par, entre os números que estão nos cartões, são as seguintes: ; ; ; ; .
Página LXXVII
Assim, há 5 possibilidades de a adição ser par. Logo, a probabilidade é .
Portanto, a alternativa b está correta.
48. Para formar números com três algarismos distintos, temos 3 algarismos possíveis para a ordem das centenas, 2 para a ordem das dezenas e 1 para a ordem das unidades. Como , podemos formar 6 números com 3 algarismos distintos.
Logo, o espaço amostral desse experimento é:
.
Sendo assim:
a) Os números pares do espaço amostral são 132 e 312.
Logo, a probabilidade de sortearmos um número par é ou .
b) Os números ímpares do espaço amostral são 123, 213, 231 e 321.
Logo, a probabilidade de sortearmos um número ímpar é ou .
c) Os números múltiplos de 4 são 132 e 312, pois e .
Logo, a probabilidade de sortearmos um número múltiplo de 4 é ou .
d) Os números múltiplos de 12 são 132 e 312, pois e .
Logo, a probabilidade de sortearmos um número múltiplo de 12 é ou .
e) Os números menores do que 320 são 123, 132, 213, 231 e 312.
Logo, a probabilidade de sortearmos um número menor do que 320 é .
49. a) O quadro de possibilidades desse experimento é:
|
Moeda / Dado |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
Cara (K) |
K, 1 |
K, 2 |
K, 3 |
K, 4 |
K, 5 |
K, 6 |
|
Coroa (C) |
C, 1 |
C, 2 |
C, 3 |
C, 4 |
C, 5 |
C, 6 |
b) Temos 6 faces no dado e 2 faces na moeda. Assim, a quantidade de resultados possíveis é igual a 12, pois .
c) • A probabilidade de obter nesse lançamento o número 1 e cara é .
Temos 3 números pares e 2 resultados possíveis na moeda, ou seja, 6 possíveis resultados, pois . Logo, a probabilidade de obter nesse lançamento um número par e qualquer resultado para a moeda é ou .
Temos um possível resultado para a moeda e 6 para o dado. Logo, a probabilidade de obter nesse lançamento coroa e qualquer número para o dado é ou .
Temos 3 números ímpares e um possível resultado para a moeda, ou seja, 3 possíveis resultados. Logo, a probabilidade de obter nesse lançamento um número ímpar e cara é ou .
50. a) O espaço amostral desse experimento é:
b) O espaço amostral apresenta 24 elementos, sendo 6 números pares em ambos os dados. Portanto, a probabilidade é ou .
c) Nesse caso, do total, 6 são lançamentos com números ímpares. Portanto, a probabilidade de obter um número ímpar em ambos os dados é ou .
d) Do total de 24 elementos do espaço amostral, 12 são lançamentos com um número par em um dos dados e um número ímpar no outro. Portanto, a probabilidade de obter resultado desse tipo em um lançamento é ou .
e) Adicionando cada uma das probabilidades anteriores, temos . Portanto, a soma das probabilidades é igual a 1.
51. a) Como 5 calças apresentam defeito para cada 120 calças fabricadas, a probabilidade de retirar do lote uma calça com defeito é ou .
b) De acordo com as informações, a cada 240 calças fabricadas 10 apresentam defeito. Assim, a probabilidade de retirar, de um lote de 240 calças, uma com defeito é ou . Logo, as probabilidades são iguais. Isso ocorre porque, ao aumentar o número de calças fabricadas, a probabilidade de encontrar calças com defeito aumenta proporcionalmente.
52. a) • Vogal: Entre as 5 letras que estão nos cartões, 2 são as vogais A e E. Logo, a probabilidade de Ana sortear uma vogal é .
Consoante: Entre as 5 letras que estão nos cartões de Ana, 3 são as consoantes B, C e D. Logo, a probabilidade de Ana sortear uma consoante é .
b) Calculando a adição das probabilidades, temos: .
Portanto, a soma das probabilidades é igual a 1.
53. a) Os divisores de 42 são 1, 2, 3, 6, 7, 14, 21 e 42. Assim, o espaço amostral desse sorteio é .
b) Como o espaço amostral apresenta 8 elementos, a probabilidade de obter cada um dos números é .
c) A adição das probabilidades do item anterior é dada por: .
Página LXXVIII
d) • Como os números pares são 2, 6, 14 e 42, a probabilidade de sortear um número par é ou .
Como os números ímpares são 1, 3, 7 e 21, a probabilidade de sortear um número ímpar é ou .
Como os números compostos por dois algarismos são 14, 21 e 42, a probabilidade de sortear um número composto por dois algarismos é .
Como os números múltiplos de 6 são 6 e 42, a probabilidade de sortear um múltiplo de 6 é ou .
Como os números divisores de 11 são 1 e 11, apenas o número 1 pode ser sorteado. Portanto, a probabilidade de sortear um divisor de 11 é .
Como os números primos são 2, 3 e 7, a probabilidade de sortear um número primo é .
54. Resposta pessoal. Sugestão de resposta:
Ao sortear uma das bolas do jogo de bilhar, qual é a probabilidade de retirar uma bola com um número maior do que 10?
Resposta: A probabilidade de retirar uma bola com um número maior do que 10 é .
O que eu estudei?
1. a) Resposta no final da seção Resoluções.
b) Do total de estudantes, 22% tem altura com medida menor do que . Portanto, 78% dos estudantes têm medida de altura maior ou igual a .
c) De acordo com a tabela construída no item a, concluímos que 6% dos estudantes têm altura medindo ou mais.
2. a) O menor e o maior salário são R$ 1.600,00 e R$ 1.870,00, respectivamente. Logo, a amplitude total é dada por , ou seja, R$ 270,00.
b) Resposta no final da seção Resoluções.
3. a) Calculando a média anual de Renata em cada componente curricular, temos:
Língua Portuguesa:
Língua Inglesa:
Matemática:
História:
Geografia:
Ciências:
Arte:
Calculando a média geral, obtemos:
Portanto, a média geral foi, aproximadamente, 7,9.
b) Pelo item anterior, a maior média anual por componente curricular foi 9,4 e a menor foi 6,3. Como , a amplitude total das médias anuais de Renata por componente curricular é 3,1.
c) Escrevendo as médias anuais de Renata em ordem crescente, temos: 6,3; 7,5; 7,5; 7,5; 8,4; 9,0; 9,4.
Como são 7 médias, a mediana é dada pelo valor central.
Portanto, a mediana é 7,5.
A média que ocorre com maior frequência é 7,5. Logo, a moda das médias anuais de Renata é 7,5.
4. a) Sugestão de resposta: O gráfico mais adequado é o de colunas, pois com ele é mais fácil comparar a quantidade de aces de cada time.
b) Sugestão de resposta: O tipo de gráfico mais adequado é o de linhas, pois ele permite uma melhor visualização da variação das medidas de temperatura.
5. a) De acordo com os dados da tabela, temos:
Portanto, foram entrevistados 300 pacientes.
b) Primeiro, calculamos a medida do ângulo central, em grau, correspondente a cada setor do gráfico que representa a quantidade de respostas com relação à qualidade do atendimento.
Como a quantidade total de respostas é igual a 300, essa quantidade representa no gráfico.
Calculando a medida do ângulo central de cada setor correspondente aos indicadores de qualidade de atendimento, temos:
Ruim:
|
Quantidade de respostas |
Medida do ângulo (em graus) |
|---|---|
|
300 |
360 |
|
45 |
x |
Portanto, a medida desse setor será .
Regular:
|
Quantidade de respostas |
Medida do ângulo (em graus) |
|---|---|
|
300 |
360 |
|
75 |
x |
Página LXXIX
Portanto, a medida desse setor será .
Bom:
|
Quantidade de respostas |
Medida do ângulo (em graus) |
|---|---|
|
300 |
360 |
|
120 |
x |
Portanto, a medida desse setor será .
Ótimo:
|
Quantidade de respostas |
Medida do ângulo (em graus) |
|---|---|
|
300 |
360 |
|
60 |
x |
Portanto, a medida desse setor será .
Com as medidas determinadas, traçamos uma circunferência e marcamos nela a medida de cada ângulo obtido. Após isso, indicamos cada setor do gráfico com uma cor diferente e usamos a cor correspondente na legenda. Por fim, inserimos o título e a fonte de pesquisa.
Pesquisa de satisfação
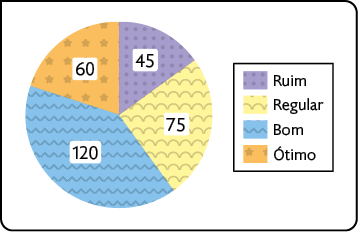
Fonte de pesquisa: setor de recursos humanos da clínica em 2023.
c) Sim, o resultado é favorável à clínica. Espera-se que os estudantes respondam que, embora 15% dos entrevistados tenham indicado a opção ruim e 25% tenham respondido regular, 60% responderam que o atendimento é bom ou ótimo.
6. a)
|
Número da face |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
1 |
1, 1 |
1, 2 |
1, 3 |
1, 4 |
1, 5 |
1, 6 |
|
2 |
2, 1 |
2, 2 |
2, 3 |
2, 4 |
2, 5 |
2, 6 |
|
3 |
3, 1 |
3, 2 |
3, 3 |
3, 4 |
3, 5 |
3, 6 |
|
4 |
4, 1 |
4, 2 |
4, 3 |
4, 4 |
4, 5 |
4, 6 |
|
5 |
5, 1 |
5, 2 |
5, 3 |
5, 4 |
5, 5 |
5, 6 |
|
6 |
6, 1 |
6, 2 |
6, 3 |
6, 4 |
6, 5 |
6, 6 |
b) Como são 2 dados de 6 faces, a quantidade de combinações é dada por , ou seja, são 36 combinações possíveis.
c) Analisando o quadro do item a, temos 9 combinações formadas apenas por números pares.
d) Analisando o quadro do item a, temos 6 combinações formadas apenas por números iguais.
e) De acordo com os possíveis resultados nas faces voltadas para cima de ambos os dados, as adições entre esses números são:
|
Número da face |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
De acordo com o quadro, temos 3 resultados em que as adições são maiores do que 10.
7. a) Juntando a quantidade de bolas de cada cor, temos:
Portanto, há 120 bolas na urna.
b) Das 120 bolas na urna, 35 são vermelhas. Então, 85 não são vermelhas, pois .
Logo, a probabilidade de retirar uma bola que não seja vermelha é ou .
c) Como na caixa há 24 bolas azuis, a probabilidade de retirar uma bola azul é ou .
d) De acordo com o item anterior, a probabilidade de retirar uma bola azul é ou .
Assim, a probabilidade de retirar:
uma bola vermelha é ou .
uma bola preta é .
uma bola amarela é ou .
Juntando essas probabilidades, temos:
Portanto, a soma das probabilidades é igual a 1.
8. Do número 1 ao 36, temos 18 números pares. Logo, sabendo que foi sorteado um número par, a probabilidade de ser o 18 é .