Página LXXX
Unidade 6
Transformações geométricas
Questão 1.
a) A alternativa é falsa, pois a transformação de reflexão da figura A em relação ao eixo e seria uma figura do lado direito do eixo, mas a figura B está sobre o eixo.
b) A alternativa é verdadeira.
c) A alternativa é falsa, pois uma transformação de translação não rotaciona a figura original.
d) A alternativa é falsa, pois a figura B é a imagem da figura A pela rotação de , e não o contrário.
Portanto, a alternativa b é a correta.
Atividades
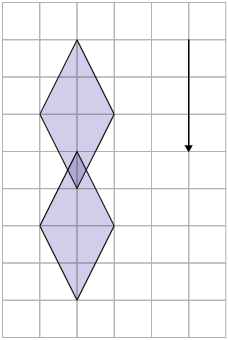
1. As figuras são simétricas na malha quadriculada A, pois, para haver uma simetria por reflexão entre duas figuras, é necessário que os vértices alinhados das figuras simétricas tenham a mesma distância até o eixo de simetria.
2. a) A transformação foi aplicada no sentido horário, pois a figura 2 está à direita da figura 1, e foi realizada uma rotação de .
b) A transformação foi aplicada no sentido horário, pois a figura 2 está à direita da figura 1, e foi realizada uma rotação de .
3. A figura 2 é simétrica à figura 1 por rotação em torno do ponto O na malha quadriculada C, pois, na malha quadriculada A, as figuras não são idênticas; na malha B, as figuras são simétricas por reflexão; na malha D, as figuras são simétricas por translação.
4. a) Para haver uma simetria por rotação de modo que as figuras coincidam, devem ser aplicados os seguintes ângulos de rotação.
Figura A:
Figura B:
Figura C:
b) Resposta pessoal.
c) Resposta pessoal.
5. Como a figura tem contorno em formato aproximadamente circular, é possível dividi-la em 3 figuras idênticas. Portanto, o menor ângulo de rotação é
6. a) Fazendo os desenhos referentes a cada uma das indicações, temos:
b)
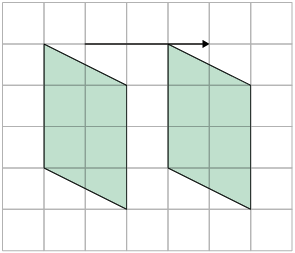
7. A figura 2 é simétrica à figura 1 por translação nas malhas quadriculadas B e C, pois nesse tipo de simetria as figuras devem ser idênticas, estando apenas transladadas em relação à original.
8. Para realizar as construções no GeoGebra, fazemos:
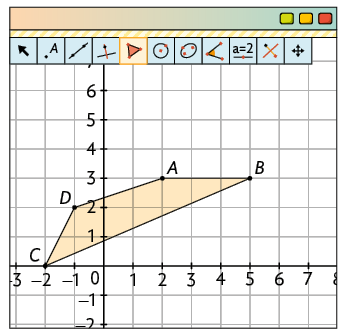
a) 1º. Clique com o botão direito sobre a Janela de visualização, habilite a opção Exibir Eixos e, na aba Exibir Malha, escolha a opção Malha Principal.
2º. Para construir os vértices do polígono, digite no campo Entrada... as coordenadas , , e e pressione Enter. Com a ferramenta Polígono, clique nos pontos A, B, C e D criados e novamente em A, para construir o retângulo .
b) Digite no campo Entrada... as coordenadas dos pontos e e pressione Enter. Em seguida, trace uma reta r passando por esses pontos. Para isso, selecione a ferramenta Reta e clique nos pontos E e F.
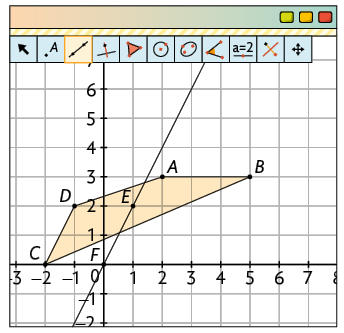
Página LXXXI
c) Com a ferramenta Reflexão em Relação a uma Reta, clique no polígono e, depois, na reta r.
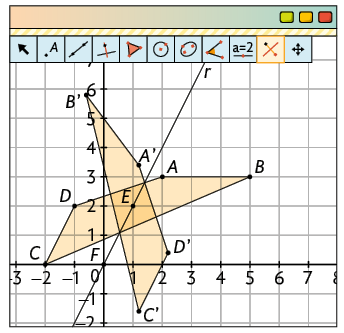
d) 1º. Construa o ponto que será a referência para a rotação.
2º. Com a ferramenta Rotação em Torno de um Ponto, clique no polígono e, depois, no ponto O. No campo Ângulo da janela que será exibida, digite , escolha o sentido anti-horário e clique em OK.
e) 1º. Construa dois pontos distintos para delimitar as extremidades da seta, que será a referência para a medida da distância, a direção e o sentido da translação. Com a ferramenta Vetor, clique nesses dois pontos, primeiro na extremidade inicial, depois na final.
2º. Com a ferramenta Translação por um Vetor, clique no polígono e, depois, na seta.
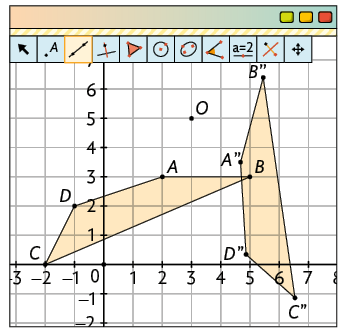
9. Rotacionando o quadrilátero em no sentido horário, encontramos o quadrilátero na posição acima e à direita de . Em seguida, fazendo a reflexão do polígono , obtemos abaixo e oposto de e abaixo e à direita de . Portanto, o item A apresenta o resultado correto obtido por Antônio.
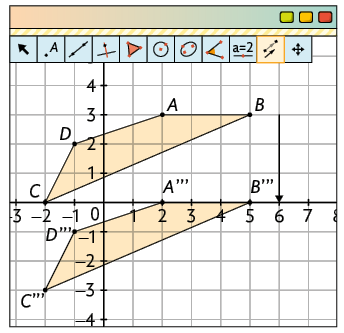
10. Copiando o desenho na malha quadriculada e seguindo as indicações da atividade, temos:
11. É possível identificar as transformações geométricas reflexão e rotação.
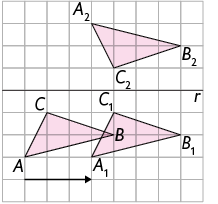
12. a) Maria pode ter usado as transformações geométricas na seguinte ordem: reflexão, reflexão, reflexão, translação e translação. Essa ordem está descrita no item B. Outra possibilidade é usar as transformações na seguinte ordem: rotação, reflexão, rotação, translação e translação. Essa ordem é descrita no item C.
b) Resposta pessoal.
13. a) O menor elemento da imagem, considerando as transformações que poderiam ser usadas, é representado pela imagem a seguir.

b) Sugestão de resposta: Reflexão, translação e rotação.
O que eu estudei?
1. O triângulo foi construído por meio da transformação de reflexão em relação ao triângulo . Portanto, a frase pode ser reescrita como:
O triângulo é a imagem do triângulo pela transformação de reflexão em relação à reta r.
2. Reproduzindo a imagem na malha quadriculada, temos:

Página LXXXII
3. A alternativa C apresenta a figura 2 como imagem da figura 1, transladada na direção horizontal 7 unidades para a direita e na vertical 4 unidades para baixo.
Unidade 7
Cálculo algébrico
Questão 1. Espera-se que os estudantes verifiquem que Al-Khowarizmi fez várias contribuições, entre elas, a idealização do sistema decimal com 10 algarismos e a resolução de equações, algo que popularizou métodos algébricos.
Questão 2. O valor de duas canetas é reais e de três cadernos é reais. Assim, o valor total a ser pago, em reais, é
Atividades
1. A metade de é representada por . Adicionando mais 2, obtemos .
O dobro de é representado por e o quadrado de , por . Adicionando esses valores, temos .
O triplo de é representado por e a quinta parte do dobro de x, por . Adicionando essas expressões, obtemos .
Portanto, podemos associar A-3, B-1 e C-2.
2. a)
b)
c)
d)
e)
Resposta pessoal. Sugestão de resposta:
O dobro do número menos cinco.
Resposta: .
Para , temos:
A metade do quadrado de um número mais um.
Resposta: .
Para , temos:
3. a) O triplo de um número mais cinco.
b) A metade de um número menos o quádruplo desse número.
c) O quadrado de um número menos três.
d) A metade do cubo de um número menos esse número.
4. a) A figura 2 tem 4 quadradinhos. A figura 4 tem 6 quadradinhos.
b) A figura 6 terá 8 quadradinhos, pois quadradinhos.
c) A expressão algébrica que representa a quantidade de quadradinhos para uma figura na posição é .
d) Utilizando a expressão obtida no item anterior, temos:
Figura 10: , isto é, 12 quadradinhos.
Figura 16: , isto é, 18 quadradinhos.
Figura 27: , isto é, 29 quadradinhos.
5. Efetuando as operações indicadas e reduzindo os termos semelhantes, temos:
a)
b)
c)
d)
e)
f)
Questão 3. Sugestão de resposta: .
Atividades
6. a) O coeficiente é 16 e a parte literal é .
b) O coeficiente é e a parte literal é .
c) O coeficiente é 1 e a parte literal é .
d) O coeficiente é 22 e a parte literal é .
e) O coeficiente é 4,2 e a parte literal é .
f) O coeficiente é e a parte literal é .
g) O coeficiente é 0,021 e a parte literal é .
h) O coeficiente é 100 e a parte literal é .
i) O coeficiente é 18 e a parte literal é .
7. a) Como o expoente da variável é 1 e da variável é 1, o grau do monômio é 2, pois .
b) Como o expoente da variável é 3, da variável é 2 e da variável é 1, o grau do monômio é 6, pois .
c) Como o expoente da variável é 1, da variável é 1 e da variável é 1, o grau do monômio é 3, pois .
d) Como o expoente da variável é 5 e a parte literal do monômio só tem essa variável, o grau do monômio é 5.
e) Como o expoente da variável é 3 e da variável é 1, o grau do monômio é 4, pois .
f) Como o expoente da variável é 1 e da variável é 1, o grau do monômio é 2, pois .
g) Como o expoente da variável é 1 e a parte literal do monômio só tem essa variável, o grau do monômio é 1.
h) Como o expoente da variável é 8 e da variável é 1, o grau do monômio é 9, pois .
Página LXXXIII
i) Como o expoente da variável é 0 e a parte literal do monômio só tem essa variável, o grau do monômio é zero.
8. a)
b)
c)
9. Os monômios semelhantes são os que apresentam a parte literal igual. Sendo assim, temos:
Monômios semelhantes a : , e .
Monômios semelhantes a : e .
Monômios semelhantes a : , e .
Monômios semelhantes a : , e .
10. Sugestão de resposta: , e .
11. Resposta pessoal. Sugestão de resposta:
Considerando as expressões algébricas que representam a medida da área e a medida do perímetro do retângulo, responda às questões a seguir.
a) Qual das expressões é um monômio?
Resposta: .
b) Qual é o grau desse monômio?
Resposta: 1.
c) Qual é o valor numérico de cada uma das expressões para ?
Resposta: Para , temos:
Sendo assim, a medida de área é igual a 156 unidades de medida de área.
Sendo assim, o perímetro tem 50 unidades de medida de comprimento.
12. a) Diofanto empregava as letras com abreviação.
b) Em geral, os gregos representavam as quantidades por meio de linhas, determinadas por uma ou duas letras, e raciocinavam como em geometria.
c) Ele substituiu sistematicamente a álgebra numérica pela álgebra dos símbolos.
d) Resposta pessoal. Espera-se que os estudantes escrevam um texto argumentando, de maneira resumida, que o uso de letras e números é importante para simplificar a escrita.
13. a)
b)
c)
d)
e)
14. Adicionando as medidas dos comprimentos dos lados das figuras, temos:
figura A: , isto é, a medida do perímetro é igual a .
figura B:
, isto é, a medida do perímetro é igual a .
figura C:
, isto é, a medida do perímetro é igual a 18w.
15. Substituindo os por monômios, temos:
a)
b)
c)
d)
16. A. A medida da área total é dada por:
B. A medida da área total é dada por:
17. Sugestão de resposta:
a)
b)
c)
18. a)
b)
c)
d)
e)
f)
19. A. A medida da área é dada por:
B. A medida da área é dada por:
C. A medida da área é dada por:
20. Aplicando a propriedade de multiplicação de potências de mesma base, temos:
a)
Assim, , ou seja, .
b)
Assim, e .
c) e
Assim, e .
d) e .
Assim, e .
Página LXXXIV
21. Efetuando as operações indicadas, temos:
a)
b)
c)
d)
e)
f)
22. A medida da área do retângulo verde é igual a . A medida da área do retângulo laranja é igual a . Dividindo a primeira medida pela segunda temos:
Portanto, a medida da área do retângulo verde corresponde a 9 vezes a medida da área do retângulo laranja.
23. a)
Portanto, o monômio procurado é .
b)
Portanto, o monômio procurado é .
c)
Portanto, o monômio procurado é .
d)
Portanto, o monômio procurado é .
24. Se a medida da área do retângulo é e a medida do comprimento de um dos lados é , então a medida A é dada por , isto é, .
25. a)
Portanto, .
b)
Portanto, .
c)
Portanto, .
d)
Portanto, .
e)
Portanto, .
f)
Portanto, .
26. Como , então , isto é, .
Substituindo A em e , temos: e
Portanto, e .
Substituindo B e C em , obtemos , isto é, .
27. Grupo 1 (monômios): D, H e J; Grupo 2 (binômios): A, C, G e I; Grupo 3 (trinômios): B, E e F.
28. A. O grau do monômio é dado por e o grau do monômio é dado por . Logo, o polinômio tem grau 7.
B. O grau do monômio é dado por , o grau do monômio é dado por e o grau do monômio é igual a 2. Logo, o polinômio tem grau 8.
C. O grau do monômio é igual a 1 e o grau do monômio é igual a 2. Logo, o polinômio tem grau 2.
D. O grau do polinômio é 6, pois .
E. O grau do monômio é dado por , o grau do monômio é igual a 2 e o grau do monômio é igual a 1. Logo, o polinômio tem grau 7.
F. O grau do monômio é dado por , o grau de é igual a 2 e o grau do monômio é dado por . Logo, o polinômio tem grau 13.
G. O grau do monômio é dado por e o grau do monômio é igual a 2. Logo, o polinômio tem grau 4.
H. O grau do polinômio é 2, pois .
I. O grau do monômio é dado por e o grau do monômio é igual a 2. Logo o polinômio tem grau 4.
J. O grau do polinômio é 5, pois .
29. Substituindo os valores correspondentes de x e y em cada polinômio, temos:
A. ;
B.
.
30. Agrupando os termos semelhantes e efetuando as operações indicadas, temos:
a)
b)
c)
31. O polinômio na forma reduzida que representa a medida do perímetro da figura é dado por:
32. a) O polinômio que representa a quantidade total de pontos de Carlos é dado por , ou seja, .
b) Sugestão de resposta:
1ª possibilidade: , e , pois .
2ª possibilidade: , e , pois .
3ª possibilidade: , e , pois .
c) Resposta pessoal. Sugestão de resposta:
Considerando que Carlos fez 21 pontos em outra partida, atribua valores para x, y e z e determine 2 possibilidades diferentes de cestas que ele pode ter feito nessa partida.
Sugestão de resposta: , e ; , e .
33. a) O polinômio que representa a medida de área do pedaço de cartolina que sobrou é dado por , ou seja, .
b) Como todos os termos são de grau 2, esse polinômio tem grau 2 ou 2º grau.
Página LXXXV
Questão 4. A adição dos polinômios B e C é dada por:
Questão 5. O polinômio oposto ao obtido na questão 4 é .
Atividades
34. Substituindo as figuras pelos polinômios indicados, temos:
A. ;
B.
C.
D.
35. O polinômio procurado em cada item é o polinômio oposto. Assim:
a) , pois:
b) , pois:
c) , pois:
36. A. A medida do perímetro do retângulo I é dada por:
A medida do perímetro do retângulo II é dada por:
Assim, o polinômio na forma reduzida que representa a diferença entre os perímetros é dado por:
B. A medida do perímetro do retângulo I é dada por:
A medida do perímetro do retângulo II é dada por:
Assim, o polinômio na forma reduzida que representa a diferença entre os perímetros é dado por:
37. Calculando a medida do volume de cada paralelepípedo reto retângulo, temos:
A: ; B: ; C: .
a) Medida do volume da pilha 1:
Medida do volume da pilha 2:
Medida do volume da pilha 3:
b) Substituindo x e y pelos valores indicados, temos:
pilha 1: , ou seja, .
pilha 2: , ou seja, .
pilha 3: , ou seja, .
38. Resposta pessoal. Sugestão de resposta:

Escreva um polinômio que represente a medida do perímetro desse retângulo. Em seguida, considerando , calcule a medida do perímetro do retângulo.
Resposta: ; .
39. A medida do paralelepípedo reto retângulo é dada por:
40. Considerando , temos:
Sendo assim, .
41. a)
b)
c)
d)
e)
f)
42. A. Medida do comprimento:
Medida da largura:
Medida de área:
B. Medida do comprimento:
Medida da largura:
Página LXXXVI
Medida da área:
43. a)
b)
c)
d)
44. a)
b)
c)
d)
45. Considerando as linhas tracejadas e as medidas de comprimento dos lados de cada parte, indicadas na figura, temos:
Assim, obtemos o polinômio A.
Assim, obtemos o polinômio C.
Assim, obtemos o polinômio D.
Portanto, o único polinômio que não pode representar a medida de área dessa figura é o polinômio B.
Questão 6. Sugestão de resposta:
Questão 7. A resposta depende do polinômio e do monômio escritos. No caso da sugestão de resposta dada, o grau do polinômio é 2 e o grau do monômio é 1.
Atividades
46. a)
b)
c)
d)
47. a)
b)
c)
48. A. A medida de comprimento do outro lado é dada por , ou seja, .
B. A medida de comprimento do outro lado é dada por , ou seja, .
49. a)
b)
c)
d)
50. a) A medida da altura do paralelepípedo 1 é dada por: , ou seja, .
b) A medida do volume do paralelepípedo 2 é dada por: , ou seja, .
Como , temos:
Portanto, o volume desse paralelepípedo mede .
51. a)
b) Como , então:
c) Como e , então:
d) Como , então:
.
e) Como e , então:
f) Como e , então:
52. a) Como , então .
b) Como , então .
c) Como , então e .
d) Como , então , e .
53. B e C estão relacionados com 1, pois .
D e F estão relacionados com 2, pois .
A e E estão relacionados com 3, pois .
54. Como as expressões algébricas de A e E não têm variáveis no denominador, apenas B, C, D e F são frações algébricas.
55. a) A medida de tempo que a máquina B demora para produzir a mesma quantidade de peças da máquina A é representada por . Assim, a fração algébrica que representa a produção da máquina B em é igual a , com .
b) A quantidade de peças que a máquina A produz por minuto é dada por , isto é, 23 peças. A quantidade de peças que a máquina B produz por minuto é dada por , isto é, 20 peças.
56. a) , com .
b) , com .
c) , com .
d) , com .
Página LXXXVII
e) , com .
f) , com .
57. , com .
58. Resposta pessoal. Sugestão de resposta:
, com .
Valor numérico para e :
, com .
Valor numérico para e :
, com .
Valor numérico para e :
59. O quadrado de um número x:
O triplo de um número x:
O quadrado de um número x:
Desse modo, a diferença é igual a e a divisão é dada por , com .
60. a) , com .
b)
c) , com .
d) Antes de 3 funcionários desistirem: , ou seja, R$ 45,00.
Depois das desistências: , ou seja, R$ 50,00.
O que eu estudei?
1. a)
b)
c)
2. Pela figura, temos:
Assim, e .
Logo, o ponto que melhor representa o valor de é T.
Portanto, a alternativa c está correta.
3. a) .
b) .
4. a)
b) Calculando o valor numérico para , temos:
Portanto, esse cliente gastou R$ 103,90.
5. a) Se a funcionária vender R$ 20.000,00, teremos:
Portanto, seu salário será R$ 1.855,00.
Para a venda de R$ 30.000,00, teremos:
Portanto, seu salário será R$ 2.155,00.
b) ou .
6. a) A quantidade de livros de Eduarda é representada pela expressão . A quantidade de livros de Bruno é representada pela expressão .
b) A quantidade de livros de Larissa é representada pela expressão . A quantidade de livros de Eduarda é representada pela expressão .
c) Como Eduarda tem 6 livros a mais do que Larissa, Larissa tem 8 livros, pois . Além disso, Bruno tem 42 livros, pois .
7. A Figura 1 é formada com 4 canudos, isto é, canudos. A Figura 2 é formada com 7 canudos, isto é, canudos. A Figura 3 é formada com 10 canudos, isto é, . Logo, a quantidade de canudos em função da quantidade de quadrados é dada por . Portanto, a alternativa b está correta.
8. A medida do volume do cubo é dada por:
9. a) A expressão não é um monômio, pois , que tem dois termos.
b) Sim, é possível expressar a medida do perímetro de um quadrado usando um monômio. Podemos expressar a medida do perímetro do quadrado por , pois .
10. a)
A expressão é um monômio.
b)
A expressão é um binômio.
c)
A expressão é um trinômio.
11. Para e , temos:
Para e , temos:
Portanto, o polinômio assume o maior valor numérico para e e esse valor é .
12. A medida da área dessa figura é dada por:
, ou seja, .
Para e , temos:
Portanto, a medida da área dessa figura é .
13. , com .
Página LXXXVIII
Unidade 8
Equações e sistemas de equações
Questão 1.
A. Indicando por a medida da massa da lata vermelha e sabendo que , a equação que possibilita determinar a medida da massa da lata vermelha é ou, ainda, .
Resolvendo essa equação, temos:
Portanto, a lata vermelha tem de medida de massa.
B. Indicando por a medida da massa da lata azul, a equação que possibilita determinar essa medida é
ou, ainda, .
Resolvendo essa equação, temos:
Portanto, a lata azul tem de medida de massa.
Atividades
1. Sendo o preço do vestido, como Júlia comprou o vestido por reais e a saia por R$ 60,00, e sabendo que o total da compra foi R$ 149,95, a equação que permite obter o preço do vestido é dada por .
Logo, a alternativa correta é a c.
2. Efetuando os cálculos, temos:
Logo, o preço do vestido é R$ 89,95.
3. Efetuando os cálculos, temos:
a)
b)
c)
d)
e)
f)
g)
h)
Página LXXXIX
4. a) Considere x o número em que Bruna pensou. Multiplicando esse número por 3 e adicionando 12, Bruna obteve 36. Assim, a equação que permite obter o número em que Bruna pensou é
Portanto, a alternativa correta é a IV.
b) Resolvendo a equação, temos:
Portanto, Bruna pensou no número 8.
5. Situação A:
Considere o número em que Letícia pensou. Ao multiplicar esse número por 5 e adicionar 17 ao produto obtido, Letícia obteve 82 como resultado. Logo, a equação que possibilita determinar o número em que Letícia pensou é .
Portanto, a situação A está associada à equação 2.
Situação B:
Considere a idade de Tiago. Como o triplo da idade de Tiago equivale a 78, a equação que possibilita determinar a idade de Tiago é .
Portanto, a situação B está associada à equação 1.
Situação C:
Indicando a quantia em reais desconhecia por e subtraindo R$ 63,00 de , que é o dobro de , obtemos como resultado R$ 153,00. Assim, a equação que possibilita determinar a quantia de dinheiro é .
Portanto, a situação C está associada à equação 3.
6. Resolvendo a equação correspondente a cada situação, temos:
1.
Portanto, Letícia pensou no número 13.
2.
Portanto, Tiago tem 26 anos.
3.
Portanto, a quantia de dinheiro que eu tenho é R$ 108,00.
7. a) Indicando por a medida da largura do jardim de Geraldo, a medida do comprimento será igual a . O perímetro do jardim mede e, considerando o formato retangular, as medidas de seus lados opostos são iguais. Assim, podemos calcular a medida da largura e do comprimento do jardim de Geraldo resolvendo a equação .
Portanto, a largura do jardim de Geraldo mede e o comprimento mede , pois .
b) A medida da área de um retângulo é dada pelo produto das medidas dos lados adjacentes. Assim, a medida da área do Jardim de Geraldo equivale a , pois .
8. Seja a medida da altura que uma sequoia pode atingir. Sabemos que o dobro dessa medida adicionado a é igual a . Então, a equação que possibilita determinar a medida da altura que a sequoia pode atingir é .
Resolvendo essa equação, temos:
Portanto, essa árvore pode atingir uma altura de .
9. a) Indicando por x o valor da conta, a equação que fornece esse valor é .
Resolvendo essa equação, temos:
Portanto, o valor da conta é R$ 28,00.
b) Indicando por x a quantia recebida, a equação que fornece esse valor é .
Resolvendo essa equação, temos:
Portanto, a quantia que recebi foi R$ 63,00.
c) Indicando por x a idade de André, a equação que fornece a idade é dada por .
Página XC
Resolvendo essa equação, temos:
Portanto, André tem 30 anos.
d) Indicando por x o número pensado, a equação que fornece o número em que pensei é dada por .
Resolvendo essa equação, temos:
Portanto, o número pensado foi 14.
10. Efetuando os cálculos, temos:
a)
Como , a solução dessa equação é .
b)
Como , a solução dessa equação é .
c)
Como devemos ter , essa equação não tem solução.
d)
Como e , a solução da equação é .
e)
Como e , a solução da equação é .
f)
Como , a solução da equação é .
Página XCI
11. A. Indicando por x a quantidade de horas, a equação que possibilita determinar a medida de tempo gasto para percorrer é .
Resolvendo essa equação, temos:
Portanto, o automóvel percorreu em 2 horas.
B. Considere x a quantidade de funcionários antes da contratação. Sendo assim, a equação que possibilita determinar a quantidade de funcionários antes da contratação é dada por .
Resolvendo essa equação, temos:
Portanto, antes da contratação, trabalhavam 75 funcionários e, depois da contratação, passaram a trabalhar 105 funcionários, pois .
12. O preço de cada caderno é dado por e o preço de cada livro é dado por . Como o preço do livro é o dobro do preço do caderno, a equação que possibilita determinar a quantidade de cadernos comprados por Marta é ou, ainda, .
Resolvendo essa equação, temos:
Portanto, Marta comprou 8 cadernos e 6 livros, pois .
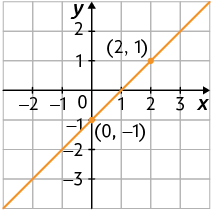
Questão 2. Em cada equação, vamos atribuir a x dois valores distintos para determinar os respectivos valores de y e formar os pares ordenados que são soluções das equações.
a) Para , temos , ou seja, ;
Para , temos , ou seja, .
Indicando os pares ordenados e no plano cartesiano e traçando a reta que passa por esses pontos, temos a representação geométrica da equação.
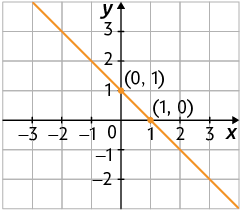
b) Para , temos , ou seja, ;
Para , temos , ou seja, .
Marcando os pares ordenados e no plano cartesiano e traçando a reta que passa por esses pontos, temos a representação geométrica da equação.
Atividades
13. As equações B, D, F, I, J e L são do 1º grau com duas incógnitas, pois podem ser escritas na forma , onde e são incógnitas e , e são números reais com e diferentes de zero (embora algumas delas tenham incógnitas diferentes, elas têm essa mesma forma).
Página XCII
As equações A, C, E, G, H e K não são do 1º grau com duas incógnitas, pois cada uma delas tem somente uma incógnita.
14. a) Considere x a minha idade e y a idade do meu filho. Como o dobro da minha idade é igual a e o triplo da idade do meu filho é igual , adicionando esses dois produtos, obteremos 84 anos de resultado. Sendo assim, a equação que representa essa situação é .
b) Considere o preço do salgado e o preço do suco. Como o valor pago em 2 salgados e 1 suco foi R$ 6,50, a equação que representa essa situação é dada por .
c) Considere o preço do par de tênis e o preço do par de sapatos. A diferença entre os preços do par de tênis e do par de sapatos é R$ 48,00. Sendo assim, a equação que representa essa situação é dada por .
d) Considere o preço do quilo do tomate e o preço do quilo da batata. O valor da compra de de tomate e de batata foi R$ 16,53. Sendo assim, a equação que representa essa situação é dada por .
15. Sejam e os números que Mariana pensou. Como a diferença entre esses números é igual a 12, a equação que relaciona esses dois números é . Além disso, um desses números está entre 20 e 23. Considerando x entre 20 e 23, temos as seguintes verificações.
Se , então . Assim, .
Se , então . Assim, .
Agora considerando y entre 20 e 23:
Se , então . Assim, .
Se , então . Assim, .
Portanto, os pares de números que Mariana pode ter pensado são , , e .
16. Para determinar a representação geométrica da equação , devemos primeiro verificar quais pares ordenados são soluções da equação.
Escolhendo o par ordenado da representação geométrica do item A, temos . Logo, não é solução da equação e A não pode ser a representação geométrica da equação.
Escolhendo o par ordenado da representação geométrica do item B, temos . Logo, é solução da equação. Além disso, os pares ordenados e também satisfazem a equação. Vejamos:
e
Portanto, o item B é a representação geométrica da equação.
Escolhendo o par ordenado do item C, temos . Logo, não é solução da equação e o item C não pode ser a representação geométrica da equação.
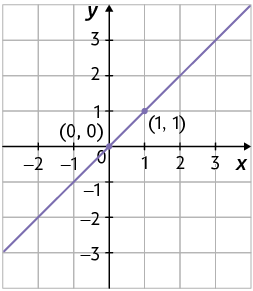
17. Para representar geometricamente as equações, devemos determinar inicialmente dois ou mais pares ordenados distintos que são soluções das equações. Depois, traçamos a reta que passa por eles.
a) Para , temos . Assim, ;
Para , temos . Assim, .
Logo, e são soluções da equação .
Com isso, podemos construir a seguinte representação geométrica dessa equação.
b) Para , temos . Assim, ;
Para , temos . Assim, .
Logo, e são soluções da equação .
Com isso, podemos construir a seguinte representação geométrica dessa equação.
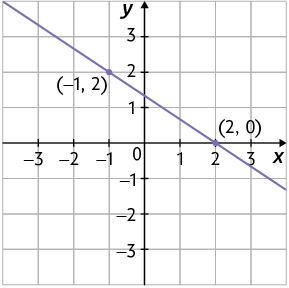
c) Para , temos . Assim, ;
Para , temos . Assim, .
Logo, e são soluções da equação .
Com isso, podemos construir a seguinte representação geométrica dessa equação.
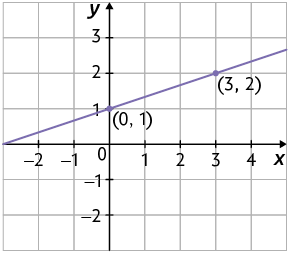
d) Para , temos . Assim, ;
Para , temos . Assim, .
Logo, e são soluções da equação .
Página XCIII
Com isso, podemos construir a seguinte representação geométrica dessa equação.
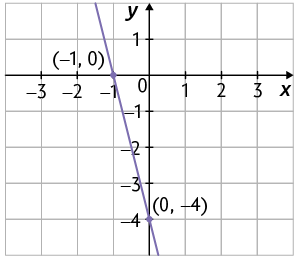
18. a) Considere x a quantidade de bolinhas vermelhas e y a quantidade de bolinhas amarelas colocadas na caixa. De acordo com as informações, na caixa há 12 bolinhas, ou seja, . Como há 2 bolinhas vermelhas a mais do que amarelas, temos ou, ainda, . Logo, o sistema de equações que representa essa situação é:
b) Como o total de doces em 2 embalagens do tipo x e em 3 embalagens do tipo y é igual a 19, escrevemos a equação . Além disso, como o total de doces em 3 embalagens do tipo x e em 2 embalagens do tipo y é igual a 21, escrevemos a equação . Logo, o sistema de equações que representa essa situação é:
c) Considere x a quantidade de meninas e y a quantidade de meninos. Como o total de estudantes é igual a 31, temos a equação . Como há 5 meninas a mais do que meninos, temos a equação ou, ainda, . Logo, o sistema de equações que representa essa situação é:
19. a) Substituindo x por y em , temos:
Substituindo por na equação , obtemos .
Portanto a solução do sistema é .
b) Isolando y em , temos:
Substituindo y por em , obtemos:
Por fim, substituindo x por 3 na equação , obtemos .
Portanto, a solução do sistema é .
c) Isolando x em , temos:
Substituindo x por em , temos:
Por fim, substituindo y por na equação , obtemos .
Portanto, a solução do sistema é .
d) Isolando y em , temos:
Substituindo y por em , obtemos:
Por fim, substituindo x na equação , temos .
Portanto, a solução do sistema é .
e) Isolando x em , temos:
Substituindo x por em , obtemos:
Página XCIV
Por fim, substituindo y por 3 na equação , temos .
Portanto, a solução do sistema é .
f) Isolando x em , temos:
Substituindo x por em , temos:
Por fim, substituindo y por 5 na equação , temos .
Portanto, a solução do sistema é .
20. Considere x e y as quantias, em reais, que Marcos e Otávio receberam, respectivamente. Como, ao todo, eles receberam R$ 980,00, escrevemos , e, como Marcos recebeu R$ 228,00 a menos que Otávio, escrevemos . Logo, temos o seguinte sistema.
Substituindo x por em , temos:
Por fim, substituindo y por 604 em , obtemos:
Portanto, Marcos recebeu R$ 376,00 e Otávio recebeu R$ 604,00.
21. Considere x a quantidade de homens e y a quantidade de mulheres que participaram dos jogos olímpicos de 2020. Ao todo, 302 atletas brasileiros participaram dos jogos olímpicos. Sendo assim, escrevemos . Nessa edição dos jogos olímpicos, a quantidade de homens participantes foi maior do que a de mulheres, com uma diferença de 22 atletas. Então, escrevemos . Desse modo, temos o seguinte sistema.
Isolando o x em , temos:
Substituindo x por em , obtemos:
Por fim, substituindo y por 140 na equação , temos:
Portanto, nos jogos olímpicos de 2020 participaram 162 homens e 140 mulheres.
22. a) Problema A:
Indicando por x e y as quantias, em reais, que Solange e Gabriel têm, respectivamente, verificamos que, juntos, eles têm R$ 776,00. Assim, . A quantia de dinheiro de Solange é o triplo da quantia de Gabriel, isto é, . Logo, podemos escrever o seguinte sistema.
Portanto, o problema A está relacionado ao sistema III.
Problema B:
Considere x e y as quantidades de figurinhas que Marcos e Renata têm, respectivamente. Como o dobro da quantidade de figurinhas de Marcos adicionado ao quíntuplo de figurinhas de Renata é igual a 125 figurinhas, temos . Além disso, como a diferença entre as quantidades de figurinhas que eles têm é igual a 10 figurinhas, escrevemos . Sendo assim, podemos escrever o seguinte sistema.
Portanto, o problema B está relacionado ao sistema I.
Problema C:
Considere x e y a quantidade de carros e de motos no estacionamento, respectivamente. Como o total de veículos nesse estacionamento é 250 veículos, escrevemos . Além disso, o dobro da quantidade de carros é igual ao triplo da quantidade de carros, ou seja, . Sendo assim, escrevemos o seguinte sistema.
Portanto, o problema C está relacionado ao sistema II.
Página XCV
Problema D:
Considere x e y as idades de Carlos e de Lúcia, respectivamente. Ao adicionarmos a idade de Carlos com o dobro da idade de Lúcia, obtemos 125 anos, ou seja, . Como Lúcia tem o dobro da idade de Carlos, escrevemos . Logo, temos o seguinte sistema.
Portanto, o problema D está relacionado ao sistema IV.
b) Vamos analisar cada problema e resolver o sistema relacionado a ele.
Problema A:
Sendo , vamos inicialmente substituir x por na equação .
Substituindo y por 194 na 2ª equação, temos:
Portanto, Solange tem R$ 582,00 e Gabriel tem R$ 194,00.
Problema B:
Isolando x na equação , temos:
Substituindo x por em , temos:
Substituindo y por 15 na equação , temos:
Portanto, Marcos tem 25 figurinhas e Renata tem 15 figurinhas.
Problema C:
Isolando x em , temos:
Substituindo x por em , temos:
Substituindo y por 100 na equação , temos:
Portanto, no estacionamento há 150 carros e 100 motos.
Problema D:
Sendo , vamos inicialmente substituir y por na equação .
Substituindo x por 25 na equação , temos:
Portanto, Carlos tem 25 anos de idade e Lúcia tem 50 anos de idade.
23. Considere x e y as quantidades de meninos e meninas nessa escola, respectivamente. Como há 2.500 estudantes nessa escola, escrevemos . Além disso, o triplo da quantidade de meninos é igual ao dobro da quantidade de meninas, ou seja, . Sendo assim, temos o seguinte sistema.
Isolando o x em , temos:
Substituindo x por em , obtemos:
Por fim, substituindo y por 1.500 na equação , temos:
Portanto, nessa escola há 1.000 meninos e 1.500 meninas.
24. Indicamos por x e y as idades de Marcela e Augusto, respectivamente. A diferença entre as idades de Marcela e de Augusto é igual a 28 anos, ou seja, . Além disso, há 6 anos, a idade de Marcela era o triplo da idade de Augusto, ou seja, . Simplificando essa última equação, obtemos:
Página XCVI
Assim, podemos escrever o seguinte sistema.
Isolando x em , temos:
Substituindo x por em , obtemos:
Por fim, substituindo y por 20 na equação , temos:
Portanto, Marcela tem 48 anos de idade e Augusto tem 20 anos de idade.
25. Como 4 embalagens do tipo x e 2 do tipo y contêm, juntas, , segue que . Além disso, 1 embalagem do tipo x e 6 do tipo y contêm, juntas, , ou seja, . Sendo assim, temos o sistema:
Isolando o x em , temos:
Substituindo x por em , temos:
Por fim, substituindo y por 1.200 na equação , temos:
Portanto, a medida da capacidade da embalagem x é e a da embalagem y é .
26. Considere x a quantidade de pessoas que pagaram a entrada inteira e y a quantidade de pessoas que pagaram meia-entrada. O total arrecadado com as vendas das entradas nessa sessão de cinema foi R$ 2.720,00, ou seja, . Com as entradas inteiras, arrecadou-se R$ 800,00 a mais do que o triplo do valor arrecadado com a venda das meias-entradas, isto é, ou, ainda, . Com isso, escrevemos o sistema a seguir.
Isolando na primeira equação, temos:
Substituindo y por em , temos:
Por fim, substituindo x por 140 em , obtemos:
Logo, 140 pessoas compraram a entrada inteira e 60 pessoas compraram a meia-entrada. Portanto, 200 pessoas pagaram para ver essa sessão, pois .
27. Considere a a medida da distância entre Londrina e Astorga e b a medida da distância entre Astorga e Maringá.
a) A medida da distância total que Adriana percorreu de Londrina até Maringá passando por Astorga foi . Essa medida de distância tem a mais do que a medida da distância de Londrina a Maringá sem passar por Astorga. Logo, a medida da distância entre Londrina e Maringá é , pois .
Página XCVII
b) A medida da distância entre Londrina e Maringá passando por Astorga é , ou seja, . Como a medida da distância entre Londrina e Astorga mede a menos do que a medida da distância entre Astorga e Maringá, segue que . Logo, temos o sistema a seguir.
Como , substituímos a na equação .
Agora, substituindo b por 90,4 em , temos:
Portanto, a medida da distância entre Londrina e Astorga é e a medida da distância entre Astorga e Maringá é .
28. Considere x e y os preços unitários da bola de futebol e da bola de voleibol, respectivamente. Com R$ 120,00, sem receber troco, é possível comprar 4 bolas de futebol e 1 bola de voleibol ou 2 bolas de futebol e 2 bolas de voleibol. Assim, temos as equações e . Essas equações formam o seguinte sistema.
Isolando o y em , temos:
Substituindo y por em , temos:
Substituindo x por 20 na equação , temos:
Portanto, cada bola de futebol custa R$ 20,00 e cada bola de voleibol custa R$ 40,00.
Questão 3. Na 1ª equação, temos o termo e, na 2ª equação, temos , que não são opostos. Desse modo, vamos multiplicar a 1ª equação por e a 2ª equação por 3, obtendo, assim, equações equivalentes com os termos opostos e .
Usando o método da adição, temos:
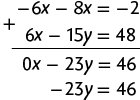
Calculando o valor de y usando a última equação obtida, temos:
Substituindo y por na equação , obtemos:
Portanto, a solução do sistema é .
Atividades
29. a) Na 1ª equação, temos o termo x e, na 2ª equação, o termo , que são opostos. Podemos, então, aplicar o método da adição.
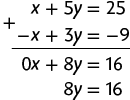
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por 2 na equação , temos:
Portanto, a solução do sistema é e .
b) Na 1ª equação, temos o termo e, na 2ª equação, temos , que são opostos. Podemos, então, aplicar o método da adição.
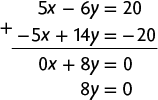
Página XCVIII
Em seguida, calculamos o valor de y usando a última equação.
Substituindo y por 0 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
c) Na 1ª equação, temos o termo e, na 2ª equação, temos , que são termos opostos. Podemos, então, aplicar o método da adição.

Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 1 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
d) Na 1ª equação, temos o termo e, na 2ª equação, temos , que são opostos. Podemos, então, aplicar o método da adição.
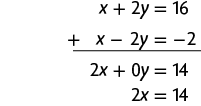
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 7 na 2ª equação do sistema, temos:
Portanto, a solução da equação é e .
e) Na 1ª equação, temos o termo e, na 2ª equação, temos , que são opostos. Podemos, então, aplicar o método da adição.
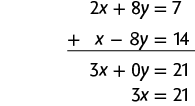
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 7 na 2ª equação do sistema, temos:
Portanto, a solução da equação é e .
f) Na 1ª equação, temos o termo e, na 2ª equação, temos , que são opostos. Podemos, então, aplicar o método da adição.
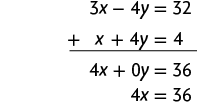
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 9 na 2ª equação do sistema, temos:
Página XCIX
Portanto, a solução da equação é e .
30. Vamos indicar os dois números por x e y. De acordo com o enunciado, temos . Como o único número primo par é o número 2, escrevemos . Desse modo, temos o sistema:
Na 1ª equação do sistema, temos o termo y e, na 2ª equação do sistema, temos , que são opostos. Podemos, então, aplicar o método da adição.
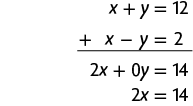
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 7 na 1ª equação do sistema, temos:
Portanto, os números são 5 e 7.
31. Vamos indicar as idades de Júlia e André por x e y, respectivamente. A soma das idades de Júlia e André é igual a 34 anos, ou seja, . Sabendo que André é mais novo e que a diferença entre as idades deles é igual a 8 anos, escrevemos . Assim, temos o sistema:
Na 1ª equação do sistema, temos o termo y e, na 2ª equação do sistema, temos o termo , que são opostos. Podemos, então, aplicar o método da adição.
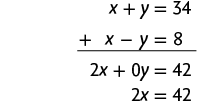
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 21 na 1ª equação do sistema, temos:
Portanto, Júlia tem 21 anos e André tem 13 anos.
32. Nessa excursão, há um total de 130 pessoas. Assim, . Como a diferença entre a quantidade de homens e a de mulheres na excursão é igual a 12 pessoas, segue que . Com isso, temos o sistema a seguir.
Na 1ª equação do sistema, temos o termo y e, na 2ª equação do sistema, temos , que são opostos. Podemos, então, aplicar o método da adição.
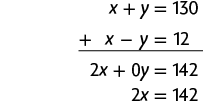
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 71 na 1ª equação do sistema, temos:
Portanto, participaram dessa excursão 71 homens e 59 mulheres.
33. Vamos indicar a medida da massa de Rafael por x e a medida da massa de Fábio por y. A diferença entre o dobro da medida da massa de Rafael e a medida da massa de Fábio é igual a , o que nos dá . Além disso, o dobro da medida da massa de Rafael adicionado à medida da massa de Fábio é igual a , isto é, . Com isso, temos o sistema a seguir.
Página C
Na 1ª equação do sistema, temos o termo e, na 2ª equação do sistema, temos o termo y, que são opostos. Podemos, então, aplicar o método da adição.
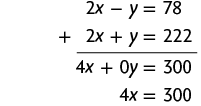
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 75 na 2ª equação do sistema, temos:
Portanto, a medida da massa de Rafael é e a medida da massa de Fábio é .
34. Resposta pessoal. Sugestão de resposta:
Em uma feira, Juliana pagou por de tomate e de cebola o total de R$ 13,00. Se tivesse comprado de tomate e de cebola, ela teria pago um total de R$ 24,00. Qual é o preço dos quilogramas do tomate e da cebola?
Resposta: O quilograma do tomate custa R$ 7,00 e o da cebola custa R$ 3,00.
35. Para resolver os itens desta atividade, vamos usar o fato de que a soma das medidas dos ângulos internos de um triângulo é igual a .
a) De acordo com as informações e a imagem, temos e . Sendo assim:
Desse modo, podemos escrever o sistema a seguir.
Na 1ª equação do sistema, temos o termo e, na 2ª equação do sistema, temos y, que são opostos. Adicionando as duas equações, temos:
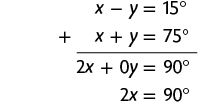
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por na 2ª equação do sistema, temos:
Portanto, e .
b) De acordo com as informações e a imagem, temos ou seja, , e . Sendo assim:
Na 1ª equação do sistema, temos o termo e, na 2ª equação do sistema, temos o termo y, que são opostos. Podemos, então, aplicar o método da adição.
Adicionando as duas equações, temos:
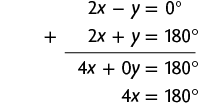
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por na 2ª equação do sistema, temos:
Portanto, e .
c) De acordo com as informações e a imagem, temos e . Sendo assim:
Desse modo, temos o sistema:
As equações desse sistema não têm termos opostos. Multiplicando a 2ª equação por , obtemos uma equação equivalente com o termo , que é oposto ao termo x da 1ª equação. Com isso, escrevemos o sistema a seguir.
Página CI
Adicionando as duas equações, temos:
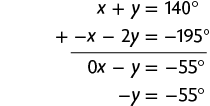
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por na 2ª equação do sistema, temos:
Portanto, e .
d) De acordo com as informações e a imagem, temos e . Sendo assim:
Desse modo, temos o sistema:
Na 1ª equação do sistema, temos o termo e, na 2ª equação do sistema, temos o termo y, que são opostos. Adicionando as duas equações, temos:
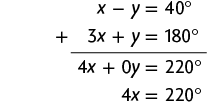
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por na 2ª equação do sistema, temos:
Portanto, e .
36. a) Multiplicando a 2ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
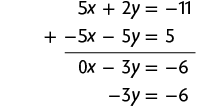
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por 2 na 2ª equação do sistema, temos:
Portanto, a solução do sistema é e .
b) Multiplicando a 1ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
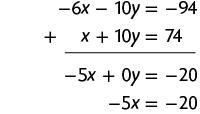
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 4 na 2ª equação do sistema, temos:
Portanto, a solução do sistema é e .
c) Multiplicando a 1ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
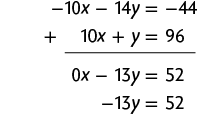
Em seguida, calculamos o valor de y usando a última equação obtida.
Página CII
Substituindo y por na 2ª equação do sistema, temos:
Portanto, a solução do sistema é e .
d) Multiplicando a 1ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
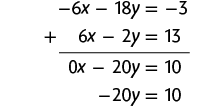
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo y por na 2ª equação do sistema, temos:
Portanto, a solução do sistema é e .
e) Multiplicando a 1ª equação por 3 e a 2ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
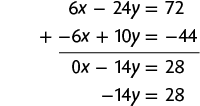
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
f) Multiplicando a 2ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
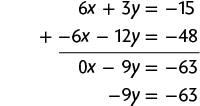
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por 7 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
g) Multiplicando a 1ª equação por 3 e a 2ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
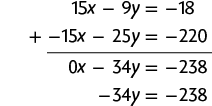
Em seguida, calculamos o valor de y usando a última equação obtida.
Página CIII
Substituindo y por 7 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
h) Multiplicando a 1ª equação por 7 e a 2ª equação por , obtemos o sistema a seguir.
Adicionando as duas equações, temos:
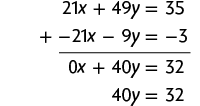
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
37. Considere o preço do coco verde e o preço do pastel. De acordo com a quantidade de cocos e pastéis comprados em cada barraca e o preço pago, temos as equações e . Desse modo, montamos o sistema a seguir.
Multiplicando a 1ª equação por 3 e a 2ª equação por , obtemos:
Adicionando as duas equações, temos:
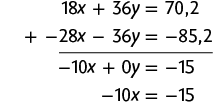
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por na 1ª equação do sistema, temos:
Portanto, cada coco verde custa R$ 1,20 e cada pastel custa R$ 1,50. Juntos, um coco verde e um pastel custam R$ 2,70. Portanto, a alternativa correta é a d.
38. Vamos indicar a medida do lado maior do cartão por a e a medida do lado menor do cartão por b. Juntando os 8 cartões pelos lados menores, Juliana obtém um retângulo com 376 cm de medida de perímetro, o que nos fornece a equação . Além disso, juntando os 8 cartões pelos lados maiores, Juliana obtém um retângulo que tem de medida de perímetro, o que nos fornece a equação . Desse modo, temos o sistema a seguir.
Multiplicando a 2ª equação por , obtemos:
Adicionando as duas equações, temos:
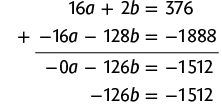
Em seguida, calculamos o valor de b usando a última equação obtida.
Página CIV
Substituindo b por 12 na 1ª equação do sistema, temos:
Logo, os lados do cartão medem e .
Como a área de um retângulo é igual ao produto das medidas de seus lados adjacentes, verificamos que a área do cartão mede , pois .
Portanto, a alternativa correta é a d.
Questão 4. Usando o método da substituição para resolver esse sistema, vamos primeiro isolar o x na 2ª equação.
Substituindo x por na 1ª equação, temos:
Por fim, substituindo y por 3 na equação , temos .
Portanto, é a solução do sistema.
Atividades
39. Em cada item, vamos primeiro determinar dois pares ordenados que são soluções de cada equação do sistema. Com eles, devemos traçar as retas que representam geometricamente as equações desse sistema, em um mesmo plano.
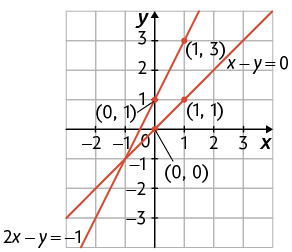
a) Considere a 1ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Considere agora a 2ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Portanto, temos a seguinte representação geométrica do sistema.
b) Considere a 1ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Considere agora a 2ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Portanto, temos a seguinte representação geométrica do sistema.
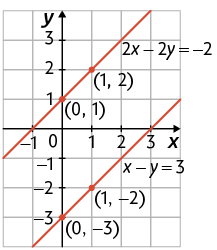
c) Considere a 1ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Considere agora a 2ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Portanto, temos a seguinte representação geométrica do sistema.
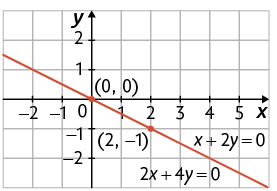
d) Considere a 1ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Considere agora a 2ª equação . Se , temos ; se , temos . Assim, e são soluções dessa equação.
Portanto, temos a seguinte representação geométrica do sistema.
Página CV
40. a) O sistema é possível e determinado, pois as retas que representam geometricamente esse sistema são concorrentes, ou seja, elas se cruzam em um único ponto.
b) Usando o método da substituição, vamos isolar x na 1ª equação.
Substituindo x por na 2ª equação, temos:
Por fim, substituindo y por 0 na equação , temos . Portanto, a solução do sistema é .
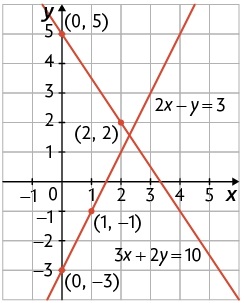
41. Na imagem, temos a representação geométrica de duas retas concorrentes que se cruzam no par ordenado . Assim, entre os sistemas a seguir, vamos procurar aquele que é possível e determinado e cuja solução seja o par ordenado .
No sistema do item a, a 2ª equação é igual à 1ª equação multiplicada por 3. Então, as retas que representam geometricamente esse sistema são coincidentes, ou seja, o sistema é possível e indeterminado.
No item b, verificamos que o par ordenado não é solução da 1ª equação, pois .
Já nas equações do sistema do item c, verificamos que e , ou seja, é solução desse sistema. Além disso, nesse sistema, os termos de uma equação não são múltiplos da outra. Consequentemente, esse sistema é possível e determinado.
O sistema do item d é um sistema impossível, pois, multiplicando a 1ª equação por , teremos um sistema com as equações e . Nesse caso, é impossível para quaisquer números x e y que a diferença entre dois números seja, ao mesmo tempo, 2 e 3.
Portanto, está representado geometricamente na imagem o sistema da alternativa c.
42. a) Falsa, pois um sistema com essa representação geométrica é impossível. Sugestão de correção:
As retas que representam um sistema possível e determinado são concorrentes.
b) Verdadeiro, pois como são retas coincidentes, o sistema terá uma solução para cada valor atribuído a x ou a y.
c) Verdadeiro, pois nesse caso sua representação geométrica será dada por duas retas concorrentes, que tenham um único par ordenado em comum.
43. a) Vamos indicar por x e y as idades de Artur e Isadora, respectivamente. Como Artur é 8 anos mais velho do que Isadora, temos ou, ainda, . Além disso, como a soma de suas idades é igual a 26 anos, temos . Logo, o sistema que possibilita determinar a idade de cada um dos irmãos é:
b) Na equação , se , temos ; se , temos . Na equação , se , temos ; se , temos .
Assim, a representação geométrica do sistema é:
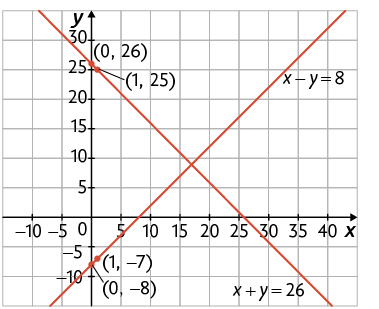
Nessa representação geométrica, as retas são concorrentes.
c) Vamos resolver o sistema usando o método da adição. Adicionando as duas equações, temos:
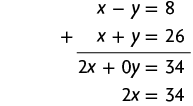
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 17 na 1ª equação do sistema, temos:
Portanto, Artur tem 17 anos e Isadora tem 9 anos.
Página CVI
44. Resposta pessoal. Sugestão de resposta:
No GeoGebra, fazemos:
1º. Clique com o botão direito sobre a Janela de visualização, habilite a opção Mostrar Eixos e, na aba Malha, escolha a opção Malha principal.
2º. Represente graficamente cada equação digitando-a no campo Entrada... e pressionando Enter, uma por vez, nesse caso, e .
3º. Selecione a ferramenta Interseção de Dois Objetos e clique nas duas retas para verificar se elas são concorrentes, coincidentes ou paralelas.
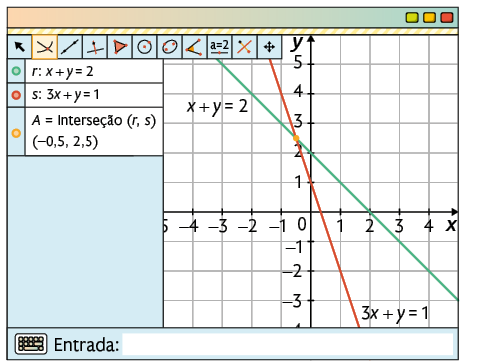
Portanto, as retas são concorrentes.
45. Resposta pessoal. Sugestão de resposta:
Em uma partida de futebol, a quantidade de gols marcados pelo time A adicionada ao dobro da quantidade de gols marcados pelo time B é igual a 2. Além disso, a diferença entre o óctuplo da quantidade de gols marcados pelo time A e o quádruplo da quantidade de gols marcados pelo time B é igual a . Quantos gols cada um desses times marcou?
Resposta: A solução desse sistema é .
Questão 5. Efetuando os cálculos, temos:
a)
b)
c)
d)
Atividades
46. a) A equação é do 2º grau do tipo , com e .
b) A equação não é do 2º grau do tipo , pois não tem o termo .
c) A equação não é do 2º grau do tipo , pois tem o termo .
d) A equação é do 2º grau do tipo , com e .
e) A equação não é do 2º grau do tipo , pois não tem o termo .
f) A equação é do 2º grau do tipo , com e .
g) A equação não é do 2º grau do tipo , pois não tem o termo .
h) A equação não é do 2º grau do tipo , pois tem o termo .
i) A equação é do 2º grau do tipo , com e .
j) A equação não é do 2º grau do tipo , pois tem o termo .
k) A equação é do 2º grau do tipo , com e .
l ) A equação não é do 2º grau do tipo , pois não tem o termo com a parte literal .
47. a) Sendo x o número que precisamos determinar, como o quadrado desse número é igual a 9, temos a equação . Desse modo, ou , pois e .
b) Sendo x o número que precisamos determinar, como o dobro do quadrado desse número é igual a 800, temos a equação . Dividindo os dois membros dessa equação por 2, obtemos . Como e , segue que ou .
c) Sendo x o número que precisamos determinar, como o triplo do quadrado desse número é igual a 1.875, temos a equação . Dividindo os dois membros dessa equação por 3, obtemos . Como e , segue que ou .
d) Sendo x o número que precisamos determinar, como o dobro do quadrado desse número é igual a 392, temos a equação . Dividindo os dois membros dessa equação por 2, obtemos . Como e , segue que ou .
e) Sendo x o número que precisamos determinar, como o triplo do quadrado desse número é igual 3.675, temos a equação . Dividindo os dois membros dessa equação por 3, obtemos . Como e , segue que ou .
48. A área de um quadrado é dada por , sendo x a medida de comprimento do lado do quadrado.
a) Como o comprimento do lado desse quadrado mede e , a área desse quadrado mede .
b) Como o comprimento do lado desse quadrado mede e , a área desse quadrado mede .
49. a) Indicando por x a medida do comprimento do lado de cada placa de vidro, a medida da área de cada placa será representada por . Como Roberto comprou 40 placas e a área total mede , a equação que representa essa situação é .
b) Para resolver esse problema no GeoGebra,, digite, no campo Entrada... da Janela Álgebra, a equação .
Página CVII
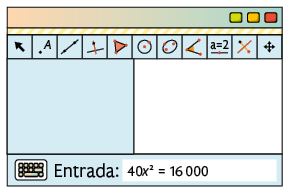
A equação ficará armazenada na Janela Álgebra, conforme apresentado a seguir.
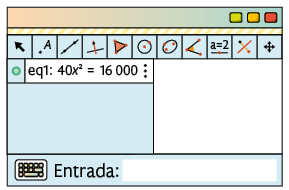
2º. Na linha correspondente a eq1, clique com o botão esquerdo do mouse em . Em seguida, selecione a opção Resolver.

Na Janela Álgebra, serão exibidas as soluções da equação (l1=Resolver(eq1)).

Como a medida de comprimento do lado de cada placa é um número positivo, então o lado de cada placa mede de comprimento.
50. No tapete confeccionado por Marcos, há 4 pedaços de retalhos em uma dimensão e 7 pedaços na outra dimensão. Desse modo, Marcos usou 28 retalhos na confecção do tapete, pois . Como os pedaços de retalhos têm dimensões de mesma medida e a área do tapete mede , verificamos que a área de cada retalho mede , pois .
Indicando por x a medida do comprimento do lado de cada retalho, representa a medida da área de cada retalho e, nesse caso, . Como e , concluímos que o lado de cada retalho mede de comprimento, visto que uma medida de comprimento só pode ser positiva.
51. Resposta pessoal. Sugestão de resposta:
Um zoológico está construindo um viveiro para jacarés. No projeto de construção do viveiro, consta que ele tem de medida de área. Para cercar esse viveiro, o zoológico usará uma tela. Quantos metros de comprimento de tela serão necessários para cercar esse viveiro?
Resposta: Serão necessários de tela para cercar esse viveiro.
O que eu estudei?
1. Indicando por x a medida de massa da caixa vermelha e por y a medida da massa da caixa azul e sabendo que , a primeira balança nos fornece a equação . Resolvendo-a, temos:
Logo, a massa da caixa vermelha mede .
A segunda balança nos fornece a equação . Resolvendo-a, temos:
Logo, a massa da caixa azul mede .
2. Vamos indicar esse número por x. Se o quádruplo desse número adicionado a 46 resulta em 118, obtemos a equação . Resolvendo-a, temos:
Portanto, esse número é igual a 18.
3. Vamos indicar por x o preço de cada pão. Como Lauro recebeu de troco R$ 5,50 ao comprar 2 caixinhas de leite e 5 pães e pagar com uma cédula de R$ 20,00, temos a equação . Resolvendo-a, obtemos:
Portanto, cada pão custou R$ 1,50.
4. Considere x a idade do irmão de Carla. Como ela é 4 anos mais velha que seu irmão e, em certo momento, ela tinha o triplo da idade dele, temos a equação . Resolvendo-a, obtemos:
Página CVIII
Portanto, no momento em que Carla tinha o triplo da idade do seu irmão, seu irmão tinha 2 anos.
5. A. Como a divisão de por x é igual a , temos a equação . Logo, podemos associar essa informação à equação 3.
B. Como a divisão de 3 por x é igual à divisão de 9 por , temos a equação . Logo, essa informação está associada à equação 1.
C. Como a divisão de 8 por x é igual a 4 dividido por , temos a equação . Logo, essa informação está associada à equação 2.
6. Efetuando os cálculos, temos:
Equação 1:
Equação 2:
Equação 3:
Portanto, .
7. Considere x a quantidade de funcionários dessa marcenaria antes das contrações. Com x funcionários, eram produzidas diariamente 2 estantes e, com funcionários, a produção de estantes passou a ser de 3 por dia. Assim, obtemos a equação . Resolvendo-a, temos:
Logo, após as contratações, a marcenaria ficou com 9 funcionários, pois .
8. a) Vamos resolver esse sistema usando o método da adição.
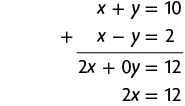
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 6 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
b) Resolvendo esse sistema usando o método da adição, temos:
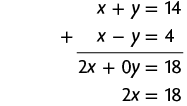
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 9 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
c) Vamos resolver esse sistema usando o método da adição.
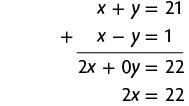
Página CIX
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 11 na 1ª equação do sistema, temos:
Portanto, a solução do sistema é e .
d) Vamos resolver esse sistema usando o método da adição.
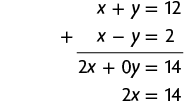
Em seguida, calculamos o valor de x usando a última equação obtida.
Substituindo x por 7 na 1ª equação do sistema, obtemos:
Portanto, a solução do sistema é e .
e) Vamos resolver esse sistema usando o método da substituição.
Na 1ª equação, temos . Substituindo y por na 2ª equação, obtemos:
Por fim, substituindo x por 7 na 1ª equação, temos:
Portanto, a solução do sistema é e .
f) Vamos resolver esse sistema usando o método da substituição.
Na 1ª equação, temos . Substituindo y por na 2ª equação, obtemos:
Por fim, substituindo x por 12 na 1ª equação, temos:
Portanto, a solução do sistema é e .
9. A. Como as balanças estão em equilíbrio, da primeira balança segue a equação e da segunda balança segue a equação .
Logo, o sistema que possibilita determinar os valores de x e y é:
Vamos resolver esse sistema usando o método da substituição.
Na 2ª equação, temos . Sendo assim, substituímos x por na 1ª equação.
Agora, substituindo y por 2 na 2ª equação, temos:
Portanto, a medida da massa da caixa azul é e a medida da massa da caixa vermelha é .
B. Como as balanças estão em equilíbrio, da primeira balança segue a equação e da segunda balança segue a equação .
Logo, o sistema que possibilita determinar os valores de x e y é:
Vamos resolver esse sistema usando o método da substituição.
Na 1ª equação, temos . Sendo assim, substituímos y por na 2ª equação.
Página CX
Por fim, substituindo por 6 na 1ª equação, temos:
Portanto, a medida da massa da caixa amarela é e a medida da massa da caixa verde é .
10. Considere x e y as quantidades de meninos e de meninas, respectivamente, na sala de aula. Como o total de estudantes nessa sala é igual a 42, escrevemos . Como há mais meninas do que meninos e a diferença entre meninos e meninas é igual a 4, segue que ou, ainda, . Desse modo, temos o sistema a seguir.
Vamos resolver esse sistema usando o método da adição.
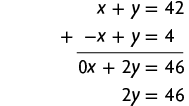
Em seguida, calculamos o valor de y usando a última equação obtida.
Substituindo y por 23 na 1ª equação do sistema, obtemos:
Portanto, há 19 meninos e 23 meninas na sala de aula.
11. Seja x a quantidade de crianças para as quais são distribuídas 40 balas. Cada criança receberá a mesma quantidade de balas se dividirmos 40 balas para x e se dividirmos 50 balas para crianças. Sendo assim, temos a equação . Resolvendo-a, obtemos:
Assim, as 40 balas são distribuídas para 4 crianças.
Portanto, cada criança recebe 10 balas, pois .
12. Considere x o preço da calça e y o preço da camiseta. Leandro pagou R$ 119,00 por 1 calça e uma camiseta, assim, . Como a camiseta custa R$ 25,00 a menos que a calça, então . Logo, temos o sistema a seguir.
Vamos resolver esse sistema usando o método da substituição.
Na 2ª equação, temos . Sendo assim, substituímos y por na 1ª equação.
Por fim, substituindo x por 72 na 2ª equação, temos:
Portanto, a calça custou R$ 72,00.
13. Considere x o preço do ingresso azul e y o preço do ingresso branco. Como 2 ingressos azuis e 2 brancos custaram R$ 140,00, temos . Além disso, 2 ingressos azuis e 3 brancos custaram R$ 180,00, isto é, . Assim, podemos escrever o seguinte sistema.
Vamos resolver esse sistema usando o método da adição.
Multiplicando a 1ª equação por , obtemos o seguinte sistema.
Adicionando as duas equações, temos:
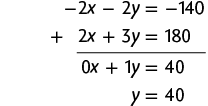
Substituindo y por 40 na 1ª equação do sistema, temos:
Portanto, o ingresso azul custa R$ 30,00 e o ingresso branco custa R$ 40,00.
14. Considere x a medida do comprimento do lado de cada quadrado. No mosaico, há 700 quadrados, totalizando uma medida de área igual a . Desse modo, . Dividindo ambos os membros da última equação por 700, obtemos . Como e e a quantidade de quadrados é um número positivo, o lado de cada quadrado mede de comprimento.