Página CXI
Unidade 9
Sequências
Questão 1. A sequência é formada pelos termos . Para defini-la de maneira recursiva, determinamos o primeiro termo como . Nesse caso, o segundo e o terceiro termo serão dados por:
Portanto, uma sugestão de resposta é e , com .
Questão 2. Considerando a sequência constante , determinamos seu primeiro termo como . Nesse caso, o segundo e o terceiro termo serão dados por:
Portanto, é possível escrever essa sequência de forma recursiva e o termo geral da sequência, com , será , com .
Atividades
1. a ) Os primeiros termos da sequência podem ser escritos como:
Assim, o termo geral dessa sequência é , .
b ) Os primeiros termos da sequência podem ser escritos como:
Assim, o termo geral dessa sequência é , .
c ) Os primeiros termos da sequência podem ser escritos como:
Assim, o termo geral dessa sequência é , .
d ) Os primeiros termos da sequência podem ser escritos como:
Assim, o termo geral dessa sequência é , .
e ) Os primeiros termos da sequência podem ser escritos como:
Assim, o termo geral dessa sequência é , .
f ) Os primeiros termos da sequência podem ser escritos como:
Assim, o termo geral dessa sequência é , .
2. a )
Portanto, os cinco primeiros termos dessa sequência são .
b )
Portanto, os cinco primeiros termos dessa sequência são .
c )
Portanto, os cinco primeiros termos dessa sequência são .
Página CXII
d )
Portanto, os cinco primeiros termos dessa sequência são .
3. a ) Cada figura tem duas bolinhas a mais que a figura anterior e, como a quinta figura tem 13 bolinhas, a sexta figura terá , ou seja, 15 bolinhas.
b ) Considerando a quantidade de bolinhas na posição de cada figura, temos a sequência .
c ) De acordo com a sequência , cada termo pode ser escrito como:
Logo, o termo geral da sequência é .
Portanto, a alternativa I está correta.
d ) Para saber quantas bolinhas haverá na figura 12, ou seja, a figura que ocupa a posição , fazemos:
Portanto, a figura 12 terá 27 bolinhas.
e ) O primeiro termo da sequência é 5, ou seja, . Como o termo seguinte, do segundo em diante, tem sempre dois termos a mais, uma sugestão de resposta é definir a sequência, de forma recursiva, como , com e .
4. Nas alternativas a e b, os termos da sequência estão definidos de tal modo que dependem apenas da posição n, enquanto, nas alternativas c e d, os termos da sequência dependem do termo anterior. Portanto, apenas as alternativas c e d estão definidas de maneira recursiva.
5. a ) De acordo com as informações do enunciado, temos:
Considerando a regra definida por Milena, os próximos termos até o 7º são:
Assim, podemos escrever a sequência .
b ) Não, pois cada termo depende dos dois termos imediatamente anteriores.
c ) Sim. Sugestão de resposta:
Como Milena definiu os termos da sequência como a adição dos dois termos anteriores, então seu termo geral é dado, na forma recursiva, como , para .
6. a ) Sugestão de resposta:
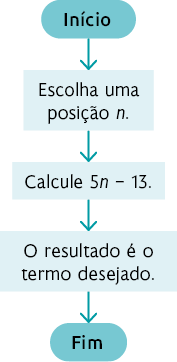
b ) Os próximos três termos da sequência são:
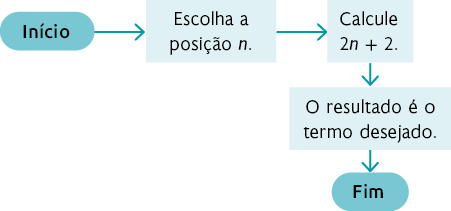
7. a ) Na sequência 1, a quantidade de bolinhas em cada posição é igual à quantidade da posição anterior acrescida de duas unidades. Assim, uma sugestão de resposta é:
Desse modo, temos a fórmula , sendo .
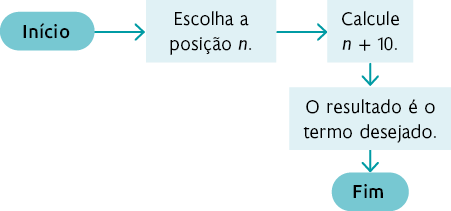
Na sequência 2, a quantidade de bolinhas em cada posição é igual ao número da posição acrescido de dez unidades. Assim, uma sugestão de resposta é:
Logo, temos a fórmula , sendo .
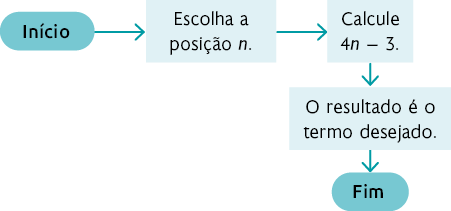
Na sequência 3, a quantidade de bolinhas é exatamente o quádruplo do número da posição subtraído de três unidades. Assim, uma sugestão de resposta é:
Portanto, temos a fórmula , com .
Página CXIII
b ) Sequência 1:
Sequência 2:
Sequência 3:
8. a )
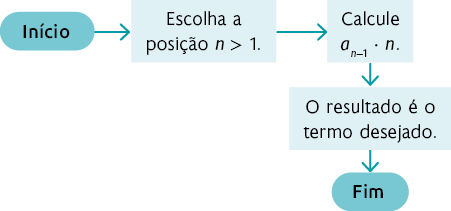
b )
Assim, podemos escrever a sequência (1, 2, 6, 24, 120, 720, ...).
9. a ) A sequência B foi definida por recorrência.
b ) A sequência A está associada ao fluxograma II e a sequência B está associada ao fluxograma I.
c ) Calculando os 8 primeiros termos da sequência A, temos:
Assim, podemos escrever a sequência (7, 9, 11, 13, 15, 17, 19, 21, ...).
Calculando os 8 primeiros termos da sequência B, temos:
Assim, podemos escrever a sequência (2, 3, 5, 9, 17, 33, 65, 129, ...).
10. Se for par, temos ; se for ímpar, temos .
a ) Sendo , então:
Logo, a sequência é .
b )
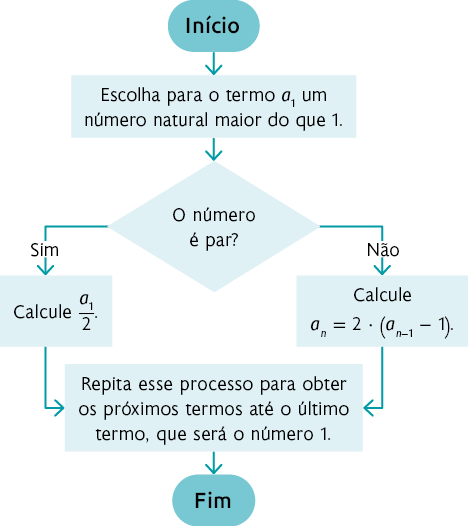
c ) Resposta pessoal. Sugestão de resposta:
Escolhendo , temos:
Portanto, a sequência é .
Página CXIV
11. a ) Considerando que, nessa sequência, cada termo é dado pela adição dos dois termos anteriores, temos:
Portanto, o 13º termo é 233.
b ) Como cada termo é a adição de dois termos anteriores, essa sequência está definida recursivamente e sua fórmula é dada por , com , e .
c ) Resposta pessoal. Espera-se que os estudantes encontrem que Leonardo Fibonacci foi responsável por popularizar os números arábicos na Europa, na época em que ainda eram usados os símbolos da numeração romana, além de explicar o sistema decimal. Seu livro Liber abaci foi muito útil aos comerciantes, ao explicar os cálculos de juros, conversões monetárias e de medidas e vários métodos e algoritmos.
O que eu estudei?
1. a ) Os numeradores são múltiplos de 3, enquanto os denominadores são ímpares. Assim:
Logo, o termo geral é dado por , com .
b ) .
2. De acordo com a sequência definida, os 5 primeiros termos são:
Assim, podemos escrever a sequência (2.048, 1.024, 512, 256, 128, ...).
3. a )
b )
c )
d )
e )
f )
4.
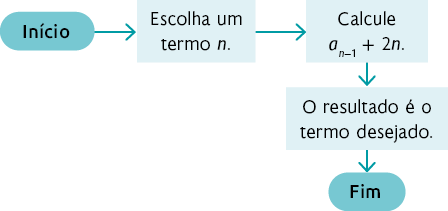
Portanto, temos a sequência .
5. A quantidade de bolinhas em cada posição da sequência é dada pelo triplo do número referente à posição adicionado a três unidades. Portanto, o termo geral da sequência é , com .
6. a ) Na alternativa I, . Como , então não é o termo geral da sequência.
Na alternativa III, . Como , então não é o termo geral da sequência.
Na alternativa II, temos, para os 4 primeiros termos:
Generalizando, verificamos que o termo geral dessa sequência coincide com a alternativa II, ou seja, , com .
Portanto, o termo geral é apresentado na alternativa II.
b )
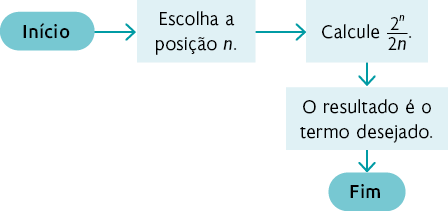
c ) .
Página CXV
7. a ) Para determinar recursivamente essa sequência, considere como a quantidade de bolinhas na primeira posição. Como os termos seguintes são obtidos ao retirar 3 bolinhas da posição anterior, essa sequência pode ser definida de maneira recursiva por , com e .
b )
Portanto, na sexta posição haverá 3 bolinhas.
Unidade 10
Polígonos e circunferência
Questão 1. Para obter as diagonais que partem de um único vértice de um polígono de 10 lados, precisamos desconsiderar da contagem o vértice de partida, uma vez que ele não pode ser ligado a si próprio nem aos dois vértices consecutivos a ele, pois seriam lados do polígono. Desse modo, restam 7 vértices aos quais ele pode ser ligado a fim de obter diagonais.
Portanto, 7 diagonais partem de um único ponto.
Questão 2. Resposta pessoal. Espera-se que os estudantes percebam que a quantidade de diagonais que partem de um único vértice em um polígono é igual à quantidade de vértices ou de lados dele menos 3, pois, para formar diagonais, esse vértice não pode ser ligado a ele mesmo nem aos dois vértices consecutivos a ele.
Questão 3. O polígono que não tem diagonais é o triângulo, pois, ao considerarmos um vértice, os outros dois restantes são consecutivos a ele, o que impossibilita a formação de diagonais.
Atividades
1. As figuras A e D são polígonos não convexos, pois podemos traçar retas que passam pelo interior deles cortando seus contornos em mais de dois pontos. A figura B é um polígono convexo, pois qualquer reta que passa pelo seu interior corta seu contorno em apenas dois pontos. A figura C não é um polígono, pois não é formada somente por segmentos de reta.
2. a ) Um polígono de 6 lados também tem 6 vértices. Logo, o número que substitui o é o 6.
b ) Um polígono tem, no mínimo, 3 lados, pois, com dois lados, teremos um ângulo e, com um lado, um segmento de reta. Logo, o número que substitui o é o 3.
c ) Aplicando a fórmula para o cálculo da quantidade de diagonais de um polígono convexo com lados ou vértices para , temos:
Portanto, um polígono convexo com 12 lados tem 54 diagonais e o deve ser substituído pelo número 54.
d ) Resposta pessoal. Sugestão de resposta:
O pentágono regular tem 5 diagonais, pois, aplicando a fórmula para o cálculo da quantidade D de diagonais desse polígono, temos:
Logo, uma substituição adequada do primeiro é a palavra pentágono e do segundo é o número 5.
3. Como o polígono convexo A tem 7 lados, então, de um único vértice, partem 4 diagonais, pois .
Como o polígono convexo B tem 12 lados, então, de um único vértice, partem 9 diagonais, pois .
4. Vamos aplicar a fórmula para calcular a quantidade de diagonais em um polígono convexo de lados em cada item.
a ) Para , temos:
Logo, um polígono convexo com 5 lados tem 5 diagonais.
b ) Para , temos:
Logo, um polígono convexo com 13 lados tem 65 diagonais.
c ) Para , temos:
Logo, um polígono convexo com 20 lados tem 170 diagonais.
Página CXVI
d ) Para , temos:
Logo, um polígono convexo com 15 lados tem 90 diagonais.
5. O polígono A é regular e tem 11 lados. Assim, a quantidade total de suas diagonais é dada por:
Como já estão traçadas 8 diagonais no polígono A, para que estejam representadas todas as diagonais, faltam 36 diagonais, pois .
O polígono B é um polígono regular com 10 lados. Assim, a quantidade total de suas diagonais é dada por:
Como já estão traçadas 5 diagonais no polígono B, para que estejam representadas todas as diagonais, faltam 30 diagonais, pois .
6. A quantidade de diagonais em um pentágono é dada por:
Logo, um pentágono tem 5 diagonais.
A quantidade de diagonais em um hexágono é dada por:
Logo, um hexágono tem 9 diagonais.
Como a figura geométrica espacial é formada por 12 faces com formato de pentágono e 20 faces com formato de hexágono, ao traçarmos todas as diagonais de cada face, a quantidade de diagonais que traçaremos é dada por:
Portanto, traçaremos ao todo 240 diagonais.
7. a ) As diagonais do polígono amarelo que não representam diagonais do polígono rosa são aquelas que não passam pelos vértices do polígono rosa. Logo, 12 diagonais do polígono amarelo não representam diagonais do polígono rosa.
b ) Como o polígono rosa tem 8 lados, a quantidade de diagonais desse polígono é dada por:
Portanto, o polígono rosa tem 20 diagonais. Como estão traçadas somente 8 diagonais no polígono rosa, para traçar todas as diagonais dele, faltam 12 diagonais, pois .
Questão 4. Aplicando a fórmula para calcular a soma das medidas dos ângulos internos de um polígono de lados ao retângulo e considerando , temos:
Portanto, a soma das medidas dos ângulos internos do retângulo é igual a .
Atividades
8. Para resolver os itens dessa atividade, vamos aplicar a fórmula que permite calcular a soma das medidas dos ângulos internos de um polígono de lados.
A. Como o polígono tem 7 lados, calculamos:
Portanto, a soma das medidas dos ângulos internos desse polígono é igual a .
B. Como o polígono tem 9 lados, calculamos:
Portanto, a soma das medidas dos ângulos internos desse polígono é igual a .
Página CXVII
C. Como o polígono tem 11 lados, calculamos:
Portanto, a soma das medidas dos ângulos internos desse polígono é igual a .
D. Como o polígono tem 8 lados, calculamos:
Portanto, a soma das medidas dos ângulos internos desse polígono é igual a .
9. A. Como o polígono tem 6 lados, a soma da medida dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos desse polígono é igual a .
Como esse polígono é regular, todos os ângulos internos têm a mesma medida.
Portanto, cada ângulo interno desse polígono mede , pois .
B. Como o polígono tem 8 lados, a soma da medida dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos desse polígono é igual a .
Como esse polígono é regular, todos os ângulos internos têm a mesma medida.
Portanto, cada ângulo interno desse polígono mede , pois .
C. Como o polígono tem 10 lados, a soma da medida dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos desse polígono é igual a .
Como esse polígono é regular, todos os ângulos internos têm a mesma medida.
Portanto, cada ângulo interno desse polígono mede , pois .
D. Como o polígono tem 12 lados, a soma da medida dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos desse polígono é igual a .
Como esse polígono é regular, todos os ângulos internos têm a mesma medida.
Portanto, cada ângulo interno desse polígono mede , pois .
10. A. Adicionando as medidas conhecidas dos três ângulos, temos:
Como o polígono tem quatro lados, a soma da medida dos seus ângulos internos é igual a .
Calculando , verificamos que a medida desconhecida é .
B. Adicionando as medidas conhecidas dos cinco ângulos, temos .
Como o polígono tem seis lados, a soma da medida dos seus ângulos internos é igual a .
Calculando , verificamos que a medida desconhecida é .
C. Adicionando as medidas conhecidas dos quatro ângulos, temos .
Como o polígono tem cinco lados, a soma da medida dos seus ângulos internos é igual a .
Calculando , verificamos que a medida desconhecida é .
11. a ) Primeiro, devemos calcular a quantidade de lados de um polígono convexo que tenha 2 diagonais. Substituindo por 2 na fórmula, temos:
Multiplicando os dois membros dessa equação por 2, obtemos:
Assim, se , vamos ter:
Com isso, verificamos que, se o polígono tem 2 diagonais, então ele tem 4 lados. Desse modo:
Portanto, a soma das medidas dos seus ângulos internos é igual a .
b ) Primeiro, devemos calcular a quantidade de lados de um polígono convexo que tenha 5 diagonais. Substituindo por 5 na fórmula, temos:
Página CXVIII
Multiplicando os dois membros dessa equação por 2, obtemos:
Assim, se , vamos ter:
Com isso, verificamos que, se o polígono tem 5 diagonais, então ele tem 5 lados. Desse modo:
Portanto, a soma das medidas dos seus ângulos internos é igual a .
c ) Primeiro, devemos calcular a quantidade de lados de um polígono convexo que tenha 0 diagonais. Substituindo por 0 na fórmula, temos:
Multiplicando os dois membros dessa equação por 2, obtemos:
Assim, se , vamos ter:
Com isso, verificamos que, se o polígono tem 0 diagonais, ele tem 3 lados. Desse modo:
Portanto, a soma das medidas dos seus ângulos internos é igual a
12. Sendo um polígono de quatro lados, a soma das medidas dos seus ângulos internos é igual a . Desse modo, podemos escrever a equação a seguir.
Resolvendo-a, temos:
Substituindo por na medida de cada ângulo interno do polígono, temos:
13. a ) O formato dos pisos indicados na imagem lembra o quadrado e o octógono.
b ) Como o quadrado tem 4 lados, então:
Logo, a soma das medidas dos ângulos internos de um quadrado é igual a .
Como o octógono tem 8 lados, então:
Logo, a soma das medidas dos ângulos internos de um octógono é igual a .
Como quadrados e octógonos são polígonos convexos, a soma das medidas dos seus ângulos externos é igual a .
c ) Como a soma das medidas dos ângulos internos de um quadrado é igual e seus quatro ângulos têm a mesma medida, verificamos que seus ângulos internos medem cada um, pois .
Como a soma das medidas dos ângulos internos de um octógono é igual e seus oito ângulos têm a mesma medida, verificamos que seus ângulos internos medem cada um, pois .
d ) Como o quadrado tem 4 lados, temos:
Logo, o quadrado tem 2 diagonais.
Como o octógono tem 8 lados, temos:
Logo, o octógono tem 20 diagonais.
14. Para resolver os itens dessa atividade, vamos aplicar a fórmula para o cálculo da soma das medidas dos ângulos internos de um polígono de lados.
Página CXIX
a ) Substituindo por na fórmula, temos:
Portanto, o polígono regular cuja soma das medidas dos ângulos internos é igual a tem 4 lados.
b ) Substituindo por na fórmula, temos:
Portanto, o polígono regular cuja soma das medidas dos ângulos internos é igual a tem 12 lados.
c ) Substituindo por na fórmula, temos:
Portanto, o polígono regular cuja soma das medidas dos ângulos internos é igual a tem 10 lados.
d ) Substituindo por na fórmula, temos:
Portanto, o polígono regular cuja soma das medidas dos ângulos internos é igual a tem 8 lados.
15. A. Como a soma das medidas dos ângulos externos de qualquer polígono é igual a e esse é um polígono regular com 5 lados, a medida de cada ângulo externo é igual a , pois seus ângulos externos são congruentes e .
B. Como a soma das medidas dos ângulos externos de qualquer polígono é igual a e esse é um polígono regular com 10 lados, a medida de cada ângulo externo é igual a , pois seus ângulos externos são congruentes e .
16. A soma das medidas de um ângulo interno com um externo, de mesmo vértice, em um polígono convexo é igual a . Desse modo, temos:
Como o polígono tem 4 lados, a soma das medidas dos seus ângulos internos é igual a . Adicionando as medidas dos três ângulos internos que são conhecidas, temos:
Como , segue que .
Além disso, temos:
17. • Quadro A:
Substituindo por na fórmula para o cálculo da soma das medidas dos ângulos internos de um polígono de lados, temos:
Assim, esse polígono tem 4 lados.
Como os seus ângulos internos têm a mesma medida, cada um desses ângulos mede e esse polígono é um retângulo.
Quadro B:
Como esse polígono tem 12 vértices, ele também tem 12 lados. Como todos os seus ângulos externos medem , ele é regular e todos os seus ângulos internos têm a mesma medida, que é , pois .
Logo, esse é um polígono regular de 12 lados, denominado dodecágono regular.
Questão 5. Resposta pessoal. Sugestão de resposta:
Considere a medida do ângulo externo ao ângulo de medida . Desse modo, temos ou, ainda, . Consequentemente:
Logo, .
Página CXX
Atividades
18. a ) O lado oposto ao ângulo de medida é o lado .
b ) A medida do ângulo oposto ao lado é .
19. A. Triângulos equiláteros têm todos os lados com a mesma medida de comprimento. Sendo assim, podemos escrever:
Resolvendo essa equação, temos:
Portanto, .
B. Triângulos equiláteros têm todos os lados com a mesma medida de comprimento. Sendo assim, podemos escrever:
Resolvendo essa equação, temos:
Portanto, .
20. Como a soma dos ângulos internos de um triângulo mede , temos:
Logo, . Assim, as medidas dos ângulos são:
Como o triângulo tem um ângulo reto, ele é um triângulo retângulo.
21. Como o triângulo é isósceles, então:
Como também é isósceles, então:
Além disso, o triângulo é isósceles. Desse modo, temos:
Considerando os ângulos do triângulo , obtemos:
22. a ) As medidas dos ângulos opostos aos lados de mesma medida em um triângulo isósceles são iguais, isto é, . Então, .
Portanto, a afirmação desse item é verdadeira.
b ) A medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não adjacentes a ele. Sendo assim, .
Portanto, a afirmação desse item é verdadeira.
c ) As medidas e são as medidas dos ângulos suplementares aos ângulos de medidas e , respectivamente, isto é, . Sendo assim, e , ou seja, . Além disso, as medidas e são iguais, pois são medidas dos ângulos opostos aos lados de mesma medida do triângulo isósceles. Nesse caso, .
Portanto, a afirmação desse item é verdadeira.
d ) Como as medidas e podem ser diferentes, a afirmação desse item é falsa.
e ) As medidas , e são medidas dos ângulos externos do triângulo. Como o triângulo é um polígono e a soma das medidas dos ângulos externos de qualquer polígono é igual a , segue que .
Portanto, a afirmação desse item é verdadeira.
23. O ângulo é alterno interno com o suplementar do ângulo que mede . Como as retas e são paralelas, esses dois ângulos têm a mesma medida. Logo, .
Resolvendo essa equação, temos:
Portanto, .
O ângulo de é o ângulo externo de um triângulo em que os ângulos que medem e são internos e não são adjacentes a ele. Assim, temos a equação .
Resolvendo essa equação, temos:
Portanto, .
24. Os ângulos que medem e são opostos pelo vértice. Por esse motivo, eles têm a mesma medida. Desse modo:
Página CXXI
Sendo assim, temos:
O ângulo externo do triângulo adjacente ao ângulo mede . Assim, calculamos .
Os ângulos , , e são ângulos internos de um polígono de quatro lados, ou seja, a soma das medidas desses ângulos é igual a . Nesse caso, obtemos:
Logo, .
Como a soma das medidas dos ângulos internos de um triângulo é igual a , temos:
Como o triângulo ABC tem um ângulo obtuso em , ele é um triângulo obtusângulo.
Questão 6. Resposta pessoal. Espera-se que os estudantes obtenham, por meio da pesquisa, o provável local e o possível período da origem do tangram, além de algumas lendas sobre sua origem.
Questão 7. Não é possível afirmar o que supõe essa questão, pois, para que dois hexágonos sejam congruentes, é necessário que seus respectivos lados sejam congruentes e os respectivos ângulos internos sejam congruentes.
Atividades
25. A. Medindo os comprimentos dos lados dos triângulos e , obtemos as seguintes considerações:
, pois ambos medem ;
, pois ambos medem ;
, pois ambos medem .
Portanto, pelo caso de congruência , esses triângulos são congruentes.
B. Medindo os comprimentos dos lados dos triângulos e , verificamos que:
mede ;
mede ;
, , e medem .
Portanto, esses triângulos não são congruentes.
26. A. Nos triângulos e temos:
, pois está indicado na figura e o lado é comum aos dois triângulos.
Portanto, pelo caso , segue que .
B. Nos triângulos e , temos:
, pois está indicado na figura.
, pois são opostos pelo vértice.
, pois são ângulos retos.
Portanto, pelo caso , segue que .
C. Nos triângulos e , temos:
, pois está indicado na figura e o lado é comum aos dois triângulos.
Portanto, pelo caso , segue que .
D. Nos triângulos e , temos:
e , pois está indicado na figura.
, pois são ângulos retos.
Portanto, pelo caso , segue que .
27. Nos triângulos e , temos:
Logo, pelo caso .
Nos triângulos e , temos:
Logo, pelo caso .
28. Considere os triângulos e . Nesses triângulos, temos:
Além disso, o lado é comum aos dois triângulos.
Logo, pelo caso , segue que . Como consequência dessa congruência de triângulos, obtemos a congruência dos respectivos ângulos, isto é, e .
29. No triângulo , temos:
Sendo assim, o triângulo é isósceles e . Como a soma das medidas dos ângulos internos de um triângulo é igual a , então .
O triângulo é um triângulo equilátero e, assim, é um polígono regular. Por esse motivo, todos os seus ângulos internos têm a mesma medida. Como a soma das medidas dos ângulos internos de um triângulo é igual a , cada ângulo do triângulo mede , pois . Com isso, nos triângulos e , temos:
Logo, pelo caso , segue que .
No triângulo , temos:
Página CXXII
Como a soma das medidas dos ângulos internos de um triângulo é igual a , segue que , pois .
No triângulo , temos:
Desse modo, nos triângulos e , temos:
Logo, pelo caso , segue que .
Por fim, os triângulos e são congruentes pelo caso . Logo, .
30. a ) Como e , segue que , pois e a soma das medidas dos ângulos internos de um triângulo é igual a .
Considerando o triângulo , temos:
Logo, pelo caso , segue que .
Considerando o triângulo , temos:
Logo, pelo caso , segue que .
Como nenhum dos lados do triângulo mede , esse triângulo não pode ser congruente ao triângulo . Portanto, os triângulos e são congruentes ao triângulo .
b ) No item anterior, mostramos que . Como o lado do triângulo corresponde, pela congruência, ao lado do triângulo e , segue que .
c ) Do item a, verificamos que . Vamos usar novamente o fato de que . Como o lado do triângulo corresponde, pela congruência, ao lado do triângulo e , segue que .
31. A. O segmento de reta vermelho divide o ângulo em dois ângulos congruentes. Logo, esse segmento de reta é uma bissetriz.
B. O segmento de reta vermelho tem uma extremidade no vértice e a outra extremidade no ponto médio do lado oposto ao vértice . Logo, esse segmento é uma mediana.
C. O segmento de reta vermelho divide o ângulo em dois ângulos congruentes. Logo, esse segmento de reta é uma bissetriz.
D. O segmento de reta vermelho tem uma extremidade no vértice e é perpendicular ao lado oposto ao vértice . Logo, esse segmento é uma altura.
32. Os segmentos e são medianas do triângulo . Desse modo, o ponto é ponto médio do segmento e o ponto é ponto médio do segmento . Como consequência disso, a medida do segmento é igual ao dobro da medida do segmento e a medida do segmento é igual ao dobro da medida do segmento . Como e , segue que e , pois e . Logo, o lado mede , o lado mede e o lado mede . Sendo assim, a medida do perímetro do triângulo é igual a , pois .
33. Resposta pessoal. Sugestão de resposta:
Ao traçarmos a mediatriz do lado , a interseção dessa mediatriz com o lado será um ponto sobre equidistante ao vértices e , pois todo ponto que está na mediatriz é equidistante às extremidades do segmento do qual ela é mediatriz.
34. a ) O ponto onde as mediatrizes de um triângulo se cruzam é um ponto equidistante aos vértices do triângulo. Desse modo, o centro da circunferência circunscrita em um triângulo é obtido pelo cruzamento de suas mediatrizes. Portanto, o deve ser substituído pela palavra mediatrizes.
b ) O ponto de encontro das medianas é o ponto de equilíbrio de um triângulo e este ponto é chamado baricentro. Desse modo, o baricentro é o centro de equilíbrio de um triângulo. Portanto, o deve ser substituído pela palavra baricentro.
c ) Se um triângulo é obtusângulo, então ele tem um ângulo obtuso. A altura traçada a partir do vértice onde está o ângulo obtuso não cruzará o seu lado oposto, mas sim uma extensão dele. O ponto onde essa altura cruza a extensão desse lado está no exterior do triângulo. Assim, nos triângulos obtusângulos, o ponto de encontro das alturas é sempre exterior ao triângulo. Portanto, o deve ser substituído pela palavra alturas.
d ) O ponto de encontro das mediatrizes de um triângulo é chamado circuncentro. Portanto, o deve ser substituído pela palavra circuncentro.
e ) O ponto em que as alturas de um triângulo se cruzam é chamado ortocentro e o baricentro é o ponto onde as medianas se cruzam. Portanto, os devem ser substituídos, respectivamente, pelas palavras ortocentro e medianas.
35. Os segmentos e são bissetrizes dos ângulos e , respectivamente. Assim, a medida do ângulo é igual ao dobro da medida do ângulo e a medida do ângulo é igual ao dobro da medida do ângulo . Como e , então e , pois e .
Além disso, como a soma dos ângulos internos de um triângulo é igual , segue que:
Página CXXIII
36. A. Os segmentos de reta traçados no triângulo dividem cada um de seus ângulos internos em dois ângulos congruentes. Logo, esses segmentos de reta são bissetrizes. Como o ponto é o ponto onde as bissetrizes se cruzam, ele representa o incentro.
B. As retas traçadas no triângulo dividem cada um de seus lados em dois segmentos congruentes e também são perpendiculares a esses lados. Logo, essas retas são mediatrizes. Como o ponto é o ponto em que as mediatrizes se cruzam, ele representa o circuncentro.
C. Os segmentos de reta traçados no triângulo têm uma de suas extremidades em um dos vértices do triângulo e a outra sobre os lados opostos a esses vértices, as quais dividem os lados opostos em dois segmentos congruentes. Logo, esses segmentos de reta são medianas. Como o ponto é o ponto onde as medianas se cruzam, ele representa o baricentro.
D. Os segmentos de reta traçados no triângulo , sendo dois deles coincidentes com os lados e , têm uma de suas extremidades em um dos vértices do triângulo e são perpendiculares aos lados opostos a esses vértices. Logo, esses segmentos de reta são alturas. Como o ponto é o ponto em que as alturas se cruzam, ele representa o ortocentro.
37. a ) O circuncentro de um triângulo é o ponto no qual as mediatrizes do triângulo se cruzam. Medindo os ângulos formados pelos segmentos de reta traçados e os lados nos triângulos desenhados por Adriana e Pedro não obtemos ângulos retos. Sendo assim, esses segmentos não são mediatrizes.
No desenho de Gilmar, medindo os ângulos formados pelas retas traçadas e os lados do triângulo, verificamos que as retas traçadas e os lados do triângulo formam ângulos retos. Além disso, medindo o comprimento do segmento de reta formado pelo ponto de interseção da reta traçada com o lado, verificamos em cada lado do triângulo que:
as retas cruzam os lados nos seus respectivos pontos médios;
o lado é dividido em dois segmentos de reta com medidas de comprimento iguais a ;
os lados e são divididos em dois segmentos de reta com medidas de comprimento iguais a .
Portanto, o estudante que obteve o circuncentro foi Gilmar.
b ) Medindo, no desenho de Adriana, os ângulos formados pelos segmentos de reta traçados com vértices coincidentes aos do triângulo, obtemos, nos vértices e , quatro ângulos medindo e, no vértice , dois ângulos medindo . Assim, os segmentos de reta que ela traçou no triângulo são bissetrizes, pois dividiram cada ângulo interno do triângulo em dois ângulos congruentes. Logo, o ponto obtido por Adriana foi o incentro.
Os segmentos de reta traçados no desenho de Pedro têm extremidades nos vértices do triângulo e em algum ponto sobre os lados opostos a esses vértices. Medindo o comprimento dos segmentos obtidos em cada lado do triângulo, verificamos que:
o lado foi dividido em dois segmentos medindo de comprimento;
o lado foi dividido em dois segmentos medindo de comprimento;
o lado foi dividido em dois segmentos de medidas de comprimento iguais a .
Assim, as extremidades dos segmentos de reta traçados que não são vértices do triângulo são os pontos médios dos respectivos lados dele.
Portanto, os segmentos de reta traçados por Pedro são medianas e o ponto obtido por ele é o baricentro.
38. a ) A frase está incorreta. Possível correção: O baricentro de um triângulo é o ponto de encontro de suas medianas.
b ) A frase está correta.
c ) A frase está incorreta. Possível correção: Em um triângulo, o segmento de reta que liga um vértice do triângulo ao ponto médio de seu lado oposto é denominado mediana.
d ) A frase está correta.
e ) A frase está correta.
39. A. Ao medirmos os ângulos formados pelos lados do triângulo e os segmentos que estão traçados no triângulo, verificamos que:
o ângulo está dividido em dois ângulos com medida igual a ;
o ângulo está dividido em dois ângulos com medida igual a ;
o ângulo está dividido em dois ângulos com medida igual a .
Portanto, o ponto representa o incentro do triângulo.
B. No triângulo , os lados e são perpendiculares e, assim, também são alturas do triângulo. O segmento de reta que tem uma extremidade em e a outra sobre o lado é perpendicular ao lado .
Portanto, o ponto é o ponto onde as alturas do triângulo se cruzam e representa o ortocentro do triângulo.
C. Cada reta traçada passando pelo triângulo é perpendicular a um dos lados do triângulo. Medindo os segmentos formados em cada lado desse triângulo, verificamos que:
o lado está dividido em dois segmentos com medida de comprimento igual a ;
o lado está dividido em dois segmentos com medida de comprimento igual a ;
o lado está dividido em dois segmentos com medida de comprimento igual a .
Assim, essas retas traçadas, além de serem perpendiculares aos lados do triângulo, os divide em segmentos congruentes, ou seja, elas são mediatrizes.
Portanto, o ponto representa o circuncentro do triângulo.
Página CXXIV
40. No triângulo , temos dois ângulos internos medindo e . Como a soma das medidas dos ângulos internos de um triângulo é igual a , segue que:
No triângulo temos dois ângulos internos medindo e . Como a soma das medidas dos ângulos internos de um triângulo é igual a , segue que:
41. O terreno onde Juliana cultiva morango tem formato triangular e as cercas que dividem esse terreno com os terrenos usados para o cultivo de alface e couve são lados desse triângulo. O ponto notável que é equidistante dos lados do triângulo é o incentro, o qual é obtido pela interseção das bissetrizes do triângulo. Assim, para que Juliana coloque esse aspersor satisfazendo à condição de estar a uma mesma distância entre as cercas que dividem o terreno do cultivo de morango com os terrenos de cultivo de alface e couve, ela deve traçar as bissetrizes dos ângulos internos do triângulo formado pela cerca do terreno usado para o cultivo de morango e colocar o aspersor no ponto em que essas bissetrizes se cruzam.
42. Resposta pessoal. Sugestão de resposta:
As mediatrizes de um triângulo podem ser traçadas, usando régua e compasso, de acordo com os seguintes procedimentos.
Desenhe um triângulo qualquer.
Com a ponta-seca em um dos vértices do triângulo e abertura maior do que a metade da medida do lado, trace dois arcos.

Com a mesma abertura, coloque a ponta-seca na outra extremidade do lado e trace mais dois arcos cruzando os anteriores.

Com uma régua, trace a reta que passa pelos pontos determinados pelos cruzamentos dos arcos.
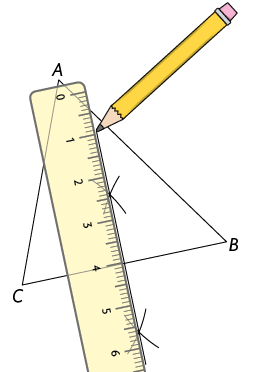
Essa reta é a mediatriz do lado . Repetindo esse processo para os outros lados, obtemos as outras mediatrizes.
43. Resposta pessoal. Sugestão de resposta:
Usando o GeoGebra, podemos construir as mediatrizes de um triângulo com os seguintes procedimentos.
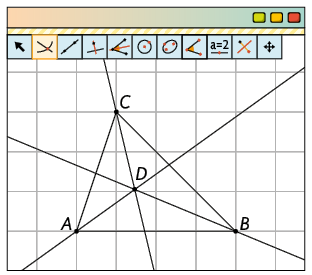
Com a ferramenta Ponto, marque três pontos (, e ) não alinhados. Depois, com a ferramenta Segmento, trace os segmentos , e .
Com a ferramenta Bissetriz, clique nos pontos , , , nessa ordem. Repita o processo clicando nos pontos , , e, em seguida, nos pontos , , .
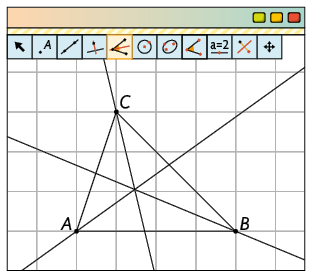
Com a ferramenta Interseção de Dois Objetos, clique em duas bissetrizes. O ponto obtido é o incentro do triângulo.
Página CXXV
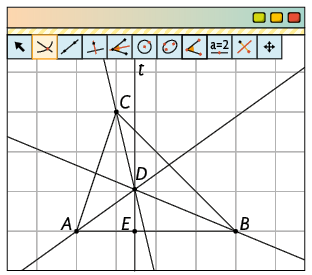
Usando a ferramenta Reta perpendicular, trace uma reta t perpendicular ao lado passando por D. Em seguida, com a ferramenta Interseção de Dois Objetos, clique em t e sobre o lado para obter o ponto E.
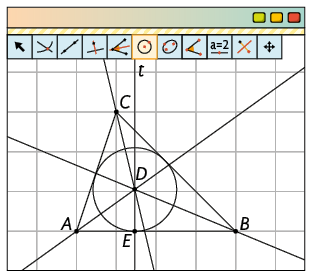
Com a ferramenta Círculo Dados Centro e Um de seus Pontos, clique em D e E, obtendo, assim, a circunferência inscrita no triângulo.
44. a ) Napoleão Bonaparte foi um dos mais famosos generais dos tempos contemporâneos e um brilhante estrategista de guerra, tornando-se o mais jovem general do Exército francês, com apenas 24 anos.
b ) Resposta pessoal. Espera-se que os estudantes citem que Napoleão Bonaparte aderiu à Revolução Francesa, era brilhante nas estratégias de guerra, foi o mais jovem general francês e realizou alguns estudos relacionados às construções geométricas.
c ) Resposta pessoal. Sugestão de resposta: Sim, o interesse dele contribuiu para o seu desempenho como estrategista de guerra, pois com a Matemática é possível fazer cálculos do contingente e do armamento necessários para enfrentar um exército inimigo.
d ) Resposta pessoal. Espera-se que os estudantes respondam que a Revolução Francesa foi responsável pelo fim do Absolutismo na França, ou seja, o fim de um sistema político de governo no qual quem governava tinha poderes sem limitações. Uma das principais consequências da Revolução Francesa foi a criação de uma constituição que definiu os direitos individuais e coletivos dos indivíduos, servindo de exemplo para muitos outros países.
e ) Resposta pessoal. Espera-se que os estudantes encontrem em sua pesquisa o teorema da base média e o teorema de Ceva.
Questão 8. Resposta pessoal. Espera-se que os estudantes construam quadriláteros cujos lados opostos não sejam paralelos.
Atividades
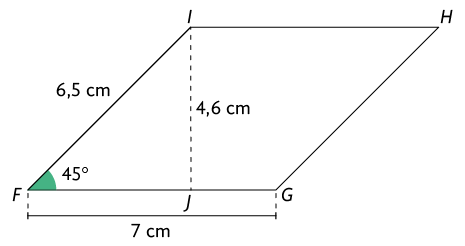
45. Lados do quadrilátero: , , e .
Vértices do quadrilátero: , , e .
Diagonais do quadrilátero: e .
Medidas dos ângulos internos do quadrilátero: , , e .
Medidas dos ângulos externos do quadrilátero: , , e .
46. A frase A está relacionada a quadriláteros, pois qualquer quadrilátero tem duas diagonais.
A frase B não está relacionada a quadriláteros, pois de cada vértice de um quadrilátero parte somente uma diagonal .
A frase C está relacionada a quadriláteros, pois a soma das medidas dos ângulos internos de um quadrilátero é igual a e a soma das medidas dos ângulos externos de qualquer polígono também é igual a .
A frase D está relacionada a quadriláteros, pois, ao traçarmos uma diagonal, os outros dois vértices não estarão sobre a reta que contém esta diagonal, formando, assim, dois triângulos.
47. Inicialmente, vamos calcular o valor de . Como a soma das medidas dos ângulos internos de um quadrilátero é igual a , temos:
Logo, .
Página CXXVI
Em seguida, vamos calcular as medidas dos ângulos internos do quadrilátero.
Assim, obtemos:
Portanto, a alternativa correta é a e.
48. a ) Como a figura é um quadrilátero, de cada vértice é possível traçar uma diagonal. Logo, parte uma diagonal do vértice e parte uma diagonal do vértice .
b ) Os ângulos internos e externos de um polígono, no mesmo vértice, são suplementares, ou seja, a soma de suas medidas é igual a . Então, o ângulo interno no vértice mede e o ângulo externo mede . Já no vértice , o ângulo interno mede e o ângulo externo mede .
c ) Sugestão de resposta:
Medidas dos ângulos internos: vértice C: ; vértice D: ;
medidas dos ângulos externos: vértice C: ; vértice D: .
49. De acordo com a figura, o menor ângulo é o de medida . Então, . Desse modo, temos:
Como a soma das medidas dos ângulos internos de um quadrilátero é , temos:
.
Por fim, como , segue que .
Questão 9. Para demonstrar essa propriedade, utilizamos o quadrado e o dividimos em duas partes.
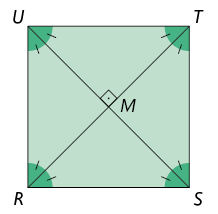
I. Considerando os triângulos e , temos:
os lados e são congruentes, pois são lados opostos de um paralelogramo;
os ângulos e medem , logo são congruentes; o segmento é lado comum aos dois triângulos.
Assim, pelo caso de congruência de triângulos , . Logo, os lados e dos triângulos, que são as diagonais do quadrado , são congruentes.
Logo, as diagonais de um quadrado são congruentes.
II. Considere os triângulos , , e obtidos ao traçar as diagonais do quadrado . Temos , pois os lados do quadrado são congruentes. E, ainda, e , pois M é ponto médio dos segmentos e , desse modo os 4 triângulos são congruentes pelo caso .
Ademais, os 4 ângulos correspondentes com vértices nas extremidades do segmento são congruentes e o mesmo ocorre com os 4 ângulos com vértices nas extremidades do segmento . Ainda da congruência dos quatro triângulos, os 4 ângulos com vértices em M são congruentes. Como a soma das medidas desses ângulos é , cada um deles mede .
Sendo assim, as diagonais do quadrado são perpendiculares entre si e correspondem às bissetrizes dos ângulos internos.
Portanto, por I e II, concluímos que as diagonais de um quadrado são congruentes, perpendiculares entre si e correspondem às bissetrizes dos ângulos internos.
Atividades
50. a ) Resposta pessoal. Espera-se que os estudantes identifiquem retângulos e quadrados.
b ) Sim. As medidas de todos os ângulos internos dos retângulos e dos quadrados são iguais a .
51. a ) Como os lados opostos de um paralelogramo são congruentes, então . Como , segue que o comprimento do lado mede .
b ) O ângulo de medida é oposto ao ângulo de . Assim, . Os ângulos e também são opostos, ou seja, . Como a soma das medidas dos ângulos internos de um paralelogramo é igual a , temos:
Logo, .
c ) Como os lados e são opostos, então . Do item a, concluímos que os lados e medem . Sabendo que o perímetro desse paralelogramo mede , temos:
Portanto, o comprimento do lado mede .
Página CXXVII
52. O quadrilátero A não é um paralelogramo, pois tem um par de lados opostos que não são congruentes. Já os quadriláteros B e C têm seus lados opostos congruentes. Como consequência disso, seus lados opostos também são paralelos. Logo, os quadriláteros B e C são paralelogramos.
53. a ) As peças que compõem o tangram têm formatos de triângulos e quadriláteros.
b ) No tangram, somente o quadrado tem os ângulos internos retos.
c ) As peças do tangram, como estão encaixadas, formam um quadrado. O quadrilátero que não é um quadrado é um paralelogramo e dois seus lados consecutivos estão sobre o lado da diagonal do quadrado formado pelas peças do tangram. Como a diagonal do quadrado é uma bissetriz dele, verificamos que o paralelogramo tem dois ângulos internos medindo . As medidas desses ângulos adicionados resultam em e, assim, restam para completar os da soma das medidas dos ângulos internos desse paralelogramo. Os dois outros ângulos do paralelogramo também são opostos e, por isso, têm a mesma medida. Logo, cada um deles mede , pois . Portanto, os ângulos internos do paralelogramo medem e .
54. Primeiro, vamos nomear , e as extremidades dos segmentos de comprimento , e , respectivamente, que estão sobre a reta .
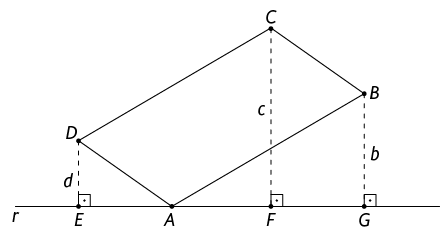
Trace uma reta perpendicular ao segmento de comprimento e indique como o ponto de interseção dessa reta com o segmento.
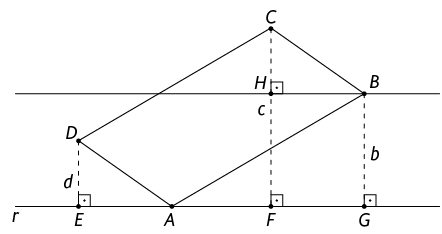
Desse modo, verificamos que os ângulos , e são ângulos retos. Como consequência disso, o ângulo do quadrilátero também é um ângulo reto e esse quadrilátero é um retângulo. Como o retângulo é um caso particular de paralelogramo, seus lados opostos são congruentes. Logo, o segmento mede .
Considere, agora, os triângulos e . Os lados e desses triângulos são congruentes, pois são lados opostos do paralelogramo . Os ângulos e são congruentes, pois são ângulos retos, e os ângulos e são congruentes, pois e . Assim, pelo caso de congruência de triângulos, segue que e, consequentemente, mede . Como é igual à adição dos comprimentos de e , segue que .
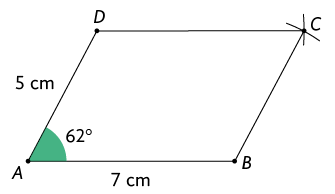
55. A. Com uma régua, trace primeiro o lado medindo de comprimento. Em seguida, usando um transferidor, construa o ângulo com medida . Depois disso, trace o lado com .
Com a ponta-seca do compasso em e abertura com a mesma medida de , trace um arco.
Com a ponta-seca em e abertura com a mesma medida de , trace um arco cruzando o arco desenhado anteriormente.
A interseção dos arcos é o vértice do paralelogramo. Traçando os lados e , obtém-se o paralelogramo.
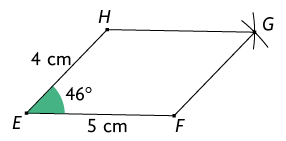
B. Com uma régua, trace primeiro o lado medindo . Em seguida, usando um transferidor, construa o ângulo com medida . Depois disso, trace o lado com .
Com a ponta-seca do compasso em e abertura com a mesma medida de , trace um arco.
Com a ponta-seca em e abertura com a mesma medida de , trace um arco cruzando o arco desenhado anteriormente.
A interseção dos arcos é o vértice do paralelogramo. Traçando os lados e , obtém-se o paralelogramo.
C. Com uma régua, trace primeiro o lado medindo . Em seguida, com um transferidor, construa o ângulo com medida . Depois disso, trace o lado com .
Com a ponta-seca do compasso em e abertura com a mesma medida de , trace um arco.
Com a ponta-seca em e abertura com a mesma medida de , trace um arco cruzando o arco desenhado anteriormente.
Página CXXVIII
A interseção dos arcos é o vértice do paralelogramo. Traçando os lados e , obtém-se o paralelogramo.

56. Como o paralelogramo tem os quatro lados congruentes, ele é um losango.
O paralelogramo tem seus ângulos internos formados por diagonais de quadrados consecutivos da malha, isto é, seus ângulos internos são retos. Como seus quatros lados não têm a mesma medida de comprimento, ele é um retângulo.
O paralelogramo não pode ser classificado, pois não é possível saber, apenas pela malha, qual é a medida dos seus ângulos internos.
Os paralelogramos e , pelo mesmo motivo do paralelogramo , têm seus ângulos internos retos, mas esses paralelogramos têm todos os seus lados congruentes. Por esse motivo, os paralelogramos e podem ser classificados como losangos, quadrados e retângulos.
57. A. Como um losango é também um paralelogramo, seus ângulos opostos são congruentes. Assim, as medidas dos ângulos e são iguais. Além disso, as diagonais de um losango são bissetrizes e, desse modo, . Resolvendo essa equação, temos:
Portanto, .
B. Em um quadrado, os quatro ângulos internos são retos e as diagonais são bissetrizes. Logo, . Resolvendo essa equação, temos:
Portanto, .
C. Em um losango, suas diagonais são bissetrizes. Assim, o ângulo mede e o ângulo mede . Esses dois ângulos, juntamente com o ângulo reto que é o encontro das diagonais do losango, são ângulos internos de um triângulo. Como a soma dos ângulos internos de um triângulo é igual a , obtemos . Resolvendo essa equação, temos:
Portanto, .
58. A. Os ângulos opostos de um paralelogramo são congruentes. Assim, os ângulos e medem . Além disso, os ângulos e também têm a mesma medida, pois são opostos. Como a soma das medidas dos ângulos internos de um quadrilátero é igual a , temos:
Portanto, as medidas dos ângulos internos do paralelogramo são:
e
.
B. Os ângulos opostos de um paralelogramo são congruentes, assim os ângulos e medem . Os ângulos e também têm a mesma medida, pois são opostos. Como a soma das medidas dos ângulos internos de um quadrilátero é igual a , temos:
Portanto, as medidas dos ângulos internos do paralelogramo são:
C. Os ângulos (interno e externo) em um mesmo vértice de um polígono são suplementares. Desse modo, o ângulo mede , pois . Como os ângulos opostos de um paralelogramo são congruentes, os ângulos e medem . Além disso, os ângulos e também têm a mesma medida, pois são opostos. Como a soma das medidas dos ângulos internos de um quadrilátero é igual a , temos:
Página CXXIX
Portanto, as medidas dos ângulos internos do paralelogramo são:
Questão 10. Para a demonstração, considere o trapézio isósceles .
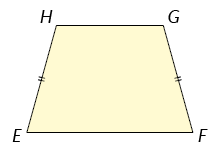
Primeiro, vamos mostrar que e são congruentes. Acompanhe:
No trapézio isósceles , temos . Traçando um segmento paralelo à com extremidade em G e outra em I sobre , obtemos um paralelogramo , assim , além disso, , pois é um trapézio isósceles.
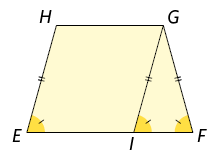
Desse modo, , ou seja, é isósceles, logo . Como , verificamos que , pois esses ângulos são correspondentes. Assim, e são congruentes.
Agora, vamos mostrar que e são congruentes.
Os ângulos e são ângulos colaterais internos, logo são suplementares. Do mesmo modo, e são suplementares, pois são colaterais internos. Desse modo, temos:
, assim
, assim
Como e são congruentes, obtemos:
Logo, e são congruentes.
Vamos provar que as diagonais de um trapézio isósceles são congruentes. Para isso, considere o trapézio .
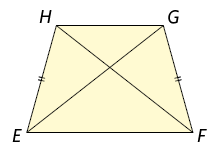
Nesse trapézio, as diagonais e formam os triângulos e . Como esse trapézio é isósceles, . Além disso, é comum aos triângulos e , e . Desse modo, pelo caso de congruência de triângulos , concluímos que . Logo, .
Portanto, em um trapézio isósceles, os ângulos internos da mesma base e as diagonais são congruentes.
Atividades
59. A. Os lados paralelos são e . Como a medida do lado é maior do que a medida do lado , então é a base maior e é a base menor.
B. Os lados paralelos são e . Como a medida do lado é maior do que a medida do lado , então é a base maior e é a base menor.
C. Os lados paralelos são e . Como a medida do lado é maior do que a medida do lado , então é a base maior e é a base menor.
60. No trapézio A, os lados que não são paralelos têm a mesma medida de comprimento. Logo, esse trapézio é isósceles. Os lados não paralelos do trapézio B têm medidas de comprimento diferentes, Logo, esse trapézio é escaleno. Os lados não paralelos do trapézio C têm medidas de comprimento diferentes. Além disso, dois de seus lados consecutivos formam um ângulo reto. Logo, esse trapézio é escaleno e retângulo. No trapézio D, os lados não paralelos têm medidas de comprimento diferentes, além disso, dois de seus lados consecutivos formam um ângulo reto. Logo, esse trapézio é escaleno e retângulo.
61. Como todo trapézio é quadrilátero, para resolver os itens dessa atividade, vamos usar o fato de que a soma das medidas de seus ângulos internos é igual a .
A. Adicionando as medidas apresentadas na imagem, temos:
Substituindo por nas medidas dos ângulos internos do trapézio, temos:
B. Adicionando as medidas apresentadas na imagem, temos:
Página CXXX
Substituindo por nas medidas dos ângulos internos do trapézio, temos:
C . Nesse trapézio, verificamos que
.
Como a soma das medidas dos ângulos internos de um quadrilátero é igual a , então a soma das medidas dos ângulos e é igual a . Sendo assim, temos:
Substituindo por nas medidas dos ângulos internos do trapézio, temos:
62. A. De acordo com as informações apresentadas, os lados e do trapézio são paralelos e . Nesse caso, temos:
Como as medidas dos ângulos e são iguais, então .
Por fim, para calcular a medida do ângulo , resolvemos o cálculo a seguir.
Portanto, .
B. De acordo com a imagem, os ângulos e são retos, ou seja, . Além disso, . Então:
Por fim, para calcular a medida do ângulo , resolvemos o cálculo a seguir.
Portanto, .
63. Como o trapézio é isósceles, os lados e têm a mesma medida de comprimento. Sendo essa medida e considerando que o perímetro do trapézio mede , temos:
Portanto, os lados e medem de comprimento cada um.
Questão 11. Resposta pessoal. Espera-se que os estudantes respondam que o contorno de uma figura circular é uma circunferência e que nessa figura geométrica todos os seus pontos estão a uma mesma distância do centro. Outra característica é que as circunferências não têm lados ou vértices.
Atividades
64. Resposta pessoal. Sugestões de resposta: Moedas, CD, copos e garrafas.
65. Em uma circunferência, o comprimento do raio tem a metade da medida de comprimento do seu diâmetro. Portanto, o comprimento do raio dessa circunferência mede , pois .
66. a ) Na circunferência de centro , identificamos que:
, , e são raios, pois unem o centro da circunferência a um de seus pontos.
e são diâmetros, pois são segmentos que unem dois pontos distintos da circunferência passando pelo seu centro (são cordas que passam pelo centro da circunferência).
, , e são cordas, pois unem dois pontos distintos da circunferência.
b ) Na circunferência de centro , identificamos que:
, , e são raios, pois unem o centro da circunferência a um de seus pontos.
e são diâmetros, pois são segmentos que unem dois pontos distintos da circunferência passando pelo seu centro (são cordas que passam pelo centro da circunferência).
, , e são cordas, pois unem dois pontos distintos da circunferência.
c ) Sugestão de resposta:
Os ângulos e são ângulos centrais, pois seus vértices estão nos centros das circunferências e seus lados passam por pontos das circunferências.
Página CXXXI
67. a ) Em uma circunferência, o comprimento do raio tem a metade da medida de comprimento do seu diâmetro. Portanto, o comprimento do raio dessa circunferência mede , pois .
b ) Em uma circunferência, o comprimento do diâmetro tem o dobro da medida de comprimento do seu raio. Portanto, o comprimento do diâmetro dessa circunferência mede , pois .
68. Como as diagonais de um retângulo têm a mesma medida de comprimento, o comprimento do segmento mede . O ponto é o centro da circunferência e o ponto está na circunferência. Então, é um raio da circunferência. Como, em uma circunferência, o diâmetro tem o dobro da medida de comprimento de seu raio, então o comprimento do diâmetro dessa circunferência mede , pois .
69. O comprimento do diâmetro da circunferência desenhada por Jade não pode medir mais de , pois, do contrário, não caberá no pedaço de cartolina. Assim, a medida do comprimento do raio da circunferência deve ser igual a , pois .
70. a ) Como o raio da roda menor terá de medida de comprimento, seu diâmetro terá , pois . Dobrando essa medida, obtemos , pois . Essa será a medida de comprimento do raio da roda maior. Sendo assim, o comprimento do diâmetro da roda maior medirá ou , visto que .
b ) Resposta pessoal: Espera-se que os estudantes obtenham, como resultado de sua pesquisa, informações sobre alguns tipos de bicicleta, entre elas as bicicletas de passeio, as bicicletas mountain bike para trilhas e as bicicletas para ciclismo. Espera-se que eles mencionem em suas produções alguns benefícios do uso da bicicleta, incluindo a melhora da musculatura, o aumento da resistência física, a redução do colesterol e o controle da pressão arterial.
Atividades
71. Um polígono está inscrito em uma circunferência se seus vértices são pontos da circunferência. Nas figuras B e C, os vértices dos polígonos não são pontos das circunferências. Logo, a figura com um polígono inscrito em uma circunferência é a figura A.
72. a ) Da definição de ângulo central de um polígono, segue que a quantidade de ângulos centrais em um polígono é igual à quantidade de lados desse polígono. Se o polígono for regular, então os ângulos centrais terão todos a mesma medida. Assim, para calcular a medida do ângulo central, basta dividir , que é referente a uma volta completa, pela quantidade de lados do polígono.
O ângulo central do triângulo mede , pois .
O ângulo central do quadrado mede , pois .
O ângulo central do hexágono mede , pois .
O ângulo central do decágono mede , pois .
b ) Sugestão de resposta:
Para calcular a medida do ângulo central de um polígono regular, dividimos pela quantidade de lados dele.
73. A. Na imagem, temos um hexágono inscrito em uma circunferência com um ângulo central de centro O. De acordo com essa imagem, o maior ângulo, representado por , tem quatro vezes a medida do ângulo central. Como, em um hexágono, o ângulo central mede , pois , verificamos que .
B. Unindo dois vértices consecutivos de um polígono regular inscrito em uma circunferência e o centro dela, obtemos um triângulo isósceles, pois dois de seus lados coincidirão com dois raios da circunferência. Assim, um polígono regular de lados pode ser visto como a junção de triângulos isósceles. Esses triângulos isósceles são todos congruentes entre si pelo caso . Como consequência disso, ângulos opostos aos lados congruentes desses triângulos são todos congruentes. Na imagem, temos um octógono inscrito em uma circunferência, cujo ângulo central mede , pois . Como a soma das medidas dos ângulos internos de um triângulo é igual a , temos:
Portanto, .
C. De acordo com a imagem, temos um quadrado inscrito em uma circunferência, cujo ângulo central mede , pois . Usando o mesmo argumento do item anterior, temos:
Portanto, .
74. a ) Como o quadrado tem 4 lados, o ângulo central mede , pois .
b ) Resposta pessoal. Sugestão de resposta:
O passo a passo para desenhar um quadrado usando régua e compasso é dado pelo fluxograma a seguir.
Página CXXXII
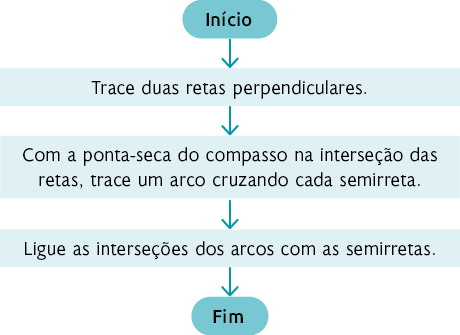
c ) Resposta pessoal. Espera-se que os estudantes sigam os passos do fluxograma do item anterior e construam um quadrado usando régua e compasso.
75. a ) Resposta pessoal. Espera-se que os estudantes justifiquem que os triângulos com vértice em O e em dois vértices consecutivos do hexágono são equiláteros. Sendo assim, o hexágono está inscrito em uma circunferência e seu ângulo central mede . Além disso, os seis lados desse polígono são congruentes, pois cada triângulo formado na construção do polígono é equilátero.
b ) Resposta pessoal. Sugestão de resposta:
Uma maneira de desenhar um hexágono regular usando régua e o esquadro é dado pelo seguinte fluxograma.

Questão 12. Efetuando os cálculos, temos:
Portanto, a medida do comprimento aproximado da circunferência é .
Atividades
76. a ) Para , temos:
Portanto, a medida do comprimento da circunferência é .
b ) Para , temos:
Portanto, a medida do comprimento da circunferência é .
c ) Para , temos:
Portanto, a medida do comprimento da circunferência é .
d ) Para , temos:
Portanto, a medida do comprimento da circunferência é .
77. a ) Usando a fórmula , vamos calcular a medida do comprimento da circunferência da roda do carro do pai do Rafael.
Logo, a circunferência da roda mede aproximadamente de comprimento.
Calculando em metro a medida da distância aproximada percorrida pelo carro quando a roda dá uma volta, obtemos , pois .
b ) Percorrer é o mesmo que percorrer . Do item anterior, verificamos que o carro percorre quando a roda dá uma volta completa. Como , então podemos concluir que a roda dá aproximadamente 704 voltas quando o carro percorre .
78.
Portanto, o comprimento do raio dessa circunferência mede .
Página CXXXIII
79. Usando a fórmula , vamos calcular a medida do comprimento da circunferência de centro cujo raio mede .
Logo, a medida de comprimento dessa circunferência é igual a . Sabemos que uma volta completa corresponde a . Assim, o ângulo de corresponde a de uma volta, visto que . Como o ângulo mede , a parte da linha vermelha que é um arco tem a medida de comprimento igual a da medida do comprimento da circunferência. Assim, essa parte da linha vermelha mede , pois . O restante dela é formado por dois segmentos com medidas de comprimento iguais , ou seja, essa parte mede . Adicionando essas medidas, obtemos .
Portanto, o comprimento aproximado da linha vermelha mede .
80. Para , temos:
Logo, essa circunferência mede aproximadamente de comprimento.
Para , temos:
Logo, essa circunferência tem aproximadamente de medida do comprimento.
Desse modo, em 10 voltas, a criança sentada no cavalo percorrerá aproximadamente , pois , e a criança sentada no cavalo percorrerá aproximadamente , pois .
Como , a criança sentada no cavalo percorrerá a mais do que a criança sentada no cavalo . Portanto, a alternativa b é a correta.
O que eu estudei?
1. Resposta pessoal. Sugestões de resposta:
a ) Vamos calcular a quantidade de lados de um polígono convexo que tenha 9 diagonais. Temos:
Sendo assim, a quantidade de lados que o polígono deve ter satisfaz .
Para , temos , isto é, o polígono convexo tem 6 lados.
b ) Vamos calcular a quantidade de lados de um polígono convexo que tenha 20 diagonais. Temos:
Sendo assim, a quantidade de lados que o polígono deve ter satisfaz .
Para , temos , isto é, o polígono convexo tem 8 lados.
c ) Vamos calcular a quantidade de lados de um polígono convexo que tenha 5 diagonais. Temos:
Sendo assim, a quantidade de lados que o polígono deve ter satisfaz .
Para , temos , isto é, o polígono convexo tem 5 lados.
2. Para resolver os itens dessa atividade, vamos usar a fórmula que permite calcular a soma das medidas dos ângulos internos de um polígono convexo.
a ) Para , temos:
Página CXXXIV
Portanto, a soma das medidas dos ângulos internos é igual a .
b ) Para , temos:
Portanto, a soma das medidas dos ângulos internos é igual a .
c ) Para , temos:
Portanto, a soma das medidas dos ângulos internos é igual a .
d ) Para , temos:
Portanto, a soma das medidas dos ângulos internos é igual a .
3. a ) Calculando a soma das medidas dos ângulos internos de um pentágono regular, temos:
Logo, a soma das medidas dos ângulos internos de um pentágono regular é igual a . Como os ângulos internos de um polígono regular são congruentes, a medida de cada ângulo interno de um pentágono regular é igual a , pois .
b ) Calculando a soma das medidas dos ângulos internos de um octógono regular, temos:
Logo, a soma das medidas dos ângulos internos de um octógono regular é igual a . Como os ângulos internos de um polígono regular são congruentes, a medida de cada ângulo interno de um octógono regular é igual a , pois .
c ) Calculando a soma das medidas dos ângulos internos de um decágono regular, temos:
Logo, a soma das medidas dos ângulos internos de um decágono regular é igual a . Como os ângulos internos de um polígono regular são congruentes, a medida de cada ângulo interno de um decágono regular é igual a , pois .
d ) Calculando a soma das medidas dos ângulos internos de um dodecágono regular, temos:
Logo, a soma das medidas dos ângulos internos de um dodecágono regular é igual a . Como os ângulos internos de um polígono regular são congruentes, a medida de cada ângulo interno de um dodecágono regular é igual a , pois .
4. Sendo um polígono convexo com lados, a quantidade de diagonais que partem de um mesmo vértice é dada por . Se partem 7 diagonais de cada vértice de um polígono, então ou, ainda, . Portanto, o polígono tem 10 lados.
5. De um vértice do hexágono convexo partem 3 diagonais, pois . Logo, do vértice comum aos três hexágonos vão partir 9 diagonais, ou seja, 3 diagonais de cada hexágono.
6. Ao traçarmos segmentos do centro de um polígono regular aos seus vértices, dividiremos esse polígono em triângulos. A quantidade de triângulos nessa divisão é igual à quantidade de lados do polígono. Esses triângulos são todos isósceles e congruentes entre si pelo caso . O fato de serem isósceles implica que os ângulos opostos aos lados congruentes são congruentes e, pela congruência, esses ângulos são congruentes em todos os triângulos. Desse modo, a soma das medidas desses ângulos em um dos triângulos é igual à medida do ângulo interno do polígono. Sendo assim, fazendo menos a medida do ângulo interno do polígono, obtemos o medida do ângulo central e, dividindo pela medida do ângulo central, encontramos a quantidade de lados do polígono.
a ) Se o ângulo interno de um polígono regular mede , a medida do ângulo central correspondente a ele é dada por . Logo, esse polígono tem 20 lados, pois . Portanto, esse polígono é icoságono regular.
b ) Se o ângulo interno de um polígono regular mede , a medida do ângulo central é dada por . Logo, esse polígono tem 3 lados, pois . Portanto, esse polígono é triângulo equilátero.
c ) Se o ângulo interno de um polígono regular mede , a medida do ângulo central é dada por . Logo, esse polígono tem 6 lados, pois . Portanto, esse polígono é hexágono regular.
7. O polígono A é um hexágono regular e a soma das medidas dos seus ângulos internos é dada por:
Página CXXXV
Logo, a soma das medidas dos ângulos internos do hexágono regular é igual a .
O polígono B é um triângulo equilátero e a soma das medidas dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos do triângulo equilátero é igual a .
O polígono C é um heptágono regular e a soma das medidas dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos do heptágono regular é igual a .
O polígono D é um pentágono regular e a soma das medidas dos seus ângulos internos é dada por:
Logo, a soma das medidas dos ângulos internos do pentágono regular é igual a .
Portanto, a soma das medidas dos ângulos internos é maior do que nos polígonos A e C.
8. A soma das medidas dos ângulos externos de qualquer polígono convexo é igual a . Desse modo, temos:
Portanto, .
9. Os ângulos opostos aos ângulos e , que têm as mesmas medidas, são ângulos internos de um polígono convexo de 5 lados no qual os outros 3 ângulos são ângulos retos.
A soma das medidas dos ângulos internos de um polígono convexo de 5 lados é dada por:
Logo, a soma das medidas dos ângulos internos desse polígono é igual a . Desse modo, temos:
Portanto, e a alternativa correta é a a.
10. O triângulo é isósceles de base . Assim, os ângulos e são congruentes. Como a soma das medidas dos ângulos internos de um triângulo é igual a e o ângulo mede , temos:
Portanto, .
O triângulo é isósceles de base . Desse modo, os ângulos e são congruentes, ou seja, .
Como a soma das medidas dos ângulos internos de um triângulo é igual a , temos:
A medida do ângulo é igual à soma das medidas dos ângulos e . Sendo assim, temos:
Portanto, a alternativa correta é a a.
11. a ) As diagonais de um losango se cruzam formando um ângulo reto, ou seja, .
b ) As diagonais de um losango são bissetrizes dos ângulos internos. Assim, . O losango é um caso particular de paralelogramo e os ângulos opostos de um paralelogramo são congruentes. Desse modo, e . Como um losango é um quadrilátero e a soma das medidas dos ângulos internos de um quadrilátero é igual a , temos:
Logo, .
Página CXXXVI
12. Seja a medida do comprimento do lado menor e a medida de comprimento do lado maior do cartão. Juntando os 8 cartões pelos lados maiores, Juliana formará a fila menor, cujo comprimento mede . Assim, temos:
Logo, o comprimento do lado menor mede . Agora, juntando os 8 cartões pelos lados menores, Juliana formará a fila maior, cujo comprimento mede . Assim, temos:
Logo, o comprimento do lado maior mede .
Adicionando as medidas dos lados, obtemos , ou seja, o perímetro de cada cartão mede .
Portanto, a alternativa correta é a b.
13. O lado da tira, antes de ser dobrado, representa um ângulo de . Ao dobrarmos a tira de papel ao longo da linha tracejada, construímos dois ângulos consecutivos, ambos medindo (o ângulo que foi dobrado e o ângulo formado pela parte dobrada).
Portanto, a medida do ângulo é e a alternativa correta é a c.
14. Qualquer corda que passa pelo centro de uma circunferência é chamada de diâmetro.
15. O segmento é um raio da circunferência de centro . Assim, o comprimento do raio dessa circunferência mede . O segmento é um diâmetro da circunferência de centro e, sendo a medida do comprimento do diâmetro igual ao dobro da medida do comprimento do raio, segue que mede . O segmento também é um raio da circunferência de centro e, como consequência disso, o comprimento do diâmetro da circunferência de centro mede . A medida do comprimento do diâmetro da circunferência de centro é igual à medida do comprimento do raio da circunferência de centro . Logo, o comprimento do diâmetro da circunferência de centro mede . Como é a medida do comprimento do diâmetro da circunferência de centro , segue que .
16. Usando a fórmula para o cálculo da medida do comprimento de uma circunferência, temos:
Logo, o comprimento da circunferência da roda-gigante mede . Portanto, uma pessoa que deu 8 voltas completas na roda-gigante percorreu aproximadamente , pois .
Unidade 11
Medidas de área
Atividades
1. A.
Portanto, a área do paralelogramo mede .
B.
Portanto, a área do paralelogramo mede .
C.
Portanto, a área do paralelogramo mede .
D.
Portanto, a área do paralelogramo mede .
2.
Portanto, o comprimento da base mede .
3. Primeiro, devemos identificar qual é a medida da altura do paralelogramo, sabendo que ela corresponde a 30% de . Como 1% de corresponde a , multiplicando o resultado obtido por 30, obtemos a medida da altura, isto é, .
Em seguida, usamos a fórmula que permite calcular a medida da área de um paralelogramo, ou seja, . Assim:
Portanto, a área desse paralelogramo mede .
4. A. Com uma régua, trace o lado com de medida de comprimento.
Posicione o centro do transferidor em e a linha de fé alinhada ao segmento e marque .
Depois disso, trace o lado com de medida de comprimento e indique o ângulo .
Com a ponta-seca do compasso em e abertura do compasso com medida de , trace um arco de circunferência.
Apoie a régua alinhada nessa marca e trace o lado de medida .
Repita os três últimos itens, mas agora em , traçando o lado de medida .
Trace o lado medindo , sabendo que .
Com a régua, meça com extremidade no vértice e marque um ponto no lado , construindo, assim, a altura .
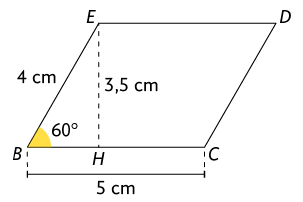
Página CXXXVII
Para obter a medida da área do paralelogramo , calculamos:
Portanto, a área do paralelogramo mede .
B. Com uma régua, trace primeiro o lado com a medida de .
Posicione o centro do transferidor em e a linha de fé alinhada ao segmento e marque . Depois disso, trace o lado com de medida de comprimento e indique o ângulo .
Com a ponta-seca do compasso em e abertura do compasso com medida de , trace um arco de circunferência.
Apoie a régua alinhada nessa marca e trace o lado de medida .
Repita os três últimos itens, mas agora em , traçando o lado de medida .
Trace o lado de medida , sabendo que .
Com a régua, meça com extremidade no vértice e marque um ponto no lado , construindo, assim, a altura .
Para obter a medida da área do paralelogramo , calculamos:
Portanto, a área do paralelogramo mede .
5. Para determinar a medida da área do jardim e da horta, devemos subtrair desse total a medida da área da casa. De acordo com as informações do enunciado, a medida da área do paralelogramo é dada por:
A medida da área da casa é dada por:
Realizando a subtração entre essas medidas, obtemos:
Portanto, a medida da área do jardim e da horta correspondem a .
6. A. Como , então a área do triângulo mede .
B. Como , então a medida da área do triângulo mede .
C. Como , então a medida da área do triângulo mede .
7. A. Para obter a área da região colorida de amarelo, devemos adicionar a medida da área dos três triângulos amarelos. De acordo com a figura, a medida da base desses triângulos é , e , respectivamente.
Medida da área do triângulo cuja base mede :
, ou seja, .
Medida da área do triângulo cuja base mede :
, ou seja, .
Medida da área do triângulo cuja base mede :
, seja, .
A adição das medidas das áreas obtidas é dada por:
Portanto, a área da região colorida de amarelo mede .
B. De acordo com a figura, a área da região colorida de amarelo é formada por um retângulo e um triângulo.
Medida da área do retângulo:
Medida da área do triângulo:
, ou seja, .
Adicionando as medidas dessas áreas, temos:
Portanto, a área colorida de amarelo mede .
8.
Portanto, a altura do triângulo mede de comprimento.
9. a ) Considere a base do triângulo como e a altura como . Assim, temos:
b ) Substituindo na equação obtida no item anterior, temos:
Assim, o valor de é .
10. a ) Sendo a medida da base e a medida da altura, podemos reescrever a fórmula de cálculo da área como .
Página CXXXVIII
De acordo com o enunciado e com a imagem, a base de ambos os triângulos mede e a altura de ambos os triângulos corresponde a . Assim, a área de ambos os triângulos é dada por .
Para obter a área total, devemos adicionar a medida da área do paralelogramo às medidas das áreas dos dois triângulos.
Substituindo as expressões que representam as medidas da área do paralelogramo e da área do triângulo, temos:
Portanto, a área total da figura é representada pela expressão .
b ) Sendo , obtemos o valor de substituindo na fórmula dada no enunciado. Assim:
Substituindo e na expressão do item anterior, temos:
.
Logo, a medida da área corresponde a .
11. Resposta pessoal. Sugestão de resposta: De acordo com as medidas indicadas, determine a medida da área do triângulo. Resposta: .
12. I: Para utilizar a fórmula de Herão, devemos primeiro calcular a medida do semiperímetro do triângulo.
Substituindo na fórmula, temos:
Portanto, a medida da área será aproximadamente .
II: Para utilizar a fórmula de Herão, devemos primeiro calcular a medida do semiperímetro do triângulo.
Substituindo na fórmula, temos:
Portanto, a medida da área será aproximadamente .
III: Para utilizar a fórmula de Herão, devemos primeiro calcular a medida do semiperímetro do triângulo.
Substituindo na fórmula, temos:
Portanto, a medida da área será .
IV: Para utilizar a fórmula de Herão, devemos primeiro calcular a medida do semiperímetro do triângulo.
Substituindo na fórmula, temos:
Portanto, a medida da área será aproximadamente .
13. Para os cálculos dessa atividade, devemos usar a fórmula , que permite calcular a área do trapézio.
A. Substituindo na fórmula os valores dados na figura, temos:
Assim, a área do trapézio mede .
B. Substituindo na fórmula os valores dados na figura, temos:
Assim, a medida da área do trapézio é .
C. Nesse trapézio, a medida da base maior corresponde à adição de três medidas.
Substituindo na fórmula os valores, temos:
Assim, a área do trapézio mede .
14. a ) Como a medida da área desse trapézio é , o comprimento da base maior mede e o comprimento da base menor e a altura medem cada. Assim, podemos efetuar o seguinte cálculo.
Página CXXXIX
Portanto, o valor de corresponde a .
b ) Como e a medida do comprimento da base maior corresponde a , substituindo o valor de , temos:
Portanto, a base maior mede de comprimento.
15. Substituindo na fórmula os valores apresentados na atividade, temos:
Portanto, a medida de comprimento da base menor do trapézio corresponde a .
16. Inicialmente, devemos determinar as medidas da base maior, da base menor e da altura de cada trapézio, sendo cada quadradinho da malha quadriculada equivalente a . Em seguida, calcularemos suas respectivas medidas de área.
Trapézio A:
Medida da base maior:
Medida da base menor:
Medida da altura:
Substituindo os valores obtidos na equação, temos:
Assim, a medida da área do trapézio A é .
Trapézio B:
Medida da base maior:
Medida da base menor:
Medida da altura:
Substituindo os valores obtidos na equação, temos:
Assim, a área do trapézio B mede .
Trapézio C:
Medida da base maior:
Medida da base menor:
Medida da altura:
Substituindo os valores obtidos na equação, temos:
Assim, a área do trapézio C mede .
Trapézio D:
Medida da base maior:
Medida da base menor:
Medida da altura:
Substituindo os valores obtidos na equação, temos:
Assim, a área do trapézio D mede .
Trapézio E:
Medida da base maior:
Medida da base menor:
Medida da altura:
Substituindo os valores obtidos na equação, temos:
Assim, a área do trapézio E mede .
17. Para calcular a medida da área do trapézio, utilizamos a fórmula .
Substituindo os valores de cada quadro na fórmula, temos:
Quadro A:
Portanto, o valor de é .
Página CXL
Quadro B:
Portanto, o valor de é .
Quadro C:
Portanto, o valor de é .
18. Para obter a medida da área da superfície do tampo da mesa, devemos adicionar a medida da área do retângulo à medida da área dos dois trapézios isósceles congruentes.
Como os trapézios são congruentes, devemos calcular a medida da área de um trapézio e multiplicar o resultado por 2. Assim, temos:
Como são 2 trapézios, multiplicamos o resultado por 2.
Adicionando as medidas obtidas, temos:
Portanto, a área da superfície do tampo mede .
19. Devemos calcular a medida da área de cada face e, em seguida, adicionar os resultados para obter a medida da área total da superfície do prisma reto.
Medida da área do retângulo menor:
Medida da área do retângulo maior:
Como os trapézios são congruentes, podemos multiplicar o resultado por 2 para obter a soma das medidas de suas áreas.
Como há 2 paralelogramos congruentes, podemos multiplicar o resultado por 2 para obter a soma da medida da área dos paralelogramos.
Logo, a medida da área total é dada por:
20. A.
Portanto, a área do losango mede .
B.
Portanto, a área do losango mede .
C.
Portanto, a área do losango mede .
D.
Portanto, a área do losango mede .
21. Usando a fórmula , temos:
Portanto, o comprimento da diagonal maior mede .
22. Usando a fórmula , temos:
Portanto, o comprimento da diagonal menor mede .
23. a ) Usando a fórmula , temos:
Assim, o valor de x é .
b ) A medida da diagonal maior é dada por , ou seja, .
24. Devemos calcular a medida da área de cada face e, em seguida, adicionar essas medidas para determinar a medida da área total da superfície do prisma reto.
Para calcular a medida da área das faces laterais, sabemos que quatro faces têm a mesma medida de altura e a mesma medida da base . Assim, podemos multiplicar por 4 a medida da área de uma face para obter a soma das medidas das áreas das faces laterais.
A área total das bases do prisma é a soma das medidas de áreas de dois losangos congruentes. Então, temos:
Página CXLI
Somando os resultados obtidos, temos:
Portanto, a área total da superfície do prisma reto mede .
25. Resposta pessoal. Sugestão de resposta:
Uma prefeitura vai revitalizar uma praça da cidade com formato de losango. Para elaborar o projeto, é preciso determinar a medida da área da praça representada pela figura. Qual é a medida da área dessa praça?
Resposta: A medida da área da praça é dada por:
, ou seja, .
26. Como a fórmula para calcular a medida da área do círculo corresponde a , substituindo os valores, temos:
A.
B.
C.
D.
E. Sabendo que a medida do comprimento do raio corresponde à metade da medida do comprimento do diâmetro, temos:
Assim, a medida da área é dada por:
F. Sabendo que a medida do comprimento do raio corresponde à metade da medida do comprimento do diâmetro, temos:
Assim, a medida da área é dada por:
27.
Portanto, a área desse círculo mede .
28. Sabemos que a fórmula da medida da área de um círculo é .
A. Medida da área do círculo inteiro:
Calculando a metade da medida da área desse círculo, temos:
, ou seja, .
B. Medida da área do círculo inteiro:
Calculando da medida da área desse círculo, temos:
, ou seja, .
C. Medida da área do círculo inteiro:
Calculando da medida da área desse círculo, temos:
, ou seja, .
D. Medida da área do círculo inteiro:
Calculando da medida da área desse círculo, temos:
, ou seja, .
29.
Desse modo, temos:
Portanto, a área da circunferência mede .
30.
Portanto, o comprimento do raio mede .
31. Método do Papiro de Rhind:
A medida do comprimento do diâmetro é dada por , e o comprimento do lado do quadrado mede . Calculando a medida da área do quadrado, obtemos . Assim, por meio do método utilizado no Papiro de Rhind, verificamos que a medida da área é .
Utilizando a fórmula, temos:
Ou seja, a medida da área obtida por meio da fórmula é .
32. a ) Para que a região circular seja máxima, a medida do comprimento do diâmetro deve ser . Assim, a medida do comprimento do raio deve ser , pois é a metade da medida do comprimento do diâmetro.
b ) A medida da área da região circular é
, ou seja, .
33. Como a medida do comprimento do raio é a metade da medida do comprimento do diâmetro, temos . Então:
Portanto, a medida da área em que será construído um parque para as crianças é .
A medida da área do terreno com formato retangular é dada por:
Logo, a medida da área aproximada do terreno que não está reservada para a construção do parque será , pois .
34. A. Devemos calcular a medida da área do retângulo e, em seguida, subtrair a medida da área das três circunferências.
Como a altura do retângulo mede de comprimento e a medida da base é dada por , então a medida da área do retângulo será:
A medida da área da circunferência de centro O será igual a:
Página CXLII
A medida da área da circunferência de centro P será igual a:
A medida da área da circunferência de centro Q será igual a:
Portanto, a medida da área em verde corresponde a , pois:
B. Devemos calcular a medida da área da circunferência, sendo , e, em seguida, subtrair a medida da área do triângulo.
Medida da área da circunferência:
Medida da área do triângulo:
Portanto, a medida da área em verde corresponde a , pois .
35. Resposta pessoal. Sugestão de resposta:
Qual é a medida da área da tampa da lata de leite em pó?
Resposta:
Portanto, a área da tampa mede .
36. Sabemos que para calcular a medida da área do setor circular utilizamos a equação .
A. Medida da área do setor circular amarelo:
Portanto, a medida da área corresponde a .
B. Medida da área do setor circular amarelo:
Portanto, a medida da área corresponde a .
37. A. A razão entre a medida do ângulo central e a volta completa no círculo é .
Medida da área total do círculo:
Calculando da medida da área total do círculo, temos:
Portanto, a medida da área aproximada do setor circular é .
B. A razão entre a medida do ângulo central e a volta completa no círculo é .
Medida da área total do círculo:
Calculando da medida da área total do círculo, temos:
Portanto, a medida da área aproximada do setor circular é .
C. A razão entre a medida do ângulo central e a volta completa no círculo é .
Medida da área total do círculo:
Calculando da medida da área total do círculo, temos:
Portanto, a medida da área aproximada do setor circular é .
38. a ) Como a figura representa um semicírculo, temos:
Assim:
b ) A medida da área do setor circular laranja é dada por:
Portanto, a área do setor circular laranja mede aproximadamente .
A medida da área do setor circular verde é dada por:
Portanto, a área do setor circular laranja mede aproximadamente .
39. a )
b ) Para obter a medida da área total da superfície do cone, devemos primeiro calcular a medida da área do setor circular.
Página CXLIII
Em seguida, calculamos a medida da área da base.
Adicionando os dois resultados, temos:
40. A medida da área do quadrado é dada por:
A medida da área do setor circular é dada por:
Calculando a diferença entre os dois resultados, temos:
Portanto, a área considerada mede aproximadamente .
41. Para os itens desta atividade, vamos usar a fórmula que permite calcular a medida da área de uma coroa circular.
A.
Portanto, a área da coroa mede .
B.
Portanto, a área da coroa mede .
C.
Portanto, a área da coroa mede .
D.
Portanto, a área da coroa mede .
42. As medidas desta atividade são aproximadas.
Região amarela:
Portanto, a área da coroa circular pintada de amarelo mede .
Região vermelha:
Portanto, a área da coroa circular pintada de vermelho mede .
Região verde:
Portanto, a área da coroa circular pintada de verde mede .
43. a ) A medida da área da folha com as etiquetas é de , isto é, .
b ) A medida da área da coroa é dada por:
Portanto, a medida da área de cada etiqueta é aproximadamente .
c ) Como a medida da área ocupada pelas etiquetas equivale a , então a medida da área da folha que não faz parte das etiquetas corresponde a , ou seja, a área corresponde a aproximadamente .
44.
Para obter a medida da área da região verde, devemos considerar que . Assim, a medida da área verde corresponde a , ou seja, aproximadamente .
45.
Sendo assim, o material disponível não será suficiente, pois a medida da área da nova região a ser pavimentada mede .
Portanto, a alternativa correta é a e.
Página CXLIV
O que eu estudei?
1.
Portanto, a altura desse paralelogramo mede de comprimento.
2. As medidas de área são iguais, porque todas as peças do quadrado foram usadas para compor o triângulo, o retângulo e o trapézio, e não foram acrescentadas outras peças na montagem.
Portanto, a medida de área do quadrado foi preservada nas medidas de área das figuras obtidas.
3. A. Medida da área do quadrado:
Medida da área de cada triângulo congruente:
Medida da área total:
Portanto, a área total da figura mede .
B. Medida da área do paralelogramo:
Medida da área de cada trapézio:
Medida da área total:
Portanto, a área total da figura mede .
C. Medida da área do retângulo maior:
Medida da área do retângulo menor:
Medida da área do trapézio:
Medida da área total:
Portanto, a área total da figura mede .
4. A.
Portanto, a altura mede de comprimento.
B.
Portanto, a base menor mede .
C.
Portanto, o comprimento da diagonal menor mede .
D.
Portanto, o comprimento da base mede .
5. Como a medida da área do triângulo maior corresponde a da medida da área do retângulo e a medida da área de cada triângulo menor corresponde a , então a adição das medidas das áreas em cinza é dada por:
Assim, a área da região sombreada corresponde a da medida da área do retângulo.
Portanto, a alternativa correta é a c.
6. A. Medida da área do quadrado:
A medida da área do setor circular:
Medida da região verde:
Portanto, a área da região verde mede aproximadamente .
B. Medida da área do quadrado:
A medida da área da região amarela corresponde à medida da área de um círculo com diâmetro medindo , ou seja, com raio medindo . Assim, temos:
Medida da região verde:
Portanto, a área da região verde mede aproximadamente .
7. Medida da área do círculo maior:
Medida da área do círculo menor:
Medida da área da região laranja:
Portanto, a área da região laranja mede aproximadamente .
Página CXLV
8. A. Medida da área do círculo:
Portanto, a área do círculo mede .
B. Como , a razão entre a medida do ângulo central e a volta completa do círculo é .
Medida da área total do círculo:
Calculando da medida da área total do círculo, temos:
Portanto, a área aproximada do setor circular mede aproximadamente .
C. A medida da área da coroa é dada por:
.
Portanto, a área da coroa circular mede .
D. Medida da área do retângulo:
Medida da área do setor circular:
.
Subtraindo os resultados, temos:
Portanto, a área da região laranja mede .
9. Dos 5 círculos, há 2 pintados de verde e 3 pintados na cor laranja. Então, a razão entre a medida da área pintada de verde e a medida da área pintada de laranja é .
Portanto, a alternativa correta é a d.
Unidade 12
Medidas de volume e de capacidade
Atividades
1. a ) Como , então .
b ) Como , então .
c ) Como , então .
d ) Como , então .
e ) Como , então .
f ) Como , então .
g ) Como , então .
h ) Como , então .
i ) Como , então .
j ) Como , então .
k ) Como , então .
l ) Como , então .
2. Para comparar a quantidade de concreto produzida pelos trabalhadores, vamos calcular quanto Armando produziu em decímetros cúbicos.
De acordo com o enunciado, José produziu . Comparando as duas produções na mesma unidade de medida, verificamos que .
Portanto, Armando produziu maior quantidade de concreto do que José neste dia.
Questão 1. Calculando a medida do volume do cubo, temos:
Portanto, a alternativa correta é a b.
Atividades
3. Realizando os cálculos, temos:
a )
b )
c )
d )
e )
4. De acordo com a medida do volume em cada um dos itens, temos as seguintes dimensões:
a )
Portanto, .
b )
Portanto, .
c )
Portanto, .
d )
Portanto, .
e ) Convertendo em centímetros cúbicos a medida do volume que está expressa em decímetros cúbicos, temos:
Página CXLVI
Assim:
Portanto, .
5. Calculando a medida do volume, temos:
Portanto, o volume desse cubo mede .
6. Para resolver essa questão, primeiro, calculamos a medida do volume do paralelepípedo reto retângulo.
Logo, o volume desse paralelepípedo mede .
Como as arestas do cubo têm a mesma medida de comprimento, fazemos:
Portanto, o comprimento da aresta do cubo deve medir .
7. A medida do volume do bloco de madeira que Carlos vai usar é dada por:
Logo, o volume desse bloco mede .
Como 20% do bloco de madeira serão destinados à construção do telhado (20% de ), temos:
Portanto, serão utilizados do bloco de madeira para a construção do telhado.
8. Indicando por a medida do volume do paralelepípedo e por a medida do volume do cubo, temos:
Logo, .
Logo, .
Convertendo em decímetros cúbicos a medida do volume do cubo, temos:
, ou seja, .
Calculando a diferença entre as medidas dos volumes, obtemos:
Portanto, a diferença entre a medida do volume desse paralelepípedo reto retângulo e desse cubo é .
9. Calculando a medida do volume desse cubo, em centímetros cúbicos, temos:
, ou seja, .
Convertendo essa medida em decímetros cúbicos, temos:
, ou seja,
Convertendo-a em metros cúbicos, temos:
, ou seja, .
Portanto, as medidas que correspondem ao volume desse cubo são , e .
10. Para resolver os itens dessa atividade, vamos calcular inicialmente a medida do volume de cada paralelepípedo reto retângulo. Depois, usaremos essa medida para calcular a parte indicada e, se necessário, efetuar a conversão entre unidades de medida.
a )
Portanto, o volume do paralelepípedo mede .
Calculando 30% desse volume, obtemos:
30% de , ou seja, .
Por fim, fazemos a conversão entre as unidades de medida.
.
Portanto, a informação apresentada nesse item é verdadeira.
b ) , ou seja, .
Calculando a quarta parte da medida desse volume, temos:
Como corresponde a, a informação apresentada nesse item é verdadeira.
c )
Portanto, o volume desse cubo mede .
Calculando da medida desse volume, temos: .
Como corresponde a e , a informação apresentada nesse item é falsa. Sugestão de correção: da medida do volume do cubo C corresponde a .
11. a ) A medida do volume interno do recipiente é dada por:
, ou seja, .
b ) Para identificar qual dos objetos tem a maior medida de massa, vamos converter todas as medidas do quadro em decímetro cúbico.
Objeto A: , ou seja, .
Objeto B: , ou seja, .
Objeto C: , ou seja, .
Objeto D: , ou seja, .
Objeto E: .
Portanto, o objeto D tem a maior medida de volume e o objeto B tem a menor medida.
Página CXLVII
c ) Sim. Para determinar qual objeto fez a água transbordar, vamos calcular a medida do volume da parte vazia do recipiente.
, ou seja, .
Logo, os objetos cujas medidas do volume são maiores do que farão a água transbordar.
Comparando os resultados, verificamos que apenas o objeto D fará a água transbordar.
d ) Para responder a esse item, vamos calcular o volume de água que a altura indicada representa no volume do recipiente e, em seguida, comparar com os objetos do experimento.
I: Como a água subiu , ou seja, , temos:
, ou seja, .
Portanto, o objeto E fez o nível da água subir .
II: Como a água subiu , ou seja, , temos:
, ou seja, .
Portanto, o objeto B fez o nível de água subir .
III: Como a água subiu , ou seja, , temos:
, ou seja, .
Portanto, o objeto C fez o nível de água subir .
De acordo com os resultados obtidos, temos a seguinte relação:
I-E; II-B; III-C.
12. Calculando a medida do volume total do vaso, temos:
, ou seja, .
Como a medida do volume de água representa metade dessa medida, então:
, isto é, .
A quantidade de pedrinhas compradas depende da medida do volume do vaso, desconsiderando 10 centímetros da medida da altura. Calculando essa medida de volume, obtemos:
, ou seja, .
Logo, a medida do volume a ser preenchido com pedrinhas é.
Cada pedrinha tem . Então:
Portanto, foram compradas 280 pedrinhas. Logo, a alternativa correta é a b.
13. A medida do volume das pastas é . Convertendo em centímetros cúbicos, temos:
, ou seja, .
Considere y a medida do volume da gaveta. Como essas pastas ocuparam 48% do total da gaveta, escrevemos e resolvemos a seguinte proporção:
Portanto, o volume total da gaveta mede .
Usando essas informações, podemos calcular a medida da altura da gaveta.
Portanto, a altura da gaveta mede .
14. Calculando a medida do volume de cada caixa, temos:
, ou seja, .
Convertendo a quantidade total de algodão doce em centímetros cúbicos, temos:
Sendo assim, calculamos a quantidade de caixas necessárias.
Portanto, são necessárias 25 caixas.
15. Indicando por a, b e c as medidas do comprimento das arestas do paralelepípedo feito por Giovana, as medidas do comprimento das arestas do paralelepípedo feito por João são , e . Logo, a medida do volume do paralelepípedo de Giovana é e o volume do paralelepípedo de João será dado por:
, ou seja, .
Portanto, a alternativa correta é a c.
16. a ) Primeiro, calculamos a medida do volume do objeto:
, ou seja, .
Em seguida, calculamos a medida do volume de cada uma das caixas.
Caixa 1: , ou seja, .
Caixa 2: , ou seja, .
Caixa 3: , ou seja, .
Caixa 4: , ou seja, .
A caixa 5 não é uma opção, pois as medidas de suas dimensões são menores do que e o objeto não caberia na caixa.
Portanto, a caixa 2 tem a menor medida de volume, ou seja, o espaço livre em seu interior será o menor possível.
b ) Como o volume desse objeto cúbico mede , então o comprimento da aresta desse objeto mede , pois . Portanto, não é possível armazenar nessa caixa esse outro objeto, pois o comprimento da aresta do outro objeto ultrapassa a medida das dimensões da caixa.
17. Como a espessura de cada face mede , então as medidas internas da caixa são diminuídas em para cada face, ou seja, no total. Logo, temos as seguintes dimensões: , e .
Calculando a medida do volume de madeira, temos:
Portanto, a alternativa correta é a c.
18. Resposta pessoal. Sugestão de resposta:
Qual é a medida do volume dessa caixa em centímetro cúbico? Resposta: .
Página CXLVIII
Questão 2.
a )
b )
Atividades
19. a ) Como , então .
b ) Como , então .
c ) Como , então .
d ) Como , então .
e ) Como , então .
f )
g ) Como , então .
h ) Como , então .
i ) Como , então .
j ) .
k ) Como , então .
l ) Como , então .
20. Primeiro, convertemos em decímetros cúbicos:
Assim, .
Como , temos: .
Portanto, a medida de capacidade desse recipiente é .
21. Calculando a medida do volume de cada um dos recipientes, temos:
Recipiente A:
, ou seja, .
Recipiente B:
, ou seja, .
Recipiente C:
, ou seja, .
Como , então os recipientes A e C têm água suficiente para completar uma garrafa de um litro.
22. a ) Calculando a quantidade de litros, temos:
Portanto, foram consumidos de água nesse mês.
b ) Como o consumo diminuiu , então foram consumidos , pois. Convertendo esse consumo em metros cúbicos, obtemos: .
Portanto, houve um consumo de nesse mês.
23. Como , então . Sendo assim, considerando x a medida do comprimento interno, em metro, temos:
Portanto, seu comprimento interno mede .
24. Primeiro, determinamos a medida do volume e, em seguida, calculamos sua capacidade.
a ) , ou seja, .
Como , nesse recipiente cabem de água.
b ) , ou seja, .
Como , nesse recipiente cabem de água.
c ) , ou seja, .
Como , nesse recipiente cabem de água.
d ) , ou seja, .
Como , nesse recipiente cabem de água.
e ) , ou seja, .
Como , nesse recipiente cabem de água.
f ) , ou seja, .
Como , nesse recipiente cabem de água.
25. A medida do volume desse reservatório é , pois . Como , verificamos que nesse reservatório cabem de água. Sendo bombeado, a cada segundo, o tempo necessário para encher o reservatório é dado por: .
Portanto, são necessários , que correspondem a , para encher o reservatório.
Página CXLIX
26. Inicialmente, vamos calcular a medida do volume da parte desse recipiente sem água.
, ou seja, .
Considere a medida do volume interno desse recipiente. Como a parte com água nesse reservatório equivale a 85%, ou seja, 0,85 da medida da capacidade total, obtemos:
Sendo assim, o volume interno do recipiente mede .
Como , calculamos:
Portanto, o volume interno desse recipiente mede .
27. Resposta pessoal. Sugestão de resposta:
Qual dos recipientes tem maior medida de capacidade?
Resposta: O recipiente com formato cilíndrico.
28. A medida do volume total dessa piscina é dada por:
, ou seja, .
Assim, a capacidade total dessa piscina mede .
Cada mangueira despeja de água por minuto. Como são 3 mangueiras, ao todo, serão despejados , ou seja, de água.
Calculando a quantidade de minutos, obtemos , ou seja, aproximadamente 1.412 minutos.
Portanto, a piscina estará cheia em, aproximadamente, 1.412 minutos.
29. a ) Calculando a medida do volume interno do recipiente, temos:
, ou seja, .
b ) Convertendo em decímetros cúbicos, temos:
, isto é, .
Assim, obtemos , que equivalem .
c ) Como a garrafa encheu completamente o recipiente, então a capacidade dessa garrafa é .
30. A medida do volume do paralelepípedo é dada por:
, ou seja, .
Assim, a medida da capacidade pode ser representada por, ou seja, .
a ) Dobrando-se a medida de uma de suas dimensões, temos:
, ou seja, .
Portanto, a afirmação apresentada nesse item é verdadeira.
b ) De acordo com os cálculos do item a, a medida da capacidade será . Logo, a afirmação desse item é falsa, ou seja, ao dobrar a medida de qualquer uma de suas dimensões, a medida da capacidade será .
c ) A afirmação desse item é falsa, pois, ao dobrar a medida de todas as arestas, temos:
, ou seja, .
Essa medida corresponde a .
d ) A afirmação é verdadeira, pois, ao triplicar a medida de qualquer uma das dimensões, temos:
, ou seja, .
Essa medida corresponde a .
e ) Essa afirmação é falsa, pois a medida de capacidade do paralelepípedo é 3 litros, o que corresponde a .
Sendo assim, são verdadeiras as afirmações dos itens a e d.
31. Resposta pessoal. Sugestão de resposta:
Um aquário tem de medida de capacidade e as medidas internas do comprimento e da largura são, respectivamente, e . Determine, em decímetros, a medida interna da altura desse aquário.
Resposta: .
32. Convertendo as medidas indicadas em centímetros cúbicos, temos:
a )
Como , vamos calcular a medida da altura que a água atingirá no recipiente, indicando por x essa medida.
, ou seja, ou, ainda, .
b )
Portanto, esse líquido ocupa uma medida de volume de . Considerando x a medida da altura que a água atingirá no recipiente, temos:
, ou seja, , ou ainda, .
c ) Medida do volume total do recipiente:
, ou seja, .
Logo, sua capacidade mede , que representa uma medida maior do que .
Portanto, a água não transbordará.
O que eu estudei?
1. Efetuando os cálculos, temos:
a )
Portanto, a igualdade é falsa.
b )
Portanto, a igualdade é falsa.
c )
Portanto, a igualdade é verdadeira.
d )
Portanto, a igualdade é verdadeira.
e )
Portanto, a igualdade é verdadeira.
Página CL
f )
Portanto, a igualdade é verdadeira.
g )
Portanto, a igualdade é verdadeira.
h )
Portanto, a igualdade é falsa.
Sendo assim, são verdadeiras as igualdades dos itens c, d, e, f e g.
2. Cada aresta mede de comprimento. Então, a medida do volume da caixa é dada por:
, ou seja, .
Como , então , ou seja, o volume da caixa mede .
Sabendo que o objeto tem , efetuamos uma subtração.
Sendo assim, obtemos uma diferença de .
Para converter esse resultado em , fazemos:
Portanto, sobrou na caixa uma medida de de volume.
3. Para esse cálculo, vamos considerar três paralelepípedos, todos com espessura de . Nesse caso, a medida do volume de concreto será dada por:
, ou seja, .
Logo, o mestre de obras deve pedir à usina um caminhão cuja capacidade máxima seja de .
Portanto, a alternativa correta é a c.
4. Como , temos:
Considerando , obtemos:
Como b representa a medida da dimensão de um paralelepípedo reto retângulo, vamos considerar o valor positivo, ou seja, .
Desse modo:
Portanto, as medidas do paralelepípedo são , e .
5. Inicialmente, calculamos a medida da altura da água.
Sendo assim, a medida do volume é dada por:
, ou seja, .
Como , a quantidade em litros de água será .
De acordo com as informações do problema, para cada , adiciona-se de produto. Então, para , serão adicionados , ou seja, .
Portanto, a alternativa correta é a b.
O que eu aprendi?
1. a )
b )
c )
d )
2. O conjunto representa , pois são os elementos que estão no conjunto A e no conjunto B simultaneamente. Portanto, .
3. Como são 5 algarismos e 5 vogais, as possibilidades serão , isto é, Oscar tem 25 possibilidades de compor essa senha.
4. Representando o triplo de um número por , podemos escrever e resolver a equação a seguir.
Portanto, o número é o 18.
5. Considere x a quantidade de carros e y a quantidade de motos nesse estacionamento. Logo, temos o seguinte sistema:
Resolvendo esse sistema pelo método da substituição, isolando x na primeira equação, temos:
Substituindo x por na segunda equação, obtemos:
Portanto, existem 10 motos nesse estacionamento.
6. a ) Para determinar a quantidade de proteínas em 10 biscoitos, vamos construir um quadro.
|
Quantidade de biscoitos |
Quantidade de proteínas (em gramas) |
|---|---|
|
6 |
3,1 |
|
10 |
x |
Portanto, em 10 biscoitos, há aproximadamente de proteínas.
b ) Para determinar a quantidade de quilocalorias no pacote, vamos construir um quadro.
Página CLI
|
Quantidade de quilocalorias () |
Medida de massa (em gramas) |
|---|---|
|
126 |
30 |
|
x |
200 |
Portanto, em todo pacote, há .
c ) Para determinar a quantidade de biscoitos nesse pacote, vamos construir um quadro.
|
Quantidade de biscoitos |
Medida de massa (em gramas) |
|---|---|
|
6 |
30 |
|
x |
200 |
Logo, há, ao todo, 40 biscoitos nesse pacote.
7. a ) Subtraindo a quantidade de água do começo do dia pela quantidade de água do final do dia, temos , ou seja, a quantidade de água utilizada nesse dia foi .
b ) Para determinar a porcentagem de água utilizada, vamos construir um quadro.
|
Quantidade de água (em ) |
Porcentagem (%) |
|---|---|
|
500 |
100 |
|
180 |
x |
Logo, a quantidade de água utilizada nesse dia representa 36% da medida da capacidade dessa caixa d'água.
8. a ) A soma das medidas dos ângulos internos de um quadrilátero é igual a . Então:
.
Logo, o quarto ângulo mede .
b ) O quadrilátero que tem todos os ângulos internos iguais é o retângulo. Portanto, cada ângulo interno desse quadrilátero mede .
c ) Como a soma das medidas dos ângulos internos de um quadrilátero é , temos:
Substituindo a medida x em cada um dos ângulos, obtemos:
; ; ; .
Portanto as medidas desses ângulos são , , e .
d ) A soma das medidas dos comprimentos dos lados de uma figura representa seu perímetro. Assim:
, ou seja, .
Substituindo a medida encontrada x, temos:
12; ; ; .
Portanto, os comprimentos dos lados desse quadrilátero medem , , e .
9. Resposta no final da seção Resoluções.
10. a ) Como , fazemos:
, ou seja, , que equivalem a .
b ) A medida do volume do cubo é dada por:
Portanto, o volume do cubo mede .
Como , temos .
11. Rotacionando a figura em no sentido horário em torno do ponto O, obtemos:
Portanto, a alternativa C está correta.
12. Para determinar a medida da área desse terreno, vamos calcular a medida da área dos dois trapézios separadamente.
, ou seja, ;
, ou seja, .
Adicionando as duas medidas, obtemos:
Portanto, a área do terreno mede .
Página CLII
Resolução referente à seção O que eu já sei?.
3. Usando a reta numérica como suporte, temos:
Com isso, podemos obter as seguintes conclusões.
a ) O número fica à esquerda de . Portanto, .
b ) O número fica à esquerda de 10. Portanto, .
c ) O número fica à direita de . Portanto, .
d ) O número 0 fica à esquerda de 6. Portanto, .
e ) O número fica à esquerda de 0. Portanto, .
f ) O número 9 fica à direita de . Portanto, .
5. Na reta numérica apresentada, cada unidade está dividida em 10 partes iguais. Nesse caso, verificamos que A: 0,2; B: 0,4; C: 0,6; D: 1,3; E: 1,5; F: 1,8; G: 2; H: 2,1; I: 2,5; J: 2,7.
Resolução referente à unidade 1.
22. a )
Portanto, a massa da Lua mede aproximadamente .
Resolução referente à unidade 2.
18. Para determinar a letra correspondente a cada número, vamos obter a forma decimal de cada número que está representado na forma fracionária.
Assim, identificamos entre quais inteiros o número decimal está localizado, conforme representado na reta numérica a seguir.
25. Para facilitar as comparações, obtemos a representação decimal das frações e dos radicais.
, , , e .
Assim, associando cada letra aos números apresentados, obtemos:
Resolução referente à unidade 5.
4. c ) Para construir a tabela, vamos calcular as frequências absoluta , relativa , acumulada e acumulada relativa para cada nota.
Nota 2,0:
Página CLIII
Nota 4,0:
Nora 5,0:
Nota 6,0:
Nota 7,0:
Nota 8,0:
Nota 9,0:
Nota 10,0:
|
Nota |
Frequência |
Frequência relativa |
Frequência acumulada |
Frequência acumulada relativa |
|---|---|---|---|---|
|
2,0 |
3 |
7,5% |
3 |
7,5% |
|
4,0 |
4 |
10% |
7 |
17,5% |
|
5,0 |
7 |
17,5% |
14 |
35% |
|
6,0 |
8 |
20% |
22 |
55% |
|
7,0 |
10 |
25% |
32 |
80% |
|
8,0 |
4 |
10% |
36 |
90% |
|
9,0 |
2 |
5% |
38 |
95% |
|
10,0 |
2 |
5% |
40 |
100% |
|
Total |
40 |
100% |
Fonte de pesquisa: registros do professor de Matemática.
Página CLIV
6. c ) Antes de construir a tabela, vamos calcular as frequências relativa, acumulada e acumulada relativa de cada faixa salarial.
Faixa salarial de :
Faixa salarial de :
Faixa salarial de :
Faixa salarial de :
Faixa salarial de :
|
Faixa salarial |
Frequência |
Frequência relativa |
Frequência acumulada |
Frequência acumulada relativa |
|---|---|---|---|---|
|
18 |
36% |
18 |
36% |
|
|
15 |
30% |
33 |
66% |
|
|
9 |
18% |
42 |
84% |
|
|
5 |
10% |
47 |
94% |
|
|
3 |
6% |
50 |
100% |
|
|
Total |
50 |
100% |
Fonte de pesquisa: departamento financeiro da empresa.
7. a ) Analisando o intervalo de classe referente à faixa salarial , concluímos que a amplitude dos intervalos deve ser 10. Nesse caso, os três intervalos considerados são:
; ; .
Para construir a tabela, determinamos as frequências: absoluta, relativa, acumulada e acumulada relativa de cada intervalo.
Faixa de medida de massa de :
Faixa de medida de massa de :
Faixa de medida de massa de :
|
Medida de massa |
Frequência |
Frequência relativa |
Frequência acumulada |
Frequência acumulada relativa |
|---|---|---|---|---|
|
12 |
50% |
12 |
50% |
|
|
9 |
37,5% |
21 |
87,5% |
|
|
3 |
12,5% |
24 |
100% |
|
|
Total |
24 |
100% |
Fonte de pesquisa: registros da professora do 3º ano.
Página CLV
12. a ) Para calcular a mediana, vamos, inicialmente, organizar as notas em ordem crescente.
4,0; 5,0; 5,0; 6,0; 6,0; 6,0; 6,0; 6,0; 6,5; 7,0;
7,0; 7,0; 7,0; 7,0; 7,5; 8,0; 8,0; 8,0; 8,0; 8,0;
8,0; 8,5; 9,0; 9,0; 9,0; 9,0; 9,5; 10; 10; 10.
A quantidade de notas é igual a 30, isto é, um número par. Assim, a mediana deve ser calculada por meio da média aritmética dos valores centrais, que nesse caso são 7,5 e 8,0.
,
então a mediana dessas notas é 7,75.
Como a nota que ocorre com mais frequência é 8,0, concluímos que 8,0 é a moda dessas notas.
A média aritmética dessas notas é dada por:
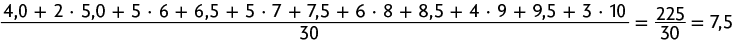
Portanto, a média aritmética dessas notas é igual a 7,5.
15. Calculando a média aritmética das medidas de temperatura, temos:
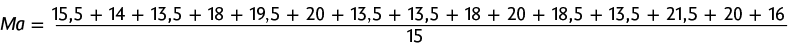
, ou seja, a média aritmética das medidas de temperatura é .
Colocando esses dados em ordem crescente, temos:
13,5; 13, 5; 13,5; 13,5; 14; 15,5; 16; 18; 18; 18,5; 19,5; 20; 20; 20; 21,5
Esse conjunto tem 15 elementos, e essa quantidade é representada por um número ímpar. Desse modo, a mediana é dada pelo valor central, que é .
A medida de temperatura com maior frequência é . Logo, a moda das medidas de temperatura é igual a .
Portanto, a alternativa correta é a b.
33. c ) No eixo horizontal, representamos os componentes curriculares que Rafael fez no 1º bimestre e, no eixo vertical, as médias. No eixo vertical, usamos uma escala tal que corresponde a 2,0 pontos de média e construímos as colunas relacionadas a cada componente curricular. Por fim, indicamos o título "Médias de Rafael de cada componente curricular do 1º bimestre de 2023" e a fonte de pesquisa "coordenação da escola de Rafael".
Médias de Rafael de cada disciplina do 1º bimestre de 2023
Fonte de pesquisa: coordenação da escola de Rafael.
Página CLVI
Questão 6. O diagrama de árvore que representa todas as possibilidades para cada algarismo é:
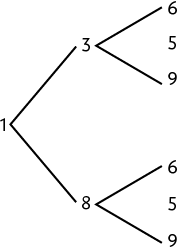
37. b ) O diagrama de árvore que indica todas as possibilidades ao retirar duas bolas, nesse caso, é:
Resolução referente à seção O que eu estudei? da unidade 5.
1. a ) Como o primeiro intervalo é , verificamos que sua amplitude é 4. Nesse caso, na tabela serão considerados os intervalos de classe:
; ; ; ; ; ; .
Para construir a tabela, vamos determinar as frequências absoluta, relativa, acumulada e acumulada relativa de cada intervalo.
Faixa de medida de altura de :
Faixa de medida de altura de :
Faixa de medida de altura de :
Faixa de medida de altura de :
Faixa de medida de altura de :
Faixa de medida de altura de :
Faixa de medida de altura de :
Página CLVII
|
Faixa de medida de altura |
Frequência (f) |
Frequência relativa (fr) |
Frequência acumulada (fa) |
Frequência acumulada relativa (far) |
|---|---|---|---|---|
|
4 |
11% |
4 |
11% |
|
|
4 |
11% |
8 |
22% |
|
|
8 |
22% |
16 |
44% |
|
|
13 |
36% |
29 |
80% |
|
|
4 |
11% |
33 |
91% |
|
|
1 |
3% |
34 |
94% |
|
|
2 |
6% |
36 |
100% |
|
|
Total |
36 |
100% |
Fonte de pesquisa: registros da professora de Educação Física.
2. b ) Mediana: Escrevendo os valores dos salários em ordem crescente, temos:
1.600, 1.600, 1.600, 1.600, 1.600, 1.640, 1.650, 1.650, 1.700, 1.720, 1.750, 1.790, 1790, 1.800, 1.870, 1.870, 1.870, 1.870, 1.870 e 1.870.
Como a quantidade de salários é um número par, a mediana é dada pela média aritmética dos valores centrais.
Portanto, a mediana dos salários dos funcionários é R$ 1.735,00.
Moda: O salário que ocorre com mais frequência é R$ 1.870,00.
Média: Calculando a média aritmética dos valores dos salários, obtemos:
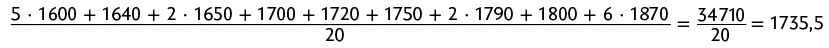
Portanto, a média dos salários dos funcionários é R$ 1.735,50.
Resolução referente à seção O que eu aprendi?.
9. A média é dada por:
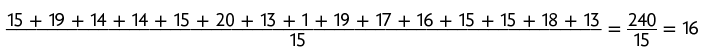
Para determinar a medida da mediana, colocamos os dados em ordem crescente.
13, 13, 14, 14, 15, 15, 15, 15, 16, 17, 17, 18, 19, 19, 20.
Como a quantidade de elementos é um número ímpar, o elemento central corresponde à medida da mediana. Como o elemento central é 15, a mediana é 15.
A moda é 15, pois é o número que mais se repete nesse conjunto de dados.
Portanto, a alternativa b está correta.