Página 43

UNIDADE

Ângulos

Fotografia. Duas meninas jogando Air Hockey. Há uma mesa lisa com desenhos circulares e as meninas seguram um suporte liso nas mãos que desliza sobre a mesa para tentar rebater um disco, que também desliza. Elas estão apoiadas em uma das mãos, enquanto disputam para acertar o disco. Há uma ilustração, em verde, indicando o ângulo formado pela trajetória do disco batendo na lateral da mesa. — Momento de disputa em uma mesa de Air Hockey, jogo no qual a principal estratégia de pontuação é o lançamento do disco em trajetórias angulares para desviá-lo do obstáculo do oponente.

Agora vamos estudar...

ângulos, seus elementos e algumas características;
bissetriz de um ângulo.

ORIENTAÇÕES AO PROFESSOR

A abertura da unidade apresenta uma partida do jogo Air Hockey, em que o objetivo é o jogador acertar o disco na caçapa adversária. Promova a análise da imagem e oriente os estudantes a relatar suas conclusões, verificando se eles relacionam o jogo com os conteúdos que serão estudados na unidade.

A ideia principal é abordar o conceito de ângulo, explorando a abertura do ângulo formada pela trajetória do disco.

Se achar conveniente, faça alguns questionamentos aos estudantes, como as sugestões a seguir.

a) Você conhece o jogo Air Hockey? Compartilhe sua experiência com os colegas da sala de aula.

b) Por que o uso de trajetórias angulares é uma boa estratégia nesse jogo?

c) Você conhece outro jogo que tem estratégia similar à do Air Hockey?

É possível que alguns estudantes reconheçam similaridades entre as jogadas do Air Hockey e as nesse jogo de bilhar. Explique a eles que, no jogo, algumas jogadas descrevem trajetórias angulares semelhantes à do Air Hockey para encaçapar uma bola.

Metodologias ativas

Para desenvolver o trabalho com esta página de abertura, avalie a possibilidade de usar a metodologia ativa Abordagem por pares. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Sugestão de avaliação

A fim de avaliar o conhecimento prévio dos estudantes sobre os conteúdos que serão trabalhados na unidade, reproduza o retângulo ABCD a seguir na lousa e peça-lhes que calculem em seu caderno a medida do ângulo x.

Resolução e comentários

Considerando que o ponto F pertence ao segmento $B C$ , o ângulo $B \hat{F} C$ mede $180 graus$ . Logo:

$36 graus mais x mais 36 graus igual a 180 graus$

$x mais 72 graus igual a 180 graus$

$x mais 72 graus menos 72 graus igual a 180 graus menos 72 graus$

$x igual a 108 graus$

Portanto, o ângulo x mede $108 graus$ .

Obtenha informações sobre avaliações no tópico Avaliação, nas orientações gerais deste manual.

Página 44

Ângulos

Em anos anteriores, vimos que os ângulos podem ser identificados em diversas situações do cotidiano. A ideia de ângulo pode ser associada, por exemplo, a situações envolvendo giro em torno de um ponto fixo ou à inclinação em relação a um eixo.

Ângulo é uma figura geométrica formada por duas semirretas de mesma origem.

Em um ângulo, identificamos os seguintes elementos:

os lados $\vec{A B}$ e $\vec{A C}$ ;
o vértice A.

Indicamos esse ângulo por $\hat{A}$ , $B \hat{A} C$ ou $C \hat{A} B$ .

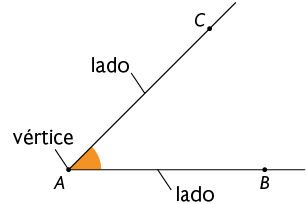
Ilustração de um ângulo demarcado entre duas semirretas, de mesma origem, marcada pelo ponto A, que é denominado 'vértice'. Em uma semirreta está marcado o ponto C e na outra o ponto B. As semirretas são denominadas 'lado' desse ângulo.

Questão 1. Em seu caderno, escreva algumas situações envolvendo objetos do cotidiano, nas quais podemos reconhecer a ideia de ângulo.

Resposta pessoal. Sugestões de resposta: Ponteiros do relógio; abertura de uma porta.

Utilizamos o grau $(°)$ como unidade de medida para medir o ângulo. O instrumento usado para medi-lo é o transferidor.

A seguir, apresentamos uma maneira de medir um ângulo utilizando um transferidor de $180 graus$ (meia volta).

Ilustração de um ângulo demarcado na menor abertura entre duas semirretas de mesma origem O, no centro de um transferidor de meia volta. Uma semirreta está alinhada com a demarcação do 0 grau e passa pelo ponto C, à direita do transferidor, e a outra com a demarcação de 75 graus, no sentido anti-horário, marcando o ponto A. Há a demarcação da linha que passa no ângulo 0 e para ela a seguinte indicação: 'linha de fé do transferidor coincide com um dos lados do ângulo'. E a demarcação no centro do transferidor com a frase 'centro do transferidor coincide com o vértice do ângulo'.

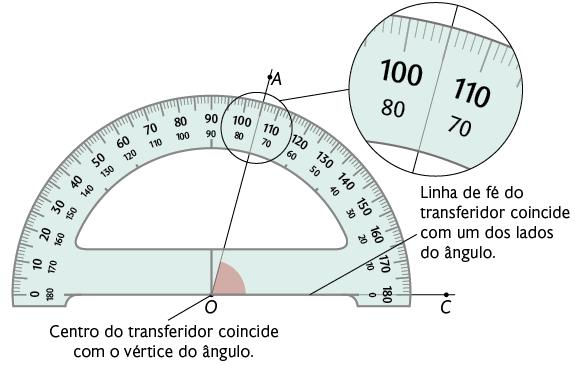
Atenção!

Para determinar qual medida do ângulo estamos considerando, indicamos um pequeno "arco". Nos casos em que não haja a indicação do "arco", vamos considerar a abertura de menor medida.

O ângulo $A \hat{O} C$ mede $75 graus$ (lê-se: sessenta e cinco graus). Podemos indicar essa medida por $medida do ângulo A O C igual a 75 graus$ ou $medida do ângulo O igual a 75 graus$ .

Ângulos cuja medida seja menor ou igual a $180 graus$ podem ser classificados em reto, agudo, raso ou obtuso.

Reto

Ângulo cuja medida é $90 graus$ . Podemos indicar o ângulo reto utilizando o símbolo .

Exemplo: $medida do ângulo A igual a 90 graus$ .

Raso

Ângulo cuja medida é $180 graus$ .

Exemplo: $medida do ângulo C igual a 180 graus$ .

Agudo

Ângulo cuja medida é maior do que $0 grau$ e menor do que $90 graus$ .

Exemplo: $medida do ângulo B igual a 48 graus$ .

Obtuso

Ângulo cuja medida é maior do que $90 graus$ e menor do que $180 graus$ .

Exemplo: $medida do ângulo D igual a 126 graus$ .

ORIENTAÇÕES AO PROFESSOR

Objetivos da unidade

Compreender a ideia de ângulo.

Reconhecer o grau $(°)$ como unidade de medida para expressar o resultado da medição de um ângulo.

Utilizar o transferidor como instrumento para medir ângulos.

Medir e classificar ângulos em reto, agudo, raso ou obtuso.

Identificar ângulos opostos pelo vértice.

Construir ângulos com régua, compasso e software de geometria dinâmica.

Construir e traçar as bissetrizes dos ângulos.

Resolver e elaborar situações-problema envolvendo ângulos.

Compreender e calcular as medidas de ângulos complementares e de ângulos suplementares.

Justificativas

Os conteúdos abordados nesta unidade são relevantes para que os estudantes avancem no trabalho com ângulos e compreendam seus elementos e suas características. Com base nesses conteúdos, pretende-se aliar teoria com atividades práticas nas quais a noção de ângulo esteja envolvida e relacionada com situações do cotidiano, de modo que os estudantes entendam a linguagem matemática como uma forma de compreender e representar o mundo em que vivem, além de incentivá-los a pensar, criar, escrever e construir conceitos geométricos.

Aos estudantes, são sugeridas algumas construções para auxiliá-los na percepção de certas características e propriedades relacionadas aos ângulos e à bissetriz de um ângulo, conceitos que estão associados à experimentação, à manipulação e à observação de elementos da realidade e do espaço físico.

Antes de apresentar o conteúdo desta página, verifique o conhecimento dos estudantes a respeito dos ângulos. Deixe que eles expliquem e conversem entre si, oportunizando que resgatem o conhecimento prévio sobre o assunto e, assim, tornem o estudo mais significativo.

Os conteúdos trabalhados nesta unidade desenvolvem a habilidade EF08MA15 ao levar os estudantes a construir, utilizando instrumentos de desenhos e softwares de geometria dinâmica, bissetrizes e ângulos de $90 graus$ , $60 graus$ , $45 graus$ e $30 graus$ .

Na questão 1, o intuito é que os estudantes identifiquem a ideia de ângulos em situações cotidianas. Para tirar maior proveito e tornar o aprendizado mais dinâmico, permita que eles realizem um passeio pela escola em busca de situações nas quais possam observar ângulos. Depois, promova a socialização das respostas dos estudantes.

Página 45

Ângulos complementares e suplementares

Dois ângulos são complementares quando a soma de suas medidas é igual a $90 graus$ .

Ilustração de duas semirretas partindo do ponto O, uma possuindo o ponto C e a outra o ponto A, entre elas há uma semirreta, de mesma origem O, com o ponto B demarcado. Os ângulos são: C O B igual a 58 graus; e B O A igual a 32 graus.

Podemos calcular a medida do ângulo $A \hat{O} C$ da seguinte maneira:

$med (A \hat{O} C) = med (A \hat{O} B) + med (B \hat{O} C)$

$medida do ângulo A O C igual a 32 graus mais 58 graus$

$medida do ângulo A O C igual a 90 graus$

Assim, $A \hat{O} B$ e $B \hat{O} C$ são ângulos complementares. Desse modo, dizemos que $A \hat{O} B$ é o complemento de $B \hat{O} C$ , e vice-versa.

Dois ângulos são suplementares quando a soma de suas medidas é igual a $180 graus$ .

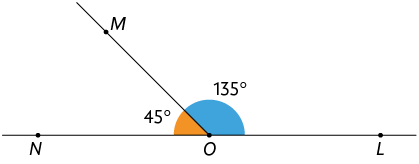
Ilustração de uma reta passando pelos pontos N O L, entre ela há uma semirreta, de mesma origem O, passando pelo ponto M. Estão demarcados os dois ângulos sendo N O M igual a 45 graus, e M O L igual a 135 graus.

Calculamos a medida do ângulo $L \hat{O} N$ da seguinte maneira:

$med (L \hat{O} N) = med (L \hat{O} M) + med (M \hat{O} N)$

$medida do ângulo L O N igual a 135 graus mais 45 graus$

$medida do ângulo L O N igual a 180 graus$

Portanto, $L \hat{O} M$ e $M \hat{O} N$ são ângulos suplementares. Assim, podemos dizer que $L \hat{O} M$ é o suplemento de $M \hat{O} N$ , e vice-versa.

Ângulos opostos pelo vértice

Duas retas concorrentes formam dois pares de ângulos chamados opostos pelo vértice. Tais ângulos têm o vértice em comum. Por exemplo, na figura apresentada a seguir há dois pares de ângulos opostos pelo vértice.

$A \hat{O} B$ e $D \hat{O} C$
$B \hat{O} C$ e $A \hat{O} D$

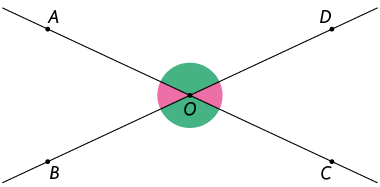
Ilustração de duas retas que se cruzam formando um X. Uma reta com os pontos A O C e a outra com os pontos B O D. Os respectivos ângulos formados estão demarcados, em que o ângulo A O D tem a mesma medida que o ângulo B O C. E o ângulo A O B tem a mesma medida de C O D.

Dois ângulos opostos pelo vértice têm medidas iguais, ou seja, são congruentes. Desse modo:

$med (A \hat{O} B) = med (D \hat{O} C)$ e $med (B \hat{O} C) = med (A \hat{O} D)$

Página 46

Construção dos ângulos

Analise como podemos construir alguns ângulos utilizando régua e compasso.

Instrumentos e softwares

Construção do ângulo cuja medida é $90 graus$

Para construir um ângulo de $90 graus$ , dada uma reta r e os pontos A e B sobre ela, podemos traçar uma reta perpendicular à reta r.

1º. Com a régua, trace uma reta r, indicando os pontos A e B sobre ela.

Ilustração de um lápis demarcando uma reta r, com os pontos A e B sobre ela, distanciados.

2º. Com a ponta-seca do compasso em A e abertura maior do que a metade da medida do comprimento de $\overline{A B}$ , trace um arco, como na imagem.

Ilustração de uma reta r, com os pontos A, B e ao meio, há um arco feito por um compasso com a ponta seca no ponto A e abertura menor que a distância de A até B.

3º. Repita os procedimentos apresentados no 2º passo, porém, com a ponta-seca do compasso em B, mantendo a mesma abertura, de modo que os arcos se cruzem em dois pontos: C e D.

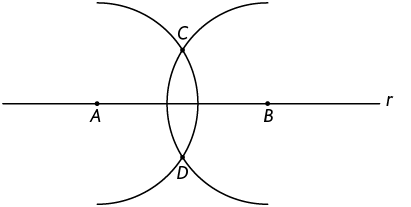
Ilustração de uma reta r, com os pontos A e B pertencentes à ela e dois pontos, C e D, entre os pontos A e B, com C acima da reta e D abaixo. Há dois arcos passando pelos pontos C e D, feitos com o compasso, com a ponta seca em A e depois em B.

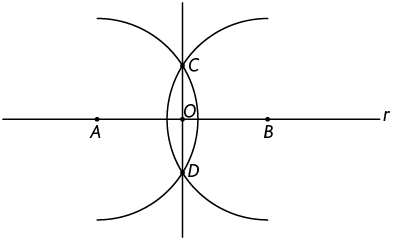
4º. Com a régua, trace a reta $C D$ .

5º. Por fim, marque o ponto O na interseção das duas retas. Os quatro ângulos obtidos são retos, ou seja, medem $90 graus$ : $A \hat{O} C$ , $B \hat{O} C$ , $A \hat{O} D$ e $B \hat{O} D$ .

Ilustração igual à anterior com uma reta desenhada com a régua e, perpendicular à reta r, passando pelo ponto C, pelo ponto O, que está na intersecção entre as duas retas e pelo ponto D.

ORIENTAÇÕES AO PROFESSOR

Antes de desenvolver o trabalho com os conteúdos apresentados nesta seção, é importante que os estudantes tenham acesso aos instrumentos necessários para esse estudo. Caso não haja compasso e régua em quantidade suficiente para todos, organize-os em grupos para que possam acompanhar o passo a passo apresentado. Além disso, alerte-os de eventuais riscos no manuseio dos instrumentos durante esta seção, de modo a garantir a integridade física de todos os envolvidos. Caso anteveja imprevistos e riscos, providencie antecipadamente suporte e medidas de segurança.

Verifique se eles perceberam que a medida da abertura do compasso deve ser maior do que a metade da medida do comprimento de $\overline{A B}$ , pois, caso contrário, os dois arcos não se cruzariam para determinar os pontos C e D.

Nesta seção, os estudantes têm a oportunidade de trabalhar aspectos da habilidade EF08MA15, uma vez que farão a construção do ângulo de $90 graus$ .

Avalie a conveniência de apresentar na lousa outra maneira de construir um ângulo de $90 graus$ com o ponto fora da reta. Para isso, dado um ponto A e uma reta r, trace uma reta perpendicular à reta r que passe por A.

Metodologias ativas

Ao desenvolver o trabalho com a seção Instrumentos e softwares, considere a possibilidade de usar a metodologia ativa Tiras de classificação. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 47

Instrumentos e softwares

Construção do ângulo cuja medida é $60 graus$

Dada uma reta s, verifique um procedimento que podemos utilizar para construir um ângulo de $60 graus$ .

1º. Com a régua, trace uma reta s e marque um ponto O sobre ela.

2º. Com a ponta-seca do compasso em O e abertura qualquer, trace dois arcos para determinar os pontos A e B equidistantes de O.

Ilustração de uma reta s, com os pontos A, B e O no meio deles. Há um compasso com a ponta seca no ponto em O, formando um pequeno arco no ponto A e outro pequeno arco no ponto B.

3º. Mantendo a abertura do compasso igual à medida do comprimento de $\overline{A B}$ , trace um arco com a ponta-seca do compasso em A.

Ilustração de uma reta s, com os pontos A, B e O no meio deles. Há um arco cruzando com a reta no ponto B e um compasso com a ponta seca em A.

4º. Repita os procedimentos apresentados no 3º passo, porém, com a ponta-seca em B, mantendo a mesma abertura. Marque o ponto C na interseção deles.

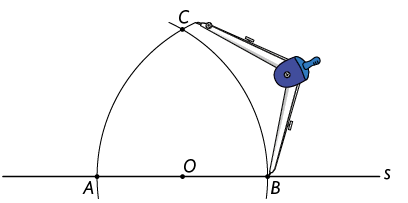
Ilustração de uma reta s, com os pontos A, B e O no meio deles. Há um arco cruzando com a reta no ponto B e um compasso com a ponta seca neste ponto, formando outro arco que cruza a reta no ponto A. Os dois arcos se cruzam no ponto C.

5º. Com a régua, trace a semirreta $A C$ .

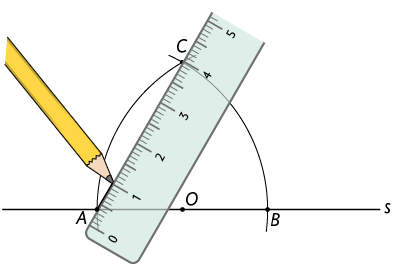
Ilustração de uma reta s, com os pontos A, B e O no meio deles. Há um arco cruzando com a reta no ponto B e outro cruzando a reta no ponto A. Os dois arcos se cruzam no ponto C. Também há um lápis traçando uma semirreta de A à C, com o auxílio de uma régua.

6º. Após esses procedimentos, obtém-se o ângulo $B \hat{A} C$ , cuja medida é $60 graus$ .

Ilustração de uma reta com os pontos A, B e O no meio deles. Há um arco cruzando com a reta no ponto B e outro cruzando a reta no ponto A. Os dois arcos se cruzam no ponto C. Também há uma semirreta partindo do ponto A e passando pelo ponto C, que faz 60 graus com a reta existente.

Atenção!

No 4º passo, se traçarmos o segmento $B C$ , construiremos o triângulo $A B C$ , que é equilátero por construção, pois $\overline{A B}$ , $\overline{A C}$ e $\overline{B C}$ têm a mesma medida de comprimento e, por ser um polígono regular de 3 lados, a medida de cada um de seus ângulos internos é $início de fração, numerador: 180 graus, denominador: 3, fim de fração igual a 60 graus$ .

Página 48

Atividades

Faça as atividades no caderno.

1. Com um transferidor, meça cada ângulo a seguir e classifique-os em reto, raso, agudo ou obtuso.

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto A e outra possui o ponto B. O ângulo tem medida de 80 graus.

Ilustração de um ângulo com medida 90 graus entre duas semirretas de mesma origem O, uma possui o ponto E, e outra possui o ponto F.

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto C e outra possui o ponto D. O ângulo tem medida de 150 graus.

Ilustração de um ângulo de 180 graus entre duas semirretas de mesma origem O, uma possui o ponto M e outra possui o ponto N.

Respostas: A. $80 graus$ ; agudo; B. $90 graus$ ; reto; C. $150 graus$ ; obtuso; D. $180 graus$ ; raso.

2. Com um transferidor, meça os ângulos apresentados e, depois, escreva no caderno a medida do complemento e do suplemento de cada um deles.

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto A e outra possui o ponto B. O ângulo tem medida 55 graus.

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto C e outra possui o ponto D. O ângulo tem medida 25 graus.

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto E, e outra possui o ponto F. O ângulo tem medida 75 graus.

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto E, e outra possui o ponto F. O ângulo tem medida 40 graus.

Respostas: A. $55 graus$ ; complemento: $35 graus$ ; suplemento: $125 graus$ ; B. $25 graus$ ; complemento: $65 graus$ ; suplemento: $155 graus$ ; C. $75 graus$ ; complemento: $15 graus$ ; suplemento: $105 graus$ ; D. $40 graus$ ; complemento: $50 graus$ ; suplemento: $140 graus$ .

3. Analise as medidas dos ângulos a seguir.

Ilustração de um ângulo com medida de 95 graus.

Ilustração de um ângulo com medida de 27 graus.

Ilustração de um ângulo com medida de 139 graus.

Ilustração de um ângulo com medida de 85 graus.

Ilustração de um ângulo com medida de 18 graus.

Ilustração de um ângulo com medida de 63 graus.

Ilustração de um ângulo com medida de 72 graus.

Ilustração de um ângulo com medida de 41 graus.

No caderno, escreva os pares de ângulos:

a) complementares;

b) suplementares.

Respostas: a) B e F; E e G; b) A e D; C e H.

ORIENTAÇÕES AO PROFESSOR

Caso não haja transferidores para todos os estudantes, reúna-os em grupos para que realizem as atividades. Além disso, antes de propor as atividades desta página, verifique se eles se recordam dos conceitos de ângulo reto, ângulo agudo, ângulo raso e ângulo obtuso. Analise a possibilidade de retomar esses conteúdos organizando as informações na lousa.

Metodologias ativas

Ao trabalhar com as atividades desta unidade, considere a possibilidade de utilizar a metodologia ativa Pensar-conversar-compartilhar. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Na atividade 1, o objetivo é usar o transferidor como instrumento de medida dos ângulos e retomar a classificação dos ângulos em reto, agudo, raso ou obtuso. Se considerar necessário, oriente os estudantes acerca do posicionamento correto do transferidor para medir os ângulos. Caso não haja transferidores para que todos os estudantes realizem as atividades propostas na unidade, verifique a possibilidade de levar alguns para a sala de aula ou reuni-los em grupos, a fim de favorecer um momento de interação e a troca de experiências entre eles.

Verifique a necessidade de retomar a explicação a respeito de ângulos complementares e de ângulos suplementares para a realização das atividades 2 e 3. Ressalte que, quando a soma das medidas de dois ângulos é igual a $90 graus$ , os ângulos são complementares, e, quando a soma das medidas de dois ângulos é igual a $180 graus$ , dizemos que os ângulos são suplementares.

Na atividade 2, o intuito é que os estudantes meçam os ângulos e escrevam o suplemento e o complemento de cada um deles. Já na atividade 3, após realizarem as medidas dos ângulos, eles precisam identificar quais pares são complementares e quais são suplementares.

Página 49

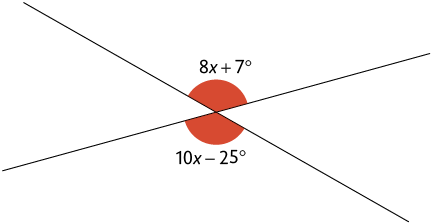
4. Na imagem estão representados os ângulos suplementares $D \hat{A} C$ e $B \hat{A} D$ .

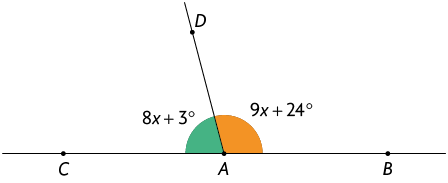
Ilustração de uma reta passando pelos pontos C e B, com o ponto A entre eles e desse ponto parte uma semirreta que contém o ponto D. O ângulo C A D mede 8 x mais 3 graus e o ângulo D A B mede 9 x mais 24 graus.

Como os ângulos são suplementares, então $medida do ângulo D A C mais medida do ângulo B A D igual a 180 graus$ . Logo, podemos determinar o valor de $x$ resolvendo a seguinte equação:

$8 x mais 3 graus mais 9 x mais 24 graus igual a 180 graus. está indicado que 8 x mais 3 graus corresponde a ângulo D A C e que 9 x mais 24 graus corresponde a ângulo b a d$

$8 x mais 9 x mais 3 graus mais 24 graus igual a 180 graus$

$17 x mais 27 graus igual a 180 graus$

$17 x mais 27 graus menos 27 graus igual a 180 graus menos 27 graus$

$17 x igual a 153 graus$

$início de fração, numerador: 17 x, denominador: 17, fim de fração igual a numerador 153 graus, denominador: 17, fim de fração$

$x igual a 9 graus$

Para obter as medidas de $D \hat{A} C$ e $B \hat{A} D$ , substituímos o valor obtido para x em cada uma das expressões que representam essas medidas.

$medida do ângulo D A C igual a 8 x mais 3 graus$

$medida do ângulo D A C igual a 8 vezes 9 graus mais 3 graus igual a 75 graus$

$medida do ângulo B A D igual a 9 x mais 24 graus$

$medida do ângulo B A D igual a 9 vezes 9 graus mais 24 graus igual a 105 graus$

Determine a medida dos ângulos $D \hat{A} C$ e $B \hat{A} D$ indicados em cada item, sabendo que os pontos A, B e C pertencem a uma mesma reta.

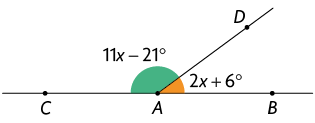
Ilustração de uma reta passando pelos pontos C e B, com o ponto A entre eles e desse ponto parte uma semirreta que contém o ponto D. O ângulo C A D mede 11 x menos 21 graus e o ângulo D A B mede 2 x mais 6 graus.

Ilustração de uma reta passando pelos pontos C e B, com o ponto A entre eles e desse ponto parte uma semirreta que contém o ponto E. Entre as semirretas que passam pelos pontos E e pelo ponto B há outra contendo o ponto D. O ângulo C A E mede 90 graus, o ângulo E A D mede 8 x menos 5 graus e o ângulo D A B mede 29 graus menos 2 x.

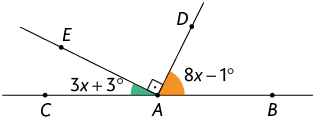
Ilustração de uma reta passando pelos pontos C e B, com o ponto O entre eles e desse ponto parte uma semirreta que contém o ponto E. Entre as semirretas que passam pelos pontos E e pelos ponto B há outra contendo o ponto D. O ângulo C A E mede 3 x mais 3 graus, o ângulo E A D mede 90 graus e o ângulo D A B mede 8 x menos 1 graus.

Respostas: A. $x igual a 15 graus$ ; $36 graus$ ; $144 graus$ ; B. $x igual a 11 graus$ ; $7 graus$ ; $83 graus$ ; C. $x igual a 8 graus$ ; $63 graus$ ; $27 graus$

5. De acordo com as figuras em cada item, escreva no caderno as medidas dos ângulos representados pelas letras.

Ilustração de duas retas que se cruzam formando um X. Uma reta passa pelos pontos A O B e a outra passa pelos pontos C O D. Os respectivos ângulos formados estão demarcados, em que o ângulo A O C indicado por r, é oposto pelo vértice ao ângulo D O B, indicado por p. O ângulo A O D, com medida igual a 68 graus, é oposto pelo vértice ao ângulo C O B, indicado por q.

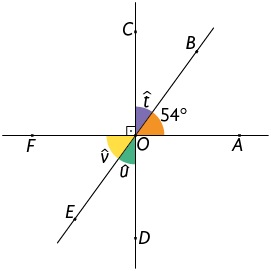
Ilustração de três retas que se cruzam no mesmo ponto. Uma reta horizontal com os pontos F O A, perpendicular à reta com os pontos C O D, entre elas, uma reta oblíqua passando pelo mesmo ponto de interseção das outras duas, essa reta contem os pontos E O B. Do cruzamento das retas D O C e A O A com a reta B O E, destaca-se os ângulos formados: C O B com medida t, B O A com medida de 54 graus, F O E com medida v, e, E O D com medida u.

Ilustração de uma reta na horizontal passando pelos pontos E, A, B, e G. Há uma reta contendo os pontos C, A e F, que intersecta a reta horizontal no ponto A de maneira oblíqua e outra reta contendo os pontos D e B, que corta a reta horizontal no ponto B também de maneira oblíqua. Os respectivos ângulos formados estão demarcados. O ângulo E A F indicado por g, o ângulo E A C, com medida igual a 116 graus, o ângulo C A B indicado por f. O ângulo A B D, indicado por h e o ângulo D B G, com medida igual a 80 graus.

Respostas: A. $medida do ângulo p igual a 112 graus$ ; $medida do ângulo q igual a 68 graus$ ; $medida do ângulo r igual a 112 graus$ ; B. $medida do ângulo t igual a 36 graus$ ; $medida do ângulo u igual a 36 graus$ ; $medida do ângulo v igual a 54 graus$ ; C. $medida do ângulo f igual a 64 graus$ ; $medida do ângulo g igual a 64 graus$ ; $medida do ângulo h igual a 100 graus$ .

Página 50

6. Nos itens a seguir, obtenha o valor de x e determine a medida dos ângulos representados pelas expressões algébricas.

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo 3 x mais 17 graus e o ângulo 6 x menos 4 graus são opostos pelo vértice.

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo 3 x mais 5 graus e o ângulo 193 graus menos x são opostos pelo vértice.

Respostas: A. $x igual a 7 graus$ ; $38 graus$ ; B. $x igual a 47 graus$ ; $146 graus$ .

7. Os ângulos $A \hat{O} B$ e $C \hat{O} B$ são suplementares e a medida de $C \hat{O} B$ é o dobro da medida de $A \hat{O} B$ . Determine a medida do complementar de $A \hat{O} B$ .

Resposta: $30 graus$ .

8. Utilizando um transferidor, construa no caderno um ângulo com medida de $140 graus$ . Para isso, desenhe ângulos adjacentes cuja medida de cada um seja igual a $70 graus$ e, em seguida, resolva os itens.

Atenção!

Quando dois ângulos têm um lado em comum e as regiões determinadas por eles não têm pontos em comum, dizemos que eles são adjacentes.

a) Escreva no caderno as etapas dessa construção.

Resposta pessoal.

b) Construa um ângulo de $160 graus$ , utilizando essas mesmas estratégias.

Resposta pessoal.

9. Na figura a seguir, os ângulos $B \hat{A} C$ e $C \hat{A} D$ são suplementares e $C \hat{A} D$ é agudo.

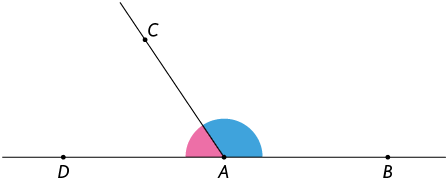
Ilustração de uma reta passando pelos pontos D e B, com o ponto A entre eles e desse ponto parte uma semirreta que contém o ponto C. O ângulo D A C tem medida menor do que 90 graus e o ângulo C A B tem medida maior do que 90 graus. O ângulo D A C mais o ângulo C A B somam a medida de 180 graus.

Utilizando essas informações, elabore um problema e troque-o com um colega. Você resolverá o dele, e ele, o seu. Depois, verifiquem se as respostas estão corretas.

Resposta pessoal.

10. Os ângulos $M \hat{O} P$ e $N \hat{O} P$ são suplementares e a diferença entre suas medidas é de $30 graus$ . Calcule no caderno a medida de $M \hat{O} P$ e $N \hat{O} P$ , sabendo que $N \hat{O} P$ é agudo.

Resposta: $medida do ângulo m o p igual a 105 graus$ e $medida do ângulo n o p igual a 75 graus$ .

11. Analise os modelos de esquadros a seguir.

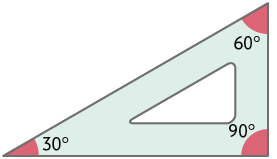
Ilustração de um esquadro, com seus ângulos internos medindo 30 graus, 60 graus e 90 graus. — Esquadro de $60 graus$ .

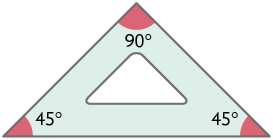
Ilustração de um esquadro, com seus ângulos internos medindo 45 graus, 90 graus e 45 graus. — Esquadro de $45 graus$ .

Verifique como Marília representou um ângulo com medida de $135 graus$ .

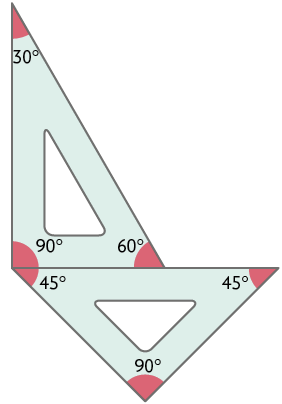
Ilustração de dois esquadros, um acima do outro. O de cima, com seus ângulos internos medindo 30 graus, 90 graus e 60 graus; o debaixo com seus ângulos internos medindo 45 graus, 90 graus e 45 graus. Eles estão encostados de maneira que o esquadro de cima, esteja alinhado no ângulo de 90 graus com o ângulo de 45 graus do esquadro debaixo.

Utilizando esse par de esquadros, represente no caderno ângulos com medidas de:

a) $75 graus$ .

b) $120 graus$ .

c) $150 graus$ .

d) $180 graus$ .

Respostas na seção Resoluções.

Versão adaptada acessível

Descreva como devemos posicionar esse par de esquadros para representar um ângulo com medida de:

a) 75°.

Resposta: posicionar o par de esquadros de maneira que a parte de 30° do esquadro de 60° se encontre com a parte de 45° do esquadro de 45°.

b) 120°.

Resposta: posicionar o par de esquadros de maneira que a parte de 30° do esquadro de 60° se encontre com a parte de 90° do esquadro de 45°.

c) 150°.

Resposta: posicionar o par de esquadros de maneira que a parte de 60° do esquadro de 60° se encontre com a parte de 90° do esquadro de 45°.

d) 180°.

Resposta: posicionar o par de esquadros de maneira que a parte de 90° do esquadro de 60° se encontre com a parte de 90° do esquadro de 45°.

ORIENTAÇÕES AO PROFESSOR

O objetivo da atividade 6 é verificar se os estudantes são capazes de determinar as medidas dos ângulos indicados por meio da resolução de expressões algébricas. Para tirar melhor proveito do trabalho com essa atividade, elabore outros itens e reproduza-os na lousa para que os estudantes possam efetuar os cálculos em seu caderno. Ao final, verifique se eles resolveram corretamente.

A resolução da atividade 7 possibilita o desenvolvimento do raciocínio lógico-matemático (indução, dedução, abdução ou raciocínio por analogia). A fim de auxiliar os estudantes, faça questionamentos que trabalhem com a capacidade de abstração e de argumentação deles. Para aproveitar melhor a atividade, proponha a resolução de outras situações parecidas com essa, como:

Jéssica descobriu que o triplo da medida do complemento de um determinado ângulo é igual a $102 graus$ . Qual é a medida desse ângulo?

Espera-se que eles obtenham a medida de $56 graus$ .

Antes de realizar a atividade 8, analise a necessidade de relembrar a definição de ângulos adjacentes. Essa atividade contribui para o desenvolvimento da habilidade EF08MA15, pois propõe que os estudantes utilizem o transferidor para construir o ângulo indicado.

Ao elaborar e resolver uma questão envolvendo o contexto da atividade 9, os estudantes são instigados a desenvolver aspectos da Competência específica de Matemática 6, enfrentando situações-problema, incluindo situações imaginadas, expressando suas respostas e sintetizando conclusões. Além disso, por exercitar a curiosidade intelectual, a empatia, o diálogo, a cooperação e a resolução de conflitos, o trabalho com as Competências gerais 2 e 9 também é favorecido.

Para tirar melhor proveito da atividade 10, proponha a resolução de outras situações parecidas com essa, como:

Qual é a medida da metade do suplemento de um ângulo que mede $124 graus$ ?

Espera-se que eles obtenham a medida de $28 graus$ .

Na atividade 11, questione-os se é possível representar ângulos com outras medidas utilizando esse par de esquadros. Além disso, leve esquadros para a sala de aula, organize os estudantes em grupos e deixe que eles os manuseiem. Nesse caso, alerte os estudantes para os eventuais riscos no desenvolvimento do trabalho com esta seção, de modo a garantir a integridade física de todos os envolvidos.

Página 51

Bissetriz de um ângulo

Uma professora de Matemática pediu aos estudantes do 8º ano que construíssem em uma folha de papel, um ângulo medindo $72 graus$ . Em seguida, orientou-os a recortar o ângulo e dobrá-lo ao meio, conforme representado a seguir.

Ilustração de uma folha de papel com uma dobradura. Uma seta indica uma nova dobradura a partir da ilustração anterior, são 4 etapas. No início, não há dobradura, a folha tem um ângulo e uma tesoura aparece indicando que o ângulo será cortado. Seta para direita indicada outra figura. A folha de papel cortada com o ângulo indicado e uma seta curva indicando o sentido da dobra. Seta para direita. O lado esquerdo da folha dobrado de cima para baixo, na diagonal. Seta aponta para outra imagem: a marca dessa dobra aparece exatamente no meio do ângulo, separando o ângulo em dois ângulos iguais.

Ao desdobrar a folha, o ângulo ficou dividido ao meio pela marca da dobra. Cada uma das partes obtidas mede $36 graus$ , pois $72 dividido por 2 igual a 36$ . Nesse caso, a marca do vinco está sobre a bissetriz do ângulo.

A bissetriz de um ângulo é uma semirreta, com origem no vértice, que o divide em dois ângulos congruentes. Na imagem, a semirreta $O E$ é a bissetriz do ângulo $A \hat{O} B$ .

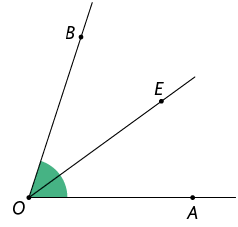
Ilustração de duas semirretas partindo do ponto O, uma possuindo o ponto B e a outra o ponto A, entre elas há uma semirreta, de mesma origem O, com o ponto E demarcado, dividindo o ângulo B O A em dois ângulos iguais.

Instrumentos e softwares

Construção da bissetriz de um ângulo

Execute o passo a passo a seguir para construir a bissetriz de um ângulo usando régua e compasso.

1º. Com a régua, trace um ângulo $A \hat{O} B$ de medida qualquer.

Ilustração de duas semirretas partindo do ponto O, uma contendo o ponto A e a outra contendo o ponto B. O menor ângulo formado entre elas está demarcado.

2º. Depois, com a ponta-seca do compasso em O e abertura qualquer, trace um arco determinando um ponto C em $\vec{O A}$ e um ponto D em $\vec{O B}$ .

Ilustração de duas semirretas partindo do ponto O, uma contendo os pontos D e B e a outra os C e A. Há um compasso com a ponta seca em O, traçando um arco que passa pelos pontos D e C.

ORIENTAÇÕES AO PROFESSOR

Antes de apresentar o conteúdo desta página, verifique o conhecimento dos estudantes relacionado à bissetriz de um ângulo. Deixe que eles deem suas explicações e conversem entre si, oportunizando o resgate do conhecimento prévio sobre o assunto e, assim, tornando o estudo mais significativo.

Antes de desenvolver o trabalho com os conteúdos apresentados na seção Instrumentos e softwares desta página, é importante garantir aos estudantes a disponibilidade dos instrumentos necessários. Caso não haja compasso e régua em quantidade suficiente para todos, organize-os em grupos para que possam acompanhar o passo a passo apresentado. Além disso, alerte-os a respeito dos eventuais riscos no desenvolvimento do trabalho desta seção, de modo a garantir a integridade física de todos os envolvidos.

Os conteúdos deste tópico desenvolvem aspectos da habilidade EF08MA15, propondo a construção da bissetriz de um ângulo com compasso e régua como instrumentos.

Metodologias ativas

Ao desenvolver o trabalho com a seção Instrumentos e softwares, avalie a possibilidade de utilizar a metodologia ativa Tiras de classificação. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Algo a mais

Sugira aos estudantes a leitura do livro referenciado a seguir, em que a autora retrata de modo ilustrativo e poético um mundo cheio de formatos, destacando as paisagens, os objetos, entre outras coisas que nos rodeiam.

ULITZKA, Irene. O país dos ângulos. São Paulo: Ciranda Cultural, 2011.

Página 52

3º. Com a ponta-seca do compasso em C e abertura maior do que a metade da medida do comprimento de $\overline{C D}$ , trace um arco, como na imagem.

Ilustração de duas semirretas partindo do ponto O, uma contendo os pontos D e B e a outra os C e A, como na ilustração anterior, com um arco passando pelos pontos D e C. Há um compasso com a ponta seca em C, marcando outro arco à frente, entre os pontos A e B.

4º. Mantendo a abertura anterior, trace um arco como na imagem com a ponta-seca em D. Marque o ponto E na interseção dos arcos.

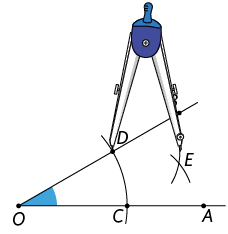
Ilustração com a mesma construção da ilustração anterior. Há dois arcos que se cruzam formando um X na região interna do ângulo, formando o ponto E. Há um compasso com a ponta-seca em D, e a outra ponta no final de um dos arcos.

5º. Com a régua, trace a semirreta $O E$ .

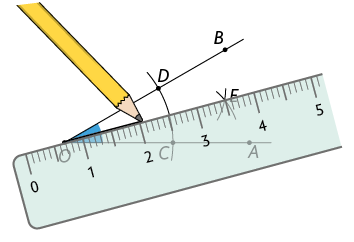
Ilustração de duas semirretas partindo do ponto O, uma contendo os pontos D e B e a outra os C e A. Entre estas duas semirretas há o ponto E. Há um arco passando pelos pontos D e C, e outros dois pequenos arcos cruzando entre si no ponto E. Também há um lápis traçando um segmento de reta que começa em O e passa por E, com o auxílio de uma régua.

6º. A semirreta $O E$ traçada no passo anterior é a bissetriz do ângulo $A \hat{O} B$ .

Atividades

Faça as atividades no caderno.

12. Na figura a seguir, a semirreta $O B$ é bissetriz do ângulo $A \hat{O} C$ e a semirreta $O D$ é bissetriz do ângulo $C \hat{O} E$ .

Ilustração de um ângulo A O E, do ponto O partem 3 semirretas, cada uma contendo um dos pontos: B, C, D. O ângulo B O C mede 41 graus e o ângulo D O E mede 32 graus.

De acordo com essas informações, calcule as medidas dos ângulos:

a) $A \hat{O} C$ .

b) $B \hat{O} D$ .

c) $C \hat{O} E$ .

d) $A \hat{O} E$ .

Respostas: a) $82 graus$ ; b) $73 graus$ ; c) $64 graus$ ; d) $146 graus$ .

ORIENTAÇÕES AO PROFESSOR

Verifique se os estudantes perceberam que a medida da abertura do compasso deve ser maior do que a metade da medida do comprimento de $\overline{C D}$ , pois, caso contrário, os dois arcos não se cruzariam para determinar o ponto E.

Acompanhe os estudantes durante cada passo da construção e avalie a necessidade de realizá-la também na lousa.

Na atividade 12, espera-se que os estudantes identifiquem que as bissetrizes indicadas na figura geométrica determinam, com seus lados, dois ângulos adjacentes congruentes.

Atividade a mais

Complemente o trabalho desta página reproduzindo, na lousa, a atividade a seguir e peça aos estudantes que efetuem os cálculos no caderno.

Na figura geométrica a seguir, $\vec{O B}$ é bissetriz do ângulo $A \hat{O} C$ e $\vec{O D}$ é bissetriz do ângulo $C \hat{O} E$ . Sabendo que $medida do ângulo A O C igual a 70 graus$ e $medida do ângulo C O E igual a 60 graus$ , calcule a medida do ângulo $B \hat{O} D$ .

Resolução e comentários

Como o ângulo $A \hat{O} C$ mede $70 graus$ , o ângulo $A \hat{O} B$ mede $35 graus$ . Da mesma maneira, como o ângulo $C \hat{O} E$ mede $60 graus$ , o ângulo $C \hat{O} D$ mede $30 graus$ e o ângulo $D \hat{O} E$ mede $30 graus$ . Assim, adicionando a medidas dos ângulos $B \hat{O} C$ e $C \hat{O} D$ , obtemos a medida do ângulo $B \hat{O} D$ .

$35 graus mais 30 graus igual a 65 graus$

Portanto, $medida do ângulo B O D igual a 65 graus$ .

Página 53

13. Junte-se a um colega e, utilizando um transferidor, construam no caderno os ângulos cujas medidas estão indicadas em cada item. Em seguida, tracem a bissetriz de cada um deles.

a) $medida do ângulo A O B igual a 48 graus$ .

b) $medida do ângulo C O D igual a 76 graus$ .

c) $medida do ângulo P O Q igual a 34 graus$ .

Respostas na seção Resoluções.

14. Determine a medida do ângulo $A \hat{O} B$ em cada item, sabendo que a semirreta $O C$ é a bissetriz dele.

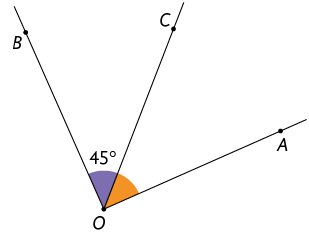
Ilustração de duas semirretas partindo do ponto O, uma passando pelo ponto B e a outra o ponto A, entre estas duas semirretas, há outra partindo da mesma origem O, passando pelo ponto C. O ângulo B O C mede 45 graus.

Ilustração de duas semirretas partindo do ponto O, uma passando pelo ponto B e a outra pelo ponto A, entre estas duas semirretas, há outra partindo da mesma origem O, passando pelo ponto C. O ângulo C O A mede 38 graus.

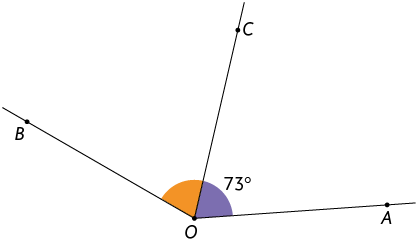
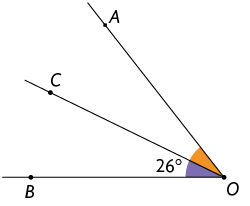
Respostas: A. $90 graus$ ; B. $76 graus$ ; C. $146 graus$ ; D. $52 graus$ .

15. No futebol, o bom treinamento do goleiro é fundamental para que o time obtenha resultados positivos. Esse treino consiste não somente no condicionamento físico, mas também na aprendizagem de técnicas, como ficar posicionado sobre a bissetriz imaginária do ângulo formado entre a bola e as traves, conforme o esquema a seguir.

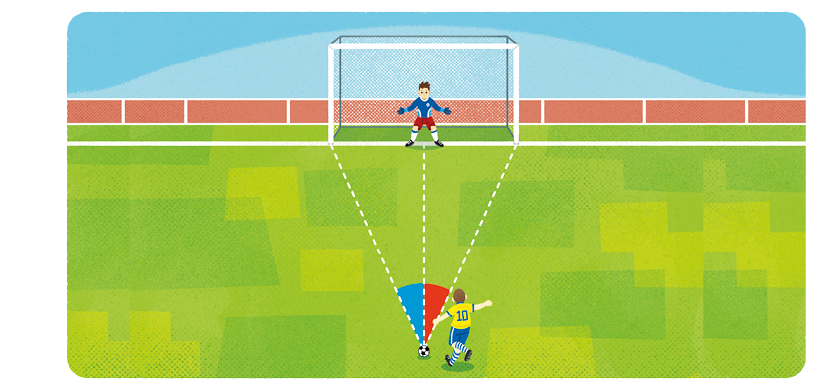
Ilustração de um goleiro, bem ao centro do gol. Em sua frente, há um jogador que se prepara para chutar a bola. Há dois ângulos iguais, com seus lados formados: um pela distância do jogador com o goleiro e os outros 2 pela distância do jogador até uma das traves laterais do gol. Há um ângulo de cada lado.

a) Em sua opinião, qual é a vantagem de o goleiro se posicionar dessa maneira diante do jogador?

Resposta pessoal. Espera-se que os estudantes respondam que, nesse posicionamento, o goleiro tem maior alcance em toda a extensão do gol e, consequentemente, mais chance de defesa.

b) No esquema, suponha que a medida do ângulo indicado em vermelho seja $18 graus$ . Nesse caso, qual é a medida do ângulo indicado em azul?

Resposta: $18 graus$ .

ORIENTAÇÕES AO PROFESSOR

Aproveite o fato de a atividade 13 ser proposta em duplas e oriente os estudantes sobre a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos, de compreender e de aceitar as necessidades e as limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Se achar conveniente, converse com eles a respeito do combate aos diversos tipos de violência, especialmente o bullying. Obtenha informações acerca desse assunto no tópico Cultura de paz e combate ao bullying, nas orientações gerais deste manual. Desse modo, propicia-se o desenvolvimento das Competências gerais 4 e 9, além da Competência específica de Matemática 8.

A fim de tirar melhor proveito desta atividade, registre na lousa outras medidas de ângulos para os estudantes construírem. Inclua ângulos com medida ímpar e, desse modo, promova uma discussão a respeito dos números decimais ou, até mesmo, aborde com eles os submúltiplos do grau.

Na atividade 14, o objetivo é que os estudantes determinem a medida dos ângulos indicados utilizando o conceito de bissetriz. Se considerar necessário, retome as explicações das páginas 51 e 52.

Na atividade 15, questione se o ângulo formado entre a bola e a trave será alterado caso o jogador se afaste ou se aproxime do travessão. Desse modo, eles podem refletir a respeito do fato de a medida do ângulo não se basear na medida de comprimento dos lados. Permita que os estudantes troquem opiniões e exercitem sua capacidade de argumentação.

Página 54

16. Márcia traçou uma linha verde no caderno e construiu um ângulo de medida $52 graus$ com base nela. Em seguida, ela representou um ângulo simétrico a ele, em relação à linha verde.

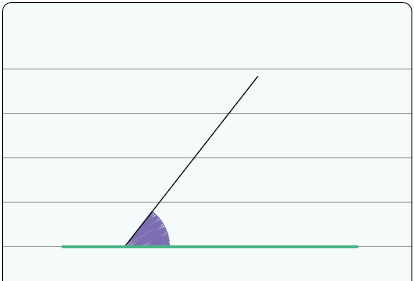
Ilustração de um caderno pautado, com um ângulo agudo desenhado. Uma de suas semirretas está destacada de verde.

a) Qual é a medida do ângulo simétrico em relação à linha verde que Márcia desenhou?

Resposta: $52 graus$ .

b) Qual é a soma das medidas desses ângulos?

Resposta: $104 graus$ .

c) Podemos dizer que a linha verde é a bissetriz do ângulo formado? Por quê?

Resposta: Sim. Espera-se que os estudantes respondam que a linha verde divide o ângulo igualmente, cada lado medindo $52 graus$ .

17. Calcule no caderno o valor de $x$ para que a semirreta $O E$ seja a bissetriz do ângulo $A \hat{O} B$ a seguir.

Resposta: $x igual a 13 graus$ .

18. (OBM-2002) Dado um triângulo $A B C$ , em que $medida do ângulo A igual a 80 graus$ e $ângulo C igual a 40 graus$ , a medida do ângulo agudo formado pelas bissetrizes dos ângulos $\hat{A}$ e $\hat{B}$ é:

a) $40 graus$

b) $60 graus$

c) $70 graus$

d) $80 graus$

e) $110 graus$

Resposta: Alternativa c.

19. A semirreta $O F$ é bissetriz do ângulo $C \hat{O} D$ .

Efetue os cálculos no caderno para obter o valor de $x$ e a medida do ângulo $C \hat{O} D$ .

Resposta: $x igual a 6 graus$ ; $medida do ângulo c o d igual a 80 graus$ .

20. No triângulo a seguir, a semirreta $C D$ está contida na bissetriz do ângulo $A \hat{C} B$ .

Ilustração de um triângulo retângulo B A C com ângulo reto em A. Está traçada uma semirreta com origem em C e passa por D, sobre o lado A B do triângulo. Estão destacados os ângulos A que mede x, B C D de medida 2 x menos 5 graus e D C A com medida igual a x mais 15 graus.

Determine as medidas dos ângulos $A \hat{B} C$ e $A \hat{C} B$ .

Resposta: $medida do ângulo a b c igual a 20 graus$ e $medida do ângulo a c b igual a 70 graus$ .

21. Na representação dos ângulos a seguir, a semirreta $O B$ é bissetriz do ângulo $A \hat{O} C$ e a semirreta $O C$ é bissetriz do ângulo $A \hat{O} D$ .

Ilustração com o ponto O e desse ponto partem 4 semirretas, cada uma contendo um dos pontos: A, B, C e D. O ângulo B O C mede 23 graus e os outros ângulos não estão indicados.

Qual é a medida do ângulo $B \hat{O} D$ ?

Resposta: $69 graus$ .

ORIENTAÇÕES AO PROFESSOR

Na atividade 16, para facilitar a compreensão dos estudantes, solicite-lhes que reproduzam a figura geométrica apresentada no caderno e tracem o ângulo simétrico em relação à linha verde.

As resoluções das atividades 17, 19 e 20 necessitam do uso de equações, o que possibilita verificar se os estudantes compreenderam o conceito de valor numérico de uma expressão algébrica, nesse caso com foco nas medidas de ângulos. Deixe que os estudantes conversem entre si, trocando informações e explicações, para favorecer a compreensão das relações entre conceitos e procedimentos de diferentes campos da Matemática, conforme solicita a Competência específica de Matemática 3.

Na atividade 18, se julgar oportuno, solicite aos estudantes que desenhem em seu caderno um triângulo com os ângulos descritos na atividade, a fim de que eles visualizem a situação apresentada no problema.

Na atividade 21, para tirar melhor proveito e sanar possíveis dificuldades, relembre o conceito de bissetriz. Em seguida, elabore outras representações de ângulos, reproduzindo-as na lousa, e peça aos estudantes que calculem a medida de alguns ângulos determinados.

Sugestão de avaliação

A fim de avaliar o aprendizado dos estudantes a respeito dos conteúdos trabalhados até esta página, proponha a seguinte atividade, reproduzindo-a na lousa, e peça-lhes que copiem e efetuem os cálculos no caderno.

No retângulo $A B C D$ a seguir, $\vec{D E}$ é bissetriz do ângulo $A \hat{D} C$ . Qual é a medida do ângulo $D \hat{E} C$ ?

Resolução e comentários

Os ângulos $A \hat{D} C$ e $D \hat{C} B$ são retos, ou seja, iguais a $90 graus$ . Como $\vec{D E}$ é bissetriz do ângulo $A \hat{D} C$ , o ângulo $E \hat{D} C$ mede $45 graus$ . Sabendo que, em todo triângulo, a soma das medidas dos ângulos internos é igual a $180 graus$ , calculamos:

$90 graus mais 45 graus mais x igual a 180 graus$

$135 graus mais x igual a 180 graus$

$x igual a 180 graus menos 135 graus$

$x igual a 45 graus$

Portanto, o ângulo $D \hat{E} C$ mede $45 graus$ .

É possível obter informações sobre avaliações no tópico Avaliação, nas orientações gerais deste manual.

Página 55

22. Na representação dos ângulos a seguir, a semirreta $Q S$ é bissetriz do ângulo $R \hat{Q} T$ e a semirreta $Q T$ é bissetriz do ângulo $S \hat{Q} U$ .

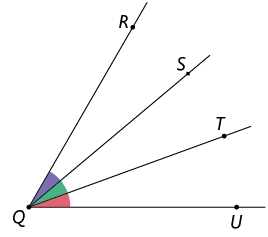
Ilustração com o ponto Q e desse ponto partem 4 semirretas, cada uma contendo um dos pontos: R, S, T e U, nessa ordem, formando três ângulos e cada um indicado por uma cor.

O que se pode afirmar sobre:

a) $med (R \hat{Q} S)$ em relação a $med (T \hat{Q} U)$ ?

Resposta: São congruentes.

b) $med (R \hat{Q} S)$ em relação a $med (S \hat{Q} U)$ ?

Resposta: A $med (R \hat{Q} S)$ é igual à metade da $med (S \hat{Q} U)$ .

c) $med (R \hat{Q} S)$ em relação a $med (R \hat{Q} U)$ ?

Resposta: A $med (R \hat{Q} S)$ é igual a um terço da $med (R \hat{Q} U)$ .

23. No triângulo a seguir, o ângulo $B \hat{A} C$ mede $30 graus$ e o segmento de reta $C D$ está contido na bissetriz de $A \hat{C} B$ .

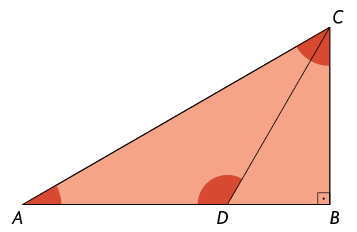
Ilustração de um triângulo retângulo A B C com ângulo reto em B. Está traçado um segmento que parte do vértice C até o ponto D, que está sobre o lado A B do triângulo. Estão destacados os ângulos A, A D C, e C.

Qual é a medida do ângulo $A \hat{D} C$ indicado?

Resposta: $120 graus$ .

24. Qual é a medida do menor ângulo formado pelas bissetrizes dos ângulos $A \hat{O} B$ e $C \hat{O} D$ ?

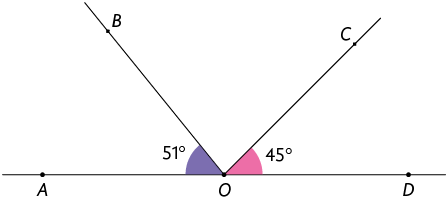
Ilustração de uma reta passando pelos pontos A e D, com o ponto O entre eles e desse ponto partem 2 semirretas, cada uma contendo um dos pontos: B e C. O ângulo A O B mede 51 graus e o ângulo C O D mede 45 graus.

Resposta: $132 graus$ .

25. (Obmep-2010) Na figura dada, $A \hat{O} D$ e $B \hat{O} Y$ são ângulos retos e a medida de $D \hat{O} Y$ está entre $40 graus$ e $50 graus$ . Além disso, os pontos C e Y estão sobre a reta r, enquanto D e E estão sobre a reta s.

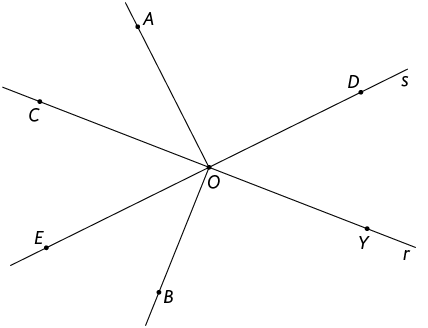
Ilustração de duas retas: r e s, que se cruzam em um ponto O. A reta r passa pelos pontos C e Y e a reta s, passa por E, e, D. Entre os pontos C e D, parte uma semireta contendo o ponto A e origem O e entre E, e, Y, uma semirreta contendo B e de origem O.

O possível valor para a medida de $A \hat{O} C$ está entre:

a) $30 graus$ e $40 graus$ .

b) $40 graus$ e $50 graus$ .

c) $50 graus$ e $60 graus$ .

d) $40 graus$ e $60 graus$ .

e) não pode ser determinado.

Resposta: Alternativa b.

26. Nas páginas 46 e 47, aprendemos a construir ângulos retos e de $60 graus$ utilizando régua e compasso. Em seu caderno, escreva quais procedimentos você faria para construir, usando régua e compasso, ângulos cujas medidas sejam 45° e 30°. Agora, usando régua, compasso e os procedimentos que você escreveu, construa no caderno os ângulos de medida:

a) $30 graus$ .

b) $45 graus$ .

Respostas na seção Resoluções.

Versão adaptada acessível

26. Nas páginas 46 e 47, aprendemos a construir ângulos retos e de 60° utilizando régua e compasso. Junte-se a um colega e escrevam quais procedimentos vocês fariam para construir, usando régua e compasso, ângulos cujas medidas sejam 45° e 30°. Agora, usando régua, compasso e os procedimentos que vocês escreveram, construam os ângulos de medida:

a) 30°.

b) 45°.

Respostas na seção Resolução.

Orientação para acessibilidade

Professor, professora: oriente os estudantes a conversar sobre o posicionamento da régua e do compasso em cada um dos passos que serão executados. Além disso, se julgar pertinente, promova uma roda de conversa para que eles exponham as estratégias desenvolvidas para construir os ângulos cujas medidas são 45° e 30°.

27. (Obmep-2011) Na figura a seguir, temos dois triângulos, $A B C$ e $A D C$ , tais que $A B = A D$ e $C B = C D = C A$ .

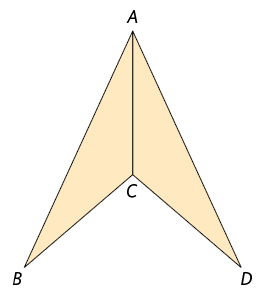
Ilustração de dois triângulos ABC e ACD. Os triângulos são iguais e simétricos, estão encostados com o lado em comum AC, de modo a formar uma figura que se assemelha a uma asa delta, com a ponta em A.

Sabendo que $medida do ângulo c b a igual a 25 graus$ , determine a medida do ângulo $B \hat{C} D$ .

Resposta: $100 graus$ .

ORIENTAÇÕES AO PROFESSOR

Na atividade 22, caso os estudantes apresentem alguma dificuldade, realize a leitura conjunta do enunciado para ajudá-los na resolução. Após todos solucionarem a atividade, proponha um bate-papo para que exponham suas conclusões e afirmações a respeito das respostas dos itens a, b e c.

Durante a execução da atividade 23, peça aos estudantes que digam quais conceitos eles precisam usar para obter a solução da atividade. Se necessário, retome algumas explicações sobre ângulos internos dos triângulos e bissetriz.

Para o desenvolvimento da atividade 24, permita que os estudantes utilizem a estratégia que julgarem adequada. Obtenha melhor proveito da tarefa, pedindo-lhes que determinem também a medida do maior ângulo formado pelas bissetrizes dos ângulos citados.

Na atividade 25, caso os estudantes apresentem dificuldade, analise se eles concluíram que $med (A \hat{O} C)$ está entre $40 graus$ e $50 graus$ . Se achar necessário, resolva a atividade na lousa para sanar possíveis dúvidas.

A atividade 26 oportuniza o trabalho com a habilidade EF08MA15, pois propõe a construção dos ângulos indicados com régua e compasso. Caso não haja compasso e régua em quantidade suficiente para todos, organize-os em grupos para realizar a atividade. Além disso, alerte os estudantes sobre os eventuais riscos no desenvolvimento do trabalho desta seção, de modo a garantir a integridade física de todos os envolvidos.

Diga aos estudantes que, por se tratar de uma atividade de prova oficial, não inserimos a palavra "medida" na atividade 27. Nesse caso, oriente-os a considerar que $medida do ângulo c b a igual a 25 graus$ indica a medida do ângulo $C \hat{B} A$ , que é $25 graus$ .

Metodologias ativas

Para desenvolver o trabalho com as atividades 24 e 27, avalie a possibilidade de utilizar a metodologia ativa Pensamento do design. Além disso, ao final do trabalho com as atividades desta unidade, verifique a possibilidade de utilizar a metodologia ativa Escrita rápida. Obtenha informações sobre essas metodologias no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 56

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

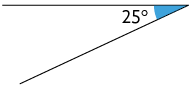
1. Determine as medidas dos ângulos complementar e suplementar dos ângulos representados em cada item.

Respostas: A: complementar: $47 graus$ ; suplementar: $137 graus$ ; B: complementar: $1 grau$ ; suplementar: $91 graus$ ; C: complementar: $65 graus$ ; suplementar: $155 graus$ ; D: complementar: $19 graus$ ; suplementar: $109 graus$ .

2. Sabendo que os pontos A, O e B pertencem a uma mesma reta, calcule em uma folha de papel avulsa a medida do ângulo:

Respostas: a) $medida do ângulo A O C igual a 139 graus$ ; b) $medida do ângulo a o d igual a 66 graus$ .

a) $A \hat{O} C$

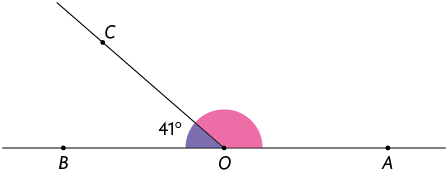
Ilustração de uma reta passando pelos pontos B e A, com o ponto O entre eles e desse ponto parte uma semirreta que contém o ponto C. O ângulo B O C mede 41 graus, o ângulo C O A é suplementar a ele.

b) $A \hat{O} D$

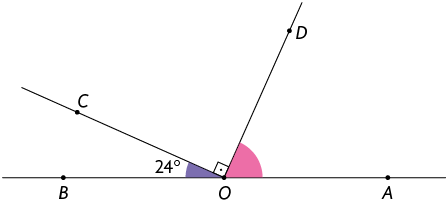
Ilustração de uma reta, passando pelos pontos B O A com uma semirreta com origem em O, passando por C, e outra semirreta com origem em O passando por D. Está demarcado que o ângulo C O D é reto. E está demarcado outros dois ângulos complementares, que são: B O C igual a 24 graus; e D O A, sem indicação.

3. Sabendo que os pontos A, B e O pertencem a uma mesma reta, determine em uma folha de papel avulsa a medida dos ângulos indicados em cada figura.

Respostas: A. $medida do ângulo a o c igual a 26 graus$ ; $medida do ângulo c o d igual a 38 graus$ ; $medida do ângulo d o e igual a 64 graus$ ; $medida do ângulo e o b igual a 52 graus$ ; B. $medida do ângulo a o c igual a 19 graus$ ; $medida do ângulo c o d igual a 71 graus$ ; $medida do ângulo d o b igual a 90 graus$ .

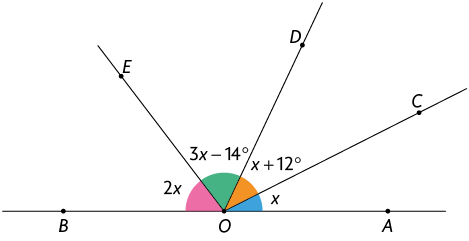
Ilustração de uma reta, passando pelos pontos B O A com uma semirreta com origem O, e do ponto O surgem 3 semirretas, cada uma contendo um dos pontos: E, D, C. O ângulo B O E mede 2 x graus, o ângulo E O D mede 3 x menos 14 graus, o ângulo D O C mede x mais 12 graus e o ângulo C O A mede x graus.

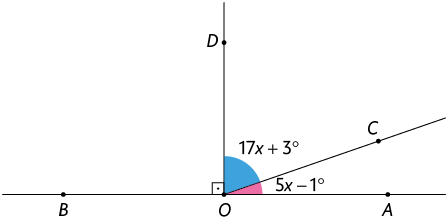
Ilustração de uma reta, passando pelos pontos B O A com uma semirreta com origem O, passando por D, e outra semirreta com origem O passando por C. Está demarcado que o ângulo B O D é reto. E está demarcado outros dois ângulos complementares, que são: D O C igual a 17 x mais 3 graus; e C O A igual a 5 x menos 1 grau.

4. Determine a medida de cada ângulo indicado nos itens a seguir.

Respostas: A. $135 graus$ ; B. $29 graus$ .

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo 8 x mais 7 graus e o ângulo 10 x menos 25 graus são opostos pelo vértice.

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo 9 x mais 2 graus e o ângulo 47 graus menos 6 x são opostos pelo vértice.

ORIENTAÇÕES AO PROFESSOR

1 e 2. Objetivo

Avaliar se os estudantes calculam a medida de ângulos complementares e suplementares.

Como proceder

Se os estudantes apresentarem dificuldade, retome com eles as explicações da página 45. No item b da atividade 2, analise se eles se lembram que a indicação é usada para indicar ângulos retos, ou seja, que medem $90 graus$ .

3. Objetivo

Conferir se os estudantes calculam a medida de ângulos resolvendo equações.

Como proceder

Verifique se os estudantes reconhecem que, no item A, como o ângulo $B \hat{O} A$ é raso, a soma das medidas dos ângulos indicados deve ser igual a $180 graus$ e, no item B, como os ângulos $D \hat{O} C$ e $C \hat{O} A$ são complementares, a soma de suas medidas deve ser igual a $90 graus$ .

4. Objetivo

Avaliar se os estudantes compreendem que dois ângulos opostos pelo vértice têm medidas iguais.

Como proceder

Analise se os estudantes recorrem ao uso de equações para calcular a medida dos ângulos. Se eles apresentarem dúvidas, auxilie-os na resolução da equação resolvendo alguns exemplos na lousa.