Página 57
UNIDADE
4
Proporcionalidade

Agora vamos estudar...
- razão e proporção;
- grandezas diretamente ou inversamente proporcionais;
- grandezas não proporcionais;
- regra de três envolvendo grandezas diretamente ou inversamente proporcionais.
Página 58
Razão e proporção
Em uma empresa de tecnologias digitais, no setor de programação, trabalham 15 mulheres e 12 homens. Nesse caso, dizemos que a razão entre a quantidade de mulheres e a quantidade de homens nesse setor é:
Nessa situação, a razão significa que, a cada 5 mulheres, há 4 homens no setor.

Sejam a e b dois números reais, com . A razão entre a e b é o quociente de a por b, ou seja, ou .
No setor administrativo da mesma empresa, trabalham 10 mulheres e 8 homens. Sabendo disso, segue que a razão entre a quantidade de mulheres e homens do setor é:
Analisando os cálculos, verificamos que as razões entre as quantidades de mulheres e homens, tanto para o setor de programação quanto para o setor administrativo, são iguais. Portanto, as duas razões formam uma proporção, a qual indicamos por:

Nesse caso, dizemos que 15 está para 12 assim como 10 está para 8.
Duas razões com termos não nulos, e , formam uma proporção quando as frações e são equivalentes, ou seja, .
Nessa proporção, a e d são chamados de extremos e b e c são chamados de meios.
Agora, enunciaremos uma propriedade das proporções.
Propriedade fundamental das proporções: o produto dos meios, em uma proporção, é igual ao produto dos extremos.
Página 59
Acompanhe alguns exemplos.
Exemplo 1. Qual é o valor de x para que a razão forme uma proporção com a razão ? Para responder a essa pergunta, escrevemos a seguinte proporção.
Aplicando a propriedade fundamental das proporções, obtemos:
Portanto, para que a razão forme uma proporção com a razão é necessário que .
Exemplo 2. Quanto é de R$ 250,00? Para responder a essa pergunta, escrevemos a seguinte proporção.
Aplicando a propriedade fundamental das proporções, obtemos:
Portanto, 30% de R$ 250,00 é igual a R$ 75,00.
Instrumentos e softwares
Calculando porcentagens no Calc
Planilhas eletrônicas, como o Calc, que faz parte do pacote gratuito LibreOffice, podem nos auxiliar nas construções de tabelas e gráficos de diferentes tipos.
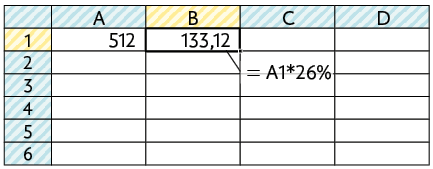
As planilhas são divididas em linhas (indicadas por números) e colunas (indicadas por letras). O cruzamento entre uma linha e uma coluna é denominado célula. Por exemplo, a célula B4 corresponde ao cruzamento da coluna B com a linha 4.
Siga as orientações do professor e o passo a passo a seguir para determinar 26% de R$ 512,00.
1º. Registre o número 512 na célula A1.
2º. Na célula B1 digite a fórmula =A1*26% e pressione Enter. Será exibida nela a porcentagem desejada.
Página 60
Atividades
Faça as atividades no caderno.
1. Escreva em seu caderno uma razão que represente a frase de cada item.
a) Jogando videogame, Carla perdeu 3 partidas e ganhou 5.
b) Em uma apresentação de teatro, 74 pessoas pagaram meia-entrada e 118 pagaram a inteira.
c) Em um escritório, 7 pessoas preferem o ar-condicionado desligado e 10 preferem o aparelho ligado.
d) Para um projeto de Ciências, Mateus tirou 14 fotos de animais invertebrados e 5 de vertebrados.
Sugestão de respostas: a) ; b) ; c) ; d) .
2. Em um dia de estudos, Rafael resolveu 27 questões de Português e 36 de Matemática.
a) Qual é a razão entre a quantidade de questões de Português e de Matemática resolvidas por ele?
Resposta: .
b) Qual é o significado da razão que você escreveu no item a?
Resposta: Significa que a cada 3 questões resolvidas de Português, 4 de Matemática foram solucionadas.
3. Indique quais das razões a seguir formam uma proporção.
a) e
b) e
c) e
d) e
e) e
f) e
g) e
h) e
Resposta: Itens b, d, e e h.
4. Em uma excursão, a cada 5 pessoas, 2 são idosas.
a) Qual é a razão entre a quantidade de pessoas idosas e de não idosas?
b) Sabendo que, ao todo, são 45 pessoas nessa excursão, quantas delas são idosas?
Respostas: a) ; b) 18 idosos.
5. Efetue os cálculos e determine o valor de x nas seguintes proporções.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ;d) ; e) ; f) ; g) ;h) .
6. Utilizando
o Calc, determine:
a) 18% de R$ 50,00.
b) 22% de R$ 75,00.
c) 38% de R$ 55,00.
d) 55% de R$ 40,00.
e) 80% de R$ 30,00
Respostas: a) R$ 9,00; b) R$ 16,50; c) R$ 20,90; d) R$ 22,00; e) R$ 24,00.
7. Escreva em seu caderno uma proporção usando os números a seguir. Depois, justifique-a usando a propriedade fundamental das proporções.
-
8
-
17
-
24
-
51
Sugestão de resposta: , pois .
Página 61
Grandezas proporcionais
Há situações em que duas ou mais grandezas podem estar relacionadas de modo que podem ser diretamente proporcionais, inversamente proporcionais ou não proporcionais.
Grandezas diretamente proporcionais
Assim como medimos a temperatura de um ambiente, o comprimento de um dos lados de um terreno ou o volume de um objeto, podemos medir o consumo de energia elétrica de um eletrodoméstico. Para isso, utilizamos uma unidade de medida chamada quilowatt-hora .
No quadro a seguir, está apresentado o consumo médio aproximado de energia elétrica em um mês, em quilowatt-hora, de um forno elétrico, de acordo com a medida do tempo de uso diário.
|
Medida do tempo |
Consumo médio mensal |
|---|---|
|
1 |
15 |
|
2 |
30 |
|
3 |
45 |
|
4 |
60 |
Analisando as informações, verificamos que o consumo de energia elétrica do forno varia de acordo com a medida do tempo de uso. Ao dobrarmos a medida do tempo de uso do forno elétrico, o consumo também dobra; ao triplicarmos a medida do tempo de uso do forno, o consumo também triplica; ao reduzirmos a medida do tempo de uso à metade, o consumo será igualmente reduzido à metade; e assim por diante. Nesse caso, dizemos que as grandezas tempo e consumo médio são diretamente proporcionais.
Com base nisso, a razão entre as medidas correspondentes às grandezas consumo médio e tempo é constante, ou seja:
Indicando por x e y, respectivamente, a medida do tempo de uso diário e o consumo médio mensal, podemos escrever:
ou
Para determinar o consumo mensal do forno elétrico com tempo de uso diário medindo , por exemplo, basta substituir x por 5 em .
Portanto, o consumo mensal do forno elétrico com uso de por dia é .
Página 62
Sejam x e y valores não nulos de duas grandezas diretamente proporcionais. Nesse caso, existe uma constante k, tal que ou .
Questão 1. Em seu caderno, determine quantos quilowatts-hora o forno elétrico consome em um mês se ficar ligado por diariamente.
Resposta: .
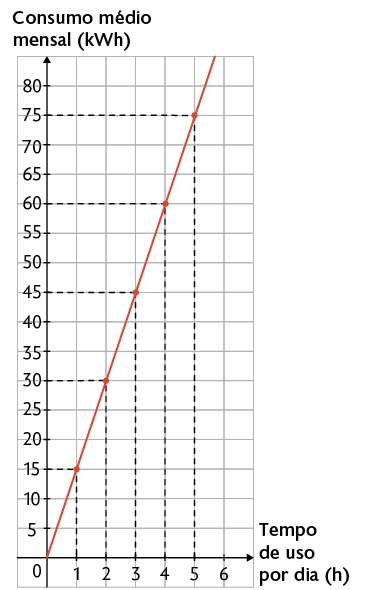
Agora, vamos representar a relação entre as grandezas da situação da página anterior em um gráfico. Para isso, inicialmente, atribuímos valores para x, na sentença , e calculamos os valores correspondentes para y. Desse modo, obtemos pares ordenados e os marcamos no plano cartesiano.
|
x |
|
|
|---|---|---|
|
1 |
|
|
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
Os pontos marcados no plano sugerem uma reta. Ao considerarmos que x pode assumir valores reais maiores do que zero, obtemos o gráfico a seguir.
Atenção!
O ponto não pertence ao gráfico apresentado.
Grandezas inversamente proporcionais
Para realizar a colheita de laranja, 2 trabalhadores levam 24 dias. Se esse mesmo trabalho for realizado por 4 pessoas, será concluído em 12 dias.
De acordo com as informações, temos:


Página 63
Analisando essas informações, percebemos que a quantidade de dias necessários para a colheita varia de acordo com a quantidade de trabalhadores, de modo que, ao dobrarmos a quantidade de trabalhadores, a quantidade de dias é reduzida à metade; ao reduzirmos à metade a quantidade de trabalhadores, dobra-se a quantidade de dias; e assim por diante. Nesse caso, dizemos que as grandezas quantidade de dias e total de trabalhadores são inversamente proporcionais.
Desse modo, o produto entre as medidas correspondentes às grandezas quantidade de trabalhadores e quantidade de dias é constante.
Indicando por x e y, respectivamente, a quantidade de trabalhadores e a quantidade de dias, podemos escrever:
ou
Sejam x e y valores não nulos de duas grandezas inversamente proporcionais. Nesse caso, existe uma constante k, tal que ou .
Agora, vamos representar a relação entre essas grandezas em um gráfico. Para isso, inicialmente, atribuímos valores para x e calculamos os valores correspondentes para y. Desse modo, obtemos pares ordenados.
|
x |
||
|---|---|---|
|
1 |
||
|
2 |
||
|
3 |
||
|
4 |
Ao representarmos esses pares ordenados no plano cartesiano, obtemos:
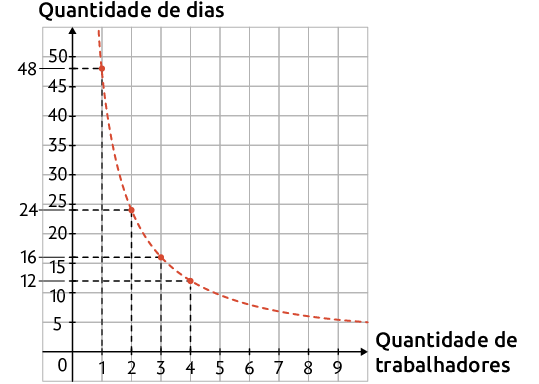
Atenção!
Ao considerarmos que x pode assumir valores reais maiores do que zero, obtemos a curva representada pela linha tracejada no gráfico anterior.
Página 64
Grandezas não proporcionais
Nos tópicos anteriores estudamos grandezas proporcionais. Porém, há situações em que trabalhamos com grandezas não proporcionais, como é o caso do tempo de duração de um filme e a quantidade de público dele.
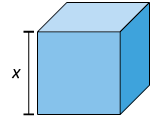
Vamos analisar uma situação envolvendo grandezas não proporcionais. Para isso, considere um cubo cujo comprimento da aresta mede x, com . Sabemos que a medida de seu volume y é igual ao cubo da medida do comprimento de sua aresta x, ou seja:
Agora, vamos representar a relação entre essas grandezas em um gráfico. Para isso, inicialmente, atribuímos valores para x e calculamos os valores correspondentes para y. Desse modo, obtemos pares ordenados.
|
x |
||
|---|---|---|
|
1 |
||
|
2 |
||
|
3 |
||
|
4 |
Atenção!
Note que a razão e o produto entre as medidas correspondentes às grandezas volume e comprimento da aresta não são constantes.
e
Portanto, essas grandezas não são diretamente nem inversamente proporcionais.
Como a medida do comprimento desse cubo pode assumir qualquer valor real maior ou igual a 1, ao representarmos a relação entre essas grandezas obtemos a curva apresentada a seguir.
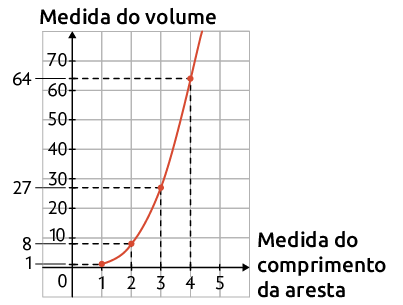
Página 65
Atividades
Faça as atividades no caderno.
8. Em cada item, verifique se as grandezas são proporcionais entre si.
a) Em uma fábrica, certa máquina produz 98 peças em de funcionamento e 196 peças em .
b) Aos 14 anos de idade, a altura de Regina media , e aos 26 anos, .
c) Em certo supermercado, 1 pacote de açúcar de de determinada marca custa R$ 2,60 e o pacote de custa R$ 5,10.
d) Uma impressora industrial imprime certa quantidade de panfletos em . Três impressoras iguais a ela imprimem a mesma quantidade em .
Respostas: a) Sim; b) Não; c) Não; d) Sim.
9. Verifique em cada item se as grandezas são proporcionais. Caso sejam, classifique-as em direta ou inversamente proporcionais.
a) O tempo de uma partida de futebol e a quantidade de gols marcados por uma das equipes.
Resposta: Não são proporcionais.
b) O tempo gasto para pintar uma casa e a quantidade de pintores, trabalhando no mesmo ritmo.
Resposta: São inversamente proporcionais.
c) O tempo de uma viagem e a velocidade média desenvolvida no percurso.
Resposta: São inversamente proporcionais.
d) A massa de carne a ser comprada e o valor a ser pago.
Resposta: São diretamente proporcionais.
e) A duração de um filme e as dimensões do DVD.
Resposta: Não são proporcionais.
10. Junte-se a um colega e identifiquem as afirmações verdadeiras.
a) O tempo da aula e a quantidade de aulas são grandezas diretamente proporcionais.
Atenção!
No item a, considere aulas com medidas de tempo iguais.
b) Um médico receita a uma pessoa tomar 3 comprimidos por dia. A quantidade de comprimidos e a quantidade de dias são grandezas inversamente proporcionais.
c) Se um bebedouro enche 1 copo em 25 segundos, encherá 3 copos de mesma medida de capacidade em 1 minuto.
d) A escala de um mapa indica que um centímetro do mapa representa 3 quilômetros no território real. A medida da distância no mapa e na realidade são grandezas diretamente proporcionais.
e) Se cada episódio de uma série tem , então 10 episódios terão .
Resposta: Alternativas a e d.
11. Luís tem uma plantação de soja e, após coletar informações, construiu o quadro a seguir relacionando a quantidade de colheitadeiras de mesmo modelo e a quantidade de dias que levam para colher a soja.
|
Quantidade de colheitadeiras |
Quantidade de dias |
|---|---|
|
1 |
24 |
|
2 |
12 |
|
3 |
8 |
|
4 |
6 |
a) Quantas colheitadeiras são necessárias para colher a soja em 8 dias?
b) As grandezas apresentadas no quadro são diretamente ou inversamente proporcionais?
Respostas: a) 3 colheitadeiras; b) Inversamente proporcionais.
Página 66
12. Usando um programa de computador, Amanda fez um triângulo com a medida do comprimento da base fixa e analisou a medida da área em relação à medida do comprimento da altura.
|
Medida da área (em ) |
Medida do comprimento da altura (em ) |
|---|---|
|
26 |
13 |
|
39 |
a |
|
65 |
32,5 |
|
b |
65 |
a) Determine os valores de a e b indicados no quadro.
b) As grandezas no quadro são diretamente ou inversamente proporcionais?
Respostas: a) e ; b) Diretamente proporcionais.
13. Em um mercado, de limões custa R$ 4,00.
a) Considere y o preço pago por quilograma de limões e x a medida de massa, em quilogramas, de limões. Determine a seguir a fórmula que representa a relação entre essas grandezas.
b) Qual dos gráficos representa a fórmula que você indicou no item a, para x maior ou igual a 1?
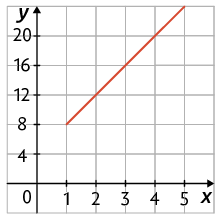
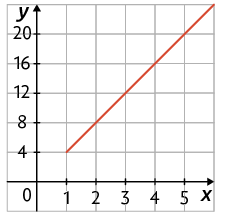
c) Se uma pessoa comprar de limões, quanto vai pagar?
Respostas: a) ; b) Alternativa B; c) R$ 6,00.
14. Junte-se a um colega e determinem a fórmula que representa a relação entre as grandezas em cada item. Depois, em uma folha quadriculada, representem a relação entre essas grandezas graficamente.
a) Certa máquina embala 600 produtos em 1 minuto. Duas máquinas iguais a essa embalam 1.200 produtos em 1 minuto.
b) Em uma página de um livro cabem 500 palavras. Em 10 páginas desse mesmo livro cabem 5.000 palavras.
Respostas na seção Resoluções.
15. Além do valor fixo de R$ 4,00, um estacionamento cobra mais R$ 1,50 por hora de permanência.
a) As grandezas são diretamente proporcionais, inversamente proporcionais ou não proporcionais?
Resposta: Não proporcionais.
b) Determine a fórmula que representa a relação entre essas grandezas.
Resposta: .
c) Qual é a quantia paga por uma pessoa que permaneceu 5 horas nesse estacionamento?
Resposta: R$ 11,50.
d) Em uma malha quadriculada, construa um gráfico para representar a relação entre essas grandezas.
Resposta na seção Resoluções.
16. Em uma plantação, são colhidos 420 tomates por hora. Considerando essas informações, elabore um problema. Em seguida, resolva-o.
Resposta pessoal.
Página 67
Regra de três simples
Para resolver situações-problema envolvendo grandezas proporcionais, podemos utilizar um método chamado regra de três.
Regra de três simples e grandezas diretamente proporcionais
Analise na tabela a seguir o consumo médio aproximado de energia elétrica em um mês, em quilowatt-hora (), de alguns eletrodomésticos de acordo com a medida de tempo de uso por dia.
|
Aparelho |
Medida de tempo de uso por dia |
Consumo médio mensal |
|---|---|---|
|
Ar-condicionado |
|
129 |
|
Chuveiro |
72 |
|
|
Computador |
15 |
|
|
Micro-ondas |
|
14 |
|
Televisor |
12 |
Fonte de pesquisa: PROCELINFO. Disponível em: https://oeds.link/hvgrrC. Acesso em: 29 mar. 2022.
De acordo com os dados da tabela, quantos quilowatts-hora um televisor consome em um mês se ficar ligado diariamente durante 16 horas?
Note que o tempo de uso por dia e o consumo de energia elétrica de um aparelho são grandezas diretamente proporcionais, pois ao dobrarmos a medida do tempo de uso do televisor, o consumo também dobrará; ao triplicarmos a medida do tempo de uso, o consumo também triplicará; e assim por diante.
Portanto, para responder à questão anterior, podemos usar a regra de três simples envolvendo grandezas diretamente proporcionais. Para isso, organizamos as informações, como mostrado a seguir.
|
Medida de tempo de uso por dia |
Consumo médio mensal |
|---|---|
|
5 |
12 |
|
16 |
x |
Escrevemos uma proporção com essas informações e a resolvemos.
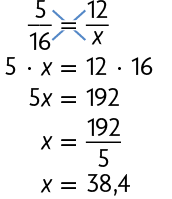
Portanto, o televisor vai consumir em média em um mês se ficar ligado diariamente durante .
Página 68
Acompanhe agora uma situação envolvendo porcentagem, que pode ser resolvida por meio de uma regra de três.
Em uma viagem que realizou, Gabriel gastou no total o valor de R$ 1.590,00. Dessa quantia, R$ 477,00 foram destinados à hospedagem. Que porcentagem corresponde ao custo da hospedagem em relação ao total gasto na viagem?
Considerando o total como 100%, podemos construir o quadro a seguir.
|
Valor gasto (R$) |
Porcentagem (%) |
|---|---|
|
1.590 |
100 |
|
477 |
? |
Representando por x a porcentagem correspondente aos gastos com a hospedagem, podemos escrever e resolver a seguinte proporção.

Portanto, a despesa com hospedagem corresponde a 30% do gasto total da viagem.
Regra de três simples e grandezas inversamente proporcionais
Vamos usar a regra de três para resolver situações envolvendo grandezas inversamente proporcionais. Acompanhe a seguinte situação.
Com certa quantidade de ração, Leonardo alimenta 8 cabeças de gado durante 18 dias. Com a mesma quantidade de ração, ele alimenta 16 cabeças de gado por 9 dias.
De acordo com as informações, temos:

Atenção!
Nessa situação, considere que os animais comem sempre uma mesma porção de ração.

Página 69
Analisando essas informações, percebemos que a quantidade de dias que Leonardo consegue alimentar os animais com a ração que tem varia de acordo com a quantidade de cabeças de gado, de modo que, ao dobrarmos essa quantidade, o total de dias será reduzido à metade; ao reduzir à metade a quantidade de cabeças de gado, dobra-se a quantidade total de dias; e assim por diante. Então, o tempo que Leonardo consegue alimentar o gado com a ração disponível e a quantidade de cabeças de gado são grandezas inversamente proporcionais.
Nesse caso, , pois e .
Contudo, se invertermos uma das frações, obtemos uma proporção.


Durante quantos dias Leonardo pode alimentar 4 cabeças de gado com essa quantidade de ração?
Para responder a essa questão, vamos considerar x a quantidade de dias e organizar as informações da seguinte maneira.
|
Quantidade de cabeças de gado |
Quantidade de dias |
|---|---|
|
8 |
18 |
|
4 |
x |
Como as grandezas são inversamente proporcionais, invertemos uma das razões e escrevemos uma proporção.
ou
Em seguida, efetuamos os cálculos e determinamos o valor de x.


Portanto, Leonardo pode alimentar 4 cabeças de gado durante 36 dias com a mesma quantidade de ração.
Página 70
Atividades
Faça as atividades no caderno.
17. Os números que estão na linha A são diretamente proporcionais aos que estão na linha B. Determine o número que corresponde a cada figura representada.
|
A |
7,5 |
12 |
||
|---|---|---|---|---|
|
B |
15 |
30 |
46 |
Resposta: , e .
18. Calcule o valor de x nos itens a seguir, sabendo que A e B são grandezas diretamente proporcionais e que C e D são inversamente proporcionais.
a)
|
A |
B |
|---|---|
|
7 |
x |
|
56 |
104 |
b)
|
C |
D |
|---|---|
|
7 |
x |
|
56 |
104 |
c)
|
A |
B |
|---|---|
|
x |
5 |
|
21 |
7 |
d)
|
C |
D |
|---|---|
|
30 |
54 |
|
x |
20 |
e)
|
C |
D |
|---|---|
|
8 |
21 |
|
14 |
x |
Respostas: a) ; b) ; c) ; d) ; e) .
19. Junte-se a um colega e, de acordo com as informações da tabela apresentada no tópico Regra de três simples e grandezas diretamente proporcionais, calculem o consumo médio de energia elétrica em um mês, em quilowatt-hora, em cada situação a seguir.
a) Um televisor ligado todos os dias durante 3 horas.
b) Um aparelho de ar-condicionado ligado todos os dias durante 6 horas.
c) Um micro-ondas ligado durante 1 hora em cada dia do mês.
d) Um chuveiro ligado durante em cada dia do mês.
Respostas: a) Aproximadamente ; b) Aproximadamente ; c) Aproximadamente ; d) Aproximadamente .
20. Renato é criador de bovinos e deve aplicar um medicamento para o controle de uma doença. De acordo com o fabricante, para cada do animal, deve ser aplicado do medicamento.
a) Em um animal com , quantos mililitros de medicamento devem ser aplicados?
b) Um animal que recebeu a aplicação de do medicamento tem quantos quilogramas?

Respostas: a) ; b) .
21. Bruno compra sacos com de bala e as empacota em saquinhos com 6 balas cada um para revendê-las.
Sabendo que um saquinho tem em média , aproximadamente quantas balas há em um saco de ?
Resposta: Aproximadamente 109 balas.
Página 71
22. A cana-de-açúcar é matéria-prima de diversos produtos, como o etanol.
Para obter de etanol, são necessários aproximadamente de cana-de-açúcar.
a) Aproximadamente quantos litros de etanol podem ser produzidos com de cana-de-açúcar?
Resposta: a) Aproximadamente .
b) Aproximadamente quantos quilogramas de cana-de-açúcar são necessários para produzir de etanol?
Resposta: b) Aproximadamente .
23. Para limpar um salão de festas, Letícia contratou 3 pessoas. Elas levaram para limpá-lo. Se Letícia contratasse 1 pessoa a mais, em quantas horas elas realizariam esse serviço, trabalhando no mesmo ritmo?
Resposta: Em .
24. Para colher as laranjas de um pomar, foram necessárias 15 pessoas trabalhando durante 7 dias. Quantas pessoas, trabalhando no mesmo ritmo, seriam necessárias para colher essas frutas em 5 dias?
Resposta: 21 pessoas.
25. Marilda recebeu uma encomenda para preparar 1.850 salgados. Trabalhando ela e mais 3 funcionários, foi possível terminar a encomenda em 3 dias.
a) Para que Marilda terminasse a encomenda em 1 dia, quantos funcionários ela deveria contratar a mais, considerando o mesmo ritmo de trabalho?
b) Se Marilda contratasse mais 2 funcionários, em quantos dias finalizaria a encomenda, considerando o mesmo ritmo de trabalho?
Respostas: a) 8 funcionários; b) 2 dias.
26. Em uma editora, trabalham 9 digitadores. Trabalhando juntos durante o mesmo período diariamente, eles digitam certo material em 20 dias. Contratando mais 6 digitadores, em quantos dias todos finalizariam o material, considerando o mesmo ritmo de trabalho?
Resposta: 12 dias.
27. (Enem-2013) Uma torneira não foi fechada corretamente e ficou pingando, da meia-noite às seis horas da manhã, com a frequência de uma gota a cada 3 segundos. Sabe-se que cada gota de água tem volume de .
Professor, professora: Diga aos estudantes que, por se tratar de uma atividade de prova oficial, não inserimos a palavra medida na atividade 27. Nesse caso, oriente-os a considerar que o termo volume indica a medida do volume.
Qual foi o valor mais aproximado do total de água desperdiçada nesse período, em litros?
a) 0,2
b) 1,2
c) 1,4
d) 12,9
e) 64,8
Resposta: Alternativa c.
28. Para encher uma caixa-d'água com medida de capacidade de , Bernardo comprou um equipamento que bombeia de água a cada .
a) Quantos minutos o equipamento vai levar para encher totalmente a caixa?
b) Se o equipamento ficar ligado durante 18 min, quantos litros de água vai bombear?
Respostas: a) ; b) .
29. Em um depósito foram colocadas lado a lado, sem empilhar, 54 caixas com formato cúbico cujas dimensões medem . Depois de um tempo, elas foram substituídas por outras, também de formato cúbico, mas com dimensões medindo . Quantas caixas com as dimensões medindo cabem nesse depósito?
Resposta: 24 caixas.
30. Fábio comprou um jogo em promoção e recebeu um desconto de R$ 9,90, que corresponde a 15% do preço sem desconto. Qual é o preço desse jogo sem o desconto? Quantos reais Fábio pagou nessa compra?
Respostas: R$ 66,00; R$ 56,10.
31. Eduardo pagou R$ 185,11 por uma conta atrasada com acréscimo de 7% de multa. Qual seria a quantia paga por ele se a conta não tivesse o acréscimo?
Resposta: R$ 173,00.
Página 72
32. Para a informação a seguir, elabore no caderno o enunciado de um problema envolvendo grandezas diretamente proporcionais. Depois, entregue-o para um colega resolver e verifique se a resposta dele foi correta.
|
Grandeza A |
Grandeza B |
|---|---|
|
7 |
77 |
|
15 |
x |
Resposta pessoal.
33. No esquema
a seguir, aparecem 3 engrenagens com tamanhos
diferentes.
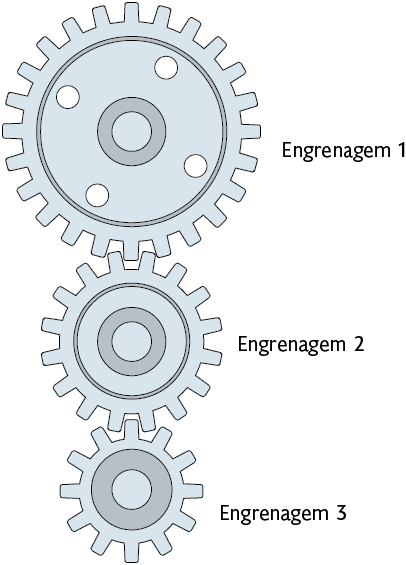
Atenção!
Para resolver esta atividade, verifique quantos "dentes" tem cada engrenagem.
a) Se a engrenagem 1 der 8 voltas completas, quantas voltas dará a engrenagem 2?
b) Enquanto a engrenagem 3 dá 28 voltas completas, quantas voltas dá a engrenagem 2? E a engrenagem 1?
Respostas: a) 12 voltas; b) 21 voltas; 14 voltas.
34. A água é indispensável para a vida. Apesar de a superfície terrestre ser coberta por 70% dela, apenas 1% dessa substância é própria para o consumo.
a) Uma torneira que despeja, em média, de água por minuto demora cerca de para encher um reservatório.
Quantas horas essa torneira levaria para encher totalmente o mesmo reservatório, se despejasse, em média, por minuto?
Para que o reservatório fique cheio em , em média quantos litros de água a torneira precisa despejar por minuto?
Respostas: ; por minuto.
b) Faça uma pesquisa a respeito de atitudes que podem ser tomadas no dia a dia para economizar água.
Resposta: Espera-se que o estudante diga para tomar banhos em menor tempo, não escovar os dentes com a torneira aberta, preferir varrer a calçada em vez de lavá-la, usar baldes para lavar automóveis em vez da mangueira, entre outras atitudes.
c) Quais atitudes obtidas na pesquisa do item anterior você e seus familiares já costumam ter? Elenque outras ações semelhantes que podem ser executadas e compartilhe-as com os colegas e o professor.
Resposta pessoal.
35. Para cada informação a seguir, elabore no caderno o enunciado de um problema envolvendo grandezas inversamente proporcionais. Em seguida, entregue-os para um colega resolver e verifique se as respostas obtidas estão corretas.
A.
|
Quantidade de funcionários |
Quantidade de dias |
|---|---|
|
3 |
12 |
|
x |
4 |
B.
|
Medida da velocidade do automóvel () |
Quantidade de horas de viagem |
|---|---|
|
80 |
10 |
|
x |
8 |
Respostas pessoais.
Página 73
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Lúcia comprou uma porção de esfirras para sua família, na qual havia 15 esfirras de carne e 10 de queijo.
a) Qual é a razão entre a quantidade de esfirras de carne e de queijo?
Resposta:
b) O que significa a razão que você escreveu no item a?
Resposta: Significa que, para cada 3 esfirras de carne, havia 2 de queijo.
2. Em um supermercado, a cada R$ 50,00 em compras, o cliente ganha 3 fichas numeradas para participar de um sorteio.
a) Guilherme fez uma compra de R$ 450,00 nesse supermercado. Quantas fichas ele ganhou?
b) Qual é a razão entre a quantidade de fichas para o sorteio e a quantia gasta no supermercado?
c) Qual é o valor mínimo que uma pessoa deve gastar para ganhar 18 fichas para o sorteio?
Respostas: a) 27 fichas; b) ; c) R$ 300,00.
3. Classifique
as grandezas em cada item como diretamente proporcionais,
inversamente proporcionais ou não proporcionais.
a) A quantidade de livros disponíveis em uma biblioteca e o total de leitores que a visitam.
b) A área de um quintal e a quantidade de pisos iguais para cobrir o chão dele.
c) A quantidade de funcionários trabalhando no mesmo ritmo e a medida de tempo necessária para concluir o trabalho.
Respostas: a) Não proporcionais; b) Diretamente proporcionais; c) Inversamente proporcionais.
4. Sabendo que para fazer determinado bolo um confeiteiro usa 3 ovos, responda às questões a seguir.
a) Considerando x o total de bolos e y a quantidade de ovos necessários para fazê-los, indique a sentença matemática que relaciona corretamente essas grandezas.
b) Qual dos gráficos representa a fórmula que você indicou no item a, para x maior ou igual a 1?
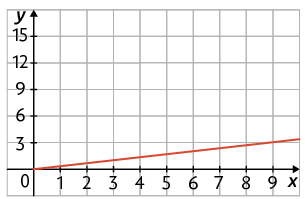
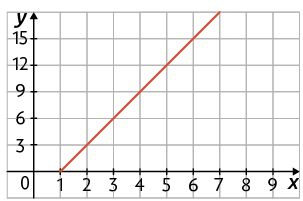
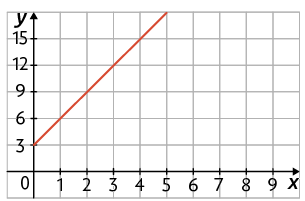
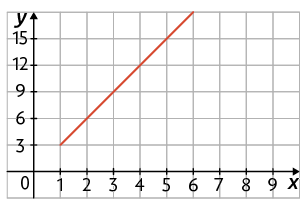
c) Em um dia, o confeiteiro utilizou 4 caixas com uma dúzia de ovos cada para fazer os bolos dessa receita. Quantos bolos ele fez?
Respostas: a) ; b) Gráfico D; c) 16 bolos.
Página 74
5. Das postagens que Fernanda faz em sua rede social, 75% são fotos. Sabendo disso, responda às questões a seguir.
a) Quais são as grandezas envolvidas?
b) Se a porcentagem de fotos postadas se mantiver, as grandezas serão diretamente ou inversamente proporcionais?
c) Se Fernanda fez 228 postagens nessa rede social, quantas fotos ela postou?
Respostas: a) Quantidade de fotos e quantidade de postagens; b) Diretamente proporcionais; c) 171 fotos.
6. Vera tem um automóvel que consome aproximadamente de etanol a cada percorridos. Ela foi a um posto e abasteceu o automóvel com a quantidade de combustível indicada a seguir.
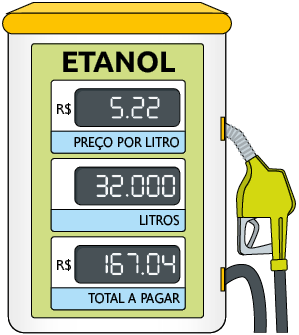
a) Antes do abastecimento, havia de etanol no tanque do carro. Aproximadamente quantos quilômetros o veículo de Vera poderá percorrer com o combustível que havia no tanque mais a quantidade colocada, sem abastecer o carro novamente?
b) Aproximadamente quantos litros de etanol o carro de Vera consome para percorrer ?
Respostas: a) Aproximadamente ; b) Aproximadamente .
7. Em uma loja, constatou-se que um funcionário leva, em média, para atender a 4 clientes. Quantos minutos ele levará para atender a 32 clientes, considerando o mesmo ritmo de atendimento?
Resposta: .
8. Para alimentar 2 cães de pequeno porte, Juliana utiliza certa quantidade de ração durante 30 dias. Por quantos dias ela poderia alimentar 5 cães desse porte com a mesma quantidade de ração, considerando que os animais comem sempre uma mesma porção de ração.
Resposta: 12 dias.
9. Os números que aparecem no quadro completam o enunciado do problema. Em uma folha de papel avulsa, reescreva-o com os números adequados e, em seguida, resolva-o.
|
Quantidade de operários |
Quantidade de meses |
|---|---|
|
4 |
9 |
|
x |
6 |
Para construir sua casa, Anselmo contratou operários. Com essa quantidade de trabalhadores, a casa ficou pronta em meses. Para que a construção fosse finalizada em meses, quantos operários Anselmo deveria ter contratado?
Resposta: Para construir sua casa, Anselmo contratou 4 operários. Com essa quantidade de trabalhadores, a casa ficou pronta em 9 meses. Para que a construção fosse finalizada em 6 meses, quantos operários Anselmo deveria ter contratado? Resposta: 6 operários.
10. Todos os produtos de uma perfumaria estavam em promoção com 30% de desconto, Gilmar fez uma compra e pagou R$ 217,70. Qual seria o preço pago se os produtos não estivessem na promoção?
Resposta: R$ 311,00.