Página 265
UNIDADE
12
Medidas de volume e de capacidade

Agora vamos estudar...
- medidas de volume;
- medidas de capacidade;
- relação entre medidas de volume e de capacidade;
- medida do volume do paralelepípedo reto retângulo.
Página 266
Medidas de volume
É bem provável que você já tenha estudado algumas unidades de medida de volume, entre elas o centímetro cúbico , o decímetro cúbico e o metro cúbico . Vamos recordá-las!
Um centímetro cúbico é a medida do volume de um cubo cujo comprimento da aresta mede .
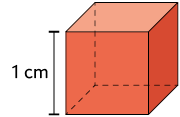
Um decímetro cúbico é a medida do volume de um cubo cujo comprimento da aresta mede .
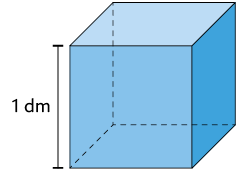
Imagens não proporcionais entre si.
Um metro cúbico é a medida do volume de um cubo cujo comprimento da aresta mede .
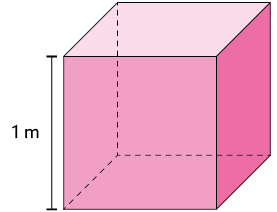
Utilizando figuras, vamos verificar as igualdades apresentadas. Para isso, considere os cubos a seguir.


Note que o volume do cubo A mede ou . Já o volume do cubo B mede ou . Desse modo, obtemos as igualdades apresentadas anteriormente.
Página 267
Agora, vamos realizar algumas transformações entre essas unidades de medida.
Decímetro cúbico em centímetro cúbico
Para transformar uma medida em decímetros cúbicos em centímetros cúbicos, basta multiplicá-la por 1.000. Analise alguns exemplos.
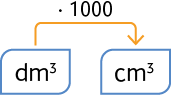
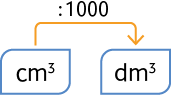
Centímetro cúbico em decímetro cúbico
Para transformar uma medida em centímetros cúbicos em decímetros cúbicos, basta dividi-la por 1.000. Analise alguns exemplos.
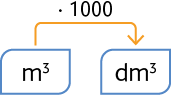
Metro cúbico em decímetro cúbico
Para transformar uma medida em metros cúbicos em decímetros cúbicos, basta multiplicá-la por 1.000. Analise alguns exemplos.
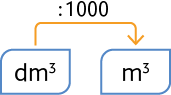
Decímetro cúbico em metro cúbico
Para transformar uma medida em decímetros cúbicos em metros cúbicos, basta dividi-la por 1.000. Analise alguns exemplos.
Atividades
Faça as atividades no caderno.
1. Copie as igualdades em seu caderno, substituindo os pelos números adequados.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
Respostas nas orientações ao professor.
2. Armando e José trabalham com construção civil. Em um dia de trabalho, Armando produziu de concreto, e José, . Qual dos trabalhadores produziu a maior quantidade de concreto nesse dia?
Resposta: Armando.
Página 268
Medida do volume do paralelepípedo reto retângulo
Já estudamos a fórmula que possibilita calcular a medida do volume de um paralelepípedo reto retângulo. Vamos relembrar!
Para calcular a medida do volume V de um paralelepípedo reto retângulo em que as dimensões medem a, b e c, fazemos:
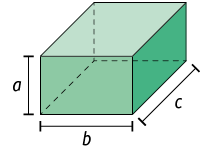
Utilizando essa fórmula, vamos calcular, por exemplo, a medida do volume do paralelepípedo reto retângulo apresentado a seguir.
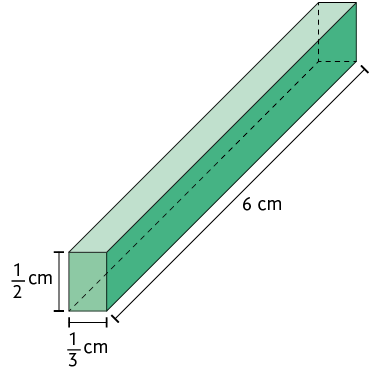
Portanto, o volume desse paralelepípedo mede .
O cubo é um caso particular de paralelepípedo reto retângulo, em que todas as dimensões têm medidas iguais. Sendo assim:
Para calcular a medida do volume V de um cubo cujo comprimento da aresta mede a, fazemos:
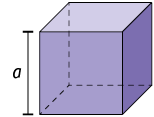
Questão 1. Em qual item é apresentada a medida do volume do cubo a seguir? Faça os cálculos em seu caderno.
a)
b)
c)
d)
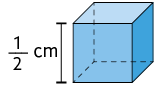
Resposta: Alternativa b.
Página 269
Atividades
Faça as atividades no caderno.
3. Calcule a medida do volume de cada um dos paralelepípedos retos retângulos.
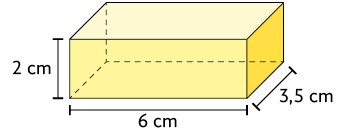

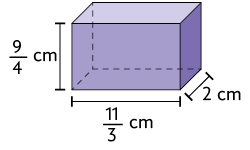
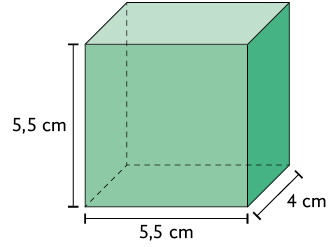
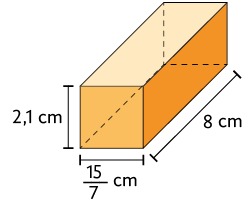
Respostas: A. ; B. ; C. ; D. ; E. .
4. Em cada item, determine a medida desconhecida.
a) O volume do paralelepípedo reto retângulo mede .
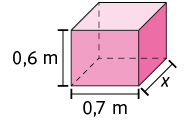
b) O volume do paralelepípedo reto retângulo mede .
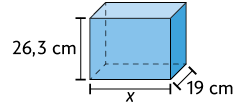
c) O volume do paralelepípedo reto retângulo mede .
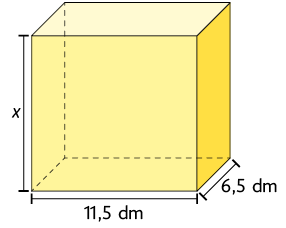
d) O volume do paralelepípedo reto retângulo mede .
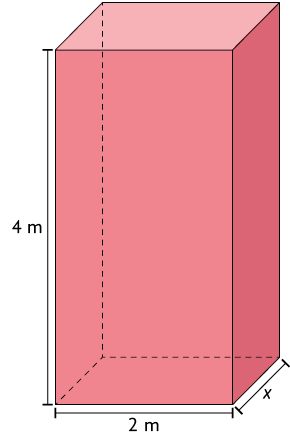
e) O volume do paralelepípedo reto retângulo mede .
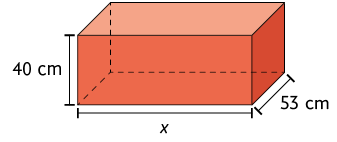
Respostas: a) ; b) ; c) ; d) ; e) .
Página 270
5. Qual é a medida do volume de um cubo cujo comprimento da aresta mede ?
Resposta: .
6. As dimensões de um paralelepípedo reto retângulo medem , e . Qual deve ser a medida do comprimento da aresta de um cubo para que ele tenha a medida do volume igual à desse paralelepípedo?
Resposta: .
7. Carlos vai construir uma casa de bonecas para suas filhas. Para isso, ele utilizará um bloco de madeira com formato de paralelepípedo reto retângulo cujas dimensões medem , e . Sabendo que 20% do bloco de madeira serão destinados à construção do telhado, determine a medida do volume de madeira usado na confecção dessa parte da casa.
Resposta: .
8. Qual é a diferença entre a medida do volume de um paralelepípedo reto retângulo cujas dimensões medem , e e a medida do volume de um cubo cujo comprimento da aresta mede ?
Resposta: .
9. Escreva no caderno quais das medidas indicadas a seguir correspondem ao volume do cubo cujo comprimento das arestas mede .
Resposta: , e .
10. Analise os paralelepípedos retos retângulos.
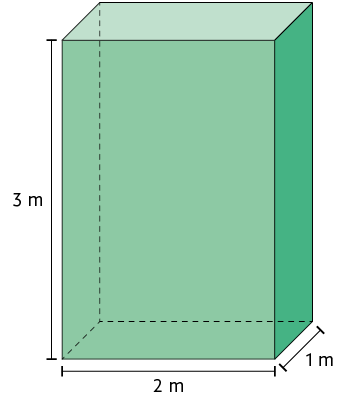
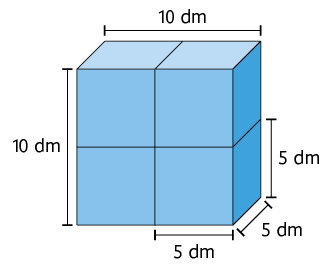
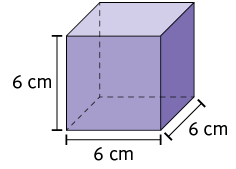
Agora, leia cada informação e classifique-a em verdadeira ou falsa. Depois, reescreva no caderno as falsas, corrigindo-as.
a) 30% da medida do volume do paralelepípedo A correspondem a .
Resposta: Verdadeira.
b) A quarta parte da medida do volume do empilhamento de cubos B equivale a .
Resposta: Verdadeira.
c) da medida do volume do cubo C é igual a .
Resposta: Falsa. Sugestão de correção: da medida do volume do cubo C corresponde a .
Página 271
11. Maria está realizando um experimento. Nele, ela deposita objetos dentro de um recipiente com água. O recipiente utilizado tem formato de paralelepípedo reto retângulo e está representado a seguir.
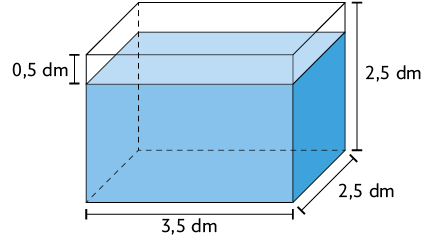
Atenção!
Na imagem estão indicadas as medidas das dimensões internas do recipiente.
No quadro está apresentada a medida do volume dos objetos que Maria depositou no recipiente, um por vez.
|
Objeto |
Medida do volume |
|---|---|
|
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
a) Qual é a medida do volume interno do recipiente usado por Maria?
Resposta: .
b) Entre os objetos, qual tem a maior medida de volume? E a menor?
Respostas: D; B.
c) Entre os objetos depositados por Maria, algum fez a água transbordar? Em caso afirmativo, qual ou quais?
Respostas: Sim; D.
d) Qual ou quais dos objetos depositados por Maria fez ou fizeram o nível da água subir:
I)?
II)?
III)?
Respostas: I-E; II-B; III-C.
12. (Enem – 2019) Para decorar sua casa, uma pessoa comprou um vaso de vidro em forma de um paralelepípedo retangular, cujas medidas internas são: de comprimento, de largura e de altura. Em seguida, foi até uma floricultura e escolheu uma planta aquática para colocar nesse vaso. Segundo uma proposta do gerente do local, essa pessoa avaliou a possibilidade de enfeitar o vaso colocando uma certa quantidade de pedrinhas artificiais brancas, de volume igual a cada uma delas, que ficarão totalmente imersas na água que será colocada no vaso. O gerente alertou que seria adequado, em função da planta escolhida, que metade do volume do vaso fosse preenchido com água e que, após as pedrinhas colocadas, a altura da água deveria ficar a do topo do vaso, dando um razoável espaço para o crescimento da planta. A pessoa aceitou as sugestões apresentadas, adquirindo, além da planta, uma quantidade mínima de pedrinhas, satisfazendo as indicações do gerente.
Nas condições apresentadas, a quantidade de pedrinhas compradas foi
a) 140.
b) 280.
c) 350.
d) 420.
e) 700.
Resposta: Alternativa b.
13. Na
imagem estão indicadas as medidas das dimensões internas da gaveta do
escritório de Gabriela. Ao guardar algumas pastas de documentos, cujo volume
total mede , Gabriela ocupou 48% da gaveta. Qual é a
medida da altura (x) dessa gaveta?
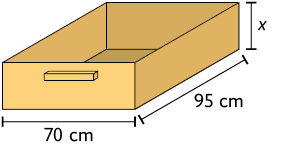
Resposta: .
Página 272
14. Como lembrancinhas da festa de aniversário de sua filha, Juliana está preparando minicaixas no formato de paralelepípedo reto retângulo com algodão-doce, conforme apresentado a seguir. No preparo das lembrancinhas, ela enche completamente as caixas.

Quantas caixas são necessárias para que Juliana acondicione de algodão-doce?
Resposta: 25 caixas.
15. Giovana e João desenharam paralelepípedos retos retângulos no caderno. Cada aresta do paralelepípedo feito por ele tem o dobro da medida de comprimento das arestas daquele representado por ela. Considerando G a medida do volume do paralelepípedo desenhado por Giovana e J a medida do volume do paralelepípedo feito por João, podemos afirmar que:
a) .
b) .
c) .
d) .
e) .
Resposta: Alternativa c.
16. Uma transportadora vai enviar um objeto para outra cidade. Esse objeto tem formato cúbico, o comprimento de sua aresta mede e não pode ser desmontado. Para armazená-lo, ela deve utilizar uma entre as 5 opções de caixa de papelão, cujas medidas das dimensões estão indicadas a seguir.
Caixa 1:
Caixa 2:
Caixa 3:
Caixa 4:
Caixa 5:
a) Qual caixa a transportadora vai utilizar para armazenar esse objeto, de modo que o espaço livre dentro da caixa seja o menor possível?
b) É possível armazenar na mesma caixa mais um objeto com formato cúbico, cujo volume mede ? Justifique sua resposta.
Resposta: Caixa 2; b) Não, pois a medida de comprimento da aresta desse objeto mede e com a medida de comprimento da aresta do outro objeto ultrapassa a medida das dimensões da caixa.
17. (Enem – 2018) Uma fábrica comercializa chocolates em uma caixa de madeira, como na figura.
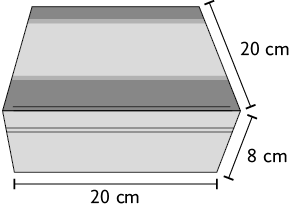
A caixa de madeira tem a forma de um paralelepípedo reto retângulo cujas dimensões externas, em centímetro, estão indicadas na figura. Sabe-se também que a espessura da madeira, em todas as suas faces, é de .
Qual é o volume de madeira utilizado, em centímetro cúbico, na construção de uma caixa de madeira como a descrita para embalar os chocolates?
a) 654
b) 666
c) 673
d) 681
e) 693
Resposta: Alternativa c.
18. Elabore um problema envolvendo a caixa em formato de paralelepípedo reto retângulo apresentada a seguir.
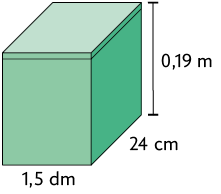
Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Resposta pessoal.
Página 273
Medidas de capacidade
Quando queremos determinar a quantidade de líquido ou gás que um recipiente pode conter, por exemplo, estamos querendo saber a medida da capacidade desse recipiente. Analise alguns exemplos.
Imagens não proporcionais entre si.

O ar quente que enche um balão e o faz subir toma sua forma e ocupa completamente seu espaço interno.

O volume de água que uma jarra pode conter é sua capacidade.
O volume interno de um recipiente é sua capacidade.
As unidades de medida de capacidade mais utilizadas são o litro e o mililitro .
As unidades de medida de capacidade e de volume podem ser relacionadas. Um recipiente cujo volume mede , por exemplo, tem capacidade medindo .
No recipiente com formato cúbico representado a seguir cabe de água.
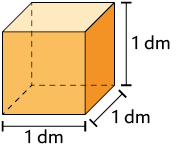
Atenção!
Um recipiente cujo volume mede , por exemplo, tem capacidade medindo .
Agora, vamos determinar uma equivalência entre litros e metros cúbicos. Sabemos que e . Nesse sentido, temos:
Portanto, .
Questão 2. Escreva em seu caderno um algoritmo que possibilite converter uma medida em:
a) litros em decímetro cúbico.
b) litros em metros cúbicos.
Respostas na seção Resoluções.
Página 274
Atividades
Faça as atividades no caderno.
19. Copie as igualdades em seu caderno, substituindo os pelos números adequados.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
Respostas na seção Respostas e na seção Resoluções.
20. O volume interno de um recipiente mede . Qual é a medida da capacidade desse recipiente em mililitros?
Resposta: .
21. As figuras a seguir representam recipientes em formato de paralelepípedos retos retângulos cheios de água.
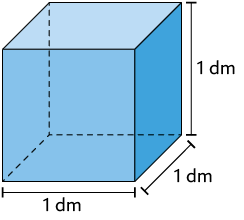
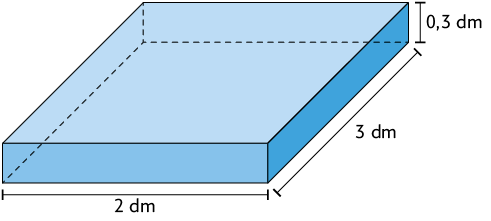
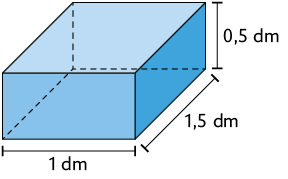
Atenção!
As medidas indicadas correspondem às dimensões internas dos recipientes.
Quais deles têm água suficiente para encher completamente uma garrafa cuja capacidade mede ?
Resposta: Alternativas A e C.
22. Em geral, a fatura de água de uma residência apresenta o consumo mensal de água em metros cúbicos. Considere a fatura de água da casa de Roberto, que indica o consumo de de água no mês de janeiro.
a) Quantos litros de água foram consumidos nesse mês?
b) No mês seguinte, o consumo de água na casa de Roberto diminuiu . De quantos metros cúbicos foi o consumo nesse mês?
Respostas: a) ; b) .
23. A capacidade de um recipiente com formato de paralelepípedo reto retângulo mede . Sabendo que a largura e a altura interna desse recipiente medem, respectivamente, e , determine a medida do comprimento interno dele.
Resposta: .
Página 275
24. Em cada item, determine a quantidade de litros de água que cabe em cada recipiente com formato de paralelepípedo reto retângulo, sabendo que as medidas indicadas correspondem às dimensões internas.

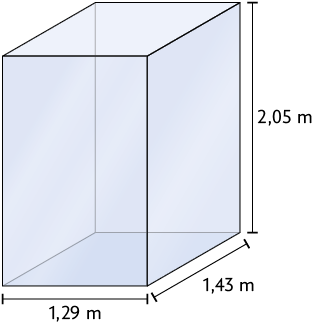
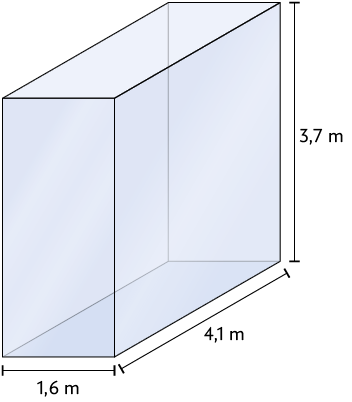
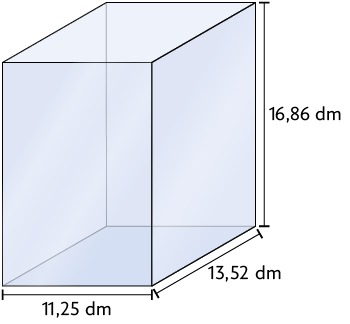
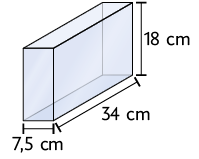
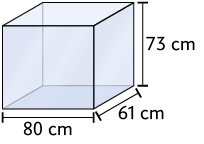
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
25. Considere o reservatório em formato de paralelepípedo reto retângulo apresentado a seguir.
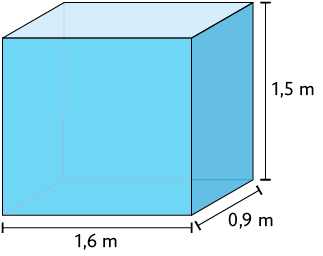
Marta vai bombear água para dentro desse reservatório. Supondo que a cada segundo seja despejado 1,8 litro de água, quantos minutos são necessários para encher completamente esse reservatório?
Resposta: .
Página 276
26. Maurício
colocou água no recipiente em formato de paralelepípedo reto retângulo
apresentado a seguir.
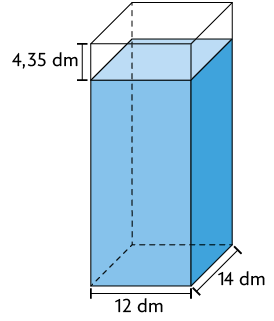
Sabendo que a quantidade de água no recipiente corresponde a 85% de sua medida de capacidade, determine a medida do volume interno desse recipiente em metros cúbicos.
Resposta: .
27. Elabore um problema envolvendo as figuras a seguir.
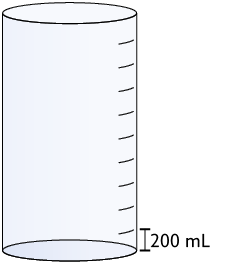
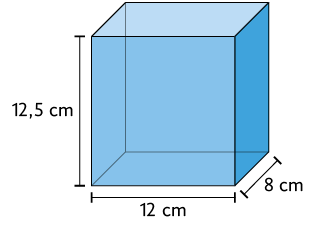
Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Resposta pessoal.
28. A figura a seguir representa uma piscina com formato de paralelepípedo reto retângulo.
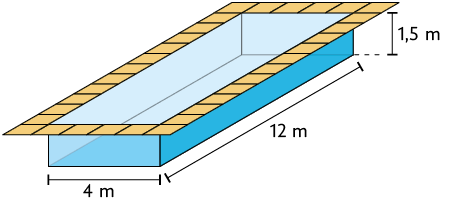
Sabendo que as medidas indicadas correspondem às dimensões internas da pisicina e que três mangueiras que despejam de água por minuto, cada uma, estão enchendo essa piscina, inicialmente vazia, calcule em quantos minutos aproximadamente ela estará cheia.
Resposta: .
29. A garrafa a seguir estava cheia e Renata despejou todo seu conteúdo no recipiente com formato de paralelepípedo reto retângulo. O conteúdo da garrafa encheu completamente o recipiente e não sobrou líquido algum.

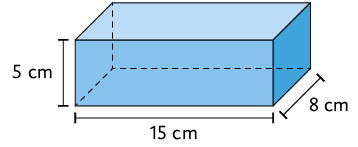
Atenção!
As medidas indicadas correspondem às dimensões internas do recipiente com formato de paralelepíedo reto retângulo.
a) Qual é a medida, em centímetro cúbico, do volume interno desse recipiente?
b) Quantos mililitros foram despejados nesse recipiente?
c) Qual é a medida da capacidade dessa garrafa, em mililitro?
Respostas: a) ; b) ; c) .
Página 277
30. Analise o paralelepípedo reto retângulo a seguir.
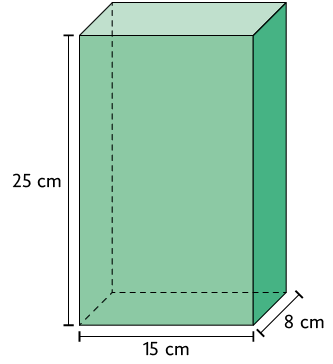
Agora, determine quais afirmações são verdadeiras.
a) Ao dobrar a medida de qualquer uma de suas dimensões, a medida da capacidade será .
b) Ao dobrar a medida de qualquer uma de suas dimensões, a medida da capacidade será .
c) Ao dobrar a medida de todas as suas dimensões a medida da capacidade será igual a .
d) Ao triplicar a medida de qualquer uma de suas dimensões, a medida da capacidade será correspondente a .
e) A medida da capacidade desse paralelepípedo reto retângulo é .
Resposta: Alternativas a e d.
31. Elabore um problema envolvendo todas as medidas apresentadas.
Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Resposta pessoal.
32. A seguir são apresentados três copos iguais com as quantidades de água indicadas.



Imagens não proporcionais entre si.
Considerando o recipiente com formato de paralelepípedo reto retângulo a seguir, responda às questões no caderno.
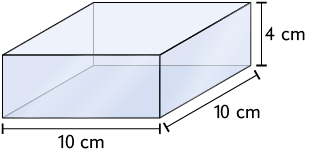
a) Que medida de altura a água atingirá ao despejar todo o conteúdo do copo A no recipiente?
b) Ao despejar todo o conteúdo dos copos A e B no recipiente, qual será a medida da altura atingida pela água?
c) Ao despejar todo o conteúdo do copo C no recipiente, a água transbordará? Justifique sua resposta.
Respostas: a) ; b) ; c) Não, pois a medida da capacidade do recipiente é maior do que .
Página 278
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Quais das igualdades a seguir são verdadeiras?
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
Resposta: Alternativas c, d, e, f e g.
2. Em uma caixa em formato cúbico cujo comprimento das arestas internas mede , Flávia guardou um objeto com . Qual é a medida de volume que sobrou na caixa?
Resposta: .
3. (Enem – 2019) Um mestre de obras deseja fazer uma laje com espessura de utilizando concreto usinado, conforme as dimensões do projeto dadas na figura.
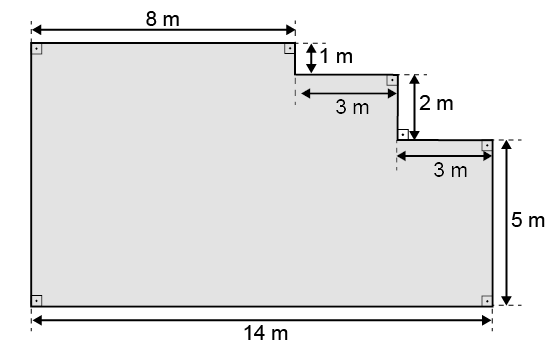
O concreto para fazer a laje será fornecido por uma usina que utiliza caminhões com capacidades máximas de , e de concreto.
Qual é a menor quantidade de caminhões, utilizando suas capacidades máximas, que o mestre de obras deverá pedir à usina de concreto para fazer a laje?
a) Dez caminhões com capacidade máxima de .
b) Cinco caminhões com capacidade máxima de .
c) Um caminhão com capacidade máxima de .
d) Dez caminhões com capacidade máxima de .
e) Um caminhão com capacidade máxima de .
Resposta: Alternativa c.
4. As dimensões de um paralelepípedo reto retângulo medem a, b e . Sabendo que o volume desse paralelepípedo mede e que , determine as medidas das dimensões dele.
Resposta: , e .
5. (ENEM – 2017) Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado desse produto para cada de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a , com largura e comprimento iguais a e , respectivamente.
O nível da lâmina d'água dessa piscina é mantido a da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é
a) 11,25
b) 27,00.
c) 28,80.
d) 32,25.
e) 49,50.
Resposta: Alternativa b.