SuperAÇÃO! matemática

Página 10

O que eu já sei?

Faça as atividades em uma folha de papel avulsa.

1. Uma possível decomposição do número 6.874 é:

a) $6 vezes 10 ao cubo mais 8 vezes 10 ao quadrado mais 7 vezes 10 elevado a 1 mais 4 vezes 10 elevado a 1$ .

b) $6 vezes 10 ao cubo mais 8 vezes 10 ao quadrado mais 7 vezes 10 elevado a 1 mais 4 vezes 10 elevado a 0$ .

c) $6 vezes 10 ao cubo mais 8 vezes 10 ao quadrado mais 7 vezes 10 elevado a 1 vezes 4 vezes 10 elevado a 0$ .

d) $6 vezes 10 elevado a 0 mais 8 vezes 10 elevado a 1 mais 7 vezes 10 ao quadrado mais 4 vezes 10 ao cubo$ .

e) $6 vezes 10 elevado a 4 mais 8 vezes 10 ao cubo mais 7 vezes 10 ao quadrado mais 4 vezes 10 elevado a 1$ .

2. Alexandre realizou uma pesquisa com 30 colegas para saber se eles já assistiram aos filmes A, B ou C. Ele percebeu que 11 deles assistiram ao filme A, 15, ao filme B, e 16, ao filme C. Além disso, em seus registros, ele percebeu que 7 colegas assistiram aos filmes A e B, 6, aos filmes B e C, 5, aos filmes A e C, e 3 assistiram a todos os filmes. Quantos colegas de Alexandre não assistiriam a nenhum dos filmes?

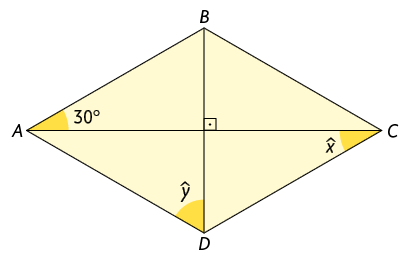
3. Sabendo que $\vec{A C}$ é a bissetriz do ângulo $B \hat{A} D$ e que $A B C D$ é um losango, determine $\hat{x}$ e $\hat{y}$ .

Ilustração de um losango A B C D dividido em quatro partes iguais. Cada parte corresponde a um triângulo retângulo. No triângulo retângulo AB e centro do losango, a medida do ângulo A igual a 30 graus. No triângulo retângulo CD e centro do losango, a medida do ângulo C igual a x. No triângulo retângulo AD e centro do losango, a medida do ângulo D igual a y.

4. Em cada item, de acordo com a informação apresentada, determine a medida do comprimento da aresta do cubo.

a) O volume do cubo mede $27 centímetros cúbicos$ .

b) O volume do cubo mede $125 centímetros cúbicos$ .

5. O preço de uma mesa de jantar que custava R$ 1.500,00 sofreu um aumento de 3% em fevereiro. Em maio, com o objetivo de vender a mesa, o comerciante decidiu fazer uma promoção e aplicou um desconto de 3% sobre o preço de fevereiro.

a) Qual era o preço dessa mesa em fevereiro?

b) Em maio, o preço da mesa voltou a ser os R$ 1.500,00 iniciais? Justifique sua resposta em uma folha de papel avulsa.

6. O comprimento do raio da circunferência de centro O apresentada a seguir mede $19 metros$ .

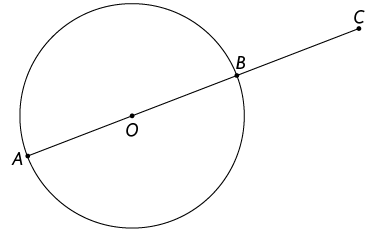
Ilustração de uma circunferência de centro O. Sobre a circunferência há um segmento de reta que tem 4 pontos alinhados: A, O e B, representam o diâmetro da circunferência e o ponto C, que está fora da circunferência na extremidade do segmento de reta.

Sabendo que $a c igual a 59 metros$ , determine a medida do comprimento do segmento de reta $B C$ .

7. Numa fábrica de embalagens, 16 funcionários produzem 240 embalagens por dia. Considerando o mesmo ritmo de trabalho, quantos funcionários seriam necessários para produzir 600 embalagens em um dia?

8. Cecília tem em sua carteira 15 moedas que totalizam R$ 5,25. Sabendo que ela tem apenas moedas de 25 e de 50 centavos, determine a quantidade de moedas de 25 centavos que há na carteira dela.

Página 11

9. Analise as notas obtidas pelos estudantes do 9º ano em uma prova de Matemática.

a) Determine a média, a moda e a mediana desse conjunto de dados.

b) Em sua opinião, qual das medidas de tendência central representa melhor esse conjunto de dados?

10. Rodolfo construiu duas figuras: A e B. Para construir a figura B, ele aplicou uma única transformação sobre a figura A.

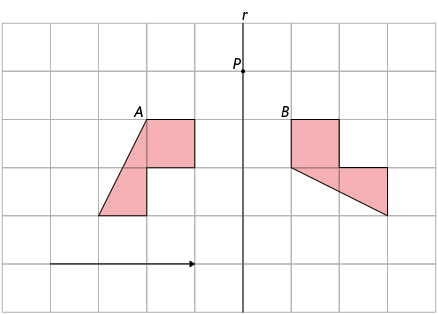
Ilustração de malha quadriculada com dois polígonos de 6 lados iguais e uma reta vertical r passando com a mesma distância entre esses polígonos e com o ponto P pertencente a ela. A figura A representa o polígono que está à esquerda da reta e o polígono parece estar em pé. Abaixo dele há uma seta que aponta para a direita e tem tamanho de 3 quadradinhos. Do outro lado da reta e na mesma linha, está a figura B que representa o outro polígono que parece estar deitado em relação ao polígono da figura A.

Qual transformação Rodolfo aplicou na figura A para obter a figura B?

11. Em uma sorveteria, há 6 tipos de casquinha, 15 sabores de sorvete e 12 tipos de cobertura. Sabendo que uma pessoa deve escolher uma de cada opção oferecida, quantas possibilidades de tomar sorvete há ao todo nessa sorveteria?

12. As imagens a seguir representam duas praças retangulares de certa cidade.

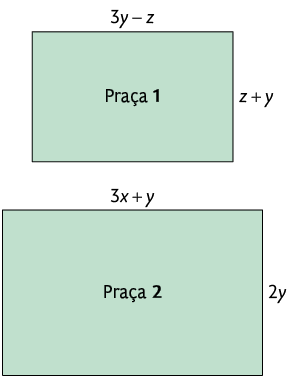
Ilustração de duas praças, nomeadas por praça 1 e praça 2 com a representação de um terreno de formato retangular. Medidas da Praça 1: 3y menos z de comprimento e z mais y de largura. Medidas da Praça 2: 3x mais y de comprimento e 2y de largura.

a) Escreva uma expressão algébrica que represente a medida do perímetro de cada uma das praças.

b) A prefeitura da cidade decidiu cercar essas praças. Se $x igual a 5 metros$ e $y igual a 7 metros$ , quantos metros de cerca serão necessários?

13. Considere a sequência a seguir.

$abre parênteses menos 2 2 6 10 14 18 reticências fecha parênteses$

Determine:

a) a lei de formação dessa sequência.

b) o vigésimo termo dessa sequência.

14. Roberto é entregador. Seu salário é constituído por um valor fixo de R$ 1.300,00 mais R$ 2,50 por quilômetro rodado.

a) Em uma folha de papel avulsa, escreva uma equação que possibilite determinar o salário y de Roberto em função da quantidade x de quilômetros rodados por ele em um mês.

b) Represente em um plano cartesiano a equação escrita por você no item a.

Página 12

15. Calcule a medida da área das figuras geométricas planas.

Ilustração de um paralelogramo com 3 centímetros de altura e a base com 5 centímetros. — Paralelogramo.

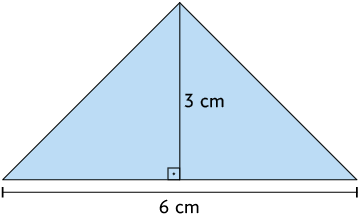
Ilustração de um triângulo com 3 centímetros de altura e a base com 6 centímetros. — Triângulo.

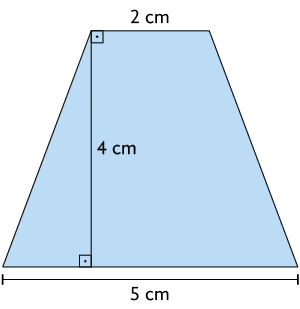
Ilustração de um trapézio, com a base maior medindo 5 centímetros, base menor medindo 2 centímetros e a altura medindo 4 centímetros. — Trapézio.

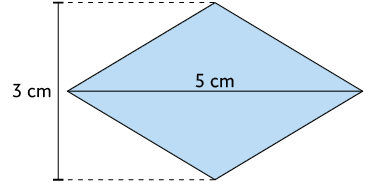
Ilustração de um losango. A medida de comprimento da diagonal maior é 5 centímetros, e da diagonal menor é 3 centímetros. — Losango.

16. Role-Playing Game (RPG) de mesa é um jogo que se parece muito com jogos de tabuleiro, mas nele você interpreta e descreve as ações de seus personagens durante uma narrativa. Para adicionar aleatoriedades nas decisões dos jogadores, usam-se dados de diversas faces, como os apresentados a seguir.

Fotografia de 7 dados usados para jogar RPG, todos com diferentes quantidades de faces e formatos. Um deles é tradicional, com 6 faces, outro tem 4 faces triangulares, outro com 8 faces triangulares, dois deles tem 10 faces quadrangulares, outro tem 20 faces triangulares e o outro tem 12 faces pentagonais. — Dados utilizados para jogar RPG de mesa.

Determine a probabilidade de:

a) sortear um número par utilizando um dado de 8 faces numeradas de 1 a 8.

b) sortear um número maior ou igual a 5 utilizando um dado de 12 faces, numeradas de 1 a 12.

c) sortear um número menor do que 15 utilizando um dado de 20 faces, numeradas de 1 a 20

17. Analise as afirmações a seguir e determine quais são verdadeiras e quais são falsas, reescrevendo as afirmações falsas em uma folha de papel avulsa de modo a corrigi-las.

a) $1 litro$ equivale a $1 decímetro cúbico$ .

b) $100 decímetros cúbicos$ equivale a $1.000 litros$ .

c) $1 metro cúbico$ equivale a $1.000 litros$ .

d) $100.000 litros$ equivale a $10 metros cúbicos$ .