Página 19
UNIDADE
2
Potenciação e radiciação

Agora vamos estudar...
- potenciação com expoentes naturais;
- potenciação com expoentes negativos;
- potenciação com expoentes fracionários;
- radiciação e cálculo de raízes;
- propriedades dos radicais;
- simplificação de raízes.
Página 20
Relembrando potenciação
A potenciação é uma operação utilizada para representar uma multiplicação de fatores iguais, na qual podemos identificar os seguintes elementos.
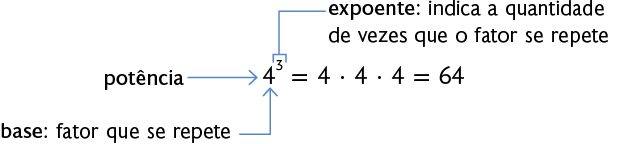
Lemos das seguintes maneiras: quatro elevado ao cubo, quatro ao cubo ou quatro elevado à terceira potência.
Analise alguns exemplos de cálculos de potências.
Denomina-se potência de base a e expoente n, em que n é um número natural maior do que 1, o número (lê-se: a elevado a n), que corresponde ao produto de n fatores a, ou seja:
Caso ou , definimos:
, isto é, a elevado a 1 é igual a a, para qualquer que seja a. Acompanhe alguns exemplos.
, isto é, a elevado a 0 é igual a 1, para qualquer que seja a. Acompanhe alguns exemplos.
Página 21
Potências com expoente negativo
Agora, estudaremos potências com expoente negativo.
Um número diferente de zero elevado a um expoente negativo é igual ao inverso desse número elevado ao oposto do expoente.
Assim, sendo a (base) um número diferente de zero e n (expoente) um número natural, temos:
ou
Atenção!
Lembre-se de que o inverso de um número a diferente de zero é .
Acompanhe alguns exemplos.
Propriedades das potências
Neste tópico, estudaremos algumas propriedades das potências decorrentes das definições apresentadas nesta unidade.
1ª propriedade
Um produto de potências de mesma base pode ser transformado em uma única potência mantendo a base e adicionando os expoentes.
De modo geral, sendo m e n números inteiros e a um número real, temos , com se ou .
Exemplos:
2ª propriedade
Um quociente de potências de mesma base pode ser transformado em uma única potência mantendo a base e subtraindo os expoentes.
De modo geral, sendo m e n números inteiros e , temos .
Exemplos:
Página 22
3ª propriedade
A potência de um produto pode ser transformada em um produto de potências elevando cada número ao expoente nela indicado.
De modo geral, sendo n um número inteiro e a e b números reais, temos , com se .
Exemplos:
4ª propriedade
A potência de um quociente pode ser transformada em um quociente de potências elevando cada número ao expoente nela indicado.
De modo geral, sendo n um número inteiro e a e b números reais, com , temos , com se .
Exemplos:
5ª propriedade
A potência de uma potência pode ser transformada em uma única potência mantendo a base dela e multiplicando os seus expoentes.
De modo geral, sendo m e n números inteiros e a um número real, temos , com se ou .
Exemplos:
Atividades
Faça as atividades no caderno.
1. Calcule as potências.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Página 23
2. A seguir, identifique quais potências são maiores do que 1.
a)
b)
c)
d)
e)
f)
3. Usando as propriedades das potências, calcule.
a)
b)
c)
d)
e)
f)
g)
h)
4. Com o
auxílio de uma calculadora, calcule:
a) o produto entre e .
b) o quociente entre e .
c) o cubo da metade de 5.
d) a metade do cubo de 5.
e) a quarta potência do dobro de 5.
f) o quadrado do dobro de .
5. Resolva as expressões em cada item.
a)
b)
c)
d)
e)
6. Em cada
item, determine o valor de x para que a
igualdade seja verdadeira.
a)
b)
c)
d)
7. Calcule.
a)
b)
c)
d)
e)
f)
Atenção!
Em uma potência de base 10 com expoente inteiro positivo, a quantidade de zeros no resultado após o algarismo 1 é igual ao valor do expoente.
Em uma potência de base 10 com expoente inteiro negativo, a quantidade de algarismos à direita da vírgula é igual ao oposto do valor do expoente.
8. Anderson colocou uma dúzia de ovos em uma caixa pequena, inseriu uma dúzia dessas caixas pequenas em caixas maiores e, por fim, acomodou uma dúzia dessas caixas maiores em um caminhão para transporte. Quantos ovos esse caminhão transportou?
9. Entre as
expressões a seguir, qual apresenta o maior valor? Justifique a resposta em seu
caderno.
Página 24
10. Leia as informações a seguir.
Imagem com elementos não proporcionais entre si.


Atenção!
Os números escritos em notação científica devem ter a forma , sendo:
a: um número maior ou igual a 1 e menor do que 10.
n: um número inteiro.
Para reduzir a quantidade de algarismos em números muito grandes, ou muito pequenos, podemos indicá-los usando a notação científica. Os números anteriores, por exemplo, podem ser representados da seguinte maneira.
A. .
B.
Represente os números destacados nas informações a seguir em notação científica.
a) A medida do volume de água dos oceanos da Terra é de aproximadamente .
b) A medida da distância média da Terra ao Sol é de .
c) Um quilograma equivale a .
d) As hemácias, cujo comprimento do diâmetro mede , estão presentes no sangue humano.
11. Para adicionarmos ou subtrairmos números em notação científica, os expoentes da base 10 devem ser iguais. Se os expoentes forem diferentes, podemos reescrever um dos números fazendo a adaptação adequada. Em seguida, efetuamos a operação com os coeficientes e conservamos a base 10. Acompanhe um exemplo.
Usando esse procedimento, efetue os cálculos a seguir.
a)
b)
Página 25
Radiciação
Neste tópico, estudaremos algumas situações envolvendo a operação radiciação.
Considere a seguinte situação.
Pedro é marceneiro e vai fabricar uma mesa cuja superfície, de forma quadrada, terá de medida de área. Para isso, é necessário que ele saiba a medida do comprimento do lado da superfície dessa mesa.
Extraindo a raiz quadrada de 4.900, é possível obter essa medida.
, pois
Logo, o comprimento do lado da superfície da mesa que Pedro vai fabricar medirá .
A radiciação, operação usada para resolver a situação anterior, é a operação inversa da potenciação.
Em uma radiciação, temos os seguintes elementos:
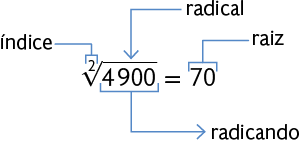
Atenção!
Usualmente, o índice 2 da raiz quadrada é omitido. Indicamos, por exemplo, por .
Agora, considere outra situação.
O cubo mágico representado a seguir tem a medida de volume igual a . Para saber a medida das dimensões desse cubo, basta calcular a raiz cúbica de 125.
, pois

Logo, as dimensões desse cubo medem .
Questão 1. Realize uma pesquisa para descobrir o inventor do cubo mágico. Depois, registre os resultados obtidos no caderno.
Atenção!
A pesquisa proposta na questão 1 pode ser feita em sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com as de outras fontes.
Página 26
Raiz enésima
Para calcular a raíz enésima de um número real a (indicada por ), devemos considerar os seguintes casos.
Atenção!
enésimo: que ocupa a posição do número n; também pode ser escrito como n-ésimo.
a) n é um número natural par, diferente de zero.
- Para , a raiz enésima de a é um número real b
não negativo, tal que .
Acompanhe alguns exemplos.
- , pois .
- (lê-se: raiz quarta de 256 é igual a 4), pois .
- (lê-se: raiz sexta de 729 é igual a 3), pois .
- Para ,
a raiz enésima de a não é definida no
conjunto dos números reais, pois não existe um número b tal que .
Exemplo: Não existe no conjunto dos números reais, pois não existe um número real que, elevado ao quadrado, seja igual a .
b) n é um número natural ímpar, diferente de 1.
A raiz enésima de a é um número real b, tal que .
Nesse caso, quando a é um número real positivo, b também é positivo, e quando a é negativo, b também é negativo.
Acompanhe alguns exemplos.
- , pois .
- (lê-se: raiz quinta de é igual a ), pois .
- (lê-se: raiz sétima de é igual a ), pois .
Questão 2. Copie as sentenças a seguir em seu caderno, substituindo os pelos números adequados.
a) A raiz sétima de é 5, pois .
b) A raiz quarta de 81 é , pois .
c) A raiz quinta de é , pois .
d) A raiz sexta de 64 é , pois .
Questão 3. Junte-se a um colega e realizem uma pesquisa sobre o surgimento do símbolo utilizado para indicar a radiciação. Depois, apresente seus resultados para os colegas e professor.
Página 27
Potências com expoente fracionário
Já estudamos em anos anteriores as potências com expoente fracionário e verificamos que elas podem ser escritas por meio de radicais, assim como radicais podem ser escritos na forma de potências. Analise alguns exemplos.
De modo geral, sendo a um número racional positivo, n e m números naturais, com e , temos:
Atenção!
O índice do radical corresponde ao denominador do expoente da potência.
Atividades
Faça as atividades no caderno.
12. Em cada item está indicada a medida da área de um quadrado. Efetue os cálculos e determine a medida do perímetro de cada quadrado.
a)
b)
c)
d)
13. Qual é a medida do comprimento da aresta do cubo cujo volume mede:
a) .
b) .
c) .
d) .
14. Utilizando
uma calculadora, efetue os cálculos, determine o valor de cada
e registre no caderno.
a)
b)
c)
d)
e)
f)
15. Nos
itens a seguir,
representa o índice das raízes. Efetue os cálculos com uma calculadora e
determine o valor de .
a)
b)
c)
d)
e)
f)
16. Sem efetuar cálculos, identifique quais das raízes a seguir são definidas no conjunto dos números reais.
A.
B.
C.
D.
E.
F.
G.
H.
17. A seguir, escreva em seu caderno as potências como raízes e as raízes como potências
a)
b)
c)
d)
e)
f)
18. Indique as igualdades verdadeiras.
a)
b)
c)
d)
Página 28
Propriedades dos radicais
Estudaremos, a seguir, algumas propriedades dos radicais. Elas podem ser úteis ao realizar cálculos com radicais.
1ª propriedade
Quando o índice do radical e o expoente do radicando são positivos e iguais, o resultado é o próprio radicando. Exemplos:
De modo geral, sendo a um número real positivo e n um número natural maior do que 1, temos .
2ª propriedade
Quando multiplicamos ou dividimos o índice do radical e o expoente do radicando por um mesmo número natural não nulo, obtemos um radical equivalente ao inicial. Exemplos:
De modo geral, sendo a um número real positivo, n um número natural maior do que 1, m e p números naturais diferentes de zero, temos:
e
3ª propriedade
A raiz de um produto é igual ao produto das raízes dos fatores e a raiz de um quociente é igual ao quociente das raízes do dividendo e do divisor. Exemplos:
De modo geral, sendo a e b número reais positivos e n um número natural maior do que 1, temos: e ou
4ª propriedade
A raiz de uma raiz pode ser escrita na forma de um único radical, na qual o índice resultante é o produto dos índices das raízes iniciais. Exemplos:
De modo geral, sendo a um número real positivo, n e q números naturais maiores do que 1, temos .
Página 29
Analise, a seguir, como podemos simplificar, por exemplo, as expressões numéricas e escrevendo cada uma na forma de uma única raiz.
Atividades
Faça as atividades no caderno.
19. Efetue os cálculos a seguir.
a)
b)
c)
d)
e)
f)
20. Escreva, no caderno, as expressões numéricas a seguir na forma de uma única raiz.
a)
b)
c)
d)
e)
f)
21. De acordo com as propriedades das raízes, copie, no caderno, as igualdades verdadeiras.
A.
B.
C.
22. Sendo e
números reais positivos e , e
números naturais maiores do que 1, quais igualdades a
seguir são verdadeiras?
A.
B.
C.
D.
E.
F.
23. Aplique as propriedades das raízes e transforme a expressão numérica de cada item em uma única raiz.
A.
B.
C.
24. Simplifique cada potência representando-a com uma única raiz.
a)
b)
c)
d)
e)
f)
25. Calcule a medida da área de cada retângulo a seguir.


Página 30
Simplificação de radicais
Existem casos em que não é possível calcular a raiz exata de um número, mas é possível simplificar a escrita dela.
Acompanhe um procedimento para simplificar .
Inicialmente, decompomos o radicando em fatores primos.
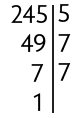
Depois, aplicamos a propriedade , com a e b números reais positivos e n um número natural maior do que 1, e transformamos em um produto de raízes.
Por último, aplicamos a propriedade , com a um número real positivo e n um número natural maior do que 1, e obtemos a escrita simplificada.
Atenção!
O fator tem o mesmo expoente do índice do radical. Portanto, pode ser extraído do radicando.
Logo, a escrita simplificada de é .
Analise como podemos simplificar usando a decomposição em fatores primos.
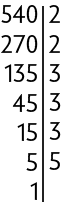
Atenção!
Os fatores e têm o expoente igual ao índice do radical. Portanto, podem ser extraídos do radicando.
Logo, a escrita simplificada de é .
Também podemos introduzir um fator externo no radicando de uma raiz. Analise alguns exemplos.
Página 31
Atividades
Faça as atividades no caderno.
26. Em cada item, retire fatores do radicando.
a)
b)
c)
d)
e)
f)
27. Simplifique as raízes.
a)
b)
c)
d)
e)
f)
28. Os quadrados a seguir são representações de terrenos e em cada um deles está indicada a sua medida de área .
Considerando ; ; e , calcule a medida aproximada do comprimento do lado de cada terreno.
Atenção!
Para obter a medida do comprimento do lado de cada terreno, use as propriedades das raízes.




29. Introduza no radicando os fatores externos.
a)
b)
c)
d)
30. Determine o valor de x em cada item de modo que a igualdade seja verdadeira.
a)
b)
c)
d)
e)
f)
31. Qual deve ser o valor de para que a igualdade a seguir seja verdadeira?
32. Simplifique
no caderno a expressão numérica.
33. Associe os itens que têm o mesmo resultado.
a)
b)
c)
d)
e)
f)
g)
h)
Página 32
Operações com radicais
Adição e subtração com radicais
Em algumas situações, precisamos realizar operações com radicais, como adição, subtração, multiplicação e divisão. Essas operações podem simplificar expressões numéricas envolvendo radicais.
Analise, por exemplo, como calcular o valor de .
Inicialmente, decompomos cada radicando em fatores primos.
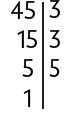
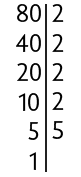
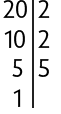
Depois, aplicamos a propriedade , com a e b números reais positivos e n um número natural maior do que 1.
Em seguida, aplicamos a propriedade , com a um número real positivo e n um número natural maior do que 1.
Por último, colocamos em evidência o fator comum dos termos da expressão numérica, nesse caso , e simplificamos a expressão numérica obtida.
Logo, .
Multiplicação e divisão com radicais
Para realizar multiplicações e divisões envolvendo radicais com o mesmo índice, basta aplicar as propriedades das raízes e depois simplificar o resultado. Analise dois exemplos.
Página 33
Agora, analise como efetuar multiplicações e divisões com radicais de índices diferentes.
Vamos calcular, por exemplo, .
Escrevemos os radicais na forma de potências com expoentes fracionários. Em seguida, calculando o mínimo múltiplo comum () dos denominadores, reduzimos os expoentes a frações com o mesmo denominador.
Agora que as frações dos expoentes estão com o mesmo denominador, escrevemos as potências com expoentes fracionários na forma de raízes.
Depois, aplicamos as propriedades das raízes e simplificamos o resultado.
Portanto, .
Seguindo os mesmos procedimentos, podemos calcular o valor de .
Atividades
Faça as atividades no caderno.
34. No caderno, simplifique as expressões numéricas a seguir.
a)
b)
c)
35. Fatore o radicando em cada item e simplifique as expressões numéricas.
a)
b)
c)
36. Sabendo que as letras representam números reais positivos, simplifique as expressões a seguir.
a)
b)
c)
37. Sabendo que , e , calcule o valor das seguintes expressões.
a)
b)
c)
d)
e)
Página 34
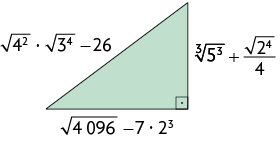
38. Calcule a medida do perímetro de cada figura representada a seguir, sabendo que as medidas estão dadas em metros.

39. Simplifique cada expressão numérica, deixando-as na forma irredutível, ou seja, até que não seja possível fazer mais simplificações.
a)
b)
c)
40. Seja e . Calcule e simplifique o resultado.
41. Considerando ; ; e , calcule o valor aproximado das seguintes expressões numéricas:
a)
b)
c)
d)
e)
42. Determine o valor de em cada item de modo que a igualdade seja verdadeira.
a)
b)
c)
d)
e)
f)
43. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
44. Analise a figura a seguir.

Sabendo que o retângulo anterior representa um terreno, elabore um problema usando as informações apresentadas e dê para um colega resolver. Depois, verifique se a resposta apresentada por ele está correta.
Página 35
45. Sabendo que as letras representam números reais positivos, resolva no caderno as expressões a seguir.
a)
b)
c)
d)
46. Sendo x um número real positivo, a expressão pode ser escrita como:
a)
b)
c)
d)
e)
47. Sabendo que , e , calcule o valor de cada expressão.
a)
b)
c)
d)
48. Simplifique cada expressão numérica a seguir, escrevendo-a no caderno com uma única raiz.
a)
b)
c)
d)
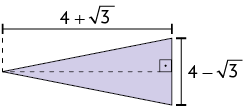
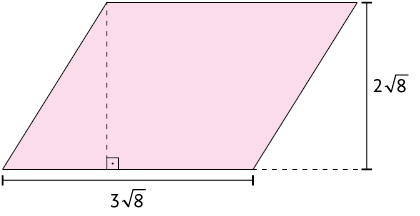
49. Calcule a medida da área de cada figura a seguir, sabendo que as medidas estão indicadas em metros.
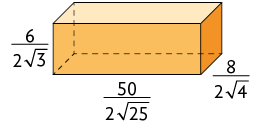
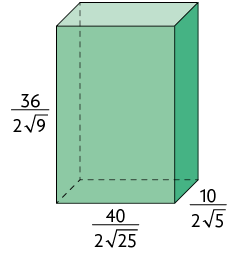
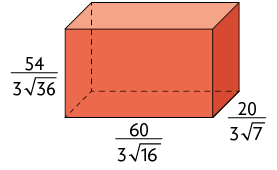
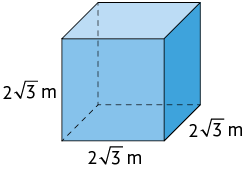
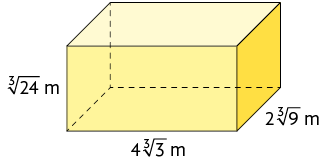
50. Calcule a medida do volume de cada paralelepípedo reto retângulo de acordo com as medidas indicadas.
Página 36
Racionalização
Cada fração escrita na lousa tem uma raiz não exata no denominador.

Na Matemática, não é comum escrevermos frações desse tipo, com raiz no denominador. Então transformamos cada uma delas em uma fração equivalente, de modo que não tenha raiz no denominador, usando um recurso chamado racionalização.
Para racionalizar o denominador de uma fração, multiplicamos o numerador e o denominador por um mesmo número diferente de zero (fator racionalizante), sem alterar seu valor.
Por exemplo, para racionalizar a fração , usamos o fator .
Atenção!
O fator foi escolhido para essa racionalização, pois e, assim, eliminamos a raiz do denominador.
Agora, vamos calcular o valor aproximado de e para verificar se essas duas frações são equivalentes. Para isso, vamos efetuar os cálculos utilizando uma calculadora e considerando .
De fato, nas duas divisões, obtemos o mesmo resultado.
Questão 4. De maneira parecida, em seu caderno, racionalize os denominadores das outras frações apresentadas na lousa da ilustração anterior.
Página 37
Podemos racionalizar o denominador da fração de duas maneiras diferentes, como mostrado a seguir.
1ª maneira
2ª maneira
Também podemos racionalizar o denominador da fração multiplicando o numerador e o denominador por , pois . Nesse caso, obtemos:
Note que:
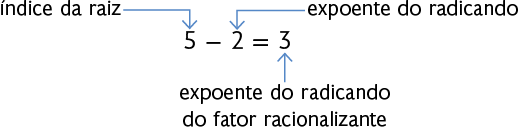
Agora, para racionalizar o denominador de , multiplicamos o numerador e o denominador por , que é a "expressão conjugada" do denominador.
Atenção!
Lembre-se que o produto da soma pela diferença de dois termos é .
Atividades
Faça as atividades no caderno.
51. Racionalize os denominadores das frações.
a)
b)
c)
d)
e)
f)
g)
h)
Página 38
52. Em cada retângulo estão indicadas as medidas de sua área A e de seu comprimento. Determine a medida da largura de cada um deles.


53. Racionalize os denominadores das frações a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
54. Racionalize os denominadores.
a)
b)
c)
d)
e)
f)
55. Sabendo que as letras que aparecem nas frações representam números reais positivos, racionalize os denominadores.
a)
b)
c)
d)
e)
f)
56. Racionalize os denominadores.
a)
b)
c)
d)
e)
f)
57. Simplifique as expressões a seguir, racionalizando os denominadores sempre que possível.
a)
b)
c)
d)
e)
f)
Página 39
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Determine as potências a seguir.
a) O quadrado do dobro de 6.
b) O dobro do quadrado de 6.
c) O quadrado do triplo de 2.
d) O cubo do dobro de 5.
2. Resolva os cálculos a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
3. No quadrado mágico a seguir, o produto das linhas, colunas ou diagonais é sempre igual. Determine as potências de base 9 que as letras representam.
A
B
C
D
E
4. Resolva as expressões a seguir.
a)
b)
c)
5. Escreva, em uma folha de papel avulsa, os números a seguir em notação científica.
a)
b)
c)
d)
6. Calcule.
a)
b)
c)
7. Sendo , calcule:
a) .
b) .
c) .
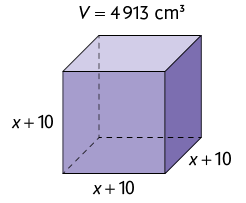
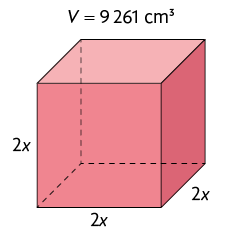
8. Nos cubos a seguir, as medidas dos comprimentos das arestas estão expressas em centímetros. Sabendo que V indica a medida do volume de cada cubo, determine o valor de x em cada item.
Página 40
9. Associe as potências com as raízes.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
10. Determine o valor de x de modo que a igualdade seja verdadeira.
a)
b)
c)
d)
e)
f)
11. Considerando ; e , calcule o valor aproximado de cada expressão numérica a seguir.
a)
b)
c)
12. Considerando e , calcule o valor aproximado de cada expressão numérica.
a)
b)
c)
d)
13. é igual a:
a)
b)
c)
d)
e)
14. Determine a medida do volume de cada paralelepípedo reto retângulo.