Página 41
UNIDADE
3
Razão e proporção

Agora vamos estudar...
- o conceito de razão e de proporção;
- algumas razões especiais;
- grandezas diretamente proporcionais e grandezas inversamente proporcionais;
- divisão em partes proporcionais;
- ângulos opostos pelo vértice;
- ângulos formados por um feixe de retas paralelas e uma transversal;
- o conceito de razão aplicado a segmentos de reta proporcionais;
- o teorema de Tales e sua aplicação nos triângulos.
Página 42
Razão
Neste tópico, estudaremos como comparar duas grandezas. Para isso, vamos analisar o seguinte exemplo.
Na prova de Matemática, Félix acertou 9 atividades e errou 4. Nesse caso, dizemos que a razão entre o número de acertos e o número de erros de Félix nessa prova é de ou .
Sejam a e b dois números reais, com . A razão entre a e b é o quociente de a por b, ou seja, ou .
Agora, considere o seguinte problema.
Em uma turma de 9º ano, há 42 estudantes. A razão entre o número de meninos e o de meninas é . Quantas meninas há nessa turma?
Para resolver o problema, podemos elaborar um quadro.
|
Meninos |
Meninas |
Total de estudantes |
|---|---|---|
|
7 |
||
|
|
14 |
|
|
21 |
||
|
42 |
Desse modo, segue que:
Portanto, na turma há meninas.
Questão 1. Quantos meninos há na turma de
9º ano?
Na sequência, estudaremos algumas razões que estão presentes em nosso dia a dia.
Velocidade média
A velocidade média é definida como a distância total percorrida dividida pelo tempo gasto para percorrê-la. Para compreender melhor, vamos analisar o seguinte exemplo:
Para ir ao trabalho, Marcelo percorreu com seu carro em . Para determinar a medida da velocidade média da viagem em quilômetros por hora, calculamos:
Atenção!
equivale a .
Portanto, a velocidade média desse trajeto mede .
Atenção!
Algumas das unidades utilizadas para expressar a velocidade média são quilômetro por hora e metro por segundo .
Página 43
Densidade demográfica
A densidade demográfica de um local é definida como a razão entre a população total de determinado lugar e a medida de sua área em quilômetros quadrados. Vamos analisar o seguinte exemplo.
Em 2021, a comunidade quilombola Sumidouro, em Queimada Nova (PI), era formada por 23 famílias, havendo nela aproximadamente 115 pessoas. Sabendo que a área da região em que eles moram mede , podemos determinar sua densidade demográfica. Para isso, devemos fazer:
Portanto, em 2021, a densidade demográfica da comunidade quilombola Sumidouro era de aproximadamente .
Atenção!
A densidade demográfica é expressa em habitantes por quilômetro quadrado .
Quilombo Sumidouro – Queimada Nova (PI)
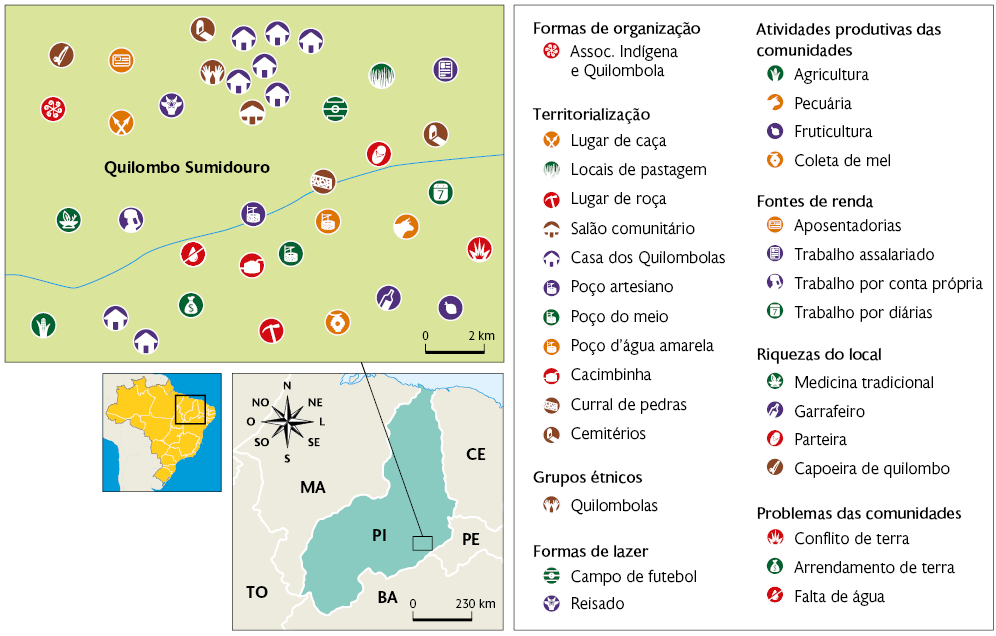
Fonte de pesquisa: MAPA – Indígenas Kariri e quilombolas do Mocambo, Sumidouro e Tapuio Queimada Nova – PI. Nova Cartografia Social da Amazônia. Disponível em: https://oeds.link/lnAhOp. Acesso em: 4 abr. 2022.
Questão 2. Alguns mapas são elaborados por
especialistas junto com
membros da comunidade. Você considera essa parceria importante? Converse com os
colegas e o professor sobre o assunto.
Página 44
Densidade
A densidade de um objeto é definida como o quociente entre sua massa e seu volume. Vamos analisar o seguinte exemplo.
Um objeto tem massa e volume medindo, respectivamente, e . Para determinar a medida da densidade desse objeto em gramas por centímetro cúbico, devemos fazer:
Portanto, a densidade do objeto mede .
Atenção!
Algumas das unidades utilizadas para expressar a densidade de um objeto são: grama por centímetro cúbico , quilograma por metro cúbico e grama por litro .
Escala
A escala de uma representação é definida como a razão entre a medida do comprimento considerado para produzir a representação e a medida do comprimento real correspondente, expressas em uma mesma unidade de medida. Acompanhe o seguinte exemplo.
No mapa apresentado a seguir, cada representa .
Mapa do Paraná
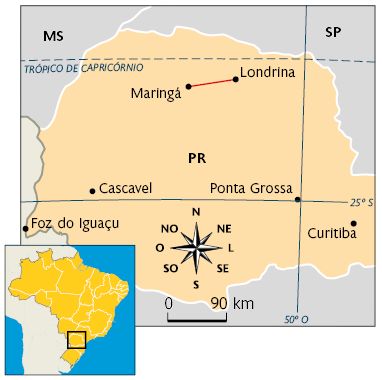
Fonte de pesquisa: Atlas geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.
Para determinar a escala do mapa, devemos fazer:
Com base nessa escala, podemos determinar, por exemplo, a medida da distância em linha reta entre as cidades de Londrina e Maringá. Como no mapa a distância em linha reta entre essas cidades mede , devemos efetuar:
Transformando essa medida em quilômetros, obtemos:
Portanto, a distância em linha reta entre as cidades de Londrina e Maringá mede .
O uso de escalas está presente no dia a dia dos arquitetos, engenheiros, biólogos, entre outros. Por exemplo, os arquitetos utilizam-na para elaborar a planta de uma casa. Já os biólogos podem usar esse conceito para representar a ampliação de uma bactéria, por exemplo.
Questão 3. Pesquise uma situação em que engenheiros utilizam o conceito de escala. Além disso, busque por outros profissionais que utilizam o conceito de razão para realizar os seus trabalhos. Registre no caderno as informações que achar relevantes.
Atenção!
Podem ser usados como fonte, para realizar a pesquisa proposta na questão 3, livros, revistas e sites. No entanto, é necessário estar atento e se certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para finalizar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Página 45
Atividades
Faça as atividades no caderno.
1. No 9º ano B, há 15 meninas e 26 meninos. Qual é a razão entre:
a) o número de meninas e o número de meninos?
b) o número de meninas e o total de estudantes?
c) o número de meninos e o total de estudantes?
2. Joana gosta de colecionar figurinhas de carros e motos, tendo ao todo 125 figurinhas. Sabendo que a razão entre o número de figurinhas de carros e o número de figurinhas de motos é , determine quantas são as figurinhas de carros.
3. Elabore um problema envolvendo velocidade média e peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
4. A escola onde Pedro estuda fica a da casa dele, e para se deslocar ele precisa utilizar o ônibus escolar para frequentar as aulas. Em determinado dia, o ônibus levou para ir da casa de Pedro até a escola, sem fazer paradas ao longo do caminho. Em seu caderno, calcule a medida da velocidade média do ônibus nesse dia.
5. A população estimada de Petrolina (PE) em 2021 era de 359.372 pessoas e a extensão territorial desse local mede .
Fonte de pesquisa: IBGE. Disponível em: https://oeds.link/zIaAdV. Acesso em: 17 maio 2022.
Em seu caderno, calcule a densidade demográfica desse município em 2021.
6. O volume de uma pedra de gelo com formato cúbico mede . Determine a densidade dela, sabendo que sua massa mede .
7. A Rodovia Transpantaneira está localizada no estado do Mato Grosso e liga o município de Poconé a Porto Jofre, em um total de de estrada de "chão".
No mapa, cada representa .
Rodovia Transpantaneira entre Porto Jofre e Poconé
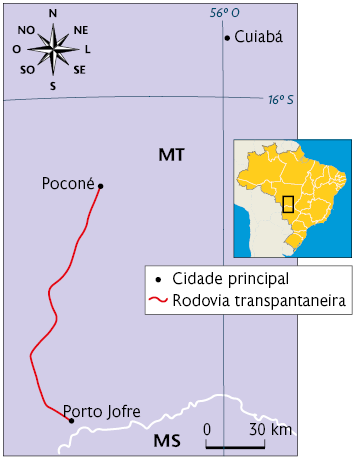
Fonte de pesquisa: Atlas geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.
a) Utilizando uma régua, determine a medida da distância real aproximada em linha reta, em quilômetros, entre Poconé e:
Porto Jofre.
Cuiabá.
b) Qual é a diferença entre a medida do comprimento da Rodovia Transpantaneira e a medida da distância real aproximada em linha reta entre o município de Poconé e Porto Jofre?
8. Escolha uma das razões estudadas, elabore um problema e peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Página 46
Proporção
O quadro a seguir apresenta o número de estudantes de duas turmas do 9º ano.
|
Turma |
Meninos |
Meninas |
|---|---|---|
|
9º ano A |
13 |
9 |
|
9º ano B |
26 |
18 |
Analisando o quadro, verificamos que no 9º ano A a razão entre o número de meninos e o de meninas é . Por outro lado, no 9º ano B, a razão entre o número de meninos e o de meninas também é , visto que, ao simplificar a fração , obtemos . Nesse caso, temos: .
Duas razões com termos não nulos, e , formam uma proporção quando as frações e são equivalentes, ou seja:
(lê-se: a está para b assim como c está para d)
Nessa proporção, a e d são chamados extremos e b e c são chamados meios.
As razões e formam uma proporção, pois . Nesse caso, dizemos que 5 está para 4 assim como 10 está para 8.
Propriedades das proporções
Neste tópico, estudaremos algumas propriedades das proporções. Para isso, considere a proporção .
Propriedade fundamental das proporções: o produto dos meios, em uma proporção, é igual ao produto dos extremos.
Demonstração: Seja a proporção . Como os termos da proporção são não nulos, podemos multiplicar ambos os membros da igualdade por bd. Desse modo, obtemos:
Assim, podemos concluir que, em uma proporção, o produto dos meios é igual ao produto dos extremos.
Se , temos:
Página 47
Demonstração: Vamos verificar que, dada a proporção , temos . De fato, considerando a propriedade fundamental, temos . Adicionando ab em ambos os membros da igualdade, obtemos:
Questão 4. Em seu caderno, mostre que se , com , é uma proporção, então , e .
Grandezas proporcionais
No ano anterior, estudamos grandezas diretamente proporcionais e grandezas inversamente proporcionais. Agora, vamos relembrar esses conceitos analisando alguns exemplos.
Grandezas diretamente proporcionais
Marcos precisa descongelar sua comida e, para isso, utiliza o micro-ondas. Para saber a medida do tempo necessária, ele fez uma busca no manual do aparelho e encontrou o quadro a seguir para o tipo de alimento que ele precisa descongelar.
|
Medida da massa |
|||||
|---|---|---|---|---|---|
|
Medida do tempo |
Analisando as informações, verificamos que, ao dobrarmos a medida da massa, a medida do tempo também dobra; ao triplicarmos a medida da massa, a medida do tempo também triplica; e assim por diante. Nesse caso, dizemos que as grandezas massa e tempo são diretamente proporcionais.
Com base nisso, a razão entre as medidas correspondentes às grandezas massa e tempo é constante, ou seja:
Indicando por x e y, respectivamente, a medida da massa de comida e a medida do tempo necessário para o descongelamento, podemos escrever:
Utilizando essa expressão, podemos calcular, por exemplo, a medida do tempo necessário para descongelar dessa comida. De fato, se , temos:
Portanto, são necessários para descongelar de comida.
Questão 5. Em seu caderno, calcule quantos minutos são necessários para descongelar dessa comida nesse micro-ondas.
Página 48
Grandezas inversamente proporcionais
Bianca vai viajar para a casa de seus pais. Como ela precisa estimar a medida do tempo necessário para completar essa viagem, realizou uma pesquisa e obteve as seguintes informações.
|
Medida da velocidade média |
|||
|---|---|---|---|
|
Medida do tempo |
Ao dobrarmos a medida da velocidade média, verificamos que a medida do tempo fica reduzida pela metade; ao triplicarmos a medida da velocidade média, a medida do tempo fica reduzida à terça parte; e assim por diante. Nesse caso, dizemos que as grandezas velocidade média e tempo são inversamente proporcionais.
Com base nisso, a razão entre as medidas da grandeza velocidade média e o inverso das medidas correspondentes da grandeza tempo é constante, ou seja:
Atenção!
Lembre-se de que é o inverso de 540.
Indicando por x e y, respectivamente, a medida da velocidade média e a medida do tempo necessário para completar a viagem, podemos escrever:
Utilizando essa expressão, podemos calcular, por exemplo, a medida do tempo necessário para completar a viagem, considerando uma velocidade média medindo . De fato, se , temos:
Portanto, serão necessários para completar a viagem.
Questão 6. Se a velocidade média medir , calcule em seu caderno quantas horas e minutos serão necessários para completar essa viagem.
Atividades
Faça as atividades no caderno.
9. Em cada item, verifique se as razões formam uma proporção.
a) e .
b) e .
c) e .
d) e .
e) e .
f) e .
g) e .
h) e .
i) e .
Página 49
10. A seguir, estão indicados os ingredientes para o preparo de um bolo de laranja que Suely vende em sua lanchonete, cujo rendimento é de 6 porções.

De quantas xícaras (chá) de óleo Suely vai precisar para preparar 24 porções desse bolo?
11. Uma empresa de construção civil vai asfaltar de uma estrada. Nos primeiros 76 dias de execução da obra, essa empresa finalizou . Quantos dias ainda são necessários para a empresa concluir o serviço, considerando que o ritmo de trabalho seja mantido?
12. Para ir de sua a casa até o museu da cidade, Pedro levou dirigindo, em média, a . Qual seria a medida do tempo gasto, tanto em minutos quanto em segundos, se tivesse dirigido, em média, a ?
13. Após uma consulta, o médico prescreveu um medicamento para Mateus com a seguinte dosagem: 3 gotas para cada de medida de massa corporal a cada . Sabendo que a massa corporal de Mateus mede , quantas gotas desse medicamento ele deve ingerir a cada ?
14. Para encher um reservatório com água, duas torneiras abertas demoram, em média, . Em quantos minutos cinco torneiras abertas iguais a essas demorariam para encher esse reservatório?
15. Para atender à alta demanda, uma estamparia decidiu adicionar 3 novas máquinas em sua linha de produção, totalizando 8 máquinas. Sabendo que antes eram estampadas 300 camisetas por dia e que todas as máquinas são iguais, qual será o aumento na produção diária?
16. Uma máquina copiadora imprime 960 páginas a cada 3 minutos. Em quantos minutos ela imprimirá 1.600 páginas?
17. Trabalhando 5 horas por dia, Juliana e seus dois funcionários produzem, diariamente, certa quantidade de refeições. Sabendo que Juliana se dedicará apenas às entregas, determine a medida de tempo necessária para que, em um dia, esses dois funcionários produzam, considerando o mesmo ritmo de trabalho, essa mesma quantidade de refeições.
18. Com certa quantidade de ração, Antônio alimenta 120 galinhas durante 12 dias. Durante quantos dias essa mesma quantidade de ração será suficiente para alimentar 80 galinhas?
19. Elabore um problema envolvendo grandezas diretamente proporcionais. Em seguida, peça a um colega que o resolva. Depois, verifique se ele respondeu corretamente.
Página 50
20. Analise a tabela nutricional a seguir.
|
Alimento |
Energia |
Proteína |
Carboidratos |
|---|---|---|---|
|
Quilocalorias () |
Grama () |
Grama () |
|
|
Arroz tipo 1 cozido |
128 |
2,5 |
28,1 |
|
Pão de trigo francês |
300 |
8,0 |
58,6 |
|
Batata doce cozida |
77 |
0,6 |
18,4 |
Fonte de pesquisa: TABELA Brasileira de composição de alimentos. TACO. Disponível em: https://oeds.link/E3x0qE. Acesso em: 22 jun. 2022.
a) Quantos gramas de arroz do tipo 1 cozido uma pessoa deve consumir para ingerir de carboidrato?
b) Qual é a medida de energia, em quilocalorias, presente em de arroz tipo 1 cozido?
c) Qual é a quantidade de proteína, em gramas, presente em de batata doce cozida?
d) Qual é a medida de energia, em quilocalorias, presente em uma porção de arroz tipo 1 cozido com de proteína?
21. A companhia de saneamento de uma cidade identificou um vazamento de água em sua rede de distribuição, cuja vazão era de 2.700 litros por hora. O reparo da tubulação foi concluído após 3 horas e 30 minutos. Determine a medida do volume de água, em litros, desperdiçada até a conclusão do reparo.
22. Em seu caderno, reescreva a atividade 21 trocando os números, mas mantendo a proporcionalidade. Em seguida, peça a um colega que o resolva. Por fim, verifique se ele respondeu corretamente.
23. A medida da massa de um objeto com certa densidade é quando seu volume mede . Determine a medida da massa de outro objeto de mesma densidade em que seu volume mede .
24. Em seu caderno, reescreva a atividade 23 trocando os números, mas mantendo a proporcionalidade. Em seguida, peça a um colega que a resolva. Por fim, verifique se ele a fez corretamente.
25. Em uma empresa de confecção de calçados, duas máquinas produziram certa quantidade de pares de sapatos em 12 horas. Quantas máquinas iguais a essas seriam necessárias para produzir a mesma quantidade de pares de sapatos em 3 horas?
26. Em seu caderno, reescreva a atividade 25 trocando os números, mas mantendo a proporcionalidade inversa. Em seguida, peça a um colega que a resolva. Por fim, verifique se ele respondeu corretamente.
27. Elabore um problema envolvendo grandezas inversamente proporcionais e, em seguida, peça a um colega que o resolva. Depois, verifique se ele o respondeu corretamente.
Página 51
Divisão em partes diretamente proporcionais
Armando, Antônio e Amarildo são irmãos e têm, respectivamente, 12, 13 e 15 anos. Acompanhe o que o pai deles está dizendo.

Para saber quantos reais cada um deles vai receber, devemos dividir os R$ 500,00 em partes diretamente proporcionais à idade deles, ou seja, 12, 13 e 15 anos.
Indicando por x, y e z a quantia que Armando, Antônio e Amarildo vão receber, respectivamente, temos:
Com base nas propriedades das proporções estudadas, segue que:
Como , temos:
Agora, calculamos a quantia recebida por eles.
Armando
Portanto, Armando vai receber R$ 150,00.
Antônio
Portanto, Antônio vai receber R$ 162,50.
Amarildo
Portanto, Amarildo vai receber R$ 187,50.
Questão 7. Se o pai deles tivesse dividido
R$ 1.250,00
de maneira diretamente proporcional à idade de cada um, quanto cada um
receberia?
Página 52
Divisão em partes inversamente proporcionais
Outro dia, o pai de Armando, Antônio e Amarildo disse a eles o seguinte:

Para saber quantos reais cada um deles vai receber, devemos dividir os R$ 1.062,00 em partes inversamente proporcionais à idade deles, ou seja, 12, 13 e 15 anos.
Indicando por x, y e z a quantia que Armando, Antônio e Amarildo vão receber, respectivamente, temos:
Com base nas propriedades das proporções estudadas, segue que:
Como , temos:
Agora, calculamos a quantia recebida por eles.
Armando
Portanto, Armando vai receber R$ 390,00.
Antônio
Portanto, Antônio vai receber R$ 360,00.
Amarildo
Portanto, Amarildo vai receber R$ 312,00.
Questão 8. Caso o pai deles tivesse
dividido R$ 1.593,00
de maneira inversamente proporcional à idade de cada um, quanto cada um
receberia?
Página 53
Atividades
Faça as atividades no caderno.
28. Decomponha o número 150 em duas partes diretamente proporcionais aos números 2 e 3.
29. Decomponha o número 120 em duas partes inversamente proporcionais aos números 2 e 3.
30. Fernando decompôs o número 1.768 em três partes x, y e z diretamente proporcionais aos números 5, 9 e 12. A resposta obtida por ele foi:
a) , e .
b) , e .
c) , e .
d) , e .
31. Três amigos fizeram um investimento em um empreendimento. O quadro a seguir apresenta o capital aplicado por eles.
|
Nome |
Capital aplicado |
|---|---|
|
Marcos |
R$ 1.000,00 |
|
Antônio |
R$ 1.200,00 |
|
Camila |
R$ 1.500,00 |
Ao final de certo período, eles receberão R$ 9.398,00. Determine a quantia que cada amigo vai receber, sabendo que a divisão desse montante deve ser diretamente proporcional ao capital aplicado por cada um deles.
32. Elabore dois problemas: um envolvendo divisão em partes diretamente proporcionais e outro envolvendo divisão em partes inversamente proporcionais. Em seguida, dê para um colega resolver. Por fim, verifique se as respostas obtidas por ele estão corretas.
33. Decomponha o número 220 em três partes inversamente proporcionais aos números 2, 4 e 6.
34. Anderson, Márcia e Gustavo prestaram um serviço para uma empresa e cobraram, ao todo, R$ 5.795,00.

|
Nome |
Quantidade de dias trabalhados |
|---|---|
|
Anderson |
12 |
|
Márcia |
9 |
|
Gustavo |
11 |
Quantos reais cada um deles vai receber?
35. A empresa para a qual Marta trabalha dará uma bonificação de final de ano. Ao todo, serão distribuídos R$ 102.920,00 entre 3 funcionários. Sabendo que o valor recebido por cada funcionário será inversamente proporcional ao seu salário, analise o quadro e determine quanto cada um vai receber.
|
Nome |
Salário |
|---|---|
|
Marlene |
R$ 2.300,00 |
|
Marcos |
R$ 2.000,00 |
|
Marta |
R$ 2.700,00 |
Página 54
Ângulos opostos pelo vértice
Estudamos em anos anteriores que duas retas concorrentes determinam 4 ângulos. Além disso, verificamos que ângulos opostos pelo vértice são congruentes, ou seja, têm medidas iguais. Na figura a seguir, temos, por exemplo, , pois esses ângulos são opostos pelo vértice.
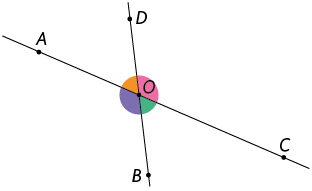
Considerando , segue que:
- , pois os ângulos e são opostos pelo vértice.
- , pois os ângulos e são suplementares e .
- , pois os ângulos e são opostos pelo vértice.
Atenção!
Lembre-se de que dois ângulos são suplementares quando a soma de suas medidas é igual a .
Ângulos formados por um feixe de retas paralelas e uma transversal
Você sabe o que são retas paralelas? Tratam-se de retas de um mesmo plano que não se cruzam.
Duas retas paralelas cortadas por uma transversal determinam 8 ângulos.
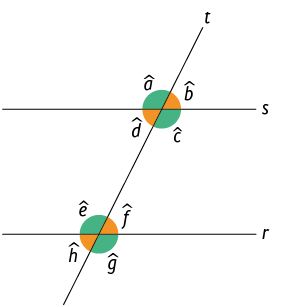
Na figura anterior, as retas r e s são paralelas , t é uma transversal a essas retas e os ângulos de medida:
- e , e , e , e são correspondentes. Ângulos correspondentes são congruentes.
- e , e são colaterais internos, pois estão entre as paralelas e do mesmo lado em relação à reta transversal.
- e , e são colaterais externos, pois estão do mesmo lado em relação à reta transversal, mas não estão entre as paralelas.
- e , e são alternos internos, pois estão em lados opostos em relação à transversal e estão entre as paralelas.
- e , e são alternos externos, pois estão em lados opostos em relação à transversal e não estão entre as paralelas.
Página 55
Agora, vamos determinar uma relação entre os ângulos de medidas e (colaterais internos). De fato, sabemos que os ângulos de medida e são suplementares e que os ângulos de medida e são correspondentes. Nesse caso, e . Logo, . Portanto, os ângulos de medidas e são suplementares.
Questão 9. Em seu caderno, determine e demonstre a veracidade da relação entre os ângulos de medida:
a) e (colaterais externos).
b) e (alternos internos).
c) e (alternos externos).
Duas retas paralelas cortadas por uma transversal determinam 8 ângulos, tais que ângulos correspondentes são congruentes, ângulos alternos são congruentes e ângulos colaterais são suplementares.
Atividades
Faça as atividades no caderno.
36. Determine o valor de x em cada item.




37. Sabendo que as retas r e s são paralelas, determine o valor de x e y.
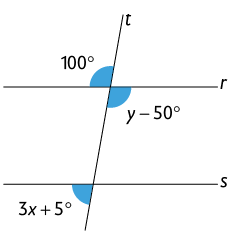

38. Considere
o paralelogramo .
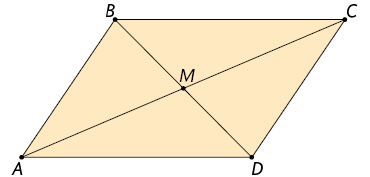
Mostre que M é o ponto médio das diagonais desse paralelogramo.
Página 56
Segmentos de reta proporcionais
Uma professora de Matemática do 9º ano entregou a seus estudantes um pedaço de papel em formato retangular. Feito isso, ela pediu a eles que dobrassem o pedaço de papel dividindo seus lados ao meio, como representado nas figuras a seguir.
Atenção!
A medida do comprimento do segmento de reta é indicada por .
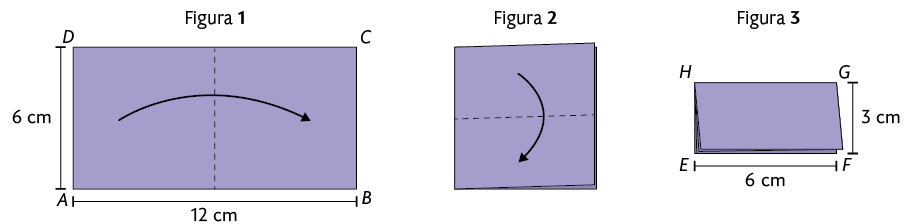
Associamos o pedaço de papel que a professora entregou ao retângulo , cujas dimensões medem e . Em relação à figura obtida, após realizadas as dobras, associamos ao retângulo , cujas dimensões medem e .
Após realizar as dobras, cada estudante obteve uma figura, também retangular, cujas dimensões medem e .
Ao calcularmos a razão entre a medida do comprimento e da largura de cada retângulo, obtemos:
As duas razões obtidas são iguais. Então, podemos escrever a seguinte proporção:
Assim, dizemos que os segmentos de reta e são proporcionais aos segmentos de reta e .
Dois segmentos de reta são proporcionais a outros dois segmentos de reta quando a razão entre as medidas dos comprimentos dos dois primeiros é igual à razão entre as medidas dos comprimentos dos dois últimos.
Atividades
Faça as atividades no caderno.
39. Os segmentos de reta e são proporcionais aos segmentos de reta e , ou seja, . Sabendo que , e , qual é a medida do comprimento do segmento de reta ?
Página 57
40. Analise o retângulo representado a seguir.

a) Determine a razão entre as medidas dos comprimentos dos lados e .
b) Ao diminuir da medida do comprimento de cada lado desse retângulo, a razão entre e permanecerá a mesma? Por quê?
41. Analise os segmentos de reta e suas respectivas medidas de comprimento.

Em cada item, determine a medida do comprimento do segmento de reta para tornar a proporção verdadeira.
a)
b)
c)
42. Em seu caderno, calcule o valor de em cada igualdade a seguir.
a)
b)
c)
d)
43. Leia atentamente as informações, analise o esquema e determine a medida da distância percorrida por Aline para ir de sua casa até a praça onde está Fábio.
- Durante o trajeto, Aline encontrou quatro outros amigos: Bruno, Celina, Douglas e Elias.
- No esquema, a casa de Aline está representada pela letra A, Bruno pela letra B, Celina pela letra C, Douglas pela letra D, Elias pela letra E e a praça onde Fábio está pela letra F.
- No esquema, os segmentos de reta e são proporcionais aos segmentos de reta e .

Página 58
Teorema de Tales
Neste tópico, estudaremos o Teorema de Tales, que recebeu esse nome em homenagem ao matemático e filósofo grego Tales de Mileto. Ele viveu por volta de 624 a.C a 548 a.C. e é considerado um dos "sete sábios" que se conhece na Antiguidade.
Questão 10. Realize uma pesquisa a respeito de Tales de Mileto. Nela, busque informações sobre ele e quais foram as suas contribuições para as ciências. Registre no caderno o que achar relevante.

Atenção!
As fontes para realizar a pesquisa proposta na questão 10 podem ser livros, revistas e sites. No entanto, é necessário estar atento e certificar-se de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Agora, vamos enunciar o Teorema de Tales e demonstrá-lo para dois casos.
Se um feixe de retas paralelas cruza duas retas transversais, então quaisquer dois segmentos de reta determinados em uma das transversais são proporcionais aos respectivos segmentos de reta determinados na outra transversal.
Atenção!
Quando três ou mais retas em um mesmo plano são paralelas entre si, duas a duas, elas formam um feixe de retas paralelas. Se r, s e t são retas paralelas, duas a duas, podemos indicar por r//s//t.
1º caso: Feixe de retas paralelas que determina, nas transversais, segmentos congruentes.
Considere o feixe de retas paralelas r, s e t. Devemos, então, traçar as retas p e q transversais, que cruzam esse feixe de retas de maneira que os segmentos e sejam congruentes, ou seja, .
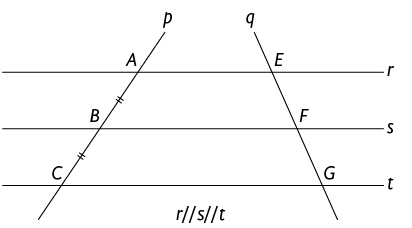
Vamos demonstrar que e são congruentes.
Página 59
Para isso, traçamos os segmentos e paralelos à reta p, de maneira que e . Como , segue que .
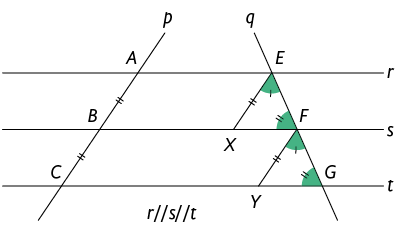
Agora, vamos considerar os triângulos e . Neles, temos:
;
, pois são ângulos correspondentes;
, pois são ângulos correspondentes.
Assim, pelo caso de congruência , os triângulos e são congruentes. Portanto, , como queríamos demostrar.
2º caso: Feixe de retas paralelas que determina, nas transversais, segmentos comensuráveis e não congruentes.
Considere o feixe de retas paralelas a, b e c. Então, devemos traçar as retas u e v transversais, que cruzam esse feixe de retas de maneira que os segmentos e sejam comensuráveis.
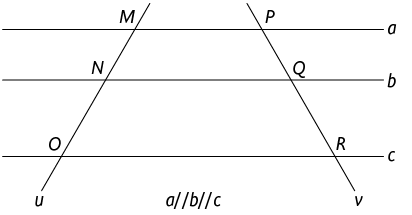
Atenção!
Dois segmentos são comensuráveis quando existe uma medida s que divide os segmentos em quantidades inteiras de partes.
Vamos demonstrar que . De fato, como os segmentos e são comensuráveis, existe uma medida s que cabe n vezes no segmento e m vezes no segmento , tal que n e m são números inteiros. Desse modo, temos:
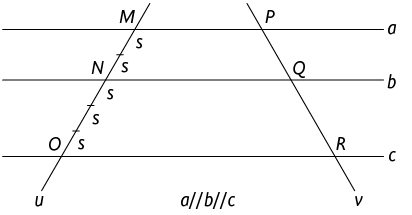
Atenção!
Na imagem, é representado o caso em que e .
Página 60
Vamos traçar retas paralelas às retas a, b e c pelos pontos obtidos na divisão dos segmentos de reta e .
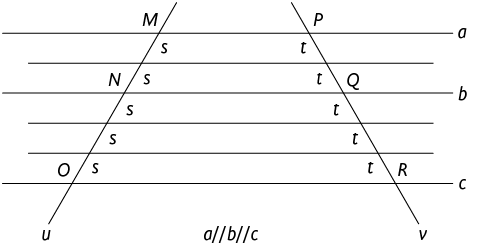
Pelo 1º caso, as retas paralelas determinam na transversal v exatamente n + m segmentos de reta congruentes. Desse modo, há um segmento de reta cujo comprimento mede contido n vezes em e vezes em . Então:
Portanto, , ou seja, os segmentos de reta e são proporcionais aos segmentos de reta e .
Apesar de termos demonstrado o teorema de Tales para dois casos, ele também é válido no caso em que o feixe de retas paralelas determina, nas transversais, segmentos não comensuráveis. Além disso, a recíproca do teorema, enunciada a seguir, é verdadeira.
Considere as retas r, s, t e duas transversais a elas. Se quaisquer dois segmentos de reta determinados em uma das transversais são proporcionais aos respectivos segmentos de reta determinados na outra transversal, então as retas r, s e t são paralelas.
Agora, analisaremos dois exemplos.
Exemplo 1. Utilizando o teorema de Tales, podemos determinar o valor de x na figura a seguir.
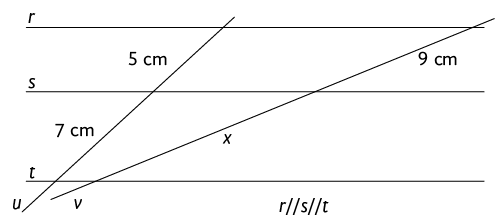
Portanto, .
Página 61
Exemplo 2. Ao analisarmos a imagem a seguir, podemos concluir que e são proporcionais a e , ou seja:
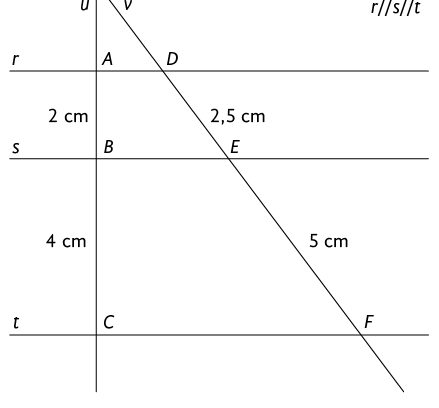
Assim, pela recíproca do teorema de Tales, podemos concluir que as retas r, s e t são paralelas.
Atividades
Faça as atividades no caderno.
44. Na figura a seguir, as retas , , e formam um feixe de retas paralelas.
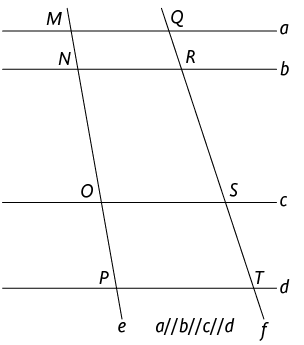
Com base na figura, copie os itens no caderno substituindo cada pela indicação da medida de um segmento de reta de modo que as igualdades sejam verdadeiras.
a)
b)
c)
d)
e)
f)
45. Em cada item, verifique se as retas p, q e r são paralelas.
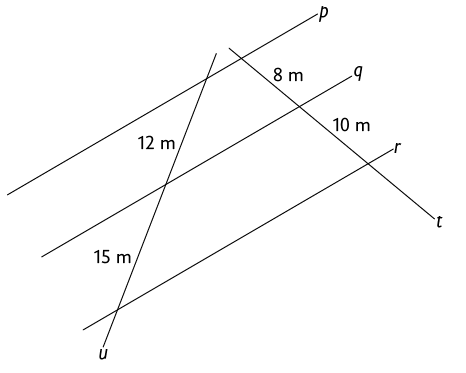
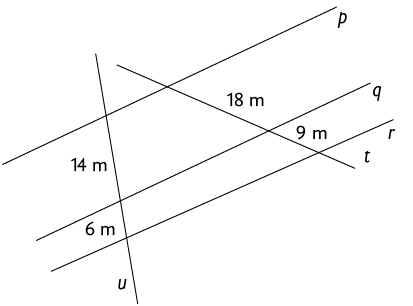
Página 62
46. Analise a figura a seguir e algumas informações sobre ela.
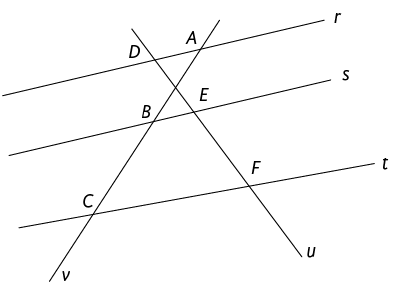
Verifique se as retas , e são paralelas e justifique sua resposta.
47. As retas , e a seguir formam um feixe de retas paralelas.
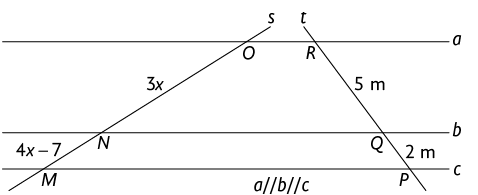
Determine e .
48. O esquema
a seguir representa dois terrenos que têm a frente voltada para a rua Manaus. O
terreno A pertence à Valquíria e o terreno B, a Marcos.
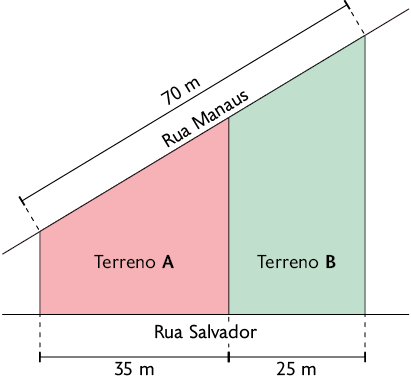
Valquíria e Marcos pretendem construir um muro na frente dos terrenos. Usando uma calculadora, determine quantos metros de muro cada um deve construir em seu terreno, sabendo que as divisas laterais dos terrenos são paralelas.
49. A figura
a seguir representa uma horta que Patrícia dividiu paralelamente em canteiros
para plantar alface, cebolinha e almeirão.
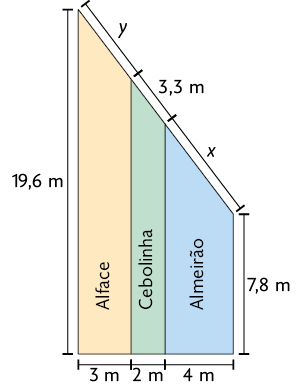
Para isso, ela cercou a horta com tela. Utilizando uma calculadora, quantos metros de tela Patrícia utilizou para cercar a horta?
50. Em seu caderno, calcule os valores de , , e representados na figura a seguir.
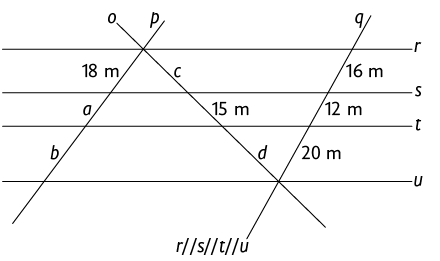
51. Elabore um problema, que, para resolvê-lo, seja necessário aplicar o teorema de Tales. Em seguida, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Página 63
Teorema de Tales nos triângulos
O teorema de Tales pode ser aplicado em situações que envolvam triângulos. Para compreender melhor sua aplicação, considere o triângulo e as retas que contêm seus lados.
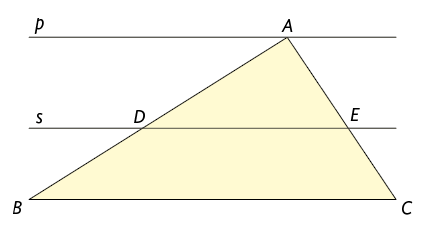
Ao traçarmos a reta:
- , paralela ao lado e que cruza os lados e , determinamos os pontos e ;
- paralela a , passando pelo vértice , temos um feixe de retas paralelas, que cruza 2 retas transversais.
Com base no teorema de Tales, temos:
Toda reta paralela a um dos lados de um triângulo e que cruza os outros dois lados os divide em segmentos de reta proporcionais.
No triângulo a seguir, é paralelo a .
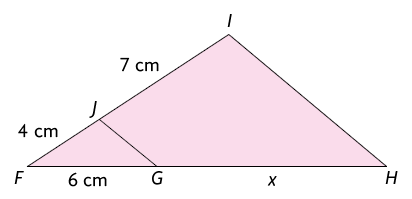
Utilizando o teorema de Tales, podemos determinar o valor de x. De fato:
Portanto, .
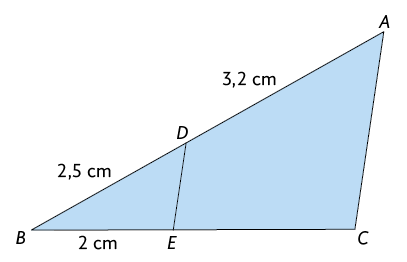
Questão 11. Considere o triângulo a seguir, em que é paralelo a . Em seu caderno, calcule a medida do comprimento do lado .
Página 64
Atividades
Faça as atividades no caderno.
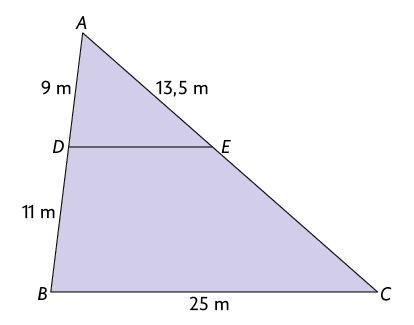
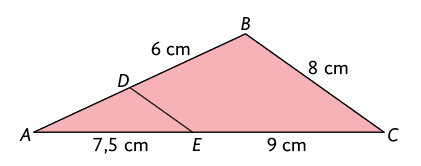
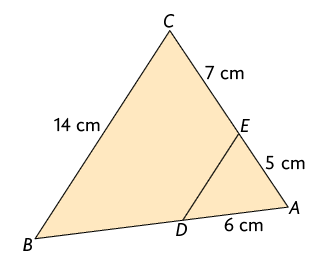
52. Em cada item, determine a medida do perímetro do triângulo, sabendo que é paralelo a .
53. Considere o triângulo a seguir.
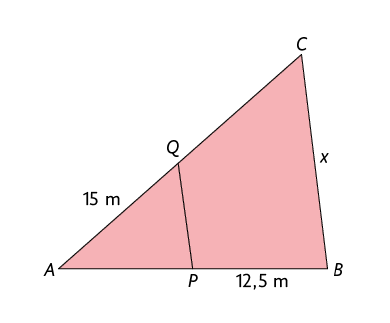
Determine o valor de x no triângulo , sabendo que:
;
o perímetro do triângulo mede ;
é o ponto médio de .
54. O triângulo é isósceles.
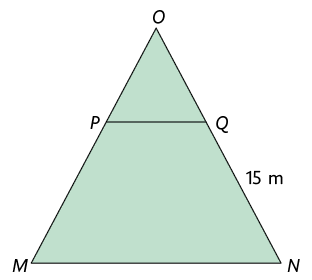
Atenção!
O triângulo isósceles apresenta pelo menos 2 lados com medidas de comprimento iguais.
Considerando que , e , determine e .
55. Em determinada hora do dia, as sombras de um poste e de uma estátua projetadas no solo atingem o ponto S, como representado no esquema a seguir.
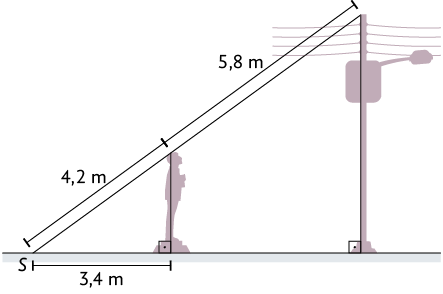
Determine a medida da distância aproximada entre o poste e a estátua.
Página 65
56. Na figura a seguir, e são paralelos.

a) Determine a medida do comprimento de em metros.
b) Quanto mede o perímetro do triângulo em metros?
57. Dirceu quer trocar o arame de parte da cerca de seu pasto, que está representado na figura a seguir. A parte da cerca que ele deseja trocar está indicada pela medida x.
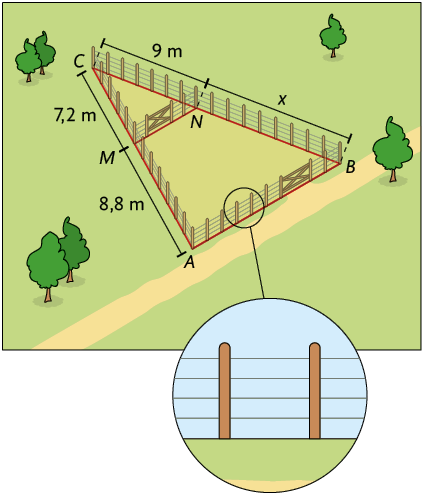
a) Sabendo que o pasto é dividido por uma cerca paralela à que está próxima da estrada, calcule no caderno o valor de x.
b) De quantos metros de arame Dirceu vai precisar para que a parte da cerca que ele deseja trocar seja feita com 4 arames paralelos, como mostra a figura?
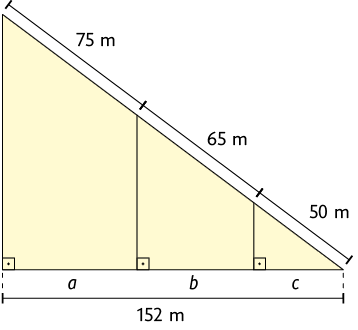
58. Determine os valores de , e .
59. Na imagem, as medidas são dadas em metros.
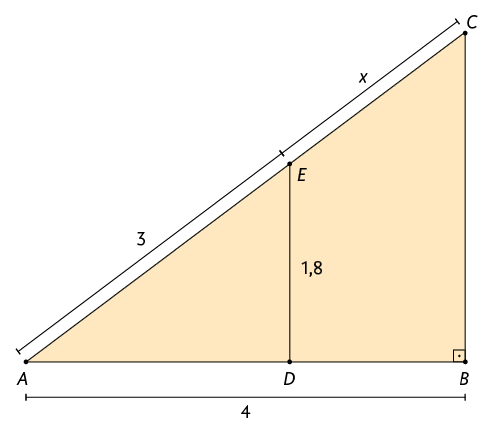
Sabendo que a área do triângulo mede e que , determine o valor de x.
60. Elabore um problema envolvendo triângulos e o teorema de Tales e, em seguida, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Página 66
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. A figura a seguir representa a planta baixa do quarto de Renata.
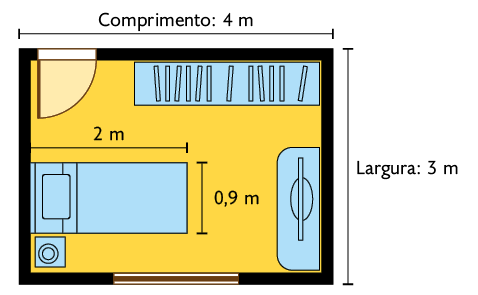
Resolva os itens a seguir em uma folha de papel avulsa.
a) Ao fazer outra planta baixa de seu quarto, Renata representou com o comprimento desse cômodo. Levando em consideração essa informação, com quantos centímetros ela representou a largura de seu quarto nessa planta baixa?
b) Nessa nova planta baixa, quais seriam as medidas das dimensões da cama de Renata?
2. Na turma de ballet da professora Marcela, há, ao todo, 36 estudantes. Sabendo que a razão entre o número de meninos e o de meninas é de , determine quantos meninos e quantas as meninas fazem parte dessa turma.
3. Para ir de sua casa até o museu, Marília percorreu, com seu automóvel, em . Determine a velocidade média, em quilômetros por hora, nesse percurso.
4. Decomponha o número 180 em duas partes inversamente proporcionais aos números 4 e 5.
5. Ana e Rebeca investiram em uma floricultura, respectivamente, R$ 7.200,00 e R$ 10.800,00. Após certo período, elas apuraram lucro de R$ 5.400,00, que deverá ser dividido entre as duas de maneira diretamente proporcional ao que cada uma investiu. Determine o valor correspondente a Ana e a Rebeca.
6. Analise a figura a seguir e determine o valor de x.
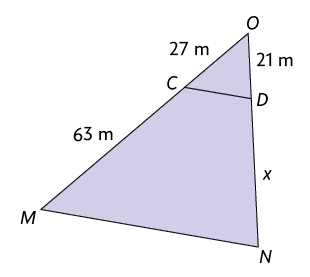
Atenção!
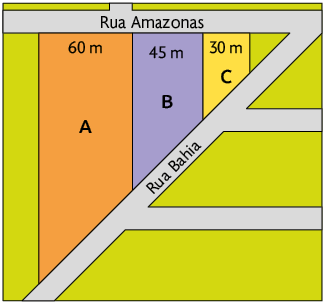
7. Três terrenos têm frente para a rua Bahia e suas divisas laterais são perpendiculares à rua Amazonas.
Qual é a medida da frente de cada terreno, sabendo que juntos têm medida igual a de frente?