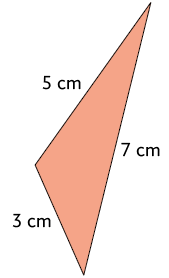Página 67
UNIDADE
4
Semelhança de figuras

Agora vamos estudar...
- figuras semelhantes;
- polígonos semelhantes;
- homotetia;
- casos de semelhança em triângulos.
Página 68
Semelhança de figuras
Ivo representou em uma malha quadriculada a fachada do prédio onde mora. Feito isso, ele ampliou e reduziu esse desenho utilizando outras malhas quadriculadas.
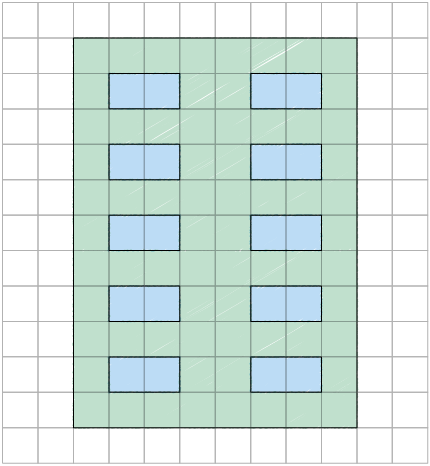
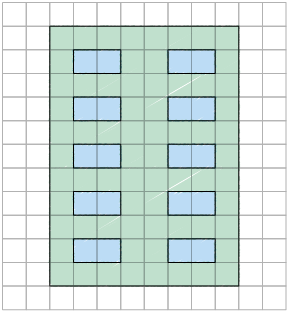
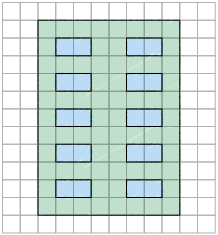
Para ampliar a figura original, Ivo precisou usar uma malha quadriculada com quadradinhos maiores do que a malha quadriculada original, enquanto que, para reduzi-la, usou uma malha quadriculada com quadradinhos menores. Porém, tanto na ampliação quanto na redução, a figura manteve o formato original.
Podemos também reproduzir, ampliar ou reduzir uma figura usando a mesma malha quadriculada. Para compreender melhor, analise a seguir outras figuras desenhadas por Ivo.
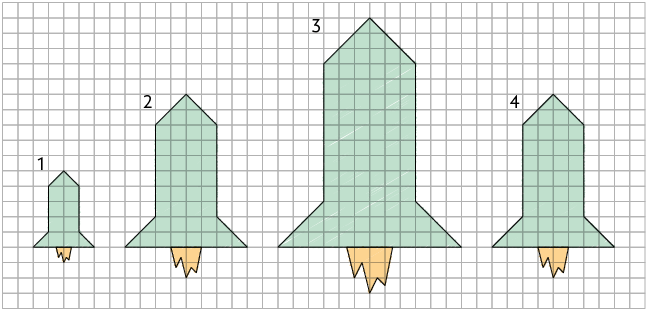
Página 69
Se uma figura for a ampliação, redução ou reprodução de outra, essas figuras serão semelhantes.
Assim, os desenhos que Ivo fez são figuras semelhantes.
Diversos artistas utilizam as técnicas de reprodução, ampliação e redução para retratar a realidade em suas obras. Um desses artistas é o australiano Ron Mueck, (1958 -), autor da obra a seguir, denominada Boy, que mede mais de de altura.

Questão 1. É possível realizar visitas em
alguns museus de maneira
virtual. Faça isso e compartilhe essa experiência com os colegas e o professor.
Atenção!
A visita virtual pode ser feita por meio do site indicado a seguir. Disponível em: https://oeds.link/SJEK11. Acesso em: 27 jul. 2022.
Atividades
Faça as atividades no caderno.
1. Considere as figuras 1, 2, 3 e 4 desenhadas em uma mesma malha quadriculada na página anterior.
a) Qual delas representa uma reprodução da figura 4?
b) Quais delas representam uma ampliação da figura 1?
c) Quais delas representam uma redução da figura 3?
d) Todas as figuras desenhadas nessa malha quadriculada são semelhantes? Por quê?
2. Nos itens a seguir, estão representadas algumas imagens que sofreram alterações em relação à imagem a seguir.




a) Qual delas representa uma reprodução da figura original?
b) Qual delas é uma ampliação da imagem original?
c) Qual delas não manteve a proporção das medidas das dimensões da foto original, ou seja, não é uma reprodução, ampliação ou redução dela?
Página 70
3. As figuras 1, 2, 3 e 4 foram obtidas com base na figura apresentada a seguir.
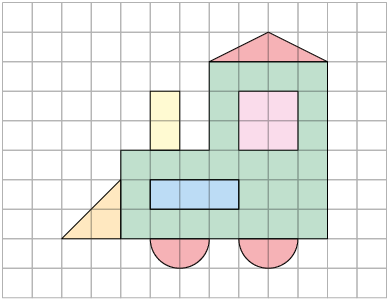

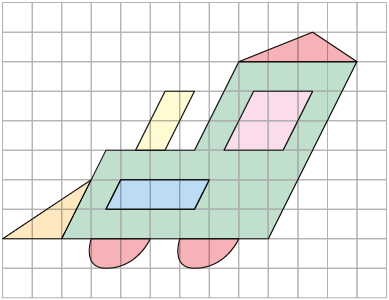
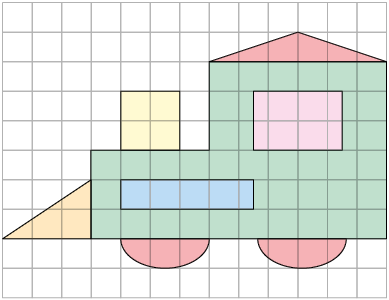
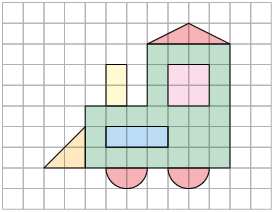
a) Qual delas representa uma reprodução da figura original?
b) Qual delas representa uma redução da figura original?
c) Quais delas são semelhantes à figura original? Por quê?
d) Quais delas não são semelhantes à figura original? Por quê?
4. Desenhe uma figura em uma malha quadriculada e peça a um colega que amplie e reduza o desenho feito por você. Depois, verifique se ele executou a tarefa corretamente.
Versão adaptada acessível
4. Junte-se a um colega, desenhem uma figura em uma malha quadriculada e peçam a outra dupla que ampliem e reduzam o desenho feito por vocês. Depois, verifiquem se eles executaram a tarefa corretamente.
Página 71
Polígonos semelhantes
Conforme estudado, ao reproduzir, ampliar ou reduzir uma figura mantendo seu formato, é possível obter figuras semelhantes à original. Agora, vamos estudar a semelhança para polígonos.
Dois polígonos são semelhantes quando satisfazem, simultaneamente, as seguintes condições:
- as medidas de comprimento dos respectivos lados são proporcionais;
- os respectivos ângulos internos são congruentes.
Considere os polígonos ABCD e a seguir.
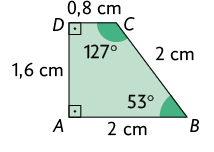
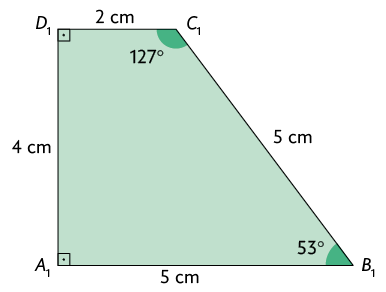
Perceba que as medidas dos respectivos ângulos internos são iguais, ou seja, os ângulos são congruentes.
As medidas de comprimento dos respectivos lados desses polígonos são proporcionais, visto que, ao dividir a medida de comprimento de cada lado do polígono pela medida de comprimento do respectivo lado do polígono , obtém-se o mesmo número.
O valor 2,5 obtido é a razão de semelhança entre os polígonos e .
Como as medidas de comprimento dos respectivos lados desses polígonos são proporcionais e os respectivos ângulos internos são congruentes, os polígonos e são semelhantes. Podemos indicar essa semelhança da seguinte maneira:
(lê-se: é semelhante a )
Atenção!
Os polígonos regulares com a mesma quantidade de lados são sempre semelhantes entre si, pois os ângulos internos são congruentes e as medidas de comprimento de seus respectivos lados são proporcionais.
Página 72
Atividades
Faça as atividades no caderno.
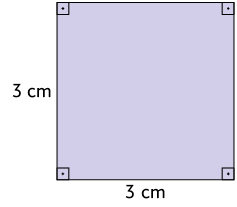
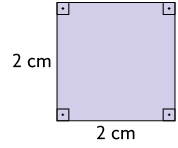
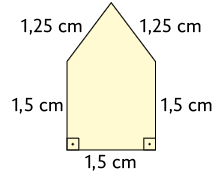
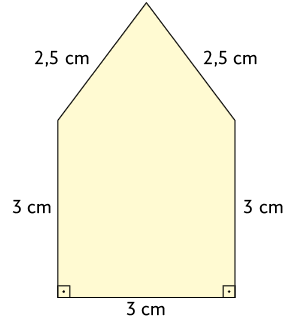
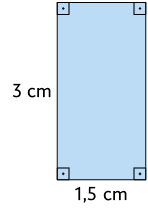
5. Verifique se o par de figuras de cada item a seguir é semelhante ou não. Sendo semelhante, determine a razão de semelhança entre as figuras.

6. Utilizando
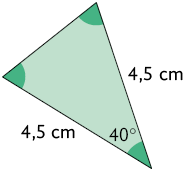
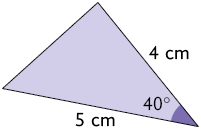
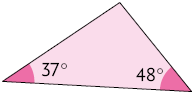
régua e transferidor, realize as medições e verifique se os triângulos de cada
par de triângulos são semelhantes.
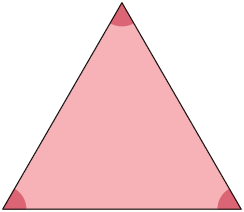
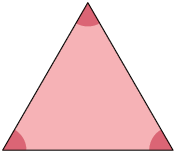


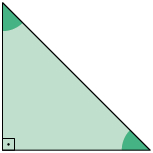

7. Com base nos pares de triângulos da atividade anterior, responda às questões a seguir no caderno.
a) Quaisquer dois triângulos são sempre semelhantes?
b) Existem pares de triângulos que são sempre semelhantes? Quais são eles? Por quê?
Página 73
8. Junte-se a um colega e, com a ajuda dele, dobre ao meio uma folha de papel com as medidas das dimensões indicadas a seguir. Feito isso, desdobrem a folha para recortar na marca da dobra.

Em seguida, repitam o processo com uma das partes da folha, para, então, obter mais 2 pedaços com o formato de um retângulo.

Repitam esse processo utilizando um dos pedaços menores da folha para obter mais 2 retângulos.
Finalizado isso, respondam às questões a seguir.
a) Quantos retângulos foram obtidos ao todo?
b) Quais são as medidas das dimensões desses retângulos?
c) Todos os retângulos são semelhantes?
d) Entre os retângulos, quais são semelhantes?
9. Considere dois triângulos equiláteros e . Sabendo que o triângulo é maior do que o triângulo , a soma das medidas dos perímetros dos dois triângulos é igual a e a razão de semelhança entre eles é , determine a medida do lado de cada triângulo.
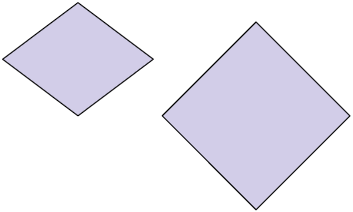
10. As
figuras geométricas representadas a seguir são semelhantes entre si? Se
necessário, utilize régua e transferidor. Justifique sua resposta.
Página 74
Homotetia
Podemos ampliar ou reduzir uma figura de diversas maneiras, como utilizando softwares, um pantógrafo ou realizando a transformação chamada homotetia. Para compreender melhor, verifique, a seguir, como ampliar o polígono na razão utilizando homotetia.
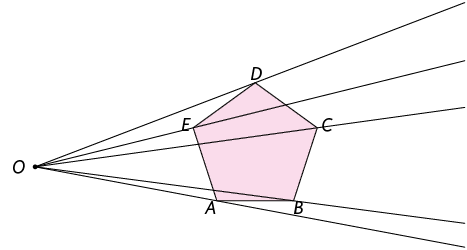
Primeiro, escolhemos um ponto O externo ao polígono e traçamos as semirretas com origem nesse ponto e que passam pelos vértices A, B, C, D e E.

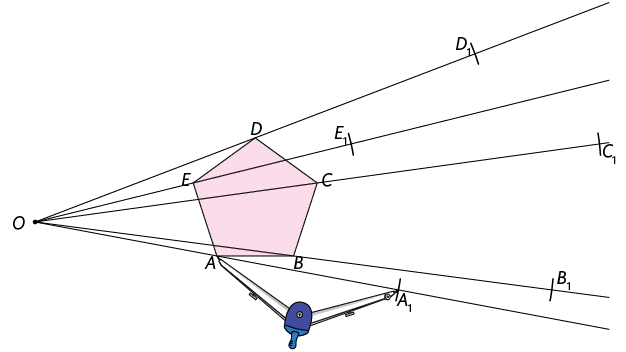
Utilizando um compasso ou uma régua, marcamos os pontos , , , e , sobre as semirretas , , , e , respectivamente, de modo que , , , e .
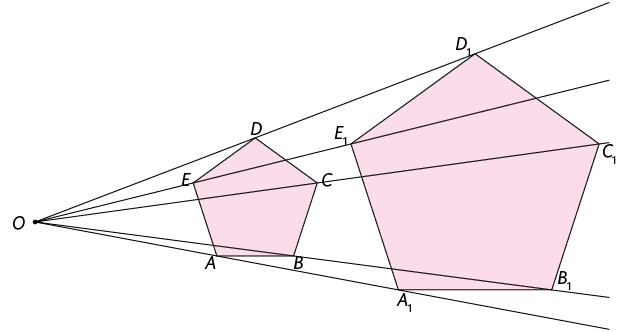
Em seguida, ligamos os pontos , , , e e determinamos, assim, o polígono , que é uma ampliação do polígono , na razão .
Página 75
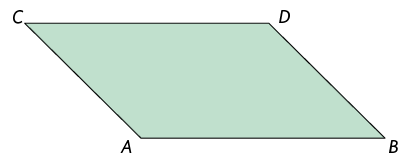
Acompanhe o procedimento de redução de um paralelogramo com razão de semelhança utilizando a homotetia.
Determinamos um ponto O interno ao paralelogramo e traçamos os segmentos , , e .
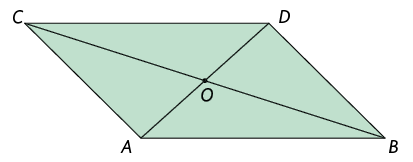
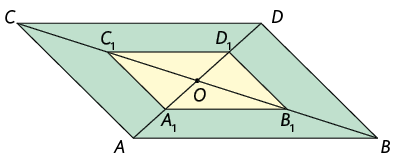
Com auxilio de um compasso, marcamos os pontos , , e em relação aos segmentos , , e , respectivamente, de maneira que , , e . Em seguida, ligamos os pontos obtidos e, assim, determinamos o paralelogramo , que é uma redução por homotetia do paralelogramo na razão .
Atividades
Faça as atividades no caderno.
11. Faça em
seu caderno o que se pede a seguir.
a) Construa um triângulo equilátero cujo comprimento do lado mede . Em seguida, usando homotetia, construa um triângulo equilátero com comprimento de lado medindo .
b) Construa um quadrado cujo comprimento do lado mede . Em seguida, usando homotetia, construa um quadrado com comprimento de lado medindo .
12. Na imagem a seguir foram construídas as figuras A e C com base na figura B, que é um hexágono regular.
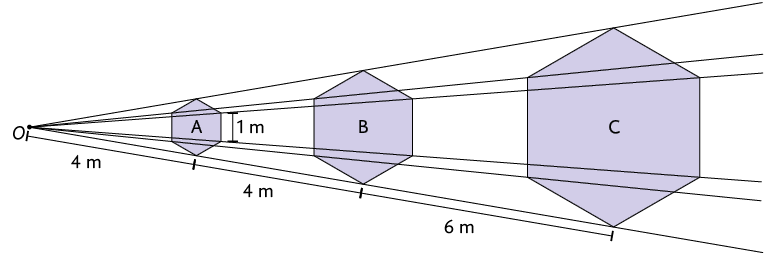
a) Qual é a medida de comprimento de cada lado das figuras B e C?
b) Qual foi a razão de redução da figura B para obter a figura A?
c) Qual seria a razão de ampliação da figura A para obter a figura C?
Página 76
13. Reproduza,
no caderno, os polígonos a seguir. Feito isso, amplie-os por homotetia na razão de semelhança .
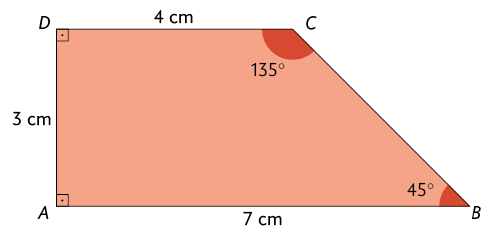
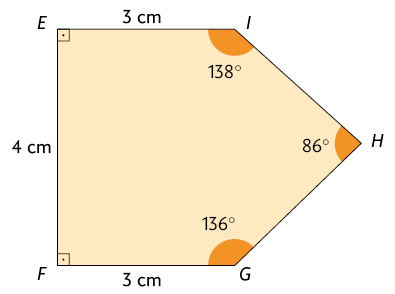
14. Reproduza, no caderno, cada polígono a seguir. Feito isso, reduza-os por homotetia na razão de semelhança .

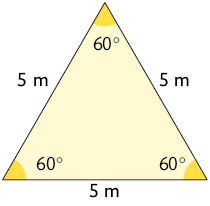
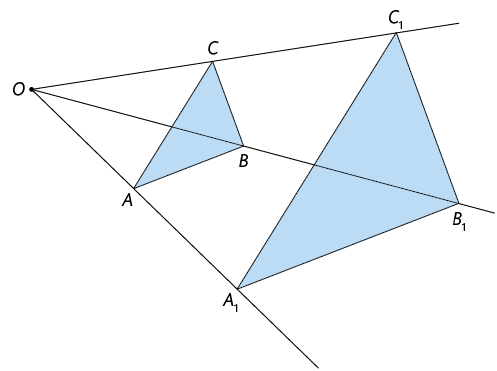
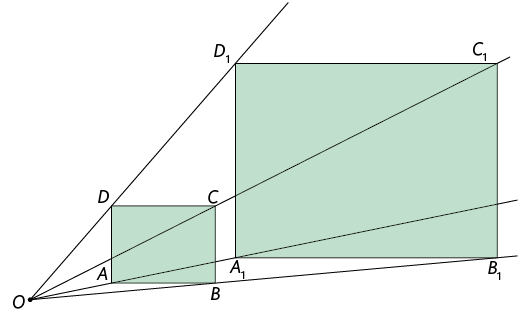
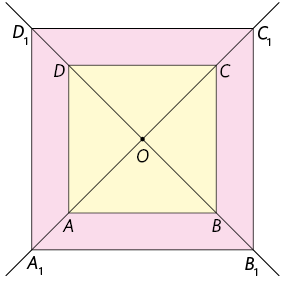
15. Em cada figura a seguir, houve uma ampliação da original. Utilizando uma régua, realize as medições necessárias e determine a razão de semelhança de cada homotetia.
Página 77
Triângulos semelhantes
Estudamos anteriormente que dois polígonos são semelhantes quando satisfazem, simultaneamente, as seguintes condições.
- As medidas de comprimento dos respectivos lados são proporcionais.
- Os respectivos ângulos internos são congruentes.
Para compreender melhor, acompanhe, por exemplo, como podemos verificar se os triângulos a seguir são semelhantes.
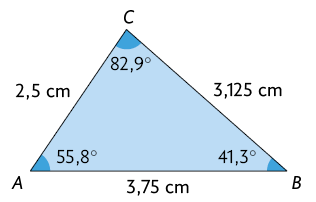
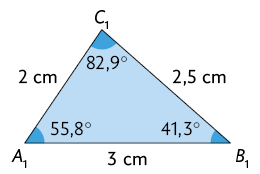
Nos triângulos, todos os respectivos lados apresentam medidas proporcionais e todos os respectivos ângulos internos são congruentes.
Portanto, como ambas as condições foram satisfeitas, os triângulos e são semelhantes, com razão de semelhança 1,25. Essa semelhança é representada por:
Atenção!
A notação também indica que esses triângulos são semelhantes.
No entanto, para determinar se dois triângulos são semelhantes, não é necessário comparar as medidas de todos os seus ângulos internos e as medidas de comprimento de todos os seus lados. Existem casos em que é possível verificar se dois triângulos são semelhantes levando em consideração apenas alguns de seus elementos.
Vamos conhecer os casos de semelhança de triângulos que estabelecem condições necessárias e suficientes para que dois triângulos sejam semelhantes.
1º caso de semelhança ()
Quando dois triângulos têm seus respectivos ângulos internos congruentes, eles são semelhantes.
Página 78
Demonstração: Vamos mostrar que, se nos triângulos e temos , e , então os triângulos e são semelhantes.
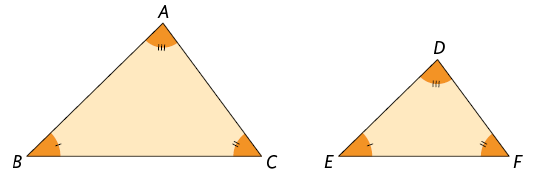
Marque um ponto P sobre o lado do triângulo , de maneira que , e trace o segmento paralelo ao lado do triângulo.
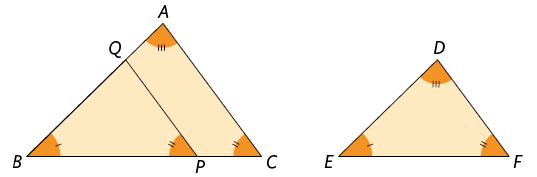
De acordo com as imagens, verificamos que , pois são ângulos correspondentes de paralelas cortadas por uma transversal. Já pelo caso de congruência de triângulos, temos .
Pelo teorema de Tales, temos:
Como , segue que .
Seguindo o mesmo procedimento, marque um ponto M sobre o lado do triângulo , de maneira que , e trace o segmento que seja paralelo ao lado .
Assim, pelo teorema de Tales, temos:
Como , pelo caso de congruência de triângulo, temos:
Logo, . Portanto, .
Atenção!
Lembre-se de que a soma das medidas dos ângulos internos de um triângulo é . Desse modo, conhecendo as medidas de dois dos ângulos internos de um triângulo, podemos determinar a medida do terceiro ângulo interno.
Agora, com base em exemplos, vamos estudar outros dois casos de semelhança de triângulos.
Página 79
2º caso de semelhança ()
Quando dois triângulos apresentam dois dos respectivos lados com medidas de comprimento proporcionais e os ângulos formados entre eles são congruentes, esses triângulos são semelhantes.
Considerando esse caso, para que dois triângulos sejam semelhantes, é suficiente verificarmos a proporcionalidade entre as medidas de comprimento dos lados correspondentes e a congruência entre os ângulos formados por eles.
Para compreender melhor, analise os seguintes triângulos.
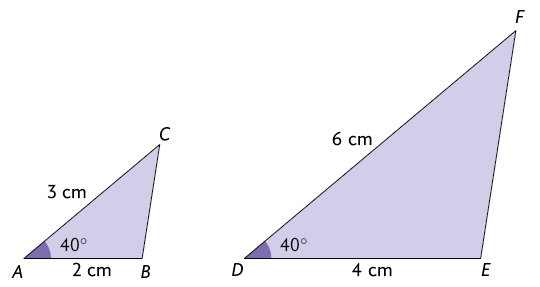
Podemos verificar que e . Portanto, os triângulos e são semelhantes.
3º caso de semelhança ()
Quando dois triângulos têm as medidas de comprimento dos lados correspondentes proporcionais, eles são semelhantes.
Levando em consideração esse caso, para que dois triângulos sejam semelhantes, é suficiente verificarmos a proporcionalidade entre as medidas de comprimento de seus lados correspondentes.
Considere os triângulos a seguir.
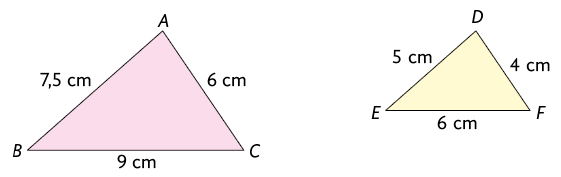
De acordo com as imagens, verificamos que . Portanto, os triângulos e são semelhantes, com razão de semelhança 1,5.
Página 80
Atividades
Faça as atividades no caderno.
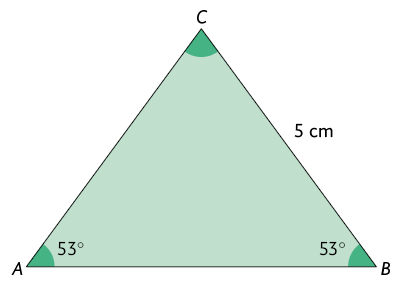
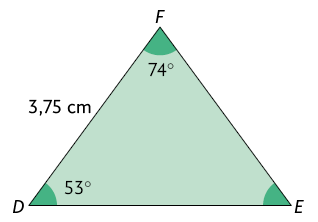
16. Verifique se os triângulos e a seguir são semelhantes. Em caso afirmativo, determine a razão de semelhança entre eles.
17. Na
imagem a seguir, estão representados
dois triângulos. Considere que
é um ponto dos segmentos e .
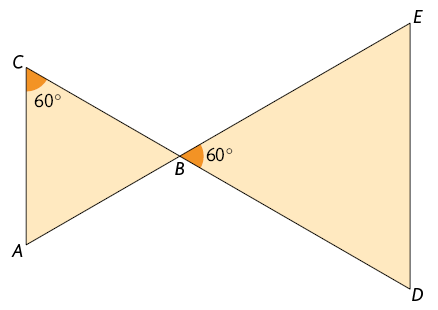
a) Junte-se a um colega para medir os lados desses triângulos usando régua. Eles são semelhantes? Justifique sua resposta.
b) Caso sejam semelhantes, qual é a razão de semelhança entre os triângulos e ?
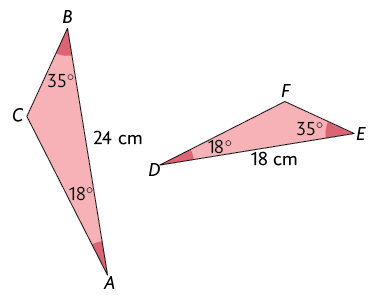
18. Analise os triângulos e a seguir.
a) Esses triângulos são semelhantes?
b) Se a resposta ao item anterior for sim, determine:
a razão de semelhança entre e .
o caso de semelhança.
19. Analisando as figuras apresentadas a seguir, identifique os pares de triângulos semelhantes e indique os casos de semelhança.
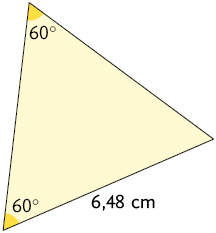

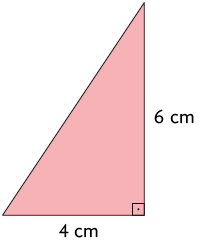
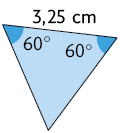

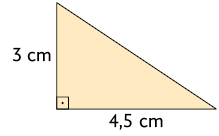
Página 81
20. Sabendo que em cada item a seguir os triângulos isósceles são semelhantes, determine o valor de x.
A.


B.
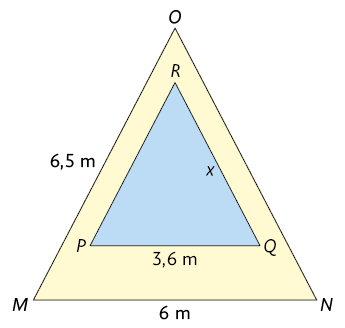
C.


21. Em cada item, calcule as medidas x e y sabendo que os triângulos são semelhantes.

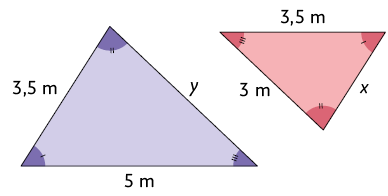
22. Considere
as informações referentes à figura a seguir.
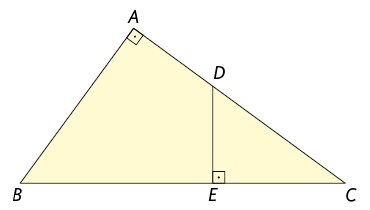
Qual é a medida do comprimento do segmento de reta ?
23. (Saresp-2007) Os triângulos e são semelhantes, com . O lado mede .
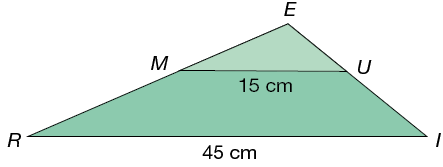
Qual é a medida, em cm, do lado ?
a) 15
b) 20
c) 24
d) 36
Página 82
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
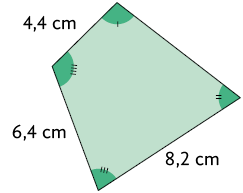
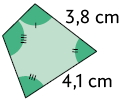
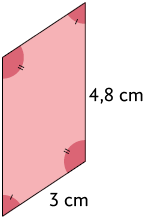
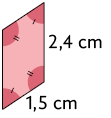
1. Sabendo que os pares de polígonos de cada quadro a seguir são semelhantes, calcule, em uma folha de papel avulsa, a medida do perímetro de cada polígono.
2. Analise os hexágonos regulares a seguir.


a) Esses hexágonos são semelhantes?
b) Qual é a razão de semelhança entre os hexágonos A e B?
c) Qual é a razão da medida do perímetro do hexágono A em relação a do hexágono B?
d) Qual é a relação entre as razões obtidas nos itens b e c? Isso também acontece com outros polígonos regulares?
3. Em uma folha de papel avulsa, por homotetia, faça a ampliação dos polígonos a seguir na razão .
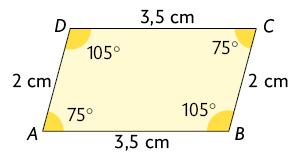
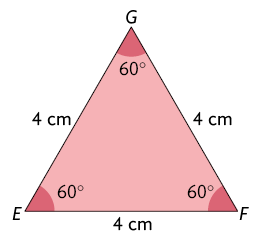
4. Determine se os triângulos indicados em cada item são semelhantes. Para isso, justifique sua resposta.