Página 83
UNIDADE
5
Produtos notáveis, fatoração de polinômios e equações do 2º grau

Agora vamos estudar...
- produtos notáveis;
- fatoração de polinômios;
- equação do 2º grau com uma incógnita;
- resolução de equações do 2º grau completas e incompletas;
- relações entre as raízes e outros elementos de uma equação do 2º grau.
Página 84
Produtos notáveis
Neste tópico, estudaremos produtos de polinômios que aparecem em problemas e apresentam algumas regularidades. Eles são chamados produtos notáveis e, ao estudá-los e conhecê-los, perceberemos que as regularidades apresentadas possibilitam, em alguns momentos, a redução da quantidade de cálculos.
Quadrado da soma de dois termos
Um dos produtos notáveis é o quadrado da soma de dois termos. Podemos indicá-lo da seguinte maneira.

Utilizando a propriedade distributiva da multiplicação, obtemos:
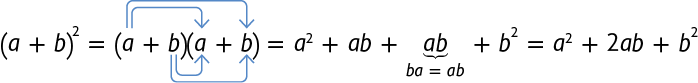
O polinômio tem três termos e é chamado trinômio quadrado perfeito.
Podemos visualizar geometricamente a igualdade anterior. Para a e b positivos, calcularemos a medida da área de um quadrado com o comprimento do lado medindo de duas maneiras diferentes.
1ª maneira
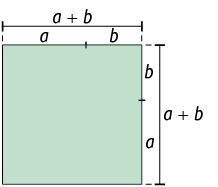
Multiplicando a medida do comprimento pela medida da largura:
2ª maneira
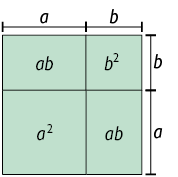
Adicionando as medidas das áreas das quatro partes:
Note que, em ambas as imagens, o quadrado cuja medida do comprimento do lado é tem a mesma medida de área. Portanto: .
Página 85
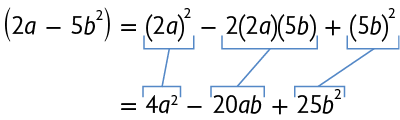
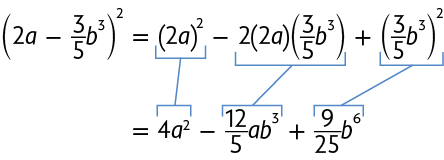
O quadrado da soma de dois termos pode ser obtido calculando o quadrado do 1º termo, mais 2 vezes o 1º termo pelo 2º, mais o quadrado do 2º termo.
A seguir, apresentamos alguns exemplos.
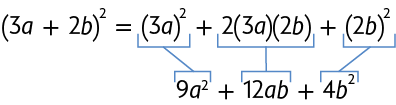
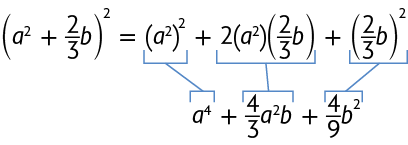
Quadrado da diferença de dois termos
Outro produto notável é o quadrado da diferença de dois termos. Podemos indicá-lo da seguinte maneira.

Aplicando a propriedade distributiva da multiplicação, obtemos:
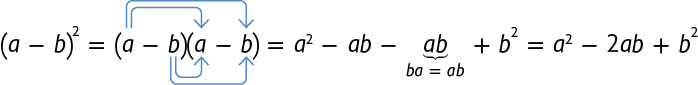
O polinômio também é um trinômio quadrado perfeito.
Podemos visualizar geometricamente a igualdade anterior. Para a e b positivos, com , calcularemos a medida da área de um quadrado cujo comprimento do lado mede .
Podemos representar a medida da área desse quadrado (em verde na figura a seguir) da seguinte maneira:
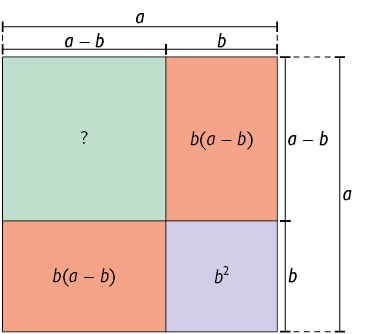
Outra maneira de representar a medida da área do quadrado verde é subtrair, da medida da área do quadrado maior, as medidas das áreas dos dois retângulos vermelhos e do quadrado roxo.
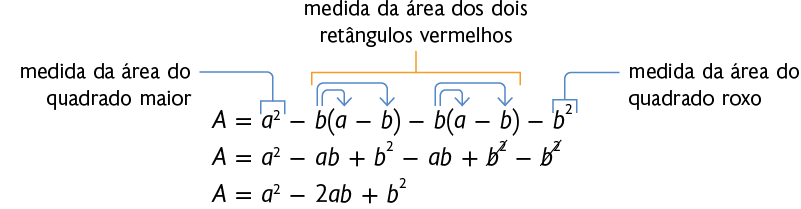
Portanto, .
Página 86
O quadrado da diferença de dois termos pode ser obtido calculando o quadrado do 1º termo, menos 2 vezes o 1º termo pelo 2º, mais o quadrado do 2º termo.
A seguir, apresentamos alguns exemplos.
Produto da soma pela diferença de dois termos
O produto também é um produto notável. Ele é conhecido como produto da soma pela diferença de dois termos. Ao desenvolver esse produto notável com o auxílio da propriedade distributiva da multiplicação, obtemos:
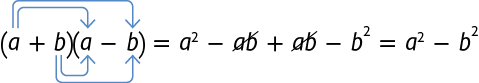
O polinômio é uma diferença de quadrados.
Podemos visualizar geometricamente o desenvolvimento desse produto notável. Para a e b positivos, com , calcularemos a medida da área de um retângulo cujos comprimentos dos lados medem e .
Podemos representar a medida da área desse retângulo (em amarelo na figura a seguir) da seguinte maneira.
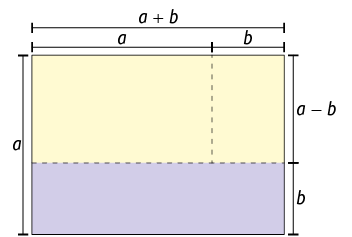
Outra maneira de representar a medida da área do retângulo amarelo é subtrair, da medida da área do retângulo maior, a medida da área do retângulo roxo.
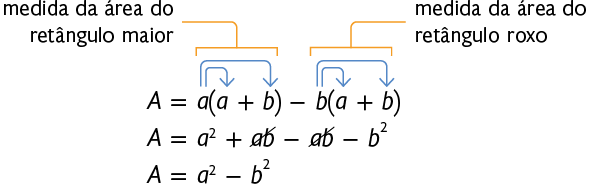
Portanto, .
Página 87
O produto da soma pela diferença de dois termos pode ser obtido calculando o quadrado do 1º termo menos o quadrado do 2º termo.
A seguir, apresentamos alguns exemplos.
Atividades
Faça as atividades no caderno.
1. Utilizando figuras geométricas, desenvolva o produto notável indicado em cada item e obtenha um trinômio quadrado perfeito.
a)
b)
c)
2. Escreva no caderno um trinômio que represente a medida da área de cada quadrado.
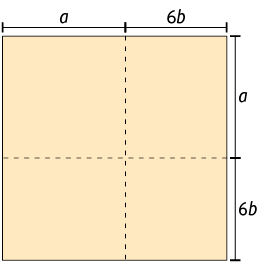

3. Represente no caderno um quadrado cuja medida do comprimento do lado seja . Em seguida, escreva o polinômio que representa a medida da área desse quadrado.
Versão adaptada acessível
3. Imagine um quadrado cuja medida do comprimento do lado seja . Em seguida, escreva o polinômio que representa a medida da área desse quadrado.
4. Escreva no caderno os termos adequados que podem substituir cada ■.
a)
b)
c)
d)
e)
f)
5. Escreva no caderno cada produto notável na forma de trinômio quadrado perfeito.
a)
b)
c)
d)
e)
6. Copie os itens no caderno substituindo cada pelo valor adequado.
a)
b)
c)
Página 88
7. Para cada item, escreva no caderno o trinômio quadrado perfeito utilizando a regra do quadrado da diferença de dois termos.
a)
b)
c)
d)
8. Simplifique as expressões algébricas.
a)
b)
9. A figura a seguir é formada por dois quadrados, um verde e um amarelo, e dois retângulos congruentes.
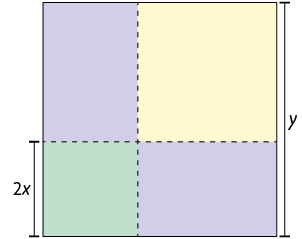
a) Qual trinômio representa a medida da área do quadrado amarelo? Ele é um trinômio quadrado perfeito?
b) Para e , qual é a medida da área:
de cada retângulo roxo?
do quadrado verde?
do quadrado amarelo?
c) Considerando , e a figura anterior, elabore duas perguntas e peça a um colega que as responda. Por último, verifique se a resposta dele está correta.
10. Copie os itens no caderno substituindo cada pelo valor adequado.
a)
b)
c)
11. Para cada item, escreva no caderno a diferença de quadrados utilizando a regra do produto da soma pela diferença de dois termos.
a)
b)
c)
12. Simplifique as expressões algébricas.
a)
b)
13. Jorge recortou, de um pedaço quadrado
de cartolina, um quadrado
menor, como indicado na imagem a seguir.
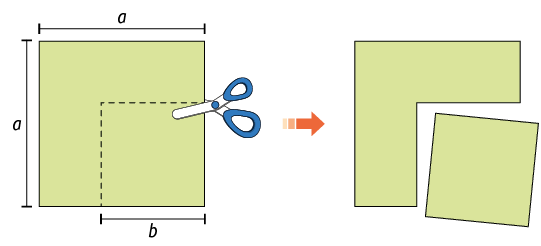
a) Que polinômio representa a medida da área da cartolina que sobrou após o quadrado ter sido recortado?
b) Sabendo que e , qual é a medida da área do pedaço de cartolina que sobrou?
Página 89
Fatoração de polinômios
Em anos anteriores, você provavelmente estudou que um número natural diferente de 1 pode ser escrito como produto de dois ou mais fatores, ou seja, podemos grafá-lo na forma fatorada. A seguir, escrevemos alguns exemplos, na forma fatorada, do número 48.
De maneira semelhante aos números, também podemos fatorar polinômios, ou seja, dado um polinômio na forma reduzida, podemos escrevê-lo como um produto de polinômios, que, em algumas situações, é útil na resolução de problemas.
A seguir, estudaremos alguns métodos de fatoração de polinômios.
Colocando um fator comum em evidência
Podemos fatorar, por exemplo, o polinômio da seguinte maneira.
Inicialmente, decompomos cada termo do polinômio em um produto de fatores.
Note que é o fator comum aos dois termos do polinômio. Assim, podemos escrevê-lo multiplicando-o pelos outros fatores que não são comuns. Nesse caso, dizemos que foi colocado em evidência.
Portanto, a forma fatorada de é .
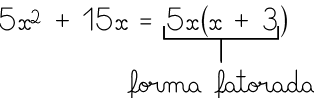
Podemos verificar se a fatoração está correta usando a propriedade distributiva da multiplicação e analisando se o resultado obtido é o polinômio inicial.

A seguir, apresentamos outros exemplos.
Página 90
Fatoração por agrupamento
Outra maneira de fatorar um polinômio é utilizando a fatoração por agrupamento.
Acompanhe, por exemplo, a fatoração do polinômio utilizando esse método.
Esse polinômio não apresenta fatores comuns a todos os termos. Por isso, agrupamos os termos que têm fatores comuns e, depois, efetuamos a fatoração.
Como é o fator comum do polinômio, podemos colocá-lo em evidência.
Portanto, a forma fatorada de é:
Atenção!
Podemos verificar se a fatoração por agrupamento foi realizada de maneira correta. Para isso, usamos a propriedade distributiva da multiplicação e o resultado obtido deve ser igual ao polinômio inicial.
A seguir, apresentamos outros exemplos.
Fatoração de um trinômio quadrado perfeito
Também podemos fatorar um trinômio quadrado perfeito.
Estudamos anteriormente que . Então, nesse caso, é a forma fatorada do polinômio .
Também verificamos que . Então, nesse caso, é a forma fatorada do polinômio .
A seguir, apresentamos alguns exemplos de fatoração de trinômios quadrados perfeitos.
Página 91
Podemos verificar, por exemplo, que . Para isso, inicialmente, fazemos:
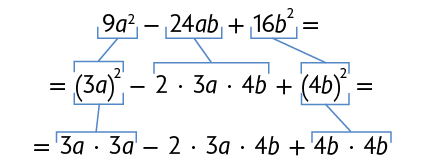
Como , escrevemos:
Agora, colocamos os fatores e em evidência:
Por fim, colocamos em evidência, pois é o fator comum da expressão.
Fatoração do produto da soma pela diferença de dois termos
Anteriormente, verificamos que . Então, nesse caso, é a forma fatorada do polinômio .
A seguir, apresentamos dois exemplos de fatoração de diferenças de quadrados.
Outros casos envolvendo fatoração de polinômios
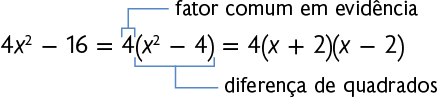
Em alguns casos, é preciso fatorar duas vezes o mesmo polinômio.
Acompanhe, por exemplo, a fatoração dos polinômios e .

Página 92
Atividades
Faça as atividades no caderno.
14. No caderno, associe os polinômios às suas formas fatoradas. Para isso, escreva a letra e o número correspondentes.
A.
B.
C.
D.
1.
2.
3.
4.
15. Em cada item, determine o fator comum a todos os termos do polinômio e fatore-o.
a)
b)
c)
d)
16. Copie os itens no caderno e substitua cada pelo monômio adequado.
a)
b)
c)
17. Fatore os polinômios por agrupamento.
a)
b)
c)
18. Fatore os trinômios quadrados perfeitos. Se necessário, desenhe figuras no caderno.
a)
b)
c)
d)
19. Fatore as diferenças de quadrados.
a)
b)
c)
d)
20. Jair fatorou algumas expressões algébricas em seu caderno.
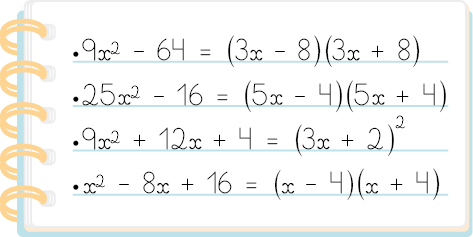
a) Ele fatorou todas as expressões algébricas corretamente?
b) Caso Jair tenha fatorado alguma expressão algébrica incorretamente, reescreva-a no caderno e a corrija.
21. Copie os itens no caderno e substitua cada pelo termo adequado.
a)
b)
c)
d)
e)
22. Utilizando os monômios a seguir, escreva no caderno três trinômios quadrados perfeitos. Em seguida, fatore os que você escreveu.
23. Fatore os polinômios.
a)
b)
c)
d)
Página 93
Equações do 2º grau com uma incógnita
Você já deve ter estudado equações nos anos anteriores. Agora, aprofundaremos um pouco esse assunto. Acompanhe, a seguir, duas situações que podem ser resolvidas usando equações.
Situação A
Carla tem certa quantia em reais e sua amiga Marcela tem o dobro dessa quantia mais R$ 2,00. Sabendo que juntas elas têm R$ 38,00, quantos reais cada uma delas tem?
Chamaremos a quantia que Carla tem de e, assim, podemos escrever a seguinte equação.
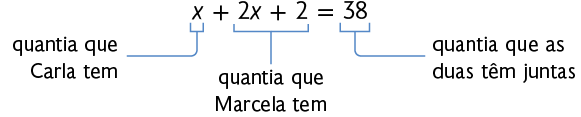
Resolvendo a equação, obtemos:
Portanto, Carla tem R$ 12,00 e Marcela tem R$ 26,00, pois .
Situação B
A figura a seguir representa um terreno com a forma de um quadrado. Sabendo que sua área mede , qual é a medida de cada um de seus lados?

Para responder a essa pergunta, escrevemos e resolvemos a equação a seguir, na qual representa a medida do lado do terreno.
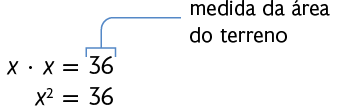
Como há dois números cujo quadrado é 36, temos:
ou
Como queremos saber a medida de um comprimento, consideramos apenas o número positivo 6, pois não existe medida de comprimento negativa.
Portanto, cada lado do terreno mede .
Página 94
Note que as equações apresentadas em cada situação da página anterior foram escritas apenas com a incógnita .
Na situação A, escrevemos uma equação cujo maior expoente da incógnita é 1. Por isso, ela é chamada equação do 1º grau.
Na situação B, escrevemos uma equação cujo maior expoente da incógnita é 2. Por isso, ela é chamada equação do 2º grau.
Atenção!
Uma equação é formada por dois membros, os quais são separados pelo sinal de igual. Exemplo:
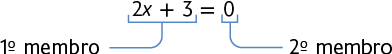
Nos quadros a seguir, estão representadas algumas equações do 2º grau, com incógnita e 2º membro igual a zero. Além disso, apresentamos algumas características dos termos do 1º membro dessas equações.
1.
No 1º membro, cada equação apresenta um termo com , um termo com e um termo sem .
2.
No 1º membro, cada equação apresenta um termo com e um termo com .
3.
No 1º membro, cada equação tem um termo com e um termo sem .
4.
No 1º membro, cada equação tem apenas um termo com .
Dizemos que as equações exibidas no quadro 1 são equações do 2º grau completas e as apresentadas nos quadros 2, 3 e 4, equações do 2º grau incompletas.
Além das equações demonstradas até o momento, existem equações do 3º grau, 4º grau, 5º grau etc. com uma incógnita. Por exemplo, o maior expoente da incógnita :
- na equação é 3, por isso essa equação é do 3º grau;
- na equação é 4, por isso essa equação é do 4º grau.
Nesta unidade, estudaremos somente as equações do 2º grau.
Questão 1. Explique para
um colega qual é
a diferença entre uma equação
do 1º grau e outra do
2º grau, ambas na incógnita x.
Página 95
Uma equação do 2º grau com incógnita pode ser escrita da seguinte forma.
, em que , e são números reais e
Essa é a forma reduzida de uma equação do 2º grau. As letras , e , que representam números reais, são os coeficientes da equação: é o coeficiente de , é o coeficiente de e é o termo independente.
A seguir, apresentamos alguns exemplos.
Equação do 2º grau completa do tipo , em que , e .
, com ; ;
Equação do 2º grau incompleta do tipo , em que , e .
, com ; ;
Equação do 2º grau incompleta do tipo , em que , e .
, com ; ;
Equação do 2º grau incompleta do tipo , em que , e .
, com ; ;
Questão 2. Identifique qual é o tipo de cada uma das equações apresentadas nos quadros 1, 2, 3 e 4 da página anterior. Depois, registre-os no caderno.
Atividades
Faça as atividades no caderno.
24. Copie no caderno as equações a seguir, separando-as em 2 grupos: equações do 1º grau e equações do 2º grau.
25. Em cada quadrado, determine o valor de x.


26. Considerando a incógnita , escreva no caderno duas equações do 2º grau:
a) completas.
b) incompletas do tipo , com e números reais e .
c) incompletas do tipo , com e números reais e .
27. Identifique os coeficientes das equações que você escreveu na atividade anterior.
28. Em cada quadro, são apresentados os coeficientes , e de uma equação do 2º grau na forma . Escreva no caderno essas equações, na forma reduzida.
A.
B.
Página 96
29. A figura a seguir representa a planta baixa de uma sala de formato retangular, cujo perímetro mede . As medidas indicadas na imagem estão em metros.
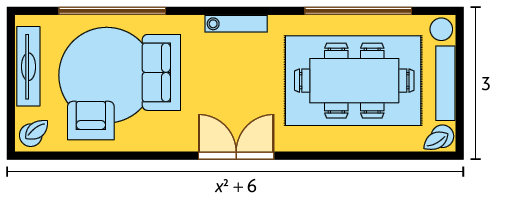
a) Escreva no caderno uma equação do 2º grau, na forma reduzida, que possibilita determinar o valor de x indicado na planta baixa.
b) A equação do 2º grau que você escreveu é completa ou incompleta? Justifique sua resposta.
c) Considerando a figura anterior, elabore uma pergunta envolvendo equação do 2º grau e peça a um colega que a resolva. Depois, verifique se a resposta dele está correta.
30. Identifique os coeficientes de cada equação.
a)
b)
c)
d)
e)
f)
31. Analise a seguinte figura.
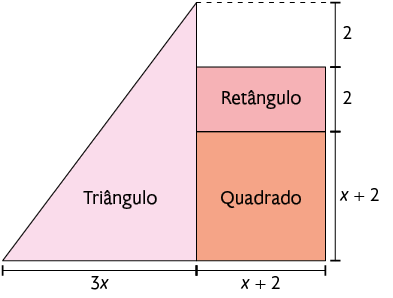
a) Sabendo que a medida da área do triângulo é igual à medida da área do quadrado mais a medida da área do retângulo, escreva no caderno uma equação do 2º grau, na forma reduzida, para representar a relação entre essas medidas de área.
b) Essa equação é completa ou incompleta? Quais são os seus coeficientes?
32. Escreva no caderno uma equação do 2º grau, na forma reduzida, para cada situação.
a) O quadrado de um número mais seu triplo é igual a 10.
b) O dobro do quadrado de um número mais sua quinta parte é igual a 12.
c) O triplo do quadrado de um número menos 6 é igual ao quíntuplo desse número.
d) A medida da área de um quadrado cujo comprimento dos lados mede é 52.
Agora, elabore em seu caderno três situações semelhantes às apresentadas nos itens e peça a um colega que as resolva. Depois, verifique se a resposta dele está correta.
33. Escreva no caderno uma equação do 2º grau, na forma , em que o produto dos coeficientes seja 35, a soma seja 13 e os coeficientes sejam números naturais tais que .
34. Em cada item, descubra o valor de para que as condições sejam atendidas.
a)
Deve ser uma equação do 2º grau.
b)
Deve ser uma equação do 2º grau completa.
c)
Deve ser uma equação do 2º grau incompleta.
Página 97
Resolvendo equações do tipo
Em anos anteriores, você deve ter estudado como resolver equações do 1º grau com uma incógnita, isto é, como determinar o valor da incógnita da equação. Nos tópicos a seguir, aprofundaremos os estudos sobre a resolução de equações, em particular das equações do 2º grau com uma incógnita, visto que muitos problemas podem ser resolvidos por meio de uma equação desse tipo.
Questão 3. Realize uma pesquisa sobre as contribuições de Luca Pacioli e a obra Aritmética, de sua autoria, para a Matemática. Após a realização da pesquisa, registre no caderno as informações mais importantes.
Atenção!
A pesquisa proposta na questão 3 pode ser feita com base em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Analise o que Aline está dizendo.

Podemos responder à pergunta de Aline escrevendo uma equação do 2º grau com uma incógnita. Chamando o número desconhecido de , temos:
Para resolver essa equação, precisamos obter um número que, multiplicado por ele mesmo, seja igual a 49. Nesse caso, temos dois números: 7 e .
ou
Assim, o número que responde à pergunta de Aline pode ser 7 ou . Dizemos que esses números são as raízes ou as soluções da equação .
Atenção!
A equação tem raízes 7 e . Então, podemos registrá-las por ou ou por e .
Analise a seguir a resolução da equação .
Como não existe um número real x que elevado ao quadrado seja igual a , essa equação não tem solução real.
Página 98
Atividades
Faça as atividades no caderno.
35. Efetue os cálculos no caderno e determine as raízes das equações.
a)
b)
c)
d)
e)
f)
36. Calcule no caderno o valor de para que a expressão:
a) seja igual a ;
b) seja igual a ;
c) seja igual a .
37. Escreva no caderno uma equação do 2º grau para representar a situação de cada item. Em seguida, resolva essas equações.
a) O quadrado de um número é igual a 121. Qual é esse número?
b) O quadrado de uma quantia em reais menos R$ 45,00 é igual a R$ 396,00. Qual é essa quantia?
38. A área do retângulo a seguir mede . Quais são as medidas de suas dimensões?

39. Uma piscina é coberta por uma lona retangular cuja área mede . A medida do comprimento da lona é o dobro da medida da largura. De acordo com essas informações, elabore em seu caderno o enunciado de um problema e peça a um colega que o resolva. Por fim, verifique se ele resolveu o problema corretamente.
40. Entre as equações a seguir, quais não têm raízes reais?
A.
B.
C.
D.
E.
F.
41. Quais são as possibilidades de quantidade de raízes de uma equação do tipo , com e números reais e ? Caso a equação tenha raízes, quais podem ser as relações entre elas?
42. A figura a seguir é formada por cinco quadrados congruentes.
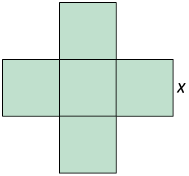
Sabendo que a área dessa figura mede , determine a medida do comprimento do lado de cada quadrado.
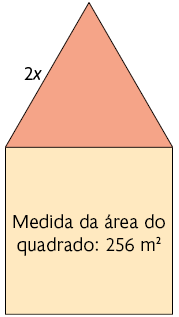
43. Calcule
no caderno a medida do perímetro da figura, sabendo que ela é formada por um
quadrado e um triângulo equilátero.
Página 99
Resolvendo equações do tipo
Antônio cortou dois pedaços de madeira, um com a forma de um quadrado e outro com a forma de um retângulo. Cada um desses pedaços está representado a seguir, e as medidas indicadas estão expressas em centímetros.


Sabendo que esses dois pedaços de madeira têm a mesma medida de área, qual é a medida do perímetro de cada um deles?
Para responder a essa pergunta, precisamos obter o valor de . Nesse caso, inicialmente escrevemos uma equação e a deixamos na forma reduzida.
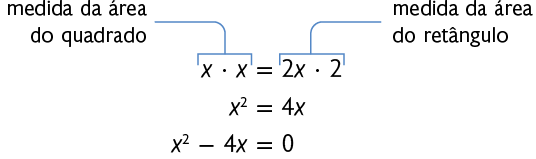
Temos que é o fator comum aos dois termos do 1º membro da equação. Por isso, podemos colocá-lo em evidência.
Se o produto de dois fatores é igual a zero, então, um deles é zero. Portanto, pode assumir dois valores:
ou
Logo, as raízes da equação são 0 e 4. Para essa situação, consideremos apenas a raiz , pois a medida de comprimento indicada em um dos pedaços de madeira é maior do que zero.
Agora, calculamos a medida do perímetro do quadrado e do retângulo.
Medida do perímetro do quadrado
Medida do perímetro do retângulo
Página 100
Atividades
Faça as atividades no caderno.
44. Determine as raízes de cada equação.
a)
b)
c)
d)
e)
f)
g)
h)
45. Quantas são as raízes de uma equação do tipo , com e números reais não nulos? Quais são as características das raízes desse tipo de equação?
46. (Saresp-2005) A equação :
a) não tem raízes reais.
b) tem uma raiz nula e outra negativa.
c) tem uma raiz nula e outra positiva.
d) tem duas raízes reais e simétricas.
47. O cubo e o paralelepípedo reto retângulo representados a seguir têm a mesma medida de volume.
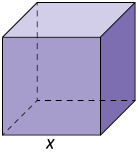
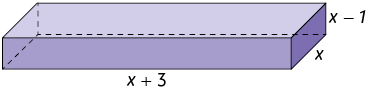
a) Sabendo que as medidas estão em centímetros, quais são as medidas dos comprimentos das arestas dessas figuras geométricas espaciais?
b) Quanto é a medida do volume de cada figura geométrica espacial?
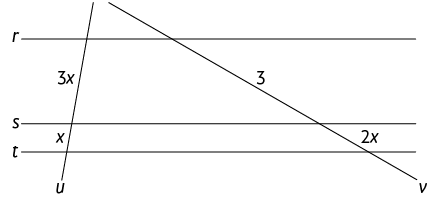
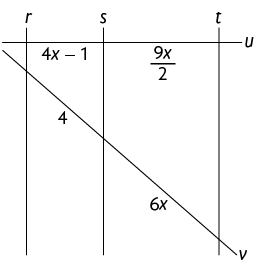
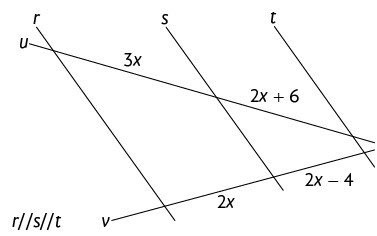
48. Em cada figura, as retas , e são paralelas. Calcule no caderno o valor de indicado em cada figura.
Atenção!
Utilize o teorema de Tales para resolver esta atividade.
49. De acordo com as figuras a seguir, elabore um problema envolvendo equações do 2º grau e o entregue para um colega resolver. Depois, verifique se a resposta dele está correta.

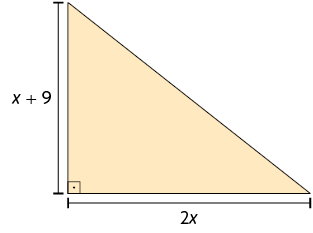
Página 101
Resolvendo equações do tipo
Acompanhamos, anteriormente, a resolução de equações do 2º grau incompletas e, agora, resolveremos equações do 2º grau completas, isto é, aquelas em que todos os coeficientes são diferentes de zero.
Podemos calcular as raízes de uma equação do 2º grau completa de várias maneiras, como por meio da fatoração, do método de completar quadrados ou da fórmula resolutiva.
Fatoração
Uma das maneiras de obter as raízes de uma equação do 2º grau completa é por fatoração.
Atenção!
Lembre-se que fatorar é escrever um número ou uma adição algébrica na forma de um produto.
Por exemplo, consideremos a equação . O 1º membro dessa equação é um trinômio quadrado perfeito. Portanto, podemos escrevê-lo da seguinte maneira:
A representação geométrica do trinômio corresponde à medida da área de um quadrado cujo comprimento dos lados mede .
Medida da área das quatro partes nas quais o quadrado foi dividido:
Medida da área do quadrado maior:

Como as duas expressões obtidas representam a medida da área da mesma figura, temos:
Assim, é a forma fatorada de .
Agora, voltamos à equação e escrevemos o 1º membro na forma fatorada:
Como há dois números que, elevados ao quadrado, são iguais a 36, temos:
ou
Portanto, os números 3 e são as raízes da equação .
Página 102
Método de completar quadrados
Em algumas equações completas do 2º grau, o 1º membro não é um trinômio quadrado perfeito. Nesses casos, para obter as raízes da equação, utilizamos o método de completar quadrados.
Questão 4. Junte-se a um colega e realizem uma pesquisa sobre as contribuições de Al-Khwarizmi e do livro Al-Jabr wa'l muqabalah, de sua autoria, para a Matemática. Depois, registre no caderno as informações que achar mais interessantes.

Atenção!
A pesquisa proposta na questão 4 pode ser feita com base em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Acompanhe como podemos obter as raízes da equação utilizando esse método.
Nessa equação, o 1º membro não é um trinômio quadrado perfeito. Assim, para que possamos fatorá-la, acrescentamos convenientemente um mesmo número aos dois membros da equação.Para obter esse número, inicialmente isolamos o termo independente da equação no 2º membro.
Agora, vamos analisar, por meio de representação geométrica, o 1º membro da equação. Para facilitar essa visualização, trocamos por .
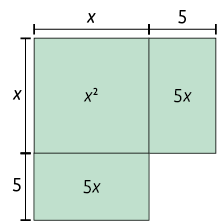
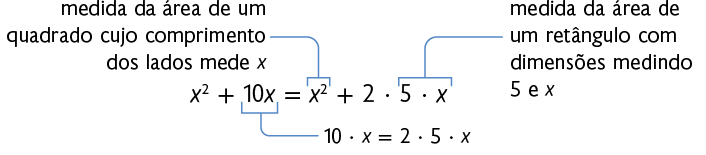
Na figura, percebemos que, para completar o quadrado, é necessário acrescentar a ela um quadrado com 5 unidades de lado.
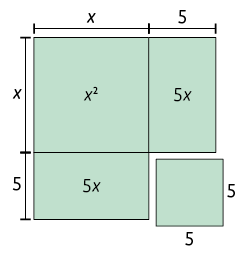
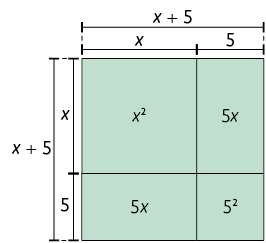
Página 103
Assim, para que a expressão seja um trinômio quadrado perfeito, precisamos acrescentar a ela.

Logo, para não alterar a igualdade , precisamos acrescentar aos dois membros:
Fatorando o 1º membro da equação, obtemos suas raízes.
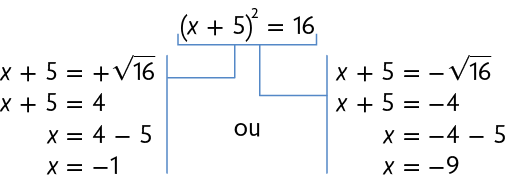
Atenção!
Para comprovar se e são as raízes, substitua cada uma na equação e verifique que a relação de igualdade permanece.
Portanto, as raízes da equação são e .
Atividades
Faça as atividades no caderno.
50. Fatore o 1º membro de cada equação e determine suas raízes.
a)
b)
c)
d)
e)
Atenção!
Em todas as equações desta atividade, o 1º membro é um trinômio quadrado perfeito.
51. Utilizando o método de completar quadrados, determine as raízes de cada equação.
a)
b)
c)
d)
e)
f)
52. De acordo com as figuras, escreva no caderno uma equação do 2º grau e determine as suas raízes.
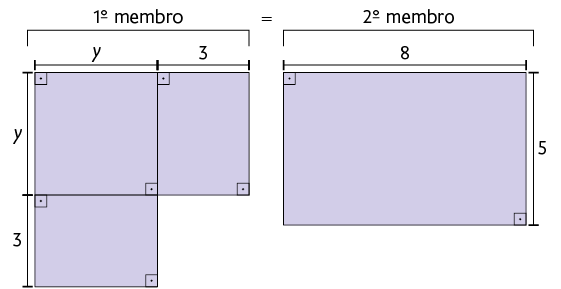
Atenção!
Para escrever a equação, considere a medida da área total das figuras em cada membro.
Página 104
Fórmula resolutiva
Anteriormente, estudamos como resolver equações completas do 2º grau por meio da fatoração e do método de completar quadrados. Outra maneira de obter as raízes desse tipo de equação é por meio da fórmula resolutiva, que é uma generalização desse método.
A seguir, deduziremos a fórmula resolutiva utilizando o método de completar quadrados.
Para isso, começamos com a equação , com , e números reais e .
Primeiro, dividimos cada termo dessa equação por e isolamos, no 2º membro, o termo independente.
Agora, representamos geometricamente o 1º membro da equação.
Para facilitar essa representação, trocamos pela expressão algébrica equivalente .
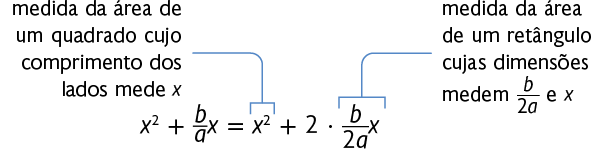
Na figura a seguir, percebemos que, para completar o quadrado, é necessário acrescentar a ela um quadrado cujo comprimento dos lados mede .
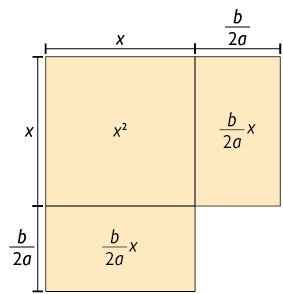
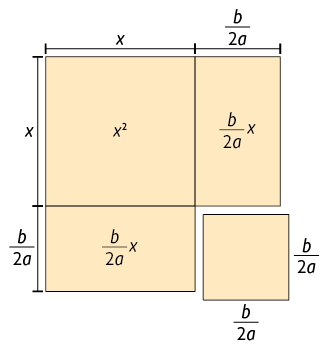
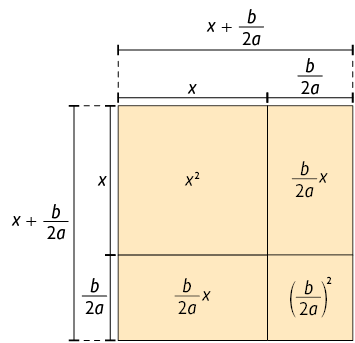
Página 105
Assim, para que o 1º termo da equação seja um trinômio quadrado perfeito, precisamos acrescentar aos dois membros da equação:
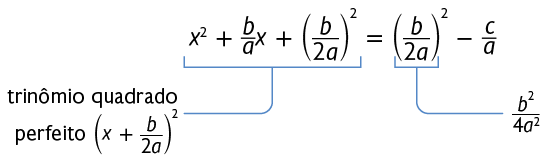
Fatoramos o 1º membro da equação obtida e a desenvolvemos até isolarmos a incógnita no 1º membro.
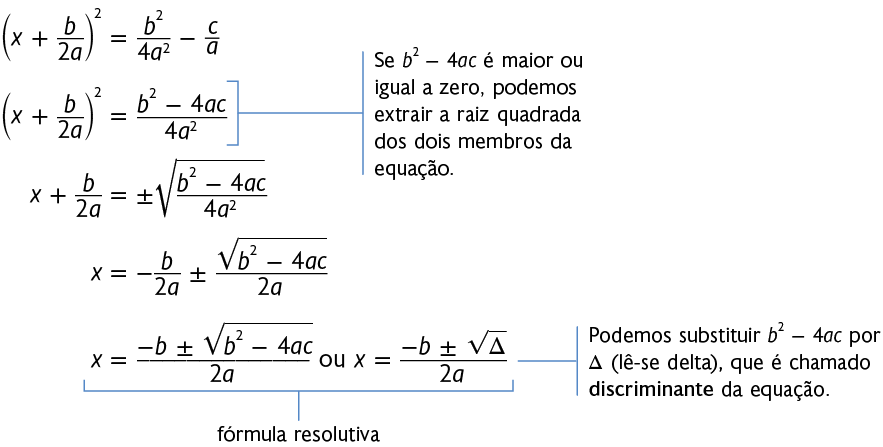
Atenção!
O símbolo (lê-se mais ou menos) indica que há dois valores associados: um positivo e outro negativo.

Página 106
Usando a fórmula resolutiva, podemos obter, por exemplo, as raízes da equação . Nela, temos , e . Assim, calculando o valor do discriminante da equação, obtemos:
Sendo assim:
Consequentemente:
Portanto, as raízes dessa equação são e .
Para verificar se a resolução está correta, substituímos os valores de e na equação .
De fato, e são as raízes da equação.
Equações literais
Na equação a seguir, de incógnita , também aparece a letra . Nesse caso, a letra , chamada parâmetro, faz parte dos coeficientes da equação.
Nessa equação, temos , e . Esse tipo de equação é chamado equação literal.
Podemos resolvê-la usando a fórmula resolutiva.
Consequentemente:
Portanto, as raízes dessa equação são e .
Página 107
Considere agora a equação , de incógnita , que tem uma das raízes igual a 3. Para obter a outra raiz dela, podemos substituir a incógnita pela raiz conhecida e, assim, determinamos o valor do parâmetro . Em seguida, resolvemos a equação.
Substituímos o valor de e resolvemos a equação.
Consequentemente, e .
Portanto, a outra raiz dessa equação é .
Equações fracionárias
As equações que apresentam pelo menos uma fração com incógnita em seu denominador são chamadas equações fracionárias. Nelas, o denominador de cada fração deve ser diferente de zero.
Acompanhe como podemos obter as raízes da equação fracionária , com e .
Calculamos inicialmente o mmc de e , que é , e multiplicamos cada termo da equação pelo mmc para eliminarmos os denominadores. Em seguida, simplificamos a equação, deixando-a na forma reduzida, e usamos a fórmula resolutiva, obtendo, assim, as raízes da equação.
Atenção!
As raízes desta equação devem ser diferentes de 0 e de 4. Caso contrário, um dos denominadores se anularia.
Utilizando a fórmula resolutiva, por exemplo, obtemos e .
Por fim, verificamos se as raízes obtidas atendem às condições de existência da equação.
Portanto, as raízes da equação são e .
Página 108
Atividades
Faça as atividades no caderno.
53. Resolva no caderno as equações do 2º grau a seguir usando a fórmula resolutiva.
a)
b)
c)
d)
e)
f)
54. Jorge é professor de Matemática e sempre que lhe fazem alguma pergunta durante a aula, gosta de usar a Matemática em sua resposta. Analise o que ele respondeu quando lhe perguntaram a idade de seus filhos.

Qual é a idade dos filhos do professor Jorge?
55. No caderno, escreva cada equação na forma reduzida e, em seguida, resolva-as da maneira que preferir.
a)
b)
c)
d)
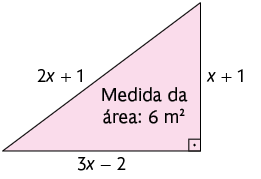
56. Sabendo que as medidas dos comprimentos dos lados das figuras a seguir estão indicadas em metros, determine o valor de e a medida do perímetro de cada figura.

57. As medidas indicadas no triângulo a seguir estão expressas em centímetros.
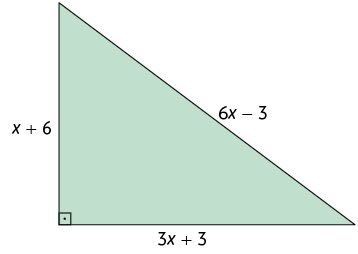
Medida do perímetro:
Medida da área:
a) Utilizando a medida do perímetro desse triângulo, escreva uma equação que possibilite determinar o valor de .
b) Utilizando a medida da área desse triângulo, escreva uma equação que possibilite determinar o valor de .
c) Entre as equações obtidas nos itens a e b, qual é do 2º grau?
d) Determine a medida do comprimento de cada lado do triângulo resolvendo a equação escrita no item b.
Página 109
58. Ao determinar as raízes da equação , obtemos dois números:
a) pares.
b) ímpares.
c) cuja soma é igual a 1.
d) cujo produto é igual a .
59. Sabendo que a soma dos quadrados de dois números inteiros e consecutivos é 113, determine esses números.
60. Calcule no caderno o valor de na figura a seguir.
61. Para obtermos a quantidade de diagonais de um polígono convexo, podemos utilizar a seguinte fórmula:
: quantidade de lados
: quantidade de diagonais
Usando essa fórmula, podemos calcular, por exemplo, quantos lados tem um polígono convexo com 14 diagonais, da seguinte maneira:
No caderno, resolva essa equação e determine quantos lados tem esse polígono convexo.
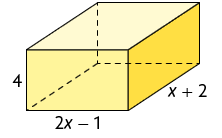
62. As medidas indicadas no paralelepípedo reto retângulo estão em centímetros. Calcule a medida do volume desse paralelepípedo, sabendo que a medida da área de sua planificação é .
63. Escreva no caderno uma equação para representar as informações de cada item, usando a incógnita , e resolva-a.
a) O quadrado de um número é igual a 8 menos o dobro desse número.
b) O quadrado de um número mais seu dobro é igual a esse número mais 2.
64. Para produzir morangos, um agricultor utiliza um terreno retangular cuja medida da área é . Com o objetivo de aumentar a produção, o agricultor decidiu aumentar as medidas do terreno em metros na largura e metros no comprimento.

Qual deve ser o valor de para que a medida da área de plantio seja aumentada em ?
Página 110
65. Usando a fórmula da atividade 61, efetue os cálculos no caderno e determine quantos lados tem um polígono convexo com:
a) 20 diagonais;
b) 35 diagonais;
c) 65 diagonais;
d) 90 diagonais.
66. O produto de um número inteiro por seu consecutivo é igual a 380. Quais são esses números?
67. Determine as raízes das equações literais, a seguir, com incógnita .
a)
b)
c)
d)
e)
f)
68. Obtenha, se existirem, as raízes das equações fracionárias a seguir.
a) , com .
b) , com .
c) , com .
d) , com e .
e) , com e .
f) , com e .
g) , com e .
69. Em cada equação, com incógnita , foi apresentada uma das raízes. Determine no caderno a outra raiz.
A.
Raiz:
B.
Raiz:
70. Para que a expressão , com , seja igual a , qual deve ser o valor de ?
71. Para divulgar uma peça de teatro que seria apresentada na escola, Leandro e alguns amigos ficaram responsáveis pela distribuição de 84 panfletos. No dia da distribuição, 3 pessoas não puderam participar dela. Com isso, cada pessoa entregou 9 panfletos a mais. Para saber quantas pessoas entregaram os panfletos, podemos representar por o número de pessoas que combinaram de distribuí-los e escrever a seguinte equação.
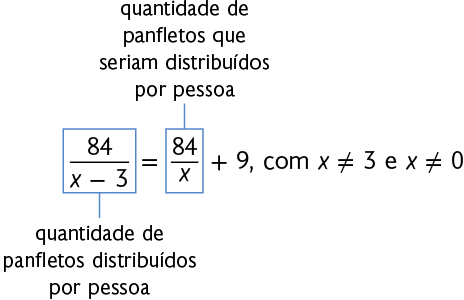
a) Resolva no caderno essa equação e determine quantas pessoas distribuíram os panfletos.
b) Quantos panfletos cada pessoa entregou?
Página 111
Estudo das raízes de uma equação do 2º grau
O discriminante e a quantidade de raízes
Analise três equações do 2º grau que Bruna resolveu. Em cada resolução, verifique o valor de e a quantidade de raízes de cada equação.
Consequentemente:
Consequentemente:
A equação não tem raízes reais, pois não existe raiz quadrada de número negativo no conjunto dos números reais.
De modo geral, na resolução de qualquer equação do 2º grau, temos três casos.
- Se é um número positivo (), a equação tem duas raízes reais e diferentes.
- Se é igual a zero (), a equação tem duas raízes reais e iguais.
- Se é um número negativo (), a equação não tem raízes reais.
Relações envolvendo as raízes e os coeficientes
Usando os coeficientes de uma equação do 2º grau na forma , podemos escrever duas relações envolvendo a soma () e o produto () de suas raízes e .
Para determinar essas relações, consideremos e da seguinte maneira:
e , em que
Podemos estabelecer essas relações da seguinte maneira.
Soma das raízes
Página 112
Produto das raízes
Assim:
Atenção!
As relações de soma e produto das raízes possibilitam resolver algumas equações do 2º grau de maneira prática.
Quando o coeficiente da equação do 2º grau é 1, podemos obter mentalmente suas raízes utilizando as relações de soma e produto.
Assim, se , a soma das raízes é o oposto do coeficiente e o produto das raízes é o próprio coeficiente .
Podemos obter as raízes da equação usando essas relações da seguinte maneira.
Inicialmente, determinamos dois números cuja soma seja o oposto do coeficiente , nesse caso, . Algumas possibilidades são:
e
e
e
e 3
e 2
Como o produto das raízes é o coeficiente , ou seja, 10, as raízes são e , pois elas satisfazem as duas relações.
e
Analise, agora, a seguinte situação.
Uma das raízes da equação é . Podemos obter a outra raiz dessa equação sem utilizar a fórmula resolutiva. Faremos isso de duas maneiras, utilizando as relações de soma () e produto () das raízes.
Note que, tanto na relação da soma das raízes quanto na de produto, chegamos à mesma solução. Logo, a outra raiz dessa equação é .
Página 113
Com as relações de soma e produto das raízes, podemos escrever uma equação do 2º grau do tipo , com , de outra maneira.
Inicialmente, vamos dividir todos os termos da equação por .
Substituindo as relações e na equação, obtemos:
Atenção!
Note que .
Essa forma é útil para escrever uma equação do 2º grau, conhecendo suas raízes. Por exemplo, para escrever uma equação do 2º grau cujas raízes são 1 e , procedemos da seguinte maneira:
Equação do 2º grau e sua forma fatorada
Vamos escrever a equação do 2º grau , com , cujas raízes reais são e , em sua forma fatorada. Para isso, executamos as seguintes etapas.
1º. Colocamos o coeficiente a em evidência.
2º. Se e , escrevemos:
3º. Colocando os fatores comuns em evidência, obtemos a forma fatorada da equação do 2º grau.
Agora, escreveremos uma equação do 2º grau cujas raízes são 2 e usando a forma fatorada.
Portanto, a equação cujas raízes são 2 e é .
Página 114
Atividades
Faça as atividades no caderno.
72. Calcule no caderno o discriminante () e descubra quantas raízes cada equação tem. Depois, obtenha, se existirem, as raízes de cada uma delas.
a)
b)
c)
d)
73. Utilizando as relações, determine a soma e o produto das raízes de cada equação.
a)
b)
c)
d)
74. Considere a equação literal , de incógnita . Nessa equação, temos , e . A fim de determinar valores de , com , para os quais a equação tem duas raízes reais diferentes, procedemos da seguinte maneira.
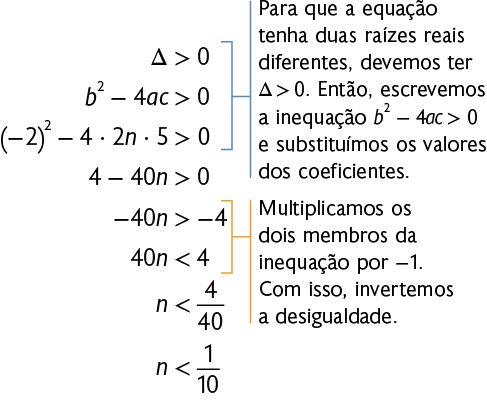
Portanto, quando , com , a equação tem duas raízes reais diferentes.
Agora, determine para quais valores de essa equação:
a) tem duas raízes reais iguais;
b) não tem raízes reais.
75. Determine as raízes de cada equação efetuando mentalmente os cálculos da soma e do produto das raízes.
a)
b)
c)
76. De acordo com as raízes em cada item, escreva uma equação do 2º grau, na forma reduzida, com incógnita e coeficiente de igual a 1.
a) e
b) e
c) e
d) e
77. Uma das raízes da equação é . Utilizando a forma fatorada, determine a outra raiz.
78. No caderno, elabore dois problemas semelhantes ao apresentado na atividade anterior e peça a um colega que os resolva. Depois, verifique se as respostas dele estão corretas.
79. Utilizando as relações de soma e produto das raízes, determine a outra raiz de cada equação.
a) ;
b) ;
c) ;
Atenção!
Em cada item é dada uma equação e uma de suas raízes.
Página 115
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
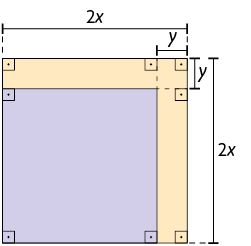
1. Escreva, em uma folha de papel avulsa, um trinômio quadrado perfeito para representar a medida da área do quadrado roxo.
2. Em uma folha de papel avulsa, associe a diferença de quadrados à sua forma fatorada. Para isso, escreva a letra e o número correspondentes.
A.
B.
C.
1.
2.
3.
3. Copie os itens em uma folha de papel avulsa e substitua cada por um dos polinômios a seguir, de modo que a igualdade permaneça.
a)
b)
c)
4. O produto da idade de João pelo dobro da idade de José é igual a 280. José tem 4 anos a menos do que João. Chamando a idade de João de , escreva, em uma folha de papel avulsa, uma equação do 2º grau, na forma reduzida, que represente essa situação.
5. A medida da área do paralelogramo a seguir é igual à medida de seu perímetro.

a) Escreva, em uma folha de papel avulsa, uma equação do 2º grau, na forma reduzida, que represente essa igualdade.
b) A equação do 2º grau que você escreveu é completa ou incompleta? Quais são seus coeficientes?
6. A soma das medidas das áreas de todas as faces de um cubo, de aresta com comprimento medindo , é igual a . Escreva, em uma folha de papel avulsa, uma equação que represente essa situação. Depois, determine a medida do comprimento de cada aresta do cubo.
7. Guilherme pediu a um amigo que descobrisse a quantia em reais que ele tinha na carteira. Para isso, deu a seguinte dica:
O dobro do quadrado da quantia que tenho mais o quádruplo da quantia que tenho é igual ao triplo do quadrado dessa quantia menos dez vezes a quantia que tenho.
Quantos reais Guilherme tinha na carteira?
8. (OBM-2006) A soma de 3 números naturais consecutivos é igual ao produto desses 3 números. A soma dos quadrados desses números é:
a) 14
b) 15
c) 18
d) 24
e) 36
Página 116
9. A medida do comprimento de um terreno retangular cuja área mede é maior do que a medida de sua largura.
a) Em uma folha de papel avulsa, escreva uma equação de incógnita que relacione as medidas dos comprimentos dos lados desse terreno com a sua medida de área.
b) Resolva, em uma folha de papel avulsa, essa equação utilizando o método de completar quadrados e determine as medidas das dimensões desse terreno.
10. Paulo vai cercar o jardim que há no terreno de sua casa, representado na figura a seguir. Na imagem, o fio em vermelho representa a cerca que será construída.
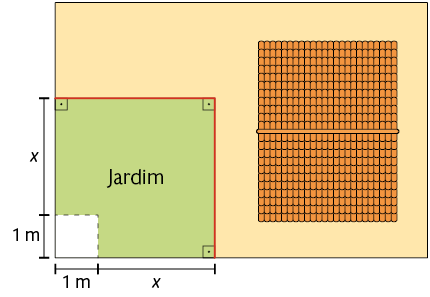
Sabendo que a área do jardim mede , calcule, em uma folha de papel avulsa o valor de que aparece na figura e a medida do comprimento dessa cerca.
11. Um triângulo com o comprimento da base e da altura medindo, respectivamente, e teve um aumento de na medida do comprimento da base e de na medida do comprimento da altura. Qual deve ser o valor de para que a medida da área do triângulo seja aumentada em ?
12. (Obmep-2006) No dia de seu aniversário, em 2006, o avô de Júlia disse a ela: "Eu nasci no ano e completei anos em 1980. Quantos anos eu completo hoje?".
a) 61
b) 64
c) 67
d) 70
e) 72
13. (IFSP-2011) Considere a equação do 2º grau, em , dada por . Se as raízes dessa equação são e , então a diferença é igual a:
a) 8
b) 14
c) 19
d) 23
e) 27
14. Eduardo pensou em um número que, dividido por 2, é igual a dividido por .
a) Represente essa situação em uma folha de papel avulsa.
b) Em que número Eduardo pensou?
15. Uma empresa de táxi compra diariamente de combustível para abastecer sua frota. Essa quantidade de combustível é dividida igualmente entre os táxis da frota. Em certo dia, 2 táxis estavam quebrados e o combustível destinado a eles foi dividido igualmente entre os demais. Sabendo que nesse dia cada táxi recebeu a mais do que recebe diariamente, qual é a quantidade de táxis da frota?
16. Se multiplicarmos as raízes reais da equação , obteremos um número:
a) primo.
b) ímpar.
c) par.
d) menor do que 2.
e) maior do que 6.