Página 117

UNIDADE

Triângulo retângulo

Fotografia em visão oblíqua, com a vista lateral de uma ponte pênsil sobre uma grande superfície de água. Ao fundo há uma cidade onde a ponte vai de encontro. — Vista de parte da estrutura de sustentação da Ponte 25 de Abril, em Lisboa, Portugal, em 2019, composta por treliças de formatos triangulares.

Agora vamos estudar...

triângulo retângulo e seus elementos;
relações métricas no triângulo retângulo;
teorema de Pitágoras.

Página 118

Relações métricas no triângulo retângulo

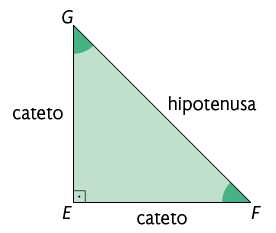
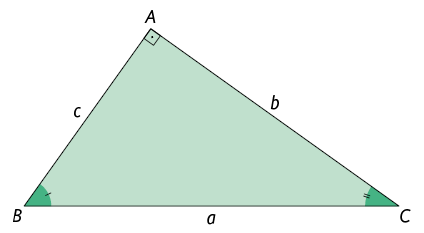
Você sabe o que é um triângulo retângulo? Um triângulo é assim chamado quando um de seus ângulos internos mede $90 graus$ . Neles, podemos destacar a hipotenusa e os catetos. A hipotenusa é o lado oposto ao ângulo reto. Os outros dois lados do triângulo retângulo, que formam o ângulo reto, são os catetos.

Atenção!

A hipotenusa é o lado de maior medida de comprimento.

No triângulo retângulo $E F G$ , $\overline{F G}$ é a hipotenusa, e $\overline{E F}$ e $\overline{E G}$ são os catetos.

Ilustração de um triângulo retângulo E F G. Os ângulos internos a esse triângulo estão demarcados e o vértice E tem ângulo reto. Está indicado que o lado oposto ao ângulo reto é denominado hipotenusa. E os outros dois lados são denominados cateto.

Atenção!

O símbolo indica o ângulo reto.

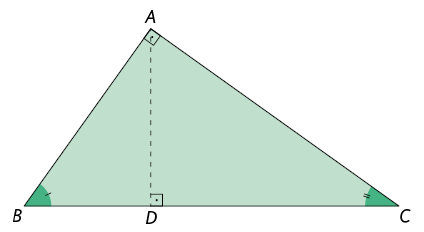
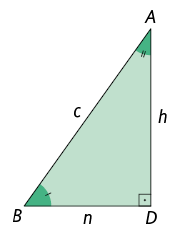
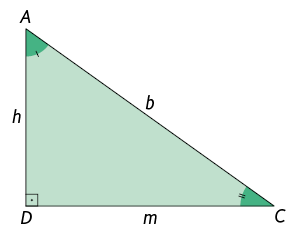
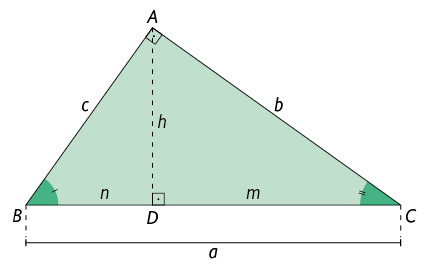
Agora, considere o triângulo retângulo $A B C$ . Nele, ao traçarmos a altura $\overline{A D}$ relativa à hipotenusa, determinamos outros dois triângulos retângulos, os quais são semelhantes entre si e semelhantes ao triângulo $A B C$ .

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado no vértice A. Os outros dois ângulos também estão demarcados. Sobre o ângulo B há um pequeno traço, e sobre o ângulo C, há dois pequenos traços. Há um segmento A D, traçado formando um ângulo de 90 graus com a hipotenusa B C.

Vamos conferir a semelhança entre esses triângulos retângulos.

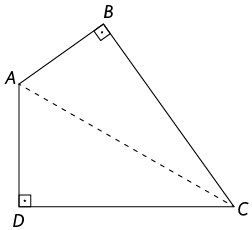
Inicialmente, imaginamos os triângulos $A B C$ , $D B A$ e $D A C$ separadamente.

Ilustração de um triângulo retângulo A D B. Ele é formado da divisão do triângulo A B C a partir do segmento A D. Nele, o ângulo reto está no vértice D. E sobre o ângulo B há um pequeno traço. — Triângulo $D B A$ .

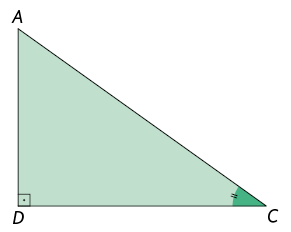
Ilustração de um triângulo retângulo A D C. Ele é formado da divisão do triângulo A B C a partir do segmento A D. Nele, o ângulo reto está no vértice D. E sobre o ângulo C há dois pequenos traços. — Triângulo $D A C$ .

Página 119

Considere os triângulos $A B C$ e $D B A$ . Note que os ângulos $B \hat{A} C$ e $B \hat{D} A$ são congruentes por serem retos, e que os ângulos $A \hat{B} C$ e $D \hat{B} A$ são congruentes por serem comuns aos dois triângulos.

Atenção!

Indicaremos o triângulo $A B C$ por $△ A B C$ .

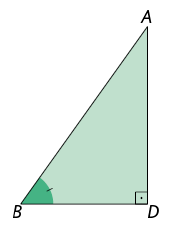
Ilustração de um triângulo retângulo A D B. O ângulo reto está indicado no vértice D. Sobre a indicação do ângulo B há um pequeno traço.

$B \hat{A} C ≅ B \hat{D} A$

$A \hat{B} C ≅ D \hat{B} A$

$△ A B C \sim △ D B A$

Considere os triângulos $A B C$ e $D A C$ . Note que os ângulos $B \hat{A} C$ e $A \hat{D} C$ são congruentes por serem retos, e que os ângulos $A \hat{C} B$ e $D \hat{C} A$ são congruentes por serem comuns aos dois triângulos.

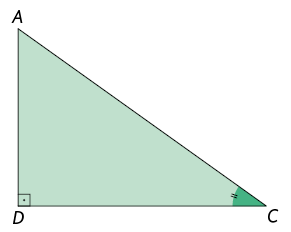
Ilustração de um triângulo retângulo A D C. O ângulo reto está indicado no vértice D. Sobre a indicação do ângulo C há dois pequenos traços.

$B \hat{A} C ≅ A \hat{D} C$

$A \hat{C} B ≅ D \hat{C} A$

$△ A B C \sim △ D A C$

Como os triângulos $D B A$ e $D A C$ são semelhantes ao triângulo $A B C$ , segue que eles são semelhantes entre si, dois a dois.

A altura relativa à hipotenusa de um triângulo retângulo divide-o em outros dois triângulos retângulos, que são semelhantes a ele e entre si.

Considerando que, em triângulos semelhantes, as medidas do comprimento são proporcionais nos respectivos lados, podemos estabelecer algumas relações entre elas.

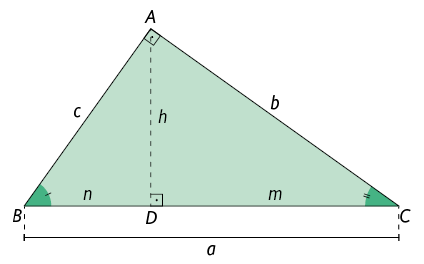
Ilustração de um triângulo retângulo A B C. O ângulo reto está no vértice A. O lado B C é hipotenusa e está indicado como a minúsculo. O lado A B é um dos catetos e está indicado como c minúsculo. E o lado A C é o outro cateto indicado como b minúsculo. Há um segmento A D, traçado formando um ângulo de 90 graus com a hipotenusa B C. Esse segmento está indicado como h minúsculo. Está indicado que a medida de comprimento de B até D é n minúsculo. E a medida de comprimento de D até C é m minúsculo. Os ângulos internos referentes ao vértice B e C estão demarcados, e sobre o ângulo B há um pequeno traço, e sobre o ângulo C, dois pequenos traços.

$a = m + n$

a: medida do comprimento da hipotenusa.

b e c: medidas dos comprimentos dos catetos.

h: medida do comprimento da altura relativa à hipotenusa.

m e n: medidas dos comprimentos das projeções dos catetos sobre a hipotenusa.

Página 120

Considerando os triângulos $A B C$ e $D B A$ , temos:

Ilustração de um triângulo retângulo A D B. Ele é formado da divisão do triângulo A B C a partir do segmento A D. Nele, o ângulo reto está no vértice D. Sobre o ângulo B há um pequeno traço. Está indicado que o lado A B tem medida de comprimento c minúsculo; o lado B D tem medida de comprimento n minúsculo; e o lado A D tem medida de comprimento h minúsculo.

$\frac{a}{c} = \frac{c}{n} \Rightarrow c^{2} = a \cdot n$

$\frac{a}{c} = \frac{b}{h} \Rightarrow b \cdot c = a \cdot h$

$\frac{b}{h} = \frac{c}{n} \Rightarrow c \cdot h = b \cdot n$

Considerando os triângulos $A B C$ e $D A C$ , temos:

Ilustração de um triângulo retângulo A D C. Ele é formado da divisão do triângulo A B C a partir do segmento A D. Nele, o ângulo reto está no vértice D. Sobre o ângulo C há dois pequenos traços. Está indicado que o lado A C tem medida de comprimento b minúsculo; o lado A D tem medida de comprimento h minúsculo; e o lado D C tem medida de comprimento m minúsculo.

$\frac{a}{b} = \frac{c}{h} \Rightarrow b \cdot c = a \cdot h$

$\frac{a}{b} = \frac{b}{m} \Rightarrow b^{2} = a \cdot m$

$\frac{b}{m} = \frac{c}{h} \Rightarrow c \cdot m = b \cdot h$

Questão 1. Em seu caderno, mostre que a relação $h^{2} = m \cdot n$ é verdadeira. Para isso, considere os triângulos $D B A$ e $D A C$ .

$a = m + n$
$b \cdot c = a \cdot h$
$b^{2} = a \cdot m$
$c^{2} = a \cdot n$
$c \cdot h = b \cdot n$
$c \cdot m = b \cdot h$
$h^{2} = m \cdot n$

Página 121

Acompanhe alguns exemplos em que as relações métricas são utilizadas para determinar medidas de comprimentos desconhecidos em um triângulo retângulo.

Vamos determinar as medidas a, b e c no triângulo $A B C$ .

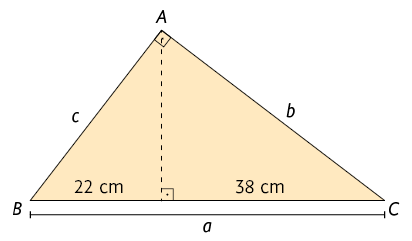
Ilustração de um triângulo retângulo A B C. Os catetos estão indicados como c minúsculo e b minúsculo e a hipotenusa com a minúsculo, que é igual a 22 centímetros mais 38 centímetros. Está traçado a altura em relação à hipotenusa a minúsculo. São formados outros dois triângulos retângulos a partir da altura. Um deles tem a hipotenusa sendo c minúsculo; um cateto tem medida 22 centímetros; e o outro cateto é a altura do triângulo A B C. O outro triângulo retângulo formado tem a hipotenusa sendo b minúsculo; um cateto tem medida 38 centímetros; e o outro cateto é a altura do triângulo A B C.

$a igual a m mais n, assim, a igual a 38 mais 22, assim, a igual a 60$

$c ao quadrado igual a a vezes n, assim, c ao quadrado igual a 60 vezes 22$ $Assim, c ao quadrado igual a 1.320, assim, c aproximadamente igual a 36 vírgula 33$

$b ao quadrado igual a a vezes m, assim, b ao quadrado igual a 60 vezes 38$ $Assim, b ao quadrado igual a 2.280, assim, b aproximadamente igual a 47 vírgula 75$

Nesse triângulo, temos $a igual a 60 centímetros$ , $b aproximadamente igual a 47 vírgula 75 centímetros$ e $c aproximadamente igual a 36 vírgula 33 centímetros$ .

Vamos determinar as medidas e, f e h no triângulo $E F G$ , sabendo que $g igual a 20 centímetros$ .

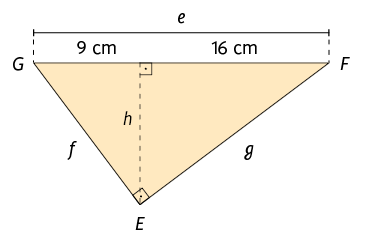
Ilustração de um triângulo retângulo E F G. Os catetos estão indicados como f minúsculo e g minúsculo e a hipotenusa como e minúsculo, que tem 9 centímetros mais 16 centímetros de medida de comprimento. Está traçado a altura h minúsculo em relação à hipotenusa e minúsculo. São formados outros dois triângulos retângulos a partir da altura h minúsculo. Um deles tem a hipotenusa sendo f minúsculo; um cateto tem medida de comprimento 9 centímetros; e o outro cateto é a altura h minúsculo. O outro triângulo retângulo formado tem a hipotenusa sendo g minúsculo; um cateto tem medida de comprimento 16 centímetros; e o outro cateto é a altura h minúsculo.

$e = m + n \Rightarrow e$ $igual a 16 mais 9, assim, e igual a 25$

$h ao quadrado igual a m vezes n, assim, h ao quadrado igual a 16 vezes 9$ $assim, h ao quadrado igual a 144, assim, h igual a 12$

$f vezes h igual a g vezes n, assim, f vezes 12 igual a 20 vezes 9$ $Assim, 12 f igual a 180, assim, f igual a 15$

Nesse triângulo, temos $e igual a 25 centímetros$ , $h igual a 12 centímetros$ e $f igual a 15 centímetros$ .

Atenção!

Nos exemplos, ao obtermos as medidas c, b e h, resolvemos uma equação que tem uma raiz positiva e outra negativa. Como são medidas de comprimentos, consideramos apenas os valores positivos.

Atividades

Faça as atividades no caderno.

1. O triângulo $A B C$ é isósceles com base $\overline{B C}$ . Sabendo que $\overline{A E}$ é a altura relativa à base, responda às questões.

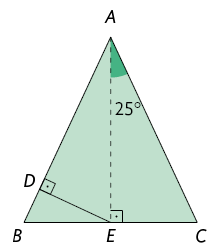
Ilustração de um triângulo isósceles A B C. Está traçado a altura A E em relação a base B C, demarcando o ângulo reto em E, formando dois triângulos retângulos. Abrangendo apenas o triângulo A E C está destacado e indicado o ângulo de medida 25 graus no vértice A. No triângulo A B E está indicado sua altura D E em relação ao lado A B, demarcando o ângulo reto em D.

a) Quais dos triângulos indicados são triângulos retângulos?

b) Quais são as medidas dos ângulos internos do triângulo $E D B$ ? E do triângulo $A D E$ ?

c) Quais dos triângulos indicados são semelhantes?

Página 122

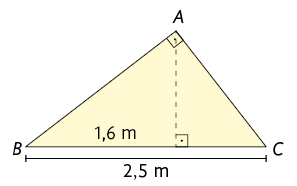
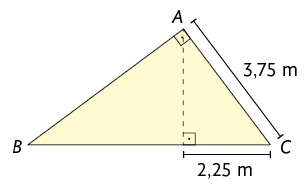
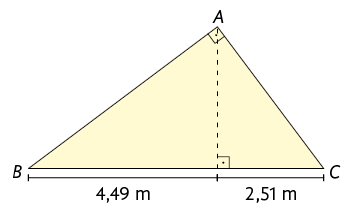
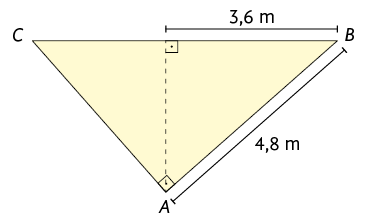
2. Nos triângulos a seguir, as letras representam medidas em centímetros. Com o auxílio de uma calculadora, faça os cálculos necessários para determinar o valor de cada uma delas.

Ilustração de um triângulo retângulo. Um dos catetos está indicado com b e a hipotenusa tem medida de comprimento 18 centímetros. Está traçado a altura relativa à hipotenusa, indicada por h. São formados outros dois triângulos retângulos a partir da altura. Um desses triângulos tem a hipotenusa indicada por b; um dos catetos é a altura h e o outro cateto tem 8 centímetros de medida de comprimento.

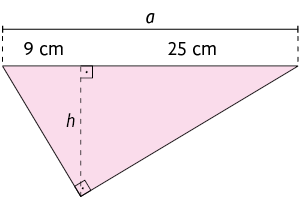
Ilustração de um triângulo retângulo. A hipotenusa tem medida a minúsculo. Está traçado a altura relativa à hipotenusa, indicada por h minúsculo. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos um dos catetos é a altura h minúsculo e o outro cateto tem medida de comprimento 9 centímetros. No outro triângulo um dos catetos é a altura h minúsculo e o outro cateto tem 25 centímetros de medida de comprimento.

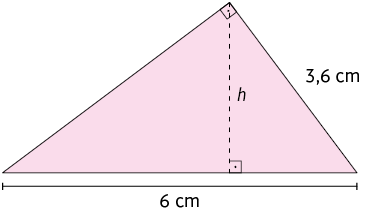
Ilustração de um triângulo retângulo. Um dos catetos tem medida de comprimento 3,6 centímetros e a hipotenusa 6 centímetros de medida de comprimento. Está traçado a altura relativa à hipotenusa, indicada por h minúsculo. São formados outros dois triângulos retângulos a partir da altura. Um deles tem a hipotenusa indicada pela medida 3,6 centímetros e o outro cateto é a altura h minúsculo.

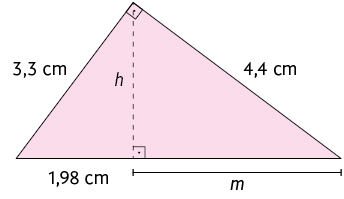
Ilustração de um triângulo retângulo. Os catetos têm as medidas de comprimento: 3,3 centímetros e 4,4 centímetros, respectivamente. A hipotenusa tem 1,98 centímetros mais m minúsculo de medida de comprimento. Está traçado a altura relativa à hipotenusa, indicada por h minúsculo. São formados outros dois triângulos retângulos a partir da altura. Um deles tem a hipotenusa indicada pela medida de comprimento 3,3 centímetros; um dos catetos é a altura h minúsculo e o outro cateto tem 1,98 centímetros de medida de comprimento. O outro triângulo tem hipotenusa de medida de comprimento 4,4 centímetros; um dos catetos é a altura h minúsculo e o outro cateto tem medida de comprimento m minúsculo.

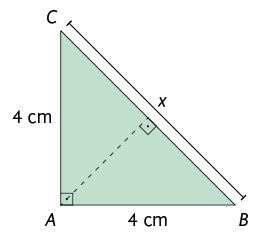
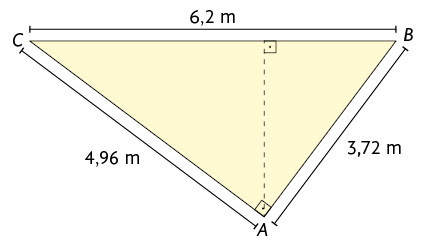
3. Qual é o valor de x no triângulo?

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. O lado B C é a hipotenusa e está indicada por x. Um dos catetos é o lado A C de medida de comprimento 4 centímetros e o outro cateto é o lado A B de medida de comprimento 4 centímetros. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado A C. No outro triângulo a hipotenusa é o lado A B.

4. Usando uma calculadora, determine a medida da área de cada triângulo.

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. O lado B C é a hipotenusa e tem medida de comprimento 2,5 metros. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado A C. No outro triângulo a hipotenusa é o lado A B, um dos catetos é a altura e o outro cateto tem medida de comprimento 1,6 metros.

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. O lado A C tem medida de comprimento 3,75 metros. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado A C, um dos catetos é a altura e o outro cateto tem 2,25 metros de medida de comprimento.

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. O lado B C é a hipotenusa e tem 4,49 metros mais 2,51 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa é A B, um dos catetos é a altura e o outro cateto tem 4,49 metros de medida de comprimento. O outro triângulo tem a hipotenusa em A C, um dos catetos é a altura e o outro cateto tem medida de comprimento 2,51 metros.

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. O lado A B tem 4,8 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado A B, um dos catetos é a altura e o outro cateto tem medida de comprimento 3,6 metros.

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. O lado A C tem 4,96 metros de medida de comprimento e o lado A B 3,72 metros. O lado B C é a hipotenusa e tem 6,2 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado A C. No outro triângulo a hipotenusa é o lado A B.

Página 123

Teorema de Pitágoras

Além das relações métricas estudadas até aqui, existe outra envolvendo as medidas dos comprimentos dos lados de um triângulo retângulo, chamada teorema de Pitágoras. Esse nome homenageia o matemático e filósofo grego Pitágoras.

Pitágoras nasceu na ilha de Samos, no Mar Egeu, por volta de 572 a.C. Em Crotona, na Magna Grécia – costa sudeste do que agora é a Itália –, fundou a escola pitagórica, que consistia em um centro de estudos de Matemática, Filosofia e Ciências naturais.

Fonte de pesquisa: EVES, Howard. Introdução à História da Matemática. Tradução: Hygino H. Domingues. Campinas: Editora da Unicamp, 2004.

Fotografia da escultura de busto de um homem de barba e bigode. Está escrito PITAGORA na própria escultura, na parte de baixo. Ao fundo há árvores e uma grade próxima. — Busto de Pitágoras. Escultura no parque Villa Borghese, em Roma, na Itália, em 2021.

Agora, enunciaremos e demonstraremos o teorema de Pitágoras.

Em todo triângulo retângulo, o quadrado da medida do comprimento da hipotenusa é igual à soma dos quadrados das medidas dos comprimentos dos catetos.

Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado no vértice A. A hipotenusa B C tem medida de comprimento a minúsculo. E os catetos A B e A C tem medidas de comprimento c minúsculo e b minúsculo, respectivamente.

$a^{2} = b^{2} + c^{2}$

Demonstração

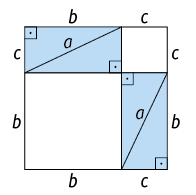
Considere um quadrado com o comprimento dos lados medindo $b + c$ . Podemos decompor esse quadrado em 4 triângulos retângulos congruentes (com o comprimento dos catetos medindo b e c) e um quadrado menor (com o comprimento dos lados medindo a).

Ilustração de um quadrado. Os quatro vértices estão indicados com ângulos retos. Cada lado tem medida b mais c. São formados quatro triângulos retângulos com os catetos de medidas b e c. Esses catetos formam os lados do quadrado. A hipotenusa de cada triângulo tem medida a e estão voltados para o interior do quadrado. Esses triângulos estão com destaque. No interior do quadrado é formado um quadrado menor inclinado, de lado a, e com os quatro ângulos retos indicados.

Atenção!

Note que a corresponde à medida do comprimento da hipotenusa de um dos triângulos e que b e c são as medidas dos comprimentos dos catetos.

Considerando o mesmo quadrado (com o comprimento dos lados medindo $b + c$ ) também podemos decompô-lo em 4 triângulos retângulos congruentes (com o comprimento dos catetos medindo b e c) e dois quadrados menores (um com o comprimento dos lados medindo c e o outro com o comprimento dos lados medindo b).

Ilustração de um quadrado. Cada lado tem medida b mais c. O quadrado está dividido em dois retângulos de lados b e c, com a diagonal indicada por a; um quadrado de lado c e outro quadrado de lado b. Os retângulos estão com destaque e são ligados por um dos vértices. Seus lados são coincidentes com os lados dos quadrados.

Página 124

Cada quadrado inicial tem área medindo ${(b + c)}^{2}$ . Retirando os 4 triângulos retângulos congruentes de cada quadrado, obtemos figuras com medidas de áreas iguais.

$a^{2} = b^{2} + c^{2}$

Assim, demonstramos o teorema de Pitágoras.

Questão 2. Existem várias demonstrações do teorema de Pitágoras. No caderno, utilizando as relações métricas $b^{2} = a \cdot m$ e $c^{2} = a \cdot n$ , faça a demonstração desse teorema.

Agora, utilizando o teorema de Pitágoras, acompanhe como podemos obter os valores de x e y nos triângulos a seguir.

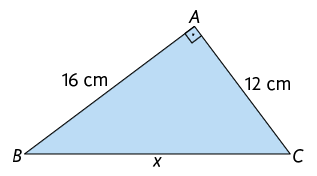
Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado no vértice A. A hipotenusa B C está indicada por x. O cateto A B tem 16 centímetros de medida de comprimento e o cateto A C tem 12 centímetros de medida de comprimento.

$a = x$

$b igual a 16 centímetros$

$c igual a 12 centímetros$

$a^{2} = b^{2} + c^{2}$

$x ao quadrado igual a 16 ao quadrado mais 12 ao quadrado$

$x ao quadrado igual a 256 mais 144$

$x ao quadrado igual a 400$

$x igual a 20$

Portanto, $x igual a 20 centímetros$ .

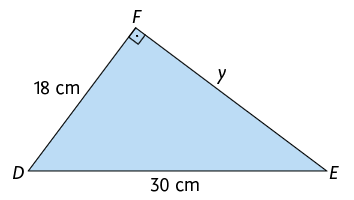
Ilustração de um triângulo retângulo D E F. O ângulo reto está demarcado no vértice F. A hipotenusa D E tem 30 centímetros de medida de comprimento. O cateto D F tem 18 centímetros e o cateto E F está indicado por y.

$a igual a 30 centímetros$

$b = y$

$c igual a 18 centímetros$

$a^{2} = b^{2} + c^{2}$

$30 ao quadrado igual a y ao quadrado mais 18 ao quadrado$

$900 igual a y ao quadrado mais 324$

$900 menos 324 igual a y ao quadrado$

$576 igual a y ao quadrado$

$y igual a 24$

Portanto, $y igual a 24 centímetros$ .

A recíproca do teorema de Pitágoras também é válida.

Em um triângulo, se o quadrado da medida do comprimento de um lado for igual à soma dos quadrados das medidas dos comprimentos dos outros dois lados, então trata-se de um triângulo retângulo.

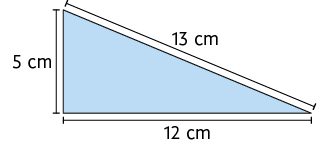
Questão 3. O triângulo indicado a seguir é um triângulo retângulo? No caderno, justifique sua resposta.

Ilustração de um triângulo. As medidas de comprimento dos lados estão indicadas por: 5 centímetros, 12 centímetros e 13 centímetros.

Página 125

Instrumentos e softwares

Cálculo da medida do comprimento da hipotenusa de um triângulo retângulo no Calc

Utilizando o Calc, vamos escrever uma fórmula que permita calcular a medida do comprimento da hipotenusa de um triângulo retângulo, conhecidas as medidas dos comprimentos dos dois catetos. Para isso, siga os passos apresentados a seguir.

1º. Nas células A1, B1 e C1, escreva "Cateto menor", "Cateto maior" e "Hipotenusa", respectivamente. Essas células serão preenchidas com as medidas dos comprimentos desses segmentos.

2º. Na célula C2, digite $igual a RAIZ abre parênteses A 2 asterisco A 2 mais B 2 asterisco B 2 fecha parênteses$ . Essa fórmula permite calcular a medida do comprimento da hipotenusa, dadas as medidas dos comprimentos dos catetos informadas nas células A2 e B2.

Ilustração de uma planilha. Na parte superior há uma barra com a fórmula: igual RAIZ abre parêntese A 2 asterisco A 2 mais B 2 asterisco B 2 fecha parêntese. Linha 1: na coluna A está escrito 'Cateto menor'; na coluna B 'Cateto maior' e na coluna C 'Hipotenusa'. Na célula C 2 há a fórmula: igual RAIZ abre parêntese A 2 asterisco A 2 mais B 2 asterisco B 2 fecha parêntese. Há um destaque na célula A 2 e no texto 'A 2 asterisco A 2' da fórmula da célula C 2, que os relaciona. Há um destaque na célula B 2 e no texto 'B 2 asterisco B 2' da fórmula da célula C 2, que os relaciona.

Atenção!

No Calc, o símbolo * indica multiplicação.

Para exemplificar, calcularemos a medida do comprimento da hipotenusa de um triângulo retângulo cujos comprimentos dos catetos medem $3 centímetros$ e $4 centímetros$ . Para isso, indique 3 na célula A2, 4 na célula B2 e tecle Enter.

Portanto, o comprimento da hipotenusa desse triângulo mede $5 centímetros$ .

Página 126

Atividades

Faça as atividades no caderno.

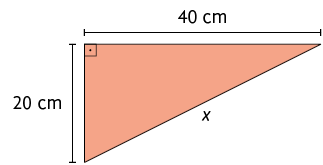
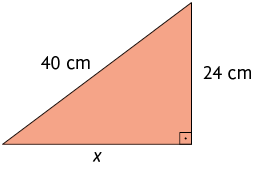
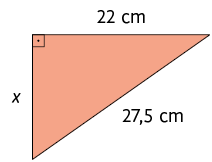
5. Determine a medida de x em cada triângulo retângulo a seguir.

Ilustração de um triângulo retângulo. A hipotenusa está indicada por x. Um dos catetos tem medida de comprimento 20 centímetros e o outro cateto 40 centímetros.

Ilustração de um triângulo retângulo. A hipotenusa tem medida de comprimento 40 centímetros. Um dos catetos tem medida de comprimento 24 centímetros e o outro cateto está indicado por x.

Ilustração de um triângulo retângulo. A hipotenusa tem medida de comprimento 27,5 centímetros. Um dos catetos tem medida de comprimento 22 centímetros e o outro cateto está indicado por x.

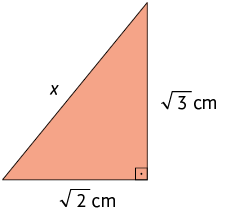
Ilustração de um triângulo retângulo. A hipotenusa está indicada por x. Um dos catetos tem medida de comprimento raiz quadrada de 2 centímetros e o outro cateto raiz quadrada de 3 centímetros.

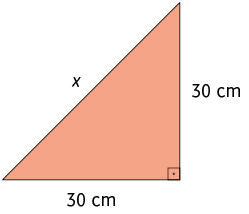
Ilustração de um triângulo retângulo. A hipotenusa está indicada por x. Um dos catetos tem medida de comprimento 30 centímetros e o outro cateto 30 centímetros.

6. Como já vimos, a recíproca do teorema de Pitágoras é válida. Em cada item, estão indicadas as medidas dos comprimentos dos lados de alguns triângulos. Com o Calc, verifique quais deles são triângulos retângulos.

a) $15 centímetros$ , $9 centímetros$ e $12 centímetros$ .

b) $20 centímetros$ , $16 centímetros$ e $12 centímetros$ .

c) $18 centímetros$ , $15 centímetros$ e $10 centímetros$ .

d) $8 centímetros$ , $7 centímetros$ e $4 centímetros$ .

e) $13 centímetros$ , $12 centímetros$ e $5 centímetros$ .

7. Calcule, em centímetros, a medida do comprimento da diagonal de cada um dos polígonos.

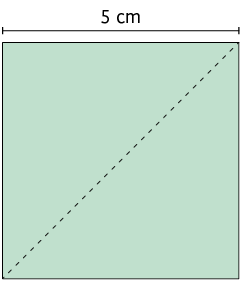
Ilustração de um polígono de quatro lados. Um dos lados tem medida de comprimento 5 centímetros. Está traçado sua diagonal. — quadrado

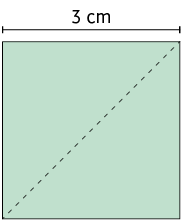
Ilustração de um polígono de quatro lados. Um dos lados tem medida de comprimento 3 centímetros. Está traçado sua diagonal. — quadrado

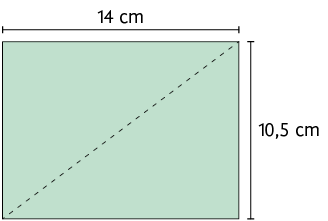
Ilustração de um polígono de quatro lados. Um dos lados tem medida de comprimento 14 centímetros e outro lado tem 10,5 centímetros. Está traçado sua diagonal. — retângulo

Página 127

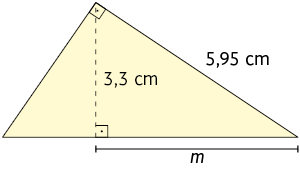
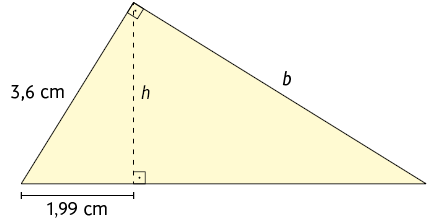
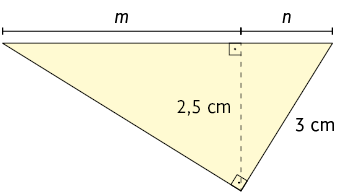
8. Utilizando uma calculadora, determine a medida aproximada, com duas casas decimais, de cada letra indicada nos triângulos retângulos.

Ilustração de um triângulo retângulo. A altura em relação à hipotenusa tem 3,3 centímetros de medida de comprimento. São formados dois triângulos retângulos a partir da altura. Um deles tem a hipotenusa com medida de comprimento 5,95 centímetros; um dos catetos é a altura de medida de comprimento 3,3 centímetros e o outro cateto tem medida de comprimento m.

Ilustração de um triângulo retângulo. Seus catetos tem as medidas de comprimento: 3,6 centímetros e b, respectivamente. A altura em relação à hipotenusa está indicada por h. São formados dois triângulos retângulos a partir da altura. Um deles tem a hipotenusa com medida de comprimento 3,6 centímetros; um dos catetos é a altura h e o outro cateto tem medida de comprimento 1,99 centímetros.

Ilustração de um triângulo retângulo. A hipotenusa tem medida de comprimento m mais n. Está traçado a altura relativa à hipotenusa, que tem 2,5 centímetros de medida de comprimento. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa tem 3 centímetros de medida de comprimento; um dos catetos é a altura de 2,5 centímetros de medida de comprimento e o outro cateto está indicado por n. No outro triângulo, um cateto é a altura de 2,5 centímetros de medida de comprimento e o outro cateto está indicado por m.

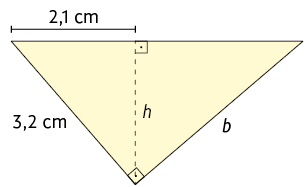
Ilustração de um triângulo retângulo. Seus catetos tem as medidas de comprimento: 3,2 centímetros e b, respectivamente. Está traçado a altura relativa à hipotenusa, indicada por h. São formados outros dois triângulos retângulos a partir da altura h. Em um dos triângulos a hipotenusa tem 3,2 centímetros de medida de comprimento; um dos catetos é a altura h e o outro cateto tem 2,1 centímetros de medida de comprimento. No outro triângulo, um dos catetos é a altura h e a hipotenusa é b.

9. Qual é a medida da área do triângulo retângulo a seguir?

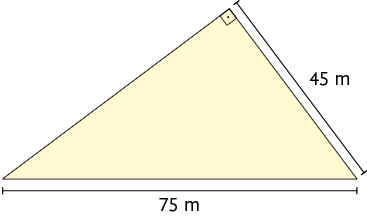
Ilustração de um triângulo retângulo. Um dos catetos tem medida de comprimento 45 metros e a hipotenusa tem 75 metros de medida de comprimento.

10. O perímetro de um triângulo equilátero mede $15 centímetros$ . Com o auxílio de uma calculadora, determine a medida aproximada, com duas casas decimais, do comprimento da altura desse triângulo.

11. Um terreno com formato retangular tem as medidas indicadas na figura.

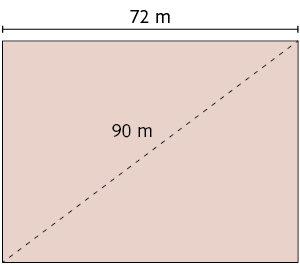
Ilustração de um retângulo. Um dos lados tem medida de comprimento 72 metros. Está traçado sua diagonal que possui medida de comprimento de 90 metros.

Qual é a medida do perímetro desse terreno?

12. A altura do trapézio isósceles representado a seguir mede $12 centímetros$ .

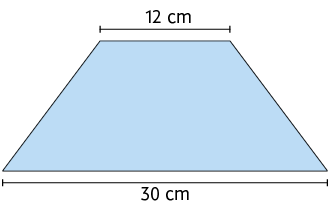
Ilustração de um trapézio isósceles. A base menor tem 12 centímetros de medida de comprimento e a base maior 30 centímetros de medida de comprimento.

Qual é a medida do perímetro desse trapézio?

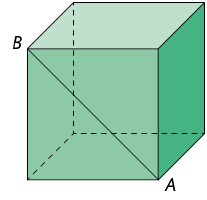
13. Calcule a medida do volume do cubo representado a seguir, sabendo que o comprimento da diagonal que liga o vértice A ao vértice B mede $15 raiz quadrada de 2 centímetros$ .

Ilustração de um cubo. Na face frontal está traçado uma diagonal ligando dois vértices, A e B.

Página 128

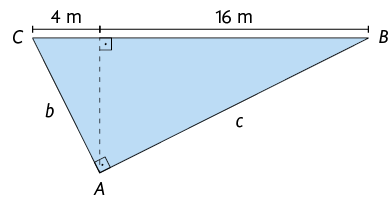
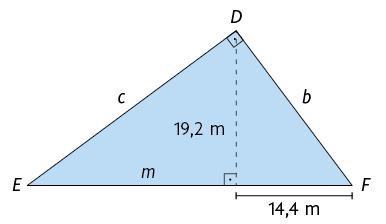
14. Determine, em metros, a medida do perímetro de cada um dos triângulos.

Ilustração de um triângulo retângulo A B C. O lado A C está indicado por b minúsculo e o lado A B está indicado por c minúsculo. O ângulo reto está demarcado em A. O lado B C é a hipotenusa e tem 4 metros mais 16 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa é A B; um dos catetos é a altura e o outro cateto tem medida de comprimento 16 metros. O outro triângulo tem a hipotenusa em A C, um dos catetos é a altura e o outro cateto tem 4 metros de medida de comprimento.

Ilustração de um triângulo retângulo D E F. O lado D E está indicado por c minúsculo e o lado D F está indicado por b minúsculo. O ângulo reto está demarcado em D. O lado E F é a hipotenusa e tem medida de comprimento m minúsculo mais 14,4 metros. Está traçado a altura relativa à hipotenusa, com medida de comprimento 19,2 metros. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa é D E; um dos catetos é a altura de medida de comprimento 19,2 metros e o outro cateto está indicado por m minúsculo. O outro triângulo tem a hipotenusa em D F, um dos catetos é a altura de medida de comprimento 19,2 metros e o outro cateto 14,4 metros.

15. Considere o quadrado $A B C D$ .

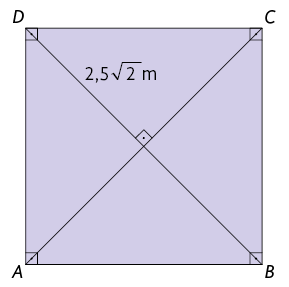
Ilustração de um quadrado A B C D. Estão indicados todos os ângulos retos dos vértices. O quadrado está dividido em quatro triângulos retângulos, formados por segmentos que são as diagonais que ligam os vértices A C e B D. No centro do quadrado está indicado um dos ângulos retos, formados pelo encontro desses segmentos. No triângulo A C D formado, está indicado sua altura com medida de comprimento 2,5 raiz quadrada de 2 metros.

a) Qual é a medida do comprimento de cada lado desse quadrado?

b) Qual é a medida do perímetro desse quadrado?

c) Qual é a medida da área do triângulo $A C D$ ?

16. Qual é a medida do comprimento da diagonal de um retângulo cujas dimensões medem:

a) $28 metros$ e $21 metros$ .

b) $5 centímetros$ e $12 centímetros$ .

c) $1 centímetro$ e $3 centímetros$ .

d) $5 centímetros$ e $início de raiz, raiz quadrada de 2 fim de raiz centímetros$ .

17. Calcule a medida do perímetro, da área e do comprimento da altura de cada um dos triângulos retângulos representados a seguir.

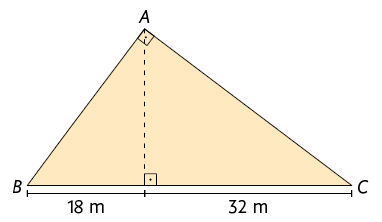
Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. A hipotenusa B C tem medida de comprimento 18 metros mais 32 metros. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa é A B, um dos catetos é a altura e o outro cateto tem 18 metros de medida de comprimento. O outro triângulo tem a hipotenusa em A C, um dos catetos é a altura e o outro cateto tem medida de comprimento 32 metros.

Ilustração de um triângulo retângulo D E F. O ângulo reto está demarcado em D. A hipotenusa E F tem medida de comprimento 25 metros mais 144 metros. Um dos catetos é o lado D E.e mede 65 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa é D F, um dos catetos é a altura e o outro cateto tem 144 metros de medida de comprimento. O outro triângulo tem a hipotenusa em D E, um dos catetos é a altura e o outro cateto é o lado D E.

18. Uma escada está apoiada em um muro, conforme mostra a imagem a seguir.

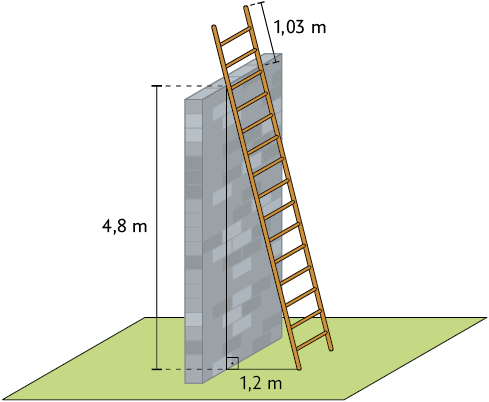
Ilustração de uma escada apoiada em um muro. O topo da escada ultrapassa o topo do muro em 1 vírgula zero 3 metros. O muro tem 4,8 metros de medida de altura e a distância horizontal entre a base do muro e a base da escada é de 1,2 metros. A altura do muro e a distância do muro para o pé da escada formam os catetos de um triângulo retângulo e a base da escada até onde ela encosta no muro, representa a hipotenusa.

a) Qual é a medida do comprimento aproximado da escada?

b) Calcule aproximadamente a que medida de distância a escada deve estar da base do muro para que seu topo coincida com o topo do muro.

Página 129

19. No esquema a seguir, está representada uma torre de energia elétrica perpendicular ao solo. Para sustentá-la, foram utilizados 4 cabos de aço com a mesma medida de comprimento.

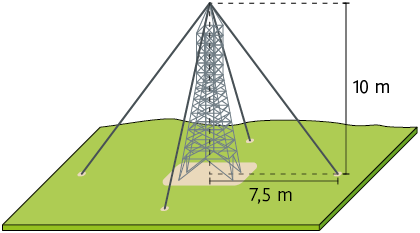
Ilustração de uma torre de energia elétrica sobre uma superfície plana. Do topo da torre saem quatro cabos inclinados e não-curvos até o chão, distantes igualmente entre si. A medida da distância horizontal entre o centro da base da torre e onde cada cabo toca o chão, é de 7,5 metros. A torre tem uma medida de altura de 10 metros.

Quantos metros de cabo de aço foram utilizados para sustentar essa torre?

20. De acordo com a imagem a seguir, elabore um problema envolvendo o teorema de Pitágoras e entregue-o para um colega resolver. Depois, verifique se ele resolveu corretamente.

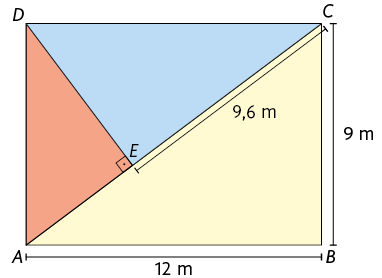
Ilustração de um retângulo A B C D. Os lados do retângulo têm 9 metros e 12 metros de medida de comprimento. O retângulo está dividido em 3 triângulos retângulos, sendo: o triângulo A B C, de catetos de medida de comprimento 12 metros em A B e 9 metros em B C; o triângulo C D E, reto em E e um dos catetos sendo C E com 9,6 metros de medida de comprimento; e o triângulo A D E, reto em E com a hipotenusa em A D. D E é a altura relativa em relação à hipotenusa A C do triângulo A C D.

21. No quadrilátero $A B C D$ , os ângulos $A \hat{B} C$ e $A \hat{D} C$ são retos. Sabendo que os comprimentos dos lados $\overline{A B}$ , $\overline{B C}$ e $\overline{C D}$ medem $7 metros$ , $24 metros$ e $20 metros$ , respectivamente, qual é a medida do perímetro desse quadrilátero em metros?

Ilustração de um quadrilátero A B C D. Os ângulos são retos em B e D. Há um traçado que liga os vértices A e C formando dois triângulos retângulos, o A B C e o A C D.

22. As raízes da equação $x ao quadrado menos 7 x mais 12 igual a 0$ correspondem às medidas do comprimento dos catetos de um triângulo retângulo, em centímetros. Determine a medida do perímetro desse triângulo, em centímetros.

23. Utilizando um programa de computador, Aroldo desenhou a seguinte figura, cuja soma das medidas das áreas dos três quadrados é $24 centímetros quadrados$ .

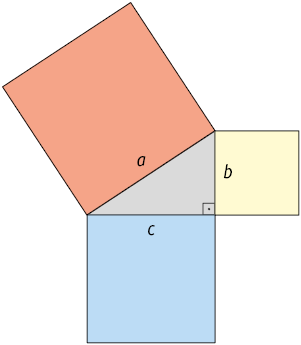
Ilustração de um triângulo retângulo e três quadrados formados pela medida de cada um de seus lados. O triângulo possui lados com medidas de comprimento a, b, c. Para cada lado do triângulo há um quadrado com arestas coincidentes de mesma medida de comprimento.

A área do quadrado maior mede:

a) $9 centímetros quadrados$ .

b) $10 centímetros quadrados$ .

c) $12 centímetros quadrados$ .

d) $8 centímetros quadrados$ .

e) $15 centímetros quadrados$ .

24. (UFRGS-2019) Na figura a seguir, está representado um cubo cuja aresta tem $2 centímetros$ de medida. O ponto P está localizado no centro da face $E F G H$ .

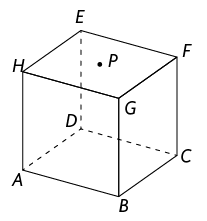
Ilustração de um cubo de arestas A B C D E F G H. A face A B C D está voltada para baixo e a face E F G H é a face superior. O ponto P está localizado no centro da face E F G H.

A medida do segmento $\overline{A P}$ é

a) $início de raiz, raiz quadrada de 2, fim de raiz$ .

b) 2.

c) $início de raiz, raiz quadrada de 6 fim de raiz$ .

d) $2 início de raiz, raiz quadrada de 3 fim de raiz$ .

e) 3.

Página 130

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Em uma folha de papel avulsa, determine a medida correspondente a cada letra.

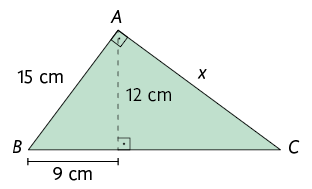
Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. Os catetos têm medidas de comprimento: x, em A C e 15 centímetros em A B. Está traçado a altura relativa à hipotenusa, com 12 centímetros de medida de comprimento. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado A C e um dos catetos é a altura de 12 cm de medida de comprimento. No outro triângulo, a hipotenusa é o lado A B; um dos catetos é a altura de 12 centímetros de medida de comprimento e o outro cateto de 9 centímetros de medida de comprimento.

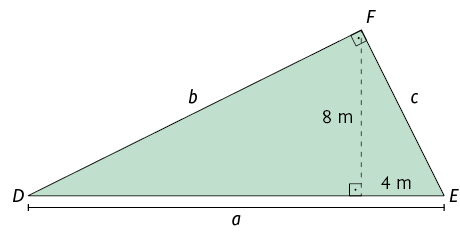
Ilustração de um triângulo retângulo D E F. O ângulo reto está demarcado em F. Os catetos têm medidas de comprimento: c minúsculo, em E F e b minúsculo em D F. A hipotenusa está indicada por a minúsculo. Está traçado a altura relativa à hipotenusa, com 8 metros de medida de comprimento. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado E F e um dos catetos é a altura de 8 cm de medida de comprimento. No outro triângulo, a hipotenusa é o lado D F e um dos catetos é a altura de 8 centímetros de medida de comprimento.

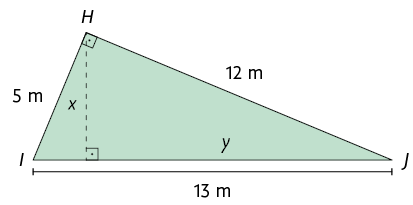
Ilustração de um triângulo retângulo H I J. O ângulo reto está demarcado em H. Os catetos têm medidas de comprimento: 5 metros, em H I e 12 metros em H J. A hipotenusa tem 13 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa, indicada por x. São formados outros dois triângulos retângulos a partir da altura. Em um desses triângulos a hipotenusa é o lado H J, um dos catetos é a altura x e o outro cateto é indicado por y. No outro triângulo, a hipotenusa é o lado H I e um dos catetos é a altura x.

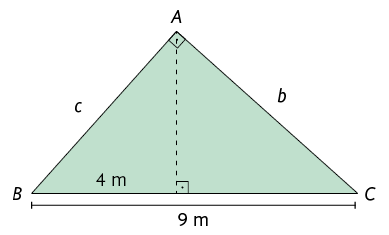
Ilustração de um triângulo retângulo A B C. O ângulo reto está demarcado em A. Os catetos estão indicados por c minúsculo em A B e por b minúsculo em A C. O lado B C é a hipotenusa e tem 9 metros de medida de comprimento. Está traçado a altura relativa à hipotenusa. São formados outros dois triângulos retângulos a partir da altura. Em um dos triângulos a hipotenusa é A B, um dos catetos é a altura e o outro cateto tem 4 metros de medida de comprimento. O outro triângulo tem a hipotenusa em A C e um dos catetos é a altura.

2. Determine a medida do comprimento da altura relativa à hipotenusa de um triângulo retângulo, sabendo que os comprimentos das projeções dos catetos sobre ela medem $9 metros$ e $25 metros$ .

3. Analise a figura.

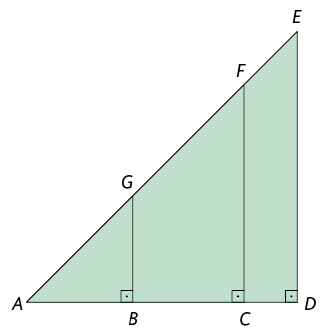
Ilustração de um triângulo retângulo A D E. O ângulo reto está demarcado em D. O lado A D é a base do triângulo. Há dois segmentos que dividem o interior do triângulo e que formam ângulos retos com a base. São os segmentos B G e C F, retos em B e C. G e F estão sobre o lado A E; B e C estão sobre o lado A D.

Agora, copie o quadro em uma folha de papel avulsa e complete-o, considerando u como unidade de medida.

Medidas de comprimento de três triângulos retângulos
Triângulo	Medida do comprimento
Triângulo	cateto	cateto	hipotenusa
$A B G$	$2 u$	$2 u$
$A C F$	$4 u$		$4 raiz quadrada de 2, u$
$A D E$		$5 u$	$5 raiz quadrada de 2, u$

4. Considere o quadrado $A B C D$ .

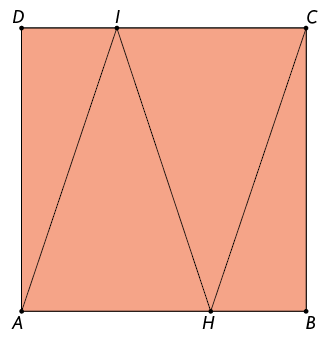
Ilustração de um quadrado A B C D. O lado A B é oposto ao lado C D. Sobre o lado A B há um ponto H. Sobre o lado D C há um ponto I. Estão ligados por segmentos os pontos A com I; I com H; H com C.

Sabendo que $a i igual a i h igual a h c igual a 10 centímetros$ , determine a medida da área de $A I H$ .