Página 159
UNIDADE
9
Funções

Agora vamos estudar...
- conjuntos;
- funções;
- função afim;
- gráfico de uma função afim;
- função quadrática;
- gráfico de uma função quadrática;
- valor máximo e mínimo de uma função quadrática.
Página 160
A noção de função
Em muitas situações do dia a dia, quando relacionamos grandezas, estamos tratando de um conceito importante na Matemática: o conceito de função. Acompanhe alguns exemplos.


Agora, considere a seguinte situação.
O consumo de energia elétrica dos eletrodomésticos é dado, em geral, em quilowatts-hora (). O quadro a seguir relaciona duas grandezas: o consumo de um chuveiro (y) e o tempo de uso (x).
|
Medida do tempo de uso em horas (x) |
Consumo em |
|---|---|
|
1 |
3,5 |
|
2 |
7 |
|
3 |
10,5 |
|
4 |
14 |
Para cada valor que atribuímos para x, obtemos um único valor correspondente para y, pois cada medida de tempo corresponde a um determinado consumo. Desse modo, a situação apresentada caracteriza um exemplo de função.
Dizemos que o consumo de energia elétrica é dado em função da medida do tempo de uso. A correspondência entre as grandezas "tempo" e "consumo de energia elétrica" é expressa pela seguinte sentença matemática.
Essa sentença é chamada lei de formação da função.
Atenção!
O consumo, que depende da medida do tempo de uso, é a variável dependente. A medida do tempo, cuja escolha é livre, é a variável independente.
Página 161
Também podemos representar a lei de formação dessa função substituindo a variável dependente y por , ou seja:
(lemos: f de x é igual a )
Nesse caso, a função chama-se f.
Podemos utilizar qualquer letra para indicar a função e a variável independente nessa notação. A seguir são apresentados alguns exemplos.
Agora, acompanhe outra situação.
Antônio é vendedor, e seu salário é calculado da seguinte maneira: salário-base de R$ 1.800,00 mais uma comissão de R$ 5,00 para cada peça de roupa vendida. O quadro a seguir apresenta o salário de Antônio de acordo com a quantidade de peças de roupa vendidas.
|
Quantidade de peças de roupa vendidas |
Salário (R$) |
|---|---|
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
12 |
|
|
|
|
|
p |
O salário de Antônio é dado em função da quantidade de peças de roupa vendidas. A lei de formação dessa função é , em que indica o salário de Antônio e p, a quantidade de peças de roupa vendidas.
Questão 1. Ao longo dos séculos, o conceito de função evoluiu muito, o que permitiu muitas aplicações da Matemática em outras ciências. Realize uma pesquisa acerca do desenvolvimento dos estudos relacionados à função. Depois, registre em seu caderno as informações mais importantes.
Questão 2. Junte-se a um colega e realizem uma pesquisa com mais informações sobre o uso das funções no cotidiano, anotando aqueles que acharem mais interessantes. Com base nas informações obtidas, escrevam no caderno um texto acerca do assunto.
Atenção!
As pesquisas propostas nas questões 1 e 2 podem ser feitas em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Página 162
O conceito de função
No tópico anterior, estudamos a noção de função. Agora, definiremos esse conceito.
Sejam os conjuntos A e B não vazios. Uma função f de A em B é uma regra que diz como associar a cada elemento um único elemento .
Dada uma função f de A em B, o conjunto A é chamado domínio da função e o conjunto B, contradomínio.
Para cada elemento , o elemento é chamado imagem de x pela função f.
Considere a seguinte situação. A medida do perímetro y de um triângulo equilátero é dada em função da medida do comprimento do seu lado x. A lei de formação dessa função é , e seu domínio é o conjunto dos números reais maiores do que zero, pois não existe medida de comprimento nula ou negativa.
Valor de uma função
Armando escreveu um programa em uma planilha eletrônica. Nele, o usuário insere um número e tem como resultado o dobro desse número. No quadro, são apresentados alguns exemplos.
|
Número inserido |
0 |
5 |
15 |
|
7,6 |
|
|---|---|---|---|---|---|---|
|
Resultado |
0 |
10 |
30 |
|
15,2 |
|
A lei de formação da função que relaciona o número inserido com o resultado é:
Agora, calcularemos o valor da função para x igual a 5, por exemplo. Para isso, substituímos x por 5 na lei de formação, ou seja: .
Portanto, o valor dessa função para x igual a 5 é 10, ou seja, ao inserir o número 5 nesse programa, o resultado exibido será 10.
Qual é o valor dessa função para x igual a ? Para responder a essa pergunta, basta substituir x por na lei de formação da função.
Questão 3. Em seu caderno, calcule qual será o resultado apresentado pelo programa caso o número inserido seja:
a) 1.210.
b) .
c) .
d) .
Página 163
Atividades
Faça as atividades no caderno.
1. No parque de diversões que Renato frequenta, o ingresso para cada brinquedo custa R$ 10,50. O quadro a seguir apresenta a quantia paga de acordo com algumas quantidades de ingressos comprados.
|
Quantidade de ingressos |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
|
Quantia paga (R$) |
10,50 |
21 |
31,5 |
42 |
a) Qual das fórmulas expressa o valor a ser pago por Renato (y) em função da quantidade de ingressos comprados (x)?
b) Quantos reais Renato vai pagar se comprar:
I. 7 ingressos?
II. 9 ingressos?
III. 12 ingressos?
IV. 15 ingressos?
c) Certo dia, Renato pagou R$ 52,50 pelos ingressos. Quantos ingressos ele comprou?
2. Escreva no caderno uma fórmula que represente cada situação a seguir.
a) A medida do perímetro (P) do retângulo em função da medida de sua largura (x).
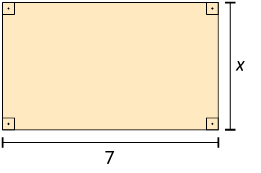
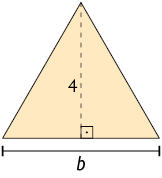
b) A medida da área A do triângulo em função da medida do comprimento de sua base b.
3. Na figura a seguir, as medidas estão indicadas em metros.

a) Escreva no caderno uma fórmula que expresse a medida do perímetro (P) dessa figura em função do valor desconhecido (x).
b) Utilizando a fórmula que você escreveu, determine o perímetro dessa figura quando:
I. .
II. .
III. .
IV. .
Página 164
4. Em uma prova, os pontos obtidos pelo estudante dependem da quantidade de questões que ele acerta. O quadro apresenta algumas pontuações em função da quantidade de acertos.
|
Quantidade de acertos |
Pontuação |
|---|---|
|
1 |
5 |
|
2 |
10 |
|
3 |
15 |
|
4 |
20 |
a) Escreva no caderno a sentença que representa a pontuação obtida (y) em função da quantidade de acertos (x) nessa prova.
b) Tiago acertou 15 questões nessa prova. Quantos pontos ele obteve?
c) Quantos acertos um estudante deve ter para obter 60 pontos nessa prova?
d) Sabendo que a quantidade máxima de pontos dessa prova é 100, qual é a quantidade de questões que ela tem?
5. O quadro a seguir apresenta alguns preços cobrados de acordo com a medida do tempo de permanência de um carro em um estacionamento.
|
Medida do tempo (em horas) |
Preço (R$) |
|---|---|
|
1 |
4,50 |
|
2 |
6,50 |
|
3 |
8,50 |
|
4 |
10,50 |
|
5 |
12,50 |
a) Escreva no caderno uma fórmula que represente o preço a pagar (y), em reais, em função da medida do tempo de permanência do carro nesse estacionamento (x), em horas.
b) Renata deixou seu carro por 8 horas nesse estacionamento. Quantos reais ela terá de pagar?
c) Com R$ 14,50, é possível deixar um carro nesse estacionamento por, no máximo, quantas horas?
6. Os alimentos trazem em sua embalagem uma tabela com informações sobre seus nutrientes, chamada tabela nutricional. Analise a seguir algumas informações acerca da medida da massa, em gramas (), e o valor calórico, em quilocalorias (), em determinada quantidade de um biscoito.
|
Quantidade de biscoito (unidade) |
Medida da massa () |
Valor calórico () |
|---|---|---|
|
1 |
15 |
70 |
|
2 |
30 |
140 |
|
3 |
45 |
210 |
|
4 |
60 |
280 |
|
5 |
75 |
350 |
|
6 |
90 |
420 |
a) Escreva no caderno uma fórmula que represente a medida da massa (m), em gramas, em função da quantidade de biscoitos (b).
b) Escreva no caderno uma fórmula que expresse o valor calórico (c), em quilocalorias, em função da quantidade de biscoitos (b).
c) Quantos gramas há em uma porção de 7 desses biscoitos? E qual é o valor calórico, em quilocalorias, nessa porção?
d) Quantos desses biscoitos há em uma embalagem de ? E qual é o valor calórico, em quilocalorias, nessa embalagem?
Página 165
Função afim
Josias trabalha em uma loja de informática, e o seu salário é composto de uma remuneração mensal fixa de R$ 1.280,00 mais R$ 7,12 por hora extra trabalhada.

Podemos expressar o salário mensal de Josias (x) em função da quantidade de horas extras trabalhadas (y).
Essa sentença é um exemplo de lei de formação de uma função afim.
Uma função de variáveis reais definida por , com a e b reais, é chamada função afim.
As constantes a e b são os coeficientes da função.
A seguir, são apresentados alguns exemplos.
- A função definida por é uma função afim. Nesse caso, temos e .
- A função dada por é uma função afim. Nesse caso, temos e .
- A função definida por é uma função afim. Nesse caso, temos e .
- A função dada por é uma função afim. Nesse caso, temos e .
Questão 4. Quais são os coeficientes da
função afim definida por ?
Agora, determinaremos o salário de Josias caso ele tenha feito 20 horas extras em um mês. Para isso, substituímos x por 20 na lei de formação da função, ou seja:
Portanto, se Josias fizer 20 horas extras em um mês, seu salário será R$ 1.422,40.
Página 166
Atividades
Faça as atividades no caderno.
7. A seguir, são apresentadas as leis de formação de algumas funções. Copie no caderno aquelas que correspondem a uma função afim.
a)
b)
c)
d)
e)
f)
8. Escreva no caderno os coeficientes da função definida por:
a) .
b) .
c) .
d) .
e) .
f) .
9. Considere a função afim definida por . Determine o valor de x para que y seja igual a:
a) 10.
b) .
c) 18.
d) .
e) .
f) .
10. A medida do perímetro (P) de um hexágono regular é dada em função da medida do comprimento (x) de seu lado.
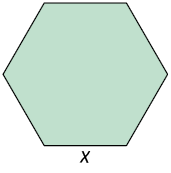
a) Em seu caderno, escreva a lei de formação da função que relaciona a medida do perímetro desse hexágono e a medida do comprimento de seu lado. A função cuja lei de formação você escreveu é afim?
b) Qual é a medida do perímetro de um hexágono regular cujo comprimento dos lados mede ?
c) Qual é a medida do comprimento de cada lado de um hexágono regular cujo perímetro mede ?
11. Você já usou a escala Celsius para medir temperaturas. E a escala Fahrenheit? Ela é usada, geralmente, nos países de língua inglesa e é indicada por . Nela, o ponto de fusão da água () é e o ponto de ebulição da água () é .
a) A escala Fahrenheit é dada por uma função afim da escala Celsius. Escreva a lei de formação dessa função.
b) Escreva em Fahrenheit.
c) Um aumento de 1 grau na escala Fahrenheit equivale a um aumento de quantos graus na escala Celsius?
Página 167
12. Para fazer uma corrida✚ em um táxi, são cobrados R$ 4,50 pela bandeirada✚ mais R$ 2,75 por quilômetro percorrido.
- Corrida:
- trajeto feito por passageiro em veículo (por exemplo, o táxi) com o devido pagamento ao motorista.↰
- Bandeirada:
- quantia fixa que é cobrada em corridas de táxi, independentemente da quantidade de quilômetros percorridos.↰
a) Escreva no caderno a lei de formação de uma função afim que represente o valor cobrado pela corrida em função da quantidade de quilômetros percorridos.
Atenção!
Indique o valor cobrado pela corrida por y e a quantidade de quilômetros percorridos por x.
b) Qual será o valor cobrado por uma corrida ao serem percorridos:
I. ?
II. ?
III. ?
c) Quantos quilômetros foram percorridos se o valor cobrado pela corrida foi:
I. R$ 7,80?
II. R$ 18,25?
III. R$ 43,00?
d) Marcelo tem R$ 60,00 para pagar uma corrida de táxi. Ele tem dinheiro suficiente para pagar uma corrida de ? Justifique sua resposta.

13. Cada embalagem de certo produto tem de medida de massa. Considerando a quantidade de embalagens como x e a medida da massa total, em gramas, como y, escreva a lei de formação de uma função que representa a medida da massa total em função da quantidade de embalagens.
14. Joice calculou o valor de uma função afim f para e . O quadro a seguir apresenta os valores obtidos por ela.
|
x |
|
|---|---|
|
1 |
3 |
|
|
9 |
Qual é o valor da função f quando ?
15. Certa papelaria utiliza o seguinte quadro de preços.
|
Produto |
Preço |
|---|---|
|
Impressão (cada folha) |
R$ 0,20 |
|
Encadernação (até 100 folhas) |
R$ 4,00 |
|
Encadernação (de 101 a 200 folhas) |
R$ 6,00 |
a) Considerando x a quantidade de folhas a serem impressas e y o valor total a ser pago, escreva a lei de formação de uma função que representa o valor total da impressão e encadernação de até 100 folhas. Faça o mesmo para a impressão e encadernação de 101 a 200 folhas.
b) Qual é o preço para imprimir e encadernar 83 folhas? E 145 folhas?
Página 168
Gráfico de uma função afim
Em uma função, ao atribuirmos valores para x, obtemos um único valor correspondente para y. Ao marcarmos os pontos obtidos no plano cartesiano, obtemos um conjunto de pontos chamado gráfico da função.
Considere, por exemplo, a função afim definida por . Vamos construir o gráfico dessa função. Para isso, inicialmente, atribuímos valores para x e determinamos o valor correspondente para y. Em seguida, marcamos os pontos obtidos no plano cartesiano.
|
x |
||
|---|---|---|
|
0 |
||
|
1 |
||
|
2 |
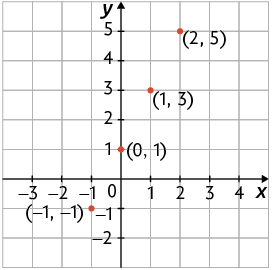
Atenção!
Note que os pontos marcados no plano cartesiano sugerem uma reta.
Como x é um número real, podemos atribuir infinitos valores para x, obtendo, para cada um deles, um único valor de y. Assim, há infinitos pontos entre os já marcados no plano cartesiano.
O gráfico da função é o conjunto de todos os pontos , com x real e , conforme apresentado a seguir.
O gráfico de uma função afim é uma reta.
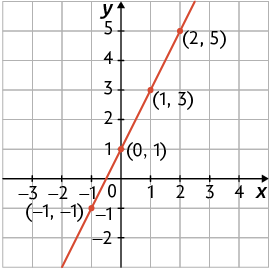

Como o gráfico de uma função afim é uma reta, para construí-lo basta marcar dois de seus pontos em um plano cartesiano e depois traçar a reta que passa por esses pontos.
Página 169
Atividades
Faça as atividades no caderno.
16. Jonas tem uma mola que se alonga de acordo com a medida da massa do corpo que é pendurado nela. Com essa mola, ele fez um experimento e pendurou alguns corpos, com diferentes medidas de massa, um de cada vez, e registrou o alongamento da mola.
No gráfico, está representado o alongamento dessa mola, em centímetros, em função da medida da massa do corpo pendurado, em quilogramas.
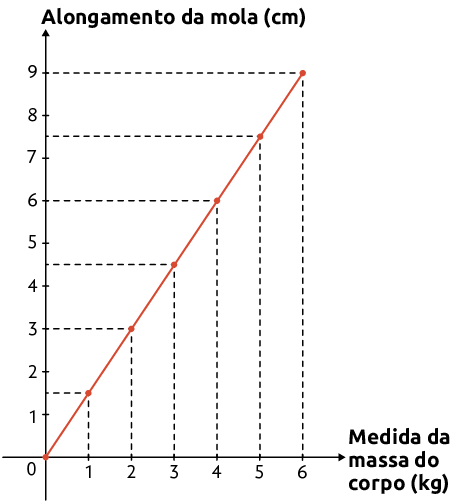
Atenção!
Após atingir determinada medida de massa, a mola vai ficar deformada de maneira permanente. No entanto, considere que, até a massa medir , a mola manterá suas características de elasticidade.
a) Qual foi o alongamento da mola quando Jonas pendurou nela um corpo com massa medindo ?
b) Qual é a medida da massa do corpo que fez a mola alongar ?
c) Escreva no caderno a lei de formação de uma função afim que permita calcular o alongamento da mola (y), em centímetros, em função da medida da massa do corpo pendurado (x), em quilogramas.
d) De acordo com a lei de formação que você escreveu, calcule qual será o alongamento da mola se Jonas pendurar nela um corpo de:
.
.
.
e) Jonas pendurou um corpo nessa mola e o alongamento foi de . Qual é a medida da massa desse corpo?
Página 170
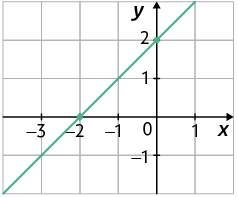
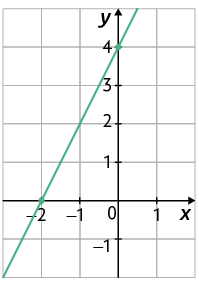
17. Considere as seguintes leis de formação que expressam função afim.
A.
B.
C.
Associe cada uma dessas leis aos gráficos apresentados a seguir. Para isso, escreva a letra e o número correspondentes.
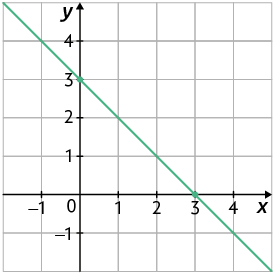
18. Construa, em um plano cartesiano, os gráficos das funções cujas leis de formação são apresentadas a seguir.
a)
b)
c)
d)
e)
f)
19. Escreva no caderno a lei de formação da função cujo gráfico está apresentado a seguir.
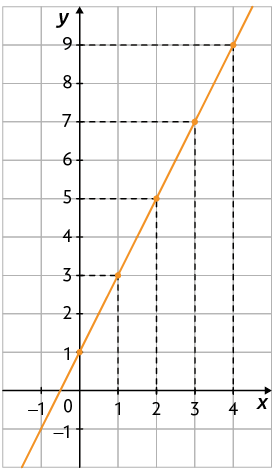
20. A seguir, é apresentado o gráfico de uma função afim que relaciona a medida da distância percorrida (y), em quilômetros, e a medida do tempo (x), em horas.
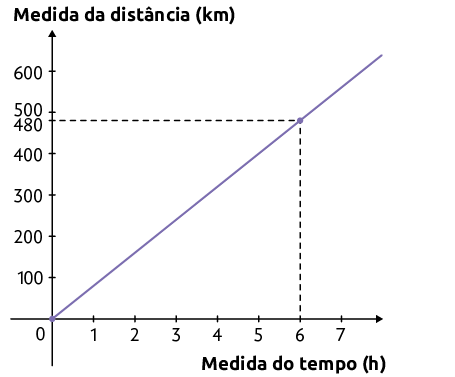
a) Escreva no caderno a lei de formação dessa função.
b) Escreva no caderno uma situação que pode ser relacionada a essa função.
Página 171
Função crescente e função decrescente
Considere o gráfico da função afim definida por .
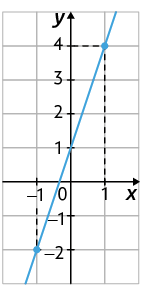
Questão 5. Nessa função, conforme
aumentamos os valores de x, o que ocorre com os valores
correspondentes de y?
Questão 6. O coeficiente a
da função é positivo ou negativo?
Quando o coeficiente a de uma função afim é positivo , a função é crescente. Nas funções crescentes, aumentando-se os valores de x, os valores correspondentes de y também aumentam.

Agora, considere o gráfico da função afim definida por .
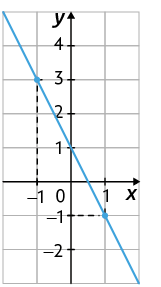
Questão 7. Nessa função, conforme
aumentamos os valores de x, o que ocorre com os valores
correspondentes de y?
Questão 8. O coeficiente a
da função é positivo ou negativo?
Quando o coeficiente a de uma função afim é negativo , a função é decrescente. Nas funções decrescentes, aumentando-se os valores de x, os valores correspondentes de y diminuem.

Atenção!
Quando o coeficiente a de uma função afim é zero , temos um caso particular de função afim, a função constante. Nesse caso, o gráfico da função afim é uma reta paralela ao eixo x.
Página 172
Atividades
Faça as atividades no caderno.
21. Em cada item, é dada a lei de formação de uma função afim. No caderno, classifique cada função em crescente ou decrescente.
a)
b)
c)
d)
e)
f)
22. Em cada item, estão representados alguns valores de x e y de uma função afim.
A.
|
x |
0 |
1 |
2 |
3 |
4 |
|---|---|---|---|---|---|
|
y |
B.
|
x |
0 |
1 |
2 |
3 |
4 |
|---|---|---|---|---|---|
|
y |
3 |
4 |
5 |
6 |
7 |
C.
|
x |
0 |
1 |
2 |
3 |
4 |
|---|---|---|---|---|---|
|
y |
0 |
1 |
2 |
D.
|
x |
0 |
1 |
2 |
3 |
4 |
|---|---|---|---|---|---|
|
y |
2 |
a) No caderno, associe cada gráfico a seguir a uma dessas funções.
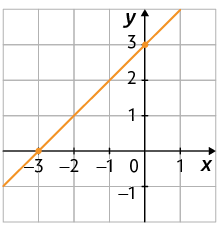
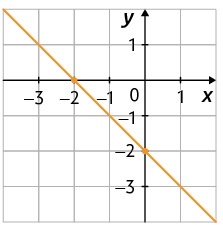
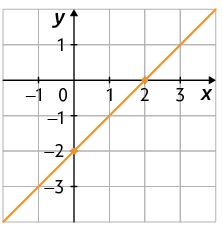
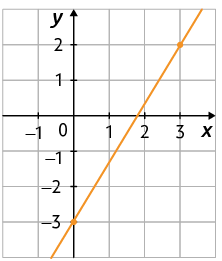
b) Escreva no caderno a lei de formação da função cujos gráficos foram apresentados no item anterior.
c) Classifique cada função cujo gráfico foi apresentado no item a em crescente ou decrescente.
Página 173
23. Em cada plano cartesiano a seguir está representado o gráfico de uma função afim.
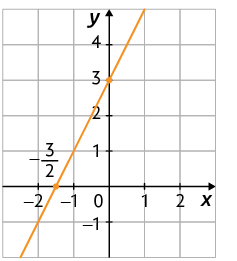
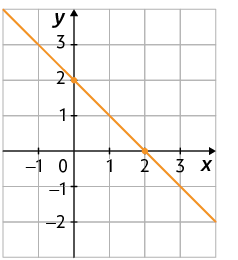
a) Classifique cada função afim em crescente ou decrescente.
b) Escreva a lei de formação de cada uma das funções cujos gráficos foram apresentados.
24. Em cada item a seguir, é apresentada a lei de formação de uma função afim de variáveis x e y. Determine os valores de k para os quais cada função afim seja decrescente.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
25. Considerando as funções cujas leis de formação foram dadas na atividade anterior, determine os valores de k em cada uma delas a fim de que seja crescente.
26. Classifique em crescente ou decrescente a função afim cujo gráfico passa pelos pontos:
a) e .
b) e .
c) e .
d) e .
e) e .
f) e .
g) e .
h) e .
i) e .
j) e .
27. Escreva no caderno a lei de formação de uma função afim crescente, na forma , com e . Depois, construa seu gráfico em um plano cartesiano.
28. O gráfico de uma função afim passa pelos pontos e . Determine valores distintos para m e n, de modo que essa função seja decrescente.
Página 174
Interseção com o eixo y
O gráfico de uma função afim definida por intersecta o eixo y quando . Nesse caso, para determinar as coordenadas do ponto de interseção com esse eixo, basta substituir x por 0 na lei de formação da função, ou seja:
Portanto, o gráfico de uma função afim intersecta o eixo y no ponto .
Acompanhe alguns exemplos.
O gráfico da função afim definida por intersecta o eixo y no ponto , pois .
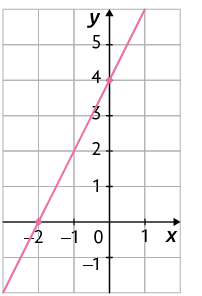
O gráfico da função afim definida por intersecta o eixo y no ponto , pois .
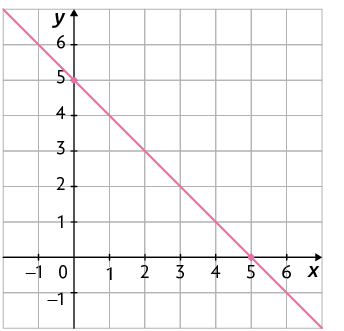
Interseção com o eixo x e zero da função afim
O gráfico de uma função afim definida por intersecta o eixo x no ponto em que . Assim:
Portanto, o gráfico de uma função afim intersecta o eixo x no ponto .
O zero de uma função afim é a abscissa do ponto de interseção de seu gráfico com o eixo x.
Considere, por exemplo, a função definida por . Seu gráfico intersecta o eixo x no ponto , pois:
Consequentemente, o zero dessa função é .
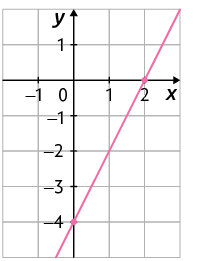
Página 175
Atividades
Faça as atividades no caderno.
29. Considere os seguintes gráficos de funções afins.
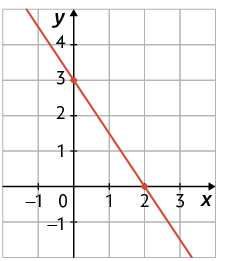
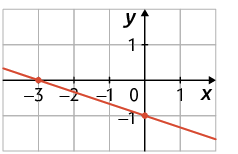
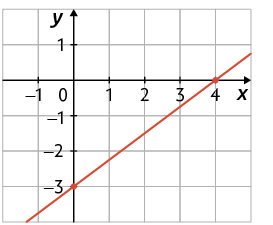
a) Quais são as coordenadas do ponto no qual cada gráfico intersecta o eixo y?
b) Qual é o zero das funções cujos gráficos foram apresentados?
c) Quais são as coordenadas do ponto no qual cada gráfico intersecta o eixo x?
d) Qual dos gráficos representa a função afim dada por ?
30. Em cada item, é apresentada a lei de formação de uma função afim. Escreva no caderno as coordenadas do ponto em que o gráfico dessas funções intersecta o eixo y.
a)
b)
c)
d)
e)
f)
g)
h)
31. Determine o zero da função afim definida por:
a) .
b) .
c) .
d) .
e) .
f) .
32. Considere a função afim definida por .
a) Construa o gráfico dessa função em um plano cartesiano.
b) Quais das afirmativas a seguir são verdadeiras?
I. Essa função é crescente.
II. O gráfico dessa função intersecta o eixo y no ponto .
III. O zero dessa função é .
IV. O gráfico dessa função intersecta o eixo x no ponto .
c) Reescreva no caderno as afirmativas falsas do item anterior, corrigindo-as.
33. Faça o que se pede.
a) Escreva no caderno a lei de formação de uma função afim, cujo gráfico intersecta o eixo y no ponto e o eixo x no ponto .
b) Em um plano cartesiano, construa o gráfico dessa função.
Página 176
Função quadrática
Pedro quer fazer uma horta para plantar espinafre e cenoura.
O esquema representa parte do terreno que ele reservou para essa horta.
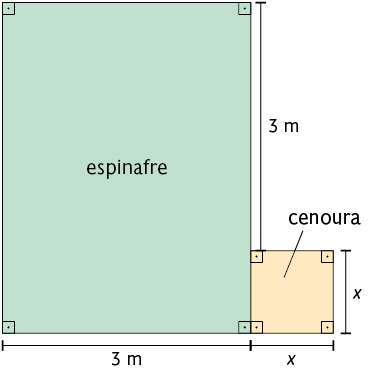
Podemos expressar a medida da área total dessa horta (y) em função de x.
A área destinada para o plantio de cenoura tem o formato de um quadrado cujo comprimento do lado mede x. Calculando a medida da área desse quadrado, temos:
A área destinada ao plantio de espinafre tem o formato de um retângulo cujas dimensões medem e . Calculando a medida da área desse retângulo, temos:
Como queremos obter a medida da área total da horta, adicionamos as medidas obtidas.
Essa sentença é um exemplo de lei de formação de uma função quadrática.
Uma função de variáveis reais definida por , com a, b e c reais e , é chamada função quadrática.
As constantes a, b e c são os coeficientes da função.
Acompanhe alguns exemplos.
- A função definida por é uma função quadrática. Nesse caso, temos , e .
- A função dada por é uma função quadrática. Nesse caso, temos , e .
- A função definida por é uma função quadrática. Nesse caso, temos , e .
Página 177
Agora, determinaremos a medida da área total da horta para , por exemplo. Para isso, substituímos x por 2 na lei de formação obtida.
Portanto, a área total da horta para mede .
Questão 9. Em seu caderno, determine a medida da área dessa horta para:
a) .
b) .
c) .
Atividades
Faça as atividades no caderno.
34. Escreva no caderno a lei de formação de uma função quadrática dada por , sabendo que:
a) , e .
b) , e .
c) , e .
d) , e .
e) , e .
f) , e .
g) , e .
h) , e .
35. Considere a função quadrática de variáveis m e y dada por . Qual é o valor de y quando:
a) ?
b) ?
c) ?
d) ?
e) ?
36. Determine os valores de x na função quadrática dada por , quando .
37. Em cada item, é apresentada a lei de formação de uma função quadrática de variáveis x e y. Para cada uma delas, determine quais valores t não pode assumir.
a)
b)
c)
d)
e)
f)
Atenção!
Para cada fórmula ser de uma função quadrática, o coeficiente de não pode ser nulo.
Página 178
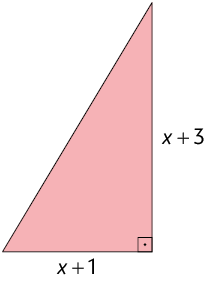
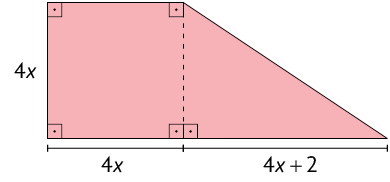
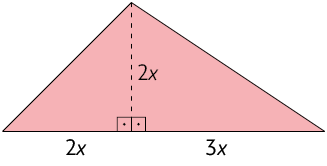
38. Escreva no caderno uma fórmula para representar a medida da área A de cada figura em função de x.

39. Para a realização de um torneio de voleibol, um terreno retangular foi utilizado para a construção da quadra e das demais instalações.
No esquema a seguir, estão representados esse terreno e a região destinada à quadra.
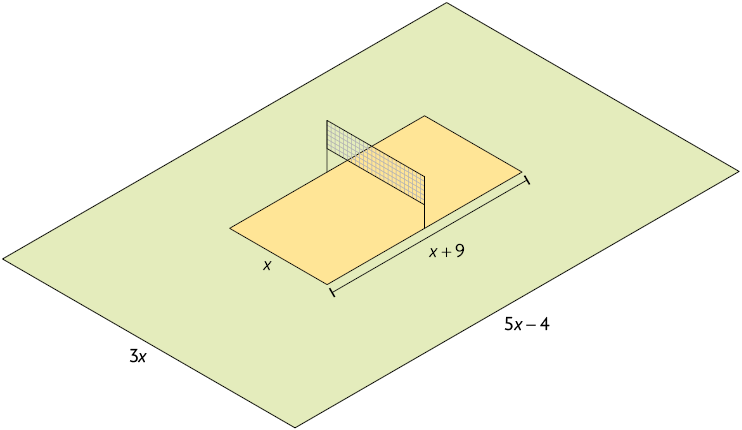
a) Escreva no caderno uma fórmula que expresse:
a medida da área do terreno (y) em função da medida x;
a medida da área da quadra (z) em função da medida x.
b) Qual é a medida da área total do terreno para ? E a medida da área da quadra?
Página 179
40. O custo y, em reais, de
produção de um lote de x peças é dado por . Qual é a diferença
entre o custo de produção de um lote de 1.000 peças
e de um lote de 998 peças?
Atenção!
Use uma calculadora para resolver a atividade 40.
a) R$ 1.210,00
b) R$ 4,20
c) R$ 1.652,00
d) R$ 444,20
e) R$ 4,02
41. Considere o retângulo a seguir.

a) Escreva no caderno uma sentença matemática que expresse a medida da área desse retângulo (y) em função de x.
b) Determine o valor de y para .
42. A medida
da área (y) da figura a seguir é dada em
função de x.
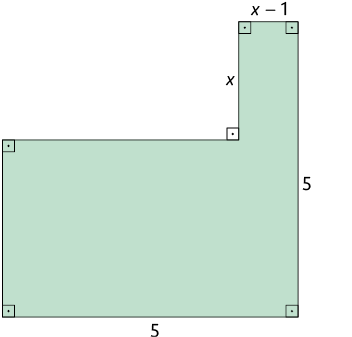
Atenção!
As medidas indicadas na imagem estão em metros.
a) Escreva no caderno a lei de formação dessa função.
b) Determine o valor de y para .
43. Em um pedaço de papel, Armando escreveu a sequência dos números ímpares positivos em ordem crescente.
1, 3, 5, 7, 9, 11, 13, ...
A soma dos n primeiros termos dessa sequência é dada por . A soma dos 3 primeiros termos, por exemplo, é 9, pois .
a) Qual é a soma dos 15 primeiros termos dessa sequência? E dos 50 primeiros?
b) Armando adicionou certa quantidade de termos a essa sequência e obteve 144 como resultado. Quantos termos ele adicionou?
Página 180
Gráfico de uma função quadrática
Estudamos anteriormente os procedimentos de construção do gráfico de uma função afim, que é uma reta. Agora, vamos construir o gráfico de uma função quadrática e, com base nela, identificar algumas de suas características.
O gráfico de uma função quadrática é uma curva chamada parábola.
A parábola tem um eixo de simetria. O ponto em que esse eixo intersecta a parábola é o vértice da parábola.
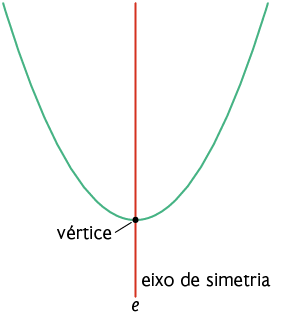
Atenção!
Indicamos o vértice da parábola por .
Considere a função quadrática definida por . Para construir seu gráfico, podemos realizar os seguintes passos.
1º. Atribuímos alguns valores para x.
2º. Substituímos os valores de x na lei de formação da função e determinamos os valores correspondentes de y. Determinamos, assim, alguns pares ordenados .
3º. Para cada par ordenado obtido, representamos um ponto no plano cartesiano.
|
0 |
||
|
1 |
||
|
2 |
Quadro referente aos passos 1 e 2.
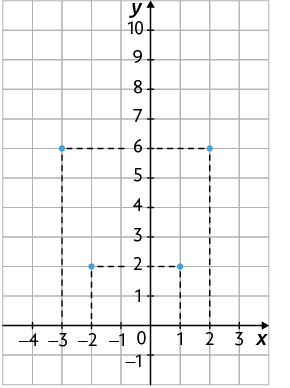
Página 181
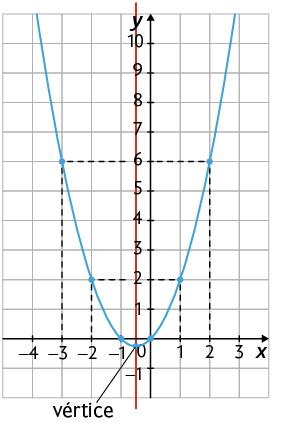
4º. Como x é um número real, podemos atribuir infinitos valores para x, obtendo, para cada um deles, um único valor de y. Assim, há infinitos pontos entre os já marcados no plano cartesiano. O gráfico da função é o conjunto de todos os pontos , com x real e , conforme apresentado a seguir.

Concavidade da parábola
Conhecendo algumas características do gráfico da função quadrática, podemos construí-lo com mais precisão.
O coeficiente a, por exemplo, determina se a parábola tem concavidade voltada para cima ou para baixo.
Se o coeficiente a é positivo , a parábola tem concavidade voltada para cima.

Se o coeficiente a é negativo , a parábola tem concavidade voltada para baixo.
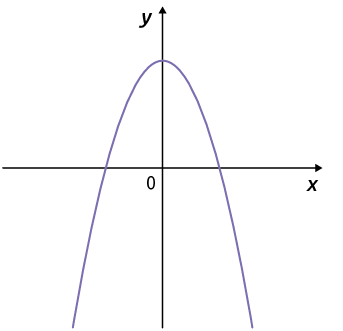
Na próxima página, apresentaremos o gráfico das funções quadráticas definidas por e .
Página 182
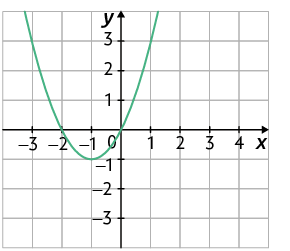
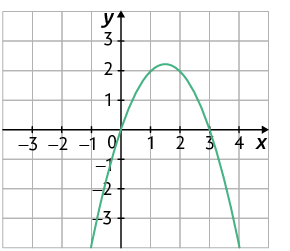
Note que o gráfico da função definida por:
- tem concavidade voltada para cima, pois o coeficiente a é positivo ;
- tem concavidade voltada para baixo, pois o coeficiente a é negativo .
Instrumentos e softwares
Gráfico de funções no GeoGebra
Com o GeoGebra, podemos construir o gráfico de funções.
Vamos construir, por exemplo, o gráfico da função quadrática definida por . Para isso, no campo Entrada..., digite a lei de formação da função e, em seguida, tecle Enter. O gráfico da função será exibido na Janela de Visualização.
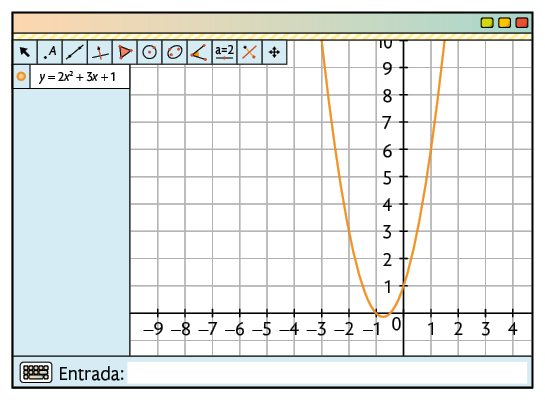
Atenção!
Para digitar , escreva x^2.
Atividades
Faça as atividades no caderno.
44. Escreva no caderno se o gráfico das funções cujas leis de formação são apresentadas a seguir têm concavidade voltada para cima ou para baixo.
a)
b)
c)
d)
e)
f)
Página 183
45. Em uma partida de futebol, Gabriel fez um lançamento no qual a trajetória da bola descreveu uma parábola. Essa trajetória tem a medida de sua altura h (em metros) dada em função da medida do tempo t (em segundos) decorrido após o chute.
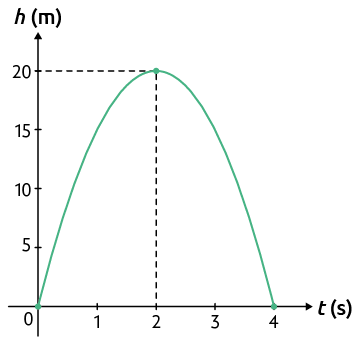
Analise a trajetória da bola e responda às questões.
a) Qual foi a medida da altura máxima atingida pela bola?
b) Quantos segundos depois do lançamento a bola tocou o solo novamente?
c) Sabendo que a trajetória da bola pode ser descrita por , determine a medida da altura atingida pela bola, após o lançamento, depois de:
I. .
II. .
III. .
d) Em quantos segundos após o lançamento a bola atingiu a altura máxima?
46. Considere os gráficos a seguir.
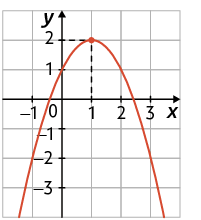
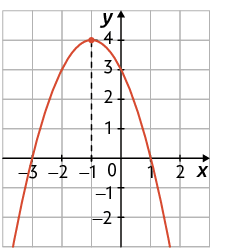
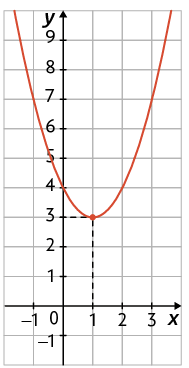
Agora, relacione os gráficos à lei de formação da função que eles representam. Para isso, escreva o algarismo romano e a letra correspondentes.
A.
B.
C.
47. Considere
as funções quadráticas dadas por e .
a) No GeoGebra, construa em um mesmo plano cartesiano os gráficos dessas funções.
b) A parábola de qual dessas funções tem concavidade voltada para baixo?
Página 184
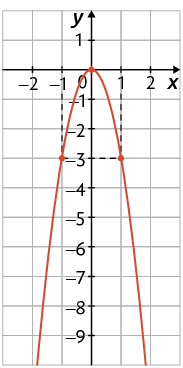
48. Em cada item está representado o gráfico de uma função quadrática. Qual é o sinal do coeficiente a dessas funções?
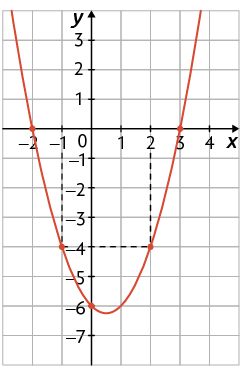
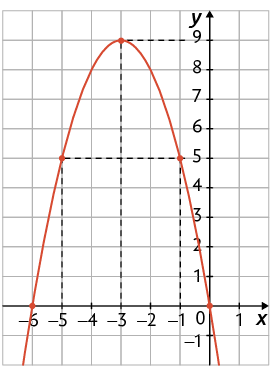
49. Considere as funções quadráticas, de variáveis x e y, cujas leis de formação estão apresentadas.
a)
b)
c)
d)
e)
f)
g)
Para quais valores de t o gráfico de cada uma dessas funções tem concavidade voltada para cima? E para baixo?
50. Construa o gráfico da função quadrática definida por:
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
i) .
j) .
k) .
l) .
51. Com o GeoGebra, construa o gráfico
da
função quadrática definida por:
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
i) .
j) .
k) .
l) .
Página 185
Interseção com o eixo y
O gráfico de uma função quadrática definida por intersecta o eixo y quando . Nesse caso, para determinar as coordenadas do ponto de interseção com esse eixo, basta substituir x por 0 na lei de formação da função, ou seja:
Portanto, o gráfico de uma função quadrática intersecta o eixo y no ponto .
Acompanhe alguns exemplos.
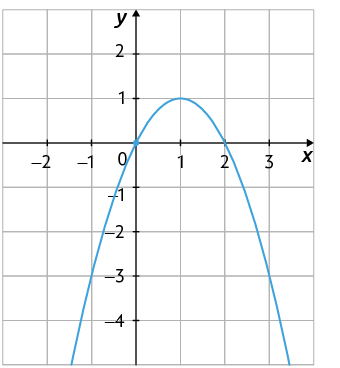
O gráfico da função quadrática definida por intersecta o eixo y no ponto , pois .
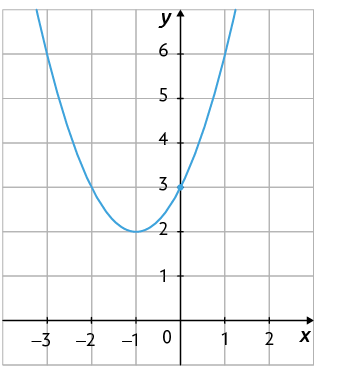
O gráfico da função quadrática definida por intersecta o eixo y no ponto , pois .
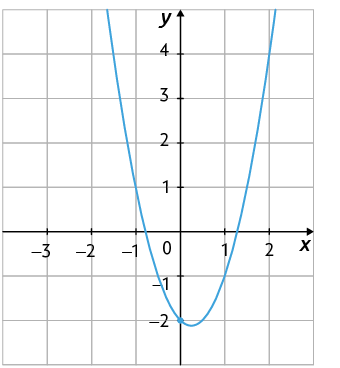
O gráfico da função quadrática definida por intersecta o eixo y no ponto , pois .
Atividades
Faça as atividades no caderno.
52. Analise os gráficos das funções quadráticas dadas por e .
Qual dos itens apresenta informações verdadeiras?

a) e
b) e
c) e
Página 186
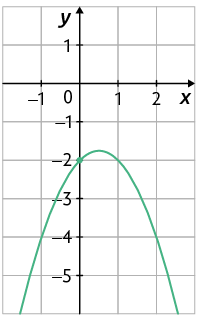
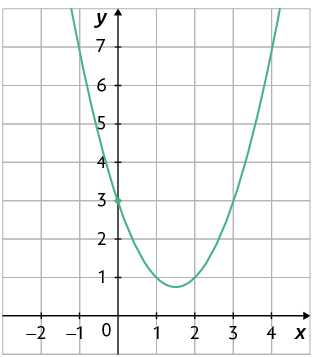
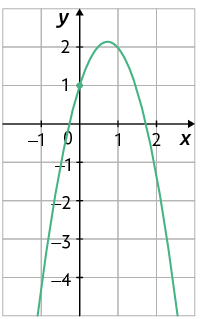
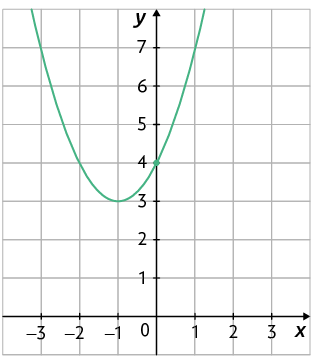
53. Considere as funções quadráticas definidas pelas leis de formação a seguir.
A.
B.
C.
D.
a) Quais dessas funções têm o gráfico com a concavidade voltada para cima?
b) Quais são as coordenadas do ponto em que o gráfico de cada uma dessas funções intersecta o eixo y?
c) Relacione no caderno cada função a um dos gráficos a seguir.
54. Qual é o ponto de interseção entre o eixo y e o gráfico da função quadrática definida por:
a) ?
b) ?
c) ?
d) ?
e) ?
f) ?
Página 187
Interseção com o eixo x e zeros da função quadrática
O gráfico de uma função quadrática, na forma , intersecta o eixo x nos pontos em que , ou seja, quando:
A equação é uma equação do 2º grau com incógnita x e coeficientes reais a, b e c, tal que . As raízes reais dessa equação são:
com .
Desse modo, o gráfico da função quadrática definida por intersecta o eixo x nos pontos e .
Os zeros de uma função quadrática são as abscissas dos pontos de interseção de seu gráfico com o eixo x.
Considere, por exemplo, a função quadrática definida por . Determinaremos as coordenadas dos pontos em que o gráfico dessa função intersecta o eixo x. Para isso, resolvemos a equação .
Atenção!
Note que , e .
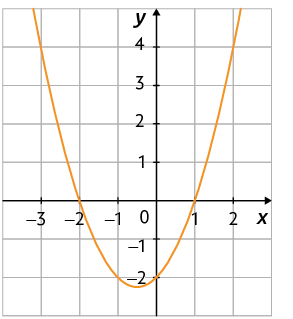
Portanto, o gráfico dessa função intersecta o eixo x nos pontos e . Então, e 1 são os zeros dessa função.
Página 188
Na unidade 5 deste livro, você viu que uma equação do 2º grau pode ter duas raízes reais diferentes, ter duas raízes reais iguais ou não ter raízes reais, dependendo do valor de seu discriminante. Assim, como os zeros de uma função quadrática são as raízes de uma equação do 2º grau, essa função também pode ter dois zeros reais diferentes, ter dois zeros reais iguais ou não ter zeros reais.
- Se é um número positivo, ou seja, , a parábola intersecta o eixo x em dois pontos distintos e a função tem dois zeros reais diferentes.
- Se é igual a zero, ou seja, , a parábola intersecta o eixo x em um único ponto e a função tem dois zeros reais iguais.
- Se é um número negativo, ou seja, , a parábola não intersecta o eixo x e a função não tem zeros reais.
De acordo com essas características, podemos organizar o seguinte quadro.

|

|

|
|

|

|
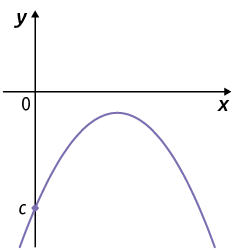
|
Acompanhe mais dois exemplos de funções quadráticas: a primeira não tem zeros reais e a segunda tem dois zeros reais iguais.
Exemplo 1. Função quadrática definida por . Nesse caso, temos:
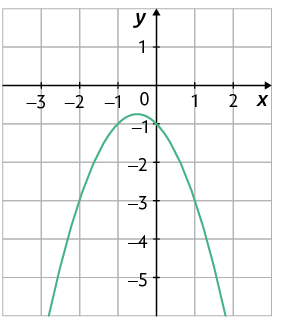
Portanto, a parábola não intersecta o eixo x.
Página 189
Exemplo 2. Função quadrática definida por . Nesse caso, temos:
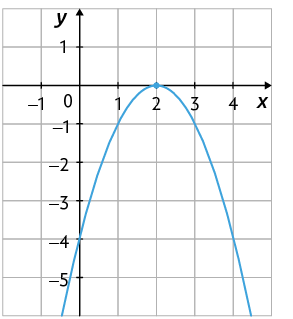
Portanto, a parábola intersecta o eixo x em um único ponto.
Conhecendo algumas informações do gráfico de uma função quadrática, podemos determinar sua lei de formação. Analise, por exemplo, as informações a seguir.
O gráfico da função quadrática intersecta o eixo y no ponto e o eixo x nos pontos e .
Analisando essas informações, concluímos que:
- , pois a interseção entre o gráfico e o eixo y ocorre em ;
- e são os zeros da função, pois a interseção entre o gráfico e o eixo x ocorre em e .
I. Substituindo x por 1 e c por 3 na equação , obtemos:
II. Agora, substituindo x por 3 e c por 3 na mesma equação, obtemos:
Com as equações obtidas em I e II, escrevemos e resolvemos o seguinte sistema de equações, obtendo, assim, os valores de a e b.
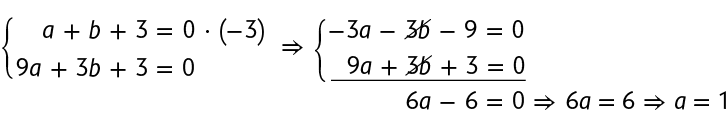
Substituindo a por 1 em , obtemos o valor de b.
Logo, , e . Portanto, a lei de formação dessa função é .
Página 190
Atividades
Faça as atividades no caderno.
55. Determine, se existirem, os zeros da função quadrática definida por:
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
i) .
j) .
k) .
56. Considere o gráfico da função quadrática apresentado a seguir.
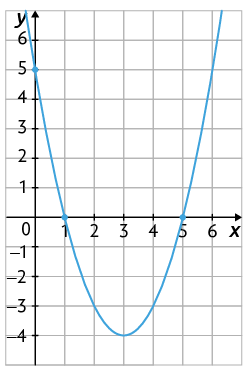
a) O coeficiente a dessa função é maior ou menor do que 0?
b) Qual é o coeficiente c dessa função?
c) Quais são os zeros dessa função?
d) Quais são as coordenadas dos pontos em que a parábola intersecta o eixo x?
e) Quais são as coordenadas dos pontos em que a parábola intersecta o eixo y?
57. Escreva no caderno se cada função cujas leis de formação são apresentadas a seguir tem dois zeros reais distintos, dois zeros reais iguais ou não tem zeros reais.
a)
b)
c)
d)
e)
f)
58. Analise o gráfico da função quadrática apresentado em cada um dos itens. Em seguida, escreva no caderno a lei de formação dessas funções.
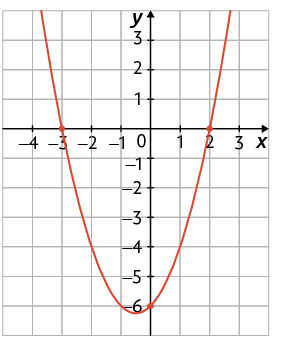
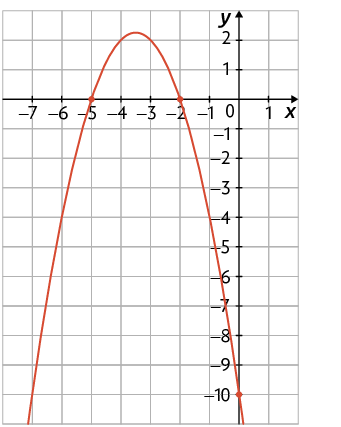
Página 191
Coordenadas do vértice da parábola
Como estudamos anteriormente, a parábola tem um eixo de simetria e seu vértice é o ponto em que esse eixo intersecta a parábola.
No gráfico da função definida por , estão destacados alguns pontos. Note que e são pontos do gráfico da função que têm ordenadas iguais. Quando isso ocorre, dizemos que os pontos são simétricos em relação ao eixo de simetria da parábola.
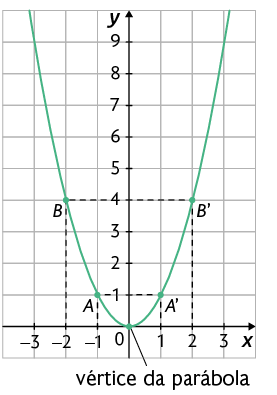
Questão 10. Os pontos B e
B' são simétricos em relação ao eixo de simetria da
parábola? Justifique sua resposta.
Como o vértice da parábola pertence ao eixo de simetria, sua abscissa pode ser calculada pela média aritmética das abscissas de quaisquer dois pontos simétricos da parábola em relação ao eixo de simetria. No caso de A e A', temos:
Para obter a ordenada do vértice da parábola, substituímos x por 0 na lei de formação da função. Assim:
Portanto, o vértice da parábola é .
Considerando uma função quadrática definida por , podemos determinar algebricamente a abscissa do vértice da parábola com base em seus coeficientes. Para isso, consideraremos os pontos e pertencentes à parábola.
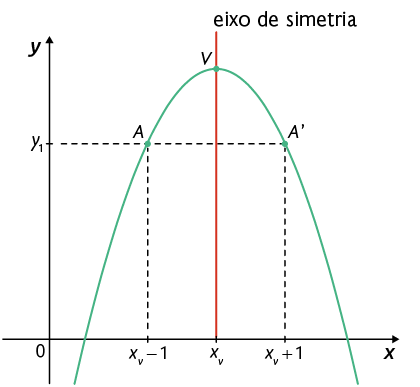
Atenção!
Note que os pontos A e A' são simétricos em relação ao eixo de simetria da parábola.
Página 192
Substituindo x por e por na lei de formação da função, temos:
Assim:
Desenvolvendo a equação, obtemos:
Para obter a ordenada do vértice, substituímos x por na lei de formação da função. Assim:
O vértice da parábola que representa a função quadrática definida por é:
, em que .
Agora, determinaremos o vértice da parábola correspondente à função quadrática definida por . Para isso, fazemos:
Atenção!
Note que , e .
Portanto, o vértice dessa parábola é .
Página 193
Valor máximo e valor mínimo da função quadrática
Toda função quadrática assume um valor máximo ou um valor mínimo, dependendo do coeficiente a de sua lei de formação.
Considere o gráfico da função quadrática definida por .
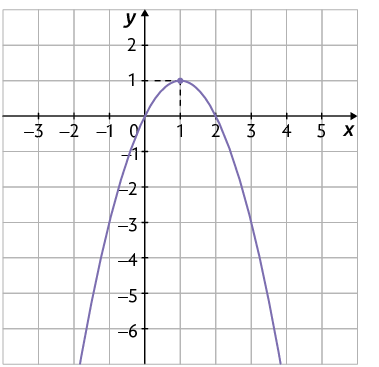
Como a é negativo, o vértice da parábola é ponto de máximo, ou seja, é o ponto em que essa função assume valor máximo. Nesse exemplo, o coeficiente a é e o vértice da parábola é . Então, é o ponto de máximo do gráfico da função e é o valor máximo da função.
Agora, considere o gráfico da função quadrática definida por .
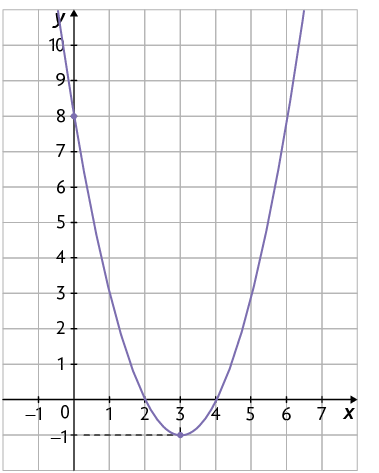
Como a é positivo, o vértice da parábola é ponto de mínimo, ou seja, é o ponto em que essa função assume valor mínimo. Nesse exemplo, o coeficiente a é 1 e o vértice da parábola é . Então, é ponto de mínimo do gráfico da função e é o valor mínimo da função.
Página 194
Considere a função quadrática definida por .
Quando a é negativo , a parábola que representa a função tem concavidade voltada para baixo. Nesse caso, é ponto de máximo do gráfico e é o valor máximo da função.
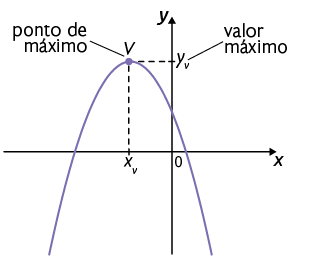
Quando a é positivo , a parábola que representa a função tem concavidade voltada para cima. Nesse caso, é ponto de mínimo do gráfico e é o valor mínimo da função.

Atividades
Faça as atividades no caderno.
59. Determine as coordenadas do vértice da parábola correspondente à função quadrática definida por:
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
60. Considere as funções quadráticas cujas leis de formação são apresentadas a seguir.
a)
b)
c)
d)
e)
f)
Em seu caderno, escreva se o gráfico dessas funções tem ponto de máximo ou ponto de mínimo.
Página 195
61. Analise o gráfico da função quadrática dada por .
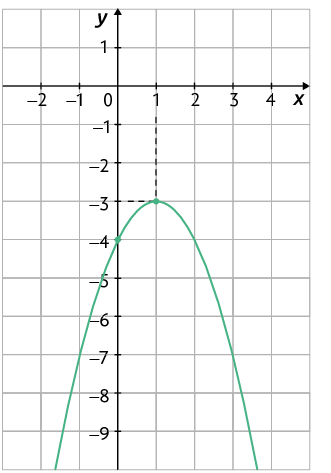
a) Qual é o sinal do coeficiente a da fórmula dessa função? Justifique sua resposta.
b) Quais são as coordenadas do ponto em que o gráfico dessa função intersecta o eixo y?
c) O gráfico dessa função intersecta o eixo x?
d) Quais são as coordenadas do vértice da parábola?
e) O vértice dessa parábola é o ponto de máximo ou de mínimo?
f) Qual é a lei de formação dessa função?
62. O gráfico da função quadrática cuja lei de formação está apresentada a seguir, de variáveis x e y, tem ponto de máximo .
a) Qual é o valor de n?
b) Construa no caderno o gráfico dessa função.
63. Mário tem de tela e quer cercar um terreno de formato retangular usando toda a tela. Para cercar esse terreno, ele vai aproveitar um muro que já está construído, conforme apresentado a seguir.
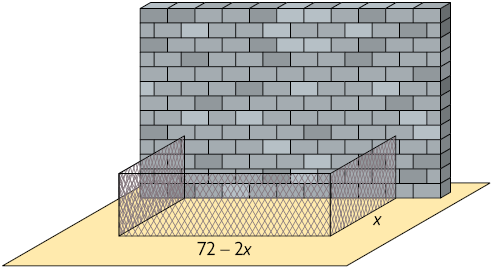
a) Escreva no caderno a lei de formação da função que expressa a medida da área do terreno cercado (y) em função de x.
b) Construa no caderno o gráfico da função cuja lei de formação você escreveu no item anterior.
c) Qual é a medida da área máxima que Mário pode cercar com essa tela?
d) Quais são as medidas do comprimento dos lados do terreno que tem essa medida de área máxima?
64. Pedro lançou um avião de papel, feito com dobradura, cuja trajetória pode ser expressa por , , em que h é a medida da altura (em metros) e t é a medida do tempo (em segundos).
a) Qual foi a medida da altura máxima atingida pelo avião de papel nesse lançamento?
b) Quantos segundos após o lançamento o avião de papel atingiu o chão?
c) Após quantos segundos do lançamento o avião de papel atingiu a altura de medida máxima?
Página 196
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. O quadro apresenta o consumo de energia elétrica de um computador de acordo com a quantidade de horas de uso.
|
Medida do tempo (em horas) |
Consumo (em ) |
|---|---|
|
1 |
0,3 |
|
2 |
0,6 |
|
3 |
0,9 |
|
4 |
1,2 |
|
5 |
1,5 |
a) Em uma folha de papel avulsa, escreva uma fórmula que represente o consumo (C), em quilowatt-hora, em função da quantidade de horas de uso (t).
b) Se uma pessoa utilizar esse computador, em média, por dia, durante 30 dias, quantos quilowatts-hora serão consumidos?
2. Uma caixa-d'água cuja capacidade mede está com de água. Em certo momento, passa-se a despejar de água por minuto nela.
a) Escreva no caderno uma fórmula que relacione a quantidade de água na caixa-d'água, em litros, em função da medida do tempo, em minutos, do momento em que a água passou a ser despejada em diante.
Indique a quantidade de água por y e a medida do tempo por x.
b) Após quantos minutos a caixa-d'água estará com de água? E com ?
c) Do momento em que a água passou a ser despejada em diante, qual é a medida de tempo necessária para que a caixa-d'água fique com ?
3. Considere o gráfico da função quadrática apresentado a seguir.
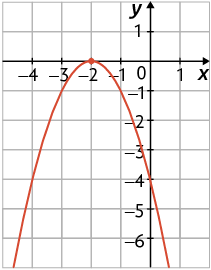
a) Quais são as coordenadas do vértice desse gráfico?
b) Quais são os zeros da função representada por esse gráfico?
c) Qual é o coeficiente c da função representada por esse gráfico?
4. As medidas das dimensões de um retângulo, em centímetros, são dadas por e .
a) Determine o valor de x de modo que a medida da área do retângulo seja máxima.
b) De acordo com o valor de x obtido no item a, determine as medidas das dimensões do retângulo.
5. Determine para quais valores de m o gráfico da função dada por intersecta o eixo x em:
a) dois pontos distintos;
b) um único ponto;
c) nenhum ponto.