Página 197

UNIDADE

Circunferência, vistas e perspectiva

Fotografia de uma torre de telecomunicação. A torre tem um formato cilíndrico. O último andar possui um diâmetro maior que os demais andares. Há antenas que lembram círculos, distribuídas em alguns andares. Por toda a extensão da superfície, na parte debaixo da foto, há uma cidade e há um lago ao fundo e à direita. — Torre de telecomunicação com antenas cujo formato do contorno lembra uma circunferência, na cidade de Curitiba (PR), em 2022.

Agora vamos estudar...

circunferência;
medida do comprimento da circunferência;
ângulos em uma circunferência;
polígonos inscritos em uma circunferência e circunscritos a ela;
vistas ortogonais;
representação em perspectiva.

Página 198

Estudando a circunferência

Em anos anteriores, você provavelmente já estudou assuntos relacionados à circunferência. Neste capítulo, vamos retomá-los e aprofundar alguns deles. Analise a seguinte situação.

Mateus construiu um poço circular cujo raio mede $1 metro$ . Antes de iniciar a escavação, ele desenhou uma circunferência no terreno para demarcar o espaço a ser escavado. Para isso, ele:

fixou uma estaca no centro do local onde o poço seria construído;
amarrou uma das pontas de um pedaço de barbante em uma vareta reta e a outra ponta na estaca, de modo que, quando o barbante estivesse esticado, a distância entre a estaca e a vareta medisse $1 metro$ ;
mantendo a vareta perpendicular ao solo e o barbante esticado, girou a vareta ao redor da estaca traçando a circunferência.

Nessa situação, Mateus desenhou uma circunferência. A estaca fixa é o centro e a medida do comprimento do barbante (desconsiderando as partes amarradas na estaca e na vareta) corresponde à medida do comprimento do raio dessa circunferência.

Ilustração de um menino agachado. O menino segura uma vareta com a ponta sobre uma circunferência desenhada no chão. A vareta está amarrada a um barbante que está esticado e preso a uma estaca posicionada no centro dessa circunferência. O menino está do lado de fora da circunferência e também fora e mais ao fundo há uma pá.

Circunferência é a figura geométrica plana formada por todos os pontos de um plano que estão a uma mesma medida de distância de um ponto fixo. Esse ponto fixo é o centro da circunferência.

Ilustração de uma circunferência de centro O. Há um segmento de reta com os pontos A e B na circunferência, passando por O. Há um segmento de reta O E, com o ponto E na circunferência. Há um segmento de reta C D com os pontos C e D na circunferência.

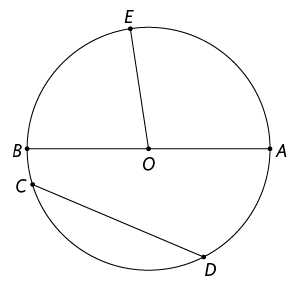
Um raio da circunferência é qualquer segmento de reta que une o centro a um de seus pontos. Na figura geométrica anterior, por exemplo, os segmentos de reta $A O$ , $O B$ e $O E$ são raios.
Uma corda da circunferência é qualquer segmento de reta que une dois pontos distintos dela. Os segmentos de reta $A B$ e $C D$ , na figura geométrica apresentada, são exemplos de corda.
Um diâmetro da circunferência é qualquer corda que passa pelo centro. Na figura geométrica anterior, o segmento de reta $A B$ é um exemplo de diâmetro.

Note que a medida do comprimento do diâmetro é igual ao dobro da medida do comprimento do raio.

Página 199

Atividades

Faça as atividades no caderno.

1. Na circunferência de centro $O$ a seguir estão traçadas algumas de suas cordas.

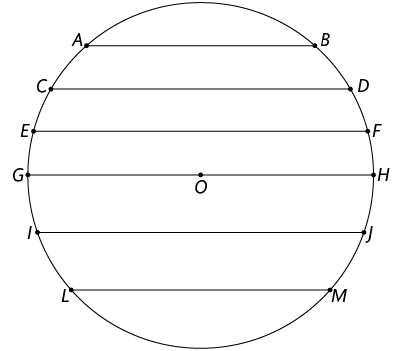
Ilustração de uma circunferência de centro O. Há seis segmentos horizontais e paralelos, com as extremidades na circunferência. De cima para baixo, os segmentos são nessa ordem: segmento A B; segmento C D; segmento E F; segmento G H, que passa pelo centro O; segmento I J; segmento L M.

a) Qual dessas cordas tem a maior medida de comprimento?

b) Se traçarmos uma corda $\overline{N P}$ que passe pelo centro $O$ , ela terá a mesma medida de comprimento de qual das cordas?

c) Imagine o segmento de reta $O B$ traçado nessa circunferência. Ele é uma corda, um diâmetro ou um raio dessa circunferência?

2. A circunferência de centro $O$ a seguir está representada em um plano cartesiano.

Ilustração de uma circunferência de centro O representada em um plano cartesiano em uma malha quadriculada. Está indicado um ponto O de coordenada 1 e menos 1. A circunferência passa pelas coordenadas 1 e 3; 5 e menos 1; 1 e menos 5; menos 3 e menos 1. Está indicado que cada quadradinho da malha tem comprimento, u, e largura, u.

a) Quais são as coordenadas do centro dessa circunferência?

b) Determine a medida do comprimento do raio $(r)$ e a medida do comprimento do diâmetro $(d)$ da circunferência. Para isso, considere como unidade $(u)$ a medida de comprimento do lado de cada quadrado da malha.

c) Qual é a medida da distância entre os pontos $coordenada 1 e 3$ e $coordenada 1 e menos 5$ ?

3. Com um compasso, desenhe no caderno uma circunferência de:

a) centro $B$ e raio com o comprimento medindo $2 centímetros$ ;

b) centro $O$ e diâmetro com o comprimento medindo $5 centímetros$ ;

c) centro $A$ cuja maior corda possível tenha comprimento medindo $3 centímetros$ .

4. Determine a medida do comprimento do raio da circunferência a seguir, considerando que:

$A B C O$ é um retângulo;

o comprimento do segmento de reta $A C$ mede $3 vírgula 2 metros$ .

Atenção!

O segmento de reta $A C$ é uma das diagonais do retângulo $A B C O$ .

Ilustração de uma circunferência de centro O. Pelo centro O passam duas retas, uma vertical e uma horizontal. Há um ponto A interno à circunferência e que está sobre a reta vertical. Também há um ponto C interno à circunferência e que está sobre a reta horizontal. Há um ponto B na circunferência. É formado um retângulo, A, B, C, O, que está em destaque. O segmento, A C, é a diagonal desse retângulo.

Página 200

Posições relativas entre retas e circunferência

Com régua e compasso, Rosana construiu uma circunferência de centro O e representou três retas em uma malha quadriculada, conforme imagem a seguir.

Ilustração de uma malha quadriculada com três retas e uma circunferência. A malha tem dimensão de 16 quadrados na horizontal e 15 na vertical. A circunferência tem centro denominado O e tem 10 quadrados de diâmetro. A reta r não toca a circunferência. A reta s cruza a circunferência em dois pontos. A reta t toca a circunferência em um ponto.

No desenho, cada reta está posicionada de maneira diferente em relação à circunferência:

a reta $t$ tem apenas um ponto comum com a circunferência;
a reta $s$ tem dois pontos comuns com a circunferência;
a reta $r$ não tem ponto comum com a circunferência.

Quando traçamos uma reta e uma circunferência em um mesmo plano, podem ocorrer três casos.

Caso 1

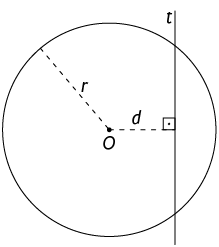
A reta e a circunferência têm apenas um ponto comum. Nesse caso, dizemos que a reta é tangente à circunferência e o ponto comum a elas é o ponto de tangência.

A medida da distância $(d)$ entre a reta tangente e o centro da circunferência O é igual à medida do comprimento do raio (r).

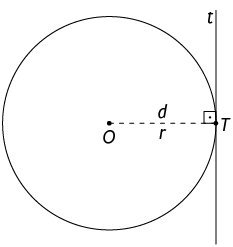
Ilustração de uma circunferência de centro O e raio r. Há uma reta t minúsculo traçada tocando a circunferência em um único ponto denominado T. A medida da distância do centro O ao ponto T está indicada como d. O raio r, e a distância, d, estão indicados em um mesmo traçado. Está indicado um ângulo reto formado com a reta t minúsculo e a traçado da distância d.

$d = r$

Caso 2

A reta e a circunferência têm dois pontos comuns. Nesse caso, dizemos que a reta é secante à circunferência.

A medida da distância $(d)$ entre a reta secante e o centro da circunferência O é menor do que a medida do comprimento do raio (r).

Ilustração de uma circunferência de centro O e raio r. Há uma reta t traçada cruzando com a circunferência em dois pontos. Está traçada a distância d, entre o ponto O e a reta t. Há um ângulo reto formado com a reta t e a traçado da distância d.

$d < r$

Caso 3

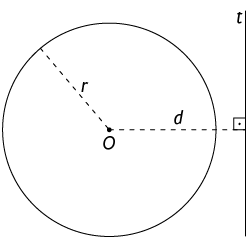
A reta e a circunferência não têm ponto comum. Nesse caso, dizemos que a reta é externa à circunferência.

A medida da distância $(d)$ entre a reta externa e o centro da circunferência O é maior do que a medida do comprimento do raio (r).

Ilustração de uma circunferência de centro O e raio r. Há uma reta t traçada ao lado da circunferência que não cruza em nenhum ponto. Está traçada a distância d entre o ponto O e a reta t. Há um ângulo reto formado com a reta t e a traçado da distância d.

$d > r$

Toda reta tangente a uma circunferência é perpendicular ao raio no ponto de tangência.

Página 201

Atividades

Faça as atividades no caderno.

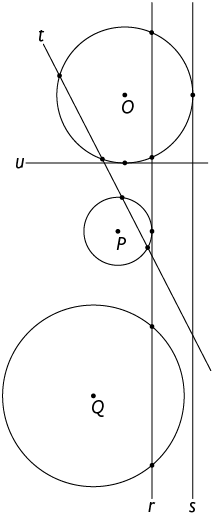
5. Nas imagens estão indicados os pontos de interseção entre as retas r, s, t e u e as circunferências de centro O, P e Q. Determine as posições relativas entre essas retas e as circunferências.

Ilustração de 3 circunferências de centros O, P, Q, dispostas respectivamente uma abaixo da outra e 4 retas denominadas r, s, t, u. As circunferências não possuem pontos em comum entre si. A reta r cruza a circunferência de centro O em dois pontos, a circunferência de centro P em um ponto e a circunferência de centro Q em dois pontos. A reta s toca a circunferência de centro O em um ponto. A reta, u, toca a circunferência de centro O em um ponto. A reta t cruza a circunferência de centro O em dois pontos e a circunferência de centro P em dois pontos.

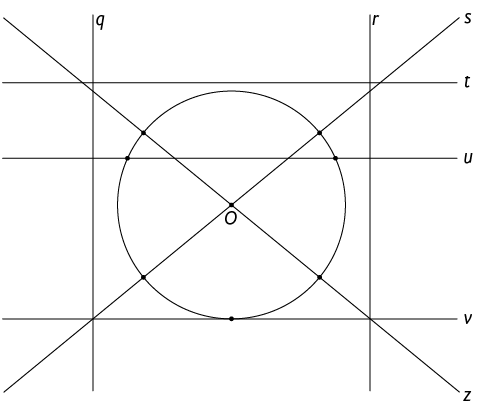
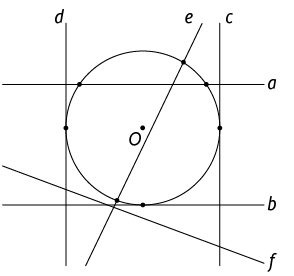
6. Na imagem a seguir, estão indicados os pontos de interseção entre as retas e a circunferência de centro O. Identifique e escreva em seu caderno as retas:

a) tangentes a essa circunferência;

b) secantes a essa circunferência;

c) externas a essa circunferência.

Ilustração de uma circunferência de centro O e sete retas, denominadas q, r, s, t, u, v, z. As retas q e r são verticais e não cruzam a circunferência. As retas t, u e v são horizontais, com a reta t não cruzando a circunferência, a reta u cruzando a circunferência em dois pontos e a reta v cruzando a circunferência em um ponto. As retas s e z passam pelo centro O se cruzando em forma de X.

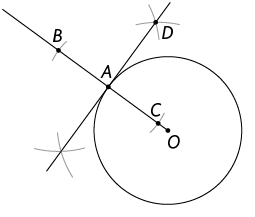
7. Analise os passos que Elza realizou para traçar uma reta tangente a uma circunferência.

1º. Elza desenhou uma circunferência de centro O, marcou um ponto A sobre ela e prolongou o raio $\overline{O A}$ . Depois, com a ponta seca do compasso em A e com abertura menor do que a medida do comprimento do raio $\overline{O A}$ , ela determinou os pontos B e C.

Ilustração de uma circunferência de centro O e uma semirreta que origina do centro O. No cruzamento da semirreta com a circunferência há um ponto A. Há um ponto B sobre a semirreta, externo a circunferência, e um ponto C, sobre a semirreta e interna a circunferência. Sobre os pontos B e C há um pequeno traço curvo.

2º. Determinou a mediatriz do segmento BC e obteve o ponto D. Por fim, traçou a reta que passa pelos pontos A e D, que é tangente à circunferência de centro O no ponto A.

Ilustração da mesma circunferência de centro O da ilustração anterior, permanecendo os mesmos pontos e marcações. Há uma reta que passa pelo ponto A, tangente à circunferência. Há um ponto D sobre essa reta, com a marcação de dois riscos em forma de X, sobre esse ponto. Há uma mesma marcação desses dois riscos em forma de X, cruzando essa reta, posicionados de forma simétrica ao ponto D em relação ao ponto A.

a) Assim como Elza, desenhe em seu caderno uma circunferência de centro $O$ e trace uma reta $t$ tangente a ela. Em seguida, desenhe uma reta $r$ externa e uma reta $s$ secante a essa circunferência.

b) Compare o desenho que você fez com o de um colega. Verifiquem o que eles têm em comum e suas diferenças.

Versão adaptada acessível

a) Junte-se a um colega e, assim como Elza, desenhem uma circunferência de centro O e tracem uma reta t tangente a ela. Em seguida, desenhem uma reta r externa e uma reta s secante a essa circunferência.

b) Comparem o desenho que vocês fizeram com o de outra dupla. Verifiquem o que eles têm em comum e suas diferenças.

Página 202

Posições relativas entre duas circunferências

No tópico anterior, Rosana desenhou em uma malha quadriculada uma circunferência e representou três retas, cada uma posicionada de maneira diferente em relação a ela, ou seja, uma reta tangente, uma secante e uma externa à circunferência.

Agora, utilizando o compasso, ela traçou em uma malha quadriculada algumas circunferências, conforme a imagem apresentada.

Ilustração de uma malha quadriculada com sete circunferências. A malha tem dimensão de 30 quadrados na horizontal e 20 na vertical. Cada circunferência está indicada com centros A, B, C, D, E, F, G, respectivamente.

Nesse desenho, algumas circunferências têm pontos comuns.

As circunferências de centros $A$ e $B$ têm dois pontos comuns.
As circunferências de centros $A$ e $D$ e de centros $D$ e $C$ têm apenas um ponto comum.

Além disso, nesta construção, alguns pares de circunferências não têm ponto comum.

A circunferência de centro $E$ é interna à de centro $D$ , e ambas não têm ponto comum.
As circunferências de centros $D$ e $B$ não têm ponto comum, e uma é externa à outra.
As circunferências de centros $F$ e $G$ , cujos centros são coincidentes, são internas e não têm ponto comum.

Quando traçamos duas circunferências em um mesmo plano, elas podem ou não ter pontos comuns.

Caso 1

Quando as circunferências têm um único ponto comum, dizemos que elas são tangentes. Nas circunferências tangentes, os dois centros e o ponto de tangência são colineares, ou seja, pertencem a uma mesma reta.

As circunferências podem se tangenciar externa ou internamente.

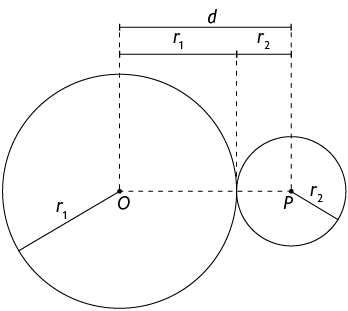
Tangentes externas

Nas circunferências tangentes externas, temos a relação a seguir.

$d igual a abre parênteses r com índice 1 mais r com índice 2 fecha parênteses$

Ilustração de duas circunferências lado a lado de centros O e P. As circunferências se cruzam em apenas um ponto. A circunferência de centro O tem raio r com índice 1 e a circunferência de centro P tem raio r com índice 2. Está indicada a distância d entre os dois centros das circunferências e indicado que r com índice 1 mais r com índice 2 tem a mesma medida de comprimento d.

Tangentes internas

Nas circunferências tangentes internas, temos a relação a seguir.

$d igual a abre parênteses r com índice 1 menos r com índice 2 fecha parênteses$

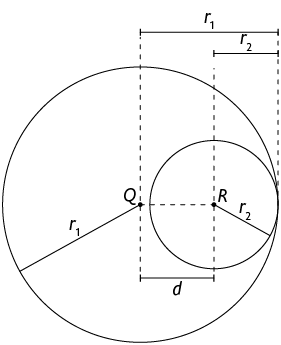
Ilustração de duas circunferências de centros Q e R. As circunferências se cruzam em um ponto e a circunferência de centro R é interna a de centro Q. A circunferência de centro R tem diâmetro menor que o raio da circunferência de centro Q. A circunferência de centro Q tem raio r com índice 1 e a circunferência de centro R tem raio r com índice 2. Está traçado a distância d entre os dois centros das circunferências. Estão indicadas as medidas de comprimento de r com índice 1 e r com índice 2.

Página 203

Caso 2

Quando as circunferências têm dois pontos comuns, dizemos que elas são secantes.

Nas circunferências secantes, temos a relação a seguir.

$abre parênteses r com índice 1 menos r com índice 2 fecha parênteses menor do que d menor do que abre parênteses r com índice 1 mais r com índice 2 fecha parênteses$

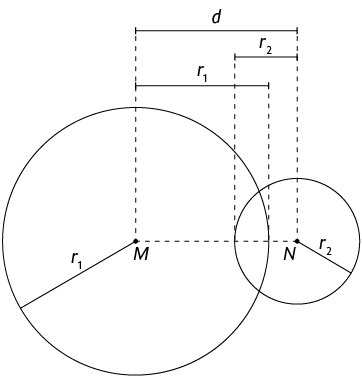
Ilustração de duas circunferências de centros M e N. As circunferências têm dois pontos em comum. A circunferência de centro M tem raio r com índice 1 e a circunferência de centro N tem raio r com índice 2. Está traçado a distância d entre os dois centros das circunferências. Estão indicadas as medidas de comprimento de r com índice 1 e r com índice 2.

Caso 3

Quando as circunferências não têm ponto comum, elas podem ser internas ou externas uma da outra.

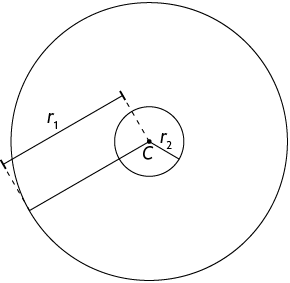
Internas

Nas circunferências internas, temos a relação a seguir.

$d menor do que abre parênteses r com índice 1 menos r com índice 2 fecha parênteses$

Ilustração de duas circunferências de centros A e B. As circunferências não tem ponto em comum e a circunferência de centro B é interna a de centro A. A circunferência de centro B tem diâmetro menor que o raio da circunferência de centro A. A circunferência de centro A tem raio r com índice 1 e a circunferência de centro B tem raio r com índice 2. Está traçado a distância d entre os dois centros das circunferências. Estão indicadas as medidas de comprimento de r com índice 1 e r com índice 2.

Quando duas circunferências internas têm centros coincidentes, dizemos que elas são concêntricas. Nesse caso, a medida da distância $(d)$ entre os centros das circunferências é igual a zero.

$d igual a 0$

Ilustração de duas circunferências de mesmo centro C. Estão indicados os dois raios respectivos sendo um com r índice 1 e outro com r índice 2. O raio r com índice 2 é menor que o raio r com índice 1.

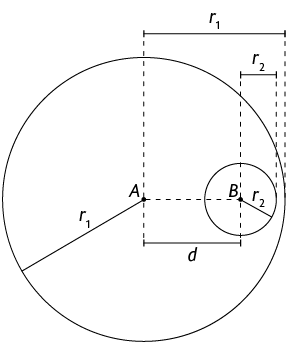
Externas

Nas circunferências externas, temos a relação a seguir.

$d maior do que abre parênteses r com índice 1 mais r com índice 2 fecha parênteses$

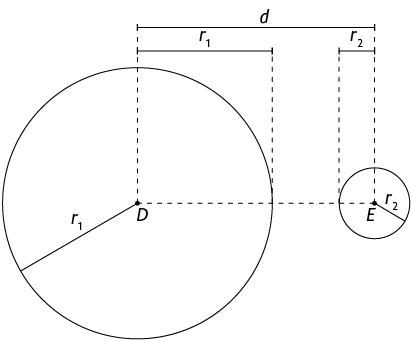
Ilustração de duas circunferências lado a lado de centros D e, E. As circunferências não tem ponto em comum. A circunferência de centro D tem raio r com índice 1 e a circunferência de centro E tem raio r com índice 2. Está indicada a distância d entre os dois centros das circunferências. Também estão indicadas as medidas de comprimento do raio r com índice 1 e do raio r com índice 2.

Página 204

Atividades

Faça as atividades no caderno.

8. Na imagem a seguir, estão representadas várias circunferências em uma malha quadriculada, cujos centros estão indicados com as letras de A a H.

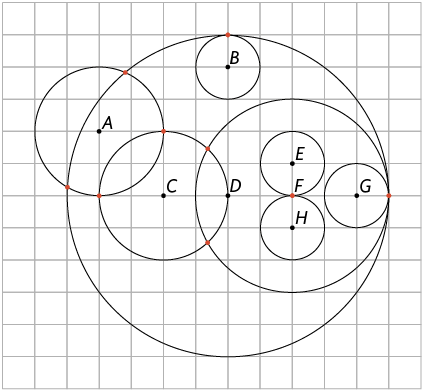
Ilustração de uma malha quadriculada com oito circunferências indicadas com centro A, B, C, D, E, F, G, H, respectivamente. Em relação a posição, as circunferências de centros B, C, E, F, G, H, são internas a D. As de centros E, G, H são internas a F. Estão destacados nove pontos, sendo eles as interseções entre circunferências. A circunferência de centro A cruza a circunferência de centro D em dois pontos e a circunferência de centro C em dois pontos. A circunferência de centro C também cruza a circunferência de centro F em dois pontos. A circunferência de centro D também cruza em um ponto as circunferências de centros B, F, G. A circunferência de centro H e a circunferência de centro E se cruzam em um ponto.

Sabendo que os pontos em laranja indicam os pontos de interseção entre elas, determine a posição relativa entre as circunferências de centros:

a) A e D.

b) B e D.

c) C e D.

d) F e G.

e) G e D.

f) E e H.

g) B e F.

h) F e C.

i) A e E.

9. Na figura geométrica a seguir, o comprimento do diâmetro da circunferência de centro $A$ mede $6 metros$ , de centro B, $8 metros$ , e de centro C, $4 metros$ .

Atenção!

As circunferências apresentadas são tangentes externas.

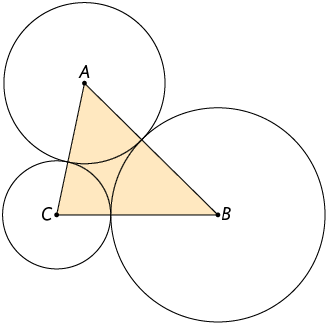
Ilustração de 3 circunferências de centros A, B, C. Cada circunferência toca a outra em um ponto. Os três pontos dos centros estão ligados por segmentos que formam um triângulo A B C, que está em destaque.

Calcule a medida do perímetro do $△ A B C$ .

10. A distância entre os centros de duas circunferências tangentes internas mede $3 centímetros$ e o comprimento do raio da maior mede $8 centímetros$ . Qual é a medida do comprimento do raio da circunferência menor?

11. De acordo com as medidas indicadas em cada item, determine a posição relativa entre as circunferências de centro $A$ e $A ’$ , cujos comprimentos dos raios medem, respectivamente, $r$ e $r ’$ , sabendo que a distância entre os centros delas mede $d$ .

a) $r igual a 5 centímetros$ ; $r linha igual a 4 centímetros$ ; $d igual a 2 centímetros$ .

b) $r igual a 4 centímetros$ ; $r linha igual a 1 centímetro$ ; $d igual a 3 centímetros$ .

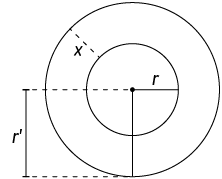
12. Determine o valor de $x$ na figura geométrica a seguir, sabendo que as circunferências são concêntricas.

$r igual a 8 centímetros$

$r linha igual a 15 centímetros$

Ilustração de duas circunferências com o centro em comum. A circunferência interna possui raio r e a maior tem raio r linha. A distância entre as duas circunferências está indicada com x.

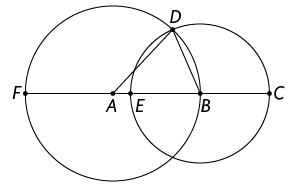
13. Na imagem, o comprimento do raio da circunferência de centro $A$ mede $5 centímetros$ e o comprimento do raio da circunferência de centro $B$ mede $4 centímetros$ . Sabendo que os pontos F, A, E, B e C são colineares, calcule mentalmente a medida do comprimento de cada segmento de reta indicado a seguir.

Ilustração de duas circunferências de centros A, B. As circunferências se cruzam em dois pontos e um desses pontos está indicado como D. Há um segmento F C que passa pelos dois centros, com o ponto F na circunferência de centro A e o ponto C na circunferência de centro B. Há um ponto E no cruzamento do segmento F C com a circunferência de centro B. Os pontos A, B, D estão ligados formando um triângulo.

a) $\overline{A B}$

b) $\overline{A F}$

c) $\overline{B F}$

d) $\overline{C F}$

e) $\overline{A D}$

f) $\overline{B D}$

g) $\overline{B E}$

h) $\overline{A E}$

Página 205

Ângulos em uma circunferência

Ângulo central

O relógio com ponteiros a seguir está marcando 3 horas. Vamos representar o menor ângulo formado pelos ponteiros do relógio em uma circunferência de centro $O$ , obtendo os pontos $A$ e $B$ sobre a circunferência.

Ilustração de um relógio de ponteiros com o ponteiro das horas no número 3, e o ponteiro dos minutos no número 12.

Ilustração de uma circunferência de centro O e dois pontos sobre ela, denominados A e B. Está marcado o ângulo interno formado pelos segmentos O A e O B.

O ângulo $A \hat{O} B$ é um ângulo central da circunferência e, nesse caso, sua medida é $90 graus$ .

Ângulo central é aquele cujo vértice é o centro da circunferência. Na figura geométrica a seguir, $A \hat{O} B$ é um ângulo central e $\vec{O A}$ e $\vec{O B}$ são os seus lados.

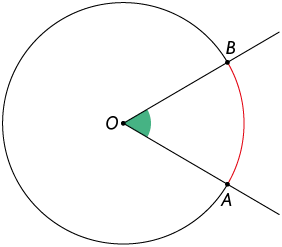
Ilustração de uma circunferência de centro O. Há duas semirretas O B e O A, estando os pontos A e B na circunferência. Essas semirretas formam um ângulo central, que está marcado. Está em destaque o arco da circunferência que está voltada para o ângulo e que está entre os pontos A e B.

O ângulo central divide a circunferência em duas partes. Cada uma delas é chamada arco da circunferência. Os pontos $A$ e $B$ são as extremidades do arco.

O arco menor dessa circunferência pode ser indicado por $\overset{⌢}{A B}$ .

A medida de um arco, em graus, é igual à medida do respectivo ângulo central. Assim, na figura geométrica anterior, $med (\overset{⌢}{A B}) = med (A \hat{O} B)$ .

Atividades

Faça as atividades no caderno.

14. Determine, em graus, as medidas $\hat{a}$ , $\hat{b}$ e $\hat{c}$ dos ângulos centrais indicados na circunferência a seguir, sabendo que elas são iguais.

Ilustração de uma circunferência dividida com quatro ângulos centrais indicados. Todos os ângulos internos estão marcados. Um dos ângulos tem medida 180 graus e os demais estão indicados com a medida: a, b, c.

15. Na circunferência de centro O a seguir estão indicadas as medidas de três ângulos centrais. Calcule a medida de cada um deles em graus.

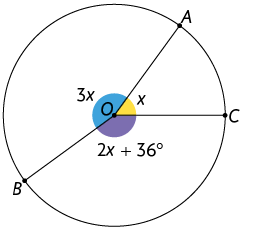
Ilustração de uma circunferência de centro O, dividida com três ângulos centrais indicados. Todos os ângulos internos estão marcados. Há três pontos na circunferência, indicados como A, B, C. Os segmentos O A com O B forma o ângulo central de medida 3 x, voltado para o arco A B. Os segmentos O A com O C forma o ângulo central de medida x, voltado para o arco A C. Os segmentos O C com O B forma o ângulo central de medida 2 x mais 36 graus, voltado para o arco B C.

a) $A \hat{O} B$

b) $A \hat{O} C$

c) $B \hat{O} C$

Página 206

Ângulo inscrito

Com o GeoGebra, Marcelo construiu uma circunferência de centro A e um ângulo central $B \hat{A} B ’$ medindo $60 graus$ . Em seguida, ele construiu o ângulo $B \hat{C} B ’$ , cujo vértice C ficou sobre a circunferência. O ângulo $B \hat{C} B ’$ é chamado ângulo inscrito.

Que tal realizar essa construção? Na seção a seguir, são apresentados os passos executados por Marcelo.

Instrumentos e softwares

Ângulos na circunferência com o GeoGebra

Para obter a construção feita por Marcelo, siga as orientações do professor e os passos apresentados.

1º. Com a ferramenta Círculo dados Centro e Um de seus Pontos, construa a circunferência de centro A que passa por B. Para isso, selecione o centro (ponto A) e, depois, o ponto B.

2º. Selecione a ferramenta Ângulo com Amplitude Fixa, clique sobre os pontos B e A, nessa ordem, e na janela Ângulo com Amplitude Fixa digite a medida do ângulo, que nesse caso é $60 graus$ . Desse modo, obtém-se o ângulo central $B \hat{A} B ’$ .

3º. Com a ferramenta Ponto, marque o ponto C sobre a circunferência de centro A, conforme indicado na imagem.

4º. Com a ferramenta Ângulo, construa o ângulo $B \hat{C} B ’$ (ângulo inscrito, cujo respectivo ângulo central é $B \hat{A} B ’$ ). Para isso, clique sobre os pontos B, C e $B ’$ , nessa ordem.

5º. Por fim, trace as semirretas AB, $A B ’$ , CB e $C B ’$ .

Ilustração de uma janela de software de geometria dinâmica, com uma circunferência de centro, A, e quatro semirretas. A ferramenta semirreta está selecionada. Os pontos B, e, B linha, estão na circunferência. As semirretas A B, e, A B linha, formam um ângulo de 60 graus, que está indicado. O ponto C está na circunferência. As semirretas C B, e, C B linha, formam um ângulo de 30 graus, que está indicado. O centro A está compreendido na região desse ângulo.

Página 207

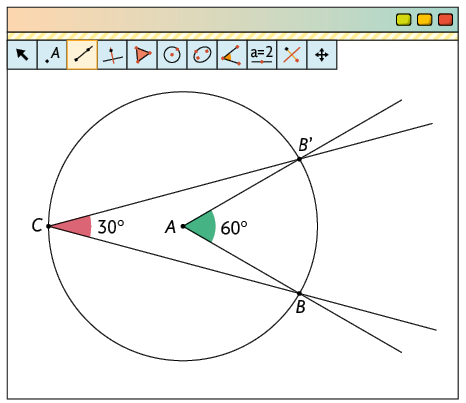
Questão 1. Qual é a medida do ângulo $B \hat{A} B ’$ ? E do ângulo $B \hat{C} B ’$ ?

Questão 2. Com a ferramenta Mover, mova o ponto C sobre a circunferência construída na seção da página anterior. A medida do ângulo variou de acordo com a posição do ponto C?

Questão 3. Considere a construção apresentada a seguir. Sabendo que $ponto O com coordenadas 1 e 1$ , $ponto A com coordenadas 3 e 2$ e $ponto C com coordenadas menos 1 e 0$ , determine a medida do ângulo $A \hat{C} B$ .

Ilustração de uma circunferência de centro O. Há três pontos sobre a circunferência, denominados A, B e C. Há uma semirreta C A que cruza o centro O. Há duas semirretas, O B e O C, que se cruzam no ponto B. Há um triângulo formado entre os pontos O B C. Está marcado um ângulo interno desse triângulo, no vértice C. Entre os segmentos O B e O A, está indicado o ângulo de medida 120 graus.

Atenção!

Utilize o GeoGebra para determinar a medida do ângulo $A \hat{C} B$ .

Questão 4. Em sua opinião, qual é a relação entre a medida do ângulo inscrito e a medida do respectivo ângulo central?

Na questão 4, caso você tenha respondido que a medida do ângulo inscrito é metade da medida do respectivo ângulo central, você está correto! Essa propriedade é válida para todos os respectivos ângulos inscrito e central em uma circunferência.

Para demonstrar essa propriedade, vamos considerar três casos.

Caso 1

Um dos lados do ângulo inscrito contém um diâmetro da circunferência. Analise a figura geométrica a seguir.

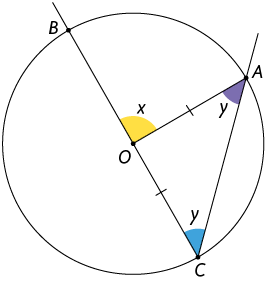
Ilustração de uma circunferência de centro O. Há três pontos na circunferência, indicados como A, B, C. Há uma semirreta C B que passa pelo centro O. Há também uma semirreta C A e um segmento O A. Está indicado um pequeno traço no meio do segmento O A e um mesmo traço no meio do segmento O C. Está indicado um ângulo central x entre os segmentos O B e O A, voltado para o arco A B. Há também um ângulo y em C, formado entre as semirretas C B e C A. Há outro ângulo y em A, formado entre o segmento O A e a semirreta C A.

Atenção!

A medida do ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não adjacentes.

O $△ A O C$ é isósceles, pois $\overline{O A} ≅ \overline{O C}$ .
Como $A \hat{O} B$ é um ângulo externo do $△ A O C$ , temos:

$x igual a y mais y assim, x igual a 2 y assim, y igual a início de fração, numerador: x, denominador: 2, fim de fração$

Assim, $medida do ângulo A C B igual a início de fração, numerador: medida do ângulo A O B, denominador: 2, fim de fração$ .

Página 208

Caso 2

O centro da circunferência não pertence à região angular do ângulo inscrito.

Traçamos o diâmetro $\overline{C D}$ , como indicado na figura geométrica a seguir.

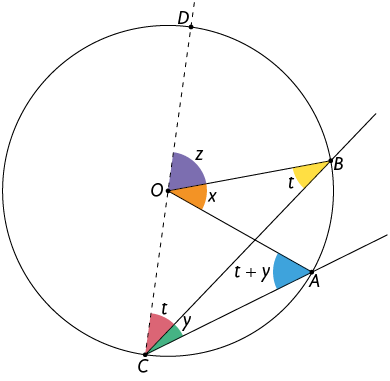
Ilustração de uma circunferência de centro O. Há 4 pontos na circunferência, denominados A, B, C, D. Há um traçado ligando os pontos C e D, passando pelo centro O. Há uma semirreta C B e uma semirreta C A. Há um segmento O B e um segmento O A. Há um ângulo central de medida z formado entre os segmentos O D e O B, voltado para o arco B D. Há outro ângulo de medida x formado entre os segmentos O B e O A, voltado para o arco A B. Está indicado um ângulo de medida t, formado entre o segmento C D e a semirreta C B. Há outro ângulo de medida t, formado entre a semirreta C B e o segmento O B. Há um ângulo de medida y, formado entre a semirreta C B e a semirreta C A e um ângulo de medida t mais y, formado pelo segmento O A e a semirreta C A.

O $△ B O C$ é isósceles, pois $\overline{O B} ≅ \overline{O C}$ . Então, pelo 1º caso, temos $z igual a 2 t$ .
O $△ A O C$ também é isósceles, pois $\overline{O A} ≅ \overline{O C}$ . Sendo assim, analogamente, temos $x mais z igual a igual a 2 abre parênteses t mais y fecha parênteses$ .
Substituindo $z$ por $2 t$ , obtemos:

$x mais 2 t igual a 2 y mais 2 t assim, x igual a 2 y assim, y igual a início de fração, numerador: x, denominador: 2, fim de fração$

Assim, $medida do ângulo A C B igual a início de fração, numerador: medida do ângulo A O B, denominador: 2, fim de fração$ .

Atenção!

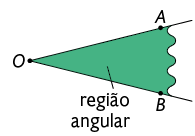
O ângulo $A \hat{O} B$ a seguir determina no plano três conjuntos de pontos compostos por:

Ilustração de um ângulo formado por semirretas. O ângulo está indicado e é formado pelas semirretas O A e O B. Entre as duas semirretas, e voltado para a região da abertura entre elas, que foi marcado o ângulo, estão indicados os pontos C e D. Fora da região da abertura das semirretas que abrange o ângulo marcado, estão indicados os pontos E, F.

pontos interiores ao ângulo $(C, D, ...)$ ;
pontos pertencentes ao ângulo $(O, A, B, ...)$ ;
pontos exteriores ao ângulo $(E, F, ...)$ .

A região angular desse ângulo é a região determinada pela união do conjunto de pontos pertencentes ao ângulo com o conjunto de pontos interiores a ele.

Ilustração de uma região angular formado por semirretas. Entre duas semirretas O A e O B, está em destaque toda região formada pela abertura entre elas. Esse destaque está indicado como 'região angular'.

Caso 3

O centro da circunferência pertence à região angular do ângulo inscrito nela.

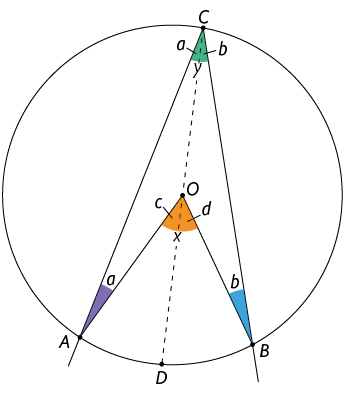
Traçamos o diâmetro $\overline{C D}$ , de modo que $y = a + b$ e $x = c + d$ .
Do 1º caso, temos $c igual a 2 a$ e $d igual a 2 b$ .
Como $med (A \hat{O} B) = c + d$ , então, $c mais d igual a 2 a mais 2 b$ , ou seja, $c mais d igual a 2 vezes abre parênteses a mais b fecha parênteses$ .

Pela construção do ângulo, temos $y = a + b$ e $x = c + d$ . Então, substituindo-os na equação anterior, obtemos:

$x igual a 2 y$ ou $y igual a início de fração, numerador: x, denominador: 2, fim de fração$

Assim, $medida do ângulo A C B igual a início de fração, numerador: medida do ângulo A O B, denominador: 2, fim de fração$ .

Página 209

Atenção!

Quando dois ângulos inscritos em uma circunferência têm o mesmo arco correspondente, as medidas desses ângulos inscritos são iguais.

Considere a figura apresentada a seguir.

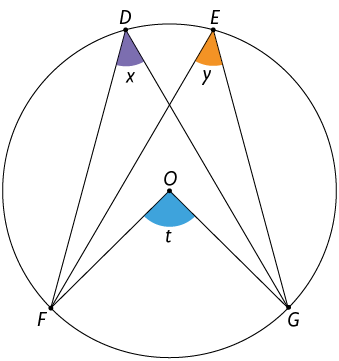
Ilustração de uma circunferência de centro O. Há 4 pontos na circunferência, denominados D, E, F, G. Há um ângulo de medida x formado entre os segmentos D F e D G. Há um ângulo de medida y formado entre os segmentos E F e E G. Também há um ângulo central de medida t, formado pelos segmentos O F e O G, voltado para o arco F G. Os ângulos de medidas x e y são formados de modo que o centro O fica compreendido em suas regiões.

Nela, $F \hat{D} G$ e $F \hat{E} G$ são ângulos inscritos e $F \hat{O} G$ é o respectivo ângulo central correspondente aos dois ângulos inscritos. Assim:

$medida do ângulo F D G igual a início de fração, numerador: medida do ângulo F O G, denominador: 2, fim de fração assim, x igual a início de fração, numerador: t, denominador: 2, fim de fração$
$medida do ângulo F E G igual a início de fração, numerador: medida do ângulo F O G, denominador: 2, fim de fração assim, y igual a início de fração, numerador: t, denominador: 2, fim de fração$

Portanto, $x = y$ , isto é, $med (F \hat{D} G) = med (F \hat{E} G)$ .

Na figura geométrica a seguir, o arco $\overset{⌢}{A B}$ , indicado em vermelho, mede $180 graus$ e é chamado semicircunferência.

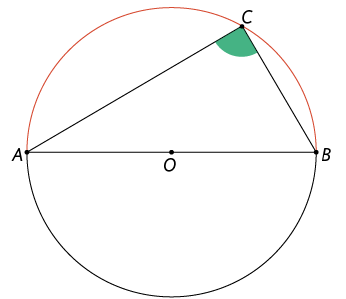
Ilustração de uma circunferência de centro O. Há 3 pontos na circunferência, denominados A, B, C. O segmento A B passa pelo centro O. Há um ângulo marcado em C, formado pelos segmentos C A e C B. O arco compreendido entre A e B, que passa pelo ponto C, está destacado em vermelho.

Qualquer ângulo inscrito em uma semicircunferência é um ângulo reto, ou seja, mede $90 graus$ .

Nessa figura geométrica, por exemplo, o ângulo $A \hat{C} B$ é um ângulo inscrito na semicircunferência, e $A \hat{O} B$ é o ângulo central correspondente. Assim:

$medida do ângulo A C B igual a início de fração, numerador: medida do ângulo A O B, denominador: 2, fim de fração igual a início de fração, numerador 180 graus, denominador: 2, fim de fração igual a 90 graus$

Página 210

Atividades

Faça as atividades no caderno.

16. Determine a medida $\hat{a}$ indicada na circunferência de centro $O$ a seguir.

Ilustração de uma circunferência de centro O. Há 3 pontos na circunferência, denominados A, B, C. Há um ângulo marcado, de medida, a, minúsculo. Esse ângulo é formado pelas semirretas C A e C B e compreendido na região desse ângulo está o centro O. Há um ângulo central de medida 50 graus formado pelos segmentos O A e O B, voltado para o arco A B.

17. Calcule o valor de $x$ e as medidas dos ângulos $B \hat{A} C$ e $B \hat{O} C$ na circunferência de centro $O$ a seguir.

Ilustração de uma circunferência de centro O. Há 3 pontos na circunferência, denominados A, B, C. Há um ângulo marcado, de medida 6 x, que é formado pelas semirretas A B e A C e compreendido na região desse ângulo está o centro O. Formado pelos segmentos O B e O C, está o ângulo central de medida 8 x mais 40 graus, voltado para o arco B C.

18. Os ângulos inscritos $A \hat{C} B$ , $A \hat{D} B$ , $A \hat{E} B$ , $A \hat{F} B$ e $A \hat{G} B$ na figura geométrica a seguir determinam o mesmo arco na circunferência. O que você pode concluir a respeito das medidas deles?

Ilustração de uma circunferência com sete pontos sobre ela denominados A, B, C, D, E, F, G. A partir do ponto A são formados os segmentos A C; A D; A E; A F; A G. A partir do ponto B são formados os segmentos B C; B D; B E; B F; B G. O arco A B está em destaque.

19. Rita desenhou uma circunferência e traçou um dos diâmetros, ao qual denominou $\overline{M N}$ . Em seguida, ela determinou o ângulo central $M \hat{O} N$ e o arco $\overset{⌢}{M N}$ . Depois, construiu os ângulos inscritos $M \hat{P} N$ e $M \hat{Q} N$ , conforme a figura a seguir.

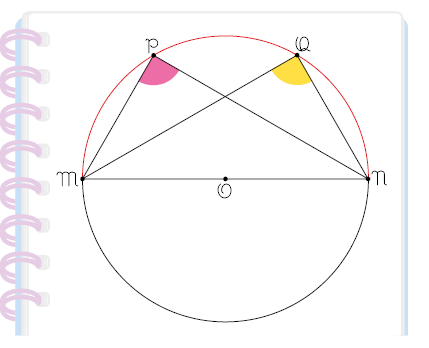
Ilustração de uma circunferência de centro O, como se estivesse desenhada em um caderno. Há quatro pontos sobre a circunferência, denominados M, N, P, Q. Os pontos P e Q estão sobre um mesmo arco M N. Há um ângulo formado pelos segmentos M P e N P, e outro ângulo formado pelos segmentos M Q e N Q. Está em destaque o arco M N que possui os pontos P e Q.

Quais são as medidas dos ângulos inscritos construídos por Rita?

20. Considere a circunferência de centro O e o triângulo ABC cujos vértices pertencem a circunferência. Reproduza essa figura no software GeoGebra. Qual é a medida de cada ângulo inscrito na circunferência?

Ilustração de uma circunferência de centro O. Há três pontos sobre a circunferência, denominados A, B, C. O segmento A C passa pelo centro O. Os pontos A, B, C são vértices de um triângulo, com os três ângulos internos marcados. Um dos ângulos internos do triângulo, de medida 52 graus, está indicado no vértice A.

Página 211

21. Determine o valor de $x$ na circunferência de centro $O$ a seguir.

Ilustração de uma circunferência de centro O. Há um ângulo de medida 44 graus, formado por duas semirretas, que se originam na circunferência e a cruzam. O centro O está compreendido dentro da região desse ângulo. Há outro ângulo com medida 4 x formado por duas semirretas, que se originam na circunferência e a cruzam. O centro O está fora da região desse outro ângulo. Cada semirreta de um ângulo se cruza com uma semirreta do outro ângulo, em um mesmo ponto da circunferência.

22. Determine a medida $\hat{x}$ na figura geométrica a seguir, sabendo que $O$ é o centro da circunferência.

Ilustração de uma circunferência de centro O. Há três pontos sobre a circunferência, denominados A, B, C. O segmento C B passa pelo centro O. Os pontos A, B, C são vértices de um triângulo. Há um ângulo marcado de medida 30 graus, no ponto C, interno a esse triângulo. Há um outro ângulo marcado chamado de x, interno ao triângulo, no vértice B.

23. Considere a circunferência de centro $O$ e alguns segmentos de reta traçados a seguir.

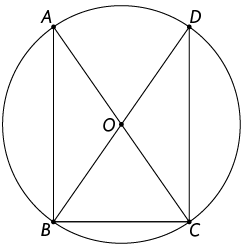
Ilustração de uma circunferência de centro O. Há quatro pontos sobre a circunferência, denominados A, B, C, D. Os segmentos A C e B D cruzam o centro O. Formam segmentos entre os pontos: A e B; B e C; C e D.

a) Quais desses segmentos de reta são diâmetros da circunferência? E quais são raios?

b) O $△ A O B$ é isósceles? Por quê?

c) Identifique os triângulos retângulos.

d) O $△ A O B$ e o $△ D O C$ são congruentes? Justifique sua resposta.

24. Considere as seguintes informações sobre a figura geométrica representada.

O comprimento do raio da circunferência de centro $O$ mede $2 vírgula 5 metros$ .

$medida do ângulo A B C igual a 65 graus$ .

$medida do segmento D A igual a 2 vírgula 11 metros$ .

Os triângulos $A B D$ e $B A C$ são congruentes.

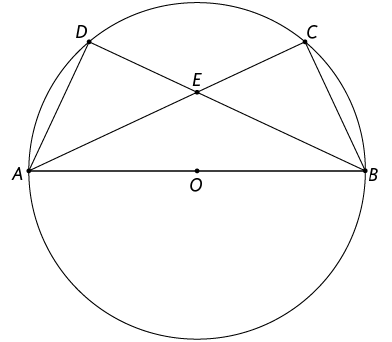
Ilustração de uma circunferência de centro O. Há quatro pontos sobre a circunferência, denominados A, B, C, D. O segmento A B cruza o centro O. Os pontos C e D estão sobre o mesmo arco A B. São formados dois triângulos, um A B D e outro A B C. Na interseção entre os segmentos A C e B D, há um ponto E.

a) O $△ A B E$ é equilátero, isósceles ou escaleno?

b) Qual é a medida do ângulo $A \hat{E} B$ ?

25. Em seu caderno, elabore um problema utilizando como referência a figura geométrica a seguir. Dê o problema para um colega resolver e, em seguida, verifique se a resposta que ele obteve está correta.

Ilustração de uma circunferência de centro O. Há um ângulo de medida 7 x mais 10 graus, formado por duas semirretas, que se originam na circunferência e a cruza. O centro O está compreendido dentro da região desse ângulo. Há outro ângulo com medida 4 x mais trinta e sete graus, formado por duas semirretas, que se originam na circunferência e a cruza. O centro O está compreendido dentro da região desse outro ângulo. Cada semirreta de um ângulo se cruza com uma semirreta do outro ângulo, em um mesmo ponto da circunferência.

Página 212

Medida do comprimento do arco de uma circunferência

Para calcular a medida do comprimento C de uma circunferência, conhecida a medida do comprimento de seu raio r ou do diâmetro d, podemos utilizar a fórmula a seguir.

$C igual a 2 vezes r vezes pi está indicado que 2 vezes r corresponde a d$ ou $C = d π$

Atenção!

O número irracional $π$ é dado por $pi igual a 3 vírgula 1 4 1 5 9 2 6 5 4 reticências$ No entanto, vamos usar uma aproximação de $π$ com duas casas decimais, isto é, $pi igual a 3 vírgula 14$ .

Considere, por exemplo, a circunferência A, cujo comprimento do diâmetro mede $5 centímetros$ , e a circunferência B, cujo comprimento do raio mede $3 vírgula 5 centímetros$ . Tomando $pi igual a 3 vírgula 14$ , vamos calcular a medida do comprimento dessas circunferências.

$C igual a d pi igual a 5 vezes 3 vírgula 14 igual a 15 vírgula 7$

$C igual a 2 pi r igual a 2 vezes 3 vírgula 14 vezes 3 vírgula 5 igual a 21 vírgula 98$

Portanto, o comprimento da circunferência A mede aproximadamente $15 vírgula 7 centímetros$ , e o da circunferência B, aproximadamente $21 vírgula 98 centímetros$ .

Também podemos determinar a medida do comprimento de apenas uma parte da circunferência, ou seja, de um arco de circunferência.

No exemplo a seguir, vamos calcular a medida do comprimento de um arco de circunferência determinado por um ângulo central.

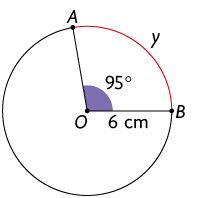
Nessa circunferência:

O é centro;
$6 centímetros$ é a medida de comprimento do raio;
$95 graus$ é a medida do ângulo central;
y é a medida do comprimento do arco.

Antes de calcular a medida do comprimento y, calculamos inicialmente a medida do comprimento da circunferência.

$C igual a 2 pi r igual a 2 vezes 3 vírgula 14 vezes 6 igual a 37 vírgula 68$

Em seguida, com o auxílio de uma regra de três simples, calculamos a medida do comprimento do arco da circunferência. Como a medida do comprimento de um arco e a medida do ângulo central que determinam esse arco são grandezas diretamente proporcionais, temos:

Medida do comprimento do arco de uma circunferência
Medida do ângulo central (em graus)	Medida do comprimento do arco ( $cm$ )
360	37,68
95	y

$início de fração, numerador: 360, denominador: 95, fim de fração igual a início de fração, numerador: 37 vírgula 68, denominador: y, fim de fração$

$360 vezes y igual a 95 vezes 37 vírgula 68$

$360 y igual a 3.579 vírgula 68$

$y aproximadamente igual a 9 vírgula 94$

Portanto, a medida aproximada do comprimento do arco é $9 vírgula 94 centímetros$ .

Página 213

Atividades

Faça as atividades no caderno.

26. O diâmetro da roda da bicicleta de Cássia mede $66 centímetros$ .

a) Calcule a medida da distância aproximada que a bicicleta de Cássia percorre quando a roda dá uma volta completa.

b) Aproximadamente, quantas voltas completas a roda da bicicleta de Cássia dá quando percorre $500 metros$ ?

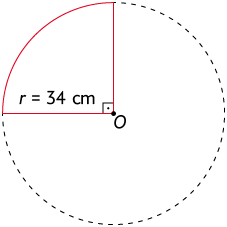
27. Em cada figura geométrica a seguir está representada uma circunferência de centro $O$ . Calcule a medida do comprimento aproximado de cada linha vermelha.

Ilustração de uma circunferência de centro O. Toda a circunferência está destacada em vermelho. O raio está traçado e está indicado com 'r igual a 15 centímetros'.

Ilustração de uma circunferência de centro O. Há dois segmentos que são raios da circunferência e que formam um ângulo reto, que está indicado. Esses dois segmentos e o arco que compreende esse ângulo, estão destacados de vermelho. O restante da circunferência está tracejado. Em um dos segmentos há a indicação 'r igual a 34 centímetros'.

28. A distância entre os eixos de duas polias^✚ mede $50 centímetros$ .

Atenção!

A correia fica em contato com metade do comprimento de cada polia.

Ilustração de duas polias. As polias tem formato circular e há um fio que as liga pelo topo e um fio que as liga abaixo. A distância entre os centros das polias está indicado com 50 centímetros de medida de comprimento.

Polia:: roda presa a um eixo, o qual recebe uma correia e transmite movimento.^↰

Sabendo que o diâmetro de cada polia mede $20 centímetros$ , determine o comprimento aproximado da correia que passa por elas.

29. Calcule a medida do comprimento aproximado de cada arco apresentado a seguir.

Ilustração de um arco de circunferência. Entre os dois segmentos que formam o arco está indicado o ângulo de 70 graus. Sobre um desses segmentos, está indicado que tem 10 centímetros de medida de comprimento.

Ilustração de um arco de circunferência. Entre os dois segmentos que formam o arco está indicado o ângulo de 145 graus. Sobre um desses segmentos, está indicado que tem 14 centímetros de medida de comprimento.

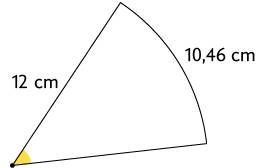
30. Marcos cortou um disco de papel até o seu centro sobre dois raios. A maior parte obtida por ele está representada a seguir.

Ilustração de um arco de circunferência. Entre os dois segmentos que formam o arco está indicado o ângulo de 240 graus. Sobre um desses segmentos, está indicado que tem 7 centímetros de medida de comprimento.

De acordo com as medidas indicadas na imagem, calcule a medida do comprimento do arco formado.

31. Calcule a medida aproximada do ângulo que corresponde ao arco a seguir.

Ilustração de um arco de circunferência. Entre os dois segmentos que formam o arco está demarcado um ângulo. Sobre um desses segmentos, está indicado que tem 12 centímetros de medida de comprimento. Ao lado do arco, está indicado que ele possui 10,46 centímetros de medida de comprimento.

Página 214

Polígonos inscritos em uma circunferência e circunscritos a ela

Um professor de Matemática do 9º ano desenhou na lousa as seguintes figuras geométricas.

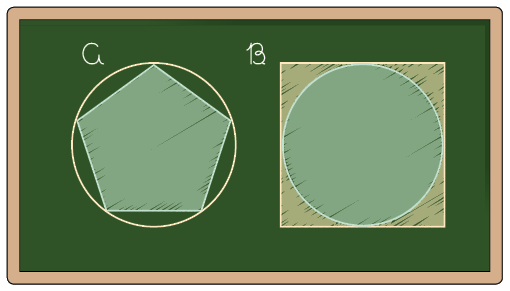
Ilustração de uma lousa. Na lousa estão desenhadas duas figuras, sendo a figura A uma circunferência com um pentágono regular em seu interior, com cada vértice sobre a circunferência. Ao lado está a figura B, sendo um quadrado com uma circunferência em seu interior. A circunferência toca o quadrado em cada lado.

Na figura A, os vértices do pentágono pertencem à circunferência. Nesse caso, temos um polígono inscrito na circunferência.

Já na figura B, os lados do quadrado são tangentes à circunferência. Portanto, temos um polígono circunscrito à circunferência.

Atenção!

Qualquer polígono regular pode ser:

inscrito em uma circunferência;
circunscrito a uma circunferência.

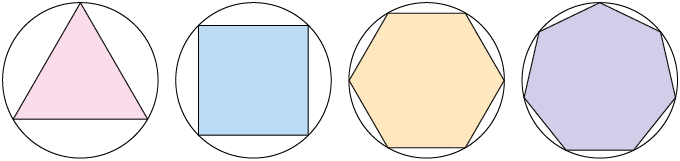
Analise a seguir outros exemplos de polígonos inscritos e circunscritos às circunferências.

Polígonos inscritos

Ilustração de 4 polígonos, com cada um inscrito em uma circunferência. Há um triângulo equilátero, um quadrado, um hexágono regular e um heptágono regular.

Polígonos circunscritos

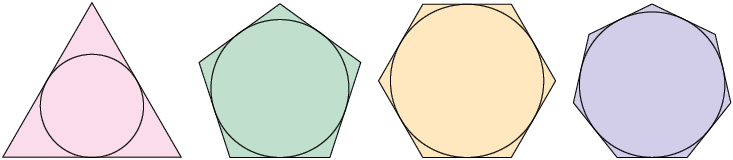
Ilustração de 4 polígonos, com cada um circunscrito em uma circunferência. Há um triângulo equilátero, um pentágono regular, um hexágono regular e um heptágono regular.

Atenção!

Em um polígono regular, podemos destacar o centro do polígono, que é o centro comum da circunferência inscrita e da circunferência circunscrita ao polígono. Além disso, podemos destacar o ângulo central, que é o ângulo cujo vértice é o centro do polígono e cujos lados contêm vértices consecutivos do polígono.

Página 215

Hexágono regular inscrito em uma circunferência

Considere a propriedade a seguir.

Propriedade: A medida do comprimento de cada lado de um hexágono regular inscrito em uma circunferência é igual à medida do comprimento do raio $r$ dela.

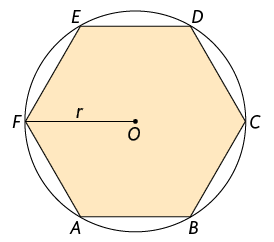
Ilustração de um hexágono regular inscrito em uma circunferência de centro O. Os vértices do hexágono estão nomeados de A até F. O raio da circunferência está indicado com r, e ele parte do centro O até o vértice F do hexágono.

Na figura apresentada, por exemplo, temos:

$A B = O F = r$

Podemos verificar essa propriedade da seguinte maneira.

Traçando os segmentos de reta $A D$ , $B E$ e $C F$ , obtemos seis triângulos, como mostra a figura geométrica a seguir.

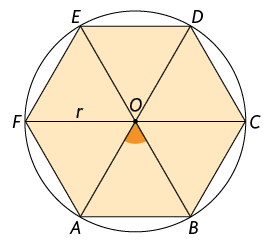
Ilustração do mesmo hexágono regular inscrito em uma circunferência de centro O, da imagem anterior. Os vértices do hexágono estão nomeados de A até F. Estão traçados os segmentos A D; B E; C F, todos passando pelo centro O. Está indica o raio r no segmento O F. Há um ângulo indicado em O, entre os segmentos O A e O B.

Atenção!

Se todos os ângulos internos de um triângulo são congruentes, então, esse triângulo é equilátero.

O triângulo $A O B$ é isósceles, pois $\overline{O A}$ e $\overline{O B}$ são raios da circunferência e, consequentemente, $O A = O B$ . Assim, $med (O \hat{A} B) = med (O \hat{B} A)$ .
$medida do ângulo O A B igual a 60 graus$ , pois $360 graus dividido por 6 igual a 60 graus$ .

Assim:

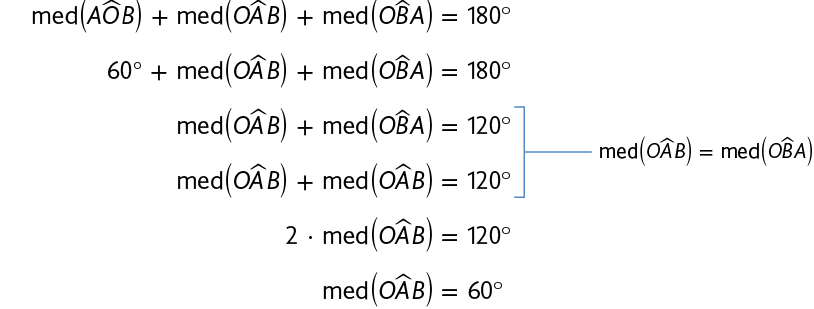
Esquema com equações. Na primeira linha, há a equação: medida do ângulo A O B mais medida do ângulo O A B mais medida do ângulo O B A é igual a 180 graus. Na segunda linha: 60 graus mais medida do ângulo O A B mais medida do ângulo O B A é igual a 180 graus. Na terceira linha: medida do ângulo O A B mais medida do ângulo O B A é igual a 120 graus. Na quarta linha: medida do ângulo O A B mais medida do ângulo O A B é igual a 120 graus. Na quinta linha: 2 vezes medida do ângulo O A B é igual a 120 graus. Na sexta e última linha: medida do ângulo O A B é igual a 60 graus. A terceira e quarta linhas estão relacionadas à indicação: medida do ângulo O A B é igual a medida do ângulo O B A.

Então, $medida do ângulo O A B igual a 60 graus$ , $medida do ângulo O A B igual a 60 graus$ e $medida do ângulo O A B igual a 60 graus$ . Portanto, o triângulo $A O B$ é equilátero.

Como $A O = A B = B O$ , temos $A B = r$ .

Página 216

Construindo polígonos regulares

A seguir apresentamos, por escrito e por meio de um fluxograma, um algoritmo que possibilita construir um eneágono regular, dada a medida do comprimento do lado a.

Algoritmo

Início

1. Desenhe um segmento $A B$ cujo comprimento mede a.

2. Calcule a medida do ângulo central:

$medida do ângulo O A B igual a início de fração, numerador: 360 graus, denominador: 9, fim de fração igual a 40 graus$

3. Calcule as medidas dos dois outros ângulos do triângulo $A O B$ :

$medida do ângulo A igual a medida do ângulo B igual a início de fração, numerador: 180 graus menos 40 graus, denominador: 2, fim de fração igual a 70 graus$

4. No sentido anti-horário, construa o ângulo $B \hat{A} X$ cuja medida é $70 graus$ . No sentido horário, construa o ângulo $A \hat{B} Y$ cuja medida é $70 graus$ .

5. Na interseção das semirretas $A X$ e $A Y$ , marque o ponto O.

6. Trace a circunferência de centro O e raio $\overline{O A}$ .

7. Desenhe as circunferências de raio $\overline{A B}$ com centros em A e B e com centros nos novos pontos obtidos sobre a circunferência de centro O.

8. Os pontos marcados sobre a circunferência de centro O são os vértices do polígono. Ligue-os para finalizar a construção.

Fim

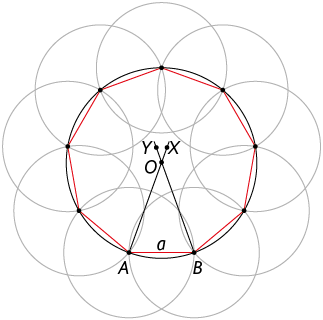
Ilustração de um eneágono regular, inscrito em uma circunferência. Cada um dos vértices é o centro de uma circunferência que possui raio da mesma medida do lado do eneágono. O eneágono tem medida de lado indicado com a minúsculo, sobre um lado A B. Há uma semirreta A X, que passa pelo centro O, e outra semirreta B Y, que também passa pelo centro O.

Fluxograma

Questão 5. Em seu caderno, escreva um algoritmo que permite construir um pentágono regular, dada a medida do comprimento do lado a. Depois, faça um fluxograma que represente o algoritmo que você escreveu.

Página 217

Instrumentos e softwares

Polígono regular no GeoGebra

Com o auxílio do GeoGebra, é possível construir um polígono regular usando os procedimentos apresentados no algoritmo ou no fluxograma da página anterior. Além disso, é possível construir um polígono regular com esse software de outra maneira, conforme apresentamos nas etapas a seguir.

1º. Com a ferramenta Segmento com Comprimento Fixo, clique em um ponto da malha e digite a medida do comprimento. No exemplo, foi digitado 3.

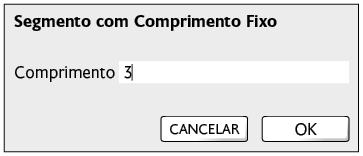
Ilustração da janela de um software. Na parte de cima da janela há o texto: Segmento com comprimento fixo. No meio há uma barra chamada comprimento, com o número 3. Na parte de baixo há os botões cancelar e ok.

2º. Com a ferramenta Polígono Regular, clique nos pontos A e B e digite a quantidade de vértices do polígono. No exemplo, foi digitado o 7.

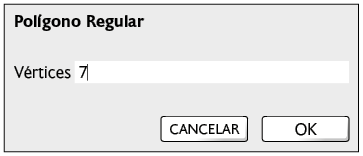
Ilustração da janela de um software. Na parte de cima da janela há o texto: polígono regular. No meio há uma barra chamada vértices, com o número 7. Na parte de baixo há os botões cancelar e ok.

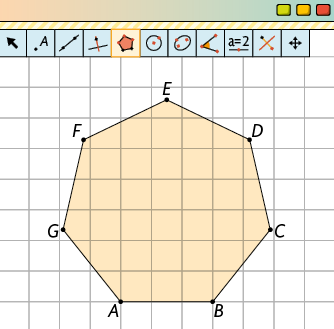
3º. O polígono construído tem a medida do comprimento do lado e a quantidade de vértices digitados.

Ilustração da janela de visualização de um software de geometria dinâmica. Está selecionado o botão da ferramenta polígono regular. Na janela, sobre uma malha quadriculada está um polígono regular de 7 lados. Os vértices estão nomeados de A até G. Observa-se, pela disposição dos vértices A e B, que o polígono tem lados do comprimento de 3 quadrados da malha.

Atividades

Faça as atividades no caderno.

32. A figura a seguir mostra um triângulo equilátero $A B C$ inscrito em uma circunferência de centro $P$ .

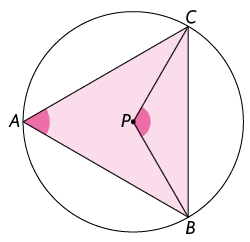
Ilustração de triângulo equilátero A B C inscrito em uma circunferência de centro P. Está indicado o ângulo interno do triângulo no vértice A, e também o ângulo em P, formado pelos segmentos P C e P B.

Determine a medida dos ângulos:

a) $B \hat{A} C$ .

b) $B \hat{P} C$ .

Página 218

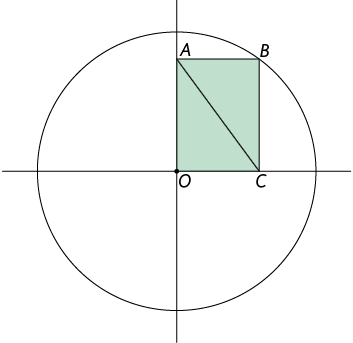
33. Na imagem, está representado um quadrado cujo comprimento do lado mede u, inscrito em uma circunferência de centro $O$ e comprimento do raio medindo $r$ .

Atenção!

Utilize o teorema de Pitágoras.

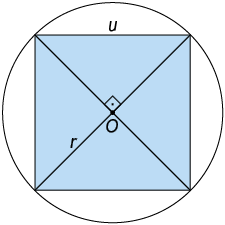
Ilustração de um quadrado inscrito em uma circunferência de centro O e raio r. As diagonais do quadrado estão traçadas, passando pelo centro O. O quadrado tem lado indicado por u. Entre duas diagonais, está indicado o ângulo reto formado no ponto O.

Sabendo que as diagonais do quadrado são perpendiculares entre si, determine a medida do comprimento do lado desse quadrado em função da medida do comprimento do raio da circunferência.

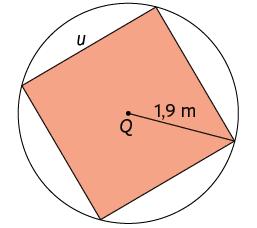
34. Utilizando a resposta que você obteve na atividade anterior, calcule a medida u indicada no quadrado inscrito na circunferência de centro Q a seguir.

Ilustração de um quadrado inscrito em uma circunferência de centro Q e raio de medida 1,9 metros. O quadrado tem lado indicado por u.

35. A figura geométrica a seguir mostra parte de um polígono regular inscrito em uma circunferência de centro $O$ .

Atenção!

O segmento de reta $A B$ é um dos lados desse polígono.

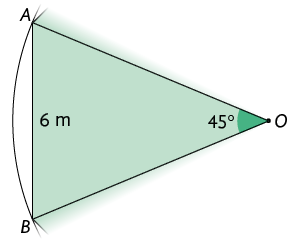
Ilustração representando parte de um polígono regular inscrito em uma circunferência de centro O. Observa-se um dos lados do polígono, que possui vértices consecutivos A e B e a medida desse lado A B tem 6 metros de comprimento. Estão traçados os segmentos O A e O B. O ângulo formado entre segmentos O A e O B, tem 45 graus de medida.

Qual é a medida do perímetro desse polígono?

36. O hexágono regular $A B C D E F$ , apresentado a seguir, está circunscrito à circunferência de centro $O$ . Os pontos de tangência do hexágono com a circunferência são os pontos médios de seus lados.

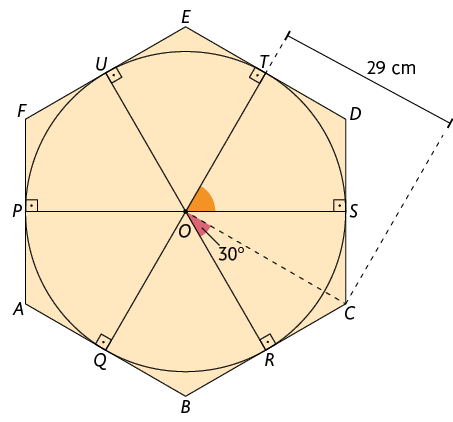
Ilustração de um hexágono regular circunscrito em uma circunferência de centro O. Os vértices do hexágono estão nomeados de A até F. Estão traçados segmentos que partem do centro O até os pontos de tangência da circunferência com o hexágono. Há os segmentos: O P, com o ponto P no lado A F do hexágono; O Q, com o ponto Q no lado A B do hexágono; O R, com o ponto R no lado B C do hexágono; O S, com o ponto S no lado C D do hexágono; O T, com o ponto T no lado D E do hexágono; O U, com o ponto U no lado E F do hexágono. Em cada um desses pontos de tangência está indicado um ângulo reto formado pelo lado do hexágono e respectivo segmento. Está marcado um ângulo em O, entre os segmentos O T e O S. Há um tracejado que liga o centro O com o vértice C do hexágono. Entre esse segmento O C formado, e o segmento O R, está indicado o ângulo de medida 30 graus. Está também indicado que o segmento O C tem 29 centímetros de medida de comprimento.

a) Calcule a medida:

do ângulo $S \hat{O} T$ ;

do comprimento do lado e a medida do perímetro do hexágono;

aproximada do comprimento do diâmetro e do comprimento da circunferência.

b) Se traçarmos os segmentos de reta $P Q$ , $Q R$ , $R S$ , $S T$ , $T U$ e $U P$ , obteremos um hexágono regular inscrito à circunferência. Calcule a medida aproximada do comprimento do lado e da medida do perímetro do hexágono $P Q R S T U$ .

37. Por meio de procedimentos semelhantes ao algoritmo da página 216, construa um hexágono regular cujo comprimento do lado meça $3 centímetros$ . Em seguida, utilizando os mesmos procedimentos apresentados na seção Instrumentos e softwares da página 217, construa esse mesmo polígono.

Versão adaptada acessível

37. Junte-se a um colega e, por meio de procedimentos semelhantes ao algoritmo da página 216, construam um hexágono regular cujo comprimento do lado meça $3 centímetros$ . Em seguida, utilizando os mesmos procedimentos apresentados na seção Instrumentos e softwares da página 217, construam esse mesmo polígono.

Página 219

Estudando vistas

A professora Alice pediu aos estudantes que levassem para a sala de aula alguns objetos e embalagens, utilizados no dia a dia, que lembrassem figuras geométricas espaciais.

Depois, ela colocou-os sobre uma mesa e pediu a quatro estudantes que desenhassem as vistas desses objetos. Cada estudante se posicionou conforme a imagem a seguir.

Ilustração de uma sala. No centro, há uma mesa marrom, com a parte superior de formato quadrado. Ao redor da mesa, há uma criança em cada lado sentadas em uma cadeira, e observando objetos que estão sobre a mesa. Considerando os lados da mesa dispostos horizontal e verticalmente, temos as seguintes posições relativas de cada criança: Otávio está no lado superior, Aline está no lado inferior, Marcos está no lado esquerdo e Adriana está no lado direito. Sobre a mesa, considerando a ordem de cima para baixo, há objetos dispostos da seguinte maneira: próximos da lateral superior, estão lado a lado três objetos dispostos da esquerda para direita: uma caixa azul em formato de paralelepípedo reto retângulo, um pote cilíndrico alaranjado com tampa marrom e ao lado desse pote uma esfera roxa. A face menor da caixa azul está voltada para Otávio, e a face maior para Marcos. Abaixo e entre o pote alaranjado e a bola roxa está um cubo verde, com uma das faces voltada para Adriana. Abaixo, próximo a lateral inferior da mesa e centralizado com o cubo verde, há um objeto amarelo em formato de pirâmide de base quadrada. Essa pirâmide tem uma face lateral voltada para Adriana e outra face voltada para Aline. O cubo e a bola têm a mesma altura; o pote cilíndrico e a pirâmide também têm a mesma altura, porém ligeiramente maior que a do cubo e da bola. A largura do pote cilíndrico tem metade da largura do cubo. A caixa tem altura da metade da altura do cubo; a largura pouco menor que a largura do cubo e seu comprimento é aproximadamente o dobro de sua própria largura. O lado da base da pirâmide é ligeiramente maior que a da base do cubo.

Analise a seguir os desenhos feitos pelos estudantes.

Ilustração de algumas figuras geométricas sobre um retângulo. Estão dispostas 5 figuras, com suas bases sobre o topo de um retângulo marrom, da seguinte forma: do lado esquerdo há um retângulo azul; no centro há um retângulo, que é dividido em duas cores pela horizontal, sendo o topo marrom e a parte de baixo alaranjado, e do lado direito desse retângulo, sugerindo que há três figuras sobrepostas, sendo: um triângulo isósceles amarelo na frente, atrás desse triângulo e centralizado com ele há um quadrado verde e atrás do quadrado há um círculo roxo, que aparece pela lateral direita do quadrado. O quadrado verde e a bola roxa têm a mesma altura. O retângulo de cores alaranjada e marrom, e o triângulo, têm a mesma altura, que é ligeiramente maior que a do quadrado e o círculo. O retângulo azul tem a metade da altura do cubo verde e comprimento pouco menor que a do quadrado. O retângulo de cores alaranjado e marrom tem metade do comprimento do quadrado. — Aline

Note que os desenhos mostram representações diferentes dos objetos, pois eles foram produzidos partindo de diferentes posições do observador. Dessa maneira, tomando um ponto de referência, definimos diferentes vistas ortogonais de objetos ou de figuras geométricas espaciais.

Em relação a Marcos, dizemos que o desenho dele representa a vista frontal dos objetos; o desenho de Aline, a vista lateral direita; e o de Otávio, a vista lateral esquerda. No caso do desenho de Adriana, ele representa a vista posterior, isto é, os objetos vistos pela parte de trás em relação a Marcos.

Questão 6. Considerando que o desenho de Aline representa a vista frontal, os desenhos dos demais estudantes representam qual tipo de vista?

Página 220

Também podemos representar os objetos da página anterior analisando-os de cima. Nesse caso, denominamos vista superior.

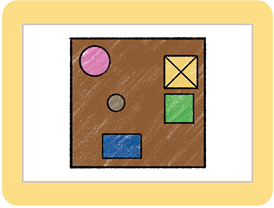
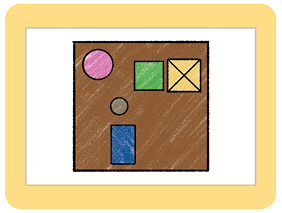
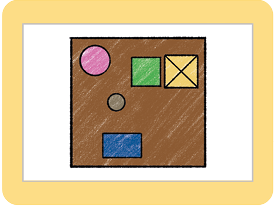
Questão 7. Qual das imagens a seguir representa uma possível vista superior dos objetos apresentados na página anterior?

Ilustração de um quadrado marrom, com 5 figuras dispostas em seu interior. Estão dispostos: no canto superior esquerdo, um círculo roxo; horizontalmente um pouco mais abaixo que o círculo roxo, mas ainda na parte superior do quadrado marrom, e próximos do lado direito, estão alinhados verticalmente, um quadrado amarelo com as diagonais traçadas e um quadrado verde; no centro do quadrado marrom, porém deslocado mais para esquerda, há um círculo marrom, que fica verticalmente alinhado à direita do círculo roxo. Próximo ao canto inferior, alinhado na vertical ligeiramente para a direita do círculo marrom, há um retângulo azul, em que seu lado maior é a base.

Ilustração de um quadrado marrom, com 5 figuras dispostas em seu interior. A ilustração possui os mesmos elementos que a ilustração anterior, porém agora o quadrado verde está à esquerda do quadrado amarelo, alinhados horizontalmente, e também agora a base do retângulo azul é seu lado menor.

Atividades

Faça as atividades no caderno.

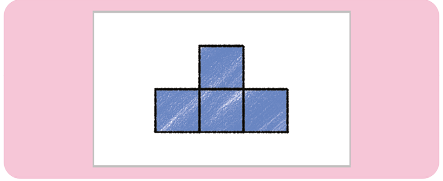
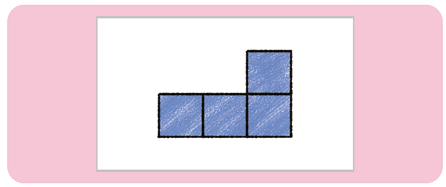
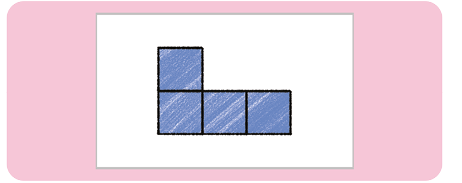
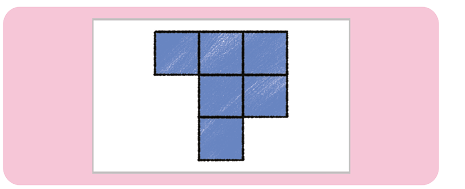
38. Em relação à posição indicada na imagem, Fábio desenhou as vistas frontal, superior, lateral esquerda e lateral direita do empilhamento de cubos.

Ilustração de um garoto sentado em um banco, observando um empilhamento formado por 7 cubos acima de uma mesa. Tendo a mesa o formato de um quadrado e considerando o garoto sentado pelo canto esquerdo, os cubos estão dispostos: alinhados ao canto direito da mesa, há uma fileira com 3 cubos, e mais 1 cubo em cima do cubo do meio; há ainda outra fileira de 2 cubos encostados no lado esquerdo da fileira anterior, nos 2 cubos inferiores; por fim, há mais um cubo encostado ao lado esquerdo do primeiro cubo da fileira do meio.

Analise os desenhos feitos por ele e determine a que vista cada um deles corresponde.

Ilustração de um retângulo branco com uma figura em seu interior. A figura é composta por 4 quadrados ao total, sendo 3 quadrados dispostos horizontalmente, ligados pela aresta, e um quadrado acima do quadrado do meio, também ligados pela aresta.

Ilustração de um retângulo branco com uma figura em seu interior. A figura é composta por 6 quadrados ao total, dispostos da seguinte forma: é formado um quadrado maior por 4 desses quadrados, ligados entre si por suas arestas; em relação a esse quadrado maior, considerando a ordem de cima para baixo, há um quadrado ao lado esquerdo do primeiro quadrado, ligados pelas arestas e outro quadrado abaixo do segundo quadrado, ligados pelas arestas.

Página 221

39. Analise a vista frontal dos vasos A e B a seguir.

Ilustração da visão frontal de um vaso. O corpo possui um formato oval e alongado, com a parte do topo que representa a boca, sendo horizontal, as laterais descendo paralelas e gradativamente seguindo o contorno oval. O corpo do vaso lembra o formato de uma raquete de tênis de ponta cabeça, como se o cabo fosse mais grosso e mais curto que o comum. Há duas hastes laterais, de formato oval, ligadas ao corpo do vaso. Na base oval do vaso, há uma estrutura retangular de sustentação, de comprimento próximo a boca do vaso.

Ilustração da visão frontal de um vaso que possui o corpo circular, com uma parte estreita de cima projetando-se um pouco para fora, com o topo reto, de modo que forma a boca do vaso. Na base do vaso há uma estrutura retangular de sustentação, de comprimento maior que a boca do vaso.

Agora, verifique as imagens a seguir, que podem ou não representar vistas desses vasos.

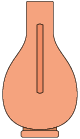
Ilustração da vista de um vaso. Observa-se o mesmo corpo, sem as hastes laterais, e a mesma base do vaso oval que aparece no cabeçalho da atividade. No meio do corpo oval, há um retângulo estreito, da mesma espessura e comprimento vertical das hastes que aparecem no vaso citado.

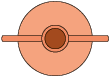
Ilustração da vista de um vaso. A imagem apresenta uma estrutura com formato de círculo, e em seu meio, outro círculo de diâmetro menor, com seu contorno com uma certa espessura, como um anel, e o interior de cor mais escura que os outros elementos. De cada lado do círculo menor, partem dois retângulos, que possuem mesma espessura das hastes do vaso de corpo oval do cabeçalho da atividade.

Ilustração da mesma visão do vaso de formato oval e com hastes laterais, que aparece no cabeçalho da atividade. A imagem tem exatamente as mesmas características e componentes.

Ilustração da mesma visão do vaso de formato circular, que aparece no cabeçalho da atividade. A imagem tem exatamente as mesmas características e componentes.

Ilustração da vista de um vaso. A imagem apresenta uma estrutura com formato de círculo com seu contorno com uma certa espessura, como um anel, e o interior de cor mais escura. De cada lado do círculo partem dois retângulos, que possuem mesma espessura das hastes do vaso de corpo oval do cabeçalho da atividade.

Ilustração da vista de um vaso. Observa-se o mesmo corpo, sem a base de sustentação, do vaso circular que aparece no cabeçalho da atividade.

a) Qual dessas imagens pode representar a vista superior do vaso A? E a vista superior do vaso B?

b) Qual delas pode representar a vista la- teral esquerda do vaso A? E a vista lateral direita do vaso B?

40. Considere as figuras geométricas espaciais a seguir.

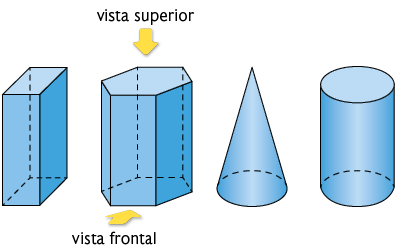
Ilustração de quatro figuras geométricas espaciais, dispostas lado a lado. As figuras tem a mesma altura. Elas são, da esquerda para direita: um paralelepípedo reto retângulo, um prisma de base hexagonal, um cone, e um cilindro. Há uma seta acima do paralelepípedo, apontada para baixo com a indicação 'vista superior'. Há outra seta, na frente do paralelepípedo, apontando para a face frontal, com a indicação 'vista frontal'.

a) Qual das sequências de figuras a seguir representa a vista superior dessas figuras geométricas nessa mesma disposição?

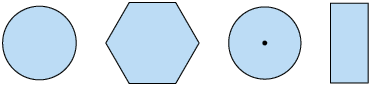
Ilustração de quatro figuras geométricas lado a lado. Da esquerda para direita: um círculo, um hexágono regular, um círculo com um ponto no centro, e um retângulo.

Ilustração de quatro figuras geométricas lado a lado. Da esquerda para direita: um retângulo, um hexágono regular, um círculo com um ponto no centro, e um outro círculo.

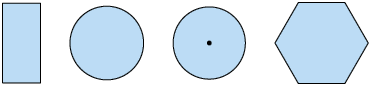
Ilustração de quatro figuras geométricas lado a lado. Da esquerda para direita: um retângulo, um círculo, outro círculo mas com um ponto no centro e um hexágono regular.

b) Desenhe em seu caderno a sequência de figuras que representa a vista frontal das figuras geométricas espaciais apresentadas.

Versão adaptada acessível

b) Descreva para um colega a sequência de figuras que representa a vista frontal das figuras geométricas espaciais apresentadas.

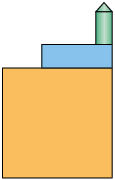
41. Analise o objeto a seguir.

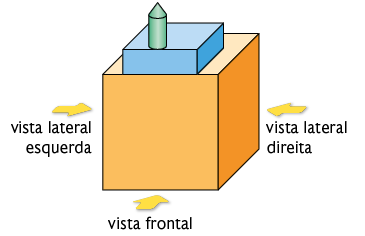
Ilustração de um objeto, formado por 4 figuras geométricas espaciais. Apontado para o lado esquerdo do objeto há uma seta horizontal com a indicação: 'vista lateral esquerda'; apontado para a face frontal do objeto, há uma seta com a indicação: 'vista frontal'; e apontado para o lado direito do objeto há uma seta horizontal com a indicação: 'vista lateral direita'. Observando cada peça do objeto como figuras específicas, temos: um cubo alaranjado, que é a base do objeto; acima do cubo há um paralelepípedo reto retângulo azul de base quadrada, que tem a medida dos lados dessa base menor que os lados do cubo alaranjado; acima do paralelepípedo azul há um objeto verde, de corpo cilíndrico com uma ponta acima, em formato de cone, se assemelhando ao formato de um lápis. O cubo alaranjado e o paralelepípedo azul estão com suas faces frontais alinhadas e centralizadas entre si. O objeto cilíndrico verde também está centralizado com essas faces frontais, e próximo a face frontal do paralelepípedo.

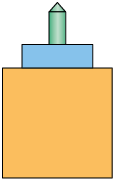
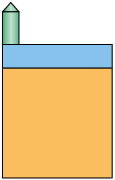
Entre as figuras geométricas a seguir, qual corresponde à:

a) vista lateral direita desse objeto?

b) vista frontal do objeto?

c) vista lateral esquerda desse objeto?

Ilustração de figuras geométricas empilhadas. Há um quadrado alaranjado; acima do quadrado há um retângulo azul de comprimento menor que o quadrado laranja; e acima do retângulo azul um retângulo verde com um triângulo verde em cima. Todas as figuras estão alinhadas verticalmente por seus centros. O retângulo azul e o quadrado alaranjado têm a mesma proporção das dimensões das faces das peças do objeto, de respectiva cor, da imagem descrita no cabeçalho da atividade, assim como a peça verde.

Ilustração de figuras geométricas empilhadas. Há um quadrado alaranjado; acima do quadrado há um retângulo azul com o mesmo comprimento do quadrado; e acima do retângulo azul um retângulo verde com um triângulo verde em cima. O retângulo e o triângulo verde estão alinhados pela esquerda com o retângulo azul e o cubo amarelo. O quadrado alaranjado e a peça verde têm a mesma proporção das dimensões das faces das peças do objeto, de respectiva cor, da imagem descrita no cabeçalho da atividade.

Página 222

Perspectivas

Na página 219, os desenhos que os estudantes fizeram representam vistas bidimensionais dos objetos, pois nelas identificamos duas dimensões (largura e altura). No entanto, os objetos colocados na mesa são tridimensionais, pois podemos identificar três dimensões (largura, altura e profundidade).

Contudo, é possível representar as três dimensões de um objeto em uma folha de papel, de modo que sua profundidade seja perceptível?

A resposta para essa pergunta é sim. Para isso, podemos usar técnicas de desenho em perspectiva, em que, por meio de conceitos geométricos, é possível representar objetos no plano de maneira que aparentem ter largura, altura e profundidade, ou seja, três dimensões.

Analise a seguir diferentes representações de uma mesma figura geométrica espacial.

Essa representação não faz uso de técnicas de perspectiva. Nela, não identificamos a profundidade do objeto.

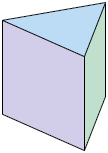
Ilustração de um prisma de base triangular em perspectiva, de modo que é possível observar a face superior e duas faces laterais.

Nessa outra representação, é usada uma técnica de perspectiva, na qual identificamos a ideia de profundidade.

Atenção!

Com base na técnica de perspectiva, podemos representar os elementos de determinada cena com profundidades diferentes.

Analise as obras de arte a seguir.

Pintura, em primeiro plano, a pintura retrata um pátio com várias pessoas em ambiente aberto. Ela está com um estilo de pintura mais próximo ao real, como uma fotografia. Está claro e aparece parte do céu com algumas nuvens. Ao fundo há alguns corredores longos, lado a lado, formados por uma sequência de dois pilares paralelos, com o topo em formato de semicírculo, como uma letra U invertida. Esses pilares vão em direção ao fundo da imagem e observa-se que vão se tornando gradativamente menores conforme estão mais longe. — *Architectural Capriccio with Jephthah and His Daughter*, de Dirk van Delen. Óleo sobre painel, $128 centímetros por 196 centímetros$ , 1633.

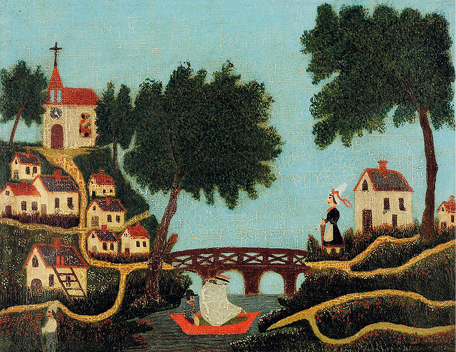
Pintura representando, do lado esquerdo, algumas casas em um morro e separado por uma ponte que passa sobre um rio, do lado direito há uma casa e uma pessoa. Há algumas árvores. No rio há um barco com uma pessoa. As casas são retratadas todas da mesma maneira, com a mesma cor em tom de amarelo, sem variação de luz ou sombra, aparecendo uma lateral com janelas e a frente. Elas variam de tamanho. Entre as casas aparecem alguns caminhos. Todas as figuras parecem estar sobre um mesmo plano, por isso não dá para reconhecer uma profundidade e uma correta relação de tamanho entre cada elemento. Os dois personagens parecem ser bem maiores que algumas casas. — *Landscape with Bridge Land*, de Henri Rousseau. Óleo sobre tela, $27 centímetros por 35 centímetros$ . 1875-1877.

Questão 8. Em qual dessas obras se faz o uso de perspectiva?

Página 223

Entre as diferentes técnicas de perspectiva, podemos citar a isométrica, a cavaleira e a cônica.

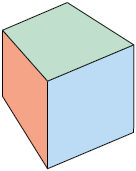
Analise a mesma figura geométrica representada por essas três técnicas de perspectiva.

Perspectiva isométrica: nessa representação, o objeto parece estar posicionado em três eixos que formam entre si um ângulo com medida de 120°.

Ilustração de 3 eixos, representados por 3 segmentos com seta na ponta, partindo de um mesmo ponto, de modo que entre eles é formado 3 ângulos de 120 graus, e a junção da indicação desses ângulos formando um círculo.

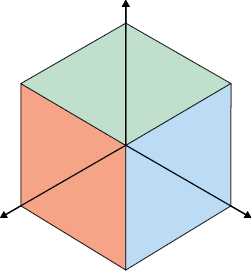
Ilustração de um cubo. O cubo está apoiado sobre os mesmos três eixos da ilustração anterior, de modo que as arestas ficam paralelas em relação ao eixo correspondente. As 3 faces do cubo possuem as arestas com o mesmo comprimento.

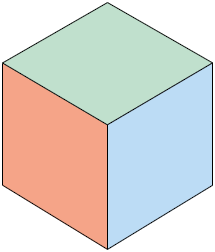
Ilustração de um cubo em perspectiva isométrica. O cubo é o mesmo da ilustração anterior.

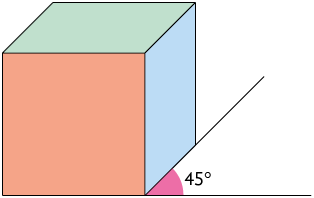
Perspectiva cavaleira: nessa representação, uma das vistas do objeto não sofre distorções, mas as demais, que estão visíveis, sim. É mantida nela uma relação entre o ângulo de inclinação na qual o objeto é verificado e a proporção entre as demais medidas de comprimento.

Ilustração de um cubo em perspectiva cavaleira de 45 graus. A face frontal do cubo é representada por um quadrado sem distorção, enquanto a face lateral, juntamente com a face superior, tem as arestas inclinadas 45 graus em relação a horizontal.

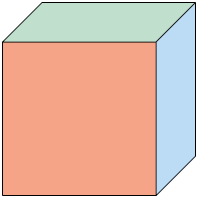
Ilustração de um cubo em perspectiva cavaleira de 45 graus. O cubo é o mesmo da ilustração anterior.

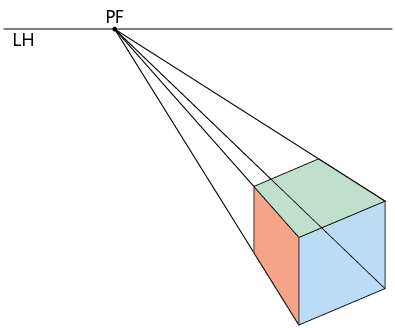
Perspectiva cônica: essa é a representação que mais se aproxima de como vemos um objeto ou de uma foto. Nesse tipo de perspectiva são usadas retas e um ponto de fuga (PF) sobre uma delas, chamada linha do horizonte (LH).

Ilustração dos elementos que geram a perspectiva cônica aplicada em um cubo. Há um traçado horizontal, denominado linha do horizonte e sobre essa linha há um ponto chamado ponto de fuga. Do ponto de fuga partem quatro seguimentos que vão se distanciando entre si conforme se distanciam da linha do horizonte. Sobre esses segmentos são traçados as arestas laterais e superiores do cubo, e em seguida completado as suas faces.

Ilustração de um cubo em perspectiva cônica. O cubo é o mesmo da ilustração anterior.

Página 224

Instrumentos e softwares

Perspectiva cônica com um ponto de fuga

Siga as orientações do professor e os passos a seguir para desenhar, partindo da vista frontal, a figura geométrica espacial representada a seguir utilizando a perspectiva cônica com um ponto de fuga.

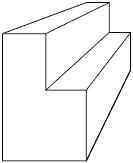
1º. Desenhe a linha do horizonte e, sobre ela, indique o ponto de fuga P. Desenhe também a face frontal da figura.

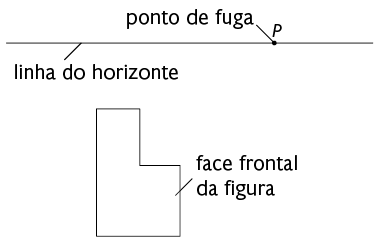
Ilustração da construção de uma figura em perspectiva cônica com um ponto de fuga. Há a linha do horizonte e sobre ela é indicado o ponto P, sendo o ponto de fuga. Abaixo da linha do horizonte está a face frontal da figura, construída como um polígono de 6 lados, semelhante a letra L.

2º. Ligue os vértices da figura até o ponto de fuga.

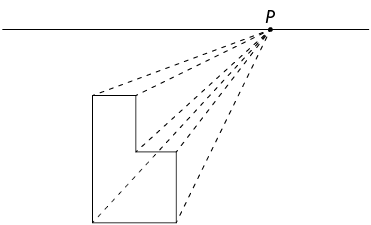
Ilustração da construção de uma figura em perspectiva cônica com um ponto de fuga, continuação da imagem anterior. Os vértices do polígono da face frontal são ligados por tracejados ao ponto P.

3º. De acordo com as linhas traçadas no passo anterior, desenhe o fundo da figura de maneira que os vértices correspondentes estejam sobre a mesma linha e as arestas correspondentes sejam paralelas.

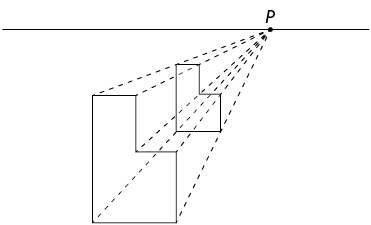
Ilustração da construção de uma figura em perspectiva cônica com um ponto de fuga, continuação da imagem anterior. Entre o ponto de fuga e o polígono que representa a face frontal, há outro polígono, semelhante ao primeiro, com os vértices sobre o tracejado.

4º. Ligue os vértices correspondentes.

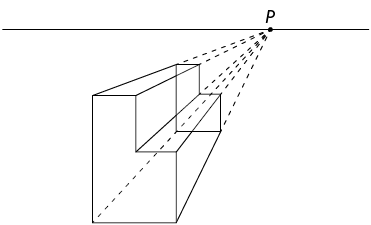
Ilustração da construção de uma figura em perspectiva cônica com um ponto de fuga, continuação da imagem anterior. Os vértices dos polígonos estão ligados, respectivamente, formando as arestas das faces laterais do prisma.

5º. Por último, apague os demais elementos que não fazem parte da figura geométrica espacial.

Questão 9. Em seu caderno, desenhe a face frontal de uma figura geométrica espacial. Seguindo os passos descritos anteriormente, desenhe essa figura na perspectiva cônica com um ponto de fuga.

Versão adaptada acessível

Questão 9. Junte-se a um colega e desenhem a face frontal de uma figura geométrica espacial. Seguindo os passos descritos anteriormente, desenhem essa figura na perspectiva cônica com um ponto de fuga.

Página 225

Instrumentos e softwares

Perspectiva central com dois pontos de fuga

Na página anterior, verificamos como construir uma figura geométrica espacial usando perspectiva cônica com um ponto de fuga a partir de uma face frontal. Agora, vamos aprender a desenhar usando outra técnica, a perspectiva central com dois pontos de fuga. Siga as orientações do professor e os passos a seguir para desenhar um paralelepípedo usando essa técnica.

1º. Desenhe a linha do horizonte e represente os pontos de fuga $F com índice 1$ e $F com índice 2$ sobre ela. Desenhe também a aresta frontal do paralelepípedo.

Ilustração de uma reta, e sobre ela dois pontos distantes entre si, que são os pontos de fuga, indicados com F com índice 1 e F com índice 2. Entre os dois pontos e abaixo da reta, há um segmento vertical, que representa uma aresta.

2º. Ligue as extremidades da aresta aos dois pontos de fuga.

Ilustração continuação da ilustração anterior. As extremidades da aresta estão ligadas aos dois pontos de fuga.

3º. Desenhe dois segmentos paralelos à aresta frontal com extremidades nas linhas traçadas no passo anterior. Em seguida, ligue as extremidades desses segmentos, conforme a imagem.

Ilustração continuação da ilustração anterior. Entre a aresta e cada ponto de fuga, há uma outra aresta vertical, delimitada pelo tracejado, com as extremidades ligadas as extremidades da aresta inicial, formando duas faces.

4º. Ligue cada uma das extremidades dos segmentos traçados no passo anterior até os pontos de fuga, conforme a imagem a seguir.

Ilustração continuação da ilustração anterior. A aresta superior de cada uma das faces formadas, está ligada a um dos pontos de fuga.

5º. Trace os segmentos que representam as arestas do paralelepípedo.

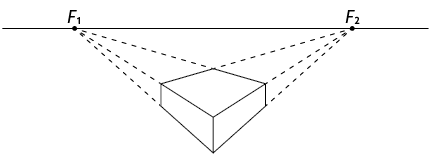
Ilustração continuação da ilustração anterior. Os vértices superiores das laterais estão ligados, formando a face superior.

6º. Por fim, apague os demais elementos que não fazem parte da figura.

Ilustração de um paralelepípedo em perspectiva cônica, sendo o mesmo construído na ilustração anterior.

Questão 10. Em seu caderno, desenhe um paralelepípedo usando a técnica de perspectiva central com dois pontos de fuga, mas, dessa vez, posicione a linha do horizonte e os pontos de fuga abaixo do paralelepípedo.

Versão adaptada acessível

Questão 10. Junte-se a um colega e desenhem um paralelepípedo usando a técnica de perspectiva central com dois pontos de fuga, mas, dessa vez, posicionem a linha do horizonte e os pontos de fuga abaixo do paralelepípedo.

Página 226

Atividades

Faça as atividades no caderno.

42. Em quais das figuras geométricas a seguir foi aplicada uma das técnicas de perspectiva?

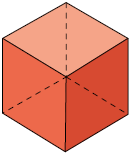
Ilustração de um cubo. É possível observar duas faces laterais e a superior, de modo que a figura parece estar posicionada sobre três eixos de mesma angulação entre si.

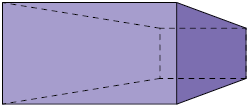
Ilustração de um paralelepípedo. Observa-se a face frontal, formada por um retângulo, e as arestas laterais se afastando ao fundo, não paralelas entre si, se encontrando nas respectivas arestas de um retângulo proporcional ao da face frontal, mas menor em escala.

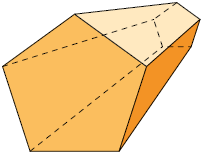
Ilustração de um prisma de base pentagonal. Observa-se a face frontal, formada por um pentágono, e as arestas laterais se afastando ao fundo, não paralelas entre si, se encontrando nas respectivas arestas de um pentágono proporcional ao da face frontal, mas menor em escala.

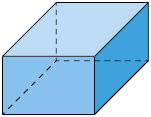
Ilustração de um paralelepípedo. Observa-se a face frontal, formada por um retângulo, e as arestas laterais se afastando ao fundo, paralelas entre si, se encontrando nas respectivas arestas de um retângulo de mesma dimensão ao da face frontal.

43. Relacione as figuras a seguir ao nome da respectiva perspectiva na qual ela foi construída. Para isso, escreva a letra e o número correspondentes.

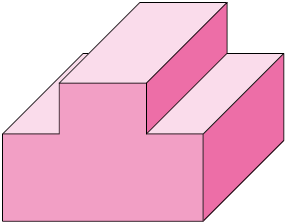
Ilustração de um prisma, cuja base é formada por um octógono irregular, semelhante ao formato de um pódio. Observa-se a face frontal, formada pelo heptágono, e as arestas laterais se afastando ao fundo, paralelas entre si, se encontrando nas respectivas arestas de um heptágono de mesma dimensão ao da face frontal.

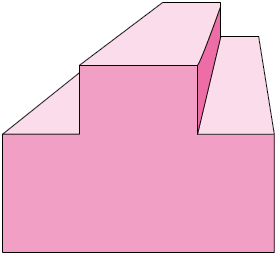
Ilustração de um prisma, cuja base é formada por um octógono irregular, como o da figura anterior. Observa-se a face frontal, formada pelo octógono, e as arestas laterais se afastando ao fundo, não paralelas entre si, se encontrando nas respectivas arestas de um octógono semelhante ao da face frontal mas em menor escala.

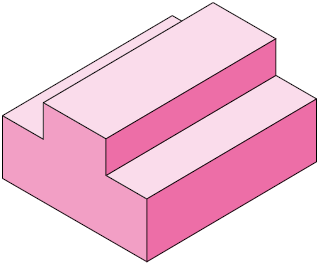
Ilustração de um prisma, cuja base é formada por um octógono irregular como o da figura anterior. Observando a disposição das faces e arestas, a figura parece estar posicionada sobre três eixos que possuem uma mesma angulação entre si.

1. Cônica.

2. Isométrica.

3. Cavaleira.

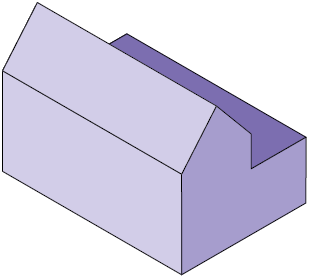
44. Qual das figuras a seguir foi construída com a perspectiva cavaleira?

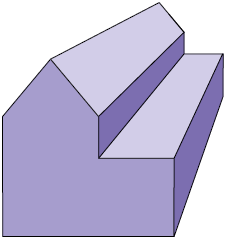
Ilustração de um prisma, cuja base é formada por um heptágono irregular lembrando a frente de uma casa. Observa-se a face frontal, formada pelo heptágono, e as arestas laterais se afastando ao fundo, não paralelas entre si, se encontrando nas respectivas arestas de um heptágono semelhante ao da face frontal, mas em menor escala.

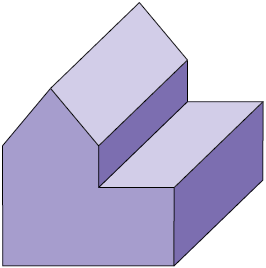
Ilustração de um prisma, cuja base é formada por um heptágono irregular como o da ilustração anterior. Observa-se a face frontal, formada pelo heptágono, e as arestas laterais se afastando ao fundo, paralelas entre si, se encontrando nas respectivas arestas de um heptágono de mesma dimensão ao da face frontal.

Ilustração de um prisma, cuja base é formada por um heptágono irregular como o da ilustração anterior. Observando a disposição das faces e arestas, a figura parece estar posicionada sobre três eixos que possuem uma mesma angulação entre si.

Página 227

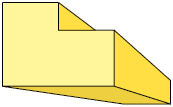
45. Para determinar o ponto de fuga de um polígono representado em perspectiva cônica, Gustavo prolongou algumas das arestas laterais, conforme a imagem a seguir.

Ilustração de um prisma em perspectiva cônica, cuja base é um hexágono irregular, semelhante a uma letra L.

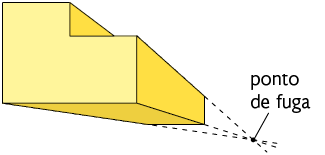
Ilustração do mesmo prisma de base hexagonal, em perspectiva cônica, da ilustração anterior. As arestas das faces laterais estão prolongadas para o fundo, se encontrando em um ponto, indicado como ponto de fuga.

Em seu caderno, construa uma figura geométrica espacial usando perspectiva cônica e um ponto de fuga. Depois, apague os elementos usados durante a construção que não fazem parte da figura. Em seguida, mostre o desenho que você fez para um colega, a fim de que ele possa determinar o ponto de fuga. Ao final, verifique se as respostas estão corretas.

Versão adaptada acessível

Junte-se a um colega e construam uma figura geométrica espacial usando perspectiva cônica e um ponto de fuga. Depois, apaguem os elementos usados durante a construção que não fazem parte da figura. Em seguida, mostrem o desenho que vocês fizeram para outra dupla, a fim de que eles possam determinar o ponto de fuga. Ao final, verifiquem se as respostas estão corretas.

46. Daniel desenhou em seu caderno as vistas frontal, lateral esquerda e superior de uma figura geométrica espacial. Analise a seguir os desenhos que ele fez.

Ilustração de um retângulo, dividido horizontalmente em 3 partes iguais. — Vista frontal.

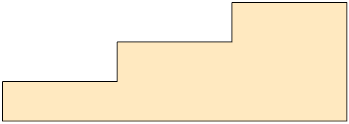
Ilustração de um octógono irregular, lembrando o formato de uma escada com 3 degraus, tendo eles a mesma altura e comprimento da parte superior. Essa figura tem a mesma altura do retângulo da ilustração anterior. — Vista lateral esquerda.

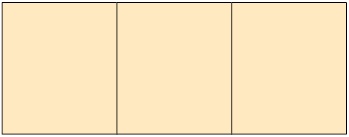
Ilustração de 1 retângulo dividido horizontalmente em 3 outros retângulos. Esse retângulo tem o mesmo comprimento da figura anterior. — Vista superior.

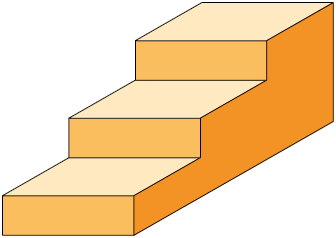
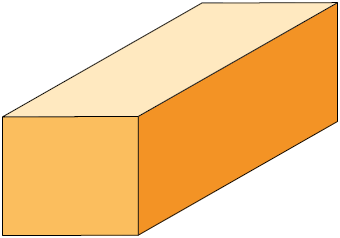
Qual das figuras geométricas espaciais a seguir representa a que Daniel usou para fazer os desenhos?

Ilustração de um prisma cuja base tem o formato de um octógono irregular. O prisma tem o formato de uma escada de 3 degraus, e está posicionado de modo que: sua base está na lateral; as faces superiores são 3 retângulos, que seriam o topo de cada degrau; e as faces frontais são 3 retângulos que seriam a altura desses degraus.

Ilustração de um paralelepípedo reto retângulo.

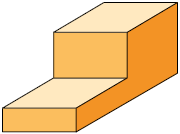
Ilustração de um prisma cuja base é um hexágono irregular. O prisma tem o formato de uma escada de 2 degraus, e está posicionado de modo que: sua base está na lateral; as faces superiores são 2 retângulos, que seriam o topo de cada degrau; e as faces frontais são 2 retângulos que seriam a altura desses degraus, sendo essas alturas diferentes entre si.

47. Considere as vistas a seguir.

Ilustração de um retângulo. Uma das laterais tem o mesmo comprimento da lateral do triângulo equilátero que está na outra ilustração desse atividade. — Vista frontal.

Ilustração de um triângulo equilátero. — Vista superior.

a) Em seu caderno, desenhe um poliedro que pode ser representado por essas vistas utilizando uma das perspectivas apresentadas.

b) Qual perspectiva você utilizou?

Versão adaptada acessível

a) Qual poliedro pode ser representado por essas vistas utilizando uma das perspectivas apresentadas?

48. Para cada item, desenhe em seu caderno uma figura geométrica espacial em perspectiva:

a) cônica usando um ponto de fuga.

b) central usando dois pontos de fuga.

Versão adaptada acessível

48. Junte-se a um colega e desenhem uma figura geométrica espacial em perspectiva:

a) cônica usando um ponto de fuga.

b) central usando dois pontos de fuga.

Página 228

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Uma lata com o formato cilíndrico será colocada dentro de uma embalagem que tem a forma de um paralelepípedo reto retângulo, conforme as figuras a seguir.

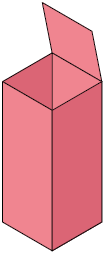
Ilustração de uma caixa, com a tampa superior levantada. A caixa tem o formato de um paralelepípedo reto retângulo.

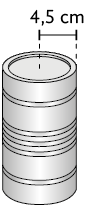
Ilustração de uma lata de formato cilíndrico. Está indicado que a face superior tem um raio de medida 4,5 centímetros.

Qual é a medida da área mínima que a tampa dessa caixa deve ter?

2. Em cada item, determine a medida do comprimento do arco.

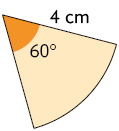
Ilustração de setor circular de um arco de circunferência de raio medindo 4 centímetros e ângulo de 60 graus.

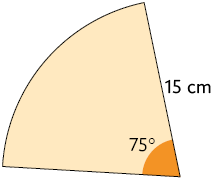
Ilustração de setor circular de um arco de circunferência de raio medindo 15 centímetros e ângulo de 75 graus.

3. Calcule a medida do comprimento aproximado da linha vermelha na figura a seguir, sabendo que:

$A B C D$ é um quadrado com o comprimento do lado medindo $7 metros$ ;

os pontos $A$ , $B$ , $C$ e $D$ são centros de circunferências;

$M$ , $N$ , $O$ e $P$ são pontos médios dos lados do quadrado $A B C D$ .

Ilustração de um quadrado A B C D. O lado A B é a base do quadrado, e os lados A D e B C, as laterais. Sobre os lados, há os pontos: P, que está sobre o lado A D; ponto O, que está sobre o lado C D; ponto N, que está sobre o lado B C; ponto M, que está sobre o lado A B. Há um segmento O M que divide o quadrado pela vertical. Há uma figura em vermelho, semelhante a um coração, formada por quatro arcos de circunferência que possuem centros em cada vértice do quadrado. Dois desses arcos são externos ao quadrado, que são: o arco de centro D, que tem uma extremidade no ponto P e a outra no ponto O; o arco de centro C, que tem uma extremidade no ponto N e outra no ponto O. Os outros dois arcos são internos ao quadrado e são: o arco de centro A, que tem uma extremidade no ponto P e a outra no ponto M; o arco de centro B, que tem uma extremidade no ponto N e outra no ponto M.

4. Nas imagens estão indicados os pontos de interseção entre as retas e a circunferências de centro O. Determine a posição relativa entre cada reta e essa circunferência.

Ilustração de uma circunferência de centro O e mais 6 retas. Observando cada reta em relação a circunferência temos: reta a, e reta e, cruzam a circunferência em dois pontos; retas b, c, d, cruzam a circunferência em um ponto; reta f, não cruza a circunferência.

5. Partindo das vistas a seguir, desenhe em seu caderno a figura geométrica espacial correspondente utilizando a técnica de perspectiva que julgar adequada.

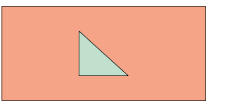
Ilustração de um retângulo alaranjado, cuja base é seu lado maior, com um triângulo retângulo verde em seu interior. — Vista lateral direita.

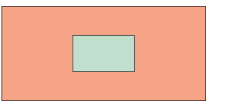
Ilustração de um retângulo alaranjado, com as mesmas dimensões do retângulo da ilustração anterior, mas agora em seu interior há um retângulo verde. — Vista lateral esquerda.

Ilustração de um quadrado alaranjado, de lados com o mesmo comprimento da base do retângulo da ilustração anterior. — Vista superior.

Versão adaptada acessível

5. Partindo das vistas a seguir, descreva para um colega a figura geométrica espacial correspondente utilizando a técnica de perspectiva que julgar adequada.