Resoluções - parte 1

O que eu já sei?

1. a) $6\cdot {10}^3+8\cdot {10}^2+7\cdot {10}^1+4\cdot {10}^1=$

$=6.000+800+70+40=6.910$

b) $6\cdot {10}^3+8\cdot {10}^2+7\cdot {10}^1+4\cdot {10}^0=$

$=6.000+800+70+4=6.874$

c) $6\cdot {10}^3+8\cdot {10}^2+7\cdot {10}^1\cdot 4\cdot {10}^0=$

$=6.000+800+70\cdot 4=7.080$

d) $6\cdot {10}^0+8\cdot {10}^1+7\cdot {10}^2+4\cdot {10}^3=$

$=6+80+700+4.000=4.786$

e) $6\cdot {10}^4+8\cdot {10}^3+7\cdot {10}^2+4\cdot {10}^1=$

$=60.000+8.000+700+40=68.740$

Comparando as decomposições dos itens, verificamos que a alternativa correta é a b.

2. Podemos representar o conjunto de colegas de Alexandre por meio de um diagrama de Venn. Primeiro, escrevemos nele as informações que são comuns a todos e, em seguida, o que é comum dois a dois, ou seja, aqueles que assistiram a apenas 1 filme. Por fim, incluímos aqueles que não assistiram aos filmes citados por Alexandre.

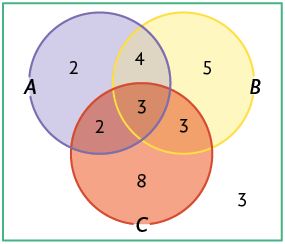
Assim, temos:

$3+2+4+3+2+5+8=27$

Subtraindo o total de colegas pelo resultado obtido, temos:

$30-27=3$

Portanto, 3 colegas de Alexandre não assistiram a nenhum dos três filmes.

3. Percebemos que o ângulo que mede $30°$ é alterno interno a $\hat{x}$. Assim, $\hat{x}=30°$. Sendo a figura apresentada um losango, podemos dividi-la em quatro triângulos congruentes. Com isso, para obter o valor de $\hat{y}$, efetuamos o seguinte cálculo.

$\hat{y}=180°-30°-90°=60°$

Logo, $\hat{x}=30°$ e $\hat{y}=60°$.

4. Para resolver os itens dessa atividade, é necessário verificar que a medida do volume de um cubo equivale ao cubo da medida de comprimento de uma de suas arestas.

a) $27=x^3$

$x=\sqrt[3]{27}$

$x=\sqrt[3]{3^3}$

$x=3$

Logo, o comprimento da aresta desse cubo mede $3\text{cm}$.

b) $125=x^3$

$x=\sqrt[3]{125}$

$x=\sqrt[3]{5^3}$

$x=5$

Logo, o comprimento da aresta desse cubo mede $5\text{cm}$.

5. a) Primeiro, devemos calcular 1% de R$ 1.500,00, ou seja, $\frac{1.500}{100}=15$. Multiplicando o resultado por 3, temos:

$15\cdot 3=45$

Desse modo, houve um aumento de R$ 45,00.

Adicionando o aumento ao valor inicial, temos:

$1.500+45=1.545$

Portanto, essa mesa custava R$ 1.545,00 em fevereiro.

b) Vamos calcular 1% do resultado obtido no item anterior, que é R$ 1.545,00. Assim, $\frac{1.545}{100}=15,45$. Multiplicando o resultado por 3, temos:

$15,45\cdot 3=46,35$

Desse modo, houve um desconto de R$ 46,35.

Retirando o desconto do preço atual da mesa, obtemos:

$1.545-46,35=1.498,65$

Portanto, o preço da mesa passou a ser R$ 1.498,65 em maio.

Sendo assim, o preço da mesa não voltou a ser R$ 1.500,00, mas passou a ser R$ 1.498,65 ao aplicar o desconto.

6. Como o raio da circunferência mede $19\mathrm{m}$ de comprimento e $\overline{AB}=2r$, temos:

$\overline{AB}=2r=2\cdot 19\text{m}=38\text{m}$

Subtraindo a medida do comprimento de $\overline{AB}$ da medida do comprimento de $\overline{AC}$, obtemos $59-38=21$.

Portanto, $\overline{BC}=21\mathrm{m}$.

7. Utilizando a regra de três simples, temos:

$\frac{16}{x}=\frac{240}{600}$

$240x=9.600$

$x=40$

Logo, considerando o mesmo ritmo de trabalho, seriam necessários 40 funcionários para produzir 600 embalagens.

8. Para resolver essa atividade, devemos considerar que a soma das moedas deve resultar em R$ 5,25, e o total de moedas deve ser igual a 15. Assim, temos as seguintes possibilidades, usando 15 moedas.

$15\cdot 0,25+0\cdot 0,5=3,75$

$14\cdot 0,25+1\cdot 0,5=4,00$

$13\cdot 0,25+2\cdot 0,5=4,25$

$12\cdot 0,25+3\cdot 0,5=4,50$

$11\cdot 0,25+4\cdot 0,5=4,75$

$10\cdot 0,25+5\cdot 0,5=5,00$

$9\cdot 0,25+6\cdot 0,5=5,25$

Portanto, para obter essa quantia, seriam necessárias 9 moedas de 25 centavos e 6 moedas de 50 centavos.

9. a) Para obter a média, adicionamos as notas obtidas (2.980) e dividimos o resultado pela quantidade de estudantes (40).

$\frac{2.980}{40}=74,5$

Logo, a média dos estudantes é 74,5.

A moda é 35, pois é o número que mais se repete nesse conjunto de valores.

Para determinar a mediana, devemos primeiro organizar os números em ordem crescente (ou decrescente).

35, 35, 35, 57, 58, 59, 59, 61, 62, 62, 63, 63, 64, 65, 67, 68, 69, 71, 73, 77, 81, 82, 82, 83, 84, 85, 85, 86, 87, 87, 88, 88, 90, 92, 94, 95, 96, 97, 97, 98

Em seguida, como a quantidade de valores nessa amostra é um número par, devemos calcular a média dos dois valores centrais.

$\frac{77+81}{2}=\frac{158}{2}=79$

Portanto, a mediana da nota dos estudantes é 79.

b) Resposta pessoal. Espera-se que os estudantes verifiquem que todas as medidas são válidas para representar esse conjunto de dados, a depender da finalidade da representação. Quanto menor for a variação entre as notas, mais próximos os valores estarão ente si.

10. Transformação de rotação de $90°$ no sentido anti-horário em relação ao ponto P.

11. Para determinar quantas possibilidades de escolha há na sorveteria, devemos multiplicar os tipos de casquinhas pelos tipos de sabores e pelos tipos de coberturas disponíveis, ou seja, $6\cdot 15\cdot 12=1.080$. Assim, há 1.080 possibilidades de tomar sorvete nessa sorveteria.

12. a) Como ambas as praças são retangulares, devemos adicionar as medidas de comprimento dos lados de cada imagem para obter os perímetros correspondentes.

Praça 1: $2\left(3y-z\right)+2\left(z+y\right)=6y-2z+2z+2y=8y$

Praça 2: $2\left(3x+y\right)+2\left(2y\right)=6x+2y+4y=6x+6y$

Portanto, a medida do perímetro da praça 1 é dada pela expressão $8y$ e a medida do perímetro da praça 2 é dada pela expressão $6x+6y$.

b) Para a praça 1 serão necessários $56\mathrm{m}$ de cerca, pois $8y=8\cdot 7=56$. Para a praça 2 serão necessários $72\mathrm{m}$ de cerca, pois $6x+6y=6\cdot 5+6\cdot 7=30+42=72$.

13. a) Sugestão de resposta:

$a_n=4n-6$, em que $n>0$.

b) Utilizando a lei de formação do item anterior, temos:

$a_{20}=4\cdot 20-6=80-6=74$

Portanto, o vigésimo termo da sequência é 74.

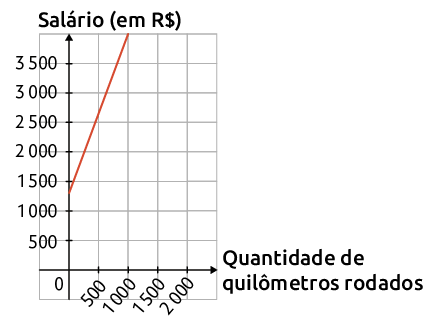
14. a) A equação que possibilita determinar o salário de Roberto é dada por $y=1.300+2,5x$.

b) Analisando essa equação, verificamos que ela representa uma função linear, ou seja, o salário de Roberto vai aumentar conforme também aumenta a quantidade de quilômetros rodados.

15. A. $A=b\cdot h=5\cdot 3=15$

Portanto, a área do paralelogramo mede $15{\text{cm}}^2$.

B. $A=\frac{b\cdot h}{2}=\frac{6\cdot 3}{2}=9$

Portanto, a área do triângulo mede $9{\text{cm}}^2$.

C. $A=\frac{\left(B+b\right)\cdot h}{2}=\frac{\left(5+2\right)\cdot 4}{2}=\frac{7\cdot 4}{2}=14$

Portanto, a área do trapézio mede $14{\text{cm}}^2$.

D. $A=\frac{D\cdot d}{2}=\frac{5\cdot 3}{2}=\frac{15}{2}=7,5$

Portanto, a área do losango mede $7,5{\text{cm}}^2$.

16. a) Existem 4 possibilidades de números pares para essa situação (2, 4, 6 e 8). Assim, a probabilidade de sortear um número par é:

$\frac{4}{8}=\frac{2}{4}=\frac{1}{2}$, ou seja, 50%.

b) Existem 8 números maiores ou iguais a 5 (5, 6, 7, 8, 9, 10, 11 e 12). Assim, a probabilidade de sortear um número maior ou igual a 5 é:

$\frac{8}{12}=\frac{4}{6}=\frac{2}{3}$, ou seja, $\frac{2}{3}\simeq 66\%$.

c) Existem 14 números menores do que 15. Assim, a probabilidade é dada por:

$\frac{14}{20}=\frac{7}{10}$, ou seja, 70%.

17. a) Afirmação verdadeira, pois $1\text{L}$ equivale a $1{\text{dm}}^3$.

b) Afirmação falsa. Sugestão de correção:

$1.000{\text{dm}}^3$ equivalem a $1.000\text{L}$.

c) Afirmação verdadeira, pois $1{\text{m}}^3$ equivale a $1.000\text{L}$.

d) Afirmação falsa. Sugestão de correção:

$100.000\text{L}$ equivalem a $100{\text{m}}^3$.

Unidade 1

Os números reais

Questão 1. Resposta pessoal. Espera-se que os estudantes efetuem a pesquisa de modo responsável, consultem dados confiáveis e validem a fonte das informações, a fim de obter bons resultados. Além disso, espera-se que eles compartilhem com os colegas o resultado do trabalho, colaborando para a construção significativa de conhecimento de todos.

Questão 2. Para representar o número irracional $\sqrt{8}$ na reta numérica, podem ser executadas as etapas apresentadas a seguir.

1ª. Construa um quadrado cujo comprimento do lado mede 4 unidades $\left(\text{4 u}\right)$.

2ª. Em seguida, faça a decomposição desse quadrado em 4 quadrados com o comprimento do lado medindo $\text{2 u}$.

3ª. Trace as diagonais em cada um dos quadrados obtidos.

Como cada um dos triângulos obtidos (destacados em verde) tem área medindo 2 unidades, consequentemente a área do quadrado verde mede 8 unidades. Portanto, cada um de seus lados mede $\sqrt{8}\text{u}$ de comprimento.

4ª. Com o auxílio de um compasso, transporte para a reta numérica a medida de comprimento do lado do quadrado verde.

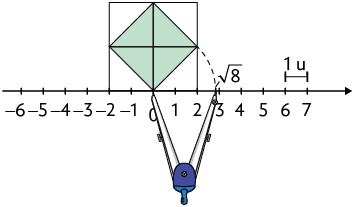
Atividades

1. Para representar o número $2\sqrt{2}$ na reta numérica, podemos utilizar o mesmo procedimento e os mesmos valores da questão 2, apresentada na página 15, já que $\sqrt{8}=2\sqrt{2}$.

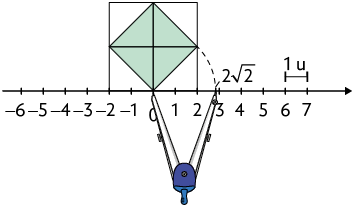
2. Os números irracionais apresentados na atividade são $\sqrt{2}$, $-\frac{\pi }{2}$, $\sqrt{3}$, $\frac{\sqrt{5}}{3}$ e $\pi$.

3. Comparando $\sqrt{3}$ com as raízes quadradas exatas mais próximas, verificamos que $\sqrt{1}<\sqrt{3}<\sqrt{4}$. Assim:

$1<\sqrt{3}<2$

$1,7^2<3<1,8^2$

$1,{73}^2<3<1,{74}^2$

$2,9929<3<3,0276$

$\sqrt{2,9929}<\sqrt{3}<\sqrt{3,0276}$

$1,73<\sqrt{3}<1,74$

Continuando esse processo, obtemos $\sqrt{3}=1,7320...$

4. O maior número é $\frac{7}{3}$, pois $\frac{7}{3}=2,3333...$ e $\sqrt{5}=2,2360...$

5. Resposta no final da seção Resoluções.

6. Resposta no final da seção Resoluções.

O que eu estudei?

1. São irracionais os números $\frac{\sqrt{3}}{2}$ e $\sqrt{21}$.

2. a) Alternativa falsa. Sugestão de correção: O número $2,\overline{21}$ adicionado ao número 5 resulta em um número racional.

b) Alternativa verdadeira.

c) Alternativa falsa. Sugestão de correção: Um número irracional é um número real cuja representação decimal é infinita e não periódica.

d) Alternativa falsa. Sugestão de correção: A representação decimal do número irracional $\sqrt{7}$ é $2,6457...$

e) Alternativa verdadeira.

3. a) Como $\sqrt{2}\simeq 1,41$ e $\sqrt{4}=2$, então $\sqrt{2}<\sqrt{4}$.

b) Podemos escrever $1,3\bar{2}$ como $1,32222...$ Sendo assim, comparando as casas decimais, verificamos que $1,3\bar{2}<1,32419...$.

c) Como $-\pi \simeq -3,14$ e $-2\sqrt{2}\simeq -2,83$, então $-\pi <-2\sqrt{2}$.

d) Como $3\sqrt{2}\simeq 4,24$ e $\frac{\sqrt{7}}{2}\simeq 1,32$, então $3\sqrt{2}>\frac{\sqrt{7}}{2}$.

e) Como $-\sqrt{81}=-9$, então $-\sqrt{81}>-10,\bar{5}$.

f) Como $3\sqrt{3}\simeq 5,2$ e $\frac{12}{5}=2,4$, então $3\sqrt{3}>\frac{12}{5}$.

g) Podemos escrever $0,\overline{15}$ como $0,151515...$ Sendo assim, comparando as casas decimais, verificamos que $0,1010010001<0\overline{15}$.

h) Como $\frac{\pi }{3}\simeq 1,05$, então $\frac{\pi }{3}>1$.

4. a) Resposta no final da seção Resoluções.

b) Resposta no final da seção Resoluções.

5. Resposta no final da seção Resoluções.

6. Para representar o número irracional $2\sqrt{8}$ na reta numérica, executamos as etapas apresentadas a seguir.

1ª. Construa um quadrado cujo comprimento do lado mede 8 unidades $\left(\text{8 u}\right)$.

2ª. Em seguida, faça a decomposição desse quadrado em 4 quadrados com o comprimento do lado medindo $\text{4 u}$.

3ª. Trace as diagonais em cada um dos quadrados obtidos.

Como cada um dos triângulos obtidos (destacados em verde) tem área medindo 8 unidades, consequentemente a área do quadrado verde mede 32 unidades. Portanto, cada um de seus lados mede $\sqrt{32}\text{u}=2\sqrt{8}\text{u}$ de comprimento.

4ª. Com o auxílio de um compasso, transporte para a reta numérica a medida de comprimento do lado do quadrado em verde.

Unidade 2

Potenciação e radiciação

Atividades

1. a) $1^{63}=1$

b) ${151}^1=151$

c) ${500}^0=1$

d) $0^9=0$

e) ${13}^2=13\cdot 13=169$

f) ${\left(7\right)}^{-3}={\left(\frac{1}{7}\right)}^3=\frac{1^3}{7^3}=\frac{1}{343}$

g) ${\left(-4\right)}^3=\left(-4\right)\cdot \left(-4\right)\cdot \left(-4\right)=-64$

h) ${\left(-\frac{2}{5}\right)}^{-2}={\left(-\frac{5}{2}\right)}^2=\left(-\frac{5}{2}\right)\cdot \left(-\frac{5}{2}\right)=\frac{25}{4}$

i) ${\left(\frac{2}{3}\right)}^5=\frac{2^5}{3^5}=\frac{2\cdot 2\cdot 2\cdot 2\cdot 2}{3\cdot 3\cdot 3\cdot 3\cdot 3}=\frac{32}{243}$

j) ${\left(-\frac{10}{21}\right)}^0=1$

2. a) ${\left(8\right)}^{-5}={\left(\frac{1}{8}\right)}^5=\left(\frac{1^5}{8^5}\right)=\frac{1}{8\cdot 8\cdot 8\cdot 8\cdot 8}=\frac{1}{32.768}<1$

b) ${\left(\frac{4}{3}\right)}^{-3}={\left(\frac{3}{4}\right)}^3=\left(\frac{3^3}{4^3}\right)=\frac{3\cdot 3\cdot 3}{4\cdot 4\cdot 4}=\frac{27}{64}<1$

c) ${\left(\frac{2}{9}\right)}^{-2}={\left(\frac{9}{2}\right)}^2=\left(\frac{9^2}{2^2}\right)=\frac{9\cdot 9}{2\cdot 2}=\frac{81}{4}>1$

d) ${\left(\frac{11}{15}\right)}^{-1}={\left(\frac{15}{11}\right)}^1=\frac{15}{11}>1$

e) ${\left(\frac{7}{3}\right)}^{-4}={\left(\frac{3}{7}\right)}^4=\frac{3^4}{7^4}=\frac{3\cdot 3\cdot 3\cdot 3}{7\cdot 7\cdot 7\cdot 7}=\frac{81}{2.401}<1$

f) ${\left(\frac{15}{14}\right)}^{-2}={\left(\frac{14}{15}\right)}^2=\frac{{14}^2}{{15}^2}=\frac{14\cdot 14}{15\cdot 15}=\frac{196}{225}<1$

Portanto, as potências das alternativas c e d são maiores do que 1.

3. a) $2^5\cdot 2^3=2^{5+3}=2^8=256$

b) ${\left(-8\right)}^{21}\cdot {\left(-8\right)}^{-18}={\left(-8\right)}^{21-18}=$

$={\left(-8\right)}^3=-512$

c) $\left(\frac{4}{3}\right)\cdot {\left(\frac{4}{3}\right)}^2={\left(\frac{4}{3}\right)}^{1+2}=$

$={\left(\frac{4}{3}\right)}^3=\frac{4\cdot 4\cdot 4}{3\cdot 3\cdot 3}=\frac{64}{27}$

d) ${\left(-3\right)}^2\cdot {\left(\frac{1}{2}\right)}^2={\left(-3\cdot \frac{1}{2}\right)}^2={\left(-\frac{3}{2}\right)}^2=\left(-\frac{3}{2}\right)\cdot \left(-\frac{3}{2}\right)=\frac{9}{4}$

e) ${\left(10\right)}^{-2}:{\left(10\right)}^3={\left(10\right)}^{-2-3}={\left(10\right)}^{-5}=$

$={\left(\frac{1}{10}\right)}^5=\frac{1}{100.000}=0,00001$

f) ${\left(\frac{3}{2}\right)}^3:{\left(\frac{6}{5}\right)}^3={\left(\frac{3}{2}\mathrm{ :}\frac{6}{5}\right)}^3={\left(\frac{3}{2}\cdot \frac{5}{6}\right)}^3={\left(\frac{15}{12}\right)}^3=$

$={\left(\frac{5}{4}\right)}^3=\frac{5^3}{4^3}=\frac{5\cdot 5\cdot 5}{4\cdot 4\cdot 4}=\frac{125}{64}$

g) ${\left(4^2\right)}^3=4^{2\cdot 3}=4^6=4.096$

h) ${\left(2^{-3}\right)}^4=2^{-3\cdot 4}=2^{-12}={\left(\frac{1}{2}\right)}^{12}=\frac{1^{12}}{2^{12}}=\frac{1}{4.096}$

4. a) ${\left(-3\right)}^2\cdot {\left(-3\right)}^7={\left(-3\right)}^{2+7}={\left(-3\right)}^9=-19.683$

b) $\frac{{11}^{-8}}{{11}^{-5}}={11}^{-8-\left(-5\right)}={11}^{-8+5}={11}^{-3}=\frac{1}{{11}^3}\simeq 0,00075$

c) ${\left(\frac{5}{2}\right)}^3=\frac{5^3}{2^3}=\frac{125}{8}=15,625$

d) $\frac{5^3}{2}=\frac{125}{2}=62,5$

e) ${\left(2\cdot 5\right)}^4={10}^4=10.000$

f) ${[2\cdot (-8)]}^2={(-16)}^2=256$

5. a) $\left(2^2\cdot 5^2\right):4^1={10}^2:4=100:4=25$

b) ${16}^3:{\left(-8\right)}^4+{15}^0-1^{11}=4.096:4.096+1-1=$

$=1+1-1=1$

c) $4^{-3}+{\left(-\frac{1}{2}\right)}^5=\frac{1}{4^3}+\frac{-1}{2^5}=\frac{1}{64}-\frac{1}{32}=\frac{1}{64}-\frac{2}{64}=-\frac{1}{64}$

d) ${\left(\frac{8}{3}\right)}^{-2}+{\left(\frac{9}{4}\right)}^3={\left(\frac{3}{8}\right)}^2+{\left(\frac{9}{4}\right)}^3=\frac{9}{64}+\frac{729}{64}=\frac{738}{64}=\frac{369}{32}$

e) ${\left(1+\frac{4}{5}\right)}^3-{\left(\frac{5}{3}\right)}^{-4}={\left(\frac{9}{5}\right)}^3-{\left(\frac{3}{5}\right)}^4=\frac{729}{125}-\frac{81}{625}=$

$=\frac{3.645}{625}-\frac{81}{625}=\frac{3.645-81}{625}=\frac{3.564}{625}$

6. a) Como $-243={\left(-3\right)}^5$ e, com isso, ${\left(-3\right)}^x=-243={\left(-3\right)}^5$, verificamos que $x=5$.

b) Todo número elevado a 0 é igual a 1. Sendo assim, ${\left(\frac{11}{7}\right)}^x=1$. Portanto, $x=0$.

c) O número 1 elevado a qualquer potência é igual a ele mesmo. Sendo assim, $x^{100}=1$. Portanto, $x=1$.

d) Como $-\frac{1}{27}={\left(-\frac{1}{3}\right)}^3={\left(-3\right)}^{-3}$ e, com isso, $x^{-3}=-\frac{1}{27}={\left(-\frac{1}{3}\right)}^3={\left(-3\right)}^{-3}$. Portanto, $x=-3$.

7. a) ${10}^2=10\cdot 10=100$

b) ${10}^5=10\cdot 10\cdot 10\cdot 10\cdot 10=100.000$

c) ${10}^8=10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10=100.000.000$

d) ${10}^7=10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10=10.000.000$

e) ${10}^3=10\cdot 10\cdot 10=1.000$

f) ${10}^0=1$

8. No caminhão, há 12 caixas maiores, cada uma com 12 caixas pequenas, e cada caixa pequena tem 12 ovos. Sendo assim, a quantidade de ovos no caminhão é dada por:

${12}^3=12\cdot 12\cdot 12=1.728$, ou seja, $1.728$ ovos.

9. Note que $4^{18}+4^{18}+4^{18}+4^{18}=4\cdot 4^{18}=4^1\cdot 4^{18}=4^{1+18}=4^{19}$.

Como $4^{20}>4^{19}$, então $4^{20}>4^{18}+4^{18}+4^{18}+4^{18}$.

10. a) $1.320.000.000=1,32\cdot 1.000.000.000=1,32\cdot {10}^9$

b) $149.600.000=1,496\cdot 100.000.000=1,496\cdot {10}^8$

c) $0,000001=1\cdot 0,000001=1\cdot {10}^{-6}$

d) $0,007=7\cdot 0,001=7\cdot {10}^{-3}$

11. a) Note que $5\cdot {10}^6=50\cdot {10}^5$ . Desse modo:

$7,93\cdot {10}^5+5\cdot {10}^6=7,93\cdot {10}^5+50\cdot {10}^5=$

$=\left(7,93+50\right)\cdot {10}^5=57,93\cdot {10}^5=5,793\cdot {10}^6$

b) Note que $3,99\cdot {10}^{-5}=399\cdot {10}^{-7}$. Desse modo:

$3,99\cdot {10}^{-5}-4,92\cdot {10}^{-7}=399\cdot {10}^{-7}-4,92\cdot {10}^{-7}=$

$=\left(399-4,92\right)\cdot {10}^{-7}=394,08\cdot {10}^{-7}=3,9408\cdot {10}^{-5}$

Questão 1. Espera-se que os estudantes concluam que o inventor do cubo mágico foi o húngaro Ernő Rubik e que o brinquedo também é chamado Cubo de Rubik em homenagem ao seu criador.

Questão 2.

a) $5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=5^7=78.125$

b) $3\cdot 3\cdot 3\cdot 3=3^4=81$

c) $\left(-2\right)\cdot \left(-2\right)\cdot \left(-2\right)\cdot \left(-2\right)\cdot \left(-2\right)={\left(-2\right)}^5=-32$

d) $2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2=2^6=64$

Questão 3. Resposta pessoal. Espera-se que os estudantes concluam com suas pesquisas que esse símbolo é uma criação do alemão Christoff Rudolff, em seu livro Die Coss, de 1525.

Atividades

12. a) O comprimento do lado do quadrado mede $16\text{cm}$, pois ${16}^2=16\cdot 16=256$.

Como um quadrado tem 4 lados, efetuamos:

$4\cdot 16\text{cm}=64\text{cm}$

Portanto, o perímetro desse quadrado mede $64\text{cm}$.

b) O comprimento do lado do quadrado mede $19\text{cm}$, pois ${19}^2=19\cdot 19=361$.

Como um quadrado tem 4 lados, efetuamos:

$4\cdot 19\text{cm}=76\text{cm}$

Portanto, o perímetro desse quadrado mede $76\text{cm}$.

c) O comprimento do lado do quadrado mede $21\text{cm}$, pois ${21}^2=21\cdot 21=441$.

Como um quadrado tem 4 lados, efetuamos:

$4\cdot 21\text{cm}=84\text{cm}$

Portanto, o perímetro desse quadrado mede $84\text{cm}$.

d) O comprimento do lado do quadrado mede $24\text{cm}$, pois ${24}^2=24\cdot 24=576$.

Como um quadrado tem 4 lados, efetuamos:

$4\cdot 24\text{cm}=96\text{cm}$

Portanto, o perímetro desse quadrado mede $96\text{cm}$.

13. a) $\sqrt[3]{512}=8$, pois $8^3=8\cdot 8\cdot 8=512$.

Portanto, o comprimento da aresta mede $\text{8 cm}$.

b) $\sqrt[3]{1.331}=11$, pois ${\text{1}1}^3=11\cdot 11\cdot 11=1.331$.

Portanto, o comprimento da aresta mede $\text{11 cm}$.

c) $\sqrt[3]{3.375}=15$, pois ${\text{1}5}^3=15\cdot 15\cdot 15=3.375$.

Portanto, o comprimento da aresta mede $\text{15 cm}$.

d) $\sqrt[3]{4.913}=17$, pois ${\text{1}7}^3=17\cdot 17\cdot 17=4.913$.

Portanto, o comprimento da aresta mede $\text{17 cm}$.

14. a) Como ${15}^3=3.375$, então $\sqrt[3]{3.375}=15$.

b) Como ${35}^2=1.225$, então $\sqrt[]{1.225}=35$.

c) Como ${41}^2=1.681$, então $\sqrt{1.681}=41$.

d) Como ${18}^3=5.832$, então $\sqrt[3]{5.832}=18$.

e) Como $8^4=4.096$, então $\sqrt[4]{4.096}=8$.

f) Como ${24}^3=13.824$, então $\sqrt[3]{13.824}=24$.

15. a) $\sqrt[n]{81}=9$

$\sqrt[n]{9^2}=9^1$

$9^{\frac{2}{n}}=9^1$

$\frac{2}{n}=1$

$n=2$

b) $\sqrt[n]{125}=5$

$\sqrt[n]{5^3}=5^1$

$5^{\frac{3}{n}}=5^1$

$\frac{3}{n}=1$

$n=3$

c) $\sqrt[\mathrm{}n]{32}=2$

$\sqrt[n]{2^5}=2^1$

$2^{\frac{5}{n}}=2^1$

$\frac{5}{n}=1$

$n=5$

d) $\sqrt[n]{128}=2$

$\sqrt[n]{2^7}=2^1$

$2^{\frac{7}{n}}=2^1$

$\frac{7}{n}=1$

$n=7$

e) $\sqrt[n]{2.187}=3$

$\sqrt[n]{3^7}=3^1$

$3^{\frac{7}{n}}=3^1$

$\frac{7}{n}=1$

$n=7$

f) $\sqrt[n]{256}=4$

$\sqrt[n]{4^4}=4^1$

$4^{\frac{4}{n}}=4^1$

$\frac{4}{n}=1$

$n=4$

16. Vamos analisar cada um dos itens.

A. $\sqrt[5]{-32}$ tem índice ímpar e radicando negativo, logo tem raiz real.

B. $\sqrt[8]{-256}$ tem índice par e radicando negativo, logo não tem raiz real.

C. $\sqrt[3]{-343}$ tem índice ímpar e radicando negativo, logo tem raiz real.

D. $\sqrt[4]{81}$ tem índice par e radicando positivo, logo tem raiz real.

E. $\sqrt[7]{2.187}$ tem índice ímpar e radicando positivo, logo tem raiz real.

F. $\sqrt[12]{-4.096}$ tem índice par e radicando negativo, logo não tem raiz real.

G. $\sqrt{-12}$ tem índice par e radicando negativo, logo não tem raiz real.

H. $\sqrt[7]{-2.187}$ tem índice ímpar e radicando negativo, logo tem raiz real.

Portanto, as raízes definidas no conjunto dos números reais são A, C, D, E e H.

17. a) ${27}^{\frac{1}{4}}=\sqrt[4]{{27}^1}=\sqrt[4]{27}$

b) ${40}^{\frac{2}{5}}=\sqrt[5]{{40}^2}=\sqrt[5]{1.600}$

c) ${\left(\frac{7}{6}\right)}^{\frac{2}{3}}=\sqrt[3]{{\left(\frac{7}{6}\right)}^2}=\sqrt[3]{\frac{49}{36}}$

d) $\sqrt{18}=\sqrt[2]{{18}^1}={18}^{\frac{1}{2}}$

e) $\sqrt[3]{6^5}=6^{\frac{5}{3}}$

f) $\sqrt[5]{81}=\sqrt[5]{9^2}=9^{\frac{2}{5}}$

18. a) ${\left(2^{\frac{3}{4}}\right)}^{\frac{1}{3}}=2^{\frac{3}{4}\cdot \frac{1}{3}}=2^{\frac{1}{4}}=\sqrt[4]{2}\ne \sqrt[4]{2^3}$

b) ${\left(5^{\frac{9}{10}}\right)}^{\frac{5}{3}}=5^{\frac{9}{10}\cdot \frac{5}{3}}=5^{\frac{3}{2}}=\sqrt[2]{5^3}=\sqrt{5^3}$

c) ${\left(3^{\frac{3}{8}}\right)}^2=3^{\frac{3}{8}\cdot \frac{2}{1}}=3^{\frac{3}{4}}=\sqrt[4]{3^3}$

d) ${\left({11}^{\frac{10}{3}}\right)}^{\frac{3}{4}}={11}^{\frac{10}{3}\cdot \frac{3}{4}}={11}^{\frac{5}{2}}=\sqrt[2]{{11}^5}=\sqrt{{11}^5}$

Portanto, as igualdades verdadeiras são aquelas presentes nos itens b, c e d.

19. a) $\sqrt{\frac{9}{4}}=\frac{\sqrt{9}}{\sqrt{4}}=\frac{3}{2}$

b) $\sqrt{\frac{25}{100}}=\frac{\sqrt{25}}{\sqrt{100}}=\frac{5}{10}$

c) $\sqrt{\frac{64}{144}}=\frac{\sqrt{64}}{\sqrt{144}}=\frac{8}{12}$

d) $-\sqrt{\frac{121}{256}}=-\frac{\sqrt{121}}{\sqrt{256}}=-\frac{11}{16}$

e) $\sqrt[3]{-\frac{1}{8}}=\frac{\sqrt[3]{-1}}{\sqrt[3]{8}}=\frac{-1}{2}=-\frac{1}{2}$

f) $\sqrt[4]{\frac{1}{81}}=\frac{\sqrt[4]{1}}{\sqrt[4]{81}}=\frac{1}{3}$

20. a) $\sqrt[3]{\sqrt[]{2}}=\sqrt[3\cdot 2]{2}=\sqrt[6]{2}$

b) $\sqrt[4]{\sqrt[3]{5}}=\sqrt[4\cdot 3]{5}=\sqrt[12]{5}$

c) $\sqrt[]{\sqrt[5]{8}}=\sqrt[2\cdot 5]{8}=\sqrt[10]{8}$

d) $\sqrt[6]{\sqrt[3]{13}}=\sqrt[6\cdot 3]{13}=\sqrt[18]{13}$

e) $\sqrt[]{\sqrt[7]{\sqrt[3]{9}}}=\sqrt[2\cdot 7\cdot 3]{9}=\sqrt[42]{9}$

f) $\sqrt[4]{\sqrt[3]{\sqrt[]{16}}}=\sqrt[4\cdot 3\cdot 2]{16}=\sqrt[24]{16}$

21. A. $\sqrt{7}\cdot \sqrt{21}=\sqrt{7\cdot 21}$ é verdadeira pela terceira propriedade.

B. $\sqrt[3]{5^{15}}=5^{\frac{15}{3}}=5^5$

$\sqrt[]{5^{20}}=5^{\frac{20}{2}}=5^{10}$

Portanto, a igualdade não é verdadeira.

C. $\sqrt[7]{\frac{19}{4}}=\frac{\sqrt[7]{19}}{\sqrt[7]{4}}$ é verdadeira pela terceira propriedade.

22. A. A igualdade em A é verdadeira pela segunda propriedade.

B. A igualdade em B não é verdadeira, pois a terceira propriedade afirma que $\sqrt[n]{a}\cdot \sqrt[n]{b}=\sqrt[n]{a\cdot b}$.

C. A igualdade em C é verdadeira, pois é a definição de expoente fracionário.

D. A igualdade em D não é verdadeira, pois a terceira propriedade afirma que $\sqrt[m\cdot n]{\frac{a}{b}}=\frac{\sqrt[m\cdot n]{a}}{\sqrt[m\cdot n]{b}}$.

E. A igualdade em E não é verdadeira, pois a quarta propriedade afirma que $\sqrt[n]{\sqrt[p]{a}}=\sqrt[n\cdot p]{a}$.

F. A igualdade em F é verdadeira pela terceira propriedade.

23. A. $\frac{\sqrt[3]{2}\cdot \sqrt[3]{5}\cdot \sqrt[3]{9}}{\sqrt[3]{4}\cdot \sqrt[3]{10}}=\frac{\sqrt[3]{2\cdot 5\cdot 9}}{\sqrt[3]{4\cdot 10}}=\frac{\sqrt[3]{90}}{\sqrt[3]{40}}=\sqrt[3]{\frac{90}{40}}=\sqrt[3]{\frac{9}{4}}$

B. $\frac{\sqrt[9]{8}\cdot \sqrt[9]{\frac{2}{3}}}{\sqrt[9]{5}\cdot \sqrt[9]{4}}=\frac{\sqrt[9]{8\cdot \frac{2}{3}}}{\sqrt[9]{5\cdot 4}}=\frac{\sqrt[9]{\frac{16}{3}}}{\sqrt[9]{20}}=\sqrt[9]{\frac{\frac{16}{3}}{20}}=\sqrt[9]{\frac{16}{60}}=\sqrt[9]{\frac{4}{15}}$

C. $\frac{\sqrt[5]{\frac{7}{6}}\cdot \sqrt[5]{\frac{8}{5}}}{\sqrt[5]{\frac{3}{2}}\cdot \sqrt[5]{\frac{1}{2}}}=\frac{\sqrt[5]{\frac{7\cdot 8}{6\cdot 5}}}{\sqrt[5]{\frac{3\cdot 1}{2\cdot 2}}}=\frac{\sqrt[5]{\frac{56}{30}}}{\sqrt[5]{\frac{3}{4}}}=\sqrt[5]{\frac{\frac{56}{30}}{\frac{3}{4}}}=\sqrt[5]{\frac{56}{30}\cdot \frac{4}{3}}=$

$=\sqrt[5]{\frac{224}{90}}=\sqrt[5]{\frac{112}{45}}$

24. a) ${\left(\sqrt[5]{13}\right)}^4={\left({13}^{\frac{1}{5}}\right)}^4={13}^{\frac{1}{5}\cdot 4}={13}^{\frac{4}{5}}=\sqrt[5]{{13}^4}$

b) ${\left(\sqrt[4]{15}\right)}^3={\left({15}^{\frac{1}{4}}\right)}^3={15}^{\frac{1}{4}\cdot 3}={15}^{\frac{3}{4}}=\sqrt[4]{{15}^3}$

c) ${\left(\sqrt[5]{3}\right)}^2={\left(3^{\frac{1}{5}}\right)}^2=3^{\frac{1}{5}\cdot 2}=3^{\frac{2}{5}}=\sqrt[5]{3^2}$

d) ${\left(\sqrt[7]{7}\right)}^6={\left(7^{\frac{1}{7}}\right)}^6=7^{\frac{1}{7}\cdot 6}=7^{\frac{6}{7}}=\sqrt[7]{7^6}$

e) ${\left(\sqrt[3]{11}\right)}^2={\left({11}^{\frac{1}{3}}\right)}^2={11}^{\frac{1}{3}\cdot 2}={11}^{\frac{2}{3}}=\sqrt[3]{{11}^2}$

f) ${\left(\sqrt[9]{5}\right)}^7={\left(5^{\frac{1}{9}}\right)}^7=5^{\frac{1}{9}\cdot 7}=5^{\frac{7}{9}}=\sqrt[9]{5^7}$

25. A. $A=\sqrt[6]{1.000}\text{m}\cdot \sqrt[6]{100}\text{m}={1.00}^{\frac{1}{6}}\cdot {100}^{\frac{1}{6}}{\text{m}}^2=$

$={\left({10}^3\right)}^{\frac{1}{6}}\cdot {\left({10}^2\right)}^{\frac{1}{6}}={10}^{\frac{3}{6}+\frac{2}{6}}{\text{m}}^2={10}^{\frac{5}{6}}{\text{m}}^2=\sqrt[6]{{10}^5}{\text{m}}^2$

B. $A=\sqrt[15]{{60}^3}\text{m}\cdot \sqrt[15]{{60}^2}\text{m}={60}^{\frac{3}{15}}\cdot {60}^{\frac{2}{15}}{\text{m}}^2={60}^{\frac{3}{15}+\frac{2}{15}}{\text{m}}^2=$

$={60}^{\frac{5}{15}}{\text{m}}^2={60}^{\frac{1}{3}}{\text{m}}^2=\sqrt[3]{60}{\text{m}}^2$

26. a) $\sqrt{3^2\cdot 6}=\sqrt{3^2}\cdot \sqrt{6}=3\sqrt{6}$

b) $\sqrt[3]{4\cdot 5^3}=\sqrt[3]{4}\cdot \sqrt[3]{5^3}=\sqrt[3]{4}\cdot 5=5\sqrt[3]{4}$

c) $\sqrt[5]{3^5\cdot 6^8}=\sqrt[5]{3^5}\cdot \sqrt[5]{6^3\cdot 6^5}=3\cdot \sqrt[5]{6^3}\cdot \sqrt[5]{6^5}=$

$=3\cdot 6\cdot \sqrt[5]{6^3}=18\sqrt[5]{216}$

d) $\sqrt[4]{2^8\cdot 7^{10}}=\sqrt[4]{2^4\cdot 2^4}\cdot \sqrt[4]{7^4\cdot 7^4\cdot 7^2}=$

$=\sqrt[4]{2^4}\cdot \sqrt[4]{2^4}\cdot \sqrt[4]{7^4}\cdot \sqrt[4]{7^4}\cdot \sqrt[4]{7^2}=2\cdot 2\cdot 7\cdot 7\cdot \sqrt[4]{7^2}=$

$=196\sqrt[4]{49}$

e) $\sqrt{2^3\cdot 3^4\cdot 5^5}=\sqrt{2^2\cdot 2\cdot 3^2\cdot 3^2\cdot 5^2\cdot 5^2\cdot 5}=$

$=\sqrt{2^2}\cdot \sqrt{3^2}\cdot \sqrt{3^2}\cdot \sqrt{5^2}\cdot \sqrt{5^2}\cdot \sqrt{2}\cdot \sqrt{5}=$

$=2\cdot 3\cdot 3\cdot 5\cdot 5\cdot \sqrt{2}\cdot \sqrt{5}=$

$=450\cdot \sqrt{2\cdot 5}=450\sqrt{10}$

f) $\sqrt[6]{2^8\cdot 3^5\cdot {10}^7}=\sqrt[6]{2^6\cdot 2^2\cdot 3^5\cdot {10}^6\cdot 10}=$

$=\sqrt[6]{2^6}\cdot \sqrt[6]{{10}^6}\cdot \sqrt[6]{2^2\cdot 3^5\cdot 10}=2\cdot 10\cdot \sqrt[6]{9.720}=$

$=20\sqrt[6]{9.720}$

27. a) Como $64=4\cdot 4\cdot 4=4^3$, podemos escrever, de modo simplificado: $\sqrt[3]{64}=\sqrt[3]{4^3}=4$

Portanto, a escrita simplificada de $\sqrt[3]{64}$ é 4.

b) Como $432=2\cdot 2\cdot 2\cdot 2\cdot 27=2^4\cdot 27$, podemos escrever, de modo simplificado:

$\sqrt[4]{432}=\sqrt[4]{2^4\cdot 27}=\sqrt[4]{2^4}\cdot \sqrt[4]{27}=2\cdot \sqrt[4]{27}$

Portanto, a escrita simplificada de $\sqrt[4]{432}$ é $2\sqrt[4]{27}$.

c) Como $896=4\cdot 4\cdot 4\cdot 14=4^3\cdot 14$, podemos escrever, de modo simplificado:

$\sqrt[3]{896}=\sqrt[3]{4^3\cdot 14}=\sqrt[3]{4^3}\cdot \sqrt[3]{14}=4\cdot \sqrt[3]{14}$

Portanto, a escrita simplificada de $\sqrt[3]{896}$ é $4\sqrt[3]{14}$.

d) Como $2.187=3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 9=3^5\cdot 9$, podemos escrever, de modo simplificado:

$\sqrt[5]{2.187}=\sqrt[5]{3^5\cdot 9}=\sqrt[5]{3^5}\cdot \sqrt[5]{9}=3\cdot \sqrt[5]{9}$

Portanto, a escrita simplificada de $\sqrt[5]{2.187}$ é $3\sqrt[5]{9}$.

e) Como $9.000=30\cdot 30\cdot 10={30}^2\cdot 10$, podemos escrever, de modo simplificado:

$\sqrt[]{9.000}=\sqrt[]{{30}^2\cdot 10}=\sqrt[]{{30}^2}\cdot \sqrt[]{10}=30\cdot \sqrt[]{10}$

Portanto, a escrita simplificada de $\sqrt[]{9.000}$ é $30\sqrt[]{10}$.

f) Como $16.384=16\cdot 16\cdot 16\cdot 4={16}^3\cdot 4$, podemos escrever, de modo simplificado:

$\sqrt[3]{16.384}=\sqrt[3]{{16}^3\cdot 4}=\sqrt[3]{{16}^3}\cdot \sqrt[3]{4}=16\cdot \sqrt[3]{4}$

Portanto, a escrita simplificada de $\sqrt[3]{16.384}$ é $16\sqrt[3]{4}$.

28. Terreno A: Como $60=2\cdot 2\cdot 3\cdot 5=2^2\cdot 3\cdot 5$, então:

$\sqrt[]{60}=\sqrt[]{2^2\cdot 3\cdot 5}=\sqrt[]{2^2}\cdot \sqrt[]{3}\cdot \sqrt[]{5}\simeq 2\cdot 1,73\cdot 2,24\simeq 7,75$

Portanto, o comprimento do lado desse terreno mede, aproximadamente, $7,75\text{m}$.

Terreno B: Como $120=2\cdot 2\cdot 2\cdot 3\cdot 5=2^2\cdot 2\cdot 3\cdot 5$, então:

$\sqrt[]{120}=\sqrt[]{2^2\cdot 2\cdot 3\cdot 5}=$

$=\sqrt[]{2^2}\cdot \sqrt[]{2}\cdot \sqrt[]{3}\cdot \sqrt[]{5}\simeq 2\cdot 1,41\cdot 1,73\cdot 2,24\simeq 10,93$

Portanto, o comprimento do lado desse terreno mede, aproximadamente, $10,93\text{m}$.

Terreno C: Como $90=2\cdot 5\cdot 3\cdot 3=2\cdot 5\cdot 3^2$, então:

$\sqrt[]{90}=\sqrt[]{2\cdot 5\cdot 3^2}=\sqrt[]{2}\cdot \sqrt[]{5}\cdot \sqrt[]{3^2}\simeq 1,41\cdot 2,24\cdot 3\simeq 9,48$

Portanto, o comprimento do lado desse terreno mede, aproximadamente, $9,48\text{m}$.

Terreno D: Como $180=2\cdot 2\cdot 5\cdot 3\cdot 3=2^2\cdot 5\cdot 3^2$, então:

$\sqrt[]{180}=\sqrt[]{2^2\cdot 5\cdot 3^2}=\sqrt[]{2^2}\cdot \sqrt[]{5}\cdot \sqrt[]{3^2}\simeq 2\cdot 2,24\cdot 3=13,44$

Portanto, o comprimento do lado desse terreno mede, aproximadamente, $13,44\text{m}$.

29. a) $6\cdot \sqrt{3}=\sqrt{6^2\cdot 3}=\sqrt{36\cdot 3}=\sqrt{108}$

b) $5\cdot \sqrt[3]{6}=\sqrt[3]{5^3\cdot 6}=\sqrt[3]{125\cdot 6}=\sqrt[3]{750}$

c) $2\cdot 4\cdot \sqrt[]{10}=8\cdot \sqrt[]{10}=\sqrt[]{8^2\cdot 10}=\sqrt[]{64\cdot 10}=\sqrt[]{640}$

d) $2\cdot 5\cdot \sqrt[5]{2}=10\cdot \sqrt[5]{2}=\sqrt[5]{{10}^5\cdot 2}=$

$=\sqrt[5]{100.000\cdot 2}=\sqrt[5]{200.000}$

30. a) Como $96=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3=2^4\cdot 2\cdot 3$, então:

$\sqrt[4]{96}=\sqrt[4]{2^4\cdot 2\cdot 3}=\sqrt[4]{2^4}\cdot \sqrt[4]{2}\cdot \sqrt[4]{3}=$

$=2\cdot \sqrt[4]{2\cdot 3}=2\cdot \sqrt[4]{6}$

Portanto, $x=6$.

b) $2\sqrt[3]{7}=\sqrt[3]{2^3\cdot 7}=\sqrt[3]{8\cdot 7}=\sqrt[3]{56}$

Portanto, $x=56$.

c) Como $32=2\cdot 2\cdot 2\cdot 2\cdot 2=2^3\cdot 2\cdot 2=2^3\cdot 4$, então:

$\sqrt[3]{32}=\sqrt[3]{2^3\cdot 4}=\sqrt[3]{2^3}\cdot \sqrt[3]{4}=2\cdot \sqrt[3]{4}$

Portanto, $x=2$.

d) $2\sqrt[]{71}=\sqrt[]{2^2\cdot 71}=\sqrt[]{4\cdot 71}=\sqrt[]{284}$

Portanto, $x=284$.

e) $4\sqrt[4]{8}=\sqrt[4]{4^4\cdot 8}=\sqrt[4]{256\cdot 8}=\sqrt[4]{2.048}$

Portanto, $x=2.048$.

f) Como $1.200=2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 5\cdot 5=2^2\cdot 2^2\cdot 3\cdot 5^2$, então:

$\sqrt[]{1.200}=\sqrt[]{2^2\cdot 2^2\cdot 3\cdot 5^2}=\sqrt[]{2^2}\cdot \sqrt[]{2^2}\cdot \sqrt[]{3}\cdot \sqrt[]{5^2}=$

$=2\cdot 2\cdot \sqrt[]{3}\cdot 5=20\cdot \sqrt[]{3}$

Portanto, $x=20$.

31. Usando as propriedades dos radicais e de potências, temos:

$2\sqrt{627}=\sqrt[]{2^2\cdot 627}=\sqrt[]{4\cdot 627}=\sqrt[]{2.508}$

Sendo assim:

$\sqrt{228\cdot a}=\sqrt[]{2.508}$

Dessa maneira, verificamos que:

$228\cdot a=2.508$

$a=\frac{2.508}{228}=11$

32. $\sqrt[]{2\cdot \sqrt[3]{4\cdot \sqrt[]{8}}}=\sqrt[]{2\cdot \sqrt[3]{\sqrt[]{4^2\cdot 8}}}=\sqrt[]{2\cdot \sqrt[3\cdot 2]{16\cdot 8}}=$

$=\sqrt[]{2\cdot \sqrt[6]{128}}=\sqrt[]{\sqrt[6]{2^6\cdot 128}}=\sqrt[2\cdot 6]{64\cdot 128}=\sqrt[12]{8.192}$

Como $8.192=2^{12}\cdot 2$, então:

$\sqrt[]{2\cdot \sqrt[3]{4\cdot \sqrt[]{8}}}=\sqrt[12]{8.192}=\sqrt[12]{2^{12}\cdot 2}=\sqrt[12]{2^{12}}\cdot \sqrt[12]{\cdot 2}=$

$=2\cdot \sqrt[12]{\cdot 2}$

Portanto, $\sqrt[]{2\cdot \sqrt[3]{4\cdot \sqrt[]{8}}}=2\sqrt[12]{2}$.