Página LVI
Resoluções - parte 2
Unidade 3
Razão e proporção
Questão 1. Como e a parte correspondente à quantidade de meninos é representada por , então a quantidade de meninos é dada por .
Questão 2. Resposta pessoal. Espera-se que os estudantes reflitam a respeito da importância da participação ativa dessas comunidades no mapeamento da região em que vivem, resguardando seus direitos e sua herança cultural.
Questão 3. Resposta pessoal. Espera-se que os estudantes realizem a pesquisa de modo responsável, utilizem dados confiáveis e validem as fontes. Além disso, espera-se que eles compartilhem com os colegas as informações coletadas, contribuindo para o enriquecimento do conhecimento coletivo.
Atividades
1. Considerando que há na turma um total de 41 estudantes, pois , então:
a) a razão entre a quantidade de meninas e a quantidade de meninos é .
b) a razão entre o número de meninas e o total de estudantes é .
c) a razão entre o número de meninos e o total de estudantes é .
2. Como a proporção é , temos:
Multiplicando essa quantidade por 2, obtemos:
Portanto, são 50 figurinhas de carros.
3. Resposta pessoal. Sugestão de problema:
Clarinha percorreu a uma velocidade média de . Quanto tempo ela levou para percorrer essa medida de distância?
Resposta: Considerando t o tempo que Clarinha levou, em horas, temos:
Como equivale à metade de uma hora, então .
Portanto, Clarinha demorou meia hora, ou seja, 30 minutos, para percorrer essa medida de distância.
4. Para determinar a velocidade média do ônibus nesse dia, devemos dividir a medida da distância pelo tempo gasto.
Portanto, a velocidade média do ônibus era nesse dia.
5. A densidade demográfica de Petrolina em 2021 era .
6. A densidade da pedra é .
7. a) Medindo as medidas no mapa para determinar a medida da distância real, obtemos os resultados a seguir.
A distância de Poconé até Porto Jofre em linha reta mede 4 centímetros no mapa. Como a escala é 1 centímetro para cada 30 quilômetros, então 4 centímetros correspondem a .
A distância de Poconé até Cuiabá em linha reta mede centímetros no mapa. Como a escala é 1 centímetro para cada 30 quilômetros, então centímetros correspondem a .
b) O comprimento da rodovia mede e a distância entre as duas cidades em linha reta é . Logo, a diferença é dada por:
8. Resposta pessoal. Sugestão de problema:
Certa cidade tem habitantes e sua densidade demográfica é habitante por quilômetro quadrado. Qual é a medida da área dessa cidade?
Resposta: Considerando x a medida da área da cidade, temos:
Logo, a área dessa cidade mede quilômetros quadrados.
Questão 4. Para a primeira igualdade, precisamos mostrar que, dada a proporção , temos .
De fato, considerando a propriedade fundamental, temos . Adicionando em ambos os membros da igualdade, obtemos:
Para a segunda igualdade, precisamos mostrar que, dada a proporção , temos .
De fato, considerando a propriedade fundamental, temos , e então . Adicionando em ambos os membros da igualdade, obtemos:
Para a terceira igualdade, precisamos mostrar que, dada a proporção , temos .
Página LVII
De fato, considerando a propriedade fundamental, temos . Subtraindo em ambos os membros da igualdade, obtemos:
Questão 5. Se , então podemos escrever e resolver a equação a seguir.
Portanto, são necessários 20 minutos para descongelar um quilograma de comida.
Questão 6. Se , então podemos escrever e resolver a equação a seguir.
Portanto, serão necessários 162 minutos (2 horas e 42 minutos) para completar a viagem.
Atividades
9. Em cada item, precisamos verificar se as razões formam uma proporção, ou seja, se são equivalentes.
a) As razões não formam uma proporção, pois .
b) As razões formam uma proporção, pois .
c) As razões não formam uma proporção, pois .
d) As razões não formam uma proporção, pois .
e) As razões formam uma proporção, pois .
f) As razões formam uma proporção, pois .
g) As razões não formam uma proporção, pois .
h) As razões formam uma proporção, pois .
i) As razões não formam uma proporção, pois .
10. Analisando as informações, verificamos que a razão entre a quantidade de porções e a quantidade de xícaras de óleo é constante, devido ao fato de serem grandezas diretamente proporcionais, ou seja:
Se meia xícara de chá de óleo rende 6 porções, então para determinar quantas xícaras renderiam 24 porções, vamos considerar x a quantidade de xícaras para render 24 porções e usar a razão obtida anteriormente, formando uma proporção.
Logo, serão necessárias 2 xícaras de óleo para que a receita renda 24 porções.
11. Analisando as informações, verificamos que a razão entre a quilometragem total e a quantidade de dias para asfaltar certa medida de distância da estrada é constante, devido ao fato de serem grandezas diretamente proporcionais, ou seja:
Como 12 quilômetros já foram finalizados de um total de 57, ainda faltam a serem asfaltados, pois . Sendo assim, considerando x a quantidade de dias necessários para concluir o serviço, temos:
Logo, serão necessários 285 dias para concluir o serviço.
12. Nesse caso, o tempo e a velocidade média são grandezas inversamente proporcionais e a razão entre a velocidade e o inverso do tempo é constante igual a:
, em que 0,3 hora corresponde a 18 minutos.
Sendo assim, considerando x o tempo gasto a uma velocidade média de , temos:
Logo, dirigindo a , Pedro teria gasto 0,36 hora, que equivale a 21,6 minutos, e 0,6 minuto corresponde a 36 segundos.
Portanto, ele teria gasto 21 minutos e 36 segundos.
13. Sendo as grandezas diretamente proporcionais, a razão entre a quantidade de gotas e a medida de massa corporal é constante e igual a . Considere x a quantidade de gotas que Mateus deve ingerir. Sendo assim, temos:
Portanto, Mateus deve tomar 24 gotas do medicamento.
14. Sendo as grandezas inversamente proporcionais, a razão entre a quantidade de torneiras e o inverso do tempo é constante. Sendo 1,5 hora correspondente a 90 minutos, temos:
Considere x o tempo, em minutos, que cinco torneiras demorariam a encher o reservatório. Nesse caso, teremos:
Página LVIII
Portanto, cinco torneiras abertas iguais a essas demorariam 36 minutos para encher esse reservatório.
15. Com as 3 máquinas novas, a estamparia passou a ter 8 máquinas. Isso significa que antes havia 5 máquinas que produziam ao todo 300 peças diariamente.
Comparando as grandezas nessa situação, verificamos que elas são diretamente proporcionais. Sendo assim, a razão entre a quantidade de peça produzida diariamente e a quantidade de máquinas é constante igual a:
Considerando x a quantidade diária de camisetas estampadas que as 3 máquinas novas produzirão diariamente, podemos escrever e calcular a equação a seguir.
Portanto, haverá aumento de 180 camisetas na produção diária dessa estamparia.
16. Comparando as grandezas nessa situação, verificamos que elas são diretamente proporcionais. Nesse caso, a razão entre a quantidade de páginas impressas e o tempo para imprimi-las é dado por:
Considerando x o tempo, em minutos, que a máquina leva para imprimir páginas, podemos escrever e resolver a equação a seguir.
Portanto, essa máquina vai imprimir páginas em 5 minutos.
17. Nessa situação, verificamos que as grandezas são inversamente proporcionais e a razão entre a quantidade de funcionários e o inverso do tempo gasto é constante igual a:
Considerando x o tempo, em horas, que dois funcionários gastariam para realizar o mesmo serviço, podemos escrever e resolver a equação a seguir.
Sendo 0,5 hora equivalente a meia hora, então 7,5 horas podem ser representadas como 7 horas e 30 minutos.
Portanto, mantendo o mesmo ritmo de trabalho, esses dois funcionários precisarão de para produzir essa mesma quantidade de refeições.
18. Comparando as grandezas nessa situação, verificamos que elas são inversamente proporcionais e a razão entre a quantidade de galinhas e o inverso da quantidade de dias é constante igual a:
Considerando x a quantidade de dias em que a ração será suficiente para alimentar 80 galinhas, podemos escrever e resolver a equação a seguir.
Portanto, essa mesma quantidade de ração será suficiente para alimentar as galinhas por 18 dias.
19. Resposta pessoal. Sugestão de resposta:
Um ônibus de certa companhia comporta 20 pessoas. Quantos ônibus serão necessários para transportar 160 pessoas em uma excursão?
Resposta: Comparando as grandezas nessa situação, verificamos que elas são diretamente proporcionais e a razão entre a quantidade de pessoas e a quantidade de ônibus é constante igual a:
Considerando x a quantidade de ônibus para transportar 160 pessoas, podemos escrever e resolver a equação a seguir.
Portanto, serão necessários 8 ônibus para transportar essa quantidade de pessoas na excursão.
20. Nos itens a seguir, todas as grandezas são diretamente proporcionais e as razões entre elas são constantes.
a) A razão entre a quantidade de carboidrato e a quantidade de arroz é dada por:
Considerando x a quantidade de arroz para ingerir de carboidratos, temos:
Portanto, uma pessoa deve consumir de arroz para ingerir de carboidrato.
b) A razão entre a medida de energia e a quantidade de arroz é dada por:
Considerando y a medida de energia presente em arroz, temos:
Portanto, em há 640 quilocalorias.
Página LIX
c) A razão entre a quantidade de proteína e a quantidade de batata-doce cozida é dada por:
Considerando z a quantidade de proteína presente em de batata-doce cozida, temos:
Portanto, em de batata-doce cozida há de proteína.
d) A razão entre a medida de energia e a quantidade de proteína é dada por:
Considerando k a medida de energia presente em uma porção de arroz com de proteína, temos:
Portanto, em uma porção de arroz com de proteína há 512 quilocalorias.
21. Nessa situação, verificamos que as grandezas são diretamente proporcionais e a razão entre a quantidade litros e o tempo é constante igual a:
Considerando x a quantidade de litros de água desperdiçada durante 3 horas e 30 minutos (ou 3,5) , temos:
Portanto, foram desperdiçados de água até a conclusão do reparo.
22. Resposta pessoal. Sugestão de resposta:
Supondo, na atividade anterior, que a vazão seja em 2 horas e 15 minutos e que o reparo da tubulação tenha demorado 6 horas e 45 minutos, determine quantos litros foram desperdiçados até a conclusão do reparo.
Resposta: Nessa situação, verificamos que as grandezas são diretamente proporcionais e a razão entre a quantidade de litros e o tempo é constante igual a .
Considerando x a quantidade de litros de água desperdiçada durante 6 horas e 45 minutos, temos:
Portanto, foram desperdiçados de água até a conclusão do reparo.
23. Analisando as grandezas nessa situação, verificamos que elas são diretamente proporcionais e a razão entre as medidas da massa e do volume é constante igual a .
Considerando x a medida da massa de um objeto cujo volume mede , temos:
Portanto, a massa do objeto mede .
24. Resposta pessoal. Sugestão de problema:
A medida da massa de um objeto com certa densidade é , quando seu volume mede . Determine a medida da massa de outro objeto de mesma densidade, em que seu volume meça .
Resposta: As grandezas são diretamente proporcionais e a razão entre as medidas da massa e do volume é constante igual a . Considere x a medida de massa desse objeto. Assim, temos:
Portanto, a massa do objeto mede .
25. As grandezas são inversamente proporcionais e a razão entre a quantidade de máquinas e o inverso do tempo gasto é constante igual a:
Considerando x a quantidade de máquinas para realizar o trabalho em 3 horas, temos:
Portanto, são necessárias 8 máquinas para produzir a mesma quantidade de sapatos em 3 horas.
26. Resposta pessoal. Sugestão de problema:
Supondo, na situação da atividade anterior, que 6 máquinas produzem certa quantidade de pares de sapatos em 10 horas, quanto tempo levaria para que 15 máquinas produzissem essa mesma quantidade de pares?
Resposta: Nessa situação, verificamos que as grandezas são inversamente proporcionais e a razão entre a quantidade de máquinas e o inverso do tempo gasto é constante igual a:
Página LX
Considerando x o tempo em que 15 máquinas levariam para produzir essa quantidade de sapatos, temos:
Portanto, essas máquinas levarão 4 horas para produzir a mesma quantidade de pares de sapatos.
27. Resposta pessoal. Sugestão de resposta:
Se 10 pedreiros levam 2 dias para erguer um muro, quantos pedreiros seriam necessários para erguer o mesmo muro em 12 horas, considerando que todos tenham o mesmo ritmo de trabalho?
Resposta: Comparando as grandezas envolvidas nessa situação, verificamos que elas são inversamente proporcionais. Nesse caso, a razão entre a quantidade de pedreiros e o inverso da quantidade de dias é constante igual a:
Considerando x a quantidade de pedreiros para erguer o muro em 0,5 dia, temos:
Portanto, seriam necessários 40 pedreiros para erguer o mesmo muro em 12 horas.
Questão 7. Se o valor a ser dividido fosse R$ 1.250,00, então teríamos a seguinte razão:
Com isso, vamos determinar a quantia correspondente a cada filho.
Armando:
Portanto, Armando receberia .
Antônio:
Portanto, Antônio receberia .
Amarildo:
Portanto, Amarildo receberia .
Questão 8. Se o valor a ser dividido fosse , então teríamos a seguinte razão:
Com isso, vamos determinar a quantia correspondente a cada filho.
Armando:
Portanto, Armando receberia R$ 585,00.
Antônio:
Portanto, Antônio receberia R$ 540,00.
Amarildo:
Portanto, Amarildo receberia R$ 468,00.
Atividades
28. Considerando x e y os valores diretamente proporcionais a 2 e 3, respectivamente, temos:
Logo, .
Logo, .
29. Considerando x e y os valores inversamente proporcionais a 2 e 3, respectivamente, temos:
Logo, .
Logo, .
30. Note que:
Logo, .
Logo, .
Logo, .
Portanto, a alternativa correta é c.
Página LXI
31. Considerando x, y e z os valores que Marcos, Antônio e Camila vão receber, respectivamente, temos:
Com isso, vamos determinar a quantia correspondente a cada um deles.
Marcos:
Logo, .
Antônio:
Logo, .
Camila:
Logo, .
Portanto, Marcos vai receber R$ 2540,00, Antônio vai receber R$ 3048,00 e Camila, R$ 3810,00.
32. Resposta pessoal. Sugestões de resposta:
O gerente de uma empresa vai pagar aos seus funcionários um bônus de R$ 1.200,00 de maneira proporcional à quantidade de horas extras trabalhadas por eles no último semestre. Pedro trabalhou 10 horas extras, Luan trabalhou 20 e Lívia, 30. Quantos reais cada um vai receber?
Resposta: Pedro vai receber R$ 200,00, Luan vai receber R$ 400,00 e Lívia vai receber R$ 600,00.
O gerente de uma empresa vai pagar aos seus funcionários um bônus de R$ 1.200,00 de maneira inversamente proporcional à quantidade de faltas que cada um teve no último semestre. Carmem teve 2 faltas e Daniel, 4. Quantos reais cada um deles vai receber?
Resposta: Carmem vai receber R$ 800,00 e Daniel, R$ 400,00.
33. Considerando x, y e z a parte correspondente a 2, 4 e 6, temos:
Logo, .
Logo, .
Logo, .
34. Considerando x, y e z as quantias que Anderson, Márcia e Gustavo vão receber, respectivamente, temos:
Calculando os valores de x, y e z:
Logo, .
Logo, .
Logo, .
Portanto, Anderson vai receber aproximadamente R$ 2.173,13, Márcia vai receber R$ 1.629,84 e Gustavo, R$ 1.992,03.
35. Considerando x, y e z as quantias que Marlene, Marcos e Marta vão receber, respectivamente, temos:
Com isso, vamos determinar a quantia correspondente a cada um deles.
Marlene:
Logo, .
Logo, .
Logo, .
Portanto, Marlene vai receber R$ 34.285,50, Marcos vai receber R$ 39.428,33 e Marta, R$ 29.206,17.
Questão 9.
a) Determinando uma relação entre os ângulos de medidas e , que são colaterais externos, temos:
Sabemos que e são suplementares, logo .
Além disso, sabemos que os ângulos de medidas e são correspondentes, ou seja, .
Portanto, e os ângulos de medidas e são suplementares.
b) Determinando uma relação entre os ângulos de medidas e , que são alternos internos, temos:
Sabemos que e são opostos pelo vértice, logo .
Além disso, sabemos que e são correspondentes, ou seja, .
Portanto, .
Página LXII
c) Determinando uma relação entre os ângulos de medidas e , que são alternos externos, temos:
Sabemos que e são correspondentes, logo .
Além disso, e são opostos pelo vértice, ou seja, .
Portanto, .
Atividades
36. a) Como os ângulos são opostos pelo vértice, temos:
b) Como os ângulos são opostos pelo vértice, temos:
c) Como os ângulos são opostos pelo vértice, temos:
d) Como os ângulos são opostos pelo vértice, temos:
37. a) Temos:
Além disso:
b) Temos:
Além disso:
38. No paralelogramo, e e . Logo, os triângulos são congruentes pelo caso .
Desse modo, e .
Portanto, M é ponto médio das diagonais desse paralelogramo.
39. Substituindo os valores na igualdade dada, temos:
Logo, .
40. a)
b) Ao diminuir dois centímetros cada lado, temos e . Assim:
.
Portanto, a razão não permanece a mesma.
41. a)
Logo, .
b)
Logo, .
c)
Logo, .
42. a)
b)
c)
d)
Página LXIII
43. Dos segmentos proporcionais, temos:
Desse modo:
Portanto, a medida da distância percorrida por Aline foi de .
Questão 10. Resposta pessoal. Espera-se que os estudantes realizem uma pesquisa sobre as contribuições para as ciências feitas por Tales de Mileto e compartilhem as informações obtidas com a turma.
Atividades
44. De acordo com o teorema de Tales, temos:
a)
b)
c)
d)
e)
f)
45. A. Se quaisquer dois segmentos de reta determinados em uma das retas transversais são proporcionais aos respectivos segmentos de reta determinados na outra reta transversal, essas duas retas são paralelas.
Analisando um exemplo, temos:
Portanto, as retas são paralelas.
B. Analisando os segmentos de retas, temos:
Portanto, as retas não são paralelas.
46. , pois .
Logo, as retas não são paralelas.
47. Como as retas são paralelas, temos:
Logo:
;
.
Podemos concluir que e .
48. Considerando x a medida do comprimento do muro, em metros, que Valquíria deve construir, Marcos deve construir . Como as retas são paralelas, temos:
Assim, sabendo que Valquíria deve construir aproximadamente , calculamos quantos metros de muro Marcos deve construir:
Portanto, Marcos deve construir aproximadamente de muro.
49. Como as retas são paralelas, temos:
Assim, para calcular a quantidade de tela que Patrícia utilizou, calculamos:
Portanto, Patrícia utilizou .
50. Para determinar o valor de a, analisamos os segmentos de reta nas retas p e q:
Portanto, ;
Para determinar o valor de b, analisamos os segmentos de reta nas retas p e q:
Portanto, ;
Para determinar o valor de c, analisamos os segmentos de reta nas retas o e q:
Portanto, ;
Para determinar o valor de d, analisamos os segmentos de reta nas retas o e q:
Portanto, .
Página LXIV
51. Resposta pessoal. Sugestão de resposta:
Dadas as retas paralelas a, b e c nesta ordem, trace duas transversais s e t tais que:
A seja interseção de s com a;
B seja interseção de s com b;
C seja interseção de s com c;
D seja interseção de t com a;
E seja interseção de t com b;
F seja interseção de t com c.
Se , e , determine a medida de .
Resposta: .
Questão 11.
Logo, .
Atividades
52. Em cada item, determinamos inicialmente a medida do comprimento do segmento desconhecido e, em seguida, calculamos a medida do perímetro:
A.
Ou seja, .
Logo, a medida do perímetro é dada por:
Portanto, .
B.
Ou seja, .
Logo, a medida do perímetro é .
Portanto, .
C.
Ou seja, .
Logo, a medida do perímetro dada por:
Portanto, .
53. Como P é ponto médio de , . Assim:
Ou seja, . Desse modo:
Portanto, .
54. Temos:
Ou seja, .
Como , temos:
Portanto, .
55. Considerando x a medida da distância entre a estátua e o poste, temos:
Portanto, a distância entre o poste e a estátua mede, aproximadamente, .
56. a)
Ou seja, .
b) Como e , temos:
Logo, a medida do perímetro é dada por:
Portanto, o perímetro mede .
57. a)
Ou seja, .
b) Como são 4 arames paralelos com comprimento medindo 11 metros cada, temos:
Portanto, Dirceu vai precisar de .
58. . Com isso, determinamos os valores de a, b e c:
Página LXV
Ou seja, .
Ou seja, .
Ou seja, .
59. Como a área de mede , temos:
Ou seja, ;
Desse modo:
Portanto, .
60. Resposta pessoal. Sugestão de resposta:
Considere o triângulo com , em que contém e contém . Se , e (com todas as medidas dadas em metro), qual é a medida do comprimento de ?
Resposta: .
O que eu estudei?
1. a) Considerando x a medida da largura:
Ou seja, .
Transformando essa medida em centímetros, temos:
Logo, .
b) Considerando y a medida do comprimento da cama na planta:
Ou seja, .
Transformando essa medida em centímetros, temos:
Logo, .
Por fim, considerando z a medida da largura da cama na planta:
Ou seja, .
Transformando essa medida em centímetros, temos:
Logo, .
Portanto, as medidas das dimensões da cama de Renata são por .
2. Temos . Assim:
Logo, a quantidade de meninos é dada por:
E a quantidade de meninas é dada por:
Portanto, 16 meninos e 20 meninas fazem parte dessa turma.
3. correspondem a . Com isso:
Portanto, a medida da velocidade média nesse percurso é .
4. Considerando x e y os valores correspondentes a 4 e 5, respectivamente, temos:
Com isso, obtemos os valores de x e y.
;
Portanto, a parte inversamente proporcional ao número 4 é 100 e ao número 5 é 80.
5. Considerando x e y os valores correspondentes a Ana e a Rebeca, respectivamente, temos:
Com isso, obtemos os valores de x e y.
Portanto, Ana deve receber R$ 2.160,00 e Rebeca, R$ 3.240,00.
Página LXVI
6. De acordo com a figura, temos:
Logo, .
7. .
Considerando , temos:
Logo, .
Logo, .
Logo, .
Unidade 4
Semelhança de figuras
Questão 1. Resposta pessoal. Espera-se que os estudantes façam visitas virtuais em alguns museus. Alguns deles são: o museu do Louvre na França, The National History Museum no Reino Unido e museu do Vaticano em Roma.
Atividades
1. a) A figura 2, pois tem o mesmo formato e as mesmas medidas de dimensões.
b) As figuras 2, 3 e 4 representam ampliações da figura 1, pois têm o mesmo formato, mas com medidas de dimensões maiores e proporcionais.
c) As figuras 1, 2 e 4 representam reduções da figura 3, pois têm o mesmo formato, mas com medidas de dimensões menores e proporcionais.
d) Sim, todas as figuras nessa malha são semelhantes, pois têm o mesmo formato e as medidas de quaisquer dois segmentos correspondentes são proporcionais.
2. a) A imagem B é uma reprodução da figura original, pois suas medidas de dimensões foram mantidas.
b) A imagem A é uma ampliação da figura original, pois suas medidas de dimensões foram aumentadas proporcionalmente.
c) A imagem C não manteve a proporção das medidas das dimensões da foto original. A medida de uma dimensão foi mantida e a medida de outra dimensão foi aumentada.
3. a) A figura 1 representa uma reprodução da figura original, pois tem as mesmas medidas de dimensões da figura original.
b) A figura 4 representa uma redução da figura original, pois tem o mesmo formato da figura original, porém foi desenhada em uma malha com quadradinhos menores.
c) As figuras 1 e 4 são semelhantes à figura original, pois têm o mesmo formato da figura original e os segmentos correspondentes têm medidas de comprimento proporcionais.
d) As figuras 2 e 3 não são proporcionais à figura original, pois não têm o mesmo formato da figura original.
4. Resposta pessoal. Espera-se que os estudantes ampliem e reduzam a figura usando malhas quadriculadas com quadradinhos menores e maiores, respectivamente, mantendo proporção entre as medidas de comprimento dos segmentos correspondentes.
5.
A. Todos os ângulos das figuras são retos e, assim, são congruentes. Desse modo, as figuras são semelhantes. Determinando a razão de semelhança, temos:
B. Os ângulos correspondentes das figuras são congruentes. Determinando a razão de semelhança, temos:
C. Dividindo as medidas de comprimento dos lados correspondentes das figuras, temos:
e
Como , os lados correspondentes dessas figuras não são proporcionais. Portanto, essas figuras não são semelhantes.
6. Utilizando régua e transferidor, obtemos as medidas do comprimento dos lados:
A. medindo e , respectivamente. Além disso, os ângulos internos desses triângulos medem . Desse modo, as medidas de comprimento dos lados correspondentes são proporcionais e os ângulos correspondentes são congruentes. Portanto, os triângulos são semelhantes.
B. do triângulo maior medindo , e , enquanto os comprimentos dos lados do triângulo menor medem , e . Ao dividirmos as medidas de comprimento dos lados correspondentes, temos:
e .
Como os lados correspondentes não têm medidas de comprimento proporcionais, os triângulos não são semelhantes.
C. dos dois triângulos iguais a , e e as medidas de seus ângulos internos iguais a , e . Desse modo, as medidas de comprimento dos lados correspondentes são proporcionais e os ângulos correspondentes são congruentes. Portanto, os triângulos são semelhantes.
Página LXVII
7. a) Não. A figura B da atividade anterior é um exemplo de dois triângulos que não são semelhantes.
b) Sim. Os triângulos equiláteros são sempre semelhantes, visto que os ângulos internos são congruentes.
8. a) 4 retângulos.
b) Um retângulo tem dimensões medindo , um retângulo tem dimensões medindo e dois retângulos têm dimensões medindo .
c) Não. Se considerarmos os retângulos com dimensões medindo e , ao dividirmos a medidas de comprimento dos lados correspondentes, temos:
e
Como , os retângulos não são semelhantes.
d) Os retângulos cujas dimensões medem e são semelhantes. Dividindo as medidas de comprimento de seus lados correspondentes, temos:
.
Logo, esses retângulos são semelhantes.
Os dois retângulos cujas dimensões medem são semelhantes, pois seus lados correspondentes têm as mesmas medidas de comprimento.
9. Indicamos por a medida de comprimento dos lados do triângulo e por a medida de comprimento dos lados do triângulo .
Logo, a medida do perímetro desses triângulos é e , respectivamente.
Como a soma das medidas de comprimento dos perímetros desses triângulos é igual a , temos:
Além disso, a razão de semelhança entre esses triângulos é . Logo, e, consequentemente, . Substituindo por na equação , temos:
Como , temos:
Portanto, os comprimentos dos lados dos triângulos e medem, respectivamente, e .
10. Os losangos não são semelhantes entre si, pois, mesmo tendo as medidas de comprimento dos respectivos lados proporcionais, eles não têm pares de ângulos internos congruentes. Os retângulos não são semelhantes, pois, mesmo tendo os respectivos ângulos internos congruentes, as medidas de comprimento dos seus lados correspondentes não são proporcionais.
11. a) Inicialmente, construímos um triângulo equilátero em que os comprimentos dos lados medem .

Em seguida, escolhemos o ponto externo a esse triângulo e traçamos as semirretas com origem nesse ponto e que passam pelos vértices , e .
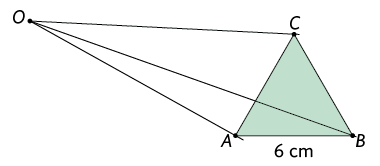
Marcamos os pontos , e sobre as semirretas , e , respectivamente, de modo que , e . Como consequência disso, os pontos , e são pontos médios dos segmentos , e , respectivamente.
Utilizando o compasso, marcamos os pontos médios , e dos segmentos , e , respectivamente.
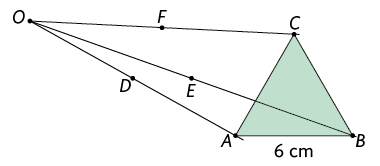
O triângulo é um triângulo equilátero com comprimento de lado medindo , obtido por meio de homotetia.
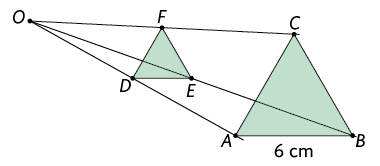
b) Construindo primeiro um quadrado com comprimento de lado medindo , temos:
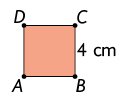
Escolhemos um ponto externo a esse quadrado e, em seguida, traçamos as semirretas com origem nesse ponto e que passam pelos vértices , , e .
Página LXVIII
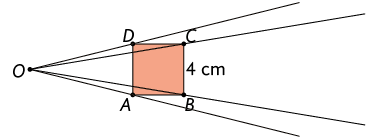
Marcamos os pontos , , e sobre as semirretas , , e , respectivamente, de modo que , , e .
Usando um compasso, com abertura igual à medida de comprimento de e ponta-seca em , marcamos o ponto sobre a semirreta . Com abertura igual à medida de comprimento de e ponta-seca em , marcamos o ponto sobre a semirreta . Com abertura igual à medida de comprimento de e ponta-seca em , marcamos o ponto sobre a semirreta . E com abertura igual à medida de comprimento de e ponta-seca em , marcamos o ponto sobre a semirreta .
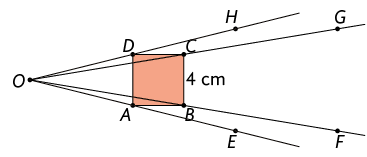
Agora, ligamos os pontos, , e , obtendo um quadrado cujo comprimento dos lados mede e que foi obtido por meio de homotetia.
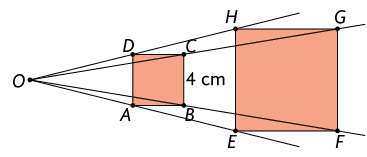
12. a) Indicando por , e o vértice de um dos lados de cada hexágono A, B e C, respectivamente, temos: , e
Como o comprimento dos lados do hexágono A mede e , a razão de semelhança entre eles é . Logo, o comprimento dos lados do hexágono B mede .
Do mesmo modo, como , a razão de semelhança entre eles é 3,5. Logo, o comprimento dos lados do hexágono C mede .
b) Usando o mesmo raciocínio do item anterior, temos:
Assim, a razão de redução é .
c) Do item a, temos .
Assim, a razão de ampliação é ou .
13.
A. Escolhemos um ponto qualquer externo ao trapézio e traçamos semirretas com origem em e que passam pelos vértices , , e .

Como a razão de ampliação é , devemos marcar pontos , , e sobre as semirretas , , e , respectivamente, tais que , , e .
Para marcar o ponto , usando um compasso com abertura igual à medida de comprimento de e ponta-seca em , marcamos um ponto sobre a semirreta . Mantendo a abertura do compasso e com a ponta-seca nesse ponto, marcamos outro ponto na semirreta , que será o ponto .
Do mesmo modo, marcamos os pontos , e .

Ligando os pontos , , e , obtemos o trapézio , que é uma ampliação do trapézio na razão de semelhança

B. Escolhemos um ponto qualquer externo ao pentágono e traçamos semirretas com origem em e que passam pelos pontos , , , e .

Como a razão de ampliação é , marcamos os pontos , , , e sobre as semirretas , , , e , respectivamente, tais que , , , e .
Página LXIX
Para marcar o ponto , usando um compasso com abertura igual à medida de comprimento de e ponta-seca em , marcamos um ponto sobre a semirreta .
Mantendo a abertura do compasso e com a ponta-seca nesse ponto, marcamos outro ponto na semirreta OE que será o ponto J. Do mesmo modo, marcamos os pontos , , e .
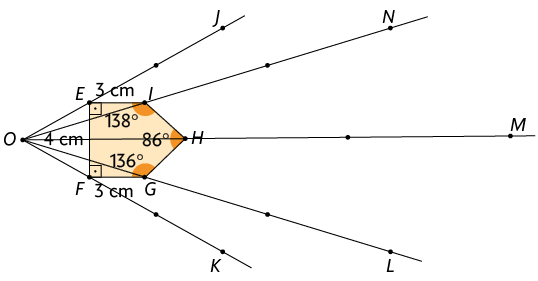
Em seguida, ligamos os pontos , , , e , obtendo o pentágono , que é uma ampliação do pentágono na razão de semelhança .
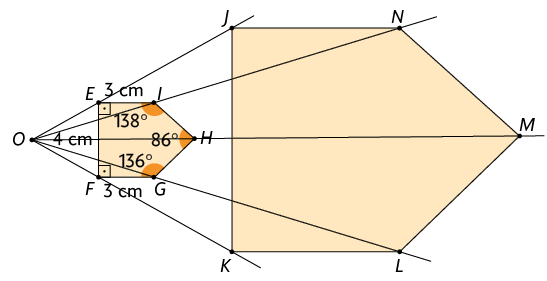
14. A. Inicialmente, marcamos os vértices , , e do trapézio e traçamos suas diagonais marcando o ponto .
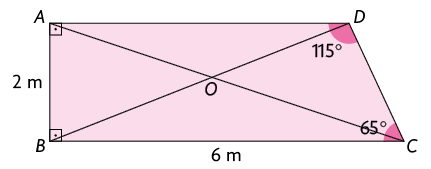
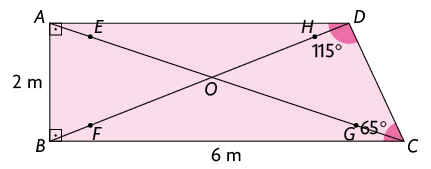
Com auxílio de uma régua e um compasso, marcamos os pontos , , e sobre os segmentos , , e de maneira que , , e .
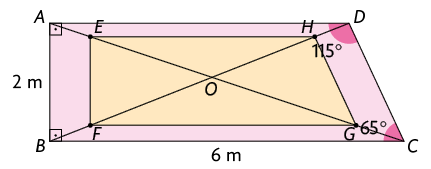
Em seguida, ligamos os pontos , , e do trapézio obtendo uma redução do trapézio na razão de semelhança .
B. Nomeando os vértices , e do triângulo, marcamos um ponto externo ao triângulo e traçamos semirretas com origem nesse ponto e que passam pelos vértices do triângulo.
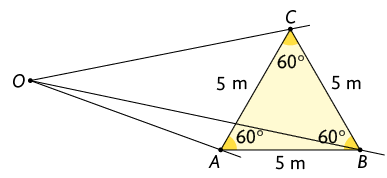
Com auxílio de régua e compasso, marcamos os pontos , e sobre as semirretas , e , de modo que satisfaça , e .
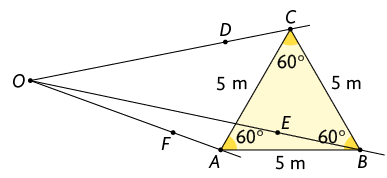
Por fim, ligamos os pontos , e , obtendo o triângulo , que é uma redução do triângulo na razão de semelhança .
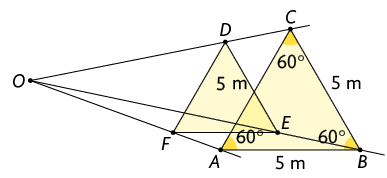
15. A. No triângulo temos e no triângulo temos . Assim:
Logo, a razão de semelhança da homotetia é igual a 2.
B. No retângulo temos e no retângulo temos . Assim:
Logo, a razão de semelhança da homotetia é igual a 2,5.
C. No retângulo temos e no retângulo temos . Assim:
Logo, a razão de semelhança da homotetia é aproximadamente 1,5.
Página LXX
16. A soma das medidas dos ângulos internos de um triângulo é igual a . Desse modo:
, pois
, pois
Logo, ,
e
.
Portanto, pelo caso de semelhança , temos .
Além disso, os triângulos são isósceles, com e . Como os lados e são correspondentes, temos:
Portanto, os triângulos são semelhantes com razão de semelhança .
17. a) A medida de comprimento dos lados do triângulo é igual a e a medida de comprimento dos lados do triângulo é igual a . Desse modo, os triângulos são equiláteros, pois polígonos regulares com a mesma quantidade de lados são sempre semelhantes entre si.
b) Calculando a razão de semelhança entre os triângulos ABC e BDE, temos:
18. a) Sim, os triângulos e são semelhantes, pois eles têm dois pares de ângulos correspondentes congruentes.
b) Como no item anterior a resposta foi afirmativa:
temos , . Como esses lados são correspondentes, calculando a razão de semelhança entre os triângulos e , temos:
os triângulos e são semelhantes pelo caso de semelhança , pois têm dois pares de ângulos correspondentes congruentes.
19. Os triângulos das figuras A e D são semelhantes pelo caso de semelhança , pois têm dois pares de ângulos congruentes que medem .
Considerando as medidas de comprimento dos lados dos triângulos das figuras B e E, temos:
Logo, esses triângulos são semelhantes pelo caso .
Considerando os lados dos ângulos retos nos triângulos das figuras C e F, temos:
Logo, esses triângulos são semelhantes pelo caso de semelhança .
20. Como os triângulos são semelhantes, os lados:
A. e são correspondentes. Calculando a razão de semelhança dos triângulos e , temos:
Além disso, os lados e também são correspondentes. Assim:
Portanto, .
B. e são correspondentes. Calculando a razão de semelhança dos triângulos e , temos:
Como o triângulo é isósceles com base , temos: .
Além disso, os lados e também são correspondentes. Assim:
Portanto, .
C. e são correspondentes. Calculando a razão de semelhança dos triângulos e , temos:
Além disso, os lados e também são correspondentes. Assim:
.
Portanto, .
21. A. Os lados que medem e são correspondentes. Assim, calculando a razão de semelhança desses triângulos, temos:
Os lados cujos comprimentos medem e são correspondentes. Desse modo, temos:
Logo, .
Além disso, os lados que medem e são correspondentes. Assim:
Portanto, .
Página LXXI
B. Os lados cujos comprimentos medem e são correspondentes. Calculando a razão de semelhança desses triângulos, temos:
Os lados que medem e são correspondentes. Desse modo:
Logo, .
Além disso, os lados cujos comprimentos medem e são correspondentes, assim:
Portanto, .
22. Na semelhança dos triângulos e , os lados e são correspondentes. Desse modo, e . Para obter a razão de semelhança desses triângulos, calculamos:
Além disso, os lados e também são correspondentes, assim, como , então:
Portanto, .
23. Na semelhança dos triângulos e , os lados e são correspondentes. Com isso, e pelo fato de e , para obter a razão de semelhança desses triângulos, fazemos:
Além disso, os lados e também são correspondentes. Assim:
Logo, o comprimento do lado mede .
Portanto, a alternativa correta é a d.
O que eu estudei?
1. A. Um dos lados do polígono 1, cujo comprimento mede , é correspondente ao lado do polígono 2, cujo comprimento mede . Como os polígonos são semelhantes, para obter a razão de semelhança, calculamos:
Logo, o lado do polígono 2 correspondente ao lado do polígono 1, cujo comprimento mede , tem medida de comprimento igual a , pois .
O lado do polígono 2 correspondente ao lado do polígono 1, cujo comprimento mede , tem medida de comprimento igual a , pois .
O lado do polígono 1 correspondente ao lado do polígono 2, cujo comprimento mede , tem medida de comprimento igual a , pois .
Calculando a medida do perímetro desses polígonos, temos:
Polígono 1:
Logo, o perímetro mede .
Polígono 2:
Logo, o perímetro mede .
B. Os polígonos 1 e 2 são paralelogramos. Além disso, os lados opostos de um paralelogramo são congruentes e a razão de ampliação é igual a . Então, as medidas de comprimento dos lados que estão faltando no polígono 1 são e e as medidas de comprimento dos lados que estão faltando no polígono 2 são e .
Assim, calculamos a medida do perímetro do polígono 1 e a medida do perímetro do polígono 2.
Polígono 1:
Polígono 2:
Portanto, o perímetro do polígono 1 mede e o perímetro do polígono 2 mede .
2. a) Sim. Quaisquer dois polígonos regulares com a mesma quantidade de lados são semelhantes, pois seus ângulos internos são congruentes.
b) Para obter a razão de semelhança entre eles, calculamos:
c) O perímetro do hexágono A mede , pois , e o perímetro do polígono B mede , pois .
Portanto, a razão da medida do perímetro dos polígonos é .
Página LXXII
d) Sim, as razões obtidas nos itens b e c são iguais a 1,25. Isso acontece com todos os polígonos regulares semelhantes. De fato, se os polígonos regulares têm lados, em que os lados de um medem e os lados do outro medem , a razão de semelhança do primeiro polígono em relação ao segundo polígono é igual a .
Portanto, a razão de semelhança entre os polígonos regulares é igual à razão de semelhança entre as medidas de seus perímetros.
3. A. Escolhemos um ponto qualquer externo ao paralelogramo e traçamos semirretas com origem em e que passam por , , e .
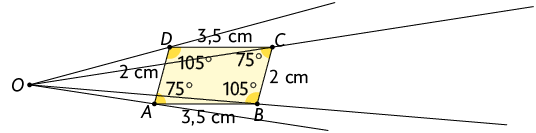
Como a razão de ampliação é , marcamos pontos , , e sobre as semirretas , , e , respectivamente, tais que , , e .
Usando um compasso com abertura igual à medida de e ponta-seca em , marcamos o ponto sobre a semirreta . De modo semelhante, marcamos os pontos , e .
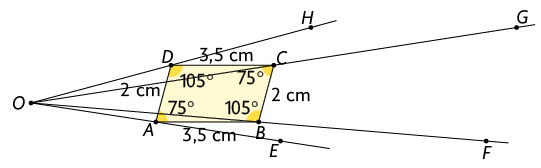
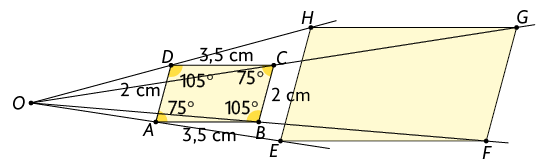
Agora, ligamos os pontos , , e .
O paralelogramo é uma ampliação do paralelogramo na razão de semelhança .
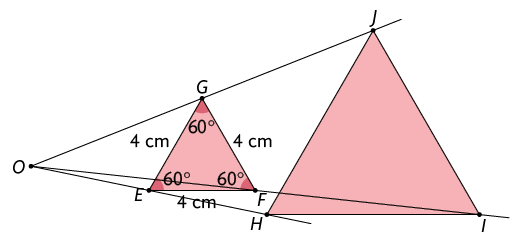
B. Escolhemos um ponto qualquer externo ao triângulo e traçamos as semirretas com origem em e que passam por , e .
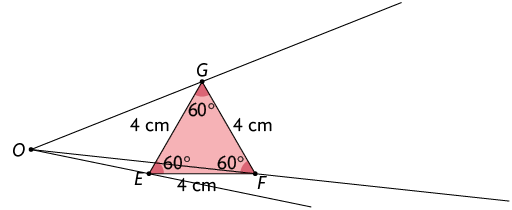
Como a razão de ampliação é igual a 2, marcamos pontos , e sobre as semirretas , e , respectivamente, tais que , e .
Usando um compasso com abertura igual à medida de e ponta-seca em , marcamos o ponto sobre a semirreta . De modo semelhante, marcamos os pontos e .
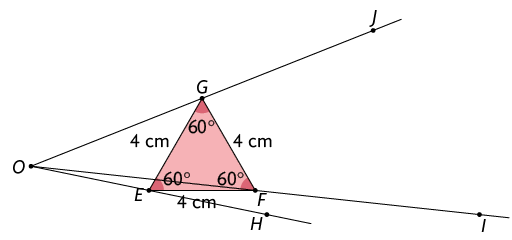
Agora, ligamos os pontos H, I e J.
O triângulo HIJ é uma ampliação do triângulo EFG na razão de semelhança .
4. A. No primeiro triângulo, os lados do ângulo que mede têm medidas de comprimento iguais a e, no segundo triângulo, os lados do ângulo que mede apresentam medidas de comprimento iguais a e .
Desse modo, os lados desses triângulos não são proporcionais e, portanto, os triângulos não são semelhantes.
B. Calculando as razões dos lados correspondentes dos triângulos, temos:
.
Logo, os triângulos são semelhantes pelo caso de semelhança de triângulos.
C. A soma das medidas dos ângulos internos de um triângulo é igual a . Assim, a medida do ângulo desconhecida do primeiro triângulo é igual a , pois .
Como consequência disso, os triângulos têm dois pares de ângulos congruentes e, portanto, os triângulos são semelhantes pelo caso de semelhança de triângulos.