Página LXXIII

Resoluções - parte 3

Unidade 5

Produtos notáveis, fatoração de polinômios e equações do 2º grau

Atividades

1. a ) Considerando um quadrado com o comprimento do lado medindo 2 a + b , temos:

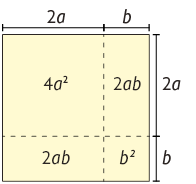
Ilustração de um quadrado dividido em dois quadrados e dois retângulos. Um quadrado fica no canto superior esquerdo. Nele está indicado que as medidas de comprimento e largura são, 2 vezes a, e, a área, indicada dentro do quadrado, tem medida igual a 4 vezes a elevado ao quadrado. Há um quadrado no canto inferior direito, está indicado que as medidas de comprimento e largura são b e a área, indicada dentro do quadrado, tem medida igual a b elevado ao quadrado. O retângulo no canto superior direito tem as medidas: comprimento b, largura 2 vezes a, e, a área, indicada dentro do retângulo, tem medida igual a 2 vezes a vezes b. O retângulo no canto inferior esquerdo tem a medida da área, indicada dentro do retângulo, igual a 2 vezes a vezes b.

Logo, ( 2 a + b ) 2 representa a medida da área desse quadrado, que, pela figura geométrica, é igual a 4 a 2 + 2 a b + 2 a b + b 2 .

Portanto, ( 2 a + b ) 2 = 4 a 2 + 4 a b + b 2 .

b) Considerando um quadrado com o comprimento do lado medindo a + 7 b , temos:

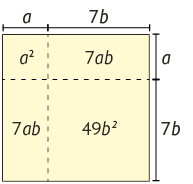
Ilustração de um quadrado dividido em dois quadrados e dois retângulos. Um quadrado fica no canto superior esquerdo. Nele está indicado que as medidas de comprimento e largura são, a, e a área, indicada dentro do quadrado, tem medida igual a, a, elevado ao quadrado. Há um quadrado no canto inferior direito, está indicado que as medidas de comprimento e largura são 7 vezes b e a área, indicada dentro do quadrado, tem medida igual a 49 vezes b elevado ao quadrado. O retângulo no canto superior direito tem as medidas: comprimento 7 vezes b, largura, a, e a área, indicada dentro do retângulo, tem medida igual a 7 vezes a vezes b. O retângulo no canto inferior esquerdo tem a medida da área, indicada dentro do retângulo, igual a 7 vezes a vezes b.

Portanto, ( a + 7 b ) 2 representa a medida da área desse quadrado, que, pela figura geométrica, é igual a: a 2 + 7 a b + 7 a b + 4 9 b 2

Portanto, ( a + 7 b ) 2 = a 2 + 14 a b + 4 9 b 2 .

c) Considerando um quadrado com o comprimento do lado medindo 5 a + 3 b , temos:

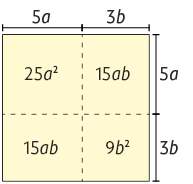
Ilustração de um quadrado dividido em dois quadrados e dois retângulos. Um quadrado fica no canto superior esquerdo. Nele está indicado que as medidas de comprimento e largura são 5 vezes a, e a área, indicada dentro do quadrado, tem medida igual a 25 vezes a elevado ao quadrado. Há um quadrado no canto inferior direito, está indicado que as medidas de comprimento e largura são 3 vezes b e a área, indicada dentro do quadrado, tem medida igual a 9 vezes b elevado ao quadrado. O retângulo no canto superior direito tem as medidas: comprimento 3 vezes b, largura 5 vezes a, e a área, indicada dentro do retângulo, tem medida igual a 15 vezes a vezes b. O retângulo no canto inferior esquerdo tem a medida da área, indicada dentro do retângulo, igual a 15 vezes a vezes b.

Logo, ( 5 a + 3 b ) 2 representa a medida da área desse quadrado, que, pela figura geométrica, é igual a 2 5 a 2 + 15 a b + 15 a b + 9 b 2 .

Portanto, ( 5 a + 3 b ) 2 = 2 5 a 2 + 30 a b + 9 b 2 .

2. Calculando o trinômio que representa a medida da área de cada um dos quadrados, temos:

A. ( a + 6 b ) 2 = ( a ) 2 + 6 a b + 6 a b + ( 6 b ) 2 = a 2 + 12 a b + 3 6 b 2

Portanto, a medida da área desse quadrado é igual a ( a + 6 b ) 2 = a 2 + 12 a b + 3 6 b 2 .

B. ( 2 a + b ) 2 = ( 2 a ) 2 + 2 a b + 2 a b + ( b ) 2 = 4 a 2 + 4 a b + b 2

Portanto, a medida da área desse quadrado é igual a ( 2 a + b ) 2 = 4 a 2 + 4 a b + b 2 .

3. Considerando um quadrado com o comprimento do lado medindo 3 x + 2 , temos:

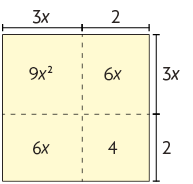
Ilustração de um quadrado dividido em dois quadrados e dois retângulos. Um quadrado fica no canto superior esquerdo. Nele está indicado que as medidas de comprimento e largura são 3 vezes x, e a área, indicada dentro do quadrado, tem medida igual a 9 vezes x elevado ao quadrado. Há um quadrado no canto inferior direito, está indicado que as medidas de comprimento e largura são 2, e a área, indicada dentro do quadrado, tem medida igual a 4. O retângulo no canto superior direito tem as medidas: comprimento 2, largura 3 vezes x, e a área, indicada dentro do retângulo, tem medida igual a 6 vezes x. O retângulo no canto inferior esquerdo tem a medida da área, indicada dentro do retângulo, igual a 6 vezes x.

Logo, ( 3 x + 2 ) 2 representa a medida da área desse quadrado, que, pela figura geométrica, é igual a 9 x 2 + 6 x + 6 x + 4 .

Portanto, ( 3 x + 2 ) 2 = 9 x 2 + 12 x + 4 .

4. Desenvolvendo os produtos notáveis e substituindo cada █ pelo valor adequado, temos:

a) 2 5 , pois ( x + 5 ) 2 = x 2 + 10 x + 2 5 .

b) 8 x , pois ( x + 4 ) 2 = x 2 + 8 x + 1 6 .

c) 9 x 2 , pois ( 3 x + 6 ) 2 = 9 x 2 + 36 x + 3 6 .

d) x 2 , pois ( x + 3 ) 2 = x 2 + 6 x + 9 .

e) 20 x , pois ( 2 x + 5 ) 2 = 4 x 2 + 20 x + 2 5 .

f) 4 x 2 , pois ( 2 x + 3 ) 2 = 4 x 2 + 12 x + 9 .

5. Escrevendo os produtos notáveis na forma de trinômio quadrado perfeito, temos:

a) ( x + 1 ) 2 = ( x + 1 ) ( x + 1 ) = x 2 + 2 x + 1 .

b) ( 9 x + 4 ) 2 = ( 9 x + 4 ) ( 9 x + 4 ) = 8 1 x 2 + 72 x + 1 6 .

c) ( x + 2 ) 2 = ( x + 2 ) ( x + 2 ) = x 2 + 4 x + 4 .

d) ( 3 x + 7 ) 2 = ( 3 x + 7 ) ( 3 x + 7 ) = 9 x 2 + 42 x + 4 9 .

e) ( 6 x + 3 4 ) 2 = ( 6 x + 3 4 ) ( 6 x + 3 4 ) = 3 6 x 2 + 9 x + 9 16 .

6. Desenvolvendo os produtos notáveis e substituindo cada █ pelo valor adequado, temos:

a) 4 a 2 , pois ( 2 a − b ) 2 = ( 2 a − b ) ( 2 a − b ) = 4 a 2 − 4 a b + b 2 .

b) a 2 e 6 a b , pois ( a − 3 b ) 2 = ( a − 3 b ) ( a − 3 b ) = a 2 − 6 a b + 9 b 2 .

c) 9 a 2 , 6 a b e b 2 , pois ( 3 a − b ) 2 = ( 3 a − b ) ( 3 a − b ) = 9 a 2 − 6 a b + b 2 .

7. Desenvolvendo os produtos notáveis e utilizando a regra do quadrado da diferença de dois termos, temos:

a) ( a − 5 b ) 2 = ( a − 5 b ) ( a − 5 b ) = a 2 − 10 a b + 2 5 b 2 .

b) ( 4 a − 5 b ) 2 = ( 4 a − 5 b ) ( 4 a − 5 b ) = 1 6 a 2 − 40 a b + 2 5 b 2 .

c) ( 3 a − 4 b ) 2 = ( 3 a − 4 b ) ( 3 a − 4 b ) = 9 a 2 − 24 a b + 1 6 b 2 .

d) ( 7 a − b ) 2 = ( 7 a − b ) ( 7 a − b ) = 4 9 a 2 − 14 a b + b 2 .

8. Simplificando cada uma das expressões, temos:

a) ( 2 a + b ) 2 + ( a − 3 b ) 2 = 4 a 2 + 4 a b + b 2 + a 2 − 6 a b + 9 b 2

Logo, ( 2 a + b ) 2 + ( a − 3 b ) 2 = 5 a 2 − 2 a b + 1 0 b 2 .

Página LXXIV

b) 3 x ( 2 − 3 y ) 2 + ( 4 x − 5 y ) 2 =

= 3 x ( 4 − 12 y + 9 y 2 ) + 1 6 x 2 − 40 x y + 2 5 y 2

Logo, 3 x ( 2 − 3 y ) 2 + ( 4 x − 5 y ) 2 =

= 12 x − 76 x y + 27 x y 2 + 1 6 x 2 + 2 5 y 2 .

9. a ) A medida do comprimento do lado do quadrado amarelo é igual a y − 2 x .

Assim, a medida da área desse quadrado é igual a ( y − 2 x ) 2 = y 2 − 4 x y + 4 x 2 .

Portanto, é um trinômio quadrado perfeito.

b) Para x = 2   cm e y = 10   cm , a medida da área:

de cada retângulo roxo ( y − 2 x ) ⋅ 2 x = ( 10 − 2 ⋅ 2 ) ⋅ 2 ⋅ 2 = 6 ⋅ 4 = 2 4 , ou seja, 24   cm 2 ;

do quadrado verde ( 2 x ) 2 = ( 2 ⋅ 2 ) 2 = 4 2 = 1 6 , ou seja, 16   cm 2 ;

do quadrado amarelo ( y − 2 x ) 2 = ( 10 − 2 ⋅ 2 ) 2 = 6 2 = 3 6 , ou seja, 36   cm 2 .

c) Resposta pessoal. Sugestão de resposta: Qual é a medida da área do quadrado verde? Resposta: 36   cm 2 .

10. Desenvolvendo os produtos notáveis e substituindo cada █ pelo valor adequado, temos:

a) x 2 , pois ( x + y ) ( x − y ) = x 2 − y 2 .

b) 4 a 2 , pois ( 2 a + b ) ( 2 a − b ) = 4 a 2 − b 2 .

c) 1 6 y 2 , pois ( 3 x − 4 y ) ( 3 x + 4 y ) = 9 x 2 − 1 6 y 2 .

11. Escrevendo a diferença de quadrados utilizando a regra do produto da soma pela diferença de dois termos, temos:

a) ( a + 4 b ) ( a − 4 b ) = a 2 − 1 6 b 2

b) ( 5 a 2 − b ) ( 5 a 2 + b ) = 2 5 a 4 − b 2

c) ( − a + 2 b 3 ) ( − a − 2 b 3 ) = a 2 − 4 b 6

12. Simplificando as expressões algébricas, temos:

a) ( a − 2 b ) ( a + 2 b ) + 3 b 2 = a 2 − 4 b 2 + 3 b 2 = a 2 − b 2

b) ( x + 3 y 2 ) ( x − 3 y 2 ) − 2 x ( x − 4 ) =

= x 2 − 9 y 4 − 2 x 2 + 8 x = − x 2 − 9 y 4 + 8 x

13. a ) Inicialmente, a figura geométrica era um quadrado de lado a com medida de área igual a 2 .

Como Jorge recortou um quadrado de lado b, a medida da área recortada é igual a b 2 .

Portanto, o polinômio que representa a medida da área da cartolina que sobrou é igual a a 2 − b 2 .

b) A medida da área do pedaço de cartolina que sobrou é igual a a 2 − b 2 .

Sabendo que a + b = 8   cm e a − b = 2   cm , temos:

a 2 − b 2 = ( a + b ) ⋅ ( a − b ) = 8 ⋅ 2 = 1 6

Logo, a medida da área do pedaço de cartolina que sobrou é igual a 16   cm 2 .

14. Resolvendo cada um dos itens da segunda coluna, temos:

1. 4 x ( 2 x + 3 ) = 4 x ⋅ 2 x + 4 x ⋅ 3 = 8 x 2 + 12 x , logo B–1;

2. 4 ( 2 x 2 + 3 ) = 4 ⋅ 2 x 2 + 4 ⋅ 3 = 8 x 2 + 1 2 , logo D–2;

3. 4 x ( 3 x + 2 ) = 4 x ⋅ 3 x + 4 x ⋅ 2 = 1 2 x 2 + 8 x , logo A–3;

4. 4 ( 3 x 2 − 2 ) = 4 ⋅ 3 x 2 − 4 ⋅ 2 = 1 2 x 2 − 8 , logo C–4.

Assim, A–3; B–1; C–4; D–2.

15. Colocando cada um dos fatores comuns em evidência, temos:

a) 5 x − 10 = 5 ⋅ x − 5 ⋅ 2 = 5 ( x − 2 )

b) 2 b 2 − 4 b = 2 b ⋅ b − 2 ⋅ 2 b = 2 b ( b − 2 )

c) 1 6 a 2 + 12 a = 4 a ⋅ 4 a + 4 a ⋅ 3 = 4 a ( 4 a + 3 )

d) 2 4 y 2 − 40 = 8 ⋅ 3 y 2 − 8 ⋅ 5 = 8 ( 3 y 2 − 5 )

16. Fatorando os polinômios e substituindo cada █ pelo valor adequado, temos:

a) 2 a 4 , pois 6 a 4 − 3 b = 3 ( 2 a 4 − b ) .

b) 1 6 n 3 , pois 1 8 m 3 + 1 6 n 3 = 2 ( 9 m 3 + 8 n 3 ) .

c) − 2 0 p 2 , pois − 2 0 p 2 + 32 q = 4 ( − 5 p 2 + 8 q ) .

17. Fatorando os polinômios por agrupamento, temos:

a) − 4 m + m n − 4 y + y n = m ( − 4 + n ) + y ( − 4 + n ) =

= ( − 4 + n ) ( m + y )

b) a m − 7 m + 8 a − 56 = m ( a − 7 ) + 8 ( a − 7 ) =

= ( a − 7 ) ( m + 8 )

c) 10 c + 20 − c v − 2 v = 1 0 ( c + 2 ) − v ( c + 2 ) =

= ( c + 2 ) ( 10 − v )

18. Fatorando os trinômios quadrados perfeitos em cada um dos itens, temos:

a) 4 a 2 + 4 a b + b 2 = ( 2 a ) 2 + 2 ⋅ 2 a ⋅ b + b 2 =

= ( 2 a + b ) 2

b) c 2 + 10 c d + 2 5 d 2 = c 2 + 2 ⋅ c ⋅ 5 d + ( 5 d ) 2 =

= ( c + 5 d ) 2

c) x 2 + 6 x y + 9 y 2 = x 2 + 2 ⋅ x ⋅ 3 y + ( 3 y ) 2 =

= ( x + 3 y ) 2

d) 4 9 a 2 − 42 a b + 9 b 2 = ( 7 a ) 2 − 2 ⋅ 7 a ⋅ 3 b + ( 3 b ) 2 =

= ( 7 a − 3 b ) 2

19. Fatorando as diferenças de quadrados, temos:

a) 16 − x 2 = 4 2 − x 2 = ( 4 + x ) ( 4 − x )

b) 4 x 2 − 64 = ( 2 x ) 2 − 8 2 = ( 2 x + 8 ) ( 2 x − 8 )

c) 9 x 2 − 4 = ( 3 x ) 2 − 2 2 = ( 3 x + 2 ) ( 3 x − 2 )

d) 49 − 2 5 x 2 = 7 2 − ( 5 x ) 2 = ( 7 + 5 x ) ( 7 − 5 x )

20. a ) Não. A quarta expressão foi fatorada de maneira incorreta.

b) Copiando a expressão e fatorando corretamente, temos:

x 2 − 8 x + 16 = x 2 − 2 ⋅ x ⋅ 4 + 4 2 = ( x − 4 ) 2

21. Desenvolvendo os produtos notáveis ou fatorando polinômios, e substituindo cada █ pelo valor adequado, temos:

a) 8 x y , pois 1 6 x 2 + 8 x y + y 2 = ( 4 x + y ) 2 .

b) a 2 , pois a 2 + 10 a b + 2 5 b 2 = ( a + 5 b ) 2 .

c) 22 5 x 2 ; 1 , pois ( 15 x − 1 ) ( 15 x + 1 ) = 22 5 x 2 − 1 .

d) 14 a b ; 7 a ; b , pois 4 9 a 2 + 14 a b + b 2 = ( 7 a + b ) 2 .

e) 3 a ; b ; 3 a ; b , pois ( 3 a + b ) ( 3 a − b ) = 9 a 2 − b 2 .

Página LXXV

22. Os três trinômios quadrados perfeitos podem ser escritos e fatorados da seguinte forma:

x 2 − 2 x y + y 2 = ( x − y ) 2 ;

9 x 2 + 6 x y + y 2 = ( 3 x + y ) 2 ;

x 2 + 6 x y + 9 y 2 = ( x + 3 y ) 2 .

23. Para responder a essa atividade, devemos fatorar os polinômios mais de uma vez, assim:

a) 3 x 2 − 27 = 3 ( x 2 − 9 ) = 3 ( x 2 − 3 2 ) =

= 3 ( x + 3 ) ( x − 3 )

b) 1 8 x 2 − 3 2 y 2 = 2 ( 9 x 2 − 1 6 y 2 ) = 2 [ ( 3 x ) 2 − ( 4 y ) 2 ] =

= 2 ( 3 x + 4 y ) ( 3 x − 4 y )

c) 5 x 2 − 20 x y + 2 0 y 2 = 5 ( x 2 − 4 x y + 4 y 2 ) =

= 5 [ x 2 − 2 ⋅ x ⋅ 2 y + ( 2 y ) 2 ] = 5 ( x − 2 y ) 2

d) 3 x 3 + 6 x 2 + 3 x = 3 x ( x 2 + 2 x + 1 ) =

= 3 x ( x 2 + 2 ⋅ x ⋅ 1 + 1 2 ) = 3 x ( x + 1 ) 2

Questão 1. Resposta pessoal. Espera-se que o estudante explique para o colega que, em uma equação do 1º grau, o maior expoente da incógnita x é o 1, enquanto na equação do 2º grau, o maior expoente da incógnita x é o 2.

Questão 2. No quadro 1, as equações do 2º grau são completas do tipo a x 2 + b x + c = 0 , em que a ≠ 0 , b ≠ 0 e c ≠ 0 .

No quadro 2, as equações do 2º grau são incompletas do tipo a x 2 + b x = 0 , em que a ≠ 0 , b ≠ 0 e c = 0 .

No quadro 3, as equações do 2º grau são incompletas do tipo a x 2 + c = 0 , em que a ≠ 0 , b = 0 e c ≠ 0 .

No quadro 4, as equações do 2º grau são incompletas do tipo a x 2 = 0 , em que a ≠ 0 , b = 0 e c = 0 .

Atividades

24. São equações do 1º grau: 3 x − 4 = 0 ; − 5 x + 18 = 0 ; − 5 x − 10 , 4 = 0 ; 2 x − 9 = 0 .

São equações do 2º grau: 5 x 2 − 7 x + 8 = 0 ; x 2 + 12 = 0 ; x 2 + 3 x + 5 = 0 ; − 2 x 2 + x 2 = 0 .

25. No quadrado A, a medida do comprimento do lado é x e a medida da área é 6 4   m 2 .

Substituindo esse valor na fórmula do cálculo da medida de área de um quadrado, temos A = x 2 , ou seja, 64 = x 2 .

Assim, x 2 = 6 4 , logo a medida do comprimento x é igual a 8   m .

No quadrado B, a medida do comprimento do lado é 2 x e a medida da área é 14 4   m 2 .

Substituindo esse valor na fórmula do cálculo da medida de área de um quadrado, temos A = x 2 , ou seja, 144 = ( 2 x ) 2 .

Assim, 4 x 2 = 14 4 , ou seja, x 2 = 3 6 , logo a medida do comprimento x é igual a 6   m .

26. Resposta pessoal. Sugestão de resposta:

a) x 2 + 8 x + 4 = 0 e − x 2 + 8 x + 9 = 0

b) − x 2 + 4 x = 0 e 3 x 2 − x = 0

c) 5 x 2 − 125 = 0 e − 2 x 2 + 72 = 0

27. As respostas dependem das equações escritas pelos estudantes na atividade anterior.

Resposta pessoal. Sugestão de resposta:

a) a = 1 ; b = 8 ; c = 4 e a = − 1 ; b = 8 ; c = 9

b) a = − 1 ; b = 4 ; c = 0 e a = 3 ; b = − 1 ; c = 0

c) a = 5 ; b = 0 ; c = − 12 5 e a = − 2 ; b = 0 ; c = 7 2

28. No quadro A, a equação é x 2 − 3 x + 7 = 0 . No quadro B, a equação é − 2 5 x 2 + 3 x = 0 .

29. a ) A medida do perímetro dessa sala é dada pelo polinômio x 2 + 6 + 3 + x 2 + 6 + 3 = 2 x 2 + 1 8 .

Assim, 2 x 2 + 18 = 2 4 . Portanto, a equação é 2 x 2 − 6 = 0 .

b) A equação é incompleta, pois o coeficiente b é igual a zero, ou seja, não tem o termo com x.

c) Resposta pessoal. Sugestão de resposta: Considerando a figura que representa a planta baixa dessa sala e sabendo que a medida de sua área é 45  m 2 , determine o valor de x . Resposta: 3   m .

30. a ) a = − 1 ; b = − 1 e c = 1

b) a = 2 ; b = 0 e c = − 3

c) a = 5 ; b = − 3 e c = − 2

d) a = 3 ; b = − 3 e c = 0

e) a = − 2 ; b = 5 e c = − 2

f) a = 1 ; b = 0 e c = 0     

31. a ) A medida da área do triângulo é dada por:

3 x ( x + 2 + 2 + 2 ) 2 = 3 x ( x + 6 ) 2 = 3 x 2 + 18 x 2 = 3 2 x 2 + 9 x

A medida da área do quadrado é dada por: ( x + 2 ) 2 = x 2 + 4 x + 4

A medida da área do retângulo é dada por:

2 ( x + 2 ) = 2 x + 4

Como a medida da área do triângulo é igual à medida da área do quadrado mais a medida da área do retângulo, temos:

3 2 x 2 + 9 x = x 2 + 4 x + 4 + 2 x + 4

Escrevendo-a na forma reduzida, obtemos x 2 + 6 x − 16 = 0 .

b) A equação é completa. Seus coeficientes são: a = 1 ; b = 6 ; c = − 1 6 .

32. Escrevendo cada uma das equações, temos:

a) x 2 + 3 x = 1 0 e, em sua forma reduzida: x 2 + 3 x − 10 = 0 .

b) 2 x 2 + x 5 = 1 2 e, em sua forma reduzida: 2 x 2 + x 5 − 12 = 0 .

c) 3 x 2 − 6 = 5 x e, na forma reduzida: 3 x 2 − 5 x − 6 = 0 .

d) ( x + 1 ) 2 = 5 2 e, na forma reduzida: x 2 + 2 x − 51 = 0 .

Resposta pessoal. Sugestão de resposta:

Página LXXVI

a) O quadrado de um número x mais seu dobro é igual a 8. Resposta: x 2 + 2 x − 8 = 0

b) A medida da área de um quadrado cujo comprimento do lado mede x − 2 é 40. Resposta: x 2 − 4 x − 36 = 0

c) A diferença entre o quadrado de um número x e o seu triplo é igual a 70. Resposta: x 2 − 3 x − 70 = 0

33. Como a b c = 3 5 , a + b + c = 1 3 e b < a < c , então: a = 5 ; b = 1 ; c = 7 . Assim, a equação é 5 x 2 + x + 7 = 0 .

34. a ) Para que a equação seja do 2º grau, o coeficiente de x 2 deve ser diferente de zero.

Assim, 3 █ + 1 ≠ 0 , isto é, █ ≠ − 1 3 .

b) Para que a equação seja do 2º grau completa, o coeficiente de x deve ser diferente de zero. Assim, █ + 8 ≠ 0 , isto é, █ ≠ − 8 .

c) Para que a equação seja do 2º grau incompleta, o coeficiente do termo independente de x deve ser igual a zero. Assim, █ + 7 = 0 , isto é, █ = − 7 .

Questão 3. Resposta: Espera-se que os estudantes verifiquem que Luca Pacioli teve várias contribuições para a Matemática, entre elas, Contabilidade, Aritmética e equações do 2º grau.

Atividades

35. Escrevendo as equações no tipo a x 2 = c e reorganizando-as, quando necessário, para x 2 = c a , ao fazer os cálculos, temos:

a) x 2 = 2 5 , logo x = − 2 5 = − 5 e x = 2 5 = 5 ;

b) x 2 − 16 = 0 , assim x 2 = 1 6 , logo x = − 1 6 = − 4 e x = 1 6 = 4 ;

c) 2 x 2 − 128 = 0 , assim x 2 = 6 4 , logo x = − 6 4 = − 8 e x = 6 4 = 8 ;

d) x 2 − 144 = 0 , assim x 2 = 14 4 , logo x = − 14 4 = − 1 2 e x = 14 4 = 1 2 ;

e) 3 x 2 + 15 = 12 3 , assim x 2 = 3 6 , logo x = − 3 6 = − 6 e x = 3 6 = 6 ;

f) x 2 − 7 = − 2 , assim x 2 = 5 , logo x = − 5 e x = 5 .

36. a ) Se x 2 − 12 = − 8 , então x 2 = 4 . Assim, x = 2 ou x = − 2 .

b) Se 2 x 2 − 7 = x 2 + 4 2 , então x 2 = 4 9 . Assim, x = 7 ou x = − 7 .

c) Se − 3 x 2 − 11 2 = − 2 x 2 + 3 5 , logo − 3 x 2 − 11 = − 4 x 2 + 7 0 , então x 2 = 8 1 . Assim, x = 9 ou x = − 9 .

37. Escrevendo uma equação para cada um dos itens, temos:

a) x 2 = 12 1 , logo esse número é x = 1 1 ou x = − 1 1 .

b) x 2 − 45 = 39 6 , logo x 2 = 44 1 e, como a quantia não pode ser um número negativo, x = 2 1 . Portanto, essa quantia é igual a R$ 21,00.

38. Calculando, primeiro, a medida da área do retângulo, temos 2 x ⋅ 3 x = 6 x 2 .

Assim, 6 x 2 = 5 4 , ou seja, x 2 = 9 , logo x = 3 .

Portanto, as medidas das dimensões desse retângulo são 6   m de largura e 9   m de comprimento.

39. Resposta pessoal. Sugestão de resposta: Uma piscina é coberta por uma lona retangular com 392   m 2 de medida de área. A medida do comprimento da lona é o dobro da medida da largura. Quais são as medidas das dimensões da lona? Resposta: As medidas das dimensões da lona são 14   m de largura e 28   m de comprimento.

40. As equações que não tem raízes reais são:

A, pois 2 x 2 + 18 = 0 resulta em x 2 = − 9 ;

D, pois − x 2 − 49 = 0 resulta em x 2 = − 4 9 ;

E, pois 2 3 x 2 + 22 = 0 resulta em x 2 = − 3 3 .

41. Espera-se que os estudantes concluam que as equações desse tipo podem ter uma (caso em que as duas raízes são iguais), duas ou nenhuma raiz. Quanto à relação entre as raízes, quando existir, espera-se que eles concluam que elas podem ser iguais ou opostas.

42. A medida da área de cada quadrado é igual a x 2 . Assim, 5 x 2 = 4 5 , ou seja, x 2 = 9 .

Como a medida do comprimento do lado não deve ser um valor negativo, a medida do comprimento do lado de cada quadrado é igual a 3   m .

43. Como o quadrado e o triângulo equilátero têm um lado comum, a medida do comprimento do lado do quadrado é igual a 2 x . Dessa maneira, ( 2 x ) 2 = 4 x 2 = 25 6 , isto é, x 2 = 6 4 .

Logo, x = 8   m .

Calculando a medida do perímetro da figura, temos 5 ⋅ 2 x = 5 ⋅ 2 ⋅ 8 .

Portanto, a medida do perímetro da figura é igual a 80   m .

44. Cada uma das equações a seguir é do tipo a x 2 + b x = 0 , nesse caso, o x é o fator comum aos dois termos. Logo, vamos reescrever a equação colocando o x em evidência para, em seguida, determinar suas raízes.

a) x ( x − 3 ) = 0 , as raízes são 0 e 3 .

b) 4 x ( x + 4 ) = 0 , as raízes são 0 e − 4 .

c) 0 , 5 x ( x + 20 ) = 0 , as raízes são 0 e − 2 0 .

d) x ( x + 5 2 ) = 0 , as raízes são 0 e − 5 2 .

e) 3 4 x ( x − 20 ) = 0 , as raízes são 0 e 2 0 .

f) 8 x ( x + 2 , 1 ) = 0 , as raízes são 0 e − 2 , 1 .

g) x ( x − 17 ) = 0 , as raízes são 0 e 1 7 .

h) x ( x − 3 5 ) = 0 , as raízes são 0 e 3 5 .

45. Espera-se que os estudantes percebam que as equações do 2º grau desse tipo têm duas raízes reais: uma igual a zero e outra diferente de zero.

Página LXXVII

46. Como a equação é incompleta do tipo a x 2 + b x = 0 , ela tem uma raiz igual a zero e outra diferente de zero, ou seja, x ( x + 3 ) = 0 . Logo, as raízes são 0 e − 3 , sendo uma raiz nula e uma negativa. Portanto, a alternativa correta é a b.

47. a ) As medidas dos volumes dos sólidos apresentados, são:

medida do volume do cubo: x ⋅ x ⋅ x = x 3 ;

medida do volume do paralelepípedo:

( x + 3 ) ⋅ x ⋅ ( x − 1 ) = x 3 − x 2 + 3 x 2 − 3 x = x 3 + 2 x 2 − 3 x .

Como as medidas dos volumes são iguais, então:

x 3 = x 3 + 2 x 2 − 3 x , ou seja, 2 x 2 − 3 x = 0 .

Resolvendo essa equação, temos:

2 x 2 − 3 x = 0

x ( 2 x − 3 ) = 0

Assim, x = 0 ou x = 3 2 = 1 , 5 .

Portanto, as medidas dos comprimentos das arestas do cubo são iguais a 1 , 5   cm e as medidas dos comprimentos das arestas do paralelepípedo são iguais a 4 , 5   cm , 1 , 5   cm e 0 , 5   cm .

b) Como as figuras têm a mesma medida de volume, o volume de ambas as figuras mede 3 , 375 ⏟ ( 1 , 5 ) 3   cm 3 .

48. Utilizando o teorema de Tales em ambos os itens da atividade, temos:

A. 3 x x = 3 2 x , ou seja, 6 x 2 − 3 x = 0 . Assim, 3 x ( 2 x − 1 ) = 0 , isto é, x = 1 2 .

B. 4 x − 1 4 = 9 x 2 6 x , logo 2 4 x 2 − 6 x = 18 x , ou seja, 2 4 x 2 − 24 x = 0 . Assim, 24 x ( x − 1 ) = 0 e, portanto, x = 1 .

49. Resposta pessoal. Sugestão de resposta: O retângulo e o triângulo representados na atividade têm a mesma medida de área. Determine o valor de x . Resposta: x = 1 5 .

Questão 4. Resposta pessoal. Sugestão de resposta: Espera-se que os estudantes verifiquem que Al-Khwarizmi teve várias contribuições para a Matemática e para a Física, entre elas, a escrita de tabelas astronômicas, tratados sobre o relógio de Sol e o desenvolvimento da Álgebra e da Aritmética.

Atividades

50. Fatorando o 1º membro de cada equação para em seguida resolvê-la, temos:

a) x 2 + 6 x + 9 = ( x + 3 ) ⋅ ( x + 3 ) = ( x + 3 ) 2

Resolvendo a equação fatorada ( x + 3 ) 2 = 4 , obtemos:

x + 3 = − 4

x + 3 = − 2

x = − 5

x + 3 = 4

x + 3 = 2

x = − 1

b) x 2 + 18 x + 81 = ( x + 9 ) ⋅ ( x + 9 ) = ( x + 9 ) 2

Resolvendo a equação fatorada ( x + 9 ) 2 = 3 6 , obtemos:

x + 9 = − 3 6

x + 9 = − 6

x = − 1 5

x + 9 = 3 6

x + 9 = 6

x = − 3

c) x 2 + 14 x + 49 = ( x + 7 ) ⋅ ( x + 7 ) = ( x + 7 ) 2

Resolvendo a equação fatorada ( x + 7 ) 2 = 1 6 , obtemos:

x + 7 = − 1 6

x + 7 = − 4

x = − 1 1

x + 7 = 1 6

x + 7 = 4

x = − 3

d) x 2 − 24 x + 144 = ( x − 12 ) ⋅ ( x − 12 ) = ( x − 12 ) 2

Resolvendo a equação fatorada ( x − 12 ) 2 = 2 5 , obtemos:

x − 12 = 2 5

x − 12 = 5

x = 1 7

x − 12 = − 2 5

x − 12 = − 5

x = 7

e) x 2 − 12 x + 36 = ( x − 6 ) ⋅ ( x − 6 ) = ( x − 6 ) 2

Resolvendo a equação fatorada ( x − 6 ) 2 = 0 , obtemos:

x − 6 = 0

x − 6 = 0

x = 6

51. a ) Isolando o termo independente na equação, temos x 2 + 8 x = − 1 2 . Como 8 x = 2 ⋅ 4 ⋅ x , obtemos:

x 2 + 2 ⋅ 4 ⋅ x = − 1 2

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 4 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 4 ⋅ x + 4 2 = − 12 + 4 2

x 2 + 8 x + 16 = − 12 + 1 6

x 2 + 8 x + 16 = 4

Página LXXVIII

Fatorando o 1º membro da equação: ( x + 4 ) 2 = 4 , assim as raízes da equação são:

( x + 4 ) 2 = 4

x + 4 = 4 , ou seja, x = − 2

x + 4 = − 4 , ou seja, x = − 6 .

b) Isolando o termo independente da equação, temos x 2 + 6 x = 1 6 . Como 6 x = 2 ⋅ 3 ⋅ x , obtemos:

x 2 + 2 ⋅ 3 ⋅ x = 1 6

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 3 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 3 ⋅ x + 3 2 = 16 + 3 2

x 2 + 6 x + 9 = 16 + 9

x 2 + 6 x + 9 = 2 5

Fatorando o 1º membro da equação: ( x + 3 ) 2 = 2 5 , assim as raízes da equação são:

x + 3 = 2 5 , ou seja, x = 2

x + 3 = − 2 5 , ou seja, x = − 8 .

c) Isolando o termo independente da equação, temos x 2 + 12 x = 2 8 . Como 12 x = 2 ⋅ 6 ⋅ x , obtemos:

x 2 + 2 ⋅ 6 ⋅ x = 2 8

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 6 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 6 ⋅ x + 6 2 = 28 + 6 2

x 2 + 12 x + 36 = 28 + 3 6

x 2 + 12 x + 36 = 6 4

Fatorando o 1º membro da equação: ( x + 6 ) 2 = 6 4 , assim as raízes da equação são:

x + 6 = 6 4 , ou seja, x = 2

x + 6 = − 6 4 , ou seja, x = − 1 4 .

d) Isolando o termo independente da equação, temos x 2 + 10 x = − 2 1 . Como 10 x = 2 ⋅ 5 ⋅ x , obtemos:

x 2 + 2 ⋅ 5 ⋅ x = − 2 1

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 5 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 5 ⋅ x + 5 2 = − 21 + 5 2

x 2 + 10 x + 25 = − 21 + 2 5

x 2 + 10 x + 25 = 4

Fatorando o 1º membro da equação: ( x + 5 ) 2 = 4 , assim as raízes da equação são:

x + 5 = 4 , ou seja, x = − 3

x + 5 = − 4 , ou seja, x = − 7 .

e) Isolando o termo independente da equação, temos x 2 + 2 x = 1 5 . Como 2 x = 2 ⋅ 1 ⋅ x , obtemos:

x 2 + 2 ⋅ 1 ⋅ x = 1 5

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 1 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 1 ⋅ x + 1 2 = 15 + 1 2

x 2 + 2 x + 1 2 = 15 + 1 2

x 2 + 2 x + 1 = 1 6

Fatorando o 1º membro da equação: ( x + 1 ) 2 = 1 6 , assim as raízes da equação são:

x + 1 = 1 6 , ou seja, x = 3

x + 1 = − 1 6 , ou seja, x = − 5 .

f) Isolando o termo independente da equação, temos x 2 + 20 x = − 9 9 . Como 20 x = 2 ⋅ 10 ⋅ x , obtemos:

x 2 + 2 ⋅ 10 ⋅ x = − 9 9

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 1 0 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 10 ⋅ x + 1 0 2 = − 99 + 1 0 2

x 2 + 20 x + 100 = − 99 + 10 0

x 2 + 20 x + 100 = 1

Fatorando o 1º membro da equação: ( x + 10 ) 2 = 1 , assim as raízes da equação são:

x + 10 = 1 , ou seja, x = − 9

x + 10 = − 1 , ou seja, x = − 1 1 .

52. De acordo com a representação do primeiro e do segundo membro da equação, temos:

y 2 + 3 y + 3 y = 8 ⋅ 5

y 2 + 6 y = 4 0

Resolvendo-a pelo método de completar quadrado:

y 2 + 6 y + 9 = 40 + 9

( y + 3 ) 2 = 4 9

y + 3 = 4 9 , ou seja, y = 4

y + 3 = − 4 9 , ou seja, y = − 1 0 .

Como o valor de y representa uma das medidas dos lados do quadrado, então y = 4 .

53. Substituindo os coeficientes na fórmula resolutiva, temos:

a) x = − ( − 7 ) ± ( − 7 ) 2 − 4 ⋅ 1 ⋅ 6 2 ⋅ 1 = 7 ± 2 5 2 = 7 ± 5 2 , ou seja, x 1 = 7 − 5 2 = 2 2 = 1 e x 2 = 7 + 5 2 = 12 2 = 6 .

b) a = − 3 ± 3 2 − 4 ⋅ 1 ⋅ ( − 18 ) 2 ⋅ 1 = − 3 ± 8 1 2 , assim a = − 3 ± 9 2 , ou seja, a 1 = − 3 − 9 2 = − 12 2 = − 6 e a 2 = − 3 + 9 2 = 6 2 = 3 .

c) y = − ( − 6 ) ± ( − 6 ) 2 − 4 ⋅ 2 ⋅ ( − 20 ) 2 ⋅ 2 = 6 ± 19 6 4 , assim y = 6 ± 14 4 , ou seja, y 1 = 6 − 14 4 = − 8 4 = − 2 e y 2 = 6 + 14 4 = 20 4 = 5 .

Página LXXIX

d) y = − 8 ± 8 2 − 4 ⋅ 4 ⋅ 3 2 ⋅ 4 = − 8 ± 1 6 8 = − 8 ± 4 8 , ou seja, y 1 = − 8 + 4 8 = − 4 8 = − 1 2

e y 2 = − 8 − 4 8 = − 12 8 = − 3 2 .

e) x = − ( − 21 ) ± ( − 21 ) 2 − 4 ⋅ 7 ⋅ 0 2 ⋅ 7 = 21 ± 44 1 14 , assim x = 21 ± 21 14 , ou seja, x 1 = 21 − 21 14 = 0 14 = 0 e x 2 = 21 + 21 14 = 42 14 = 3 .

f) a = − ( − 2 ) ± ( − 2 ) 2 − 4 ⋅ 1 ⋅ ( − 9 ) 2 ⋅ 1 = 2 ± 4 0 2 , assim a = 2 ± 2 1 0 2 , ou seja, a 1 = 2 − 2 1 0 2 = 2 ⋅ ( 1 − 1 0 ) 2 = 1 − 1 0 e a 2 = 2 + 2 1 0 2 = 2 ⋅ ( 1 + 1 0 ) 2 = 1 + 1 0 .

54. Resolvendo a equação pela fórmula resolutiva, temos:

x = − ( − 26 ) ± ( − 26 ) 2 − 4 ⋅ 1 ⋅ 16 5 2 ⋅ 1 = 26 ± 1 6 2 , assim x = 26 ± 4 2 , ou seja, x 1 = 26 − 4 2 = 22 2 = 1 1 e x 2 = 26 + 4 2 = 30 2 = 1 5 .

Assim, Paula tem 15 anos, pois é a mais velha, e Henrique tem 11 anos.

55. a ) Realizando os cálculos:

3 ( 6 x − 6 ) + 2 x 2 = x 2 + 11 x − 2 8

18 x − 18 + 2 x 2 = x 2 + 11 x − 2 8

2 x 2 − x 2 + 18 x − 11 x − 18 + 28 = 0

Escrevendo na forma reduzida, obtemos x 2 + 7 x + 10 = 0 . Resolvendo a equação, obtemos:

Δ = ( 7 ) 2 − 4 ⋅ 1 ⋅ 10 = 9

x = − 7 ± 9 2 ⋅ 1 = − 7 ± 3 2

Portanto, as raízes da equação são x 1 = − 7 + 3 2 = − 2 e x 2 = − 7 − 3 2 = − 5 .

b) Realizando os cálculos:

− 5 ( − 2 x + 3 ) − 3 x 2 = 1 − 2 x 2

10 x − 15 − 3 x 2 = 1 − 2 x 2

− 3 x 2 + 2 x 2 + 10 x − 15 − 1 = 0

Escrevendo na forma reduzida, obtemos − x 2 + 10 x − 16 = 0 .

Resolvendo a equação, obtemos:

Δ = ( 10 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 16 ) = 3 6

x = − 10 ± 3 6 2 ⋅ ( − 1 ) = − 10 ± 6 − 2

Portanto, as raízes da equação são x 1 = − 10 + 6 − 2 = 2 e x 2 = − 10 − 6 − 2 = 8 .

c) Realizando os cálculos:

2 x ( x − 4 ) + 5 = − x 2 + 7 x − 7

2 x 2 − 8 x + 5 = − x 2 + 7 x − 7

2 x 2 + x 2 − 8 x − 7 x + 5 + 7 = 0

Escrevendo na forma reduzida, obtemos 3 x 2 − 15 x + 12 = 0 .

Resolvendo a equação, obtemos:

Δ = ( − 15 ) 2 − 4 ⋅ 3 ⋅ 12 = 8 1

x = − ( − 15 ) ± 8 1 2 ⋅ 3 = − 10 ± 9 6

Portanto, as raízes da equação são x 1 = 15 + 9 6 = 4 e x 2 = 15 − 9 6 = 1 .

d) Realizando os cálculos:

( x + 2 ) ( 2 x − 3 ) = 5 x 2 + x − 11 4

2 x 2 − 3 x + 4 x − 6 = 5 x 2 + x − 11 4

2 x 2 − 5 x 2 − 3 x + 4 x − x − 6 + 114 = 0

Escrevendo na forma reduzida, obtemos − 3 x 2 + 108 = 0 .

Resolvendo a equação, obtemos:

Δ = 0 2 − 4 ⋅ ( − 3 ) ⋅ 108 = 1 . 296

x = ± 1 . 296 2 ⋅ ( − 3 ) = ± 36 − 6

Portanto, as raízes da equação são x 1 = 36 − 6 = − 6 e x 2 = − 36 − 6 = 6 .

56. A. A medida da área do retângulo é dada por 2 x ( x + 1 ) = 2 x 2 + 2 x .

Assim, temos 2 x 2 + 2 x = 2 4 , resolvendo-a:

2 x 2 + 2 x − 24 = 0

Δ = 2 2 − 4 ⋅ 2 ⋅ ( − 24 ) = 19 6

x = − 2 ± 19 6 2 ⋅ 2 = − 2 ± 14 4

As raízes da equação são x 1 = − 2 + 14 4 = 3 e x 2 = − 2 − 14 4 = − 8 .

Como x representa a medida do lado de um retângulo, segue que x = 3 . Desse modo, os lados desse retângulo medem respectivamente 6   m e 4   m , pois 2 ⋅ 3 = 6 e 3 + 1 = 4 .

Portanto, o perímetro dessa figura mede P = 6 + 4 + 6 + 4 = 2 0 , ou seja, 20   m .

Página LXXX

B. A medida da área do triângulo é dada por

( 3 x − 2 ) ( x + 1 ) 2 = 3 x 2 + x − 2 2 .

Assim, temos: 3 x 2 + x − 2 2 = 6

3 x 2 + x − 2 = 1 2

3 x 2 + x − 2 − 12 = 0

3 x 2 + x − 14 = 0

Resolvendo a equação:

Δ = 1 2 − 4 ⋅ 3 ⋅ ( − 14 ) = 16 9

x = − 1 ± 16 9 2 ⋅ 3 = − 1 ± 13 6

As raízes da equação são x 1 = − 1 + 13 6 = 2 e x 2 = − 1 − 13 6 = − 7 3 .

Como x representa a medida do lado de um triângulo, segue que x = 2 . Desse modo, o comprimento dos lados desse triângulo medem respectivamente 5   m , 4   m e 3   m , pois 2 ⋅ 2 + 1 = 5 , 3 ⋅ 2 − 2 = 4 e 2 + 1 = 3 .

Portanto, o perímetro dessa figura mede P = 4 + 3 + 5 = 1 2 , ou seja, 12   m .

57. a ) Calculando a medida do perímetro do triângulo, temos 3 x + 3 + x + 6 + 6 x − 3 = 10 x + 6 .

Assim, uma equação que possibilite calcular o valor de x é 10 x + 6 = 3 6 , ou seja, 10 x − 30 = 0 .

b) A medida da área do triângulo é dada por

( 3 x + 3 ) ( x + 6 ) 2 = 3 x 2 + 21 x + 18 2 .

Assim, 3 x 2 + 21 x + 18 2 = 5 4 , ou seja, 3 x 2 + 21 x − 90 = 0 .

c) A equação obtida no item b é do 2º grau.

d) Resolvendo a equação:

3 x 2 + 21 x − 90 = 0

Δ = 2 1 2 − 4 ⋅ 3 ⋅ ( − 90 ) = 1 . 521

x = − 21 ± 1 . 521 2 ⋅ 3 = − 21 ± 39 6

As raízes da equação são x 1 = − 21 + 39 6 = 3 e x 2 = − 21 − 39 6 = − 1 0 .

Como x representa a medida do lado de um triângulo, segue que x = 3 .

Assim, as medidas dos comprimentos dos lados do triângulo são: 9   cm , 12   cm e 15   cm .

58. Resolvendo a equação x 2 − x − 6 = 0 , temos:

Δ = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 2 5

x = − ( − 1 ) ± 2 5 2 ⋅ 1 = 1 ± 5 2

As raízes da equação são x 1 = 1 + 5 2 = 3 e x 2 = 1 − 5 2 = − 2 .

Como − 2 + 3 = 1 , a alternativa correta é a c.

59. Considerando os dois números consecutivos como x e x + 1 , temos:

x 2 + ( x + 1 ) 2 = 11 3

x 2 + x 2 + 2 x + 1 = 11 3

2 x 2 + 2 x − 112 = 0

x 2 + x − 56 = 0

Assim, x = 7 ou x = − 8 .

Portanto, os números procurados são 7 e 8 ou − 8 e − 7 .

60. Pelo teorema de Tales, temos 3 x 2 x = 2 x + 6 2 x − 4 , ou seja, 2 x 2 − 24 x = 0 ou, ainda, x 2 − 12 x = 0 . Resolvendo essa equação, temos:

x ( x − 12 ) = 0

x = 0 ou x − 12 = 0 , isto é, x = 0 ou x = 1 2

Portanto, x = 1 2 .

61. Ao resolver a equação n 2 − 3 n − 28 = 0 , temos:

Δ = ( − 3 ) 2 − 4 ⋅ 1 ⋅ ( − 28 ) = 12 1

n = − ( − 3 ) ± 12 1 2 ⋅ 1 = 3 ± 11 2

Assim, as raízes da equação são n 1 = 3 + 11 2 = 7 e n 2 = 3 − 11 2 = − 4 .

Como n representa a quantidade de lados do polígono, concluímos que n = 7 .

Logo, esse polígono tem 7 lados.

62. A medida da área da planificação desse paralelepípedo é dada por 2 ⋅ 4 ⋅ ( 2 x − 1 ) + 2 ⋅ 4 ⋅ ( x + 2 ) + 2 ⋅ ( 2 x − 1 ) ( x + 2 ) = 18 8 , ou seja, 2 x 2 + 15 x − 92 = 0 .

Assim, x = 4 .

Portanto, a medida do volume desse paralelepípedo é igual a 4 ⋅ 7 ⋅ 6 = 16 8 , isto é, 168   cm 3 .

63. a ) A equação é x 2 = 8 − 2 x , ou seja, x 2 + 2 x − 8 = 0 .

Resolvendo-a:

x = − 2 ± 3 6 2 ⋅ 1 = − 2 ± 6 2

Assim, temos x 1 = − 2 + 6 2 = 2 e x 2 = − 2 − 6 2 = − 4 .

b) A equação é x 2 + 2 x = x + 2 , ou seja, x 2 + x − 2 = 0 .

Resolvendo-a:

x = − 1 ± 9 2 ⋅ 1 = − 2 ± 3 2

Assim, temos x 1 = − 1 + 3 2 = 1 e x 2 = − 1 − 3 2 = − 2 .

64. A medida da área depois do aumento passará a ser 1 . 600   m 2 .

Assim, ( x + 20 ) ( x + 38 ) = 1 . 600 , ou seja, x 2 + 58 x − 840 = 0 .

Página LXXXI

Resolvendo essa equação:

x = − 58 ± 6 . 724 2 ⋅ 1 = − 58 ± 82 2

Assim x 1 = − 58 + 82 2 = 1 2 e x 2 = − 58 − 82 2 = − 7 0 .

Consideramos x = 1 2 , pois representa uma medida de comprimento, em metros.

Portanto, x = 12   m .

65. Utilizando a fórmula, temos:

a) n ( n − 3 ) 2 = 2 0 , logo n 2 − 3 n − 40 = 0 , encontramos n = − 5 ou n = 8 .

Portanto, esse polígono tem 8 lados.

b) n ( n − 3 ) 2 = 3 5 , logo n 2 − 3 n − 70 = 0 , encontramos n = − 7 ou n = 1 0 .

Portanto, esse polígono tem 10 lados.

c) n ( n − 3 ) 2 = 6 5 , logo n 2 − 3 n − 130 = 0 , encontramos n = − 1 0 ou n = 1 3 .

Portanto, esse polígono tem 13 lados.

d) n ( n − 3 ) 2 = 9 0 , logo n 2 − 3 n − 180 = 0 , encontramos n = − 1 2 ou n = 1 5 .

Portanto, esse polígono tem 15 lados.

66. Indicando os dois números consecutivos como sendo x e x + 1 , verificamos que x ( x + 1 ) = 38 0 , ou seja, x 2 + x − 380 = 0 .

Assim, x = 1 9 ou x = − 2 0 .

Portanto, os números procurados são 1 9 e 2 0 ou − 2 0 e − 1 9 .

67. a ) Resolvendo a equação x 2 − 3 p x − 4 p 2 = 0 :

Δ = ( − 3 p ) 2 − 4 ⋅ 1 ⋅ ( − 4 p 2 ) = 9 p 2 + 1 6 p 2 = 2 5 p 2

x = − ( − 3 p ) ± 2 5 p 2 2 ⋅ 1 = 3 p ± 5 p 2

Assim, as raízes da equação são x 1 = 3 p + 5 p 2 = 4 p e x 2 = 3 p − 5 p 2 = − p .

b) Resolvendo a equação − 9 x 2 + 6 p x + 3 p 2 = 0 :

Δ = ( 6 p ) 2 − 4 ⋅ ( − 9 p ) ⋅ ( 3 p 2 ) = 3 6 p 2 + 10 8 p 2 = 14 4 p 2

x = − 6 p ± 14 4 p 2 2 ⋅ ( − 9 ) = − 6 p ± 12 p − 18

Assim, as raízes da equação são x 1 = − 6 p + 12 p − 18 = − p 3 e x 2 = − 6 p − 12 p − 18 = − 18 p − 18 = p .

c) Resolvendo a equação 3 p x 2 + 2 p x − 5 p = 0 :

Δ = ( 2 p ) 2 − 4 ⋅ ( 3 p ) ⋅ ( − 5 p ) = 4 p 2 + 6 0 p 2 = 6 4 p 2

x = − 2 p ± 6 4 p 2 2 ⋅ 3 p = − 2 p ± 8 p 6 p

Assim, as raízes da equação são x 1 = − 2 p + 8 p 6 p = 1 e x 2 = − 2 p − 8 p 6 p = − 5 3 .

d) Resolvendo a equação 3 p 2 x 2 − 5 p x − 2 = 0 :

Δ = ( − 5 p ) 2 − 4 ⋅ ( 3 p 2 ) ⋅ ( − 2 ) = 2 5 p 2 + 2 4 p 2 = 4 9 p 2

x = − ( − 5 p ) ± 4 9 p 2 2 ⋅ 3 p 2 = 5 p ± 7 p 6 p 2

Assim, as raízes da equação são x 1 = 5 p + 7 p 6 p 2 = 2 p , com p ≠ 0 , e x 2 = 5 p − 7 p 6 p 2 = − 1 3 p , com p ≠ 0 .

e) Resolvendo a equação 6 x 2 − 12 p x = 0 :

Δ = ( − 12 p ) 2 − 4 ⋅ ( 6 ) ⋅ 0 = 14 4 p 2

x = − ( − 12 p ) ± 14 4 p 2 2 ⋅ 6 = 12 p ± 12 p 12

Assim, as raízes da equação são x 1 = 12 p + 12 p 12 = 2 p e x 2 = 12 p − 12 p 12 = 0 .

f) Resolvendo a equação 2 p x 2 − 8 p = 0 :

Δ = 0 2 − 4 ⋅ ( 2 p ) ⋅ ( − 8 p ) = 6 4 p 2

x = ± 6 4 p 2 2 ⋅ 2 p = ± 8 p 4 p

Assim, as raízes da equação são

x 1 = 8 p 4 p = 2 e x 2 = − 8 p 4 p = − 2 .

68. a ) Calculando o mmc entre os denominadores da equação: 2 ⋅ 2 x . Assim:

x 2 ⋅ ( 2 ⋅ 2 x ) + 9 2 x ⋅ ( 2 ⋅ 2 x ) = − 5 ⋅ ( 2 ⋅ 2 x )

2 x 2 + 18 = − 20 x

2 x 2 + 20 x + 18 = 0

Resolvendo a equação, obtemos x 1 = − 9 e x 2 = − 1 .

Como os valores obtidos são diferentes de 0, as raízes da equação são x 1 = − 9 e x 2 = − 1 .

b) Calculando o mmc entre os denominadores da equação, obtemos x. Assim:

x ⋅ x + 10 x ⋅ x = 5 ⋅ x

x 2 + 10 = 5 x

x 2 − 5 x + 10 = 0

Essa equação não tem raízes reais.

c) Calculando o mmc entre os denominadores da equação: ( x + 1 ) ⋅ 1 1 . Assim:

x − 21 11 ⋅ ( x + 1 ) ⋅ 11 = − 11 x + 1 ⋅ ( x + 1 ) ⋅ 1 1

x 2 − 20 x − 21 = − 12 1

x 2 − 20 x + 100 = 0

Página LXXXII

Resolvendo essa equação, obtemos x 1 = x 2 = 1 0 .

Como os valores obtidos são diferentes de − 1 , as raízes da equação são x 1 = x 2 = 1 0 .

d) Calculando o mm entre os denominadores da equação: ( x − 2 ) ⋅ x . Assim:

4 x − 2 ⋅ ( x − 2 ) ⋅ x = 2 ⋅ ( x − 2 ) ⋅ x − 6 x ⋅ ( x − 2 ) ⋅ x

4 x = 2 x 2 − 4 x − 6 x + 1 2

2 x 2 − 4 x − 4 x − 6 x + 12 = 0

2 x 2 − 14 x + 12 = 0

x 2 − 7 x + 6 = 0

Resolvendo essa equação, obtemos x 1 = 6 e x 2 = 1 .

Como os valores obtidos são diferentes de 0 e de 2, as raízes da equação são x 1 = 6 e x 2 = 1 .

e) Calculando o mmc entre os denominadores da equação: ( x + 1 ) ⋅ x . Assim:

4 x ⋅ ( x + 1 ) ⋅ x + 2 ⋅ ( x + 1 ) ⋅ x = 3 x + 1 ⋅ ( x + 1 ) ⋅ x

4 x + 4 + 2 x 2 + 2 x = 3 x

2 x 2 + 4 x + 2 x − 3 x + 4 = 0

2 x 2 + 3 x + 4 = 0

Essa equação não tem raízes reais.

f) Resposta no final da seção Resoluções.

g) Resposta no final da seção Resoluções.

69. a ) Como 2 é uma raiz, temos 2 2 + 6 ⋅ 2 − 4 m = 0 , ou seja, m = 4 .

Assim, a equação é x 2 + 6 x − 16 = 0 , logo a outra raiz é − 8 .

B. Substituindo x por − 7 , temos ( − 7 ) 2 − 9 m − 4 = 0 , ou seja, m = 5 .

Assim, a equação é x 2 − 49 = 0 e a outra raiz é 7 .

70. Resolvendo a equação x + 1 x = 2 x − 3 4 , temos:

x + 1 x ⋅ x ⋅ 4 = 2 x − 3 4 ⋅ x ⋅ 4

2 x 2 − 7 x − 4 = 0

Assim, x = − 1 2 ou x = 4 .

71. a ) Resolvendo a equação, temos:

84 x − 3 = 84 x + 9

84 x − 3 = 84 + 9 x x

84 x = 84 x − 252 + 9 x 2 − 27 x

x 2 − 3 x − 28 = 0

Resolvendo essa equação, obtemos x 1 = 7 e x 2 = − 4 .

Como x representa a quantidade de pessoas, consideramos x = 7 .

Portanto, 4 pessoas distribuíram os panfletos.

b) A quantidade de panfletos distribuídos por cada pessoa é dada por 84 : 4 = 2 1 , isto é, cada pessoa distribuiu 21 panfletos.

72. a ) Temos Δ = 8 2 − 4 ⋅ ( − 4 ) ⋅ 32 = 576 > 0 .

A equação tem duas raízes reais diferentes. Resolvendo a equação:

x = − 8 ± 57 6 2 ⋅ ( − 4 ) = − 8 ± 24 − 8 , assim x 1 = − 8 + 24 − 8 = − 2 e x 2 = − 8 − 24 − 8 = 4 .

b) Temos Δ = ( − 5 ) 2 − 4 ⋅ 3 ⋅ 3 = − 11 < 0 . A equação não tem raízes reais.

c) Temos Δ = 3 2 − 4 ⋅ 1 2 ⋅ ( − 8 ) = 25 > 0 .

A equação tem duas raízes reais diferentes. Resolvendo a equação:

x = − 3 ± 2 5 2 ⋅ ( 1 2 ) = − 3 ± 5 1 , assim x 1 = − 3 + 5 = 2 e x 2 = − 3 − 5 = − 8 .

d) Temos Δ = ( − 1 ) 2 − 4 ⋅ 1 8 ⋅ 2 = 0 .

A equação tem duas raízes reais iguais. Resolvendo a equação:

x = − ( − 1 ) ± 0 2 ⋅ ( 1 8 ) = 1 1 4 , assim x 1 = x 2 = 4 .

73. Utilizando as relações de soma e produto, temos:

a) S = − 2 1 = − 2 e P = − 8 1 = − 8 .

b) S = − 25 5 = − 5 e P = − 3 5 = − 3 5 .

c) S = − 0 2 = 0 e P = 16 2 = 8 .

d) S = − 0 1 = 0 e P = − 7 1 = − 7 .

74. a ) Como Δ = 4 − 40 n , a equação terá duas raízes reais iguais quando 4 − 40 n = 0 , isto é, n = 1 10 .

b) A equação não terá raízes reais se 4 − 40 n < 0 , isto é, quando n > 1 10 .

75. a ) Como S = − ( − 8 1 ) = 8 e P = 15 1 = 1 5 , as raízes são 3 e 5 .

b) Como S = − ( − 3 1 ) = 3 e P = 2 1 = 2 , as raízes são 1 e 2 .

c) Como S = − 11 1 = 1 1 e P = 28 1 = 2 8 , as raízes são 4 e 7 .

76. De acordo com as raízes apresentadas, temos:

a) S = 9 e P = 2 0 , assim a equação é x 2 − 9 x + 20 = 0 .

b) S = 1 e P = − 2 , assim a equação é x 2 − x − 2 = 0 .

Página LXXXIII

c) S = 0 e P = − 3 , assim a equação é x 2 − 3 = 0 .

d) S = 1 5 e P = 0 , assim a equação é x 2 − 15 x = 0 .

77. Como a = 1 e x 1 = − 2 , a forma fatorada da equação x 2 − 3 x − 10 = 0 é ( x + 2 ) ( x − x 2 ) = 0 .

Assim, temos 2 − x 2 = − 3 e − 2 x 2 = − 1 0 . Logo, x 2 = 5 .

Portanto, a raiz da equação é igual a 5.

78. Resposta pessoal. Sugestão de resposta:

a) Uma das raízes da equação x 2 − 5 x + 6 = 0 é 3 . Utilizando a forma fatorada, determine a outra raiz. Resposta: x 2 = 2 .

b) Uma das raízes da equação x 2 + 7 x + 12 = 0 é − 4 . Utilizando a forma fatorada, determine a outra raiz. Resposta: x 2 = − 3 .

79. a ) Como S = 5 + x 2 = 3 e P = 5 x 2 = − 1 0 , temos x 2 = − 2 .

b) Como S = 2 + x 2 = 7 3 e P = 2 x 2 = 2 3 , temos x 2 = 1 3 .

c) Como S = 5 2 + x 2 = 3 2 e P = 5 x 2 2 = − 5 2 , temos x 2 = − 1 .

O que eu estudei?

1. Escrevendo a medida da área do quadrado roxo, temos ( 2 x − y ) 2 .

Desenvolvendo esse produto notável, temos 4 x 2 − 4 x y + y 2 .

Portanto, a medida da área do quadrado roxo é igual a 4 x 2 − 4 x y + y 2 .

2. Escrevendo a forma fatorada dos polinômios da primeira coluna, temos:

A. x 2 − 9 = x 2 − 3 2 = ( x + 3 ) ( x − 3 ) , logo A–3;

B. x 2 − 16 = x 2 − 4 2 = ( x + 4 ) ( x − 4 ) , logo B–2;

C. x 2 − 25 = x 2 − 5 2 = ( x + 5 ) ( x − 5 ) , logo C–1.

3. a ) ( x + 7 ) , pois ( x + 7 ) ( x − 7 ) = x 2 − 4 9 .

b) ( 2 y + 3 ) ; ( 2 y − 3 ) , pois ( 2 y + 3 ) ( 2 y − 3 ) = 4 y 2 − 9 .

c) ( − 2 x + 2 y ) ; ( 2 x + 2 y ) , pois 9 x + ( − 2 x + 2 y ) ( 2 x + 2 y ) = − 4 x 2 + 4 y 2 + 9 x .

4. Indicando por x a idade de João, a idade de José será x − 4 .

Assim, temos x ⋅ 2 ( x − 4 ) = 28 0 , ou seja, 2 x 2 − 8 x − 280 = 0 .

5. a ) A medida da área do paralelogramo é ( 5 x − 4 ) ( x + 1 ) = 5 x 2 + x − 4 .

A medida de seu perímetro é

5 x − 4 + x + 2 + 5 x − 4 + x + 2 = 12 x − 4 .

Como essas medidas são iguais, temos

5 x 2 + x − 4 = 12 x − 4 , isto é, 5 x 2 − 11 x = 0 .

b) A equação é incompleta. Seus coeficientes são:

a = 5 , b = − 1 1 e c = 0 .

6. Como o cubo tem 6 faces quadradas e, nesse caso, as medidas de suas arestas têm comprimento igual a x, a equação que representa a situação é 6 x 2 = 1 . 176 .

Resolvendo essa equação, encontramos x = 1 4 e x = − 1 4 .

Portanto, a medida do comprimento de cada aresta do cubo é igual a 14   cm .

7. Indicando a quantia que Guilherme tinha de x , de acordo com a dica, temos 2 x 2 + 4 x = 3 x 2 − 10 x . Escrevendo essa equação em sua forma reduzida: x 2 − 14 x = 0 .

Resolvendo-a:

x ( x − 14 ) = 0

x = 0 ou x − 14 = 0 , assim x = 0 ou x = 1 4

Portanto, x = 1 4 , isto é, Guilherme tinha R$ 14,00 na carteira.

8. Considerando os três números naturais consecutivos como x − 1 , x e x + 1 , temos:

x − 1 + x + x + 1 = ( x − 1 ) ⋅ x ⋅ ( x + 1 ) , isto é, x 3 − 4 x = 0 .

Fatorando essa equação, temos x ( x 2 − 4 ) = 0 .

Resolvendo a equação, encontramos as raízes x 1 = 0 , x 2 = − 2 e x 3 = 2 , mas apenas o resultado de x 3 torna os três números naturais (1; 2; 3).

Assim, a soma dos seus quadrados será 1 2 + 2 2 + 3 2 = 1 4 .

Portanto, a alternativa correta é a a.

9. a ) Representando a medida da largura do terreno por x , a medida do comprimento será x + 8 .

Assim, x ( x + 8 ) = 24 0 , ou seja, x 2 + 8 x − 240 = 0 .

b) Isolando o termo independente na equação, temos x 2 + 8 x = 24 0 .

Como 8 x = 2 ⋅ 4 ⋅ x , obtemos:

x 2 + 2 ⋅ 4 ⋅ x = 24 0

Para que a expressão seja um trinômio quadrado perfeito, acrescentamos 4 2 aos dois membros da equação, assim:

x 2 + 2 ⋅ 4 ⋅ x + 4 2 = 240 + 4 2

x 2 + 8 x + 16 = 240 + 1 6

x 2 + 8 x + 16 = 25 6

Fatorando o 1º membro da equação: ( x + 4 ) 2 = 25 6 , as raízes dela são:

( x + 4 ) 2 = 25 6

x + 4 = 25 6 , ou seja, x = 1 2 e x + 4 = − 25 6 , logo x = − 2 0 .

Como x representa a medida da largura de um terreno, x = 1 2 .

Portanto, a medida da largura do terreno é igual a 12   m e a medida do comprimento é 20 ⏟ 12 + 8   m .

10. A medida da área do jardim é dada por ( x + 1 ) 2 − 1 = 1 5 .

Assim, temos x 2 + 2 x + 1 − 1 = 1 5 , ou seja, x 2 + 2 x − 15 = 0 .

Página LXXXIV

Nessa equação, temos a = 1 ; b = 2 ; c = − 1 5 .

Assim, Δ = 2 2 − 4 ⋅ ( 1 ) ⋅ ( − 15 ) = 4 + 60 = 64 .

x = − 2 ± 6 4 2 ⋅ ( 1 ) = − 2 ± 8 2

Desse modo, as raízes da equação são:

x 1 = − 2 + 8 2 = 3 e x 2 = − 2 − 8 2 = − 5 .

Como x é uma medida de comprimento, logo x > 0 .

Portanto, x = 3   m .

A medida do comprimento da cerca é igual a 4 + 4 = 8 , isto é, 8   m .

11. De acordo com o enunciado da atividade, podemos escrever:

( 8 + 2 x ) ( 6 + x ) 2 = 8 ⋅ 6 2 + 39 ⏟   medida   da área   aumentada , ou seja, 2 x 2 + 20 x + 48 = 12 6 .

Logo, 2 x 2 + 20 x − 78 = 0 .

Dividindo a equação por 2, obtemos x 2 + 10 x − 39 = 0 .

Resolvendo essa equação, temos:

a = 1 ; b = 10 ; c = − 39

Assim, Δ = 1 0 2 − 4 ⋅ 1 ⋅ ( − 39 ) = 25 6

x = − 10 ± 25 6 2 ⋅ 1 = − 10 ± 16 2

Portanto, as raízes da equação são x 1 = − 10 + 16 2 = 3 e x 2 = − 10 − 16 2 = − 1 3 .

Como x é uma medida de comprimento, logo x > 0 .

Portanto, x = 3   cm .

12. Pelo enunciado, temos x 2 = 1 . 980 − x , isto é, x 2 + x − 1 . 980 = 0 .

Resolvendo essa equação, temos:

a = 1 ; b = 1 ; c = − 1 . 980

Assim, Δ = 1 2 − 4 ⋅ 1 ⋅ ( − 1 . 980 ) = 7 . 921

x = − 1 ± 7 . 921 2 ⋅ 1 = − 1 ± 89 2

Portanto, as raízes da equação são x 1 = − 1 + 89 2 = 4 4 e x 2 = − 1 − 89 2 = − 4 5 .

Logo, x = 4 4 , ou seja, o avô de Júlia nasceu no ano de 1936 e em 1980 ele completou 44 anos.

Em 2006, ele completou 70 anos.

Portanto, a alternativa correta é a d.

13. Como as raízes da equação 2 x 2 + b x + c = 0 são iguais a x 1 = 2 e x 2 = − 3 , temos: S = x 1 + x 2 = 2 + ( − 3 ) = − 1

Como S = − b a e b = a , então b = 2 .

P = x 1 ⋅ x 2 = 2 ⋅ ( − 3 ) = − 6 .

Como P = c a e c = − 6 a , então: c = − 6 ( 2 ) = − 1 2

b − c = 2 − ( − 12 ) = 2 + 12 = 1 4

Portanto, a alternativa correta é a b.

14. a ) De acordo com a atividade, podemos escrever a seguinte equação:

x 2 = − 32 x − 16 , com x ≠ 1 6 .

b) Escrevendo a equação do item a na forma reduzida, temos:

x 2 ⋅ 2 ( x − 16 ) = − 32 x − 16 ⋅ 2 ( x − 16 )

x 2 − 16 x = − 6 4

x 2 − 16 x + 64 = 0

Resolvendo a equação:

Δ = ( − 16 ) 2 − 4 ⋅ 1 ⋅ 64 = 0

x = − ( − 16 ) 2 ⋅ 1 = 16 2 = 8

Assim, x = 8 . Portanto, Eduardo pensou no número 8.

15. Representando a quantidade de táxis por x , temos:

560 x − 2 = 560 x + 5

Escrevendo-a na forma reduzida:

560 x − 2 ⋅ x ( x − 2 ) = 560 x ⋅ x ( x − 2 ) + 5 ⋅ x ( x − 2 )

560 x = 560 x − 1 . 120 + 5 x 2 − 10 x

5 x 2 − 10 x − 1 . 120 = 0

x 2 − 2 x − 224 = 0

Resolvendo essa equação, obtemos:

x = − ( − 2 ) ± 90 0 2 ⋅ 1 = 2 ± 30 2

As raízes dessa equação são x 1 = 2 + 30 2 = 1 6 e x 2 = 2 − 30 2 = − 1 4 .

Assim, temos x = 1 6 , ou seja, na frota, há 16 táxis.

16. O produto das raízes da equação é c a = 24 6 = 4 . Portanto, a alternativa correta é a c.

Unidade 6

Triângulo retângulo

Questão 1. Considerando os triângulos D B A e D A C , temos:

n h = h m

Consequentemente, h 2 = m ⋅ n .

Atividades

1. a ) Os triângulos que apresentam um de seus ângulos medindo 90 ° , ou seja, os triângulos retângulos são A E C , A E B , A D E e E D B .

Página LXXXV

b) No △ A E C , temos:

25 ° + 90 ° + C ˆ = 180 °

C ˆ = 180 ° − 115 ° = 65 °

Como △ A B C é isósceles, B ˆ = C ˆ , logo B ˆ = 65 ° .

No △ E D B , temos:

65 ° + 90 ° + E ˆ = 180 °

E ˆ = 180 ° − 155 ° = 25 °

Logo, no △ E D B , E ˆ = 25 ° .

No △ A D E , E ˆ = 90 ° − 25 ° = 75 ° , assim:

75 ° + 90 ° + A ˆ = 180 °

A ˆ = 180 ° − 165 ° = 15 °

Portanto, no △ A D E , A ˆ = 15 ° , D ˆ = 90 ° e E ˆ = 75 ° .

c) Nos triângulos, temos:

A E ˆ C ≡ A E ˆ B , A D ˆ E ≡ E D ˆ B , A B ˆ E ≡ D B ˆ E ≡ A C ˆ E e C A ˆ E ≡ B A ˆ E

Logo, os triângulos apresentam um ângulo reto e um ângulo em comum, com isso, os triângulos A E C , A E B , A D E e E D B são semelhantes.

2. A. Para determinar o valor de b, calculamos:

b 2 = a ⋅ m

b 2 = 18 ⋅ 8

b 2 = 14 4

b = 14 4

b = 1 2

Logo, b = 12   cm .

Para determinar o valor de h, calculamos:

h 2 = m ⋅ n

h 2 = 8 ⋅ 1 0

h 2 = 8 0

h = 4 5

Logo, h ≃ 8 , 94   cm .

B. Para determinar os valores de a e h, calculamos:

a = 25 + 9 = 3 4

Logo, a = 34   cm .

h 2 = m ⋅ n

h 2 = 25 ⋅ 9

h 2 = 22 5

h = 22 5 = 1 5

Logo, h = 15   cm .

C. Primeiro, calculamos os valores de m e n:

b 2 = a ⋅ m

( 3 , 6 ) 2 = 6 ⋅ m

12 , 96 = 6 m

m = 12 , 96 6 = 2 , 1 6

Logo, m = 2 , 16   cm .

Como a = m + n , temos:

6 = 2 , 16 + n

n = 3 , 8 4

Logo, n = 3 , 84   cm .

E, para determinar o valor de h, calculamos:

h 2 = m ⋅ n

h 2 = 2 , 16 ⋅ 3 , 8 4

h 2 = 8 , 294 4

h = 2 , 8 8

Logo, h = 2 , 88   cm .

D. Para determinar o valor de h, calculamos:

c ⋅ h = b ⋅ n

3 , 3 ⋅ h = 4 , 4 ⋅ 1 , 9 8

3 , 3 h = 8 , 71 2

3 , 3 h = 8 , 71 2

h = 8 , 712 3 , 3 = 2 , 6 4

Logo, h = 2 , 64   cm .

Para determinar o valor de m, fazemos:

h 2 = m ⋅ n

( 2 , 64 ) 2 = m ⋅ 1 , 9 8

6 , 9 696 = 1 , 98 m

m = 6 , 9 696 1 , 98 = 3 , 5 2

Logo, m = 3 , 52   cm .

3. Temos x = a e b = c = 4 . Substituindo b e c em c 2 = a ⋅ n e b 2 = a ⋅ m , temos os seguintes resultados:

4 2 = x ⋅ n

16 = x n

n = 16 x

e

4 2 = x ⋅ m

16 = x m

m = 16 x

Além disso, x = m + n . Desse modo:

x = 16 x + 16 x

x = 32 x

x 2 = 3 2

x = 3 2 = 4 2

Logo, x = 4 2   cm .

4. A. Como n = 1 , 6 e m = 2 , 5 − 1 , 9 = 0 , 9 , para determinar o valor de h, fazemos:

h 2 = m ⋅ n

h 2 = 1 , 6 ⋅ 0 , 9 = 1 , 4 4

h = 1 , 4 4 = 1 , 2

Logo, h = 1 , 2   m .

Página LXXXVI

Calculando a medida da área do triângulo, temos:

A = 2 , 5 ⋅ 1 , 2 2 = 1 , 5

Logo, A = 1 , 5   m 2 .

B. Como b = 3 , 7 5 e m = 2 , 2 5 , então:

b 2 = a ⋅ m

( 3 , 75 ) 2 = a ⋅ 2 , 2 5

14 , 0 625 = 2 , 25 a

a = 14 , 0 625 2 , 25 = 6 , 2 5

Logo, a = 6 , 25   m .

Assim, n = 6 , 25 − 2 , 25 = 4 . Calculando o valor de h, obtemos:

h 2 = m ⋅ n

h 2 = 2 , 25 ⋅ 4 = 9

h = 9 = 3

Logo, h = 3   m .

Calculando a medida da área do triângulo, temos:

A = 6 , 25 ⋅ 3 2 = 9 , 37 5

Logo, A = 9 , 37 5   m 2 .

C. Para determinar o valor de h, fazemos:

h 2 = m ⋅ n

h 2 = 2 , 51 ⋅ 4 , 49 = 11 , 269 9

h = 11 , 269 9 ≃ 3 , 3 6

Como a = 7 ⏟ 4 , 49 + 2 , 5 1 , calculando a medida da área, temos:

A = 7 ⋅ 3 , 36 2 ≃ 11 , 7 6

Logo, a área mede, aproximadamente, 11 , 7 6   m 2 .

D. Como c = 4 , 8 e n = 3 , 6 , calculando o valor de a, temos:

c 2 = a ⋅ n

( 4 , 8 ) 2 = a ⋅ 3 , 6

23 , 04 = 3 , 6 a

a = 23 , 04 3 , 6 = 6 , 4

Logo, a = 6,4 m .

Desse modo, m = 6 , 4 − 3 , 6 = 2 , 8 , ou seja, 2,8 m .

Calculando o valor de h, obtemos:

h 2 = m ⋅ n

h 2 = 2 , 8 ⋅ 3 , 6 = 10 , 0 8

h = 10 , 0 8 ≃ 3 , 1 7 , ou seja, 3,17 m

Calculando a medida da área:

A = 6 , 4 ⋅ 3 , 17 2 ≃ 10 , 1 4

Logo, a área mede aproximadamente 10 , 1 4   m 2 .

E. Temos a = 6 , 2 , b = 4 , 9 6 e c = 3 , 7 2 . Calculando o valor de m e n, obtemos:

b 2 = a ⋅ m

( 4 , 96 ) 2 = 6 , 2 ⋅ m

24 , 6 016 = 6 , 2 m

m = 24 , 6 016 6 , 2 = 3 , 96 8 , ou seja, 3 , 968   m

Assim, n = 6 , 2 − 3 , 968 = 2 , 23 2 , isto é, 2 , 232   m .

Calculando o valor de h, temos:

h 2 = m ⋅ n

h 2 = 3 , 968 ⋅ 2 , 2 328 = 8 , 85 657 6

h = 8 , 85 657 6 = 2 , 97 6 , ou seja, 2 , 976   m

Calculando a medida da área, temos:

A = 6 , 2 ⋅ 2 , 976 2 ≃ 9 , 2 3

Logo, a área mede aproximadamente 9 , 2 3   m 2 .

Questão 2. Temos b 2 = a ⋅ m e c 2 = a ⋅ n . Adicionando essas duas relações métricas, temos:

b 2 + c 2 = a ⋅ m + a ⋅ n

b 2 + c 2 = a ⋅ ( m + n )

Como a = m + n , fazemos:

b 2 + c 2 = a ⋅ a

b 2 + c 2 = a 2

Portanto, a 2 = b 2 + c 2 , o que demonstra esse teorema.

Questão 3. Utilizando o teorema de Pitágoras, temos:

1 3 2 = 5 2 + 1 2 2

169 = 25 + 14 4

169 = 16 9

Portanto, o triângulo indicado é um triângulo retângulo.

Atividades

5. Utilizando o teorema de Pitágoras, temos:

A. x 2 = 2 0 2 + 4 0 2

x 2 = 400 + 1 . 600

x 2 = 2 . 000

x = 2 . 000

x = 2 0 5

Logo, x = 2 0 5   cm .

B. 4 0 2 = x 2 + 2 4 2

1 . 600 = x 2 + 57 6

x 2 = 1 . 600 − 57 6

x 2 = 1 . 024

x = 1 . 024

x = 3 2

Logo, x = 32   cm .

Página LXXXVII

C. ( 27 , 5 ) 2 = x 2 + 2 2 2

756 , 25 = x 2 + 48 4

x 2 = 756 , 25 − 48 4

x 2 = 272 , 2 5

x = 272 , 2 5

x = 16 , 5

Logo, x = 16 , 5   cm .

D. x 2 = ( 2 ) 2 + ( 3 ) 2

x 2 = 2 + 3

x 2 = 5

x = 5

Logo, x = 5   cm .

E. x 2 = 3 0 2 + 3 0 2

x 2 = 900 + 90 0

x 2 = 1 . 800

x = 1 . 800

x = 3 0 2

Logo, x = 3 0 2   cm .

6. Para inserir os valores no Calc, fazemos:

1º. Nas células A1, B1 e C1, escreva "Cateto menor", "Cateto maior" e "Hipotenusa", respectivamente. Nessas colunas, serão exibidas as medidas dos comprimentos desses segmentos.

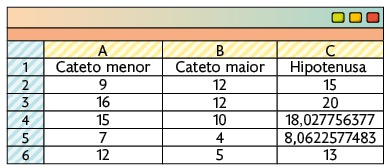
Ilustração da tela de uma tabela em uma planilha. A tabela tem 7 linhas e 3 colunas. Na primeira linha, que não está identificada, estão as colunas A, B e C. Na linha 1, coluna A está escrito 'Cateto menor', linha 2: 9; linha 3: 16; linha 4: 15; linha 5: 7 e linha 6: 12. Na linha 1, coluna B está escrito 'Cateto maior', linha 2: 12; linha 3: 12; linha 4: 10; linha 5: 4 e linha 6: 5. Na linha 1, coluna C está escrito 'Hipotenusa', linha 2: 15; linha 3: 20; linha 4: 18 vírgula 027756377; linha 5: 8 vírgula 0622577483 e linha 6: 13.

2º. Na célula C2, digite = RAIZ ( A 2 * A 2 + B 2 * B 2 ) . Essa fórmula permite calcular a medida do comprimento da hipotenusa, dadas as medidas dos comprimentos dos catetos, informadas nas células A2 e B2.

Portanto, as medidas apresentadas nas alternativas a, b e e representam as medidas dos comprimentos dos lados de triângulos retângulos.

7. Em todos os itens, a diagonal do polígono representa a hipotenusa do triângulo retângulo e o:

polígono A é um quadrado cujo lado mede 5   cm , assim:

a 2 = 5 2 + 5 2

a 2 = 25 + 2 5

a = 5 0 = 5 2

Logo, o comprimento da diagonal mede 5 2   cm .

polígono B é um quadrado cujo lado mede 3 cm , assim:

a 2 = 3 2 + 3 2

a 2 = 9 + 9

a = 1 8 = 3 2

Logo, o comprimento da diagonal mede 3 2   cm .

polígono C é um retângulo cujos comprimento e a largura medem, respectivamente, 14 cm e 10,5 cm . Desse modo:

a 2 = 1 4 2 + ( 10 , 5 ) 2

a 2 = 196 + 110 , 2 5

a = 306 , 2 5 = 17 , 5

Logo, o comprimento da diagonal mede 17 , 5   cm .

8. A. Como m representa a medida de um dos catetos, temos:

( 5 , 95 ) 2 = m 2 + ( 3 , 3 ) 2

35 , 4 025 = m 2 + 10 , 8 9

m 2 = 35 , 4 025 − 10 , 89 = 24 , 512 5

m = 24 , 512 5 ≃ 4 , 9 5

Logo, m = 4 , 95   cm .

B. Como h representa a medida de um dos catetos, calculamos:

( 3 , 6 ) 2 = h 2 + ( 1 , 99 ) 2

12 , 96 = h 2 + 3 , 960 1

h 2 = 12 , 96 − 3 , 9 601 = 8 , 99 9

h = 8 , 99 9 ≃ 3

Logo, h ≃ 3   cm .

Calculando o valor de m, temos:

h 2 = m ⋅ n

( 3 ) 2 = m ⋅ 1 , 9 9

9 = 1 , 99 m

m = 9 1 , 99 ≃ 4 , 5 2

Logo, m ≃ 4 , 52   cm .

Assim, o valor de b é dado por:

b 2 = 3 2 + ( 4 , 52 ) 2

b 2 = 9 + 20 , 430 4

b = 29 , 430 4 ≃ 5 , 4 2

Portanto, b ≃ 5 , 42   cm .

C. Para determinar o valor de n, calculamos:

3 2 = ( 2 , 5 ) 2 + n 2

9 = 6 , 25 + n 2

n 2 = 9 − 6 , 25 = 2 , 7 5

n = 2 , 7 5 ≃ 1 , 6 6

Logo, n ≃ 1 , 66   cm .

Página LXXXVIII

E para determinar o valor de m, fazemos:

h 2 = m ⋅ n

( 2 , 5 ) 2 = m ⋅ 1 , 6 6

6 , 25 = 1 , 66 m

m = 6 , 25 1 , 66 ≃ 3 , 7 7

Logo, m = 3 , 77   cm .

D. Para determinar o valor de h, calculamos:

( 3 , 2 ) 2 = ( 2 , 1 ) 2 + h 2

10 , 24 = 4 , 41 + h 2

h 2 = 10 , 24 − 4 , 41 = 5 , 8 3

h = 5 , 8 3 ≃ 2 , 4 1

Logo, h = 2 , 41   cm .

Calculando o valor de m, temos:

h 2 = m ⋅ n

( 2 , 41 ) 2 = m ⋅ 2 , 1

5 , 8 081 = 2 , 1 m

m = 5 , 8 081 2 , 1 ≃ 2 , 7 7

Logo, m ≃ 2 , 77   cm .

Calculando o valor de b:

b 2 = ( 2 , 77 ) 2 + ( 2 , 41 ) 2

b 2 = 7 , 6 729 + 5 , 808 1

b = 13 , 48 1 ≃ 3 , 6 7

Portanto, b ≃ 3 , 67   cm .

9. Indicando a medida do outro cateto por x e realizando os cálculos, temos:

7 5 2 = 4 5 2 + x 2

5 . 625 = 2 . 025 + x 2

x 2 = 5 . 625 − 2 . 025 = 3 . 600

x = 3 . 600 = 6 0

Logo, x = 60   m .

Calculando a medida da área:

A = 45 ⋅ 60 2 = 1 . 350

Portanto, a área desse triângulo mede 1 . 350   m 2 .

10. Como o triângulo é equilátero e o perímetro mede 15   cm , o comprimento de cada um dos lados mede 5   cm . A altura de um triângulo equilátero é a mediana relativa ao lado B C ‾ , assim:

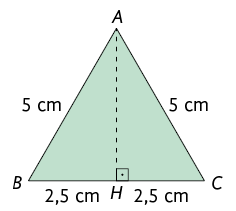
Ilustração de um triângulo equilátero A B C com medida de comprimento dos lados igual a 5 centímetros. Há um segmento A H traçado, relativo à altura, em que H está sobre o lado B C. Esse segmento divide o ângulo A em duas partes iguais e também divide o lado B C em duas partes iguais, B H e H C. Essas duas partes tem medida 2,5 centímetros. Além disso, esse segmento A H separa o triângulo equilátero em dois triângulos retângulos.

Calculando a medida da altura A H ‾ , temos:

5 2 = ( 2 , 5 ) 2 + ( A H ) 2

25 = 6 , 25 + ( A H ) 2

( A H ) 2 = 25 − 6 , 25 = 18 , 7 5

A H = 18 , 7 5 ≃ 4 , 3 3

Portanto, o comprimento da altura desse triângulo mede, aproximadamente, 4 , 33   cm .

11. Utilizando o teorema de Pitágoras para determinar a medida da largura do outro lado do terreno, indicando essa medida por x, temos:

9 0 2 = 7 2 2 + x 2

x 2 = 9 0 2 − 7 2 2

x 2 = 8 . 100 − 5 . 184 = 2 . 916

x = 2 . 916 = 5 4

Logo, x = 54   m .

Assim, fazemos:

P = 72 + 54 + 72 + 54 = 25 2

Portanto, o perímetro desse terreno mede 252   m .

12. Podemos decompor o trapézio isósceles da seguinte maneira:

Ilustração de um trapézio formado por um quadrado e dois triângulos retângulos. Há a demarcação de que medida do comprimento do quadrado é 12 centímetros, que representa a medida da base menor do trapézio e a medida da base maior é igual a 30 centímetros.

Calculando a medida do comprimento da base de cada triângulo retângulo, temos:

( 30 − 12 ) : 2 = 18 : 2 = 9 , ou seja, 9   cm

Utilizando o teorema de Pitágoras para determinar a medida do comprimento do lado e indicando essa medida por x, temos:

x 2 = 1 2 2 + 9 2

x 2 = 1 2 2 + 9 2 = 144 + 81 = 22 5

x = 22 5 = 1 5

Logo, o comprimento do lado mede 15   cm .

Adicionando as medidas do comprimento dos lados, calculamos a medida do perímetro desse trapézio:

P = 15 + 15 + 30 + 12 = 7 2

Portanto, o perímetro desse trapézio mede 72   cm .

13. A face do cubo é um quadrado, ou seja, todos os lados têm a mesma medida. Como a diagonal mede 1 5 2   cm , indicando a medida de comprimento de sua aresta por x, temos:

Página LXXXIX

( 1 5 2 ) 2 = x 2 + x 2

225 ⋅ 2 = 2 x 2

x 2 = 22 5

x = 22 5 = 1 5

Logo, o comprimento da aresta desse cubo mede 15   cm .

Calculando a medida do volume do cubo:

V = x 3 = 1 5 3 = 3 . 375

Portanto, o volume desse cubo mede 3 . 375   cm 3 .

14. A. Calculando a medida do comprimento da altura:

h 2 = m ⋅ n

h 2 = 4 ⋅ 16 = 6 4

h = 6 4 = 8

Logo, o comprimento da altura mede 8   m .

Para determinar o valor de b, fazemos:

b 2 = 4 2 + 8 2

b 2 = 16 + 64 = 8 0

b = 8 0 = 4 5

Ou seja, b = 4 5   m .

Temos a = 20 ⏟ 4 + 1 6 , calculando o valor de c:

2 0 2 = ( 4 5 ) 2 + c 2

400 = 16 ⋅ 5 + c 2

c 2 = 400 − 8 0

c 2 = 400 − 80 = 32 0

c 2 = 32 0 = 8 5

Ou seja, c = 8 5   m .

Assim, calculando a medida do perímetro, temos:

P = 20 + 4 5 + 8 5 = 20 + 1 2 5

Portanto, o perímetro mede 20 + 1 2 5   m .

B. Calculando a medida de b:

b 2 = ( 14 , 4 ) 2 + ( 19 , 2 ) 2

b 2 = 207 , 36 + 368 , 64 = 57 6

b = 57 6 = 2 4

Ou seja, b = 24   m .

Calculando a medida de m:

h 2 = m ⋅ n

( 19 , 2 ) 2 = m ⋅ 14 , 4

368 , 64 = 14 , 4 m

m = 368 , 64 14 , 4 = 25 , 6

Ou seja, m = 25 , 6   m .

Desse modo, temos:

a = 25 , 6 + 14 , 4 = 4 0

Logo, a = 40   m .

Calculando a medida de c:

4 0 2 = 2 4 2 + c 2

1 . 600 = 576 + c 2

c 2 = 1 . 600 − 576 = 1 . 024

c = 1 . 024 = 3 2 , ou seja, 32   cm .

Desse modo, calculando a medida do perímetro, temos:

P = 40 + 24 + 32 = 9 6

Portanto, o perímetro mede 96   cm .

15. a ) Como as diagonais do quadrado se cruzam no ponto médio de cada segmento, temos:

A C = B D = 5 2 ⏟ 2 ⋅ 2 , 5 2

Logo, o comprimento de cada diagonal mede 5 2   cm .

Indicando a medida do comprimento do lado do quadrado por x, como a medida da hipotenusa do triângulo A B C mede 5 2   cm , temos:

( 5 2 ) 2 = x 2 + x 2

25 ⋅ 2 = 2 x 2

x 2 = 2 5

x = 2 5 = 5

Portanto, o comprimento do lado desse quadrado mede 5   m .

b) Calculando a medida do perímetro desse quadrado, temos:

P = 5 + 5 + 5 + 5 = 2 0

Logo, o perímetro mede 20   m .

c) Calculando a medida da área, temos:

A = 5 ⋅ 5 2 = 25 2 = 12 , 5

Portanto, a área do triângulo A C D mede 12 , 5   m .

16. A diagonal do retângulo representa a hipotenusa do triângulo retângulo formado por ela. Em cada item, usando as medidas dos catetos e indicando a medida da hipotenusa por x, temos:

a) x 2 = 2 8 2 + 2 1 2

x 2 = 784 + 441 = 1 . 225

x = 1 . 225 = 3 5

Portanto, o comprimento da diagonal desse retângulo mede 35   m .

b) x 2 = 5 2 + 1 2 2

x 2 = 25 + 144 = 16 9

x = 16 9 = 1 3

Página XC

Portanto, o comprimento da diagonal desse retângulo mede 13   m .

c) x 2 = 1 2 + 3 2

x 2 = 1 + 9 = 1 0

x = 1 0

Portanto, o comprimento da diagonal desse retângulo mede 1 0   m .

d) x 2 = 5 2 + ( 2 ) 2

x 2 = 25 + 2

x = 2 7 = 3 3

Portanto, o comprimento da diagonal desse retângulo mede 3 3   m .

17. A. Para determinar a medida da altura, calculamos:

h 2 = m ⋅ n

h 2 = 18 ⋅ 32 = 57 6

h = 57 6 = 2 4

Logo, a altura mede 24   m .

Como a base desse triângulo mede 50 ⏟ 18 + 3 2   m , a medida da área é dada por:

A = b ⋅ h 2

A = 50 ⋅ 24 2 = 60 0

Logo, a área mede 60 0   m 2 .

Para determinar a medida do perímetro, precisamos calcular a medida dos outros lados. Assim, indicando-os por a e b e usando o teorema de Pitágoras, temos:

a 2 = 1 8 2 + 2 4 2

a 2 = 324 + 576 = 90 0

a = 90 0 = 3 0 , ou seja, a = 30   m

b 2 = 3 2 2 + 2 4 2

b 2 = 1 . 024 + 576 = 1 . 600

b = 1 . 600 = 4 0 , ou seja, b = 40   m

Assim, P = 50 + 30 + 40 = 12 0 , ou seja, 120   m .

Portanto, o perímetro mede 120   m , a área mede 60 0   m 2 e o comprimento da altura mede 24   m .

B. Para calcular a medida da base, precisamos determinar a medida de n. Assim:

h 2 = m ⋅ n

h 2 = 144 ⋅ 25 = 3 . 600

h = 3 . 600 = 6 0 , ou seja, h = 60   m .

Como E F = 169 ⏟ 25 + 14 4   m , a medida da área é dada por:

A = b ⋅ h 2 = 169 ⋅ 60 2 = 5 . 070

Logo, a área mede 5 . 070   m 2 .

Calculando a medida do comprimento do lado D F ‾ :

( D F ) 2 = 6 0 2 + 14 4 2

( D F ) 2 = 3 . 600 + 20 . 736

( D F ) 2 = 24 . 336

D F = 24 . 336 = 15 6

Ou seja, D F = 156   m .

Logo, o perímetro mede:

P = 156 + 169 + 65 = 39 0

Ou seja, P = 390   m .

Portanto, o perímetro mede 390   m , a área mede 5 . 070   m 2 e o comprimento da altura do triângulo mede 60 m .

18. a ) Calculando a medida do comprimento da parte da escada que está apoiada até a sua base e indicando essa medida por x, temos:

x 2 = ( 4 , 8 ) 2 + ( 1 , 2 ) 2

x 2 = 23 , 04 + 1 , 44 = 24 , 4 8

x = 24 , 4 8 ≃ 4 , 9 5

Ou seja, x mede aproximadamente 4 , 95   m .

Portanto, o comprimento aproximado da escada mede 5 , 98 ⏟ 4 , 95 + 1 , 0 3   m .

b) Para que o topo da escada coincida com o topo do muro, a medida do comprimento total da escada representará a hipotenusa. Indicando a medida da distância entre a base da escada e o muro por x, temos:

( 5 , 98 ) 2 = ( 4 , 8 ) 2 + x 2

35 , 7 604 = 23 , 04 + x 2

x 2 = 35 , 7 604 − 23 , 04 = 12 , 72 4

x = 12 , 72 4 ≃ 3 , 5 7

Portanto, para que o topo da escada coincida com o topo do muro, a base da escada deve estar a, aproximadamente, 3 , 57   m de distância do muro.

19. Indicando a medida do comprimento do cabo de aço por x e calculando a medida de seu comprimento, temos:

x 2 = 1 0 2 + ( 7 , 5 ) 2

x 2 = 100 + 56 , 25 = 156 , 2 5

x = 156 , 2 5 = 12 , 5

Ou seja, x mede 12 , 5   m .

Página XCI

Como foram utilizados 4 cabos de aço com mesma medida de comprimento, temos:

4 ⋅ 12 , 5 = 5 0

Portanto, foram utilizados 50   m de cabo de aço para sustentar essa torre.

20. Resposta pessoal. Sugestão de resposta:

Determine a medida do comprimento do segmento A E .

Resposta: A E ‾ = 5 , 4   m .

21. De acordo com a imagem, A B C é um triângulo retângulo. Calculando, inicialmente, a medida do comprimento do lado A C ‾ , temos:

( A C ‾ ) 2 = 7 2 + 2 4 2

( A C ‾ ) 2 = 49 + 576 = 62 5

A C ‾ = 62 5 = 2 5

Ou seja, A C ‾ = 25   m .

Calculando a medida do comprimento do lado A D ‾ , temos:

2 5 2 = 2 0 2 + ( A D ‾ ) 2

625 = 400 + ( A D ‾ ) 2

( A D ‾ ) 2 = 625 − 400 = 22 5

A D ‾ = 22 5 = 1 5 , ou seja, A D ‾ = 15   m .

Assim, calculando a medida do perímetro desse quadrilátero, temos:

P = 15 + 20 + 24 + 7 = 6 6

Portanto, o perímetro mede 66   m .

22. Determinando, inicialmente, as raízes da equação x 2 − 7 x + 12 = 0 , temos:

Δ = b 2 − 4 ⋅ a ⋅ c = ( − 7 ) 2 − 4 ⋅ 1 ⋅ 12 = 49 − 48 = 1

x = − b ± Δ 2 a = − ( − 7 ) ± 1 2 ⋅ 1 = 7 ± 1 2

Assim, x 1 = 7 + 1 2 = 4 e x 2 = 7 − 1 2 = 3 .

Logo, as raízes da equação são x 1 = 4 e x 2 = 3 .

Como as raízes da equação correspondem às medidas dos catetos de um triângulo retângulo, em centímetros, temos b = 4   cm e c = 3   cm .

Calculando a medida da hipotenusa:

a 2 = 4 2 + 3 2

a 2 = 16 + 9 = 2 5

a = 2 5 = 5

Ou seja, a mede 5   cm .

Calculando a medida do perímetro desse triângulo, temos:

P = 5 + 4 + 3 = 1 2

Portanto, o perímetro mede 12   cm .

23. De acordo com a figura desenhada por Aroldo, temos: a 2 + b 2 + c 2 = 2 4 . Assim:

b 2 + c 2 = 24 − a 2 (I)

Além disso, podemos escrever a 2 = b 2 + c 2 (II)

Substituindo I em II, temos:

a 2 = 24 − a 2

2 a 2 = 2 4

a 2 = 1 2

Como o lado do quadrado maior mede a, a sua área mede 1 2   cm 2 ⏟   medida de   a 2 .

Portanto, a alternativa c está correta.

24. A medida do segmento A P ‾ representa a hipotenusa do triângulo retângulo A H P . Nesse triângulo, o cateto A H ‾ mede 2   cm , pois representa a medida da aresta do cubo. O outro cateto é a metade da diagonal do quadrado E F G H . Realizando os cálculos, temos:

d = l 2 = 2 2

2 2 2 = 2

Logo, a metade da diagonal desse quadrado mede 2   cm .

Agora, vamos usar o teorema de Pitágoras para determinar a medida do segmento A P ‾ :

( A P ) 2 = ( 2 ) 2 + 2 2

( A P ) 2 = 2 + 4 = 6

A P = 6 , ou seja, 6   cm .

Portanto, a alternativa correta é a c.

O que eu estudei?

1. A. Inicialmente, calculamos a medida da projeção ortogonal do cateto A C ‾ . Assim:

h 2 = m ⋅ n

1 2 2 = m ⋅ 9

144 = 9 m

m = 144 9 = 1 6

Ou seja, m mede 16   cm .

Calculando a medida de x, temos:

x 2 = 1 2 2 + 1 6 2

x 2 = 144 + 256 = 40 0

x = 40 0 = 2 0

Ou seja, x = 20   cm .

Página XCII

B. Determinando a medida de c:

c 2 = 4 2 + 8 2

c 2 = 16 + 64 = 8 0

c = 8 0 = 4 5

Ou seja, c = 4 5   m .

Para obter o valor de a, fazemos:

h 2 = m ⋅ n

8 2 = m ⋅ 4

64 = 4 m

m = 64 4 = 1 6

Ou seja, m mede 16   m .

Assim:

a = 16 + 4 = 2 0

Ou seja, a = 20   m .

O valor de b é dado por:

b 2 = 1 6 2 + 8 2

b 2 = 256 + 64 = 32 0

b = 32 0 = 8 5

Ou seja, b = 8 5   cm .

C. Calculando a medida de y, temos:

1 2 2 = 13 ⋅ y

144 = 13 y

y = 144 13

Ou seja, y = 144 13   m .

Calculando o valor de x:

1 2 2 = ( 144 13 ) 2 + x 2

144 = 20 . 736 169 + x 2

x 2 = 144 − 20 . 736 169 = 3 . 600 169

x = 3 . 600 169 = 3 . 600 16 9 = 60 13

Ou seja, x = 60 13   m .

D. Para determinar a medida da altura, fazemos:

h 2 = 4 ⋅ ( 9 − 4 )

h = 2 0 = 2 5

Ou seja, 2 5   m .

Calculando o valor da medida de b, temos:

b 2 = ( 2 5 ) 2 + 5 2

b 2 = 4 ⋅ 5 + 25 = 20 + 25 = 4 5

b = 4 5 = 3 5

Ou seja, b = 3 5   m .

Calculando o valor de c, temos:

c 2 = ( 2 5 ) 2 + 4 2

c 2 = 4 ⋅ 5 + 16 = 20 + 16 = 3 6

c = 3 6 = 6

Ou seja, c = 6   m .

2. Calculando a medida de h, temos:

h 2 = m ⋅ n

h 2 = 9 ⋅ 25 = 22 5

h = 22 5 = 1 5

Portanto, o comprimento da altura mede 15   m .

3. Realizando os cálculos, temos:

△ A B G : a 2 = 2 2 + 2 2 = 4 + 4 = 8

Assim, a = 8 = 2 2

Ou seja, a = 2 2   u .

△ A C F : ( 4 2 ) 2 = 4 2 + b 2

Assim: b 2 = ( 4 2 ) 2 − 4 2 = 16 ⋅ 2 − 16 = 1 6

b = 1 6 = 4

Ou seja, b = 4   u .

△ A D E : ( 5 2 ) 2 = 5 2 + c 2 . Assim:

c 2 = ( 5 2 ) 2 − 5 2 = 25 ⋅ 2 − 25 = 2 5

c = 2 5 = 5

Ou seja, c = 5   u .

Completando o quadro, temos:

Medidas de comprimento de três triângulos retângulos

Triângulo

Medida do comprimento

cateto

cateto

hipotenusa

A B G

2   u

2   u

2 2   u

A C F

4 u

4 u

4 2   u

A D E

5 u

5 u

5 2   u

4. O quadrado ABCD pode ser decomposto em seis triângulos retângulos. Considerando, incialmente, a medida dos catetos e indicando por x a medida do cateto D I ‾ , o quadrado contém o lado do triângulo A D I , cuja medida de comprimento é igual a 3 x . Assim:

10 ⏟ A I ‾ 2 = x ⏟ D I ‾ 2 + ( 3 x ⏟ A D ‾ ) 2

100 = 1 0 x 2

x = 1 0   cm

Calculando a medida da área do triângulo A D I , temos:

A = x ⋅ 3 x 2

A = 1 0 ⋅ 3 1 0 2 = 1 5 , ou seja, 1 5   cm 2

Como a medida do triângulo A I H corresponde ao dobro da medida da área do triângulo A D I , sua medida de área é igual a 30 cm 2 .