Página CII
Resoluções - parte 5
Unidade 9
Funções
Questão 1. Resposta pessoal. Espera-se que os estudantes obtenham em suas pesquisas que de acordo com observações realizadas, os cientistas procuravam a fórmula de uma função para explicar consecutivos resultados obtidos e que esse importante conceito desenvolveu-se com o trabalho de grandes matemáticos, como Newton, Leibniz, Bernoulli, Euler, entre outros.
Questão 2. Resposta pessoal. Espera-se que os estudantes utilizem dados confiáveis, validem as informações com mais de uma fonte e tenha respeito com o colega durante a realização da pesquisa, contribuindo assim para enriquecer o conhecimento de todos.
Questão 3.
a) Usando a função para , obtém-se .
b) Usando a função para , obtém-se .
c) Usando a função para , obtém-se .
d) Usando a função para , obtém-se .
Atividades
1. a) Considerando que a quantia a ser paga y é igual à quantidade de ingressos x multiplicada pelo preço da unidade, a fórmula que expressa o valor a ser pago por Renato em função da quantidade de ingressos é .
b) Renato pagará:
I . R$ 73,50, pois ;
II . R$ 94,50, pois ;
III . R$ 126,00, pois ;
IV . R$ 157,50, pois .
c) Substituindo em , temos:
Portanto, Renato comprou 5 ingressos.
2. a)
b)
3. a)
b) Considerando , temos:
I .
Logo, o perímetro mede .
II .
Logo, o perímetro mede .
III .
Logo, o perímetro mede .
IV .
Logo, o perímetro mede .
4. a) Considerando que cada acerto vale 5 pontos, x representa a quantidade de acertos e y a pontuação obtida, a sentença que representa a pontuação obtida em função da quantidade de acertos é .
b) Tiago acertou 15 questões. Logo, .
Substituindo em , obtemos:
Portanto, ele obteve 75 pontos.
c) Substituindo em , obtemos:
Logo, .
Ou seja, para obter 60 pontos, um estudante deve acertar 12 questões.
d) Considerando e substituindo em , temos
e .
Ou seja, a prova tem 20 questões no total.
5. a) O preço aumenta R$ 2,00 a cada hora, começando com valor de R$ 4,50 na primeira hora. Desse modo, , pois:
|
Medida do tempo (em horas) |
Preço (R$) |
|---|---|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
x |
b) Considerando e substituindo em , temos:
Ou seja, R$ 18,50.
c) Considerando e substituindo em , temos:
Desse modo, , ou seja, 6 horas.
Página CIII
6. a) Cada biscoito contém . Assim, a medida da massa m em função da quantidade de biscoito b pode ser representada por .
b) Cada biscoito contém . Assim, o valor calórico c em função da quantidade de biscoitos b pode ser representado por .
c) Considerando e , temos:
Ou seja, .
Considerando e , temos:
Ou seja, .
d) Considerando e , temos:
Assim, , ou seja, 12 biscoitos. Como cada biscoito tem 70 kcal, temos:
Ou seja, .
Questão 4. e .
Atividades
7. As funções definidas por com a e b reais são ; ; ; .
8. a) e .
b) e .
c) e .
d) e .
e) e .
f) e .
9. Considerando a função .
a) Seja , temos:
b) Seja , temos:
c) Seja , temos:
d) Seja , temos:
e) Seja , temos:
f) Seja , temos:
10. a) Considerando que o hexágono é regular, podemos afirmar que todos os lados têm medida de comprimento igual. Denominando essa medida por x, temos:
Ou seja, . Essa é uma função afim.
b) Considerando e , temos:
Ou seja, a medida do perímetro é .
c) Considere e , temos:
Assim:
Ou seja, o comprimento de cada lado mede .
11. a) Como a medida da temperatura em graus Fahrenheit (F) é dada em função da medida da temperatura em graus Celsius (C), podemos definir a função afim .
Para , sabemos que , e para , temos .
Substituindo na função os respectivos valores, temos:
(I): e (II):
Página CIV
Por (I), concluímos que . Substituindo em (II), temos:
Logo, a função afim será .
b) Considere e . Assim:
Ou seja, .
c) Isolando C em , temos:
Assim, cada grau na escala Fahrenheit corresponde a grau na escala Celsius.
12. a) Considerando que R$ 4,50 é o valor fixo e R$ 2,75 é o valor variável de acordo com a quilometragem, a lei de formação da função afim é , que expressa o valor cobrado y em função da quantidade de quilômetros percorridos x.
b) Considerando , temos:
I . , então , ou seja, R$ 10,00.
II . , então , ou seja, R$ 30,35.
III . , então , ou seja, R$ 45,75.
c) Considerando :
I . . Logo:
, ou seja, .
II . . Logo:
, ou seja, .
III . . Logo:
Ou seja, .
d) Considerando e , temos:
Ou seja, são necessários R$ 59,50 para percorrer . Desse modo, é possível sim percorrer com R$ 60,00, pois .
13.
|
Quantidade de embalagens (unidade) |
Medida da massa (em gramas) |
|---|---|
|
1 |
|
|
2 |
|
|
3 |
|
|
x |
14. Considerando que uma função afim tem uma lei de formação que pode ser escrita na forma , calculando os valores dos coeficientes utilizando os valores de x e apresentados, obtemos e , que podemos representar como um sistema de equações lineares. Assim:
Ao utilizar o método da adição, podemos multiplicar a 2ª equação por .
Logo, .
Substituindo em , concluímos que .
Desse modo, obtemos a sentença . Para , temos:
15. a) Para 100 folhas, será pago R$ 0,20 por unidade, ou seja . Além disso, a encadernação para 100 folhas tem valor fixo de R$ 4,00. Desse modo, a lei de formação é dada por , em que , e .
Para uma quantidade de folhas entre 101 e 220, obtemos a lei de formação , em que , e .
b) Considerando e .
Para 83 folhas, , ou seja, R$ 20,60.
Para 145, folhas , ou seja, R$ 35,00.
16. a) Analisando o eixo horizontal podemos verificar que está ligado com no eixo vertical. Logo, o alongamento da mola para um corpo de medida de massa será de .
Página CV
b) Analisando o eixo vertical, podemos verificar que está ligado com no eixo horizontal. Logo, a medida de massa do corpo que fez a mola alongar é .
c) De acordo com o gráfico, temos:
e , ou seja,
e , ou seja,
e , ou seja,
Como , a lei de formação dessa função é dada por ou .
d) • Considerando e , temos:
Ou seja, de alongamento da mola.
Considerando e , temos:
Ou seja, de alongamento da mola.
Considerando e , temos:
Ou seja, de alongamento da mola.
e) Considerando e , temos:
Ou seja, .
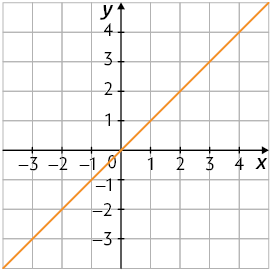
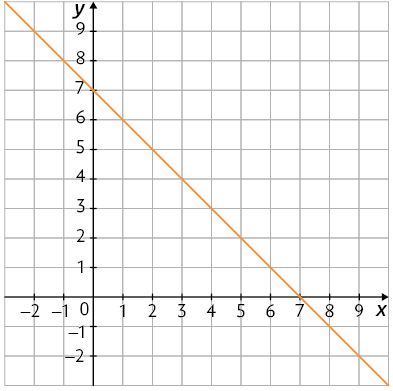
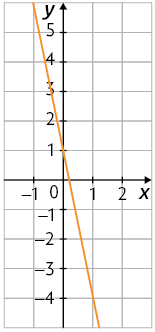
17. A. Considerando , para , obtemos . Essa relação é apresentada no gráfico 2.
B. Considerando , para , obtemos . Essa relação é apresentada no gráfico 1.
C. Considerando , para , obtemos . Essa relação é apresentada no gráfico 3.
Portanto, associamos A-2; B-1; C-3.
18. a)
|
x |
|
|
|---|---|---|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
b)
|
x |
|
|
|---|---|---|
|
|
||
|
0 |
||
|
1 |
c)
|
x |
|
|
|---|---|---|
|
|
||
|
0 |
||
|
1 |
d)
|
x |
|
|
|---|---|---|
|
|
||
|
0 |
||
|
1 |
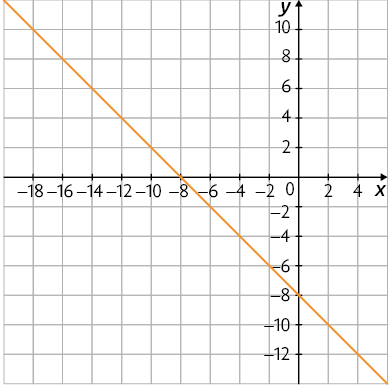
Página CVI
e)
|
x |
||
|---|---|---|
|
0 |
||
|
1 |
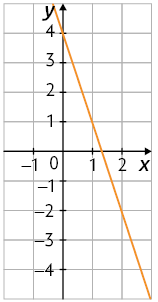
f)
|
x |
||
|---|---|---|
|
|
||
|
0 |
||
|
1 |
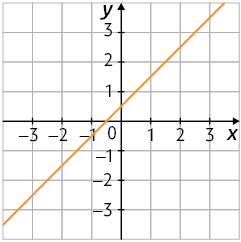
19. Considerando que o gráfico representa uma função afim , podemos utilizar dois pontos quaisquer indicados no gráfico. Escolhendo e , podemos substituir cada um respectivamente na lei de formação, assim e .
Da primeira equação, temos . Substituindo na segunda equação, temos:
Logo, .
Assim, a lei de formação da função representada no gráfico é dada por .
20. a) Podemos utilizar os pontos e em . Pelo primeiro ponto, podemos concluir que . Substituindo o segundo ponto, temos:
Assim, .
Logo, a lei de formação da função é dada por .
b) Resposta pessoal. Sugestão de resposta: Em determinado mapa, foi utilizada uma escala na qual cada corresponde a .
Questão 5. Eles aumentam.
Questão 6. Positivo.
Questão 7. Eles diminuem.
Questão 8. Negativo.
Atividades
21. Considerando que a função é crescente quando e decrescente quando , então a função é:
a) Decrescente, pois .
b) Crescente, pois .
c) Decrescente, pois .
d) Decrescente, pois .
e) Crescente, pois .
f) Crescente, pois .
22. a) Considerando o quadro A, podemos verificar que a função é decrescente, pois à medida que x aumenta, y diminui. A função está representada no gráfico II.
Considerando o quadro B, podemos verificar que a função é crescente, pois à medida que x aumenta, y aumenta. A função está representada no gráfico I.
Considerando o quadro C, podemos verificar que a função é crescente, pois à medida que x aumenta, y aumenta. A função está representada no gráfico III.
Considerando o quadro D, podemos verificar que a função é crescente, pois à medida que x aumenta, y aumenta. A função está representada no gráfico IV.
b) Considerando os pontos e apresentados no gráfico I e substituindo os valores em , obtemos:
Do segundo caso, concluímos que . Assim, substituindo em , obtemos:
, ou seja, .
A lei de formação que representa o gráfico I é dada por .
Considerando os pontos e apresentados no gráfico II e substituindo os valores em , obtemos:
Do segundo caso, concluímos que . Assim, substituindo em , obtemos:
Ou seja,
A lei de formação que representa o gráfico II é dada por .
Considerando os pontos e apresentados no gráfico III e substituindo os valores em , obtemos:
e
Do segundo caso, concluímos que . Assim, substituindo em , obtemos:
Ou seja, .
A lei de formação que representa o gráfico III é dada por .
Considerando os pontos e apresentados no gráfico IV e substituindo os valores em , obtemos:
Página CVII
Do primeiro caso, concluímos que . Assim, substituindo em , obtemos:
Ou seja, .
A lei de formação que representa o gráfico IV é dada por .
c) A. Decrescente, pois .
B. Crescente, pois .
C. Crescente, pois .
D. Crescente, pois .
23. a) A. Crescente, pois à medida que x aumenta, y também aumenta.
B. Decrescente, pois à medida que x aumenta, y diminui.
b) Considerando os pontos e apresentados em A e substituindo os valores em , obtemos:
e
Do segundo caso, concluímos que . Assim, substituindo em , obtemos:
Ou seja, .
A lei de formação é dada por .
Considerando os pontos e apresentados em B e substituindo os valores em , obtemos:
e
Do segundo caso, concluímos que . Assim, substituindo em , obtemos:
Ou seja, .
A lei de formação é dada por .
24. a) Para que a função seja decrescente, devemos ter . Assim, .
b) Para que a função seja decrescente, devemos ter . Assim, .
c) Para que a função seja decrescente, devemos ter . Assim, , logo . Portanto, .
d) Para que a função seja decrescente, devemos ter . Assim, , logo .
e) Para que a função seja decrescente, devemos ter . Assim, , logo .
f) Para que a função seja decrescente, devemos ter . Assim, , logo .
g) Para que a função seja decrescente, devemos ter . Assim, , logo .
h) Para que a função seja decrescente, devemos ter . Assim, , logo .
i) Para que a função seja decrescente, devemos ter . Assim, .
j) Para que a função seja decrescente, devemos ter . Assim, , logo .
25. Na atividade anterior, consideramos para cada função a condição de ser decrescente, ou seja, os valores de para os quais . Agora, devemos considerar os valores de para os quais , ou seja, a função será crescente. Assim:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
26. a) Crescente, pois x aumenta e y aumenta.
b) Decrescente, pois x diminui e y aumenta.
c) Crescente, pois x aumenta e y aumenta.
d) Crescente, pois x aumenta e y aumenta.
e) Crescente, pois x aumenta e y aumenta.
f) Crescente, pois x aumenta e y aumenta.
g) Crescente, pois x aumenta e y aumenta.
h) Decrescente, pois x diminui e y aumenta.
i) Decrescente, pois x diminui e y aumenta.
j) Decrescente, pois x diminui e y aumenta.
27. Resposta pessoal. Sugestão de resposta: .
|
x |
y |
|---|---|
|
0 |
1 |
|
1 |
3 |
|
2 |
5 |
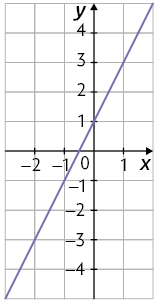
28. Resposta pessoal. Sugestão de resposta: , . Desse modo, temos os pontos e . Considerando uma função afim, podemos utilizar esses pontos para determinar a lei de formação. Substituindo cada um respectivamente na lei de formação , temos:
e
Da primeira equação, temos . Substituindo na segunda equação, temos:
Logo, , então .
Assim, a lei de formação da função é dada por .
29. a) A.
B.
C.
b) O zero da função é representado pelo ponto de interseção com o eixo x, sendo assim, o zero da função é:
A.
B.
C.
c) A.
B.
C.
Página CVIII
d) Considerando , podemos obter as coordenadas dos pontos de interseção com os eixos x e y usando e . Desse modo, no primeiro caso, temos:
Ou seja, o gráfico dessa função intersecta .
No segundo caso , temos:
, ou seja, o gráfico intersecta .
Dessa forma, o gráfico da função está representado em C.
30. O ponto em que o gráfico da função intersecta o eixo y pode ser determinado substituindo na lei de formação. Desse modo, temos:
a)
b)
c)
d)
e)
f)
g)
h)
31. O zero da função pode ser determinado quando . Desse modo, temos:
a)
b)
c)
d)
e)
f)
32. a) Considerando e usando e , podemos determinar os pontos de interseção como os eixos. Assim, para , temos:
Logo, o gráfico passa por .
Para :
Logo, o gráfico passa por .
Sendo assim, o gráfico pode ser representado por:
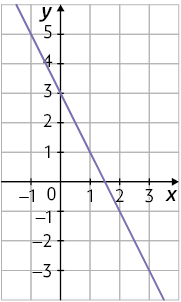
b) I. Falsa, pois .
II . Verdadeira.
Página CIX
III . Falsa, o zero dessa função é .
IV . Verdadeira.
c) Sugestão de resposta:
I . Essa função é decrescente.
III . O zero dessa função é .
33. a) Sugestão de resposta: Consideramos , que passa por e .
No primeiro caso, temos:
Logo, .
No segundo caso, temos:
Substituindo , obtemos: .
Logo, .
Desse modo: .
b)
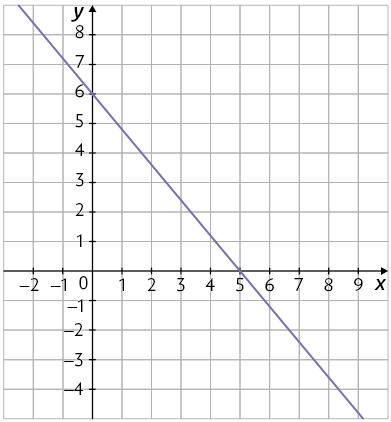
Questão 9.
a) Considerando e , temos:
Ou seja, para , a área mede .
b) Considerando e , temos:
Ou seja, para , a área mede .
c) Considerando e , temos:
Ou seja, para , a área mede .
Atividades
34. Considerando e substituindo os valores indicados, temos:
a)
b)
c)
d)
e)
f)
g)
h)
35. Considerando , para:
a) , temos:
b) , temos:
c) , temos:
d) , temos:
e) , temos:
36. Considerando e , temos:
Logo, ou .
37. Para que a função seja quadrática, a deve ser diferente de zero . Desse modo:
a)
b)
c)
d)
Página CX
e)
f)
e .
38. A. Considerando a medida da área do triângulo, temos:
, para , pois .
B. A figura pode ser decomposta em um triângulo e um quadrado. Assim, considerando e para representar as respectivas medidas das áreas, a medida da área da figura é dada por . Logo:
para , pois .
Ou seja, a medida da área total da figura é dada por , para .
C. Considerando a medida da área do retângulo, temos:
, para .
D. Considerando a medida da área do triângulo, temos:
, para .
39. a) A medida da área é dada pela multiplicação das medidas do comprimento dos lados. Desse modo, temos:
b) Considerando e , temos:
Ou seja, a área total do terreno mede .
Considerando que a medida da área da quadra é dada por e substituindo , temos:
Ou seja, a área da quadra mede .
40. Considerando e , temos:
Ou seja, o custo é de R$ 1.210,00.
Para , temos:
Ou seja, o custo é de R$ 1.205,98.
Calculando a diferença, temos:
Portanto, a resposta correta é indicada na alternativa e.
41. a) Considerando as medidas do comprimento dos lados do retângulo apresentado, temos:
, para , pois .
b) Considerando e , temos:
42. a) Decompondo a figura em dois retângulos cujas medidas de área são dadas por e por , podemos obter a medida da área total da figura calculando:
, para , pois .
b) Calculando para , obtemos:
Ou seja, .
43. a) Calculando a soma dos 15 primeiros termos, temos:
Calculando a soma dos 50 primeiros termos, temos:
Página CXI
b)
Armando adicionou 12 termos.
44. Analisando o coeficiente a, podemos concluir que a concavidade da parábola está voltada:
a) para cima, pois (positivo).
b) para baixo, pois (negativo).
c) para baixo, pois (negativo).
d) para cima, pois (positivo).
e) para cima, pois (positivo).
f) para baixo, pois (negativo).
45. a) Analisando o gráfico apresentado, podemos verificar que a medida da altura máxima foi .
b) De acordo com o gráfico, a bola tocou o solo novamente após .
c) I. Considerando e , temos:
Ou seja, a altura atingida pela bola após mede .
II . Considerando e , temos:
Ou seja, a altura atingida pela bola após mede .
III . Considerando e , temos:
Ou seja, a altura atingida pela bola após mede .
d) De acordo com o gráfico, a bola atingiu a medida da altura máxima após ser lançada.
46. Verificando qual é o ponto de interseção com o eixo y em cada lei de formação, substituindo x por 0, temos:
A:
Assim, a função cuja lei de formação é passa pelo ponto , que corresponde ao gráfico III.
B:
Assim, a função cuja lei de formação é passa pelo ponto , que corresponde ao gráfico I.
C:
Assim, a função cuja lei de formação é passa pelo ponto , que corresponde ao gráfico II.
47. a)
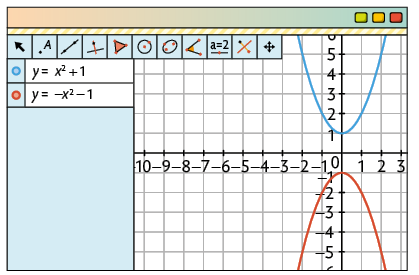
b) A parábola de tem a concavidade voltada para baixo, pois .
48. A. Como a parábola tem a concavidade voltada para cima, .
B. Como a parábola tem a concavidade voltada para baixo, .
C. Como a parábola tem a concavidade voltada para baixo, .
49. a) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
b) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
c) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
d) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
e) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
f) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
g) Para que a concavidade esteja voltada para cima: , ou seja, .
Logo, para concavidade voltada para baixo: .
50. a)
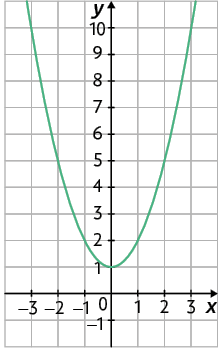
Página CXII
b)
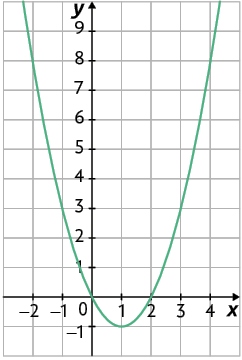
c)
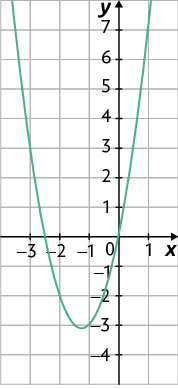
d)
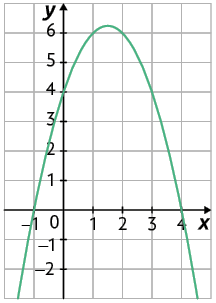
e)
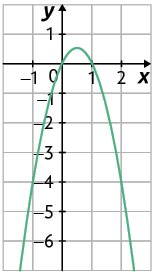
f)
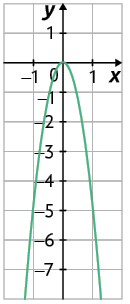
g)
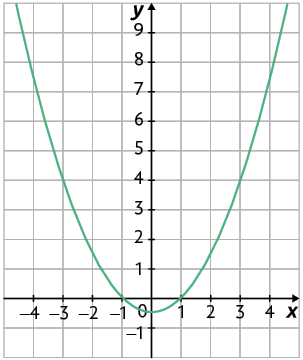
h)
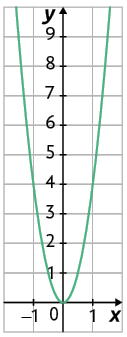
i)
Página CXIII
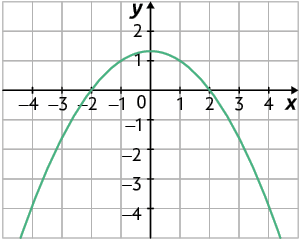
j)
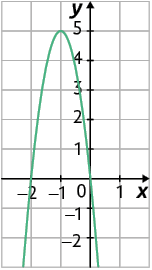
k)
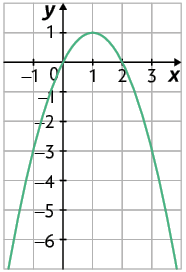
l)
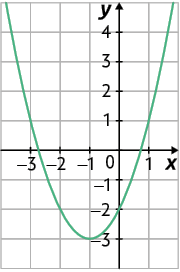
51. a)
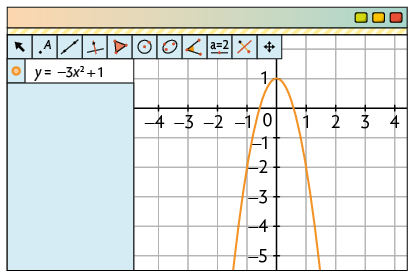
b) Resposta no final da seção Resoluções.
c)
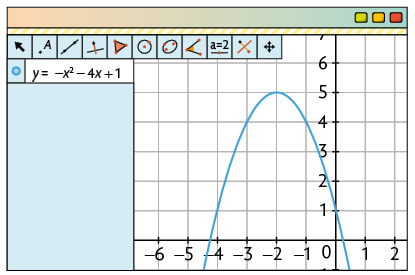
d) Resposta no final da seção Resoluções.
e) Resposta no final da seção Resoluções.
f) Resposta no final da seção Resoluções.
g) Resposta no final da seção Resoluções.
h) Resposta no final da seção Resoluções.
i) Resposta no final da seção Resoluções.
j) Resposta no final da seção Resoluções.
k) Resposta no final da seção Resoluções.
52. Analisando cada um dos itens, temos:
a) Falso, pois é negativo e é positivo. Assim, .
b) Verdadeiro, pois é negativo e também. Logo, .
No segundo caso, é positivo e também. Logo, .
c) Falso, pois é negativo e é positivo. Assim, .
Desse modo, o item que apresenta informações verdadeiras é a alternativa b.
53. a) Os itens A e B indicam funções cujos gráficos apresentam parábolas com a concavidade para cima.
b) Para descobrir o ponto de interseção com o eixo y, devemos substituir x por 0, ou seja, . Desse modo, a função intersecta o eixo y em:
A. , .
B. , .
C. , .
D. , .
c) Considerando os pontos obtidos no item anterior, podemos relacionar a lei de formação ao gráfico, ou seja, A-II, B-IV, C-I, D-III.
54. Considerando que no ponto de interseção com o eixo y o valor de x é zero, ou seja e , temos:
a)
b)
c)
d)
e)
f)
55. a) Considerando , e , temos:
Duas raízes iguais a 3.
Página CXIV
b) Considerando , e , temos:
Assim, as raízes são:
c) Considerando , e , temos:
Assim, as raízes são:
d) Considerando , e , temos:
Assim, as raízes são:
e) Considerando , e , temos:
Sendo assim, como não existe raiz real de números negativos, a função não tem raiz.
f) Considerando , e , temos:
Assim, as raízes são:
g) Considerando , e , temos:
Assim, as raízes são:
h) Considerando , e , temos:
Página CXV
Assim, as raízes são:
i) Considerando , e , temos:
Assim, as raízes são:
j) Considerando , e , temos:
Assim, as raízes são:
k) Considerando , e , temos:
Assim, as raízes são:
56. a) Como a concavidade da parábola está voltada para cima, então: .
b) O coeficiente c da lei de formação dessa função pode ser determinado quando . Assim, analisando o gráfico, quando . Logo, .
c) Analisando o gráfico, podemos verificar que os zeros da função são e .
d) Analisando o gráfico, temos dois pontos de interseção com o eixo x, em que : e .
e) Analisando o gráfico, temos um ponto de interseção com o eixo y, em que : .
57. a) Calculando o valor de , temos:
Como , podemos concluir que a função tem dois zeros reais distintos.
b) Calculando o valor de , temos:
Como , podemos concluir que a função tem dois zeros reais iguais.
c) Calculando o valor de , temos:
Como , podemos concluir que a função não tem zeros reais.
d) Calculando o valor de , temos:
Como , podemos concluir que a função tem dois zeros reais iguais.
Página CXVI
e) Calculando o valor de , temos:
Como , podemos concluir que a função tem dois zeros reais distintos.
f) Calculando o valor de , temos:
Como , podemos concluir que a função não tem zeros reais.
58. A. Considerando os pontos de interseção com os eixos, verificamos que . Usando as coordenadas e em , temos:
Para :
Para :
Desse modo, temos:
ou
Adicionando as sentenças, obtemos:
Logo, .
Substituindo em , obtemos:
Assim, .
Concluímos que a lei de formação da função representada no gráfico é .
B. Considerando os pontos de interseção com os eixos, verificamos que . Usando as coordenadas e em , obtemos:
Para :
Para :
Desse modo, temos:
ou
Subtraindo as sentenças, obtemos:
Logo, .
Substituindo em , obtemos:
Assim, .
Concluímos que a lei de formação da função representada no gráfico é .
Questão 10. Sim, pois pertencem ao gráfico da função quadrática e têm ordenadas iguais.
Atividades
59. a) Considerando os valores dos coeficientes apresentados na lei de formação, temos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
b) Considerando os valores dos coeficientes apresentados na lei de formação, temos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
Página CXVII
c) Considerando os valores dos coeficientes apresentados na lei de formação, obtemos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
d) Considerando os valores dos coeficientes apresentados na lei de formação, obtemos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
e) Considerando os valores dos coeficientes apresentados na lei de formação, obtemos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
f) Considerando os valores dos coeficientes apresentados na lei de formação, obtemos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
g) Considerando os valores dos coeficientes apresentados na lei de formação, obtemos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Ou seja, .
h) Considerando os valores dos coeficientes apresentados na lei de formação, obtemos , e .
Desse modo, calculando as coordenadas do vértice, temos:
Página CXVIII
Ou seja, .
60. Considerando que, se , a função tem ponto de mínimo, e se , a função tem ponto de máximo, temos:
a) Ponto de mínimo.
b) Ponto de máximo.
c) Ponto de máximo.
d) Ponto de mínimo.
e) Ponto de máximo.
f) Ponto de mínimo.
61. a) Considerando o gráfico apresentado, verificamos que , ou seja, o coeficiente a tem sinal negativo, pois a concavidade está voltada para baixo.
b) Analisando o gráfico, obtemos as coordenadas .
c) Não, pois seu ponto de máximo está abaixo do eixo x e sua concavidade está voltada para baixo.
d)
e) Ponto de máximo, pois .
f) Considerando que o gráfico da função passa por , . Utilizando a fórmula das coordenadas do vértice para calcular os outros coeficientes, temos:
Usando , obtemos:
Sendo assim, temos:
Logo, a lei de formação da função representada no gráfico é .
62. a) Considerando que as coordenadas do ponto de máximo é e substituindo em , temos:
Logo, .
b)
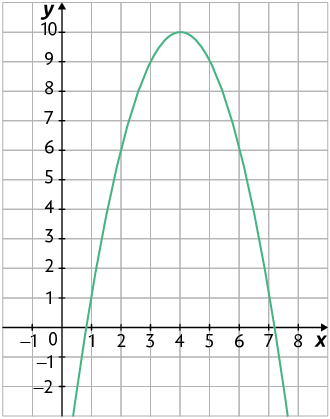
63. a)
, com .
b)
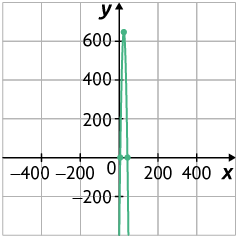
c) Calculando a medida da área máxima, ou seja, a ordenada do ponto de máximo da função , temos:
Logo, a medida da área máxima do terreno é .
d) Considerando a medida do comprimento dos lados e x, temos:
Assim, as medidas do comprimento dos lados referentes à medida da área máxima do terreno retangular são e .
Página CXIX
64. a) Considerando os coeficientes , e , temos:
Logo, a medida da altura máxima atingida pelo avião foi de .
b) Considerando , temos:
e
Logo, o avião atingiu o solo após .
c) Para isso, obtemos a média entre 0 e 2 segundos. Ou seja, após o lançamento, o avião atingiu a medida da altura máxima.
O que eu estudei?
1. a) Analisando a tabela, temos .
b) Calculando durante 30 dias, obtemos o total de 240 horas. Desse modo:
Ou seja, .
2. a) Considerando que a caixa já está com , então esse será um valor constante. Além disso, o despejo de por minuto é dado por . Desse modo, podemos escrever a lei de formação em que y representa a medida do volume da caixa-d'água em função do tempo x.
b) Considerando e , temos:
Como , a caixa-d'água está com após aproximadamente .
Considerando e , temos:
Ou seja, .
c) Para , temos:
Como , para encher a caixa-d'água, a medida de tempo necessária será de aproximadamente .
3. a) Analisando o gráfico, podemos verificar que as coordenadas do vértice são .
b) O gráfico da função apresenta apenas um zero em .
c) O coeficiente c é dado pelo ponto de interseção com o eixo y: .
4. a) Seja y a medida da área do retângulo em função de x, temos:
O valor de x para a medida da área máxima é dado por . Desse modo:
, ou seja, o valor de x para a medida da área máxima é .
b) Considerando e as medidas das dimensões do retângulo, temos:
Ou seja, as medidas das dimensões são e .
5. a) Considerando que o valor de determina as possibilidades, temos:
Para que tenham dois pontos distintos , ou seja, , calculamos:
Desse modo:
e
O vértice da parábola está voltada para cima, ou seja, . Assim, quando e .
b) Para que a função intersecte o eixo x em apenas um ponto, ou seja, , devemos ter ou .
c) Para que não tenha interseção com nenhum ponto do eixo x: .
Página CXX
Unidade 10
Circunferência, vistas e perspectiva
Atividades
1. a) A corda tem a maior medida de comprimento, pois ela também é o diâmetro.
b) A corda terá a mesma medida de comprimento da corda , pois ambas serão diâmetros.
c) O segmento de reta é um raio da circunferência, pois qualquer segmento de reta que une o centro a um de seus pontos é um raio de circunferência.
2. a) As coordenadas do centro dessa circunferência são .
b) Para calcular a medida do comprimento do raio, vamos calcular a distância do ponto até qualquer ponto da circunferência. O ponto pertence à circunferência e, como as coordenadas do centro da circunferência são , a medida do comprimento do raio pode ser calculada por . Logo, a medida do comprimento do raio é igual a .
A medida do comprimento do diâmetro é igual ao dobro da medida do comprimento do raio, assim, o diâmetro da circunferência mede .
c) Esses pontos são extremidades de um diâmetro, assim, pelo item anterior, o comprimento da distância entre esses dois pontos mede .
3. a) Marque um ponto B qualquer e, com a abertura do compasso medindo , coloque a ponta-seca em B, traçando uma circunferência.
b) Como a medida de comprimento do raio é igual à metade da medida do comprimento do diâmetro, o raio dessa circunferência mede .
Marque um ponto O qualquer e, com abertura do compasso medindo , coloque a ponta-seca em O, traçando uma circunferência.
c) A maior corda possível de uma circunferência é o seu diâmetro. Então, para desenhar uma circunferência com diâmetro medindo , devemos desenhar uma circunferência com raio medindo , visto que a medida do comprimento do raio é igual à metade da medida do comprimento do diâmetro.
Marque um ponto A qualquer e, com abertura do compasso medindo , coloque a ponta-seca em A, traçando uma circunferência.
4. As diagonais de um retângulo têm a mesma medida de comprimento. Desse modo, tem a mesma medida de comprimento de , ou seja, . O ponto O é o centro da circunferência e B é um ponto da circunferência, logo é um raio da circunferência. Portanto, a medida do comprimento do raio da circunferência é .
5. A reta r é secante às circunferências de centros O e Q e tangente à circunferência de centro P.
A reta s é externa às circunferências de centros P e Q e tangente à circunferência de centro O.
A reta t é secante às circunferências de centros O e P e externa à circunferência de centro Q.
A reta u é tangente à circunferência de centro O e externa às circunferências de centros P e Q.
6. a) A reta v é tangente à circunferência, pois a medida da distância entre a reta tangente e o centro da circunferência é igual à medida de comprimento do raio.
b) As retas s, u e z são secantes à circunferência, pois a medida da distância entre cada reta secante e o centro da circunferência é menor do que a medida de comprimento do raio.
c) As retas q, r e t são externas à circunferência, pois a medida da distância entre cada uma das retas externas à circunferência e o centro da circunferência é maior do que a medida de comprimento do raio.
7. a) Resposta pessoal. Sugestão de resposta:
1º. Desenhe uma circunferência de centro O, marque um ponto A sobre ela e prolongue o raio . Em seguida, com a ponta-seca do compasso em A e com abertura menor do que o raio , determine os pontos B e C.
2º. Determine a mediatriz entre os pontos B e C, obtendo o ponto D. Por fim, trace a reta que passa pelos pontos A e D, que é tangente à circunferência de centro O no ponto A.
Página CXXI
3º. Com a ponta-seca do compasso em A e abertura igual a , trace dois arcos sobre a circunferência, marque os pontos E e F e, em seguida, trace uma reta que passe por esses pontos, que é secante à circunferência de centro O.
4º. Com a ponta-seca do compasso em B e abertura igual a , marque um ponto H sobre a reta que passa por A e B. Com a ponta-seca do compasso em A e abertura maior do que , trace um arco. Em seguida, com a ponta-seca do compasso em H e a mesma abertura do compasso, trace outro arco e marque o ponto I na interseção desses arcos.
5º. Por fim, trace uma reta que passe pelos pontos B e I, que é externa à circunferência de centro O.

b) Resposta pessoal. Espera-se que os estudantes confiram que traçaram as retas t, r e s corretamente.
8. a) As circunferências de centros A e D são secantes, pois têm dois pontos de interseção.
b) As circunferências de centros B e D são tangentes internas, pois a de centro B é interna à de centro D e têm somente um ponto em comum.
c) As circunferências de centros C e D são internas, pois a de centro C é interna à de centro D e não têm pontos em comum.
d) As circunferências de centros F e G são tangentes internas, pois a de centro G é interna à de centro F e têm somente um ponto em comum.
e) As circunferências de centros G e D são tangentes internas, pois a de centro G é interna à de centro D e têm somente um ponto em comum.
f) As circunferências de centros E e H são tangentes externas, pois a de centro E é externa à de centro H e têm somente um ponto em comum.
g) As circunferências de centros B e F são externas, pois a de centro B é externa à de centro F e não têm pontos em comum.
h) As circunferências de centros F e C são secantes, pois têm dois pontos em comum.
i) As circunferências de centros A e E são externas, pois a de centro A é externa à de centro E e não têm pontos em comum.
9. Primeiramente, precisamos calcular as medidas de comprimento dos segmentos , e . Essas medidas são iguais às medidas das distâncias do ponto A ao ponto B, do ponto B ao ponto C e do ponto A ao ponto C, respectivamente. Como as circunferências são tangentes externas, a medida dessas distâncias é igual à soma das medidas do comprimento de seus raios.
Assim:
, ou seja, .
, ou seja, .
, ou seja, .
Logo, a medida do perímetro do triângulo é , ou seja, .
10. Denominando x a medida do comprimento do raio da circunferência maior. A medida da distância entre os centros de duas circunferência internas é igual à diferença entre a medida do raio maior e a medida do raio menor. Desse modo, temos:
Portanto, o comprimento do raio da circunferência menor mede .
11. a) Subtraindo a medida do comprimento do raio menor da medida do comprimento do raio maior, temos , ou seja, . Adicionando as medidas de comprimento dos raios, temos , ou seja, . Como a distância entre os centros das circunferências mede e , segue que as circunferências são secantes.
b) A diferença entre a medida de comprimento do raio maior e a medida de comprimento do raio menor é igual a. Como a distância entre os centros das circunferências é igual a , segue que as circunferências são tangentes internas.
12. Como as circunferências são concêntricas, e o valor de x corresponde à diferença entre as medidas de comprimento dos raios, temos:
.
Portanto, .
13. a) , pois corresponde à medida de comprimento do raio da circunferência de centro A.
b) , pois corresponde à medida de comprimento do raio da circunferência de centro A.
c) é diâmetro da circunferência de centro A, assim . Logo, .
d) . Como , pois é um raio da circunferência de centro B e , então e, portanto, .
Página CXXII
e) , pois é um raio da circunferência de centro A.
f) , pois é um raio da circunferência de centro B.
g) Temos , pois é um raio da circunferência de centro B.
h) Temos . Como e , segue que .
Logo, .
14. Temos e .
Desse modo:
Portanto, .
15. Primeiro, vamos calcular o valor de x. Como uma volta completa mede , temos:
Assim, obtemos as seguintes medidas para cada um dos ângulos:
a)
b)
c)
Questão 1. O ângulo mede e o ângulo mede .
Questão 2. Espera-se que os estudantes concluam que a medida do ângulo é fixa.
Questão 3. O ângulo mede .
Questão 4. Resposta pessoal. Espera-se que os estudantes concluam que a medida do ângulo inscrito é a metade da medida do ângulo central.
Atividades
16. O ângulo é um ângulo central e o ângulo é um ângulo inscrito e eles determinam o mesmo arco.
Assim, .
17. O ângulo é um ângulo central e o ângulo é um ângulo inscrito e eles determinam o mesmo arco. Assim:
.
Dessa igualdade, obtemos:
Portanto, e .
18. Ângulos inscritos com um mesmo arco correspondente têm a mesma medida. Sendo assim, as medidas dos ângulos , , , e são iguais.
19. De acordo com o desenho de Rita, e os ângulos e são ângulos inscritos em uma semicircunferência.
Portanto, .
20. Reproduzindo a imagem no GeoGebra, temos:
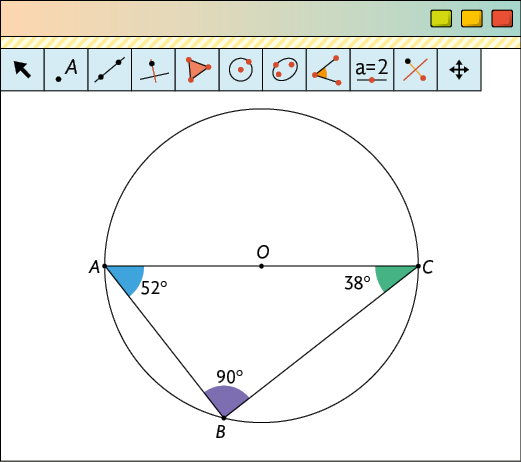
Portanto, a medida de cada ângulo inscrito na circunferência é:, e .
21. Os ângulos inscritos na circunferência têm o mesmo arco correspondente, logo eles têm a mesma medida. Desse modo, temos:
22. O segmento é um diâmetro da circunferência, logo .
Página CXXIII
Assim, é um ângulo inscrito em uma semicircunferência, logo .
Como a soma das medidas dos ângulos internos de um triângulo é igual a , temos:
23. a) Os segmentos e são diâmetros da circunferência de centro O e os segmentos , , e são raios da circunferência.
b) O triângulo é isósceles, pois dois de seus lados são formados por segmentos que representam o comprimento do raio da circunferência. Sendo assim, têm medidas iguais.
c) Os ângulos e são retos, pois estão inscritos em uma semicircunferência.
Logo, os triângulos e são triângulos retângulos.
d) Os segmentos , , e são congruentes.
Portanto, os triângulos e são congruentes, pois seus respectivos lados são congruentes e seus respectivos ângulos internos também são congruentes.
24. a) Sabemos que os triângulos e são congruentes, assim , segue que os triângulos e são congruentes, pois , , e são raios da circunferência.
Desse modo, os ângulos centrais e são congruentes, pois são correspondentes nessa congruência.
Logo, , pois os ângulos e são ângulos internos do triângulo ABE.
Portanto, o triângulo é isósceles.
b) O segmento é um diâmetro da circunferência, sendo assim o ângulo é um ângulo inscrito em uma semicircunferência, ou seja, .
Considerando o triângulo e a soma das medidas de seus ângulos internos, temos:
Logo, do item anterior, temos: .
Desse modo, considerando a soma das medidas dos ângulos internos do triângulo , temos:
Portanto, .
25. Resposta pessoal. Sugestão de resposta:
Calcule a medida dos ângulos destacados na circunferência de centro O.
Resposta: .
26. a) Para calcular a medida aproximada da distância que a bicicleta de Cássia percorre quando a roda dá uma volta completa, vamos calcular a medida C do comprimento da circunferência da roda de sua bicicleta. Como o diâmetro da roda mede , temos:
Portanto, a medida da distância aproximada que a bicicleta de Cássia percorre quando a roda dá uma volta completa é .
b) Pelo item anterior, o comprimento aproximado da circunferência da roda da bicicleta de Cássia mede , o que é equivalente a . Assim:
Portanto, percorrendo , a roda da bicicleta de Cássia dá aproximadamente 241 voltas.
27. A. Sendo , e indicando a medida aproximada do comprimento da linha vermelha por C, obtemos:
Portanto, a medida do comprimento aproximada da linha vermelha é .
B. A linha vermelha é composta de três partes, duas delas são raios da circunferência e a outra é um arco de circunferência.
Para calcular a medida de comprimento aproximada da linha vermelha, vamos primeiramente calcular a medida de comprimento aproximada do arco de circunferência:
Página CXXIV
Logo, a medida de comprimento aproximada da circunferência é .
O arco de circunferência corresponde a um ângulo central que mede .
Indicando por x a medida do comprimento do arco, temos:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
213,52 |
|
90 |
X |
Efetuando os cálculos:
Logo, a medida de comprimento aproximada do arco é . Como as outras duas partes da linha vermelha são raios do círculo, a medida de comprimento aproximada da linha vermelha é .
28. As duas polias têm seus diâmetros com mesma medida de comprimento, ou seja, . Desse modo, seus raios medem e a medida do comprimento da circunferência de cada polia é dada por:
Logo, a medida aproximada do comprimento da circunferência de cada polia é . Podemos separar a correia que passa pelas polias em quatros partes, duas que tocam metade de cada polia e duas que não tocam as polias.
As partes da correia que tocam metade das polias medem , pois , e as partem que não tocam medem , pois essa é a medida da distância entre os centros das polias.
Portanto, a medida de comprimento aproximada da correia é .
29. A. Primeiramente, vamos calcular a medida aproximada do comprimento da circunferência com raio medindo :
Logo, a medida aproximada do comprimento da circunferência é .
A medida do ângulo central correspondente ao arco é igual a . Então:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
62,8 |
|
70 |
x |
Efetuando os cálculos, temos:
Portanto, a medida de comprimento aproximada do arco é .
B. Primeiramente, vamos calcular a medida aproximada do comprimento da circunferência com raio medindo :
Logo, a medida aproximada do comprimento da circunferência é .
A medida do ângulo central correspondente ao arco é igual a , assim:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
87,92 |
|
145 |
x |
Efetuando os cálculos, temos:
Portanto, a medida de comprimento aproximada do arco é .
Página CXXV
30. Primeiramente, vamos calcular a medida aproximada do comprimento da circunferência com comprimento do raio medindo :
Logo, a medida aproximada do comprimento da circunferência é .
A medida do ângulo central correspondente ao arco é igual a , assim:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
43,96 |
|
240 |
x |
Efetuando os cálculos, temos:
Portanto, a medida de comprimento aproximada do arco é .
31. Calculando a medida aproximada do comprimento da circunferência com raio medindo :
Logo, a medida aproximada do comprimento da circunferência é .
A medida do comprimento do arco é igual a , assim:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
75,36 |
|
x |
10,46 |
Efetuando os cálculos, temos:
Portanto, a medida aproximada do ângulo que corresponde ao arco é .
Questão 5. Resposta no final da seção Resoluções.
Atividades
32. a) Todo triângulo equilátero tem as medidas de seus ângulos internos iguais a .
Portanto, .
b) Os ângulos e são, respectivamente, o ângulo inscrito e o central que determinam o mesmo arco.
Portanto, .
33. Como as diagonais do quadrado são perpendiculares entre si, elas dividem o quadrado em quatro triângulos retângulos. Os catetos desses triângulos retângulos medem r, pois são raios da circunferência, e as hipotenusas medem u, pois são lados do quadrado. Aplicando o teorema de Pitágoras em qualquer um desses triângulos retângulos, temos:
Portanto, .
34. Na circunferência de centro Q, a medida de comprimento do raio é igual a .
Assim, pela resposta da atividade anterior, temos .
Portanto, a medida do lado do quadrado é igual a .
35. Como o polígono é regular, podemos escrever a seguinte relação:
, em que n representa a quantidade de lados do polígono regular. Nesse caso, o polígono regular tem 8 lados. Portanto, seu perímetro mede , ou seja, .
36. a) Como o hexágono é regular e a circunferência tangencia o polígono em seus respectivos pontos médios, temos . Por outro lado, .
Portanto, .
A medida da distância do ponto O até o ponto C é igual a . Essa medida é igual à medida do raio da circunferência que circunscreve esse hexágono. Em um hexágono regular qualquer, a medida do raio da circunferência que o circunscreve é igual à medida do comprimento do seu lado, assim, o comprimento do lado desse hexágono mede .
Página CXXVI
Como , a medida do perímetro do hexágono é igual a .
Considere o triângulo . Esse triângulo é retângulo, pois .
Temos e , usando o teorema de Pitágoras, temos:
Logo, a medida do diâmetro da circunferência é aproximadamente , pois .
Considerando como aproximação para a medida do comprimento do raio da circunferência, vamos calcular a medida de comprimento aproximada da circunferência:
Logo, a medida aproximada do comprimento da circunferência é .
b) Considerando o hexágono regular , a medida de seu lado é igual à medida do comprimento do raio da circunferência que o circunscreve. Do item anterior, a medida do comprimento do raio dessa circunferência é aproximadamente .
Logo, o comprimento do lado desse hexágono regular mede aproximadamente . Como todos os seus lados têm a mesma medida, seu perímetro mede , ou seja, aproximadamente .
37. Resposta no final da seção Resoluções.
Questão 6. Marcos – vista lateral esquerda; Adriana – vista lateral direita; Otávio – vista posterior.
Questão 7. A imagem que representa uma possível vista superior dos objetos apresentados na página anterior é a imagem 3.
Atividades
38. A imagem A corresponde à vista frontal, a imagem B corresponde à vista lateral direita, a imagem C corresponde à vista lateral esquerda e a imagem D corresponde à vista superior.
39. a) A imagem 2 pode representar a vista superior do vaso A e a imagem 6 pode representar a vista superior do vaso B.
b) A imagem 1 pode representar a vista lateral esquerda do vaso A e a imagem 4 pode representar a vista lateral direita do vaso B.
40. a) A sequência de figuras 2 representa a vista superior das figuras geométricas espaciais.
b) A imagem a seguir representa a vista frontal das figura.
41. a) A figura B corresponde à vista lateral direita do objeto.
b) A figura A corresponde à vista frontal do objeto.
c) A figura D corresponde à vista lateral esquerda do objeto.
Questão 8. A perspectiva foi usada na obra A, pois podemos perceber que alguns dos desenhos parecem estar mais perto enquanto outros parecem estar mais afastados. Na obra B, os desenhos parecem estar todos em um mesmo plano.
Questão 9. Resposta pessoal. Sugestão de resposta: Considere a seguinte figura como face frontal de uma figura geométrica espacial.
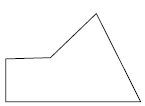
1º. Desenhe a linha do horizonte e sobre ela marque o ponto de fuga P. Em seguida, desenhe também a face frontal da figura.
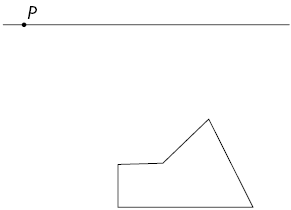
2º. Ligue os vértices da figura até o ponto de fuga.

Página CXXVII
3º. Seguindo as linhas traçadas no passo anterior, desenhe o fundo da figura de maneira que os vértices correspondentes estejam sobre a mesma linha e as arestas correspondentes sejam paralelas.
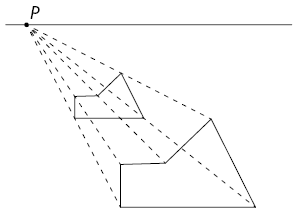
4º. Ligue os vértices correspondentes.
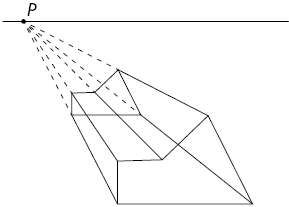
5º. Por último, apague os demais elementos que não fazem parte da figura geométrica espacial.
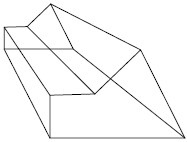
Questão 10. Resposta pessoal. Sugestão de resposta: Para desenhar um paralelepípedo reto retângulo usando a técnica da perspectiva central, execute os passos a seguir.
1º. Desenhe a linha do horizonte e represente os pontos de fuga e sobre ela. Acima da linha do horizonte, desenhe a aresta frontal do paralelepípedo.

2º. Ligue as extremidades da aresta aos dois pontos de fuga.
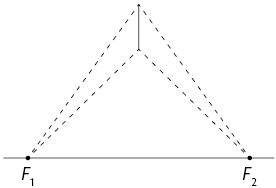
3º. Desenhe dois segmentos paralelos à aresta frontal com extremidades nas linhas traçadas no passo anterior. Em seguida, ligue as extremidades desses segmentos, conforme a imagem.
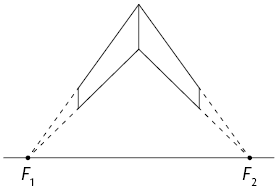
4º. Ligue as extremidades dos segmentos traçados no passo anterior até os pontos de fuga, conforme a imagem a seguir.
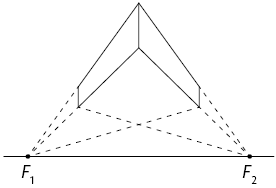
5º. Ligue os segmentos que representam as arestas do paralelepípedo reto retângulo.
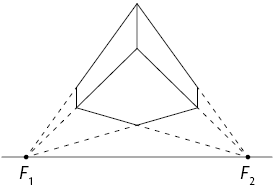
6º. Por fim, apague os demais elementos que não fazem parte da figura.
Atividades
42. Na figura A, foi aplicada a técnica de perspectiva isométrica, na figura C, foi aplicada a técnica de perspectiva cônica, na figura D, também foi aplicada a técnica de perspectiva cônica e na figura E, foi aplicada a técnica da perspectiva cavaleira. As figuras B e F apresentam somente duas dimensões e, portanto, nelas não foram aplicadas técnicas de perspectiva.
43. Na figura A, foi usada a técnica de perspectiva cavaleira, ou seja, a perspectiva 3; na figura B, foi usada a técnica de perspectiva cônica, ou seja, a perspectiva 1 e na figura C, foi usada a técnica de perspectiva isométrica, ou seja, a perspectiva 2.
Página CXXVIII
44. A figura apresentada na alternativa B foi desenhada usando a técnica de perspectiva cavaleira.
45. Resposta pessoal. Sugestão de resposta:
46. Daniel usou o poliedro A, pois esta figura é a única que tem a vista lateral esquerda de acordo com a que Daniel desenhou.
47. Resposta pessoal. Sugestões de respostas:
a) Um possível poliedro que pode ser representado por essas vistas é o prisma triangular reto.
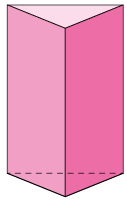
b) Para desenhar o prisma triangular reto foi usada a perspectiva isométrica.
48. a) Seguindo os passos apresentados na página 224 é possível obter uma figura geométrica espacial em perspectiva cônica usando um ponto de fuga. Resposta pessoal. Sugestão de resposta:
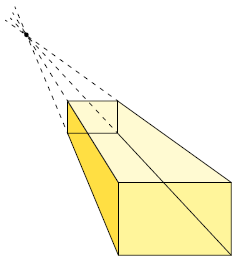
b) Seguindo os passos apresentados na página 225 é possível obter uma figura geométrica espacial em perspectiva central usando dois pontos de fuga. Resposta pessoal. Sugestão de resposta:
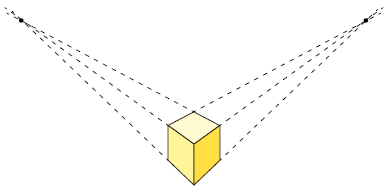
O que eu estudei?
1. Para que a lata cilíndrica entre na caixa que tem o formato de um paralelepípedo reto retângulo, a medida do comprimento das arestas da tampa da caixa deve ser igual à medida do comprimento do diâmetro da base da lata. Como o comprimento do raio da base da lata mede , verificamos que seu diâmetro mede . Assim, a tampa da caixa deve ter o formato de um quadrado cujo comprimento das arestas meça . Portanto, a área mínima da tampa da caixa deve medir .
2. a) Primeiro, vamos calcular a medida aproximada do comprimento da circunferência com raio medindo .
Logo, a medida aproximada do comprimento da circunferência é .
A medida do ângulo central correspondente ao arco é igual a , assim:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
25,12 |
|
60 |
x |
Efetuando os cálculos, temos:
Portanto, a medida de comprimento aproximada do arco é .
b) Primeiro, vamos calcular a medida aproximada do comprimento da circunferência com raio medindo .
Logo, a medida aproximada do comprimento da circunferência é .
A medida do ângulo central correspondente ao arco é igual a , assim:
|
Medida do ângulo central (em graus) |
Medida do comprimento do arco (em ) |
|---|---|
|
360 |
94,2 |
|
75 |
x |
Página CXXIX
Efetuando os cálculos, temos:
Portanto, a medida de comprimento aproximada do arco é .
3. As circunferências de centros A, B, C e D têm raios medindo , pois os pontos M, N, O e P são pontos médios dos lados , , e , respectivamente, e o lado do quadrado mede . Como os ângulos internos do quadrado são retos, os arcos e têm a mesma medida de comprimento dos arcos e . Assim, para calcular a medida de comprimento da linha vermelha, basta calcular a medida do comprimento da circunferência com centro em D e multiplicar por 2. Fazendo isso, temos:
Logo, a medida do comprimento da circunferência com centro em D é . Portanto, a medida de comprimento aproximada da linha vermelha é igual a .
4. A retas a e e são secantes em relação à circunferência, pois a cruzam em dois pontos; as retas b, c e d são tangentes em relação à circunferência, pois têm somente um ponto em comum com a circunferência e a reta f é exterior à circunferência, pois não apresenta pontos em comum com a circunferência.
5. Resposta pessoal. Sugestão de resposta: Com base nas vistas frontal, laterais e superior, vamos desenhar a figura geométrica correspondente utilizando a perspectiva central com dois pontos de fuga. Para isso, executamos os seguintes passos:
1º. Desenhe a linha do horizonte e represente os pontos de fuga e sobre ela. Abaixo da linha do horizonte, desenhe uma aresta da figura espacial, de modo que sua vista lateral esquerda fique à esquerda da aresta e a vista frontal fique à direita da aresta.

2º. Ligue as extremidades da aresta aos dois pontos de fuga.
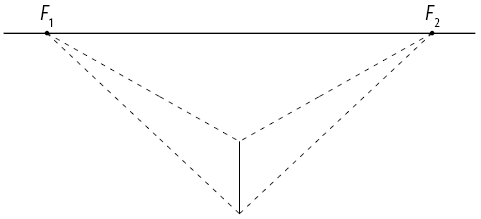
3º. Desenhe dois segmentos paralelos à aresta frontal com extremidades nas linhas traçadas no passo anterior. Em seguida, ligue as extremidades desses segmentos, conforme a imagem. Temos aqui as vistas laterais esquerda e direita.
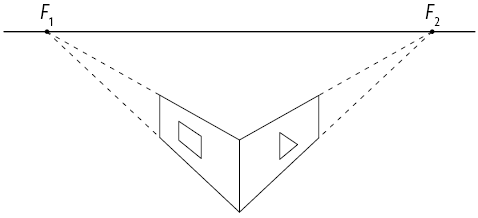
4º. Ligue as extremidades dos segmentos traçados no passo anterior até os pontos de fuga, conforme a imagem a seguir.
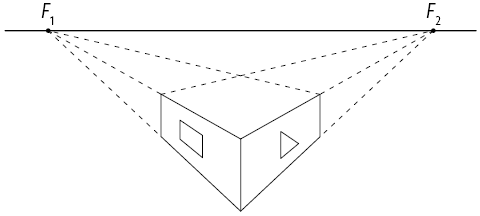
5º. Ligue os segmentos que representam as arestas do paralelepípedo reto retângulo.
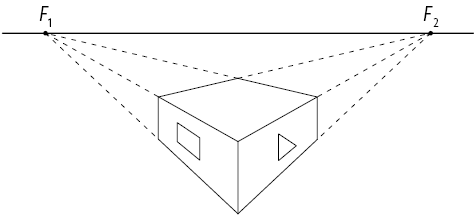
6º. Por fim, apague os demais elementos que não fazem parte da figura.