Página CXLI
Resoluções - parte 7
Unidade 12
Acréscimo, desconto e juro
Questão 1. Inicialmente, calculamos 8% de R$ 1.705,62.
Em seguida, adicionamos esse valor ao salário de abril, ou seja:
Por fim, calculamos o segundo aumento, ou seja, 8% de R$ 1.842,07, e adicionamos o valor obtido ao salário após o primeiro acréscimo.
Portanto, o salário de Adriana seria R$ 1.989,44.
Questão 2. Ao aplicarmos, sobre uma quantia x, dois acréscimos sucessivos de 8% cada, obtemos , pois: . Nesse caso, dois acréscimos sucessivos de 8% cada um equivalem a um único acréscimo de 16,64%.
Questão 3. Resposta pessoal. Sugestão de resposta: O cliente que paga à vista pode receber possíveis descontos, e essa opção de pagamento facilita o planejamento financeiro e reduz o risco de endividamento. A desvantagem é a possibilidade de parcelar o valor à vista e investir o dinheiro das parcelas.
Questão 4. Ao aplicarmos, sobre uma quantia x, dois descontos sucessivos de 14% e 5%, respectivamente, obtemos , pois: . Assim, esses descontos sucessivos equivalem a um único desconto de 18,3%, pois:
Questão 5. Ao aplicarmos, sobre uma quantia x, dois descontos sucessivos de 15% e 8%, respectivamente, obtemos , pois: . Assim, esses descontos sucessivos equivalem a um único desconto de 21,8%, pois:
Portanto, é melhor para o cliente um desconto único de 25%.
Atividades
1. Inicialmente, calculamos o acréscimo, ou seja, 8% de R$ 1.240,00.
Em seguida, adicionamos o valor obtido ao aluguel, ou seja:
Portanto, caso seja pago com 1 mês de atraso, o aluguel será R$ 1.339,20.
2. O valor do desconto é igual a . Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
15 |
100 |
|
6,9 |
x |
Portanto, o desconto aplicado é de 46%.
3. Inicialmente, calculamos o desconto aplicado na baixa temporada, ou seja, 25% de R$ 2.230,00.
Na sequência, subtraímos o valor obtido do preço da alta temporada, ou seja:
Portanto, um cliente vai pagar R$ 1.672,50 nesse pacote turístico na baixa temporada.
4. O valor do desconto é R$ 6,00, pois:
Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
40 |
100 |
|
6 |
x |
Portanto, o desconto aplicado foi de 15%.
5. O valor do aumento é R$ 270,00, pois:
Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
1.800 |
100 |
|
270 |
x |
Portanto, o aumento aplicado foi de 15%.
6. a) Seja x o preço do produto antes do aumento. Nesse caso, temos:
Portanto, o preço do produto antes do aumento era de R$ 42,00.
b) O valor do desconto é R$ 2,52, pois:
Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
44,52 |
100 |
|
2,52 |
x |
Portanto, foi aplicado desconto de, aproximadamente, 5,66%.
Página CXLII
7. Seja uma taxa de x% aplicada sobre o preço inicial do produto. Nesse caso, temos:
Isto significa que . Consequentemente:
Portanto, cada um dos aumentos foi de 10%.
8. a) Ao aplicarmos, sobre uma quantia x, dois descontos sucessivos de 12% cada, obtemos , pois: . Assim, esses descontos sucessivos equivalem a um desconto único de 22,56%, pois:
b) Ao aplicarmos, sobre uma quantia x, dois acréscimos sucessivos de 5% e 7,2%, respectivamente, obtemos , pois: . Assim, esses acréscimos sucessivos equivalem a um acréscimo único de 12,56%.
c) Ao aplicarmos, sobre uma quantia x, três descontos sucessivos de 2% cada um, obtemos , pois: . Assim, esses descontos sucessivos equivalem a um desconto único de 5,88%, pois:
d) Ao aplicarmos, sobre uma quantia x, três acréscimos sucessivos de 3% cada um, obtemos , pois: . Assim, esses acréscimos sucessivos equivalem a um acréscimo único de 9,2727%.
e) Ao aplicarmos, sobre uma quantia x, doze acréscimos sucessivos de 5% cada um, obtemos , pois: . Assim, esses acréscimos sucessivos equivalem a um acréscimo único de 79,59%.
9. Ao aplicarmos, sobre uma quantia x, dois acréscimos sucessivos de 20% e 30%, respectivamente, obtemos , pois: . Portanto, o aumento percentual dessa mercadoria nesse bimestre foi de 56%.
10. Com os dois descontos dados pela loja de Rafael, o jogo passará a custar R$ 207,86, pois:
Com o desconto dado pela loja de Francisco, o jogo passará a custar R$ 209,10, pois:
Portanto, é mais vantajoso comprar o jogo na loja de Rafael.
11. Com os dois descontos dados pela loja, o preço à vista do smartphone será R$ 1.691,28, pois:
12. Com o desconto de 20%, o produto que custava R$ 50,00 passará a custar R$ 40,00, pois:
Com o desconto do cartão fidelidade, o produto custará R$ 36,00, pois:
Portanto, para o cliente que tem o cartão fidelidade, a economia adicional é de R$ 4,00 (). A alternativa correta é a e.
13. Resposta pessoal. Sugestão de resposta:
a) Supondo que foram aplicados dois acréscimos sucessivos de 10% e 15%, respectivamente, qual é o novo preço do caderno?
b) Determine o aumento percentual do preço do caderno, após os dois acréscimos sucessivos.
Resposta: a) R$ 26,57; b) 26,5%.
14. Nessa aplicação foi obtido juro de R$ 585,00, pois:
15. O período de 1 ano e 6 meses é equivalente a 18 meses. O montante obtido nessa aplicação é de R$ 2.448,00, pois:
16. a) No regime de juro simples, o rendimento será de R$ 352,00, pois:
Agora, calculamos o rendimento no regime de juro composto.
Nesse sistema, o rendimento é de R$ 366,08, pois:
Portanto, no sistema de juro simples o rendimento é de R$ 352,00 e no de juro composto, R$ 366,08.
b) A diferença entre os rendimentos dessas duas aplicações é de R$ 14,08, pois:
17. O montante obtido por Fernanda é igual a R$ 1.500,04, pois:
18. O montante pago ao banco é igual a R$ 1.177,58, pois:
19. Para determinar a alternativa correta, vamos calcular o montante obtido por Jaime ao final de cada mês.
Montante obtido ao final do 1º mês de aplicação.
Montante obtido ao final do 2º mês de aplicação.
Página CXLIII
Montante obtido ao final do 3º mês de aplicação.
Montante obtido ao final do 4º mês de aplicação.
Montante obtido ao final do 5º mês de aplicação.
Montante obtido ao final do 6º mês de aplicação.
Montante obtido ao final do 7º mês de aplicação.
Analisando os montantes, concluímos que Jaime deve deixar a quantia aplicada por seis meses, e sobrarão menos de R$ 100,00. Portanto, a alternativa correta é a d.
20. Utilizando procedimentos semelhantes aos apresentados na seção Instrumentos e softwares, obtemos:
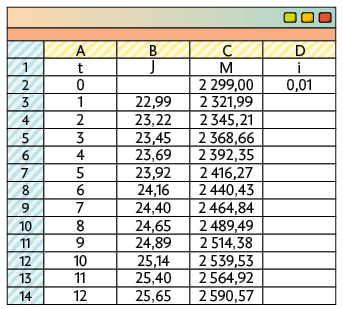
Portanto, Mariana irá pagar R$ 2.590,57 por esse notebook.
21. Para resolver essa atividade, consideramos, sem perda de generalidade, que Armando vai aplicar R$ 2.299,00. Utilizando procedimentos semelhantes aos apresentados na seção Instrumentos e softwares, determinaremos o montante obtido em cada um dos investimentos.
Investimento A.
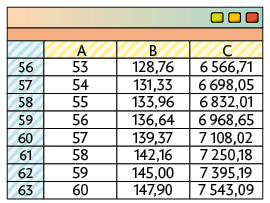
Investimento B.
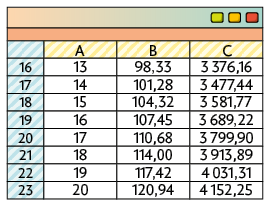
Investimento C.
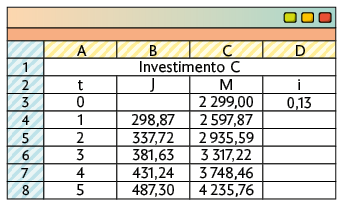
Portanto, o investimento A é o mais vantajoso.
22. O valor total pago a prazo é igual a R$ 1.377,27, pois:
Assim, a diferença entre o valor à vista e o valor total pago a prazo é R$ 78,27, pois:
23. a) Depois do 1º mês, o valor do montante é R$ 105,00, isso representa um aumento de R$ 5,00 sobre o capital de R$ 100,00. Portanto, a taxa de juro é igual a 5% ao mês.
b) No 10º mês, a diferença entre os montantes é R$ 12,89, pois:
c) Resposta pessoal. Sugestão de resposta: Qual será, ao final do 12º mês, o montante obtido no regime de juro simples? E no regime de juro composto? Resposta: R$ 160,00; R$ 179,59.
24. a) O capital aplicado é o valor no tempo 0, isto é, R$ 500,00.
b) Depois do 1º mês, o valor do montante é R$ 515,00, o que representa um aumento de R$ 15,00 sobre o capital de R$ 500,00. Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
500 |
100 |
|
15 |
x |
Portanto, a taxa de juro é de 3% ao mês.
c) O montante dessa aplicação ao final do 8º mês é igual a R$ 633,39.
d) O montante dessa aplicação ao final do 11º mês é R$ 692,12, pois:
25. Pagando R$ 90,00 no ato da compra, faltará pagar R$ 80,00, pois:
Como depois de um mês, o valor pago será de R$ 90,00, o juro correspondente é de R$ 10,00. Aplicando uma regra de três, temos:
Página CXLIV
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
80 |
100 |
|
10 |
x |
Portanto, a taxa de juro mensal é 12,5%.
26. Sendo x% a taxa de juro, temos:
Portanto, a taxa de juro mensal é 4,5%.
27. Utilizando procedimentos semelhantes aos apresentados na seção Instrumentos e softwares e adicionando uma coluna que apresenta o juro acumulado recebido, temos:
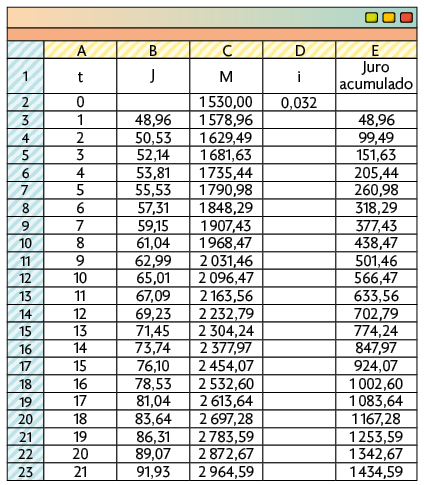
Portanto, o capital deve ficar aplicado por 20 meses.
28. Utilizando procedimentos semelhantes aos apresentados na seção Instrumentos e softwares e adicionando uma coluna que apresenta o juro acumulado recebido, temos:
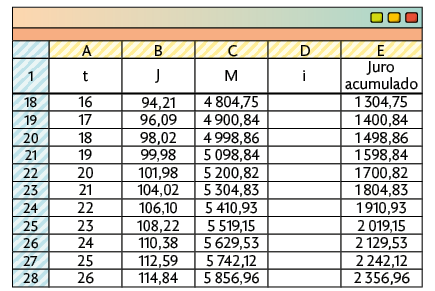
Portanto, o capital deve ficar aplicado por 24 meses, ou seja, 2 anos.
O que eu estudei?
1. Seja x o preço do produto. Nesse caso, temos:
Portanto, o preço a prazo apresenta um acréscimo de aproximadamente 8,7%.
2. Nessa compra, Adalberto gastou R$ 600,00, pois: . Com o aumento de 20%, o quilograma de carne passou a custar R$ 48,00. Dividindo o valor gasto pelo novo preço do quilograma, obtemos:
Portanto, Adalberto pôde comprar . A alternativa correta é a e.
3. Seja x o preço cobrado pelo livro antes do acréscimo. Assim:
Portanto, o valor do livro antes do acréscimo era de R$ 45,00.
4. Inicialmente, determinamos a mensalidade que Giovana pagou em cada um dos anos.
1º ano: R$ 250,00.
2º ano: R$ 300,00, pois .
3º ano: R$ 360,00, pois .
4º ano: R$ 432,00, pois .
Desse modo, o total pago por ela é:
A alternativa correta é a d.
5. Com o aumento de 15%, o preço do tênis passou a ser R$ 207,00, pois:
Com o desconto de 22%, o tênis custará R$ 161,46, pois:
6. Com os descontos sucessivos de 20% e 5%, o valor da mensalidade passou a ser R$ 94,24, pois:
7. Ao final do 6º mês o montante obtido será R$ 637,83, pois:
8. Indicando o capital inicial por C e a quantidade de meses transcorridos para a duplicação do capital por x, temos:
Portanto, para duplicar o capital aplicado deverão ser transcorridos 25 meses ou 2 anos e 1 mês.
Página CXLV
9. Seja x a quantidade de meses que Olívia deixou o capital aplicado. Assim:
Portanto, Olívia retirou esse montante ao final do 7º mês.
10. Sendo o valor de entrada 50% do valor à vista, restará pagar os outros 50%, que correspondem a R$ 932,75, pois:
Como após um mês será pago o valor de R$ 993,38, o juro é de R$ 60,63, pois:
Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
932,75 |
100 |
|
60,63 |
x |
Portanto, a taxa de juro mensal cobrada na compra a prazo é de aproximadamente 6,5%.
11. O preço a prazo é R$ 1.558,70, pois . A diferença entre o preço a prazo e o preço à vista é dada por:
Aplicando uma regra de três, temos:
|
Quantia (R$) |
Porcentagem (%) |
|---|---|
|
1.199 |
100 |
|
359,70 |
x |
Portanto, o aumento percentual no preço a prazo, quando comparado ao preço à vista, é de 30%.
12. O rendimento será de R$ 63,41, pois: .
13. a) No investimento A, após o 1º mês, há um juro de R$ 55,00 sobre o capital de R$ 1.000,00. Isto representa uma taxa de juro de 5,5% ao mês. No investimento B, após o 1º mês, há um juro de R$ 60,00 sobre o capital de R$ 1.000,00. Isto representa uma taxa de juro de 6% ao mês.
b) Após 2 meses, o investimento mais rentável é o B. Após 6 meses, o investimento mais rentável é o A.
c) A partir de 5 meses.
d) No 5º mês, a diferença entre os montantes dos investimentos é de R$ 6,96, pois:
O que eu aprendi?
1. Resposta no final da seção Resoluções.
2. Em a luz percorre , e em a luz percorre , ou seja, . Além disso, a distância média entre o Sol e a Terra mede aproximadamente .
Esta medida de distância pode ser reescrita como . Assim:
Portanto, a luz do Sol demora aproximadamente para chegar à Terra.
3. equivale a . Assim, equivale a .
Desse modo, a razão é dada por:
Portanto a alternativa correta é a e.
4. Inicialmente, devemos obter a medida da hipotenusa do triângulo :
Logo, a hipotenusa do triângulo maior mede .
A medida do comprimento do lado é dada pela subtração da medida do comprimento da base do triângulo maior pela medida do comprimento da base do triângulo menor:
.
Analisando os ângulos internos do triângulo menor , notamos que ele é semelhante ao triângulo maior . Assim, considerando em relação ao triângulo menor , a medida da altura como x e hipotenusa como z, e como y, temos:
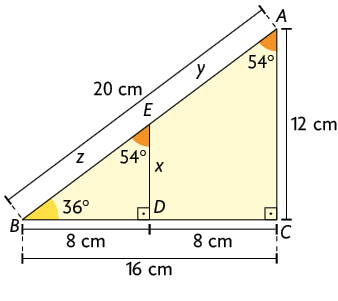
Assim, utilizando a proporcionalidade temos , em que:
Página CXLVI
Logo, a altura menor do quadrilátero mede .
Subtraindo a medida da hipotenusa do triângulo maior da medida da hipotenusa do ângulo menor, temos o lado do quadrilátero, Assim:
Calculando a medida do perímetro do quadrilátero , temos:
Portanto, a medida do perímetro do quadrilátero é .
5.
Assim, ao simplificarmos a expressão, obtemos 9 como resultado.
Portanto, a resposta correta é a alternativa d.
6. Inicialmente, devemos calcular a medida do comprimento da altura do triângulo. Assim, como , temos:
Considerando a medida da base do triângulo como y, temos:
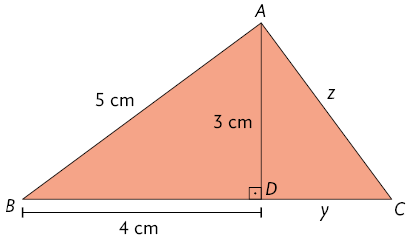
Utilizando uma das relações métricas, temos:
ou
Calculando a medida da área do triângulo, temos:
Logo, a área do triângulo mede .
7. a) As coordenadas dos vértices desse retângulo são , , e .
b) Como , temos:
Portanto, a medida do comprimento da diagonal do retângulo é unidades de comprimento.
8. O ângulo suplementar de é e o ângulo suplementar de é .
Além disso, representa a soma dos ângulos alternos internos dos ângulos suplementares e . Assim:
Portanto, o ângulo mede .
9. a) De 1 e 40 existem 20 números ímpares.
Assim, a proporção é dada por e a probabilidade é de
Ou seja, 40%.
O desconto será de 5%. Desse modo:
Logo, calculando quantos reais o estudante vai pagar, temos:
Ou seja, R$ 21,85.
b) 3 estudantes obtiveram um desconto de 5% e 1 estudante não obteve desconto. Assim, como não há reposição, o quinto estudante não poderá sortear os 4 números já sorteados.
Como , ele poderá sortear um dos 46 números possíveis.
Além disso, existe apenas 1 número que é par e primo: o número 2. Assim, a proporção será de , que pode ser escrita como .
Ou seja, a probabilidade de sortear um número par e primo é de 2,17%.
Página CXLVII
Com um desconto de 50%, o estudante pagará metade da compra, pois:
Portanto o estudante pagará R$ 18,75.
10. Resposta pessoal. Sugestão de resposta: No gráfico de linhas, podemos ter uma noção mais clara da variação dos dados ao verificar a continuidade das linhas e sua tendência de crescimento ou decrescimento, enquanto no gráfico de setores não temos a noção de continuidade, apenas a proporção entre os dados.
11. a) Como , então:
b) Como , então:
c) Como , então:
Resoluções referentes à unidade 1.
5. Analisando as posições indicadas na reta com letras, verificamos que A está mais próximo de 1 do que B. Dos números apresentados, o mais próximo de 1 é 1,3. Sendo assim, .
Como e a letra B está logo na sequência de A e antes do 2, concluímos que .
Como e, dos números apresentados, temos , então .
Além disso, verificamos que e . Sendo assim, .
Por fim, como e , concluímos que .

6. Representando os números na forma decimal, verificamos que , e . Usando essa representação, podemos localizá-los com mais facilidade na reta numérica.

Resoluções referentes à seção O que eu estudei? da unidade 1.
4. a) Primeiro, representamos cada número na forma decimal. Assim, temos:
; ; .
Em seguida, identificamos a letra correspondente a cada número na reta numérica para substituí-lo.
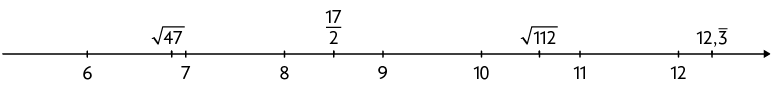
b) Como apenas um dos números não está representado na forma decimal, fazemos primeiro essa conversão.
Em seguida, identificamos a letra correspondente a cada número na reta numérica para substituí-lo.
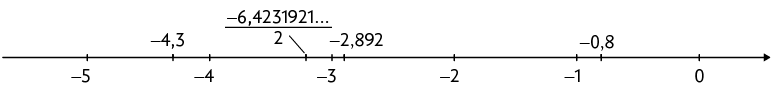
5. Primeiro, obtemos a representação de cada número na forma decimal.
; ; ; .
Página CXLVIII
Em seguida, identificamos sua localização aproximada na reta numérica.
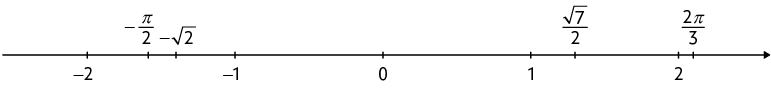
Resoluções referentes à unidade 5.
68. f) Calculando o mmc entre os denominadores da equação: . Assim:
Resolvendo essa equação obtemos e .
Como os valores obtidos são diferentes de , as raízes da equação são e .
g) Calculando o mmc entre os denominadores da equação: . Assim:
Essa equação não tem raízes reais.
Resoluções referentes à unidade 9.
51. b)
d)
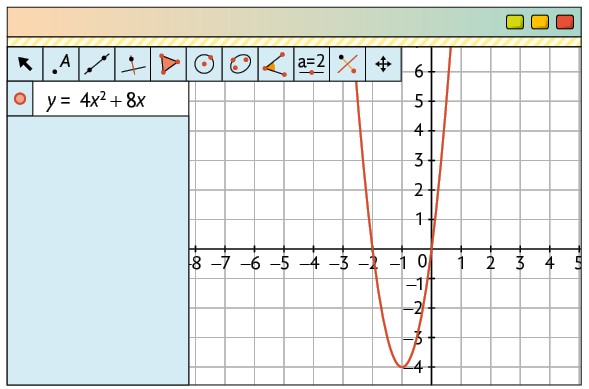
Página CXLIX
e)
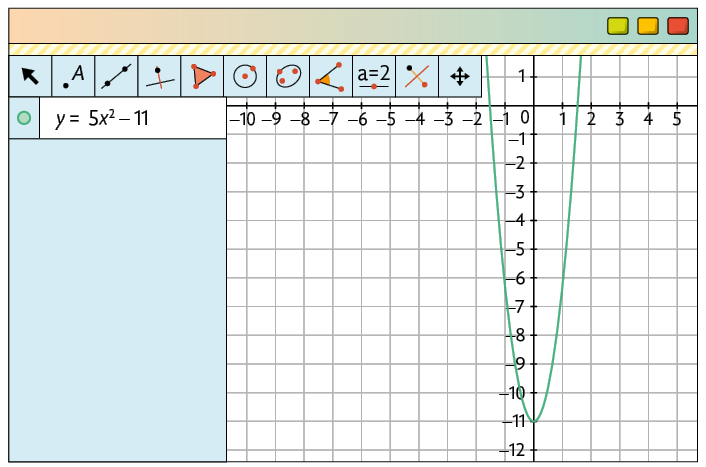
f)
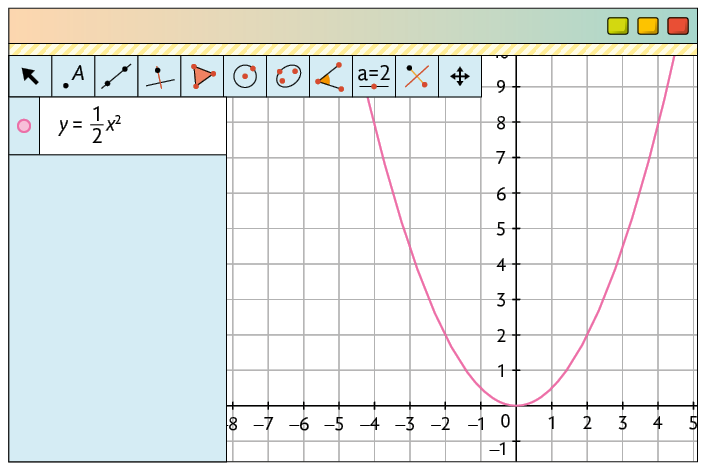
g)
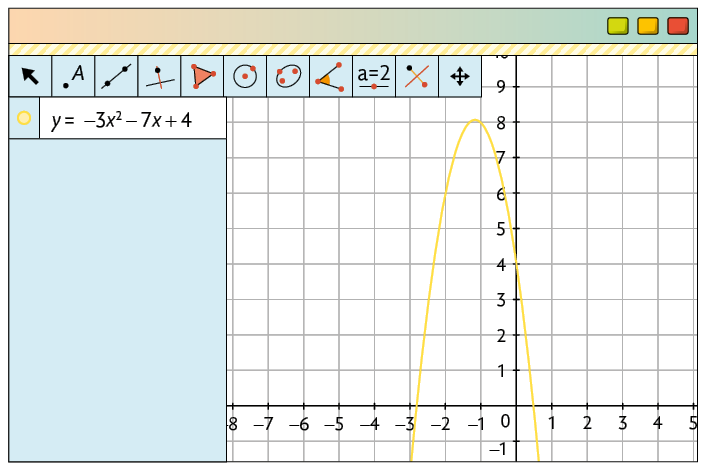
Página CL
h)
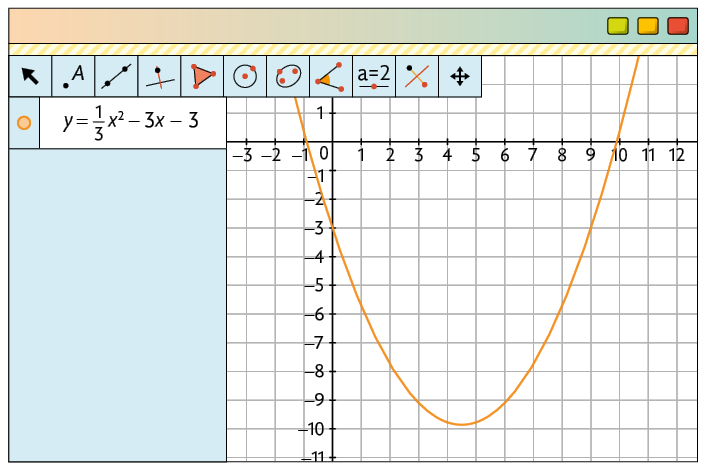
i)
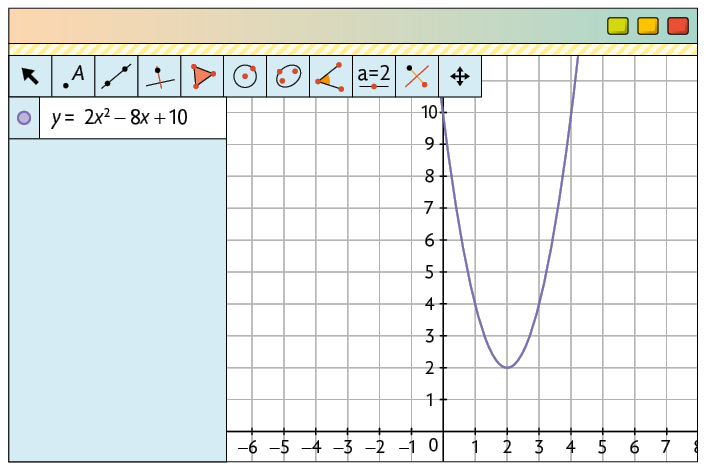
j)
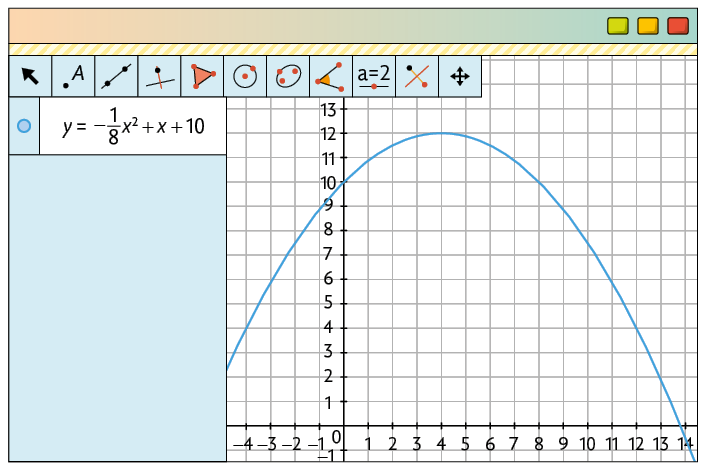
Página CLI
k)
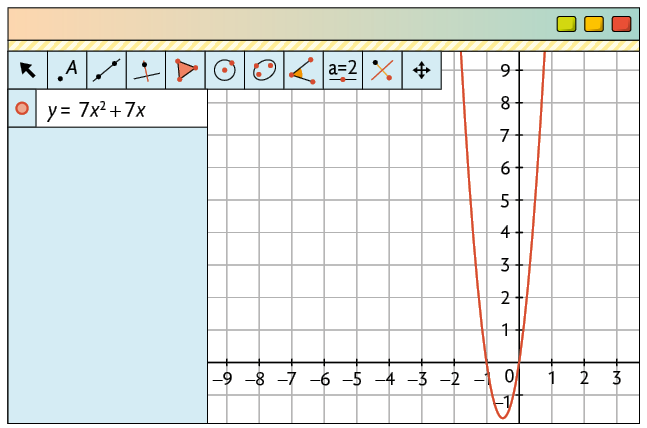
l)
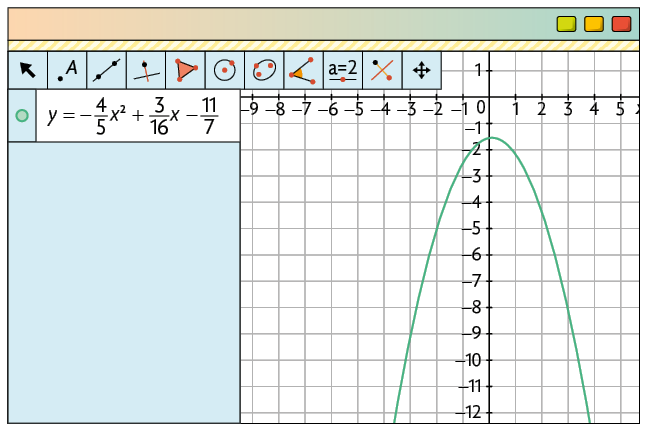
Resoluções referentes à unidade 10.
Questão 5.
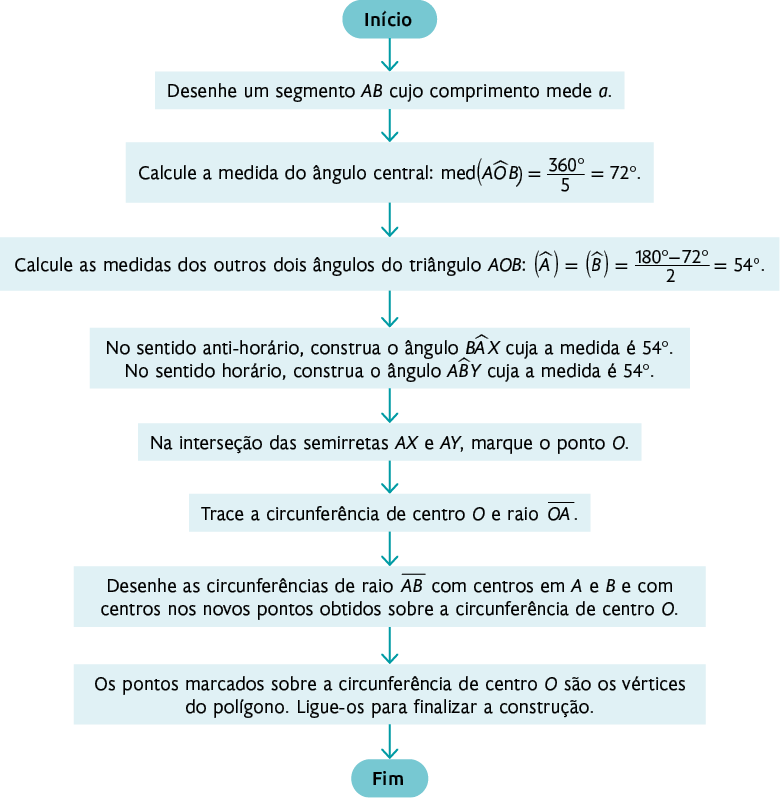
Início
1. Desenhe um segmento cujo comprimento mede a.
2. Calcule a medida do ângulo central: .
3. Calcule as medidas dos outros dois ângulos do triângulo : .
4. No sentido anti-horário, construa o ângulo cuja a medida é . No sentido horário, construa o ângulo cuja medida é .
5. Na interseção das semirretas e , marque o ponto O.
6. Trace a circunferência de centro O e raio .
7. Desenhe as circunferências de raio com centros em A e B e com centros nos novos pontos obtidos sobre a circunferência de centro O.
8. Os pontos marcados sobre a circunferência de centro O são os vértices do polígono. Ligue-os para finalizar a construção.
Fim
Página CLII
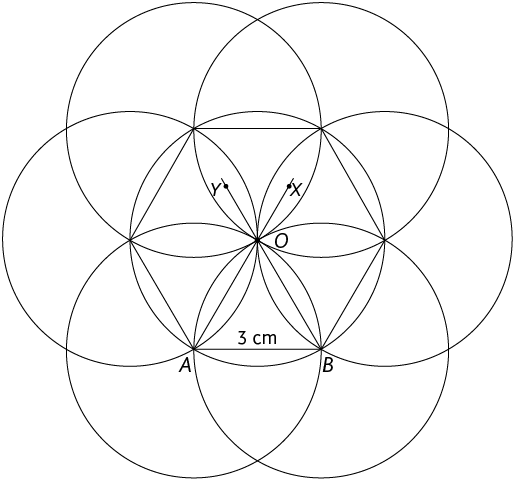
37. Para construir um hexágono regular com o comprimento do lado medindo , siga as etapas a seguir.
1º. Desenhe um segmento cujo comprimento mede .
2º. Calcule a medida do ângulo central, isto é, .
3º. Calcule as medidas dos dois outros ângulos do triângulo , .
4º. No sentido anti-horário, construa o ângulo cuja a medida é . No sentido horário, construa o ângulo cuja a medida é .
5º. Na interseção das semirretas e , marque o ponto O.
6º. Em seguida, trace a circunferência de centro O e raio .
7º. Desenhe as circunferências de raio com centros em A e B e com centros nos novos pontos obtidos sobre a circunferência de centro O.
8º. Os pontos marcados sobre a circunferência de centro O são os vértices do polígono. Por fim, ligue-os para finalizar a construção.
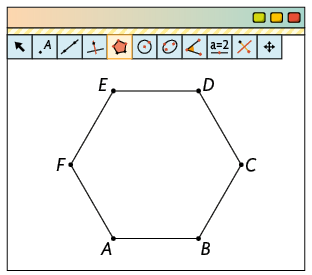
Página CLIII
Para construir um hexágono regular com lado medindo no GeoGebra, execute as etapas a seguir.
1º. Com a ferramenta Segmento com Comprimento Fixo, clique em um ponto da malha e digite a medida do comprimento, ou seja, 3.
2º. Com a ferramenta Polígono Regular, clique nos pontos A e B e digite a quantidade de vértices do polígono, nesse caso, 6.
3º. O polígono construído tem o comprimento do lado medindo e 6 vértices.
Resoluções referentes à unidade 11.
17. Para realizar as conversões das medidas no Calc, devemos executar os passos a seguir.
1º Nas células A1, B1, C1, D1 e E1 do Calc, escreva "Medida em B", "Medida em KB", "Medida em MB", "Medida em GB" e "Medida em TB", respectivamente.
2º Na célula:
A2 digite , para converter a medida expressa em megabaites em baites;
D3 digite , para converter a medida expressa em megabaites em gigabaites;
D4 digite , para converter a medida expressa em megabaites em gigabaites;
B5 digite , para converter a medida expressa em megabaites em terabaites;
A6 digite , para converter a medida expressa em megabaites em baites;
E7 digite , para converter a medida expressa em megabaites em terabaites.
3º Por fim, digite os valores em megabaites nas células C2 até C7.
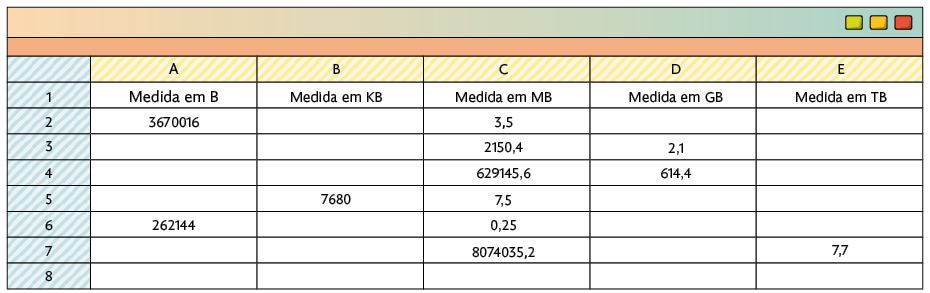
Assim, obtemos:
a) é igual a .
b) é igual a .
c) é igual a .
d) é igual a .
e) é igual a .
f) é igual a .
Resolução referente à seção O que eu aprendi.
1.
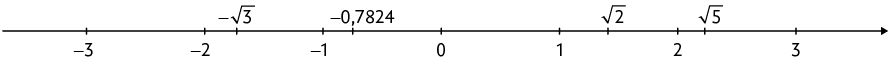
Analisando a reta numérica, temos: A: ; B: ; C: ; D: .