Página 13
UNIDADE
1
Os números reais

Agora vamos estudar...
- o conjunto dos números irracionais;
- alguns números irracionais;
- a representação geométrica de um número irracional;
- o conjunto dos números reais.
Página 14
Números irracionais
No ano anterior, estudamos o conjunto dos números racionais. Vimos que a representação decimal de um número racional pode ser finita ou infinita e que, no segundo caso, a representação se dá por meio de dízimas periódicas.
Porém, existem números que têm representações decimais infinitas e não periódicas, os quais são chamados números irracionais.
Analise alguns exemplos.
Os números irracionais não podem ser escritos na forma , com a e b inteiros e .
Questão 1. Realize uma pesquisa a respeito
do surgimento dos números
irracionais. Em seguida, apresente as informações que julgar interessante para a turma.
Resposta pessoal.
Atenção!
A pesquisa proposta na questão 1 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
O número irracional
Acompanhe o que a professora de Fábio está dizendo.


Para responder a essa pergunta, precisamos determinar um número que elevado ao quadrado resulte em 2. Nesse caso, segue que, em centímetros, a medida do comprimento do lado desse quadrado é expressa pelo número "raiz quadrada de 2", que é denotado por .
O número irracional
O número irracional (lê-se: pi) é definido como o quociente entre a medida do comprimento da circunferência de um círculo e a medida do comprimento de seu diâmetro.
Página 15
Representação geométrica
Agora, vamos representar o número irracional na reta numérica. Para isso, executaremos as etapas apresentadas a seguir.
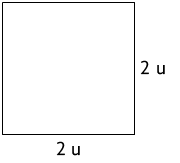
1ª. Construímos um quadrado cujo comprimento do lado mede 2 unidades ().
2ª. Em seguida, realizamos a decomposição desse quadrado em 4 quadrados com o comprimento do lado medindo , conforme apresentado na imagem a seguir.
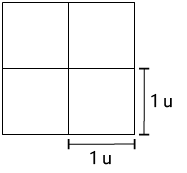
Cada um dos quadrados obtidos na 2ª etapa tem área medindo 1 unidade.
3ª. Traçamos as diagonais em cada um dos quadrados obtidos.
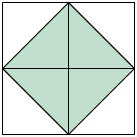
Cada um dos triângulos obtidos (destacados em verde) tem área medindo 0,5 unidade. Consequentemente, o quadrado em verde tem área medindo 2 unidades. Portanto, cada um de seus lados tem comprimento medindo .
4ª. Com o auxílio de um compasso, transportamos para a reta numérica a medida do comprimento do lado do quadrado em verde.
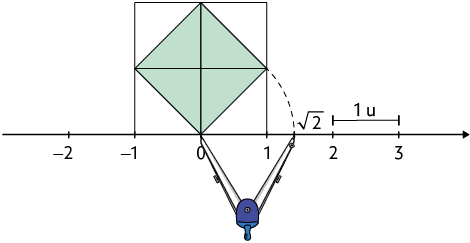
Questão 2. Junte-se a um colega e, de maneira semelhante à apresentada nesta página, representem na reta numérica o número irracional . Façam essa representação no caderno.
Resposta na seção Resoluções.
Página 16
Números reais
Reunindo todos os números racionais e todos os números irracionais, obtém-se o conjunto dos números reais, denotado por .
Atenção!
Um conjunto é um agrupamento qualquer de objetos distintos.


As operações com números reais satisfazem às mesmas propriedades referentes às operações com números racionais. Além disso, os procedimentos de comparação de números racionais se estendem aos números reais.
Podemos representar números reais em uma reta numérica. Analise alguns exemplos.
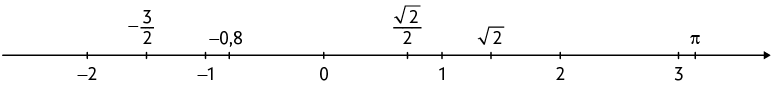
Podemos estimar a localização do número real na reta numérica.
O número está entre 1,3 e 1,4, porém mais próximo de 1,3. Nesse caso, na reta numérica, indicamos o ponto correspondente ao número entre 1,3 e 1,4, mais próximo de 1,3, conforme apresentado na imagem.

No tópico O número irracional , vimos que . Agora, vamos ver uma maneira de obter essa representação decimal. Sabemos que , então:
Página 17
Utilizando o mesmo procedimento, obtemos:
Sendo assim, verificamos que:
Atenção!
Para determinar o intervalo utilizado, efetuamos:
- ;
- ;
- ;
- ;
- .
Repetindo o procedimento, obtemos:
Logo:
.
Prosseguindo com esse procedimento, obtemos:
Atenção!
Para determinar o intervalo utilizado, efetuamos:
- ;
- .
Atividades
Faça as atividades no caderno.
1. Junte-se a um colega e escrevam quais procedimentos vocês utilizariam para representar o número na reta numérica. Em seguida, representem esse número na reta.
Resposta na seção Resoluções.
2. Entre os números apresentados a seguir, determine quais são irracionais.
-
5
-
-
2,45
-
-
1.045
-
12,4587
-
25
Resposta: , , , e .
3. Em seu caderno, obtenha a representação decimal, com 4 casas, do número irracional .
Resposta na seção Resoluções.
4. Qual número é maior: ou ?
Resposta: .
5. As letras indicadas na reta numérica representam números reais.

Os números correspondentes a cada uma dessas letras estão representados a seguir.
-
1,3
Em seu caderno, escreva a letra e o número correspondentes.
Resposta: , , , e .
6. Copie a reta numérica apresentada em seu caderno.

Em seguida, estime a localização dos números a seguir nessa reta.
Resposta na seção Resoluções.
Versão adaptada acessível
6. Junte-se a um colega e copiem a reta numérica apresentada.

Depois, estimem a localização dos números a seguir nessa reta.
Resposta na seção Resoluções.
Orientação para acessibilidade
Professor, professora: aproveite que os estudantes estarão organizados em duplas e instigue-os a desenvolver estratégias de estimativa. Se julgar necessário, estime a localização do número com eles. Por fim, após todos concluírem a atividade, organize uma roda de conversa para que as estratégias utilizadas sejam compartilhadas.
Página 18
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Copie em um folha de papel avulsa apenas os números irracionais apresentados a seguir.
-
5
Resposta: e .
2. Classifique as afirmações a seguir em verdadeira ou falsa. Em seguida, em uma folha de papel avulsa, reescreva as falsas corrigindo-as.
a) O número adicionado ao número 5 resulta em um número irracional.
Resposta: Falsa. Uma sugestão de correção é: O número adicionado ao número 5 resulta em um número racional.
b) O comprimento do lado de um quadrado de área medindo mede .
Resposta: Verdadeira.
c) Um número irracional é um número racional cuja representação decimal é infinita e não periódica.
Resposta: Falsa. Uma sugestão de correção é: Um número irracional é um número real cuja representação decimal é infinita e não periódica.
d) A representação decimal do número racional é .
Resposta: Falsa: Uma sugestão de correção é: A representação decimal do número irracional é .
e) Os números ; 2; 5,3458; ; e são exemplos de números reais.
Resposta: Verdadeira.
3. Copie as sentenças em uma folha de papel avulsa, substituindo cada pelo símbolo , ou
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
4. Em cada item, determine, entre os números indicados, aqueles correspondentes às letras apresentadas nas retas numéricas.
a) , , e .
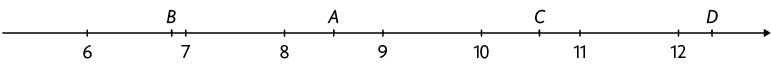
Resposta: , , e .
b) , , e .

Resposta: , , e .
5. Em uma folha de papel avulsa, copie a reta numérica apresentada.
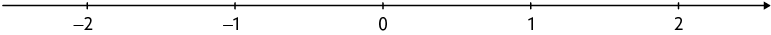
Em seguida, estime a localização dos seguintes números nessa reta.
Resposta na seção Resoluções.
Versão adaptada acessível
5. Junte-se a um colega e copiem a reta numérica apresentada.
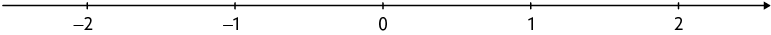
Depois, estimem a localização dos seguintes números nessa reta.
Resposta na seção Resoluções.
6. Em uma folha de papel avulsa, desenhe uma reta numérica. Em seguida, represente, nela, o número irracional .
Resposta na seção Resoluções.
Versão adaptada acessível
6. Explique para um colega os procedimentos utilizados por você para representar o número em uma reta numérica. Depois, com ele, representem esse número em uma reta numérica.
Resposta na seção Resoluções.