Página 151
UNIDADE
8
Algumas representações no plano cartesiano

Agora vamos estudar...
- medida da distância entre dois pontos no plano cartesiano;
- ponto médio de um segmento de reta;
- medida do perímetro e da área de figuras planas construídas no plano cartesiano.
Página 152
Medida da distância entre dois pontos no plano cartesiano
Imagine um plano cartesiano construído em uma malha quadriculada na qual estão indicados os pontos A e B, cujas coordenadas são diferentes. Considerando como unidade de medida o comprimento de cada lado dos quadradinhos da malha, traçamos um segmento AB que une os pontos A e B. A medida do comprimento desse segmento é igual à medida da distância entre os pontos A e B.
A seguir, vamos calcular a medida da distância entre dois pontos no plano cartesiano. Para isso, analisaremos inicialmente dois casos.
Abscissas iguais
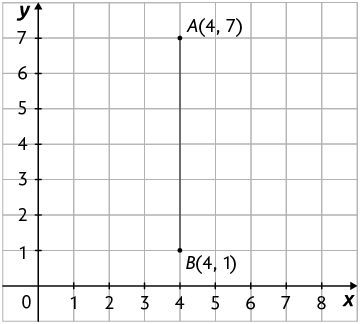
Atenção!
Nos planos cartesianos apresentados, considere como unidade de medida o comprimento de cada lado dos quadradinhos da malha.
Os pontos A e B têm abscissas iguais. Nesse caso, a medida da distância entre esses pontos é dada por , ou seja, 6 unidades de comprimento ().
Ordenadas iguais

Os pontos C e D têm ordenadas iguais. Nesse caso, a medida da distância entre esses pontos é dada por , ou seja,
E como fazer para determinar a medida da distância entre dois pontos que têm abscissas e ordenadas respectivamente diferentes?
Nesses casos, podemos utilizar o teorema de Pitágoras, assunto que você estudou na unidade 6 deste volume.
Página 153
Como exemplo, vamos calcular a medida da distância entre os pontos e no plano cartesiano. Para isso, vamos construir inicialmente um plano cartesiano na malha quadriculada, indicar esses pontos e traçar o segmento EF, cuja medida do comprimento é igual à medida da distância entre os pontos E e F.
Note que não é possível contar quantas unidades de comprimento há entre E e F, mas podemos determinar quantas unidades têm a projeção de no eixo x e no eixo y.

Indicando no plano cartesiano o ponto G, de forma que seja paralelo ao eixo x e que seja paralelo ao eixo y, obtemos o triângulo retângulo EFG, cujos catetos medem 4 e 3 unidades de comprimento.
Assim, para determinar a medida da distância entre E e F, calculamos a medida do comprimento da hipotenusa do triângulo retângulo EFG usando o teorema de Pitágoras.
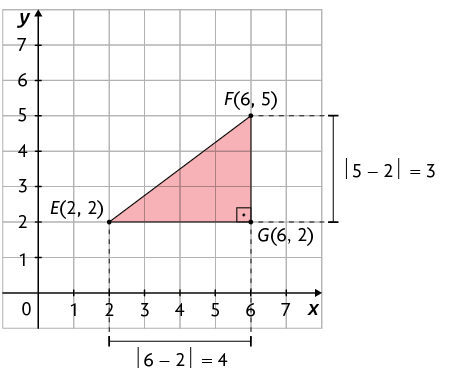
Portanto, a medida da distância entre os pontos E e F é 5 u.c.
Questão 1. Apresentamos, anteriormente, um
caso em que foi necessário
utilizar o teorema de Pitágoras para determinar a medida da distância entre
dois pontos no plano cartesiano e casos em que o teorema não foi necessário. Explique
a um colega por que isso ocorreu.
Resposta pessoal. Espera-se que os estudantes digam que, nos casos em que as abscissas ou as ordenadas dos pontos são iguais, é possível contar quantas unidades de comprimento há entre os pontos, bastando realizar a projeção nos eixos e efetuar uma subtração. Já no caso em que as abscissas ou as ordenadas dos pontos são respectivamente diferentes, é necessário utilizar o teorema de Pitágoras, pois não é possível contar quantas unidades de comprimento há entre os pontos.
Página 154
Medida da área e do perímetro de figuras planas construídas no plano cartesiano
De acordo com o que foi estudado até agora, vamos determinar a medida do perímetro e a medida da área de polígonos no plano cartesiano.
A seguir, apresentamos um retângulo e um triângulo retângulo no plano cartesiano.
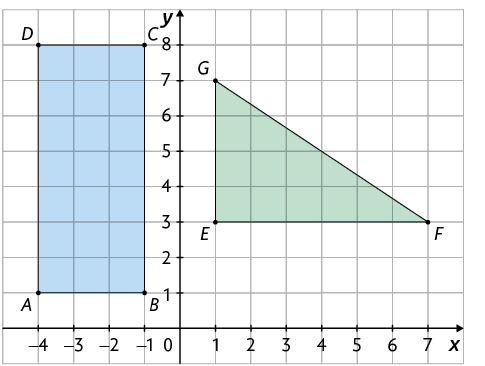
Atenção!
Note que as coordenadas dos vértices do retângulo são , , e e as coordenadas dos vértices do triângulo são , e .
Para calcular a medida do perímetro do triângulo, por exemplo, vamos determinar inicialmente a medida do comprimento de todos os lados.
Agora, calculamos a medida do perímetro P.
Conhecendo a medida do comprimento dos lados EF e EG, podemos calcular a medida da área A do triângulo retângulo da seguinte maneira:
Portanto, a medida do perímetro e a medida da área do triângulo são u.c. e 12 u.a. (unidades de área), respectivamente.
Questão 2. Utilizando os mesmos procedimentos apresentados, determine em seu caderno a medida da área e a medida do perímetro do retângulo representado no plano cartesiano.
Resposta: 21 unidades de área; 20 unidades de comprimento.
Página 155
Ponto médio de um segmento de reta
Analise o que Fábio está falando.

No plano cartesiano a seguir, está representado o segmento AB e seu ponto médio M.
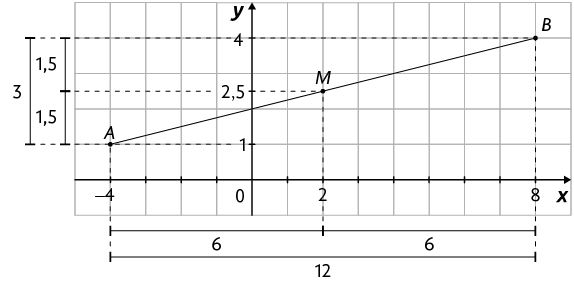
Quais são as coordenadas do ponto médio M do segmento AB?
Para responder a essa pergunta, vamos considerar as projeções do segmento AB nos eixos x e y e fazer a seguinte análise.
- Em relação ao eixo x, o valor 2 divide a projeção de em dois segmentos congruentes.
- Em relação ao eixo y, o valor 2,5 divide a projeção de em dois segmentos congruentes.
Portanto, as coordenadas do ponto médio do segmento AB são .
Questão 3. No caderno, determine as coordenadas do ponto médio do segmento CD indicado no plano cartesiano a seguir.

Resposta: .
Página 156
Atividades
Faça as atividades no caderno.
1. No plano cartesiano a seguir, foram dispostos alguns pontos.

a) Determine as coordenadas desses pontos.
b) Calcule a medida da distância entre a origem e cada um desses pontos.
Respostas: a) ; ; ; ; ; b) A: ; B: ; C: ; D: ; E:
2. Calcule a medida do perímetro de cada polígono a seguir.
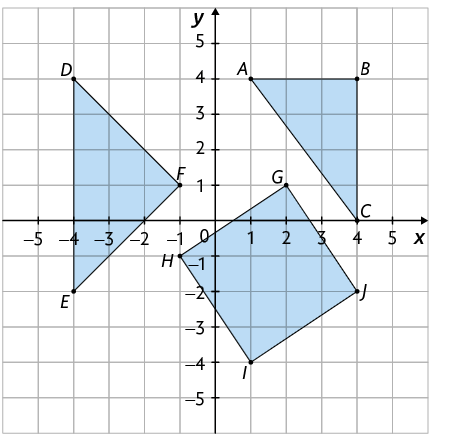
Resposta: ; ;
3. Sabendo que são as coordenadas do ponto médio de e , determine a medida do comprimento do segmento .
Resposta: 10 u.c.
4. A seguir, estão representados dois polígonos no plano cartesiano.
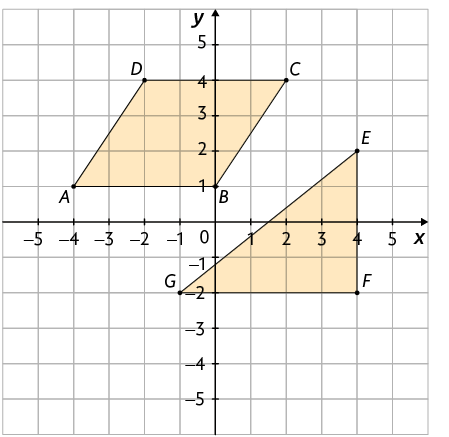
Calcule:
a) a medida do perímetro de cada polígono.
Resposta: ;
b) a medida da área de cada polígono.
Resposta: ;
5. Analise
o polígono a seguir.
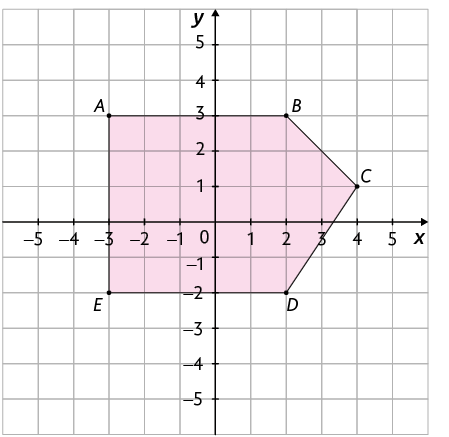
Agora, pense em uma estratégia para calcular a medida da área desse polígono e calcule essa medida.
Resposta:
Página 157
6. Considere o triângulo a seguir.
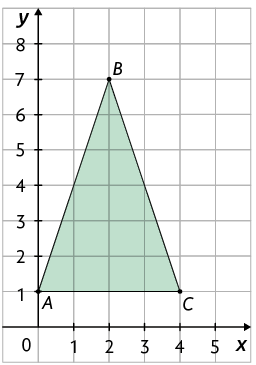
a) O triângulo é isósceles?
b) Determine as coordenadas dos pontos , e sabendo que:
- é o ponto médio do lado .
- é o ponto médio do lado .
- é o ponto médio do lado .
c) O triângulo é isósceles?
d) Calcule a medida da área e do perímetro dos triângulos e .
Respostas: a) Sim; b) ; ; ; c) Sim; d) ; ; ;
7. Os pontos , e são vértices de um triângulo em um plano cartesiano. Sabendo que esse triângulo é retângulo em B, responda às questões.
a) Esse triângulo é isósceles?
b) Calcule as medidas do perímetro e da área desse triângulo.
Respostas: a) Sim; b) ;
8. Se é a mediana relativa ao lado , calcule a medida do comprimento de .
Atenção!
Lembre-se de que a mediana é o segmento de reta em que uma das extremidades é um vértice do triângulo e a outra é o ponto médio do lado oposto a esse vértice. Sendo assim, para resolver esse problema, é necessário determinar inicialmente as coordenadas do ponto médio M do lado e, depois, calcular a medida da distância entre o vértice A do triângulo e o ponto médio do lado obtido.
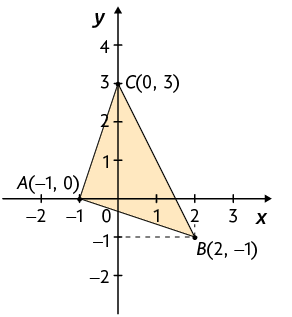
Resposta:
9. As localizações das casas de Alice e Bianca foram representadas pelos pontos A e B, respectivamente, no plano cartesiano a seguir.
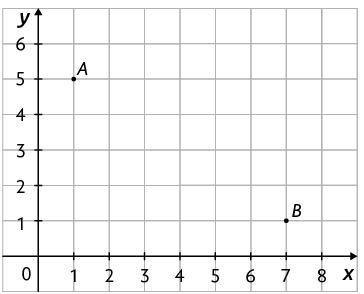
Se a escola em que elas estudam fica no ponto médio entre suas casas, calcule as coordenadas do ponto que representa a localização da escola nesse plano cartesiano.
Resposta:
10. Construa um plano cartesiano em uma malha quadriculada e elabore o enunciado de um problema que envolva o ponto médio de um segmento. Depois, troque com um colega para que ele o resolva. Por último, juntos, verifiquem se as respostas dos problemas estão corretas.
Resposta pessoal.
Página 158
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Alguns pontos foram marcados no plano cartesiano a seguir.

Calcule a medida da distância entre:
a) os pontos A e B.
b) os pontos A e C.
Respostas: a) 5 u.c.; b)
2. Determine as coordenadas do ponto médio de cada segmento de reta representado no plano cartesiano a seguir.

Resposta: ; ; ; .
3. Analise o paralelogramo a seguir.

a) Calcule a medida do comprimento das diagonais desse paralelogramo.
b) Calcule a medida da área desse paralelogramo.
Respostas: a) ; ; b)
4. Determine a medida da distância do ponto até o ponto:
a) .
b) .
c) .
Respostas: a) ; b) ; c)
5. Considerando os pontos A, B, C e D da atividade anterior, determine as coordenadas do ponto médio de , , e .
Resposta: : ; : ; : e .