Página 261

UNIDADE

Acréscimo, desconto e juro

Fotografia de uma rua de um conjunto residencial popular. Além da rua, aparecem várias casas iguais e uma ao lado da outra. — Modelo de conjunto residencial popular cuja aquisição individual está prevista mediante financiamentos à taxa baixa de juro.

Agora vamos estudar...

matemática financeira;
acréscimo e desconto;
juro simples e juro composto.

ORIENTAÇÕES AO PROFESSOR

A abertura da unidade apresenta imagem de um conjunto residencial, em que a aquisição de uma unidade habitacional normalmente se dá por meio de financiamento.

O objetivo é que os estudantes estabeleçam relação com os conteúdos que serão estudados na unidade, pois a taxa de juro de um financiamento imobiliário envolve diversos fatores, como valor do imóvel, quantidade de parcelas do financiamento, renda dos adquirentes etc. Assim, explora-se o uso da Matemática financeira no cotidiano, particularmente o conceito de juro.

Apresente aos estudantes outros contextos que envolvam taxa de juro, como o atraso no pagamento da fatura de cartão de crédito, compras parceladas e rendimento da caderneta de poupança.

Se achar necessário, faça questionamentos aos estudantes como os dos exemplos a seguir.

a) Você sabe o que é um financiamento bancário?

b) Você sabe o que é taxa de juro?

c) Em sua opinião, por que as pessoas optam por um financiamento bancário?

Metodologias ativas

Para desenvolver o trabalho com esta página de abertura, avalie a possibilidade de utilizar a metodologia ativa Abordagem por pares. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Sugestão de avaliação

A fim de avaliar o conhecimento prévio dos estudantes sobre os conteúdos que serão trabalhados na unidade, escreva na lousa o problema a seguir.

Certo produto custa R$ 120,00. Se for comprado à vista, seu valor cai para R$ 108,00. Qual é o valor do desconto, em percentual, se o pagamento desse produto for à vista?

Resolução e comentários

Inicialmente, calculamos o valor do desconto:

$120 menos 108 igual a 12$

Em seguida, calculamos a que percentual R$ 108,00 corresponde:

Desconto em um produto ao realizar o pagamento à vista
Quantia (R$)	Porcentagem (%)
120	100
108	x

$120 x igual a 100 vezes 108$

$x igual a início de fração, numerador: 10.800, denominador: 120, fim de fração igual a 90$

Assim, como o valor do produto pago à vista corresponde a 90% do preço total, o desconto corresponde a 10% $abre parênteses 100 menos 90 igual a 10 fecha parênteses$ .

Informações sobre avaliações podem ser encontradas no tópico Avaliação, nas orientações gerais deste manual.

Página 262

Matemática financeira

Um dos objetivos da Matemática financeira é estudar as variações do dinheiro em operações financeiras, como compras, vendas, aplicações, pagamentos e empréstimos. Operações como essas estão presentes e são muito utilizadas no dia a dia.

Nesta unidade, vamos estudar alguns assuntos da Matemática financeira, como descontos, acréscimos e juro. Analise as seguintes situações.

Fernanda comprou o televisor a seguir em 12 prestações iguais. Ela pagou um acréscimo por ter realizado a compra em prestações. Esse acréscimo é chamado juro e, nesse caso, foi calculado usando uma taxa de $0 vírgula 82 por cento ao mês$ (ao mês).

Imagens não proporcionais entre si.

Fotografia de um televisor de 32 polegadas. — Televisor de 32".

Promoção

À vista: R$ 1.250,00 ou em 12 vezes de R$ 109,80, sem entrada, com taxa de $0 vírgula 82 por cento ao mês$

Atenção!

Nesse caso, dizemos que a taxa percentual de acréscimo é 0,82% ao mês.

Fotografia de uma pessoa utilizando um caixa eletrônico em um banco. Ela está com uma das mãos à frente, esperando sair o comprovante da operação. — Pessoa usando o caixa eletrônico de um banco.

Anderson fez uma aplicação de R$ 900,00 em um banco. Após 1 mês, essa aplicação rendeu 0,7%. Assim, o valor aplicado por Anderson teve rendimento de R$ 6,30, que corresponde ao juro sobre o dinheiro que ele aplicou. Nesse caso, a taxa de juro foi de 0,7% ao mês.

Fotografia de três pessoas sentadas ao redor de uma mesa: um casal e uma gerente de banco. Ela aponta para algumas informações em um caderno sobre a mesa. — Pessoas fazendo cálculos referentes a um empréstimo.

Marcos fez um empréstimo de R$ 500,00 a uma taxa de juro de 5% ao mês. Após 1 mês, a dívida dele teve um acréscimo de R$ 25,00. Nesse caso, Marcos pagou um "aluguel" de R$ 25,00 pela medida do tempo que ficou com o dinheiro emprestado, ou seja, ele pagou um valor que corresponde aos 5% da taxa de juro.

Nas instituições financeiras, as taxas, por exemplo, são calculadas com o auxílio de cálculos estatísticos, Matemática financeira e porcentagem.

ORIENTAÇÕES AO PROFESSOR

Objetivos da unidade

Reconhecer e identificar operações financeiras no dia a dia.

Calcular acréscimos, descontos e juro.

Calcular porcentagens em situações do dia a dia.

Calcular acréscimos e descontos sucessivos em diferentes situações.

Resolver e elaborar situações-problema envolvendo acréscimos sucessivos e taxas percentuais.

Resolver e elaborar situações-problema envolvendo juro simples e juro composto.

Calcular a taxa de juro simples e de juro composto.

Justificativas

Os conteúdos abordados nesta unidade são relevantes para contribuir na formação dos estudantes referente à Matemática financeira, destacando situações que envolvem acréscimo, desconto, juro simples e composto.

Compreender Matemática financeira é importante para que, desde jovens, os estudantes adquiram hábitos de consumo adequado, responsável e consciente, além de saber escolher a melhor forma de pagamento na compra de um produto e calcular a taxa de juro em um empréstimo. Assim, espera-se capacitá-los para interpretar operações financeiras do cotidiano e compreendê-las com um olhar cada vez mais crítico.

Na situação A, avalie a conveniência de pedir aos estudantes que analisem os cálculos utilizando a Calculadora do Cidadão e confiram se o valor das parcelas está condizente ao que está no anúncio. Para isso, devem acessar o site do Banco Central do Brasil e clicar na opção Financiamento com prestações fixas. Nesse caso, a simulação consiste em inserir o número de meses (12), a taxa de juros (0,82) e o valor financiado (1.250). Feito isso, é só clicar em Calcular para obter o valor das prestações.

Disponível em: https://oeds.link/PdZYDe.

Acesso em: 4 ago. 2022.

O trabalho com os conteúdos desta unidade desenvolve a habilidade EF09MA05, ao levar os estudantes a resolver problemas que envolvem porcentagens e a elaborá-los, sempre com a ideia de aplicação de percentuais sucessivos e determinação das taxas percentuais, com e sem o uso de tecnologias digitais, no contexto da educação financeira.

Os dados apresentados nesta página sobre o televisor são fictícios.

Página 263

Acréscimo e desconto

Vamos estudar duas situações: uma envolvendo acréscimo e outra, desconto. Para isso, utilizaremos alguns conceitos relacionados à porcentagem, assunto que você provavelmente já estudou em anos anteriores.

Acompanhe a seguinte situação envolvendo acréscimos sucessivos.

O salário de Adriana sofreu dois reajustes durante dois meses consecutivos. No mês de abril, o salário dela era R$ 1.500,00 e sofreu um acréscimo de 8,5%. No mês de maio do mesmo ano, o salário teve outro acréscimo, cuja taxa percentual foi de 4,8%. Qual passou a ser o salário de Adriana após os dois acréscimos?

Fotografia de uma carteira de trabalho e previdência social, que está sendo segurada por uma pessoa. Na fotografia só aparece a mão da pessoa e a carteira. — Carteira de Trabalho e Previdência Social.

Atenção!

A Carteira de Trabalho e Previdência Social é um documento que registra a carreira profissional do trabalhador. Alterações salariais, bem como outras informações do trabalhador, são registradas nesse importante documento.

Para responder a essa pergunta, inicialmente, calculamos de quantos reais foi o primeiro acréscimo. Para isso, calculamos 8,5% de 1.500.

Atenção!

Podemos calcular 8,5% de 1.500 efetuando $0 vírgula 0 8 5 vezes 1.500$ , pois:

$início de fração, numerador: 8 vírgula 5, denominador: 100, fim de fração igual a 0 vírgula 0 8 5$

$0 vírgula 0 8 5 vezes 1.500 igual a 127 vírgula 5$

Em seguida, adicionamos esse valor ao salário de abril, ou seja:

$1.500 mais 127 vírgula 5 igual a 1.627 vírgula 5$

Por fim, calculamos o segundo aumento, ou seja, 4,8% de 1.627,5, e adicionamos o valor obtido ao salário após o primeiro acréscimo.

$0 vírgula 0 4 8 vezes 1.627 vírgula 5 igual a 78 vírgula 12$

$1.627 vírgula 5 mais 78 vírgula 12 igual a 1.705 vírgula 62$

Portanto, após os dois acréscimos, o salário de Adriana passou a ser R$ 1.705,62.

Os dois acréscimos no salário de Adriana equivalem a um único acréscimo de quantos por cento?

Para responder a essa pergunta, podemos usar regra de três.

Acréscimos no salário de Adriana
Quantia (R$)	Porcentagem (%)
1.500	100
$205 vírgula 62 que corresponde a 1.705 vírgula 62 menos 1.500$	x

$1.500 x igual a 100 vezes 205 vírgula 62$

$x igual a início de fração, numerador: 20.562, denominador: 1.500, fim de fração igual a 13 vírgula 708$

Portanto, dois acréscimos sucessivos de 8,5% e 4,8%, respectivamente, equivalem a um único acréscimo de 13,708%. Nesse caso, a porcentagem resultante é diferente da adição de 8,5% e 4,8%.

Página 264

Indicando por $P com índice 0$ o valor inicial e por $i com índice 1$ , $i com índice 2$ , $i com índice 3$ , $\dots$ , $i_{n}$ as taxas de acréscimos sucessivos na forma decimal, os valores obtidos após cada acréscimo, indicados por $P com índice 1$ , $P com índice 2$ , $P com índice 3$ , $\dots$ , $P_{n}$ , respectivamente, são dados por:

1º acréscimo

$A maiúsculo com índice 1 igual a P maiúsculo com índice 0 vezes i com índice 1$

$P com índice 1 igual a P com índice 0 mais A com índice 1$

2º acréscimo

$A com índice 2 igual a P com índice 1 vezes i com índice 2$

$P com índice 2 igual a P com índice 1 mais A com índice 2$

3º acréscimo

$A com índice 3 igual a P com índice 2 vezes i com índice 3$

$P com índice 3 igual a P com índice 2 mais A com índice 3$

$\dots$

enésimo acréscimo

$A com índice n igual a P com índice n menos 1 fim de índice vezes i com índice n$

$P com índice n igual a P com índice n menos 1 fim de índice mais A com índice n$

Atenção!

A indicação enésimo significa que ocupa a posição do número n; também pode ser escrito como n-ésimo.

Questão 1. Calcule no caderno qual seria o valor do salário de Adriana após os acréscimos, caso sofresse dois acréscimos sucessivos de 8% cada.

Resposta: R$ 1.989,44.

Questão 2. Responda no caderno: dois acréscimos sucessivos de 8% cada um equivalem a um único acréscimo de quantos por cento?

Resposta: 16,64%.

Agora, analise a seguinte situação envolvendo descontos sucessivos.

Uma loja está oferecendo um desconto de 14% na compra de certo modelo de notebook que custa R$ 2.850,00. Caso o pagamento seja à vista, a loja ainda concede um desconto de 5%, que é calculado após o desconto de 14%. Qual será o preço desse notebook se um cliente pagar à vista?

Fotografia de um notebook. — *Notebook.*

Para responder a essa pergunta, inicialmente, determinamos o preço do notebook com o desconto de 14%. Para isso, calculamos 14% de 2.850 e, em seguida, subtraímos a quantia obtida do preço inicial do produto.

$0 vírgula 14 vezes 2.850 igual a 399$

$2.850 menos 399 igual a 2.451$

Na sequência, calculamos o preço do notebook caso o cliente pague à vista. Para isso, calculamos 5% de 2.451 e, depois, subtraímos esse valor do preço do notebook após o primeiro desconto.

$0 vírgula 0 5 vezes 2.451 igual a 122 vírgula 55$

$2.451 menos 122 vírgula 55 igual a 2.328 vírgula 45$

Portanto, o preço à vista desse notebook é R$ 2.328,45.

Questão 3. Em sua opinião, quais são as vantagens e desvantagens de realizar um pagamento à vista? Por quê?

Resposta pessoal. Sugestão de resposta: O cliente que paga à vista pode receber possíveis descontos, e essa opção de pagamento facilita o planejamento financeiro e reduz o risco de endividamento. A desvantagem de realizar um pagamento à vista é a possibilidade de parcelar o valor à vista e investir o dinheiro das parcelas.

Questão 4. Responda no caderno: dois descontos sucessivos de 14% e 5%, respectivamente, equivalem a um único desconto de quantos por cento?

Resposta: 18,3%.

ORIENTAÇÕES AO PROFESSOR

Nas fórmulas indicadas no topo desta página, explique aos estudantes que $A com índice 1$ , $A com índice 2$ , $A com índice 3$ , ..., $A_{n}$ indicam os valores de cada acréscimo.

As questões 1 e 2 abordam acréscimos sucessivos. Se necessário, diga aos estudantes que acréscimos sucessivos ocorrem quando cada acréscimo acontece em um momento diferente. Além disso, deixa de ocorrer sobre o valor inicial e passa a ocorrer sobre o valor anterior.

Na questão 3, caso julgue necessário, ressalte aos estudantes a importância de programar para fazer a aquisição de algo, realizando o pagamento à vista e reduzindo o risco de endividamento. Desse modo, aborda-se o tema contemporâneo transversal Educação financeira.

Metodologias ativas

Para desenvolver o trabalho com a questão 3, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Na questão 4, chame a atenção dos estudantes para o fato de a resposta não ser 19% e verifique se todos chegam à mesma conclusão: que os 19% de desconto não acontece pelo fato de os descontos serem sucessivos, ou seja, aplicar dois descontos sucessivos de 14% e 5% equivale a multiplicar por $abre parênteses 1 menos 0 vírgula 14 fecha parênteses abre parênteses 1 menos 0 vírgula 0 5 fecha parênteses igual a 0 vírgula 817$ , isto é, um desconto de 18,3% $abre parênteses 100 menos 81 vírgula 7 fecha parênteses$ .

Página 265

Indicando por $P com índice 0$ o valor inicial e por $i com índice 1$ , $i com índice 2$ , $i com índice 3$ , $\dots$ , $i_{n}$ as taxas de descontos sucessivos na forma decimal, os valores obtidos após cada desconto, indicados por $P com índice 1$ , $P com índice 2$ , $P com índice 3$ , $\dots$ , $P_{n}$ , respectivamente, são dados por:

1º desconto

$D maiúsculo com índice 1 igual a P maiúsculo com índice 0 vezes i com índice 1$

$P com índice 1 igual a P com índice 0 menos D com índice 1$

2º desconto

$D com índice 2 igual a P com índice 1 vezes i com índice 2$

$P com índice 2 igual a P com índice 1 menos D com índice 2$

3º desconto

$D com índice 3 igual a P com índice 2 vezes i com índice 3$

$P com índice 3 igual a P com índice 2 menos D com índice 3$

$\dots$

enésimo desconto

$D com índice n igual a P com índice n menos 1 fim de índice vezes i com índice n$

$P com índice n igual a P com índice n menos 1 fim de índice menos D com índice n$

Questão 5. O que vai custar menos a um cliente na compra de um produto: dois descontos sucessivos, um de 15% e outro de 8%, respectivamente, ou um único desconto de 25%? Justifique sua resposta.

Resposta: Um único desconto de 25%.

Atividades

Faça as atividades no caderno.

1. O aluguel de um imóvel residencial é R$ 1.240,00 ao mês. Para pagamento em atraso, após 1 mês, esse valor sofre um acréscimo de 8%. Qual é o valor desse aluguel ao ser pago com 1 mês de atraso?

Resposta: R$ 1.339,20.

2. Em certo cinema, o ingresso custa R$ 15,00. Às segundas-feiras e quartas-feiras, é feita uma promoção, na qual os ingressos são vendidos a R$ 8,10. Qual é o desconto percentual aplicado sobre o preço do ingresso nesses dias?

Resposta: 46%.

3. Uma das atividades de grande importância para uma localidade é o turismo, pois contribui para a economia e gera empregos. Na alta temporada, uma agência de viagens vendeu pacotes turísticos para a praia de Porto de Galinhas, em Pernambuco, por R$ 2.230,00 cada um. Já na baixa temporada, a agência concedeu desconto de 25% sobre o preço da alta temporada. Quanto um cliente vai pagar nesse pacote turístico na baixa temporada?

Resposta: R$ 1.672,50.

4. Uma camiseta que custava R$ 40,00 foi comprada por R$ 34,00. De quanto foi o desconto percentual?

Resposta: 15%.

5. O salário de Clóvis era R$ 1.800,00 e, após um reajuste, ele passou a receber R$ 2.070,00. De quanto foi o aumento percentual?

Resposta: 15%.

6. Em abril, certa loja aumentou o preço de venda de um de seus produtos em 6%, passando a vendê-lo por R$ 44,52. Com esse acréscimo, as vendas diminuíram. Por isso, em setembro do mesmo ano, o gerente da loja resolveu comercializar o produto pelo antigo preço, ou seja, antes do aumento de 6%.

a) Determine o preço do produto antes do aumento.

b) De quantos por cento foi o desconto aplicado sobre o preço do produto em setembro?

Respostas: a) R$ 42,00; b) Aproximadamente 5,66%.

7. O preço de um produto sofreu aumentos mensais constantes durante 2 meses. Sabendo que, antes desses aumentos, o produto custava R$ 100,00 e que, após os 2 aumentos, ele passou a custar R$ 121,00, determine de quantos por cento foi cada um desses aumentos.

Resposta: 10%.

ORIENTAÇÕES AO PROFESSOR

Na questão 5, promova uma conversa em sala de aula e peça aos estudantes que expressem suas opiniões. Se achar necessário, explore os cálculos, resolvendo-os na lousa.

Metodologias ativas

Ao trabalhar com as atividades desta unidade, avalie a possibilidade de utilizar a metodologia ativa Pensar-conversar-compartilhar. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

O trabalho com os conteúdos desta unidade favorecem o desenvolvimento da Competência geral 6, por promover autonomia e capacitar os estudantes a fazer escolhas alinhadas à cidadania, contribuindo para que se tornem consumidores responsáveis, agindo com criticidade.

Na atividade 1, diga aos estudantes que é possível calcular 8% de $1.240$ efetuando $0 vírgula 0 8 vezes 1.240$ , pois $início de fração, numerador: 8, denominador: 100, fim de fração igual a 0 vírgula 0 8$ .

A atividade 2 se relaciona com as culturas juvenis ao explorar o tema cinema. Aproveite esse momento e promova um diálogo perguntando aos estudantes se eles têm o hábito de ir ao cinema e de que gênero de filme gostam mais. Obtenha informações sobre culturas juvenis nas orientações gerais deste manual.

As atividades 3 e 4 abordam descontos sobre o preço de um produto. Converse com os estudantes perguntando se, ao comprar determinado produto, eles têm o hábito de procurar estabelecimentos que oferecem descontos. Diga que o acesso à internet permite pesquisas de preços de forma rápida, principalmente em lojas on-line, o que contribui para a economia de dinheiro.

Caso os estudantes apresentem dificuldades nas resoluções das atividades 5 e 6, sugira que utilizem a regra de três.

Se achar necessário, explore a resolução do item b da atividade 6 na lousa, de modo que os estudantes percebam que a porcentagem do desconto não é a mesma porcentagem do aumento, e que isso acontece porque são diferentes os valores sobre os quais se calculam as porcentagens.

Na atividade 7, para sanar possíveis dúvidas, explique aos estudantes que podemos denominar o percentual procurado por x e utilizar a expressão $100 vezes abre parênteses 1 mais início de fração, numerador: x, denominador: 100, fim de fração fecha parênteses vezes abre parênteses 1 mais início de fração, numerador: x, denominador: 100, fim de fração fecha parênteses igual a 121$ para obtê-lo. Nessa expressão, 100 e 121 correspondem aos valores inicial e final do produto, respectivamente, e $1 mais início de fração, numerador: x, denominador: 100, fim de fração$ corresponde ao percentual de cada aumento.

Metodologias ativas

Para desenvolver o trabalho com a atividade 7, avalie a possibilidade de utilizar a metodologia ativa Pensamento do design. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 266

8. Resolva os itens no caderno com o auxílio de uma calculadora.

a) Dois descontos sucessivos de 12% cada um equivalem a um único desconto de quantos por cento?

b) Dois acréscimos sucessivos de 5% e 7,2%, respectivamente, equivalem a um único acréscimo de quantos por cento?

c) Três descontos sucessivos de 2% cada um equivalem a um único desconto de quantos por cento?

d) Três acréscimos sucessivos de 3% cada um equivalem a um único acréscimo de quantos por cento?

e) Doze acréscimos sucessivos de 5% cada um equivalem a um único acréscimo de quantos por cento?

Respostas: a) 22,56%; b) 12,56%; c) 5,88%; d) 9,2727%; e) 79,59%.

9. O preço de uma mercadoria sofreu dois aumentos sucessivos em uma loja: um de 20% em janeiro e outro de 30% em fevereiro. Determine o aumento percentual do preço dessa mercadoria nesse bimestre.

Resposta: 56%.

10. Na loja de Rafael, certo jogo de videogame custa R$ 273,50. O mesmo jogo, na loja de Francisco, custa R$ 255,00. Em uma semana, Rafael ofereceu 20% de desconto no jogo e, na semana seguinte, outro desconto de 5%. Francisco ofereceu um único desconto de 18%. Após os reajustes nos preços, em qual loja é mais vantajoso comprar o jogo?

Resposta: Na loja de Rafael.

11. Na promoção "Queima de estoque", uma loja ofereceu desconto de 25% na compra de um smartphone. Caso o pagamento fosse à vista, ainda era concedido um desconto de 4%, calculado após o desconto de 25%. Nessa promoção, qual é o preço à vista de um smartphone que, sem os descontos, custa R$ 2.349,00?

Resposta: R$ 1.691,28.

12. (Enem-2013) Para aumentar as vendas do início do ano, uma loja de departamentos remarcou os preços de seus produtos 20% abaixo do preço original. Quando chegam ao caixa, os clientes que possuem o cartão fidelidade da loja têm direito a um desconto adicional de 10% sobre o valor de suas compras.

Um cliente deseja comprar um produto que custava R$ 50,00 antes da remarcação de preços. Ele não possui o cartão fidelidade da loja.

Caso esse cliente possuísse o cartão fidelidade da loja, a economia adicional que obteria ao efetuar a compra, em reais, seria de:

a) 15,00

b) 14,00

c) 10,00

d) 5,00

e) 4,00

Resposta: Alternativa e.

13. Em uma papelaria, um caderno custava R$ 21,00. O preço desse produto teve dois acréscimos. De acordo com essas informações, elabore dois problemas: um envolvendo acréscimos sucessivos e outro sobre a determinação de taxas percentuais. Depois, dê para um colega resolver. Por fim, verifique se ele resolveu corretamente.

Resposta pessoal.

ORIENTAÇÕES AO PROFESSOR

Caso não haja calculadora para todos os estudantes, reúna-os em duplas para resolverem a atividade 8. Desse modo, eles podem conversar entre si e compartilhar as estratégias.

A atividade 9 é uma ótima oportunidade para verificar se todos os estudantes compreenderam como calcular aumentos sucessivos. Caso algum deles não obtenha a resposta 56%, forneça as explicações necessárias na lousa.

As atividades 10 e 11 possibilitam o desenvolvimento dos temas contemporâneos transversais Educação para o consumo e Educação financeira. Converse com os estudantes sobre a importância de fazer pesquisas de preços ao comprar um produto, com o intuito de economizar dinheiro, e leve-os a pensar sobre despesas que são realmente necessárias, pois, muitas vezes, podemos comprar coisas supérfluas e portanto, o gasto com elas pode ser revisto. Desse modo, abordam-se aspectos da Competência geral 10 ao tomar decisões com base em princípios éticos e sustentáveis.

Metodologias ativas

Para desenvolver o trabalho com as atividades 10 e 11, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Na atividade 12, diga aos estudantes que o cartão fidelidade, oferecido por alguns estabelecimentos, trata-se de um programa criado pelas empresas para recompensar os clientes que adquirem produtos ou serviços com determinada frequência.

Na atividade 13, pelo fato de o estudante elaborar e resolver situações-problema, interagindo com pares de modo cooperativo, trabalhando coletivamente, respeitando o modo de pensar dos colegas e aprendendo com eles, é favorecido o desenvolvimento das Competências específicas de Matemática 6 e 8 e das Competências gerais 2 e 4.

Página 267

Juro

Joana fez um empréstimo no banco. Após certo período, ela deve pagar, além da quantia emprestada, um valor a mais, correspondente ao juro, ou seja, um tipo de "aluguel" pelo período em que o dinheiro ficou emprestado.

Em outro momento, Joana fez uma aplicação de certa quantia em um investimento oferecido no banco. Nesse caso, ela recebe juro de acordo com o período em que essa quantia ficou aplicada.

Outra circunstância envolvendo juro ocorre quando uma pessoa realiza o pagamento de uma fatura com atraso, pois, além do valor da fatura, é acrescentado o juro correspondente à medida do tempo de atraso.

Fotografia de uma tábula de argila dos sumérios. Placa de argila com formato quadrado, mas com as pontas arredondadas, nela há alguns símbolos que foram perfurados e desenhados, representando tipos de anotações da civilização da Mesopotâmia. — Tábula de argila dos sumérios.

Assuntos relacionados a juro, faturas, recibos, escrituras de venda etc. já eram encontrados em tábulas de argila dos sumérios. Essa civilização viveu na Mesopotâmia por volta de 2100 a.C.

Conheça alguns termos importantes e muito utilizados na Matemática financeira.

Capital (c): quantia disponível em determinada data para ser investida ou emprestada.
Juro (j): rendimento ou acréscimo recebido pelo investimento de uma quantia, ou, por outro lado, acréscimo ou "aluguel" pago pelo empréstimo de uma quantia.
Taxa de juro (i): porcentagem por um período (dia, mês etc.) que se recebe ou se paga sobre o capital.
Medida do tempo (t): período em que certa quantia é investida ou emprestada, podendo ser indicada em dias, meses, bimestres, anos etc.
Montante (M): soma do capital com o juro obtido por uma aplicação ou pago por um empréstimo. Ele pode ser expresso por: $M = c + j$ .

O juro pode ser simples ou composto. Nas próximas páginas, vamos estudar algumas diferenças entre eles.

Página 268

Juro simples

Elisângela aplicou R$ 1.500,00 em um investimento e recebeu 2% de juro ao mês.

Se Elisângela aplicou essa quantia à taxa de juro simples, então, qual será o montante recebido ao final de um período de 3 meses?

Acompanhe a seguir como podemos calcular esse montante.

Capital (quantia aplicada): R$ 1.500,00
Medida do tempo: 3 meses
Taxa de juro: 2% ao mês

Inicialmente calculamos o juro simples de 1 mês de aplicação, isto é, calculamos 2% de 1.500.

$0 vírgula 0 2 vezes 1.500 igual a 30$

Como a quantia ficou aplicada durante 3 meses, multiplicamos o juro de 1 mês por 3.

$3 vezes 30 igual a 90$ , ou seja, R$ 90,00 de juro nos 3 meses

Para determinar esse valor (juro), multiplicamos o capital aplicado pela taxa de juro e pela medida do tempo de aplicação.

$j = c \cdot i \cdot t$

$j igual a 1.500 vezes 0 vírgula 0 2 vezes 3 igual a 90$

Agora, calculamos o montante após os 3 meses de aplicação.

$M = c + j$

$m igual a 1.500 mais 90 igual a 1.590$

Portanto, ao final dos 3 meses, à taxa de juro simples, Elisângela terá o montante de R$ 1.590,00.

O juro simples (j) é calculado sempre sobre o capital inicial (c), à determinada taxa de juro (i), em um período de tempo (t). Para calcular o juro simples, podemos utilizar a fórmula:

$j = c \cdot i \cdot t$

Ao substituir a taxa de juro na fórmula, devemos escrevê-la na forma decimal.

Atenção!

Para determinar o valor do juro utilizando a fórmula $j = c \cdot i \cdot t$ , tanto a taxa de juro (i) quanto a medida do tempo (t) devem estar na mesma unidade de medida de tempo. Se isso não ocorrer, é preciso converter uma delas para que fiquem na mesma unidade de medida.

Atividades

Faça as atividades no caderno.

14. Um investidor aplicou R$ 3.250,00 durante 6 meses, a uma taxa de juro simples de 3% ao mês. Qual foi o juro obtido por ele ao final da aplicação?

Resposta: R$ 585,00.

15. Solange aplicou um capital de R$ 1.800,00 durante 1 ano e 6 meses, a uma taxa de juro simples de 2% ao mês. Qual foi o montante obtido ao final da aplicação?

Atenção!

Transforme 1 ano e 6 meses em meses.

Resposta: R$ 2.448,00.

ORIENTAÇÕES AO PROFESSOR

Verifique a possibilidade de propor aos estudantes a situação apresentada nesta página antes de abordá-la no livro, a fim de que, em duplas, eles determinem o montante ao final de 3 meses. Para isso, escreva a situação-problema na lousa ou leia-a para eles. Depois, considerando as estratégias e resoluções propostas que eles desenvolveram, apresente as explicações encontradas no livro.

As atividades 14 e 15 apresentam contextos de aplicações de certo capital. Aproveite estas atividades e converse com eles sobre a importância de economizar dinheiro para atingir o objetivo de comprar algo, ou ainda para alguma eventual emergência e, nesse sentido, ter autocontrole e realizar planejamentos a longo prazo. Assim, aborda-se o tema contemporâneo transversal Educação financeira.

Metodologias ativas

Para desenvolver o trabalho com as atividades 14 e 15, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Algo a mais

No livro indicado a seguir, a autora utiliza linguagem simples e exemplos para explorar o uso da calculadora em situações que envolvem conceitos da Matemática financeira. VERAS, Lilia Ladeira. Matemática financeira. 6. ed. São Paulo: Atlas, 2007.

Atividade a mais

A seguir estão apresentadas informações de uma loja sobre o preço de uma máquina de lavar roupas.

R$ 1.699,00 à vista, ou entrada de R$ 800,00 e mais R$ 1.042,84 ao final de 2 meses

Nessa loja, qual é a taxa de juro simples cobrada pela compra a prazo da máquina de lavar roupas?

Resoluções e comentários

Inicialmente, determinamos o valor do juro cobrado.

$800 mais 1.042 vírgula 84 igual a 1.842 vírgula 84$

$1.842 vírgula 84 menos 1.699 igual a 143 vírgula 84$

Assim, temos o valor do juro cobrado $abre parênteses j igual a 143 vírgula 84 fecha parênteses$ , o valor do capital $abre parênteses c igual a 899 fecha parênteses$ e o tempo de 2 meses $abre parênteses t igual a 2 fecha parênteses$ . Substituindo esses valores na fórmula, temos:

$j = c \cdot i \cdot t$

$143 vírgula 84 igual a 899 vezes i vezes 2$

$143 vírgula 84 igual a 1.798 i$

$i igual a 0 vírgula 0 8 igual a início de fração, numerador: 8, denominador: 100, fim de fração$

Portanto, o valor da taxa é de 8% ao mês.

Página 269

Juro composto

No dia a dia, a maioria das operações financeiras faz uso do regime de juro composto, e, nesse caso, o juro é calculado sobre o montante do período anterior. Neste tópico, vimos anteriormente que Elisângela fez uma aplicação à taxa de juro simples. E se ela aplicar a mesma quantia à taxa de juro composto, qual será o montante ao final de 3 meses?

Acompanhe, a seguir, como podemos calcular esse montante.

Capital (quantia aplicada): R$ 1.500,00

Montante ao final do 1º mês:

$j com índice 1 igual a c vezes i vezes t igual a 1.500 vezes 0 vírgula 0 2 vezes 1 igual a 30$

$m com índice 1 igual a c mais j com índice 1 igual a 1.500 mais 30 igual a 1.530$

Montante ao final do 2º mês:

$j com índice 2 igual a m com índice 1 vezes 0 vírgula 0 2 vezes 1 igual a 1.530 vezes 0 vírgula 0 2 vezes 1 igual a 30 vírgula 6$

$m com índice 2 igual a m com índice 1 mais j com índice 2 igual a 1.530 mais 30 vírgula 6 igual a 1.560 vírgula 6$

Montante ao final do 3º mês:

$j com índice 3 igual a m com índice 2 vezes 0 vírgula 0 2 vezes 1 igual a 1.560 vírgula 6 vezes 0 vírgula 0 2 vezes 1 igual a 31 vírgula 21$

$m com índice 3 igual a m com índice 2 mais j com índice 3 igual a 1.560 vírgula 6 mais 31 vírgula 21 igual a 1.591 vírgula 81$

Atenção!

Em cada mês, o juro composto é calculado sobre o montante obtido ao final do mês anterior.

Portanto, ao final dos 3 meses, à taxa de juro composto, Elisângela terá o montante de R$ 1.591,81.

Ao utilizar o juro composto, apenas no 1º período o juro é calculado sobre o capital inicial. Nos períodos seguintes, o juro é calculado sobre o montante obtido no período anterior.

Se Elisângela deixasse o dinheiro aplicado por mais 3 meses à taxa de juro composto, qual seria o montante obtido ao final do 6º mês?

Para responder a essa pergunta, vamos utilizar uma calculadora.

1º. Para determinar o montante ao final do 4º mês, multiplicamos 1.591,81 por 1,02 $abre parênteses 100 por cento que corresponde a 1 mais 2 por cento que corresponde a 0 vírgula 0 2 fecha parênteses$ , que corresponde ao montante ao final do 3º mês acrescido de 2%. Para isso, digitamos em uma calculadora a seguinte sequência de teclas:

Ilustração do visor de uma calculadora apresentando no visor o número 1623 ponto 6 4 6 2. — 4º mês.

Página 270

2º. Para determinar o montante ao final do 5º mês, multiplicamos o montante obtido ao final do 4º mês por 1,02. E, para obter o montante ao final do 6º mês, multiplicamos o montante obtido ao final do 5º mês por 1,02.

Ilustração do visor de uma calculadora apresentando no visor o número 1656 ponto 1 1 9 1. — 5º mês.

Ilustração do visor de uma calculadora apresentando no visor o número 1689 ponto 2 4 1 5. — 6º mês.

Portanto, ao final do 6º mês, Elisângela terá o montante de R$ 1.689,24.

Instrumentos e softwares

Juro simples e juro composto no Calc

Com o Calc, podemos resolver problemas envolvendo juro simples e juro composto. Nesta seção, apresentaremos os procedimentos necessários para solucionar dois problemas: um envolvendo juro simples e outro, juro composto.

Acompanhe a situação a seguir.

Amanda aplicou R$ 100,00 a uma taxa de juro simples de 5% ao mês. Qual será o montante obtido por ela ao final de 10 meses?

Nesse caso, o capital aplicado é R$ 100,00 – o capital equivale ao montante correspondente à medida de tempo 0 –; a medida do tempo é 10 meses; e a taxa de juro é 5% ao mês. Sabendo disso, podemos executar os seguintes passos no Calc para solucionar o problema proposto.

1º. Nas células A1, B1, C1, A2, A3 e C2, digite t, j, M, 0, 1 e 100 respectivamente.

2º. Selecione as células A2 e A3, clique na Alça de Preenchimento Automático e arraste até a célula A12.

3º. Na célula B3, digite $igual a 0 vírgula 0 5 asterisco C cifrão 2$ e pressione Enter. Em seguida, clique na Alça de Preenchimento Automático e arraste até a célula B12. Note que 0,05 corresponde à taxa de juro de 5% escrito na forma decimal.

Atenção!

No 3º passo, para que o valor da célula C2 seja mantido nos cálculos das células abaixo, com o uso da Alça de Preenchimento Automático, usamos o símbolo $ (cifrão) em $igual a 0 vírgula 0 5 asterisco C cifrão 2$ .

4º. Na célula C3, digite $igual a C 2 mais B 3$ e pressione Enter. Por fim, clique na Alça de Preenchimento Automático da célula C3 e arraste até a célula C12.

ORIENTAÇÕES AO PROFESSOR

É possível desenvolver o trabalho com esta seção utilizando o programa Calc, que é uma planilha eletrônica do pacote LibreOffice, versão gratuita de aplicativos que inclui, além da planilha eletrônica, editores de textos, apresentações, desenhos e banco de dados. Para fazer o download e instalar o programa, basta acessar o site. Disponível em: https://oeds.link/w0Z1Uy. Acesso em: 4 ago. 2022.

O trabalho com esta seção permite compreender e utilizar tecnologias digitais de informação e comunicação de maneira crítica na resolução de problemas cotidianos, favorecendo o desenvolvimento da Competência geral 5 e da Competência específica de Matemática 5.

Metodologias ativas

Ao desenvolver o trabalho com a seção Instrumentos e softwares, avalie a possibilidade de utilizar a metodologia ativa Tiras de classificação. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 271

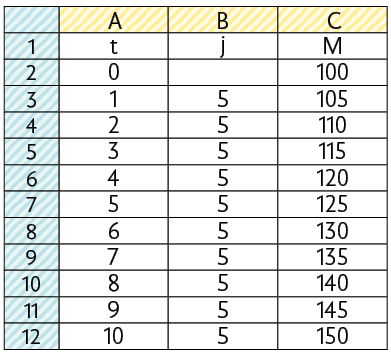
Ilustração de tela de uma tabela em uma planilha. A tabela tem 12 linhas e 3 colunas identificadas por A, B e C. linha 1: coluna A: está a letra t; coluna B: está a letra j; coluna C: letra M; linha 2: coluna A: 0; coluna B: em branco; coluna C: 100; linha 3: coluna A: 1; coluna B: 5; coluna C: 105; linha 4: coluna A: 2; coluna B: 5; coluna C: 110; linha 5: coluna A: 3; coluna B: 5; coluna C: 115; linha 6: coluna A: 4; coluna B: 5; coluna C: 120; linha 7: coluna A: 5; coluna B: 5; coluna C: 125; linha 8: coluna A: 6; coluna B: 5; coluna C: 130; linha 9: coluna A: 7; coluna B: 5; coluna C: 135; linha 10: coluna A: 8; coluna B: 5; coluna C: 140; linha 11: coluna A: 9; coluna B: 5; coluna C: 145; linha 12: coluna A: 10; coluna B: 5; coluna C: 150.

Portanto, ao final de 10 meses, Amanda obterá R$ 150,00.

Agora, acompanhe outra situação.

Joice aplicou R$ 100,00 a uma taxa de juro composto de 5% ao mês. Qual será o montante obtido por ela ao final de 10 meses?

Nessa situação, na qual a aplicação é sob juro composto, o capital inicial é R$ 100,00 – o capital equivale ao montante correspondente à medida de tempo 0 –; a medida do tempo é 10 meses; e a taxa de juro é 5% ao mês. Sabendo disso, podemos executar os seguintes passos no Calc para solucionar o problema proposto.

1º. Nas células A1, B1, C1, D1, A2, A3, C2 e D2, digite t, j, M, i, 0, 1, 100 e 0,05 respectivamente.

2º. Selecione as células A2 e A3, clique na Alça de Preenchimento Automático e arraste até a célula A12.

3º. Na célula B3, digite $igual a C 2 asterisco D cifrão 2$ e pressione Enter. Em seguida, clique na Alça de Preenchimento Automático e arraste até a célula B12.

4º. Na célula C3, digite $igual a C 2 mais B 3$ e pressione Enter. Em seguida, clique na Alça de Preenchimento Automático e arraste até a célula C12.

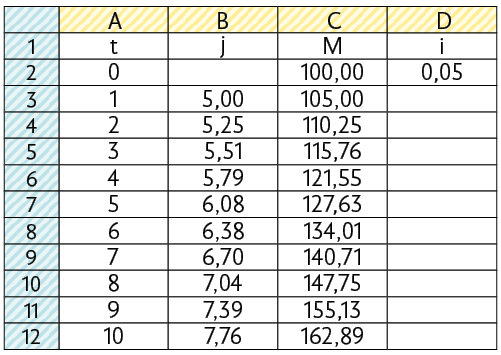
Ilustração de tela de uma tabela em uma planilha. A tabela tem 12 linhas e 4 colunas. As colunas estão identificadas por A, B, C e D. Linha 1: coluna A está a letra t; coluna B: j minúsculo; coluna C: M; coluna D: i. Linha 2: coluna A: 0; coluna B: está em branco; coluna C: 100; coluna D: 0 vírgula 0 5. Linha 3: coluna A: 1; coluna B: 5; coluna C: 105; coluna D: em branco. Linha 4: coluna A: 2; coluna B: 5,25; coluna C: 110,25; coluna D: em branco. Linha 5: coluna A: 3; coluna B: 5,51; coluna C: 115,76; coluna D: em branco. Linha 6: coluna A: 4; coluna B: 5,79; coluna C: 121,55; coluna D: em branco. Linha 7: coluna A: 5; coluna B: 6 vírgula 08; coluna C: 127,63; coluna D: em branco. Linha 8: coluna A: 6; coluna B: 6,38; coluna C: 134 vírgula 01; coluna D: em branco. Linha 9: coluna A: 7; coluna B: 6,70; coluna C: 140,71; coluna D: em branco. Linha 10: coluna A: 8; coluna B: 7 vírgula 04; coluna C: 147,75; coluna D: em branco. Linha 11: coluna A: 9; coluna B: 7,39; coluna C: 155,13; coluna D: em branco. Linha 12: coluna A: 10; coluna B: 7,76; coluna C: 162,89; coluna D: em branco.

Portanto, ao final de 10 meses, Joice obterá R$ 162,89.

ORIENTAÇÕES AO PROFESSOR

Após finalizar o 4º passo do cálculo do juro composto, para deixar os números com duas casas decimais, oriente os estudantes a selecionar as células das colunas B e C, que contêm as taxas de juro e os valores de montagem, clicar na ferramenta Formatar Células, selecionar a categoria Moeda, indicar no campo Casas decimais o número 2 e, por fim, clicar em Ok.

Para complementar o trabalho com esta seção, peça aos estudantes que, utilizando o Calc, simulem outros investimentos com juro simples e juro composto.

Um texto a mais

[...]

Leia o trecho do texto a seguir sobre a história do dinheiro como conhecemos hoje.

[...] A moeda e o dinheiro, como hoje conhecemos e calculamos, são o resultado de uma longa evolução. No início não havia moeda. Praticava-se o escambo, uma simples troca de mercadoria por mercadoria, praticamente sem a equivalência de valor. Algumas mercadorias, pela sua utilidade, passaram a serem mais requeridas do que outras. Demandadas por todos, assumiram a finalidade de moeda, circulando como elemento trocado com diversos produtos e servindo para avaliar-lhes o valor. Quando a civilização descobriu o uso do metal, logo passou a utilizá-lo para fabricação dos seus utensílios e armas, anteriormente feitos com pedra. Surgem, então, no século VII a.C., as primeiras moedas com características das atuais: são pequenas peças de metal com peso e valor definidos e com a impressão do cunho oficial, isto é, a marca de quem as emitiu e garante o seu valor. Durante muitos séculos os países cunharam em ouro suas moedas de maior valor, reservando a prata e o cobre para os valores menores. Estes sistemas monetários se mantiveram até o final do século passado, quando o cuproníquel e, posteriormente, outras ligas metálicas passaram a serem grandemente empregadas, passando a moeda a circular pelo seu valor extrínseco, isto é, pelo valor gravado em sua face, não dependente do metal nela contido.

[...]

ROSETTI JÚNIOR, Hélio; SCHIMIGUEL, Juliano. História do dinheiro, matemática financeira e a educação matemática. Revista Gestão Universitária, 256 ed. Disponível em: https://oeds.link/dZJ1WC. Acesso em: 4 ago. 2022.

Página 272

Atividades

Faça as atividades no caderno.

16. Um capital de R$ 2.200,00 foi aplicado durante 2 anos à taxa de juro de 8% ao ano.

a) Calcule o rendimento dessa aplicação no regime de juro:

simples.

composto.

b) Qual é a diferença, em reais, entre os rendimentos dessas duas aplicações?

Respostas: a) Simples: R$ 352,00; composto: R$ 366,08; b) 14,08.

17. Fernanda aplicou R$ 920,00 a uma taxa de juro composto de 13% ao ano. Utilizando uma calculadora, determine o montante obtido por Fernanda ao final de 4 anos.

Resposta: R$ 1.500,04.

18. Daniele realizou a simulação virtual de um empréstimo em um banco, à taxa de juro composto. Analise os dados que ela obteve.

Resultado da simulação
Valor do empréstimo	Medida do tempo do empréstimo	Taxa de juro ao mês	Valor a ser pago ao final do 3º mês
R$ 1.000,00	3 meses	5,60%	$█$

Caso Daniele faça esse empréstimo, ao final do contrato, qual terá sido o montante pago ao banco?

Resposta: R$ 1.177,58.

19. Jaime pretende comprar uma motocicleta cujo preço à vista é R$ 16.500,00. Para isso, deixará aplicado R$ 14.300,00 a uma taxa de juro composto de 2,5% ao mês, até que tenha o montante necessário para comprar a motocicleta à vista.

Considerando que o preço dessa motocicleta não será reajustado nos próximos meses, para pagá-la à vista, Jaime deve deixar a quantia aplicada por:

a) cinco meses, e terá a quantia exata.

b) cinco meses, e sobrarão menos de R$ 100,00.

c) seis meses, e terá a quantia exata.

d) seis meses, e sobrarão menos de R$ 100,00.

e) sete meses, e ainda sobrarão R$ 83,62.

Resposta: Alternativa d.

20. Em uma loja, o preço à vista de um notebook é R$ 2.299,00.

Mariana comprou esse notebook sem entrada e vai realizar o pagamento total ao final do 12º mês, a uma taxa de juro composto de 1% ao mês. Com o Calc, determine quantos reais Mariana vai pagar por esse produto.

Atenção!

Uma compra sem entrada acontece quando um objeto ou serviço é adquirido e não ocorre o pagamento de certa quantia no momento da compra.

Resposta: R$ 2.590,57.

ORIENTAÇÕES AO PROFESSOR

As atividades 16 e 17 apresentam contextos de aplicações de certo capital a uma taxa de juro simples e composto. Aproveite estas atividades e crie um ambiente para que os estudantes possam conversar sobre o uso do dinheiro de forma consciente, contribuindo para que se tornem adultos que saibam controlar os próprios gastos. Desse modo, aborda-se o tema contemporâneo transversal Educação financeira.

Caso não tenha calculadora para todos, reúna-os em duplas para resolverem a atividade 17.

Na atividade 18, aborda-se a questão do empréstimo virtual. Converse com os estudantes comentando que, quando imprevistos financeiros acontecem e a situação aperta, a primeira opção que vem à mente de muitas pessoas é a contratação de um empréstimo. Alerte-os dizendo que, para fazer um empréstimo, devemos ficar atentos para o fato de que ele não ultrapasse 30% do orçamento mensal, conforme alertam os especialistas da área.

As atividades 19 e 20 apresentam contextos envolvendo compra de produtos. Aproveite estas atividades e converse com os estudantes sobre o consumo responsável e a importância de realizar pesquisas de preços, antes de efetuar uma compra. Além disso, a atividade 19 permite as reflexões sobre as vantagens de aplicar o dinheiro até que tenha o montante necessário para efetuar a compra à vista, abordando o tema contemporâneo transversal Educação financeira.

Metodologias ativas

Para desenvolver o trabalho com as atividades 16, 17, 19 e 20, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 273

21. Armando pretende investir certa quantia. Ele está em dúvida entre os investimentos apresentados a seguir.

A: Investimento a uma taxa de juro composto de 2% ao mês.

B: Investimento a uma taxa de juro composto de 3% ao trimestre.

C: Investimento a uma taxa de juro composto de 13% ao ano.

Considerando que Armando vai fazer uma única aplicação e deixará a quantia rendendo durante 60 meses, qual dos investimentos é o mais vantajoso para ele? Para resolver essa atividade, utilize o Calc.

Resposta: Investimento A.

22. Ronaldo vai comprar um televisor cujo valor à vista é R$ 1.299,00. A loja oferece a seguinte opção para pagamento a prazo: entrada de R$ 200,00 e o restante em uma parcela única após 2 meses, com taxa de juro composto de 3,5% ao mês.

Qual é a diferença entre o valor à vista e o valor total pago a prazo?

Resposta: R$ 78,27.

23. A fim de comparar o rendimento de um mesmo capital, sob uma mesma taxa de juro, no regime de juro simples e no regime de juro composto, Maurício construiu o seguinte gráfico.

Montantes obtidos mês a mês – 2023

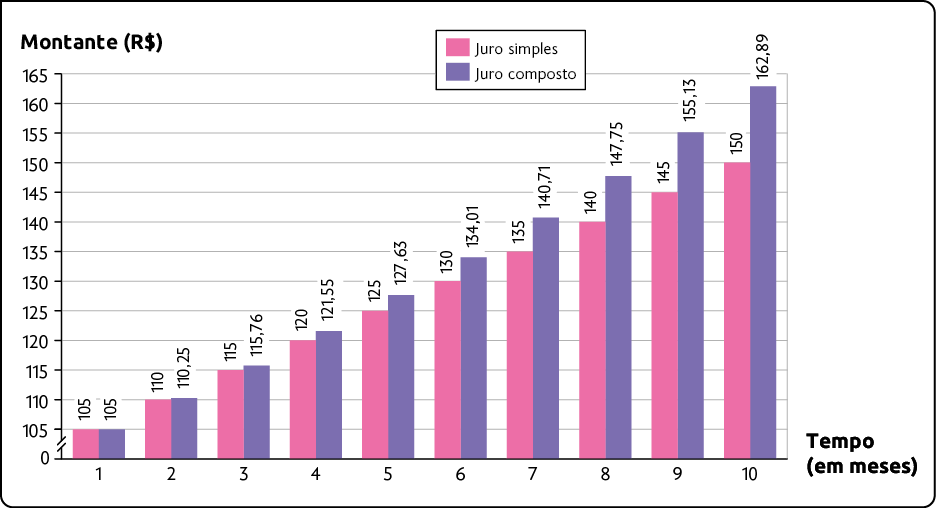
Gráfico de colunas duplas. No eixo horizontal está a medida do tempo, em meses, indo de 0 a 10 e no eixo vertical está o montante, em reais, indo de 0 a 165, sendo que entre o zero e o 105 há uma supressão e depois os valores estão indo de 5 em 5. Os dados são: um mês: juro simples: 105; juro composto: 105; dois meses: juro simples: 110; juro composto: 110,25; três meses: juro simples: 115; juro composto: 115,76; quatro meses: juro simples: 120; juro composto: 121,55; cinco meses: juro simples: 125; juro composto: 127,63; seis meses: juro simples: 130; juro composto: 134 vírgula 01; sete meses: juro simples: 135; juro composto: 140,71; oito meses: juro simples: 140; juro composto: 147,75; nove meses: juro simples: 145; juro composto: 155,13; dez meses: juro simples: 150; juro composto: 162,89.

Fonte de pesquisa: simulador de investimentos.

a) Sabendo que o capital considerado por Maurício foi R$ 100,00, determine qual é a taxa de juro dessas aplicações.

Resposta: 5% a.m.

b) Qual é a diferença entre esses montantes no 10º mês?

Resposta: R$ 12,89.

c) Elabore uma questão envolvendo as informações do gráfico e as duas formas de investimento. Depois, dê para um colega resolver e, por fim, verifique se a resposta está correta.

Resposta pessoal.

ORIENTAÇÕES AO PROFESSOR

Na atividade 21, verifique se todos os estudantes chegaram à mesma conclusão fazendo análise com a utilização do Calc.

Na atividade 22, converse com os estudantes sobre o consumo responsável e a importância de pesquisar preços antes de efetuar uma compra. Assim, permite-se a promoção de reflexões sobre as vantagens de fazer compras à vista ou a prazo e de analisar condições de pagamentos, abordando o tema contemporâneo transversal Educação financeira.

Metodologias ativas

Para desenvolver o trabalho com a atividade 22, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Na atividade 23, pelo fato de os estudantes elaborarem situações-problema e resolvê-las, interagindo com seus pares de forma cooperativa, trabalhando coletivamente, respeitando o modo de pensar dos colegas e aprendendo com eles, abordam-se as Competências específicas de Matemática 6 e 8 e as Competências gerais 2 e 4.

Os dados apresentados no gráfico da atividade 23 são fictícios.

Página 274

24. André representou no gráfico a seguir o montante obtido em uma aplicação ao final de cada mês.

Montante obtido em certa aplicação financeira – 2023

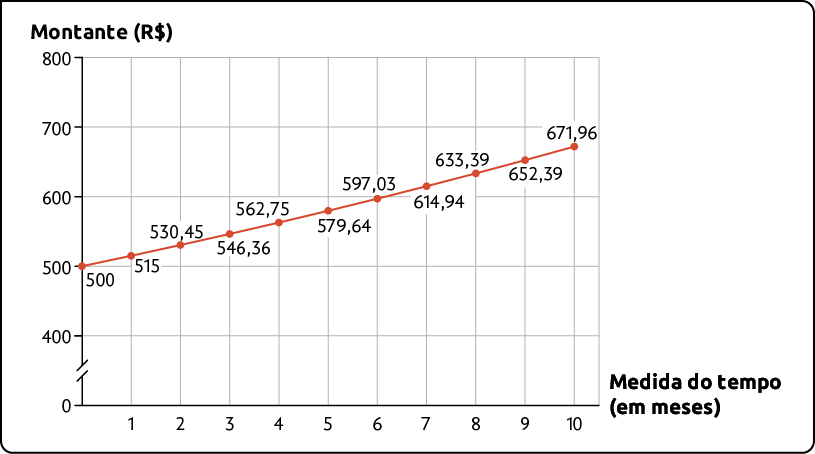
Gráfico de linhas. É apresentado o montante obtido em certa aplicação financeira em alguns meses. No eixo horizontal está a medida do tempo, em meses, indo de 1 a 10 e no eixo vertical o montante, em reais, indo de zero a 800, sendo que entre o zero e o 400 há uma supressão e depois os valores estão indo de 100 em 100. Os dados são: zero meses: 500; um mês: 515; dois meses: 530,45; três meses: 546,36; quatro meses: 562,75; cinco meses: 579,64; seis meses: 597 vírgula 03; sete meses: 614,94; oito meses: 633,39; nove meses: 652,39; dez meses: 671,96.

Fonte de pesquisa: registros de André.

a) Qual foi o capital aplicado?

b) Qual é a taxa de juro dessa aplicação?

c) Qual é o montante dessa aplicação ao final do 8º mês?

d) Qual será o montante dessa aplicação ao final do 11º mês?

Respostas: a) R$ 500,00; b) 3% ao mês; c) R$ 633,39; d) R$ 692,12.

25. Uma calça jeans que custa R$ 170,00 pode ser adquirida em duas parcelas de R$ 90,00, uma no ato da compra e outra um mês depois. Qual é a taxa de juro mensal que a loja está cobrando?

Resposta: 12,5%.

26. Victor aplicou R$ 1.000,00 em um investimento a juro composto de taxa constante ao mês. Ao final de 2 meses seu montante era R$ 1.092,00. Qual era a taxa de juro mensal desse investimento? Utilize uma calculadora para resolver esse problema.

Resposta: 4,5%.

27. Um capital de R$ 1.530,00 foi aplicado a uma taxa de juro composto de 3,2% ao mês. Utilizando o Calc, determine a quantidade de meses que esse capital deve ficar aplicado para que o juro recebido seja R$ 1.342,67.

Resposta: 20 meses.

28. Leia o que Bruna está dizendo.

Ilustração de uma mulher e ao lado um balão de fala em que está escrito: 'Vou fazer um investimento de 3 mil e 500 reais.'. — Bruna

Durante quantos anos esse capital deve ficar aplicado à taxa de juro composto de 2% ao mês, para que o juro total obtido nesse período seja R$ 2.129,53? Utilize o Calc para resolver esse problema.

Resposta: 2 anos.

ORIENTAÇÕES AO PROFESSOR

Os dados apresentados no gráfico da atividade 24 são fictícios.

Se achar conveniente, organize os estudantes em duplas para a realização das atividades 24 e 25, de modo que possam conversar e compartilhar estratégias.

Na atividade 25 analise se os estudantes notam que precisam calcular a taxa de juro apenas sobre a parcela que será paga um mês depois.

As atividades 26, 27 e 28 apresentam contextos envolvendo a aplicação de certo capital. Aproveite estas atividades e converse com os estudantes sobre a importância de economizar dinheiro para atingir o objetivo de comprar algo, ou ainda para alguma eventual emergência e, nesse sentido, ter autocontrole e realizar planejamentos a longo prazo. Assim, aborda-se o tema contemporâneo transversal Educação financeira.

Metodologias ativas

Para desenvolver o trabalho com as atividades 26, 27 e 28, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria.

Ao final do trabalho com as atividades desta unidade, avalie a possibilidade de utilizar a metodologia ativa Escrita rápida.

Obtenha informações sobre essas metodologias no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 275

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Certa loja de eletrodomésticos calcula o preço a prazo de seus produtos dividindo o preço à vista por 0,92. O preço a prazo dos produtos dessa loja apresenta um acréscimo ou um desconto em relação ao preço à vista? De quantos por cento?

Respostas: Acréscimo; aproximadamente 8,7%.

2. Adalberto, que é cozinheiro em um restaurante, comprou $15 quilogramas$ de determinado tipo de carne por R$ 40,00 o quilograma. No mês seguinte, o preço do quilograma da carne aumentou 20%. Adalberto, com a mesma quantia gasta na primeira vez, pôde comprar:

a) $13 vírgula 8 quilogramas$ da carne.

b) $12 vírgula 2 quilogramas$ da carne.

c) $14 vírgula 2 quilogramas$ da carne.

d) $12 vírgula 8 quilogramas$ da carne.

e) $12 vírgula 5 quilogramas$ da carne.

Resposta: Alternativa e.

3. Depois de um acréscimo de 12%, o valor de um livro passou a ser R$ 50,40. Qual era o valor cobrado pelo livro antes do acréscimo?

Atenção!

O valor do livro com acréscimo corresponde a $100 por cento mais 12 por cento igual a 112 por cento$ .

Resposta: R$ 45,00.

4. Giovana pretende fazer um curso por quatro anos. As mensalidades em um mesmo ano são todas iguais, porém, a cada ano, sofrem um acréscimo de 20% relativo ao anterior. Sabendo que a primeira mensalidade foi R$ 250,00 e que Giovana pagou sempre em dia, a quantia total paga pelo curso foi:

a) R$ 15.023,00.

b) R$ 15.875,50.

c) R$ 16.027,10.

d) R$ 16.104,00.

e) R$ 16.412,00.

Resposta: Alternativa d.

5. Em uma loja, houve um aumento de 15% em um tênis cujo preço inicial era R$ 180,00. Percebendo que as vendas desse produto diminuíram, foi decidido realizar uma promoção oferecendo 22% de desconto para pagamentos à vista. Nessa promoção, qual é o preço à vista desse tênis?

Resposta: R$ 161,46.

6. A matrícula em uma escola de idiomas custa R$ 124,00. Dos estudantes que já estudam outros idiomas na escola, essa taxa é cobrada uma única vez com 20% de desconto. Para completar as turmas de estudantes rapidamente, foi ofertado um desconto adicional de 5% em um período de promoção. Qual é o valor pago, no período da promoção, por um estudante dessa escola que vai fazer aulas de um outro idioma?

Resposta: R$ 94,24.

7. Elisa pretende aplicar R$ 550,00 a uma taxa de juro composto de 2,5% ao mês. Qual será o montante obtido por ela ao final do 6º mês? Utilize uma calculadora para resolver esse problema.

Resposta: R$ 637,83.

8. Responda à pergunta que Juliana está fazendo.

Fotografia de uma menina com cadernos nas mãos, e acima, um balão de fala: 'Certo capital, à taxa de juro simples de 4% ao mês, duplica seu valor em quantos meses?'.

Resposta: 25 meses ou 2 anos e 1 mês.

ORIENTAÇÕES AO PROFESSOR

1, 2 e 3. Objetivo

Avaliar se os estudantes identificam e resolvem situações-problema envolvendo acréscimo de preço e porcentagens.

Como proceder

Em caso de dificuldade na atividade 1, proponha a divisão do preço de um produto que custa R$ 100,00 por 0,92.

Ao constatar dificuldade na atividade 2, sugira que os estudantes calculem o valor total pago por Adalberto e, em seguida, determinem o novo preço do quilograma de carne.

Verifique se os estudantes usam a informação do boxe Atenção! da atividade 3. Para calcular o preço antes do aumento, eles podem aplicar a regra de três, considerando que o preço anterior corresponde a 100% e o preço após o aumento, a 112%.

4. Objetivo

Analisar se os estudantes resolvem uma situação-problema envolvendo acréscimos sucessivos.

Como proceder

Se necessário, enfatize que o acréscimo de 20% é feito sobre o valor da mensalidade do ano anterior. Depois, oriente os estudantes a calcular o custo anual com as mensalidades em cada ano.

5. Objetivo

Avaliar se os estudantes calculam o preço de um produto após um aumento e um desconto, respectivamente.

Como proceder

Verifique se os estudantes percebem que um aumento de 15% corresponde a $100 por cento mais 15 por cento igual a 115 por cento$ ou 1,15 do preço inicial. Analogamente, um desconto de 22% sobre o preço de um produto corresponde a $100 por cento menos 22 por cento igual a 78 por cento$ ou 0,78 desse preço.

6. Objetivo

Acompanhar o desempenho dos estudantes em situações-problema envolvendo percentual de descontos.

Como proceder

Analise a estratégia dos estudantes e, se necessário, enfatize que se trata de descontos sucessivos, de 20% e 5%, respectivamente. Assim, o desconto de 5% será sobre o preço após a incidência do desconto de 20%.

7 e 8. Objetivo

Avaliar se os estudantes calculam um montante sob o regime de juro simples e juro composto.

Como proceder

Em cada uma das atividades, analise se os estudantes identificam corretamente o capital aplicado, o prazo e a taxa de juro. Se necessário, retome as explicações das páginas 268 e 269.

Página 276

9. Olívia aplicou um capital de R$ 5.300,00, a uma taxa de juro simples de 2,5% ao mês. Ao final do período em que deixou o dinheiro aplicado, ela retirou o montante acumulado e verificou que era R$ 6.227,50. Após quantos meses Olívia retirou esse montante?

Resposta: 7 meses.

10. Uma geladeira está sendo vendida à vista por R$ 1.865,50 ou a prazo com 50% desse valor de entrada e mais R$ 993,38 após um mês. Qual é a taxa de juro mensal cobrada na compra a prazo?

Resposta: Aproximadamente 6,5%.

11. Um televisor, cujo preço à vista é R$ 1.199,00, está sendo vendido em 10 parcelas mensais de R$ 155,87.

Qual é o aumento percentual no preço a prazo, quando comparado ao preço à vista?

Resposta: 30%.

12. Determine o rendimento de um capital de R$ 500,00 aplicado, durante um ano, a uma taxa de juro composto de 1% ao mês.

Resposta: R$ 63,41.

13. Danilo pretende fazer um investimento de R$ 1.000,00 e está em dúvida entre duas opções. O investimento A é realizado a juro composto, e o investimento B, a juro simples. O gráfico a seguir mostra os montantes mensais nas duas opções, durante 6 meses.

Montantes mensais dos investimentos A e B – 2023

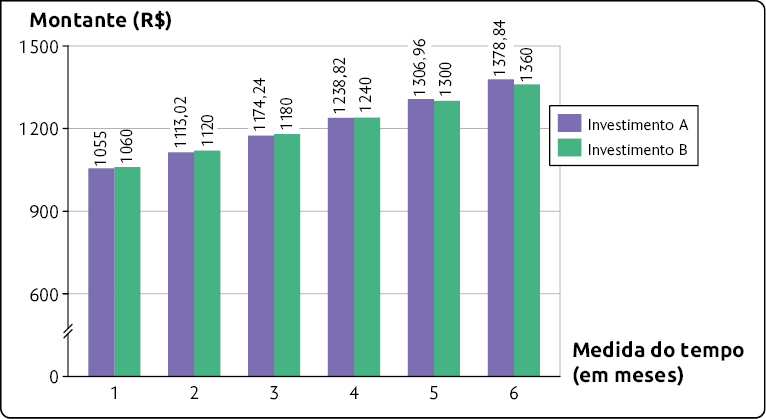
Gráfico de colunas duplas. No eixo horizontal está a medida do tempo, em meses, indo de 0 a 6 e no eixo vertical está o montante, em reais, indo de 0 a 1500, sendo que entre o zero e o 600 há uma supressão e depois os valores estão indo de 300 em 300. Os dados são: um mês: Investimento A: 1055, Investimento B: 1060; dois meses: Investimento A: 1113 vírgula 02, Investimento B: 1120; três meses: Investimento A: 1174,24, Investimento B: 1180; quatro meses: Investimento A: 1238,82, Investimento B: 1240; cinco meses: Investimento A: 1306,96, Investimento B: 1300; seis meses: Investimento A: 1378,84, Investimento B: 1360.

Fonte de pesquisa: registros do banco.

a) Qual é a taxa de juro no investimento A? E no investimento B?

b) Se Danilo pretende investir durante 2 meses, então qual dos investimentos é mais rentável? E se fossem 6 meses?

c) A partir de quantos meses decorridos o investimento A torna-se mais rentável do que o investimento B?

d) Qual é a diferença, em reais, entre os montantes nos investimentos A e B no 5º mês?

Respostas: a) investimento A: 5,5% ao mês; investimento B: 6% ao mês; b) investimento B; investimento A; c) 5 meses; d) R$ 6,96.

ORIENTAÇÕES AO PROFESSOR

9. Objetivo

Analisar a aprendizagem dos estudantes em atividades envolvendo juro simples.

Como proceder

Se necessário, peça aos estudantes que identifiquem as informações do problema e utilizem a fórmula $M = C + J$ , em que $J$ é obtido pela fórmula de juro simples.

10. Objetivo

Avaliar se os estudantes resolvem uma situação-problema envolvendo taxa de juro em uma compra parcelada.

Como proceder

Verifique se eles percebem que o valor da segunda parcela, após um mês, será maior do que o da primeira parcela paga no ato da compra. Assim, sugira que calculem o percentual de acréscimo na segunda parcela, em relação à primeira.

11. Objetivo

Conferir se os estudantes calculam o percentual de aumento de uma compra parcelada em relação ao seu preço à vista.

Como proceder

Ao constatar dificuldade, sugira aos estudantes que calculem o preço final do televisor na compra parcelada e determinem o valor pago a mais em relação ao preço à vista. Depois, peça a eles que calculem esse acréscimo em percentual.

12. Objetivo

Avaliar se os estudantes calculam o rendimento de um capital aplicado no regime de juro composto.

Como proceder

Verifique se eles percebem que 1 ano corresponde a 12 meses e que o rendimento é igual ao montante menos o capital aplicado.

13. Objetivo

Constatar se os estudantes comparam o crescimento de um capital no regime de juro simples e composto.

Como proceder

Para calcular a taxa de juro no item a, peça a eles que analisem o rendimento em cada investimento após o primeiro mês. Nos demais itens, peça aos estudantes que analisem o gráfico de cada tipo de investimento. Enfatize que, a médio e longo prazo, o investimento no regime de juro composto é sempre mais vantajoso.

Os dados apresentados no gráfico desta atividade são fictícios.