MP196

Comentários para o professor:

Introdução da Unidade 7

Como nas demais Unidades, a abertura desta apresenta, em página dupla, uma imagem que pode e deve ser explorada pelo professor a fim de resgatar conhecimentos matemáticos adquiridos no 2º ano e de incentivar a continuidade dos estudos.

Enquanto na Unidade 3 prevalecem atividades que levam os estudantes a desenvolverem as habilidades de leitura e registro de medidas e intervalos de tempo, utilizando relógios (analógico e digital) para informar os horários de início e término de realização de uma atividade e sua duração, além de reconhecerem a relação entre hora e minutos e entre minuto e segundos, esta Unidade amplia os conhecimentos sobre Grandezas e medidas, propondo atividades que exploram as medidas de comprimento, de capacidade e de massa.

Tais atividades levam os estudantes a reconhecerem que o resultado de uma medida depende da unidade de medida empregada e a escolherem a unidade de medida e o instrumento mais apropriados para medições de comprimento, tempo e capacidade.

Há também atividades que trabalham o registro, estimativas e comparações de comprimentos utilizando unidades não padronizadas e padronizadas mais usuais, além de medidas de massa e de capacidade por suas unidades de medida mais presente nas lidas cotidianas (litro, mililitro, quilograma, grama e miligrama).

O conceito da congruência, basilar para o desenvolvimento da Geometria no Ensino Fundamental 2 e Ensino Médio, empreende, nesta Unidade, os seus primeiros passos e é contemplado com atividades em que os estudantes devem comparar as áreas de figuras planas visualmente ou por superposição de figuras planas ou de desenhos.

Para reforçar e ampliar o trabalho iniciado na seção Compreender informações da Unidade 4, exploramos nesta Unidade outras situações-problema que instigam os estudantes a identificarem, em eventos aleatórios, todos os resultados possíveis, estimando os que têm mais ou menos chances de ocorrência. Dessa maneira, fica contemplada a Unidade Temática Probabilidade e estatística. As habilidades referentes a essa Unidade Temática também são desenvolvidas em problemas propostos cujos dados estão apresentados em tabelas de dupla entrada e em gráficos de barras ou de colunas.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.

Competências específicas favorecidas

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

Sugestão de roteiro de aula

Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.

Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção Jogo.

Os jogos são recursos valiosos para o desenvolvimento simultâneo de habilidades matemáticas, motoras, sociais e éticas de estudantes em qualquer faixa etária. Sempre que a atividade demandar a fixação de prazo para ser realizada, o tempo sugerido desse prazo deve ser comunicado com antecedência.

MP197

Roteiro de aula – Memória de medidas 1 ª parte – Preparação – Tempo sugerido: 20 minutos

Organize as carteiras de modo que os estudantes possam trabalhar em duplas, porém, fique atento e auxilie aqueles que estiverem com dificuldade em encontrar um par para realizar a atividade.

Para obter as 12 cartas a serem usadas no jogo, oriente os estudantes a destacarem, com o auxílio de uma tesoura de ponta arredondada, a folha indicada da parte final do livro (Material complementar). Convém que ela seja colada em outro papel de maior consistência (cartolina ou papelão) antes de ser recortada uma a uma. Para isso, solicite com antecedência que providenciem tesoura, cartolina e cola. Basta um jogo de cartas para cada dupla.

Faça a leitura coletiva das regras do jogo e certifique-se de que elas foram compreendidas por todos. Embora esse jogo proponha um procedimento simples, avalie a necessidade de simular, com um dos grupos, um início de procedimento, que sirva como exemplo e elimine possíveis dúvidas. Esta orientação é válida para os jogos em geral, portanto, pode ser adaptada para outras atividades semelhantes.

2 ª parte – Jogo – Tempo sugerido (teto): 30 minutos

O tempo de cada rodada depende da dinâmica da dupla e, de certa forma, do acaso do jogo. É provável que esses tempos sejam diferentes para as equipes. Por isso, convém estabelecer de antemão um teto que julgar adequado dentro da sua disponibilidade e programação.

Deixe-os jogar livremente, mas acompanhe as ações dos grupos para administrar impasses caso considere necessário.

3 ª parte – Questões sobre o Jogo – Tempo sugerido: 10 minutos

As questões propostas devem ser respondidas também em dupla e, muito provavelmente, elas estiveram presentes em algumas das passagens do jogo. É razoável supor que não haja dificuldade na resolução delas, mas é importante o acompanhamento de possíveis dúvidas.

Ao final, peça a cada dupla que confeccione um conjunto de 12 cartas similares às desse jogo, porém, usando medidas de massa e de capacidade. Agende um dia para repetirem o jogo com esse novo conjunto de cartas.

MP198

UNIDADE 7. Mais grandezas e medidas

Ilustração. No centro, uma senhora está sentada e na frente dela há um prato com comida sobre uma mesa. À esquerda, outra senhora está de costas e na frente dela, uma mulher com touca está segurando cédulas com a mão estendida. Entre elas há uma balança sobre um balcão. Abaixo, placa com a informação: Suco natural de laranja - Jarra (1 L): 15 reais, Copo (200 mL): 4 reais. Em seguida, três adultos e duas crianças estão segurando pratos com comida e ao lado deles há comida sobre bandejas e uma placa com a informação: 50 reais por kg. Atrás das bandejas há um homem com uniforme de cozinheiro, Melissa, Caio e duas crianças com touca. Atrás delas há uma parede de azulejos, uma porta e um relógio de ponteiro indicando 11:37. Abaixo há uma placa com a informação: Visitem nossa cozinha.
MANUAL DO PROFESSOR

Objetivos da Unidade

Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

Escolher a unidade de medida e o instrumento mais apropriado para medições.

Estimar, medir e comparar comprimentos, utilizando unidades de medida não padronizadas e padronizadas mais usuais (metro, centímetro e milímetro) e diversos instrumentos de medida.

Estimar, medir e comparar capacidades e massas, utilizando unidades de medida não padronizadas e padronizadas mais usuais (litro, mililitro, quilograma, grama e miligrama).

Comparar, visualmente ou por superposição, áreas de figuras planas.

Resolver problemas cujos dados estão apresentados em gráficos de barras.

Ler e registrar medidas de tempo (dias e meses).

Identificar todos os resultados possíveis de um experimento aleatório e estimar quais eventos desse experimento têm maiores ou menores chances de ocorrência.

Na abertura, os estudantes entram em contato com cenas do cotidiano que remetem à ideia de medida e ao uso de instrumentos adequados a cada grandeza a ser medida. BNCC em foco:

EF03MA17, EF03MA18, EF03MA19, EF03MA20, EF03MA21, EF03MA25, EF03MA26

MP199

Boxe complementar:

Para refletir...

Ícone: oral.

Em diversas situações do dia a dia temos de fazer medições.

Nessa lanchonete, que instrumento é usado para pesar o prato de comida?

PROFESSOR Resposta: A balança.

Quanto custa o quilograma da comida?

PROFESSOR Resposta: 50 reais.

Observe o relógio da lanchonete. Quantos minutos faltam para o meio-dia?

PROFESSOR Resposta: 23 minutos.

Fábio vai comprar um litro de suco para dividir com os colegas. O que é mais barato: comprar uma jarra ou cinco copos?

PROFESSOR Resposta: Uma jarra.

Fim do complemento.

MANUAL DO PROFESSOR

Para refletir…

Na primeira questão, espera-se que os estudantes identifiquem que a balança é o instrumento que faz a medição da quantidade de comida que há em cada prato (massa) e o preço de cada quilograma: 50 reais (indicado na placa).

A segunda questão possibilita aos estudantes retomarem alguns conhecimentos já adquiridos sobre medidas de tempo. Eles terão de analisar que horas o relógio marca (11 horas e 37 minutos) e determinar quanto tempo falta para o meio-dia (23 minutos).

Na terceira questão, os estudantes terão de realizar um cálculo a fim de verificar se é mais barato comprar uma jarra com 1 litro de suco ou 5 copos com 200 mililitros de suco. Para fazer essa comparação, eles devem buscar na ilustração o preço de cada copo de suco (4 reais) e multiplicar o valor por 5, totalizando 20 reais a serem pagos por 5 copos de suco. Se Fábio comprar uma jarra, ele pagará 15 reais pelo litro de suco, ou seja, é mais barato comprar uma jarra de 1 litro para dividir com os amigos do que comprar um copo para cada um.

MP200

Unidades de medida: padronizadas e não padronizadas

  1. Observe as situações que envolvem medições.

Observação: Os elementos não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.

Ilustração. 1) Um homem fala: Esse canteiro deve medir 10 passos de comprimento. Na frente dele, outro homem o observa e ao lado há um carrinho com terra e um canteiro com flores. 2) Um homem está com o dedo indicador levantado. Ele diz: Preciso de 2 pacotes de frango. Na frente dele há um balcão e um homem com touca. 3) Um homem com chapéu e uniforme de cozinheiro está lendo um livro. Ele fala: A receita pede 1 copo de água. 4) Um homem aponta para um muro e diz: O muro tem 6 metros de largura. 5) Uma mulher está com a mão esquerda virada para cima. Ela fala: Para fazer quibe de forno, vou usar 500 gramas de carne moída. Na frente dela há um pacote de carne e frascos sobre uma mesa. 6) Uma mulher sorri e diz: Comprei 20 litros de água. Ao seu lado há um galão grande sobre uma mesa.
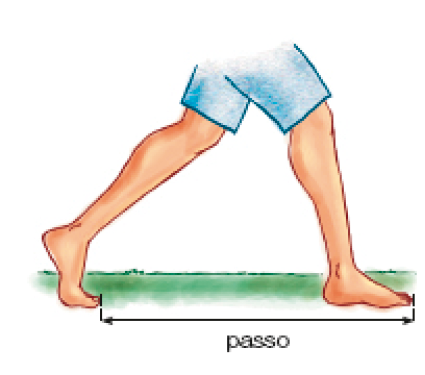
  1. A medida do comprimento do passo de uma pessoa é sempre igual à medida do comprimento do passo de todas as pessoas? _____
    PROFESSOR Resposta: Não.
  1. Um pacote de frango tem sempre a mesma massa? _____
    PROFESSOR Resposta: Não.
  1. Em todos os copos cabe a mesma quantidade de água? _____
    PROFESSOR Resposta: Não.

O passo, o pacote e o copo são exemplos de unidades de medida não padronizadas.

O metro, o grama e o litro são exemplos de unidades de medida padronizadas.

MANUAL DO PROFESSOR

Objetivos

Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

Escolher a unidade de medida e o instrumento mais apropriado para medições.

As atividades propostas nesta Unidade promovem a reflexão sobre o uso de diferentes unidades de medida que envolvem grandezas variadas e sobre os instrumentos de medição associados a cada uma delas.

É importante os estudantes entenderem que a adoção de medidas padronizadas possibilita reproduzir um procedimento, por exemplo, obter 1 kg de determinado alimento, a qualquer tempo e em qualquer lugar, pois elas são invariáveis.

Atividade 1

As situações apresentadas na atividade possibilitam aos estudantes comparar os procedimentos adotados em cada situação em que a medição estava envolvida. Para cada grandeza, foi empregada uma unidade de medida não padronizada (unidade cujo valor é variável, dependendo de quem a usa) e uma unidade de medida padronizada.

O objetivo das perguntas é evidenciar a diferença entre esses dois tipos de unidade de medida: os passos de pessoas diferentes podem não ter o mesmo comprimento; os pacotes podem não conter a mesma quantidade de massa; há copos com diferentes capacidades.

BNCC em foco:

EF03MA17

Sugestão de leitura para o professor

Textos complementares

SANTOS, Eliane Costa et al. A medida em nossas vidas. Pacto Nacional pela Alfabetização na Idade Certa. Grandezas e Medidas. Brasília: MEC/SEB, 2014. p. 13-17.

MUNHOZ, Danilo Pereira; PAULA, Mabi Katien Batista de; MORAES, Mara Sueli Simão. A importância de ensinar Grandezas e Medidas. Pacto Nacional pela Alfabetização na Idade Certa. Grandezas e Medidas. Brasília: MEC/SEB, 2014. p. 18-23.

MP201

Ícone: oral.

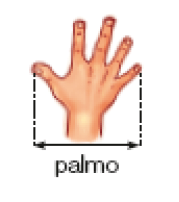
  1. O palmo, o passo e a largura do polegar de uma pessoa são unidades de medida não padronizadas. Qual delas você usaria para medir:
    1. o comprimento da parede de uma casa?
    1. o comprimento de uma borracha escolar?
    1. a largura de uma porta?
      PROFESSOR Respostas pessoais.
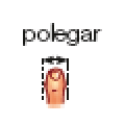
Ilustração. um dedo polegar com uma seta em cima (polegar).
Ilustração. uma mão aberta com uma seta em cima (palmo).
Ilustração. um pé na frente do outro com as pernas abertas e abaixo há uma seta (passo).

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.

  1. Cerque com uma linha cada um dos instrumentos que faz medições em unidades de medida padronizadas.
Ilustração. Uma régua.
Ilustração. Um relógio redondo de ponteiros.
Ilustração. Um lápis vermelho.
Ilustração. Uma trena.
Ilustração. uma colher.
Ilustração. Uma lata cilíndrica.
PROFESSOR Resposta: régua; relógio; trena.
  1. Complete com o nome do instrumento de medida adequado.
  1. Para medir o tempo obtido em uma prova de natação, usamos

    _____.

    PROFESSOR Resposta: o cronômetro
  1. Para medir o comprimento de um pedaço de madeira, usamos

    _____.

    PROFESSOR Resposta: a fita métrica
  1. Para medir a massa de um bolo, usamos _____.
    PROFESSOR Resposta: a balança
Fotografia. Uma mão segurando um cronômetro.

Legenda: cronômetro. Fim da legenda. cronômetro

Fotografia. Uma fita métrica.

Legenda: fita métrica. Fim da legenda. cronômetro

Fotografia. Uma balança.

Legenda: balança. Fim da legenda. cronômetro

MANUAL DO PROFESSOR

Atividade 2

Na atividade, os estudantes devem identificar a unidade de medida de comprimento não padronizada mais adequada para expressar cada medição. É importante eles reconhecerem que é possível usar qualquer uma das unidades sugeridas (palmo, passo ou largura do polegar). Entretanto, usar o polegar não seria prático para medir o comprimento de uma parede ou a largura de uma porta, porque, por ser muito pequeno em relação ao que deve ser medido, exigiria um número muito grande de repetições. Por outro lado, o uso do passo ou do palmo para medir o comprimento de uma borracha é igualmente inconveniente, porque, nesse caso, essas unidades de medida ultrapassam muito o comprimento a ser medido.

Atividade 3

Espera-se que os estudantes percebam que nas imagens dessa atividade há diversos objetos que até podem ser usados como unidades de medida (não padronizadas), como é o caso da colher, muito utilizada em receitas. No entanto, espera-se que eles reconheçam como instrumentos que fazem medições em unidades padronizadas apenas a régua, o relógio e a trena.

Atividade 4

Espera-se que os estudantes associem facilmente cada instrumento à respectiva situação de seu uso. Peça a eles que citem outros exemplos de situações de medições para um colega dizer o instrumento utilizado nessa situação. Socialize e valide as ideias com a turma.

Se julgar oportuno, conte à turma que, por muitos anos, reis, imperadores e governantes determinaram as unidades de medida-padrão adotadas em seus domínios. Usavam medidas do próprio corpo, como o palmo, ou a medida de pedaços de corda. Essas unidades de medida não padronizadas eram eficientes para o comércio local, mas prejudicavam o comércio com outros reinos, pois geravam grande confusão nas negociações. Por volta de 1790, alguns estudiosos criaram o sistema métrico decimal, unificando as unidades de medida.

BNCC em foco:

EF03MA17, EF03MA18

MP202

Medidas de comprimento

  1. O pai de Alice e Rafael vai comprar um porta-retratos. Ele mediu as dimensões da fotografia e dos porta-retratos com clipes.

    Conte e escreva a quantidade de clipes de cada comprimento (C) e de cada largura (L).

Ilustração. Fotografia quadrada com a imagem de duas crianças sorrindo. À esquerda há cinco clipes empilhados e abaixo há seis clipes enfileirados.

C: 6 clipes.

L: 5 clipes.

Ilustração. Um porta-retratos colorido e quadrado. À esquerda há cinco clipes empilhados e abaixo há seis clipes enfileirados.

C: _____ clipes.

PROFESSOR Resposta: 6

L: _____ clipes.

PROFESSOR Resposta: 5
Ilustração. Um porta-retratos colorido e retangular. À esquerda há cinco clipes empilhados e abaixo há sete clipes enfileirados.

C: _____ clipes.

PROFESSOR Resposta: 7

L: _____ clipes.

PROFESSOR Resposta: 5

Para medir comprimentos, podemos usar diversos objetos ou partes do corpo.

  1. Com uma borracha, meça o comprimento e a largura de uma régua, conforme mostrado no esquema abaixo. Depois, responda às questões.

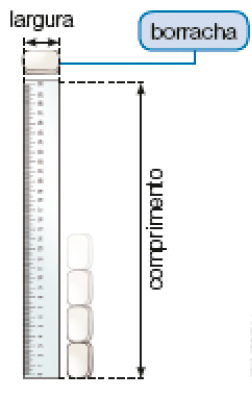
    Ilustração. Uma régua de 30 centímetros em pé. Acima há uma borracha pequena, indicando a largura. Ao lado há borrachas empilhadas, indicando o comprimento.

    1. Quantas vezes sua borracha cabe na largura da régua? _____
    1. E no comprimento da régua? _____
      PROFESSOR Respostas pessoais.

      Ícone: oral.

      Ícone: dupla.

      • Agora, compare suas respostas com as de um colega. Elas são iguais? Conversem a respeito disso.
MANUAL DO PROFESSOR

Objetivos

Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

Estimar, medir e comparar comprimentos, utilizando unidades de medida não padronizadas e padronizadas mais usuais (centímetro).

Nessa página, a ideia de medida é apresentada em situações que envolvem unidades de medida não padronizadas, como o clipe e a borracha. Comente que, nessas situações, compara-se o comprimento desses objetos com o comprimento do que se deseja medir.

Atividade 1

Os estudantes devem observar que as dimensões da fotografia são dadas pela quantidade de clipes dispostos no seu comprimento (6 clipes) e na sua largura (5 clipes) e comparar tais dimensões com as de cada porta-retratos, também determinadas pelos clipes. Verifique se os estudantes entendem a atividade e como procedem para resolvê-la. Em uma roda de conversa, propicie que exponham suas ideias.

Atividade 2

Nessa atividade, como a unidade de medida empregada (o comprimento da borracha) é variável, dependendo do tipo da borracha que cada estudante tem, provavelmente os estudantes não obterão valores iguais em suas medições. Promova uma discussão com eles sobre a necessidade de uso de uma unidade de medida padronizada.

A ideia de medição é por vezes de difícil compreensão pelos estudantes porque, ao contrário da contagem de uma quantidade, como 5 canetas, o objeto a ser medido em comprimento não está separado em pedaços, cada qual correspondendo a uma unidade de medida. No caso da atividade 2, por exemplo, os estudantes devem comparar o comprimento e a largura da régua com o comprimento da unidade de medida estabelecida – a borracha. Para isso, a borracha (em seu comprimento) deve ser colocada lado a lado com a régua em seu comprimento e em sua largura para que se faça a contagem de quantas vezes a unidade cabe no comprimento e na largura a serem medidos.

BNCC em foco:

EF03MA17, EF03MA19

MP203

Metro, centímetro e milímetro

  1. Veja como Rodolfo, Cristiano e Rodrigo mediram o comprimento do clipe.
Ilustração. Na parte superior há um clipe deitado e abaixo, uma régua com a ponta do clipe no número 0 e a outra ponta no número 3. Na parte inferior, Rodolfo, menino com camiseta azul está com os braços cruzados. Ele fala: A medida do comprimento do clipe é igual a 3 centímetros.
Ilustração. Na parte superior há um clipe deitado e abaixo, uma régua com a ponta do clipe no número 1 e a outra ponta no número 4. Na parte inferior, Cristiano, menino com cabelo encaracolado e blusa verde está com o dedo indicador apontado para cima. Ele diz: A medida do comprimento do clipe é igual a 4 centímetros.
Ilustração. Na parte superior há um clipe deitado e abaixo, uma régua com a ponta do clipe no número 4 e a outra ponta no número 7. Na parte inferior, Rodrigo, menino loiro com óculos está sorrindo. Ele fala: A medida do comprimento do clipe é igual a 3 centímetros.

Ícone: oral.

PROFESSOR Resposta: Cristiano.
PROFESSOR Exemplo de explicação: Porque a medida do comprimento do clipe não é indicada pela marca final, 4 centímetros, mas pela diferença entre a marca final e a marca inicial: 4 centímetros menos 1 centímetro são 3 centímetros.
  1. Com uma régua, meça o comprimento de cada figura.
Ilustração. Um grampo de cabelo deitado, medindo 5 centímetros.

______

PROFESSOR Resposta: 5 centímetros.
Ilustração. Uma chave deitada, medindo 4 centímetros.

______

PROFESSOR Resposta: 4 centímetros.

Ícone: Material complementar.

Ícone: grupo.

  1. Recorte e monte a fita métrica de 1 metro da página 221.

    Agora, reúna-se com 4 colegas e escolham alguns objetos da sala de aula para medir com a fita métrica montada. Depois, registrem no caderno se a medida do comprimento de cada objeto é maior que 1 metro ou menor que 1 metro.

    PROFESSOR Respostas pessoais.
MANUAL DO PROFESSOR

Atividade 1

Talvez Cristiano tenha apenas observado em qual marca indicadora de centímetros a extremidade direita do clipe se encontra, ou tenha contado o número de marcas indicadoras dos centímetros na escala da régua, demostrando, assim, que não compreende que a medição compara quantas vezes a unidade de medida centímetro (portanto, um segmento de 1 centímetro de comprimento) cabe no comprimento que está sendo medido.

A atividade é importante para verificar a compreensão dos estudantes a respeito de uma medição. O erro cometido por Cristiano, comum entre estudantes dessa faixa etária, indica mais que um erro aritmético: aponta provavelmente a falta de compreensão do que está sendo medido.

Atividade 2

Explore a medição com régua pedindo aos estudantes que alinhem o início da figura com outra marca da régua (1 cm ou 2 cm, por exemplo), e não com a marca correspondente ao zero. Depois, peça a eles que comparem os resultados com as respostas dadas.

Observe se os estudantes utilizam a ideia da atividade anterior e medem corretamente as figuras ao alinhar o início da figura com outra marca da régua que não o zero ou se cometem o mesmo erro de Cristiano.

Caso ainda haja estudantes que cometam erro na leitura da régua, peça a eles que resolvam novamente a atividade 1 para perceberem o equívoco.

Atividade 3

Solicite aos estudantes que, em grupos, meçam comprimentos de alguns objetos da sala de aula com a fita métrica que eles montaram e registrem as medições. Peça a eles que separem e agrupem os objetos:

com mais de 1 metro de comprimento;

com menos de 1 metro;

com exatamente 1 metro de comprimento.

Mostre que, para objetos que têm mais de 1 metro de comprimento (por exemplo, 1 metro e 23 centímetros), a medida pode ser expressa de forma mista, em metros e em centímetros, o que também favorece o estabelecimento da relação entre essas unidades.

Aproveite para reforçar que, ao expressar uma medição, o número sozinho não indica a medida: é preciso que a unidade de medida o acompanhe para que faça sentido.

BNCC em foco:

EF03MA19

MP204

  1. Resolva os problemas.
    1. Artur cortou 4 placas de madeira com 25 centímetros de comprimento cada uma para montar uma prateleira. Qual é a medida do comprimento das 4 placas juntas, em centímetro? E em metro?

      Ilustração. Artur, homem com boné, camiseta, calça e tênis está agachado e segurando uma fita métrica. Ele fala: Deu 1 metro de comprimento. Na frente desse há quatro placas de madeira lado a lado.

      CRÉDITO: SERGIO NG

      PROFESSOR Resposta: 100 centímetros; 1 metro.
    1. Durante a aula, Alice usou uma malha quadriculada, conforme a imagem ao lado, em que o lado de cada quadradinho da malha media 5 milímetros de comprimento. Ela pintou dois quadradinhos, um ao lado do outro, para representar um retângulo. Quantos milímetros mede um dos maiores lados desse retângulo? E em centímetro?

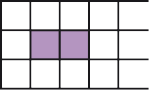
      Ilustração. Retângulo com cinco colunas e três fileiras de quadrados. Os quadrados da coluna dois, fileira dois e coluna três, fileira dois estão pintados de roxo.

      PROFESSOR Resposta: 10 milímetros; 1 centímetro.

Indicamos:

• 1 metro por 1 m

• 1 centímetro por 1 cm

• 1 milímetro por 1 mm

100 centímetros correspondem a 1 metro.

100 cm = 1 m

10 milímetros correspondem a 1 centímetro.

10 mm = 1 cm

  1. Estime e complete com a unidade de medida adequada: metro ou centímetro.
    1. O prédio em que moro tem 25 _____ de altura.
      PROFESSOR Resposta: metros
    1. O carro de Augusto tem 4 _____ de comprimento.
      PROFESSOR Resposta: metros
    1. O palmo de Larissa mede 15 _____ de comprimento.
      PROFESSOR Resposta: centímetros
    1. Meu gato tem 20 _____ de altura.
      PROFESSOR Resposta: centímetros
  1. Estime as medidas e complete com mais de ou com menos de.
    1. O comprimento da minha perna mede _____ 1 metro.
      PROFESSOR Resposta: menos de
    1. A altura da sala de aula mede _____ 1 metro.
      PROFESSOR Resposta: mais de
    1. A largura do meu livro mede _____ 1 metro.
      PROFESSOR Resposta: menos de
MANUAL DO PROFESSOR

Objetivos

Estimar, medir e comparar comprimentos, utilizando unidades de medida padronizadas mais usuais (metro, centímetro e milímetro) e diversos instrumentos de medida.

Escolher a unidade de medida e o instrumento mais apropriado para medições de comprimento.

Atividade 4

Na resolução dos dois problemas, discuta com os estudantes o uso da unidade mais adequada para expressar as medições efetuadas.

Utilize uma fita métrica para relacionar metro e centímetro (1 m = 100 cm) e uma régua para explorar a relação entre centímetro e milímetro (1 cm = 10 mm).

Se houver possibilidade, distribua pedaços grandes de barbante para os estudantes e peça a eles que, em duplas, cortem um pedaço de 1 metro. Para auxiliar na medição, sugira que usem uma fita métrica. Depois, peça aos estudantes que expressem o comprimento do pedaço de barbante que cortaram em centímetros.

Atividade 5

Observe se os estudantes percebem a ordem de grandeza dos objetos citados para não confundir as possíveis unidades de medida a serem utilizadas. Se julgar conveniente, proponha outras estimativas alterando a proposta: em vez de pedir aos estudantes a unidade de medida, forneça-a em cada caso e peça que estimem o valor da medida a ser preenchida.

Atividade 6

Leve os estudantes a outros locais da escola (pátio, quadra, biblioteca etc.) e peça que meçam comprimentos de objetos variados. Eles podem utilizar a fita métrica da atividade 3. Essa experimentação os auxiliará no momento de realizar as estimativas pedidas na atividade.

BNCC em foco:

EF03MA19

MP205

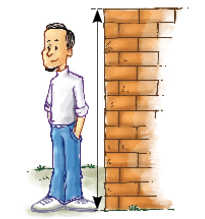
  1. Estime a medida da altura indicada em cada figura. Depois, ligue as figuras às medidas correspondentes.

Linha 1

Ilustração 1. Um homem está em pé, ao lado de um muro maior do que ele.
Ilustração 2. Um homem está segurando uma bandeja com lanche e andando em direção a uma mesa média, menor do que ele.
Ilustração 3. Um homem está segurando um regador com o corpo inclinado para frente e regando um vaso com planta pequeno.

Linha 2

80 cm

20 cm

2 m

PROFESSOR Resposta: imagem 1 - 2m; imagem 2 - 80 cm; imagem 3 - 20 cm.
  1. Observe os instrumentos de medida abaixo e, em seguida, responda.
Ilustração. Um metro muito comprido. Abaixo, uma régua média e em seguida, uma trena.
  1. Qual desses instrumentos é o mais indicado para Jaime, que é costureiro, usar em seus trabalhos? _____
    PROFESSOR Resposta: O metro.
  1. Para um estudante do 3º ano, qual é o instrumento mais adequado?

    _____

    PROFESSOR Resposta: A régua.
  1. Cite uma profissão que utilize a trena como instrumento de medida.

    _____

    PROFESSOR Exemplo de resposta: Marcenaria.
  1. Helena fez uma lista de materiais que precisará comprar para fazer algumas fantasias.
Ilustração. Folha pautada com a informação: Materiais: 300 cm de fita dourada. 150 cm de fita roxa. 150 cm de fita verde. 1 m de fita laranja.

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.

MANUAL DO PROFESSOR

Atividade 7

Realizar estimativas exige o uso da experiência pessoal dos estudantes, que devem observar, por exemplo, que a altura do muro não pode ser 20 centímetros porque é maior que a altura do homem, assim como a mesa não poderia ter altura de 2 metros.

Atividade 8

Os estudantes devem identificar a situação em que o uso de cada instrumento de medida é mais adequado ou não, na opinião deles, para fazer a medição de comprimentos. Por exemplo, peça a eles que meçam o contorno do punho com uma régua, de modo que verifiquem que o resultado obtido é impreciso. Se for possível, leve esses instrumentos de medida para a classe e verifique se a turma conhece outras situações de uso social para eles.

Atividade 9

Para realizar a atividade, os estudantes devem compreender que, para adicionar medidas (de grandezas de mesma espécie), precisam expressá-las em uma mesma unidade de medida, como nos exemplos a seguir.

Expressar 1 m em centímetros, ou seja, 100 cm, e adicionar todas as medidas em centímetros: 300 cm + 150 cm + 150 cm + 100 cm = 700 cm.

E, por fim, expressar o total obtido em metros: 7 metros.

Adicionar as medidas em centímetros, expressar o total obtido em metros e acrescentar ao 1 m de fita laranja: 300 cm + 150 cm + 150 cm = 600 cm

600 cm = 6 m

6 m + 1 m = 7 m

Socialize as estratégias utilizadas e valide-as com os estudantes.

BNCC em foco:

EF03MA18, EF03MA19

MP206

Comparando áreas

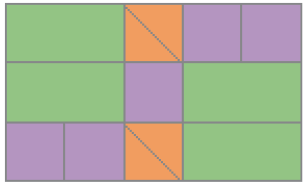
  1. Paula e Luciano fizeram um mosaico retangular cada um, usando algumas peças coloridas.

Mosaico de Paula

Ilustração. Mosaico de Paula, composto por quatro retângulos verdes, quatro triângulos laranja e cinco quadrados roxos.

Mosaico de Luciano

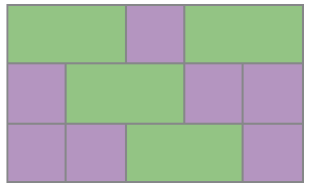
Ilustração. Mosaico de Luciano, composto por quatro retângulos verdes e sete quadrados roxos.

As peças roxas usadas pelos dois são todas iguais, assim como as verdes são iguais entre si, e todas as de cor laranja também são idênticas.

  1. Complete com a quantidade de cada tipo de peça usada por Paula e por Luciano na composição do mosaico.

Paula:

_____ Ilustração. Retângulo verde.

PROFESSOR Resposta: 4

_____ Ilustração. Quadrado roxo.

PROFESSOR Resposta: 5

_____ Ilustração. Triângulo laranja.

PROFESSOR Resposta: 4

Luciano:

_____ Ilustração. Retângulo verde.

PROFESSOR Resposta: 4

_____ Ilustração. Quadrado roxo.

PROFESSOR Resposta: 7

_____ Ilustração. Triângulo laranja.

PROFESSOR Resposta: 0
  1. Se Paula tivesse usado apenas peças laranjas qual seria a medida da área de seu mosaico, usando a peça laranja como unidade de medida?

    _____

    PROFESSOR Resposta: 30 peças laranjas.
  1. Caso Luciano tivesse usado apenas peças roxas, qual seria a medida da área de seu mosaico, usando a peça roxa como unidade de medida?

    _____

    PROFESSOR Resposta: 15 peças roxas.
  1. Sabendo que 2 peças laranjas ocupam a mesma área de 1 peça roxa, é possível dizer que a área ocupada pelo mosaico de Paula e pelo mosaico de Luciano é igual ou diferente?

    _____

    PROFESSOR Resposta: Igual.
MANUAL DO PROFESSOR

Objetivos

Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

Comparar, visualmente ou por superposição, áreas de figuras planas.

Nessas páginas, iniciamos o trabalho com medidas de superfície. Para desenvolver essa noção, dê exemplos de superfícies variadas, como o tampo de uma mesa, a superfície na lousa, uma folha do caderno, a face de um cubo, a face de uma pirâmide, a base circular de um cilindro ou de um cone etc., de modo que eles percebam que à noção de superfície associamos duas dimensões (comprimento e largura, por exemplo).

Comente com os estudantes que a medida de uma superfície é denominada área.

Para dar mais significado a esse conceito, nesse primeiro estudo trabalhamos com a comparação de áreas de figuras planas por meio da visualização ou da superposição, utilizando unidades de medida de modo que sejam obtidas medidas inteiras.

Atividade 1

Se possível, confeccione as peças dos mosaicos (pode ser com a turma) para que os estudantes possam manusear, sobrepor uma peça à outra, cobrir uma peça com outra e, assim, perceber as relações entre as áreas dessas peças e compará-las. Depois dessa exploração, proponha as questões do livro.

Essa atividade tem por objetivo levar o estudante à importante conclusão de que toda medida depende da unidade de medida adotada.

BNCC em foco:

EF03MA17, EF03MA21

MP207

  1. Observe as figuras abaixo.
Ilustração. Quadrado laranja, triângulo azul e retângulo verde.

Com 2 figuras azuis, podemos formar 1 figura laranja. E com 2 figuras laranjas podemos formar 1 figura verde.

  1. Quantas figuras azuis são necessárias para formar 1 figura verde?

    _____

    PROFESSOR Resposta: 4 figuras.
  1. Quantas figuras são necessárias para formar 2 figuras verdes, usando pelo menos 1 figura azul e 1 figura laranja?

    _____

    PROFESSOR Exemplo de resposta: 1 figura laranja e 6 figuras azuis.
  1. Qual das 3 figuras tem a maior área? Por quê?

    _____

    PROFESSOR Resposta: A figura verde, pois uma figura verde pode ser formada com as outras figuras.
  1. Se 1 figura verde pode ser formada com 2 figuras laranjas, a área da figura laranja é a metade ou o dobro da área da figura verde?

    _____

    PROFESSOR Resposta: Metade.

    Ícone: oral.

  1. Imagine um painel formado por 6 figuras laranjas e um painel formado por 3 figuras verdes. Qual terá a maior área? Justifique sua resposta.
    PROFESSOR Resposta: Os dois painéis terão área igual, pois 2 figuras laranjas equivalem a 1 figura verde; assim, uma área formada por 6 figuras laranjas equivale a uma área formada por 3 figuras verdes.

Boxe complementar:

Desafio

Quantas tábuas são necessárias para cobrir o piso?

_____

Resposta: 6 tábuas.

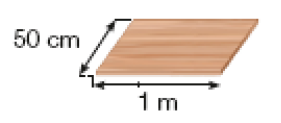
Tábua

Ilustração. Tábua de madeira medindo 50 cm de comprimento e 1 m de largura.

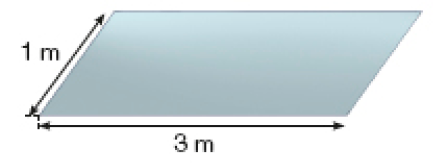
Piso

Ilustração. Piso medindo 1 m de comprimento e 3 m de largura.

CRÉDITO: GEORGE TUTUMI

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 2

Se possível, confeccione as peças para essa atividade também.

Depois que os estudantes responderem às questões, peça a eles que compartilhem as respostas com os colegas.

No item b, explore com a turma as possibilidades de resposta.

1 figura laranja e 6 figuras azuis;

2 figuras laranjas e 4 figuras azuis;

3 figuras laranjas e 2 figuras azuis.

Converse com os estudantes sobre a impossibilidade de usar apenas 1 figura azul para compor com figuras laranjas e obter a figura verde. Eles podem ainda listar a situação em que se usam 4 figuras laranjas para obter 2 figuras verdes. Ressalte que essa opção não é válida, pois é dada a condição de que deve ser usada pelo menos 1 figura azul e 1 figura laranja.

Desafio

Para saber quantas tábuas cabem no piso, sugira aos estudantes que decalquem a imagem da tábua e superponham essa figura ao piso, fazendo coincidir um dos vértices. Desse modo, eles poderão comparar o comprimento de cada lado das duas figuras e estimar quantas vezes cada lado da tábua, tomada como unidade de medida, cabe nos respectivos lados do piso. Assim, os estudantes poderão perceber que o lado da tábua que tem 1 metro de comprimento cabe 3 vezes no lado do piso de 3 metros de comprimento, e o lado da tábua de 50 centímetros de comprimento cabe 2 vezes no lado do piso de 1 metro (ou 100 centímetros) de comprimento, o que mostra que são necessárias 6 tábuas dessas para cobrir esse piso.

BNCC em foco:

EF03MA21

MP208

Jogo: Memória de medidas

Ícone: dupla.

Material: 12 cartas da página 219.

Jogadores: 2

Ícone: Material complementar.

Regras:

Ilustração. Doze cartas viradas para baixo. Em cada uma, a frase: Memória de medida e no centro há uma fita métrica.
MANUAL DO PROFESSOR

Objetivos

Estimar, medir e comparar comprimentos, utilizando unidades de medida padronizadas mais usuais (metro, centímetro e milímetro).

Escolher a unidade de medida mais apropriada para expressar medições de comprimento.

Ajude os estudantes na leitura e na compreensão das regras. Para facilitar a manipulação e melhorar a durabilidade das cartas, oriente-os a, antes de recortarem as cartas, colarem a folha retirada do livro em outro papel, mais consistente (cartolina, por exemplo). Proponha a eles que joguem uma rodada para verificar se entenderam o funcionamento do jogo.

Os estudantes devem se lembrar das equivalências entre as unidades de medida envolvidas. Se julgar necessário, antes do início do jogo, lembre-os de que 1 cm = 10 mm e que 1 m = 100 cm.

BNCC em foco:

EF03MA18, EF03MA19

MP209

Questões sobre o jogo

  1. Quais são as unidades de medida de comprimento apresentadas no jogo?

    _____

    PROFESSOR Resposta: Milímetro, centímetro e metro.
  1. Joana e Clóvis estão jogando o jogo Memória de medidas.
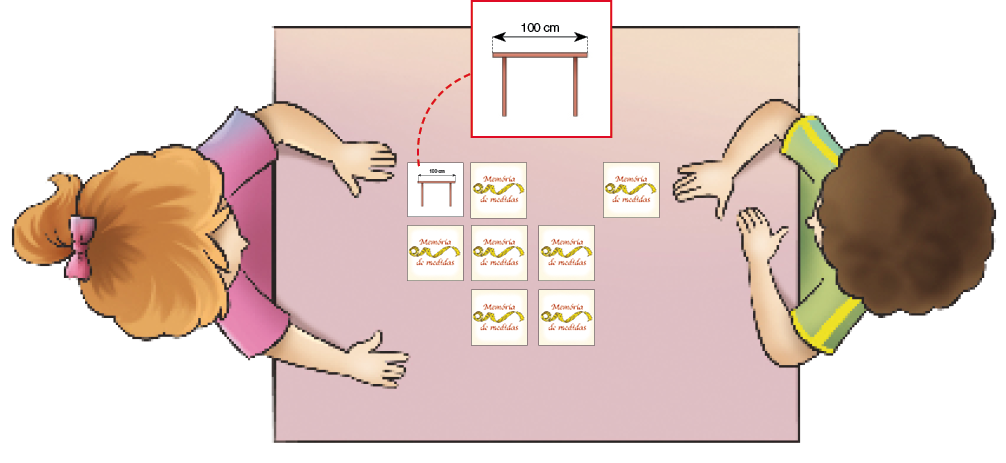
Ilustração. Vista de cima de Joana, menina loira com cabelo preso e camiseta rosa e Clóvis, menino com cabelo encaracolado e camiseta verde. Eles estão nas laterais de uma mesa e entre eles há sete cartas viradas para baixo. À esquerda, uma carta está virada para cima com o desenho de uma mesa e a largura de 100 cm.

( )

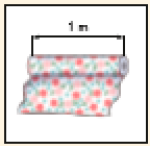
Ilustração. Carta com o desenho de um rolo de tecido florido, medindo 1 m de largura.

( )

Ilustração. Carta com o desenho de um jacaré medindo 400 cm de largura.

( )

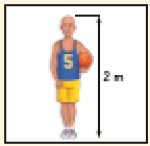
Ilustração. Carta com o desenho de um homem em pé medindo 2 m de comprimento.
PROFESSOR Resposta: tecido.
  1. Clóvis virou a carta a seguir.
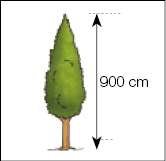
Ilustração. Carta com o desenho de uma árvore medindo 900 cm de comprimento.
  1. Das unidades de medida presentes no jogo, qual delas é a mais adequada para expressar medida de comprimentos bem pequenos?

    _____

    PROFESSOR Resposta: Milímetro.
MANUAL DO PROFESSOR

Questões sobre o jogo

Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões propostas. Elas auxiliam na compreensão das estratégias de jogo.

Na questão 1, espera-se que os estudantes já percebam que as unidades de medida que aparecem no jogo são o milímetro, o centímetro e o metro.

Na questão 2, espera-se que os estudantes associem a carta que indica 1 m à carta que Joana virou (que indica 100 cm). Caso escolham outra, solicite que exponham como pensaram e que um colega voluntário verifique em que ponto o colega se equivocou.

Na questão 3, verifique se os estudantes compreenderam o jogo e que 100 cm correspondem a 1 m.

Na questão 4, espera-se que o estudante mobilize os conhecimentos que construiu acerca das medidas de comprimento e identifique o milímetro como a unidade mais adequada.

BNCC em foco:

EF03MA18, EF03MA19

MP210

Medidas de massa

  1. Observe os dois pacotes de batata palito a seguir.

Pacote 1

Ilustração. pacote 1 de batata palito grande.

Pacote 2

Ilustração. pacote 2 de batata palito pequeno.

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.

Cirlene precisa comprar a maior massa de batatas que puder. Qual dos dois pacotes ela deve escolher? Explique sua resposta.

_____

PROFESSOR Resposta: O pacote 1, pois, sendo maior, ele terá uma quantidade maior de batatas e, assim, uma massa maior.
  1. Gabriel e Miguel estão preparando o cimento para fazer o chão da garagem da casa onde moram. Cada um deles comprou um saco de cimento, observe.
Ilustração. saco de cimento de Gabriel: saco pequeno de cimento.
Ilustração. saco de cimento de Miguel: saco de cimento grande.
  1. Avaliando a massa total dos sacos de cimento, quem conseguirá uma quantidade maior de cimento: Gabriel ou Miguel? _____
    PROFESSOR Resposta: Miguel.
  1. Se o saco de cimento de Gabriel tivesse a metade da massa do saco de cimento de Miguel, quantos sacos de cimento iguais ao de Gabriel seriam necessários para produzir a mesma quantidade de cimento que um saco de cimento de Miguel? _____
    PROFESSOR Resposta: 2 sacos.
MANUAL DO PROFESSOR

Objetivo

Estimar, medir e comparar massas, utilizando unidades de medida não padronizadas e padronizadas mais usuais (quilograma, grama e miligrama).

Atividade 1

Na atividade, os estudantes devem associar ao maior pacote a maior massa e ao menor pacote a menor massa. Porém, é importante explicar a eles que essa é uma premissa verdadeira apenas porque, nesse caso, o produto das duas embalagens é exatamente o mesmo (batatas palito). Se os produtos fossem diferentes, não seria possível comparar a massa dos dois pacotes com base apenas no tamanho.

Atividade 2

Promova situações similares para os estudantes vivenciarem em sala de aula. Se necessário, retome com eles a noção de metade.

BNCC em foco:

EF03MA20

MP211

Quilograma, grama e miligrama

  1. Ademar trabalha em uma fábrica de sal refinado. Ele opera a máquina que embala o sal refinado em pacotinhos de 1.000 miligramas cada um.

Para vender esses pacotinhos, a fábrica os embala em caixas com 1.000 pacotinhos cada uma.

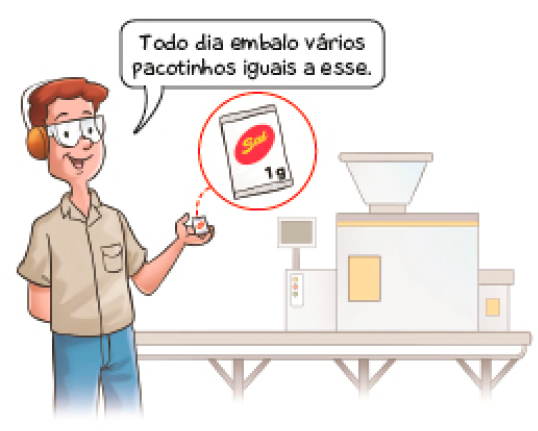
Ilustração. Ademar, homem com cabelo castanho, óculos e fones de proteção está segurando um pacote pequeno de sal. Ele fala: Todo dia embalo vários pacotinhos iguais a esse. Ao lado, destaque para o pacote com a informação: Sal 1 g. Ao fundo, uma máquina.
  1. 1 grama corresponde a quantos miligramas?

    _____

    PROFESSOR Resposta: 1.000 miligramas.
  1. 1 quilograma corresponde a quantos gramas?

    _____

    PROFESSOR Resposta: 1.000 gramas.

Indicamos:

  1. Estime e complete com a unidade de medida adequada: miligrama, grama ou quilograma.
    1. Emagreci 3 _____ no mês de janeiro.
      PROFESSOR Resposta: quilogramas
    1. Comprei na padaria 200 _____ de salame fatiado.
      PROFESSOR Resposta: gramas
    1. O comprimido que Carina tomou é de 10 _____.
      PROFESSOR Resposta: miligramas
  1. Estime e complete as frases com mais ou com menos.
    1. Um automóvel tem _____ de 150 kg.
      PROFESSOR Resposta: mais
    1. Uma lapiseira tem _____ de 1 kg.
      PROFESSOR Resposta: menos
MANUAL DO PROFESSOR

Atividade 1

Aproveite a situação apresentada no texto para perguntar:

Quantos gramas de sal refinado há em cada caixa?

E quantos quilogramas de sal refinado cada uma dessas caixas comporta?

Apresente aos estudantes a relação 1 kg = 1.000 g e discuta com eles essa questão. Espera-se que os estudantes percebam que, como cada caixa contém 1.000 pacotinhos de sal e cada um desses pacotinhos tem 1.000 mg, ou seja, 1 g, cada caixa tem 1.000 g, ou 1 kg, de sal refinado.

Atividade 2

Nessa atividade, os estudantes devem estimar a massa descrita e associá-la à unidade de medida mais adequada em cada caso.

É importante utilizar a linguagem adequada com os estudantes, para que eles possam reconhecer os equívocos ocorridos nas práticas sociais. Comente que a leitura correta do item b é “Comprei duzentos gramas de...”, pois a unidade de medida de massa grama é um substantivo masculino. No item a, o correto é“Emagreci 3 quilogramas”, em vez de “Emagreci 3 quilos”.

Atividade 3

Leve os estudantes a outros locais da escola (pátio, quadra, biblioteca etc.) e peça a eles que estimem a massa de objetos variados para depois comparar a estimativa feita com um pacote que tenha massa de 1 quilograma. Essa experimentação os auxiliará a realizar as estimativas pedidas na atividade.

BNCC em foco:

EF03MA20

MP212

Ícone: mental.

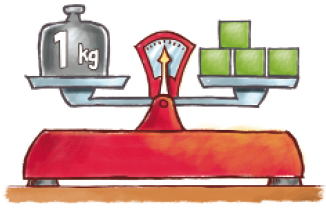
  1. A balança abaixo está em equilíbrio, e as caixas verdes têm a mesma massa.

    Qual é a massa, em grama, de cada caixa verde?

    _____

    PROFESSOR Resposta: 250 gramas.
Ilustração. Balança de pratos em equilíbrio. No prato à esquerda, um peso de 1 kg e no prato à direita, quatro caixas verdes.

Ícone: Desenho ou pintura.

  1. Pinte os quadradinhos conforme a medida de massa indicada em cada caso.

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.

Ilustração. Uma menina loira com muletas fala: Cada quadradinho representa 100 g.
fotografia. um cacho de uvas dentro de uma sacola e uma etiqueta indicando 500 g.
Ilustração. vinte quadradinhos. Há cinco quadradinhos pintados.
fotografia de laranjas dentro de uma sacola e uma etiqueta indicando 2 kg.
Ilustração. vinte quadradinhos. Todos os quadradinhos estão pintados.
fotografia de maçãs dentro de uma sacola e uma etiqueta indicando 1 kg.
Ilustração. vinte quadradinhos. Há dez quadradinhos pintados.
  1. José e Lúcia compraram, em supermercados diferentes, 2 kg de café cada um, da mesma marca e do mesmo tipo.
Ilustração. José, homem com cabelo grisalho está segurando dois pacotes de café com 1 kg cada. Na frente dele há uma prateleira com vários pacotes de café. Acima há uma placa com a informação: PACOTE DE 1 KG POR 5 REAIS.
Ilustração. Lúcia, mulher ruiva está segurando quatro pacotes de café com 500 g cada. Na frente dela há uma prateleira com vários pacotes de café. Acima há uma placa com a informação: PACOTE DE 500 G POR 3 REAIS.
MANUAL DO PROFESSOR

Objetivos

Estimar, medir e comparar massas, utilizando unidades de medida padronizadas mais usuais (quilograma e grama).

Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.

Estimar, medir e comparar capacidade, utilizando unidades de medida não padronizadas.

Atividade 4

Retome com os estudantes o princípio da balança de dois pratos e pergunte: “O que significa dizer que a balança está em equilíbrio?”. (Quando os pratos estão na mesma altura, ou seja, os dois pratos estão com a mesma massa.) Como as caixas verdes têm massas iguais e usando a relação 1 kg = 1.000 g, eles poderão perceber que a massa de cada caixa verde é de 250 gramas, pois:

4 × 250 g = 1.000 g = 1 kg.

Atividade 5

O uso de sequências de quadradinhos de mesmo tamanho para representar a massa total de pacotes de alimentos possibilita aos estudantes relacionar as unidades de medida quilograma e grama. Como cada quadradinho representa 100 gramas, uma massa de 2 quilogramas, como a do segundo item, será representada por 20 quadradinhos.

Para explorar mais a atividade, pode-se perguntar o contrário:

Se foram pintados 15 quadradinhos, quantos gramas havia de fruta?

Espera-se que os estudantes concluam que havia 1 500 gramas de frutas.

Uma estratégia que eles podem usar é observar a representação dos pacotes de 500 g e de 1 kg (ou 1.000 g) e verificar que, ao serem adicionados os quadradinhos pintados nessas duas representações, são obtidos 15 quadradinhos.

Atividade 6

Os estudantes podem pensar assim:

Compra de José

Cada pacote de 1 kg custa 5 reais; são necessários 2 pacotes de 1 kg para formar 2 kg.

Logo, José pagou 10 reais.

Compra de Lúcia

Cada pacote de 500 g custa 3 reais; são necessários 4 pacotes de 500 g para formar 2 kg.

Logo, Lúcia pagou 12 reais.

Assim, eles podem concluir que Lúcia pagou 2 reais a mais que José.

BNCC em foco:

EF03MA20

MP213

Medidas de capacidade

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.

  1. Jurema e Roberta foram à padaria e pediram uma xícara de um mesmo tipo de achocolatado cada uma. Observe as xícaras que cada uma recebeu e responda às questões.
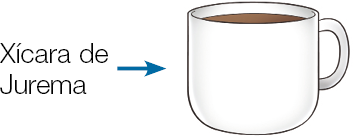
Ilustração. uma xícara grande (Xícara de Jurema).
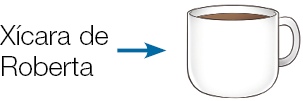
Ilustração. uma xícara pequena (Xícara de Roberta).
  1. A quantidade de achocolatado de Jurema e de Roberta é a mesma?

    _____

    PROFESSOR Resposta: Não.
  1. É justo que Jurema e Roberta paguem o mesmo valor pela xícara de achocolatado recebida? Explique sua resposta.

    _____

    PROFESSOR Resposta: Não.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que o certo é Jurema pagar um valor maior, visto que sua xícara é maior e contém mais achocolatado que a de Roberta. Fim da observação.
  1. Jeremias vai limpar a caixa-d'água de sua casa e, para isso, é necessário esvaziá-la. Na sua área de serviço, há dois baldes, mas ele só poderá usar um deles. Observe os baldes abaixo.
Ilustração. Um balde grande rosa e um balde pequeno e azul.
  1. Jeremias precisa escolher o balde que, ao usar sua capacidade, ajude-o a esvaziar a caixa-d'água mais rapidamente.

    Qual balde ele deve escolher? _____

    PROFESSOR Resposta: O balde maior.
  1. Por que o balde a ser escolhido por Jeremias vai ajudá-lo a esvaziar a caixa-d'água mais rapidamente que o outro? Explique sua resposta.

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que, quanto maior for o balde escolhido, menor será o tempo e a quantidade de baldes a ser retirados da caixa-d’água. Assim, pode realizar o trabalho mais rapidamente. Fim da observação.
MANUAL DO PROFESSOR

Objetivo

Estimar, medir e comparar capacidades, utilizando unidades de medida não padronizadas.

Desde a Educação Infantil, os estudantes desenvolvem diversos processos mentais que possibilitam a aprendizagem matemática, entre eles o processo da conservação.

No caso da grandeza capacidade, trata-se de compreender que a transferência de uma quantidade de líquido de um recipiente para outro, de formato diferente, não altera a quantidade de líquido. Essa noção possibilita ao estudante a comparação entre capacidades.

Atividade 1

Nessa atividade, os estudantes precisam comparar a capacidade das xícaras de Jurema e de Roberta e concluir que quem deve pagar mais é aquela que recebeu a xícara de maior capacidade.

Atividade 2

Espera-se que os estudantes percebam que, quanto maior for o balde, menores serão o tempo e a quantidade de baldes a serem retirados da caixa-d’água.

BNCC em foco:

EF03MA17, EF03MA20

MP214

Litro e mililitro

  1. Paula está fazendo um suco. Ela colocou 4 copos cheios de água em uma jarra.
Ilustração. Paula, menina ruiva com regata laranja. Ela está virando um copo e despejando água dentro de um jarro de 1 litro. Ela fala: 4 copos, com 250 mililitros de água cada um, encheram esta jarra em que cabe 1 litro de água. Ao lado há três copos.

Indicamos:

  1. Qual foi a quantidade de água que Paula colocou na jarra?

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes compreendam que 1 litro é o mesmo que 1.000 mililitros. Fim da observação.
  1. Quantos mililitros de água cabem em cada copo de Paula?

    _____

    PROFESSOR Resposta: 250 mililitros.
  1. 1 litro corresponde a quantos mililitros?

    _____

    PROFESSOR Resposta: 1.000 mililitros.
  1. Faça estimativas e responda, em cada caso, se no recipiente cabe mais de 1 litro ou menos de 1 litro de água.

a)

Ilustração. Uma mulher com cabelo castanho e camisa verde está sorrindo e segurando um copo com água.

_____

PROFESSOR Resposta: Menos de 1 litro.
Ilustração. Um menino com cabelo encaracolado e camiseta amarela está sorrindo. Na frente dele há um galão de água sobre um filtro.

_____

PROFESSOR Resposta: Mais de 1 litro.

c)

Ilustração. Um homem com camisa bege está sorrindo e segurando um balde amarelo.

_____

PROFESSOR Resposta: Mais de 1 litro.
MANUAL DO PROFESSOR

Objetivo

Estimar, medir e comparar capacidades, utilizando unidades de medida padronizadas mais usuais (litro e mililitro).

Atividade 1

A atividade possibilita aos estudantes estabelecerem, por meio de medidas exatas, a relação entre as unidades litro e mililitro. Comente com eles que, apesar de em receitas culinárias serem utilizadas medidas em xícaras e copos, essas unidades de medida de capacidade não são padronizadas. Pergunte:

Quantos copos devem ser usados para medir a quantidade de leite necessária para fazer uma receita na qual se usa 1 litro de leite?

Os estudantes devem perceber que a resposta depende da quantidade de leite que cabe no copo utilizado.

No item c, se julgar oportuno, pergunte aos estudantes: “Meio litro corresponde a quantos mililitros?“ (500 mililitros).

Atividade 2

Na atividade, é explorada a habilidade de os estudantes fazerem estimativas em relação a 1 litro, muito útil no cotidiano. Se possível, leve para a sala de aula embalagens vazias de recipientes cuja capacidade seja 1 litro, para que os estudantes desenvolvam a noção dessa quantidade de líquido. Essa observação os auxiliará no momento de realizar as estimativas.

BNCC em foco:

EF03MA20

MP215

  1. Observe o folheto de propaganda e responda à questão.

    Em qual dos recipientes cabe mais suco? Por quê?

Ilustração. Folheto com a informação: Ofertas. À esquerda, uma garrafa com etiqueta e a informação: SUCO DE MAÇÃ 350 ML. À direita, uma garrafa com etiqueta e a informação: SUCO DE UVA 600 ML.

Atenção! Compare apenas as medidas de capacidade dos recipientes, pois eles não estão representados proporcionalmente entre si.

_____

PROFESSOR Resposta: Na garrafa de suco de uva. Exemplo de explicação: Porque a garrafa de suco de uva tem capacidade de 600 mL e a capacidade da garrafa de suco de maçã é de apenas 350 mL.

Ícone: mental.

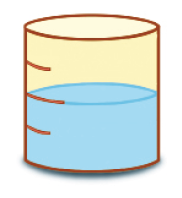
  1. Em cada recipiente cheio, cabe 1 litro de água. Quantos mililitros de água há em cada recipiente?

a)

Ilustração. Um copo medidor com três riscos. Dentro há água até o segundo risco.

_____ mililitros

PROFESSOR Resposta: 500

b)

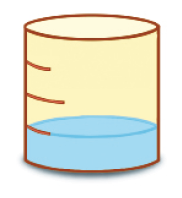
Ilustração. Um copo medidor com três riscos. Dentro há água até o primeiro risco.

_____ mililitros

PROFESSOR Resposta: 250

c)

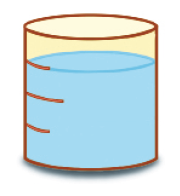
Ilustração. Um copo medidor com três riscos. Dentro há água até o terceiro risco.

_____ mililitros

PROFESSOR Resposta: 750
  1. Observe o que as crianças estão dizendo e responda à questão.
Ilustração. À esquerda, Ricardo, menino com cabelo encaracolado e camiseta amarela. Ele levanta dois dedos e fala: Eu bebi 2 copos cheios de suco. Na frente dele há um copo com 250 mL. No centro, Ana, menina ruiva com tiara e camiseta verde está com as mãos para cima. Ela diz: Eu bebi 4 copos cheios de suco. Na frente dela há um copo com 150 mL. À direita, Carolina, menina com cabelo encaracolado e camiseta roxa está com a mão direita sobre o peito. Ela fala: Eu bebi 2 copos cheios de suco. Na frente dela há um copo com 375 mL.
MANUAL DO PROFESSOR

Atividade 3

Na atividade, o risco é de os estudantes associarem o tamanho aparente da embalagem com a quantidade de líquido que ela contém. Para a resolução correta, eles devem considerar a capacidade impressa em cada embalagem.

Espera-se que os estudantes percebam que, apesar de o recipiente da esquerda estar representado em tamanho maior que o da direita, sua capacidade é menor.

Situações como essa possibilitam a formação de um raciocínio matematicamente crítico, muito desejável nas decisões de compra, sobretudo na comparação entre custo e benefício. Chame a atenção dos estudantes para a observação de folhetos publicitários, em que a imagem mostrada não retrata o tamanho real do produto.

Atividade 4

Antes da resolução, comente com os estudantes que os recipientes são idênticos e explique o que significam as marcas nas laterais dos recipientes. Sabendo que as marcas determinam intervalos iguais, peça a eles que observem que, no item a, a água ocupa metade da capacidade do recipiente; no item b, a água ocupa metade da metade da capacidade do recipiente; e, no item c, a água ocupa a metade mais a metade da metade da capacidade do recipiente. Aproveite para perguntar:

Como é possível saber a quantos mililitros corresponde o intervalo entre duas marcas sucessivas do recipiente?

Espera-se que os estudantes percebam que, como 1 litro equivale a 1.000 mililitros e há quatro intervalos iguais, cada intervalo representa 250 mL de capacidade (4 × 250 mL = 1.000 mL).

Atividade 5

Para responder à questão proposta, os estudantes precisam fazer o cálculo com as diferentes medidas dos copos utilizados pelas crianças.

BNCC em foco:

EF03MA20

MP216

Compreender problemas

Para resolver

Problema 1

Durante os quatro primeiros meses de 2023, Isolda anotou os milímetros de precipitação pluviométrica da cidade onde mora. Depois, organizou os dados no gráfico abaixo.

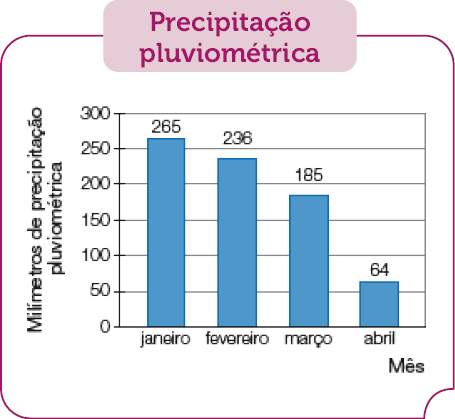
Gráfico de colunas. Precipitação pluviométrica. No eixo vertical, os milímetros de precipitação pluviométrica e no eixo horizontal, o mês. janeiro: 265 milímetros. fevereiro: 236 milímetros. março: 185 milímetros. abril: 64 milímetros.

Fonte: Anotações de Isolda. (abr. 2023)

  1. Qual foi o total, em milímetro, de precipitação acumulado nesses quatro meses de 2023?

    _____

    PROFESSOR Resposta: 750 milímetros.
  1. Esses milímetros correspondem a quantos centímetros? _____
    PROFESSOR Resposta: 75 centímetros.

Problema 2

Paulo, Felipe e Jonas treinam arremesso de disco. O gráfico a seguir mostra a distância que cada um arremessou.

Gráfico em barras. Distância dos arremessos. No eixo vertical, o atleta e no eixo horizontal, a distância (em centímetro). Paulo: 680 cm. Felipe: 940 cm. Jonas: 420 cm.

Fonte: Os três atletas. (ago. 2023)

  1. Qual atleta arremessou mais longe? _____
    PROFESSOR Resposta: Felipe.
  1. Quais atletas obtiveram o arremesso com a distância maior que 5 metros? _____
    PROFESSOR Resposta: Paulo e Felipe.
  1. Qual atleta realizou o arremesso com a distância mais próxima de 10 metros? _____
    PROFESSOR Resposta: Felipe.

    Ícone: oral.

    Ícone: dupla.

  1. Explique para um colega como você pensou para responder à pergunta anterior e ouça a explicação dele.
    PROFESSOR Resposta: Resposta pessoal.
MANUAL DO PROFESSOR

Objetivos

Estimar, medir e comparar comprimentos, utilizando unidades de medida padronizadas mais usuais (metro, centímetro e milímetro).

Resolver problemas cujos dados estão apresentados em gráficos de barras.

Os problemas propostos nessa página exploram a busca de dados em gráficos. Peça aos estudantes que observem atentamente todas as informações apresentadas nos gráficos.

Para resolver

Para responder ao item a do Problema 1, os estudantes devem ler os dados referentes à precipitação pluviométrica de cada mês e adicioná-los.

Para os estudantes responderem ao item b, devem expressar 750 mm em centímetros. Lembre-os de que 1 centímetro tem 10 milímetros, ou seja, os estudantes precisam determinar quantos grupos de 10 milímetros é possível formar com 750 milímetros. Espera-se que eles concluam que são 75. Logo, 750 mm = 75 cm.

Aproveite o momento para conversar com a turma sobre a importância de economizar água.

No Problema 2, além de ler e interpretar as informações do gráfico, os estudantes precisam fazer estimativas e arredondamentos.

Para responder ao item b, os estudantes precisam comparar cada distância de arremesso com 5 metros, ou seja, com 500 centímetros, observando que:

680 cm > 500 cm;

940 cm > 500 cm e

420 cm < 500 cm

No item c, para fazer os arredondamentos, os estudantes devem observar que 10 metros correspondem a 1.000 centímetros. Assim, espera-se que eles percebam que 940 centímetros é a distância de arremesso mais próxima dos 10 metros.

O Problema 1 enseja um trabalho interdisciplinar com Ciências da Natureza. Talvez seja oportuno explicar sobre precipitação pluviométrica. Informações disponíveis em: http://fdnc.io/eU3 e http://fdnc.io/eU4. Acesso em: 27 jan. 2021.

BNCC em foco:

EF03MA19, EF03MA26

MP217

Para resolver

  1. Para responder às perguntas do Problema 1, você usou todos os números do gráfico? Precisou usar algum número que não estava no gráfico?

    _____

    PROFESSOR Resposta: Respostas pessoais.
  1. Veja como Glória resolveu o Problema 1.
Ilustração. Folha de papel com o texto: Janeiro, fevereiro, março e abril: 265 milímetros, mais 236 milímetros, mais 185 milímetros, mais 64 milímetros são 750 milímetros. Como 1 centímetro tem 10 milímetros, 750 milímetros são o mesmo que 75 centímetros. Conclusão: nesses quatro meses de 2023, o total de precipitação acumulado foi de 75 centímetros.

Ícone: mental.

  1. Marque com um X todas as afirmações abaixo que estão corretas de acordo com o gráfico do Problema 2.

    ( ) A diferença entre as distâncias dos arremessos de Paulo e Jonas é maior que 1 metro.

    ( ) O dobro da distância do arremesso de Jonas é menor que a distância do arremesso de Felipe.

    ( ) O arremesso de Felipe ultrapassou 10 metros.

    PROFESSOR Respostas corretas: A diferença entre as distâncias dos arremessos de Paulo e Jonas é maior que 1 metro. O dobro da distância do arremesso de Jonas é menor que a distância do arremesso de Felipe
  1. Quantos centímetros representa cada quadradinho do gráfico do Problema 2? _____
    PROFESSOR Resposta: 200 centímetros.
MANUAL DO PROFESSOR

Para refletir

Na atividade 1, espera-se que os estudantes afirmem que, para responder às perguntas do Problema 1, usaram o número de milímetros de precipitação pluviométrica correspondente a cada um dos 4 meses: 265, 236, 185 e 64. Também se espera que respondam que precisaram usar a informação de que 1 centímetro tem 10 milímetros, e essa informação não está no gráfico.

Na atividade 2, peça aos estudantes que comparem a resolução de Glória com a solução dada por eles para o Problema 1, de modo que percebam similaridades e diferenças.

Explore a atividade 3 pedindo aos estudantes que criem duas novas perguntas com base nos dados do gráfico do Problema 2 e que troquem as novas questões com um colega, para resolvê-las. Eles podem fazer perguntas do tipo: “Qual é a diferença entre a distância do arremesso de Felipe e de Paulo? Quanto faltou para o arremesso de Felipe chegar à distância de 1.000 cm?”. (260 cm; 60 cm.)

Na atividade 4, espera-se que os estudantes observem os quadradinhos completamente pintados associando às centenas completas dos valores das medidas. Verifique se os estudantes respondem corretamente, indicando o número e a unidade da medida correspondente a cada quadradinho: 200 centímetros.

BNCC em foco:

EF03MA19

Sugestão de leitura para o professor

Artigo

MONTEIRO, Carlos Eduardo Ferreira; SELVA, Ana Coelho Vieira. Investigando a atividade de interpretação de gráficos entre professores do Ensino Fundamental. Disponível em: http://fdnc.io/eU5. Acesso em: 11 fev. 2021.

Esse artigo mostra uma pesquisa sobre a interpretação de gráficos da mídia impressa, realizada por professores de 2ª e 4ª séries do Ensino Fundamental (atuais 3º e 5º anos). O objetivo é identificar os fatores que interferem nessa interpretação, investigar as estratégias dos professores para abordar os gráficos e fornecer subsídios para outras pesquisas sobre o tema.

MP218

A Matemática me ajuda a ser

... uma pessoa que respeita os animais

Você já viu uma tartaruga marinha? Conheça um pouco sobre ela.

Ilustração. Tartarugas verdes nadando no mar. No centro, vários filhotes de tartaruga estão andando na areia em direção ao mar. À esquerda, alguns filhotes estão nadando no mar.

Observação: Os elementos da imagem não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.

Nome popular:

Tartaruga-verde ou aruanã

Nome científico:

Chelonia mydas

Descrição

As tartarugas-verdes recebem esse nome porque seu casco tem cor verde ou verde-acinzentado. Elas chegam a ter 143 centímetros de comprimento curvilíneo do casco. A cabeça é pequena e elas possuem mandíbula serrilhada, que facilita sua alimentação. Geralmente, sua massa pode chegar a 200 kg.

Alimentação

O que comem varia ao longo da vida delas. Enquanto jovens, alimentam-se de plantas e organismos como águas-vivas, caranguejos, moluscos e vermes. Quando seu casco atinge o tamanho de 25 a 35 centímetros, tornam-se herbívoras (passam a se alimentar de vegetais).

Hábitat

Vivem em águas costeiras com muita vegetação, ilhas ou baías, onde estão protegidas. Raramente são vistas em alto-mar.

Ilustração. um buraco na areia da praia e dentro há ovos e um filhote de tartaruga

Reprodução

Quando a fêmea está pronta para pôr seus ovos, ela sai da água e rasteja até a areia, onde cava por horas. Ela, então, coloca de 100 a 200 ovos e cobre-os com areia para protegê-los do Sol, do calor e dos predadores. O período de incubação é de 40 a 72 dias, dependendo da localização.

Informações obtidas em: http://fdnc.io/eTX e http://fdnc.io/eTY. Acesso em: 13 fev. 2021.

A tartaruga-verde é muito ameaçada. Além dos predadores naturais, ela enfrenta os humanos. Os caçadores se alimentam de sua carne e usam seu casco na fabricação de bijuterias, como brincos, anéis e colares. As dificuldades não param por aí: muitas tartarugas se enroscam acidentalmente nas redes dos pescadores e morrem.

Para ajudar a proteger as tartarugas marinhas foi criado, pelo Instituto Brasileiro do Meio Ambiente e dos Recursos Naturais Renováveis (Ibama), o Projeto Tamar — o nome vem da combinação de letras do termo ta rtaruga mar inha. Esse projeto tem como principal missão a pesquisa, a conservação e o manejo das tartarugas marinhas que vivem no Brasil.

Tome nota

  1. Qual é a medida máxima do comprimento do casco de uma tartaruga-verde? Essa medida é maior ou menor que 1 metro?

    _____

    PROFESSOR Resposta: 143 centímetros; maior que 1 metro.
MANUAL DO PROFESSOR

Objetivos

Estimar, medir e comparar comprimentos.

Estimar, medir e comparar massas.

Ler e registrar medidas de tempo (dias e meses).

A leitura e a discussão dos textos apresentados nessa seção incentivam atitudes positivas em relação ao meio ambiente, em especial aos animais. Interpretando as várias informações aqui fornecidas, os estudantes conhecerão um pouco da vida das tartarugas marinhas. Caso os estudantes não compreendam alguma palavra do texto, explique a eles ou motive-os a buscar o significado em um dicionário.

Tome nota

Leia o texto principal com os estudantes. Escolha alguns voluntários para ler cada quadro informativo. Peça a eles que registrem um resumo dos dados na lousa. Incentive-os a sempre buscar as informações necessárias para responder às questões, relendo os textos (ou consultando os resumos na lousa).

Na atividade 1, os estudantes devem mobilizar seus conhecimentos e relembrar a relação 1 m = 100 cm para fazer a comparação do comprimento com 1 metro.

BNCC em foco:

EF03MA19, EF03MA20; competência específica 2

MP219

  1. Quantos dias dura a incubação de uma tartaruga fêmea? Esse período de tempo dura mais ou menos que 3 meses?

    _____

    PROFESSOR Resposta: De 40 a 72 dias; menos que 3 meses.
  1. Quando vai se reproduzir, a tartaruga fêmea coloca quantos ovos?

    _____

    PROFESSOR Resposta: De 100 a 200 ovos.
  1. Qual é a massa de uma tartaruga-verde? Essa massa é maior ou menor que 500 quilogramas?

    _____

    PROFESSOR Resposta: Geralmente, até 200 quilogramas; menor que 500 quilogramas.

Reflita

Ícone: oral.
MANUAL DO PROFESSOR

Nas atividades 2 e 3, discuta com os estudantes os intervalos de tempo e de quantidade de ovos que aparecem nas situações dessas atividades: de 40 a 72 dias; de 100 a 200 ovos.

Explique aos estudantes que, nesse tipo de intervalo, os valores das extremidades também são válidos. Além disso, para facilitar, considera-se cada mês com 30 dias, a fim de facilitar a comparação solicitada ao entender que 3 meses correspondem a 90 dias.

Na atividade 4, discuta com os estudantes o significado da expressão “até 200 kg”. Eles devem compreender que essa informação indica o valor máximo de massa, e não o valor exato dela. É possível encontrar tartarugas-verdes com massa menor que 200 kg, mas não maior.

Reflita

Pergunte sobre questões polêmicas, que envolvem o âmbito ético:

A natureza existe apenas para servir aos interesses humanos?

Por que é importante a preservação de animais e plantas?

Que riscos os próprios seres humanos correm ao destruir o meio ambiente?

Promover discussões sobre temas sociais relevantes e incentivar os estudantes a expressar suas opiniões é um modo muito produtivo de desenvolver a consciência cidadã.

BNCC em foco:

EF03MA19, EF03MA20; competência específica 2

Sugestão de trabalho interdisciplinar

O conteúdo da seção pode ser trabalhado de forma interdisciplinar com Ciências, discutindo a importância de preservar o meio ambiente e respeitar os animais. Reflexões sobre as consequências da extinção das espécies de alguns animais e da destruição do meio ambiente podem contribuir para a formação de cidadãos mais conscientes e atuantes.

MP220

Compreender informações

Estimar a chance de ocorrer

  1. Um dado comum lembra um cubo com suas faces compostas de figuras ou representações numéricas (de 1 a 6). Sofia vai jogar um dado e observar o número representado na face voltada para cima.
Fotografia. Um dado com o número 5 para cima.

Agora, responda às questões.

  1. Quais os resultados que Sofia pode obter no lançamento desse dado? _____
    PROFESSOR Resposta: 1, 2, 3, 4, 5 ou 6
  1. Quais resultados ímpares Sofia pode obter? _____
    PROFESSOR Resposta: 1, 3 ou 5
  1. E quais resultados pares? _____
    PROFESSOR Resposta: 2, 4 ou 6
  1. Qual resultado tem maior chance de ocorrer: par ou ímpar?

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que o resultado par e o resultado ímpar têm chances iguais de ocorrer. Fim da observação.

    e) Lucas, irmão de Sofia, observou os lançamentos e fez a seguinte afirmação.

Ilustração. Lucas, menino com cabelo castanho e camiseta azul está sentado e jogando um dado sobre uma mesa. Ele fala: O resultado 6 tem maior chance de ocorrer que os outros. Na frente dele, Sofia, menina loira com camiseta rosa observa e sorri.
MANUAL DO PROFESSOR

Objetivo

Identificar todos os resultados possíveis de um experimento aleatório e estimar quais eventos desse experimento têm maiores ou menores chances de ocorrência.

Embora estudos recentes indiquem que os estudantes são capazes de atribuir algum significado a situações que envolvam noções de chance, a organização das ideias sobre probabilidade não é um processo intuitivo para eles e, portanto, requer um trabalho mais atento.

Algumas falsas concepções nesse campo precisam ser rompidas, como a ideia de que tirar o número 6 no dado é mais difícil que tirar os demais números. Oferecer aos estudantes situações, reais ou simuladas, que envolvam ideias probabilísticas é um meio eficiente de desenvolver esse trabalho.

Atividade 1

A atividade explora a ideia de, maior ou menor chance de ocorrer um evento de um experimento aleatório. A situação é simples: lançamento de um dado comum (cúbico).

Comece perguntando aos estudantes quantas e quais são as faces do dado (item a) para que eles verifiquem todos os resultados possíveis desse experimento. Discuta com a turma o fato de, apesar de os resultados que podem ocorrer serem conhecidos, não se pode afirmar com certeza quais desses resultados ocorrerão.

No item e, espera-se que os estudantes discordem da afirmação de Lucas porque, apesar de o número 6 ser o maior entre os resultados possíveis, ele tem a mesma chance de ocorrer em relação aos demais resultados.

BNCC em foco:

EF03MA25; competência específica 4

MP221

  1. Marina e Juliana jogam futebol e são capitãs de dois times que se enfrentam. Antes de iniciar a partida, elas decidiram lançar uma moeda de 1 real para o alto para definir qual time começa com a bola.
    1. Complete a lacuna com os possíveis resultados:
Fotografia. Moeda de um real. No centro há o desenho em relevo do rosto de um homem.

_____

PROFESSOR Resposta: Cara
Fotografia. Moeda de um real. No centro há o número 1 e parte da bandeira do Brasil.

_____

PROFESSOR Resposta: Coroa

Ícone: oral.

  1. Se Marina escolher cara e Juliana escolher coroa, qual time tem a maior chance de sair com a bola?
PROFESSOR Atenção professor: Espera-se que os estudantes percebam que a chance de sair com a bola é a mesma para os dois times. Fim da observação.
  1. Cristiano e Rodrigo decidiram brincar com um dado cujas faces estão numeradas de 1 a 6. Veja o que cada um escolheu:
Ilustração. Cristiano, menino ruivo com cabelo encaracolado está com o dedo indicador apontado para frente. Ele fala: Acho que vai sair um número menor que 5. Na frente dele, Rodrigo, menino loiro com óculos está olhando para o lado. Ele diz: Acho que vai sair um número maior que 4.

Ícone: dupla.

  1. Para Cristiano acertar seu palpite, que números podem sair no lançamento do dado? _____
    PROFESSOR Resposta: 1, 2, 3 ou 4.
  1. E, para Rodrigo acertar, quais números podem sair no lançamento do dado? _____
    PROFESSOR Resposta: 5 ou 6.
  1. A chance de Cristiano acertar é maior ou menor que a de Rodrigo? Justifiquem.

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que Cristiano tem maior chance de acertar porque há mais números menores que 5 do que maiores que 4 entre os resultados possíveis no lançamento do dado. Fim da observação.
MANUAL DO PROFESSOR

Atividade 2

Inicialmente, proponha um jogo de cara ou coroa com os estudantes, com o intuito de discutir falsas concepções a respeito do assunto, como a ideia de que, ao sair cara em uma jogada, na próxima é mais provável sair coroa e vice-versa. Explique a eles que a moeda não tem “memória”, isto é, não se “lembra” do último resultado, de modo que a cada nova jogada a chance é sempre a mesma e igual tanto para cara como para coroa.

Atividade 3

Peça aos estudantes que comparem esta com a atividade 1 e verifiquem as diferenças. Espera-se que eles percebam que, na atividade 1, a chance de obter um resultado par é igual à de obter um resultado ímpar. Já na atividade 3, a chance de obter um número menor que 5 é maior que a de obter um número maior que 4.

BNCC em foco:

EF03MA25; competência específica 4

MP222

O que você aprendeu

  1. Osvaldo encomendou duas camas iguais com os irmãos Andrade. As camas deveriam ter 10 palmos de comprimento.
Ilustração. Duas camas, uma grande e uma média.

Cada irmão fez uma das camas usando seu próprio palmo como unidade de medida. Quando Osvaldo foi buscar as camas, ficou surpreso porque elas tinham medidas de comprimentos diferentes apesar de terem 10 palmos de comprimento.

  1. A unidade de medida usada pelos irmãos Andrade é padronizada?

    _____

    PROFESSOR Resposta: Não.
  1. Por que as camas ficaram com medidas diferentes?

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que a unidade de medida usada (palmo) é diferente para cada irmão. Fim da observação.
  1. Para que as camas ficassem com medidas iguais de comprimento, o que Osvaldo poderia ter feito quando realizou a encomenda?

    _____

    PROFESSOR Exemplo de resposta: Osvaldo poderia ter realizado a encomenda usando uma unidade de medida padronizada para indicar o comprimento que cada cama deveria ter.
MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

Propicie conversas entre os estudantes a respeito das estratégias que usaram para resolver as atividades.

Atividade 1

Na atividade, espera-se que os estudantes percebam que a unidade de medida utilizada (palmo) para medir o comprimento da cama não é padronizada. Logo, o comprimento mensurado pelos irmãos é diferente um do outro; por isso as camas ficaram com comprimentos diferentes.

BNCC em foco:

EF03MA17, EF03MA18, EF03MA19

Sugestão de atividade

Criando figuras geométricas e medindo seu contorno

Organize a turma em grupos de cinco estudantes e distribua canudinhos * a todos. Peça a eles que cortem os canudinhos em pedaços de 5 centímetros de comprimento (medidos com régua e cortados com tesoura com pontas arredondadas) e que, com esses pedaços, formem representações de figuras geométricas (como as sugeridas a seguir). Depois, os estudantes deverão colar as figuras construídas em uma folha de papel sulfite e determinar, em centímetros, o comprimento do contorno de cada figura.

Quatro pedaços de canudinho para formar uma figura que lembra um quadrado.

20 cm (5 + 5 + 5 + 5 = 4 × 5 = 20)

Oito pedaços de canudinho para formar uma figura que lembra um quadrado.

40 cm (10 + 10 + 10 + 10 = 4 × 10 = 40)

Três pedaços de canudinho para formar uma figura que lembra um triângulo.

15 cm (5 + 5 + 5 = 3 × 5 = 15)

Seis pedaços de canudinho para formar uma figura que lembra um retângulo.

30 cm (10 + 5 + 10 + 5 = 30)

Se julgar necessário, antes de eles fazerem a colagem, mostre que o comprimento do contorno corresponde a colocar os canudinhos alinhados e justapostos a fim de formar uma única linha, a qual pode ser medida com uma régua ou fita métrica.

Nota de rodapé: (*) Oriente os estudantes a fazerem, com antecedência, canudinhos enrolando folhas de revistas ou de jornal velhos. Fim da nota.

MP223

Avaliação processual

  1. Para ir de sua casa até o local de trabalho, Maurício percorre 3.000 m e passa em frente a um posto de combustível. Se o posto está na metade do caminho, Maurício percorre mais ou menos de 1.000 metros da sua casa até o posto? Explique sua resposta.
Ilustração. Um homem está dentro de um carro azul. Atrás dele há um portão aberto.

_____

PROFESSOR Exemplo de resposta: Metade de 3.000 m é 1.500 m e 1.500 m é maior que 1.000 m. Portanto, Maurício percorre mais de 1.000 metros de sua casa até o posto.

Ícone: mental.

  1. Leia o que Vilma, Aldair e Gina estão dizendo.
Ilustração. À esquerda, Vilma, menina ruiva com óculos fala: Eu sou 20 cm mais alta que Gina. No centro, Aldair, menino com cabelo preto sorri e diz: Eu tenho 1 m e 30 cm de altura. À direita, Gina, menina loira com cabelo preso fala: Eu sou 30 cm mais baixa que Aldair.
  1. Flávia encheu as duas garrafas ao lado usando a água que estava em um recipiente de 1 litro cheio. Quantos mililitros de água sobraram no recipiente?
Ilustração. Uma garrafa com 350 mL e uma garrafa com 500 mL.

Sobraram _____ mililitros de água no recipiente.

PROFESSOR Resposta: 150

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.

Autoavaliação

Ícone: oral.
MANUAL DO PROFESSOR

Atividade 2

Leia o enunciado com os estudantes e verifique se compreenderam a questão. Sugira que anotem os dados apresentados, até mesmo os pontos de referência (casa, posto de combustível e trabalho), e façam, em seguida, um esquema da situação.

Atividade 3

Para calcular a altura de Vilma, é necessário saber a altura de Gina. A altura de Gina pode ser determinada com a informação a respeito da altura de Aldair. Como Aldair tem 1 m e 30 cm de altura, e Gina é 30 centímetros mais baixa que ele, conclui-se que Gina tem 1 m de altura. Como Vilma é 20 centímetros mais alta que Gina, Vilma tem 1 m e 20 cm (ou 120 cm) de altura.

Verifique como os estudantes procedem ao fazer operações com a medida mista “1 m e 30 cm”. Pode-se sugerir a eles que, inicialmente, expressem essa medida em centímetros antes de realizarem os demais cálculos.

Atividade 4

Uma possibilidade de cálculo para a situação apresentada seria subtrair 500 mL de 1.000 mL, restando 500 mL, e, dessa quantidade, subtrair 350 mL, restando 150 mL.

Autoavaliação

O foco desta Unidade está nas grandezas e medidas. Portanto, a primeira questão orienta a autoavaliação dos estudantes no sentido de reconhecerem unidades padronizadas adequadas a cada situação. Na primeira questão, podem verificar se percebem quando o uso de metros é mais apropriado do que o uso de centímetros, ou quando as situações estão relacionadas à massa ou à capacidade.

Na segunda questão, os estudantes poderão avaliar quanto conseguem fazer leituras de gráficos, reconhecendo o tipo de registro e como os dados podem ser organizados.

BNCC em foco:

EF03MA19, EF03MA20

MP224

Comentários para o professor

Conclusão da Unidade 7

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Reconhece e aplica unidades de medida padronizadas e não padronizadas?

_____

_____

Percebe que o resultado de uma medida depende da unidade de medida utilizada?

_____

_____

Identifica a unidade de medida e o instrumento mais apropriados para determinada medição?

_____

_____

Compara, faz o registro e faz estimativa de comprimentos empregando unidades de medida não padronizadas e padronizadas mais usuais e utiliza diversos instrumentos de medida?

_____

_____

Compara, faz o registro e faz estimativa de medidas de capacidade e de massa?

_____

_____

Faz leitura, interpretação e representação de dados em gráficos de barras ou de colunas?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____