Página 265
UNIDADE
12
Coordenadas, ampliação e redução de figuras

Agora vamos estudar...
- plano cartesiano;
- pares ordenados;
- ampliação e redução.
Página 266
Coordenadas
Em um supermercado, as vagas do estacionamento foram marcadas com letras e números para facilitar a localização dos veículos. A seguir, está representada a vista superior desse local.
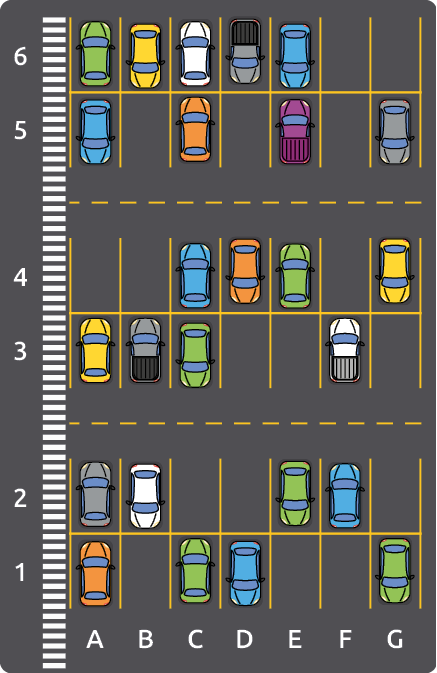
Nele, as colunas são identificadas por letras, de A a G, e as linhas são numeradas de 1 a 6.
Uma das vagas desocupadas localiza-se na coluna A e na linha 4. Podemos indicar essa vaga de maneira simplificada, dizendo que ela está na posição .
De maneira semelhante, podemos dizer, por exemplo, que o carro roxo está na posição e que as vagas , e estão ocupadas por carros brancos.
Questão 1. Quais são
as posições das vagas ocupadas pelos carros:
a) azuis?
Resposta: e .
b) amarelos?
Resposta: e .
c) verdes?
Resposta: e .
Questão 2. Quais são as posições das vagas
desocupadas?
Resposta: e .
Atividades
Faça as atividades no caderno.
1. Letras do alfabeto estão indicadas no quadro a seguir, cada uma delas ocupando uma posição. A letra J, por exemplo, ocupa a posição

Nos itens a seguir, troque cada posição pela respectiva letra indicada no quadro e descubra o que está escrito.
a)
b)
c)
d)
Respostas: a) QUADRADO; b) PENTÁGONO; c) HEXÁGONO; d) TRIÂNGULO.
2. De acordo com o quadro da atividade anterior, escreva no caderno as coordenadas das seguintes letras.
a) B
b) F
c) J
d) M
e) S
f) C
g) V
h) K
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h)
Página 267
3. Uma das peças do jogo de xadrez é o cavalo, a qual se movimenta da seguinte maneira: avançam-se duas casas na direção vertical (para cima ou para baixo) e uma na direção horizontal (para a esquerda ou para a direita); ou avançam-se duas casas na direção horizontal e uma na direção vertical.
Na imagem estão indicadas duas casas para as quais o cavalo pode se deslocar, saindo da posição em que está.
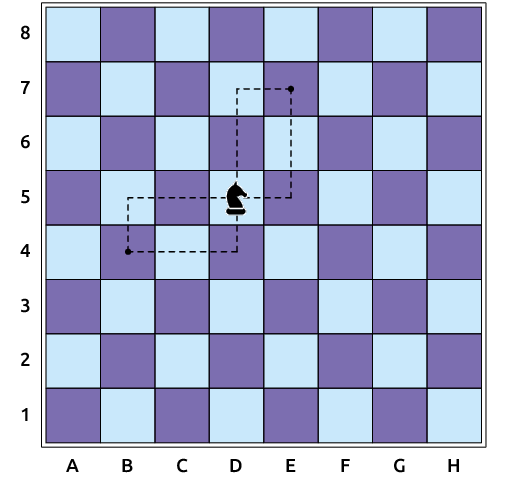
Escreva no caderno as posições das outras casas para as quais o cavalo pode ser deslocado.
Resposta: e .
4. A imagem a seguir mostra dois polígonos desenhados em uma malha quadriculada.
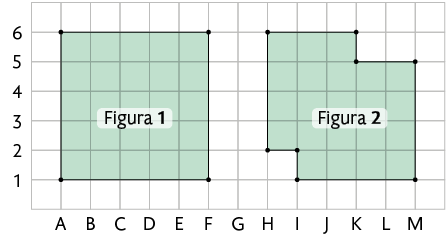
a) Quais são as coordenadas dos vértices da Figura 1? E da Figura 2?
Respostas: Figura 1: e ; Figura 2: e .
b) Sabendo que o comprimento do lado de cada quadradinho da malha mede , determine a medida do perímetro de cada uma das figuras.
Respostas: Figura 1. ; Figura 2. .
5. Camila e Daniela estão lançando dardos. Se o dardo atingir a região vermelha, então o jogador ganha 100 pontos; se atingir a região amarela, ganha 50 pontos; e se atingir a região verde, 25 pontos.
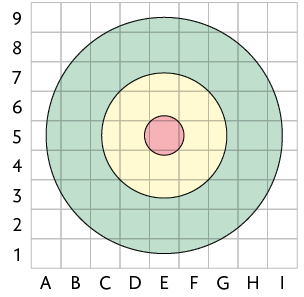
Cada jogador lançou 3 dardos e adicionou os pontos marcados.
a) Camila acertou os dardos em , e . Qual foi sua pontuação?
b) Qual foi a pontuação de Daniela, sabendo que seus dardos acertaram , e ?
Respostas: a) 125 pontos; b) 150 pontos.
Página 268
Pares ordenados
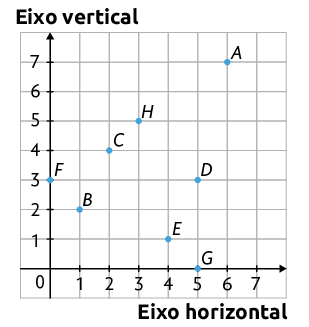
Robson indicou alguns pontos em um diagrama composto de dois eixos perpendiculares numerados, um vertical e outro horizontal.

Questão 3. Faça uma pesquisa a respeito de René Descartes e algumas de suas contribuições para a Matemática. Depois, compartilhe as informações obtidas com os colegas.
Resposta nas orientações ao professor.
Atenção!
A pesquisa proposta na questão 3 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Esse diagrama recebe o nome de plano cartesiano.
A localização dos pontos no plano cartesiano é indicada por um par ordenado de números, no qual o primeiro número refere-se ao eixo horizontal e o segundo, ao eixo vertical. O par ordenado , por exemplo, indica o ponto A.
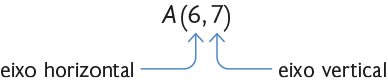
Atenção!
A ordem dos números em um par ordenado é muito importante. Ao invertermos essa ordem, obtemos a localização de pontos diferentes.
Questão 4. Quais são as coordenadas dos
outros pontos representados no
plano cartesiano?
Resposta: ; .
Questão 5. Os pares ordenados e indicam a
localização de um mesmo ponto? Em caso negativo, quais pontos esses pares ordenados indicam?
Respostas: Não; indica o ponto D e indica o ponto H.
Atividades
Faça as atividades no caderno.
6. Construa um plano cartesiano em uma malha quadriculada. Em seguida, represente os polígonos cujas coordenadas dos vértices estão indicadas em cada item.
a) Triângulo com vértices em e .
b) Losango com vértices em e .
Respostas na seção Resoluções.
Página 269
7. Considere o pentágono representado no plano cartesiano a seguir.
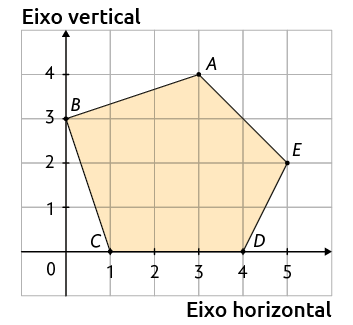
Em seu caderno, escreva as coordenadas dos vértices desse pentágono.
Resposta: e .
8. Para fazer o deslocamento do ponto A para o ponto B no plano cartesiano 1 a seguir, Lucas se orientou pelos seguintes comandos:
- avançar 3 unidades para baixo;
- avançar 2 unidades para a direita;
- avançar 4 unidades para baixo;
- avançar 6 unidades para a direita;
- avançar 5 unidades para cima;
- avançar 3 unidades para a esquerda.
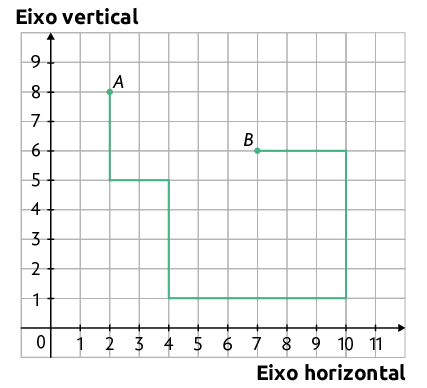
a) Quais são as coordenadas do ponto A e do ponto B no plano cartesiano 1?
Resposta: e .
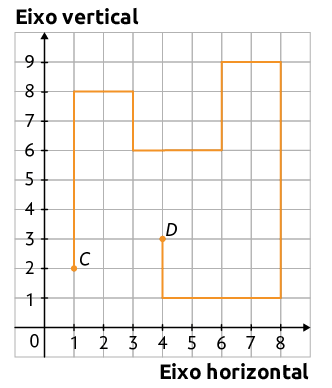
b) Agora, escreva no caderno os comandos que Lucas seguiu para fazer o deslocamento do ponto C ao ponto D no plano cartesiano 2.
Respostas na seção Respostas e na seção Resoluções.
c) Quais são as coordenadas do ponto C e do ponto D no plano cartesiano 2?
Resposta: e .
Página 270
9. Em cada
item, determine a coordenada do ponto que completa os pontos que indicam os
vértices de um quadrado.
a) e
b) e
c) , e
Respostas: a) ; b) ; c) .
10. A seguir estão indicadas as coordenadas de alguns pontos.
Se representarmos esses pontos no plano cartesiano a seguir, alguns deles estarão localizados na região da mancha. Quais são esses pontos?

Resposta: F, G e K.
11. O
triângulo a seguir está representado em um plano cartesiano no qual não estão
indicados os eixos horizontal e vertical.
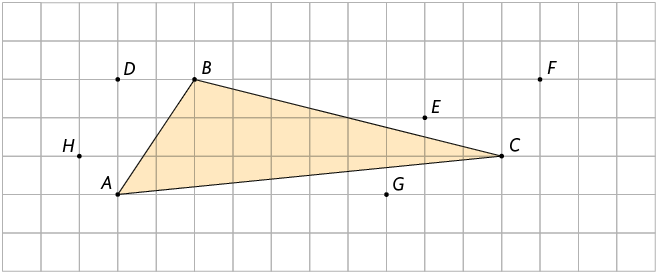
Sabendo que as coordenadas dos vértices desse triângulo são , e , escreva no caderno as coordenadas dos pontos D, E, F, G e H.
Resposta: e .
Página 271
Ampliação, redução e reprodução de figuras planas
Na malha quadriculada a seguir é apresentada uma ampliação (figura B), uma redução (figura C) e uma reprodução (figura D) da figura A.
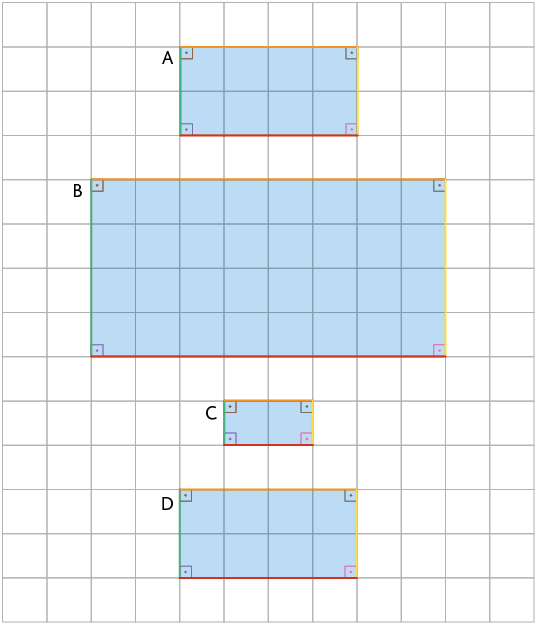
Atenção!
Nesses retângulos, os lados indicados com a mesma cor são chamados correspondentes, bem como os ângulos internos indicados com a mesma cor.
Ao serem comparadas com a figura original (figura A), a ampliação, a redução e a reprodução apresentam o mesmo formato, e as medidas dos ângulos internos são iguais às medidas dos ângulos correspondentes da figura original.
Analisando as figuras, note que:
- para obter a medida do comprimento de cada lado da ampliação (figura B), multiplicamos a medida do comprimento de cada lado da figura A por 2.
- para obter a medida do comprimento de cada lado da redução (figura C), dividimos a medida do comprimento de cada lado da figura A por 2.
- a medida do comprimento de cada lado da reprodução é igual à medida do comprimento de cada lado da figura A.
Página 272
Também podemos ampliar ou reduzir figuras em uma malha quadriculada aumentando ou diminuindo as medidas dos comprimentos dos lados dos quadradinhos.
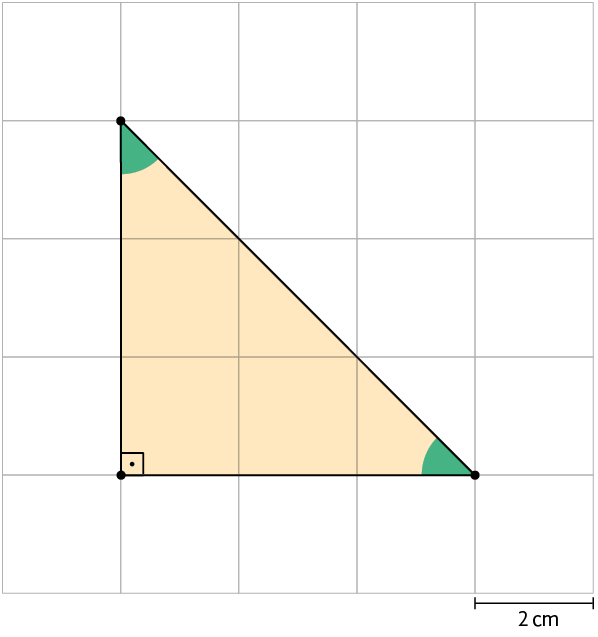
A medida de cada lado dos quadradinhos na figura ampliada (figura B) tem o dobro da medida de cada lado dos quadradinhos da figura original (figura A). Assim, as medidas dos comprimentos dos lados da figura A também foram dobradas na figura B.
Nesse caso, dizemos que a figura foi ampliada em relação à figura original na razão .
Atenção!
Note que na figura ampliada corresponde a na figura original.

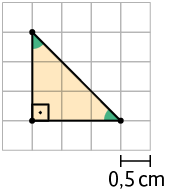
A medida de cada lado dos quadradinhos na figura reduzida (figura C) corresponde à metade da medida de cada lado dos quadradinhos da figura original (figura A). Assim, as medidas dos comprimentos dos lados da figura A também foram reduzidas à metade na figura C.
Nesse caso, dizemos que a figura foi reduzida em relação à figura original na razão .
Atenção!
Note que na figura reduzida corresponde a na figura original.

Se uma figura for a ampliação, redução ou reprodução de outra, essas figuras serão semelhantes.
Página 273
Instrumentos e softwares
Ampliando e reduzindo figuras planas com o GeoGebra
Siga as orientações do professor e os passos a seguir para construir figuras planas semelhantes.
1º. Clique com o botão direito do mouse em um ponto da Janela de visualização e, em Exibir Malha, habilite a opção Malha quadriculada principal. Com a ferramenta Polígono, construa um polígono qualquer clicando sobre os nós da malha.
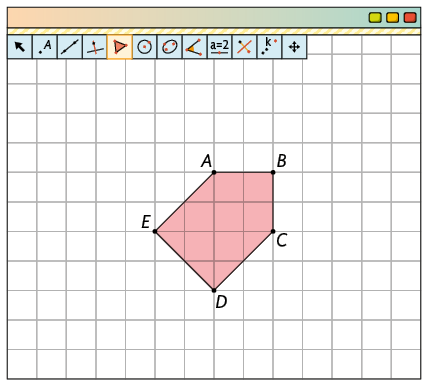
2º. Selecione a ferramenta Homotetia, clique no polígono e, depois, em um local qualquer da malha. Uma janela vai abrir solicitando o fator de multiplicação a ser aplicado nas medidas dos comprimentos dos lados da figura original.
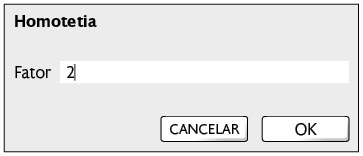
Na imagem a seguir:
- foi digitado 2 para obter o polígono , cujas medidas dos comprimentos dos lados são o dobro das medidas de comprimento dos lados do polígono .
- foi digitado 0.5 para obter o polígono , cujas medidas dos comprimentos dos lados são a metade das medidas de comprimento dos lados do polígono .
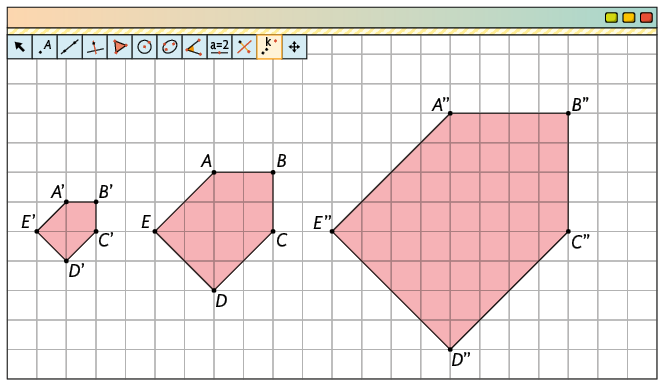
Faça o teste: com a ferramenta Mover, clique e arraste um dos vértices do polígono e verifique que os polígonos semelhantes se ajustam automaticamente.
Página 274
Atividades
Faça as atividades no caderno.
12. Analise os polígonos na malha quadriculada a seguir.
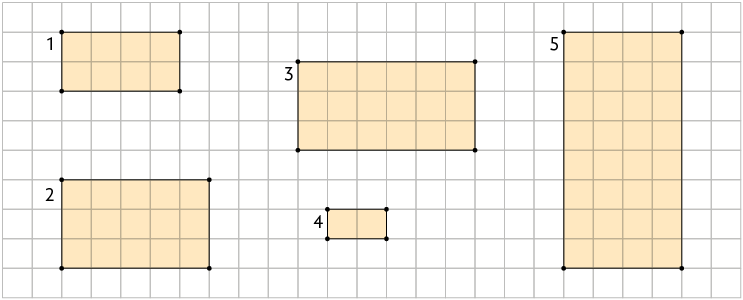
Agora, classifique as informações a seguir em verdadeiras ou falsas.
a) O polígono 2 é uma ampliação do polígono 1.
b) O polígono 4 é uma ampliação do polígono 1.
c) O polígono 4 é uma redução do polígono 5.
d) O polígono 3 é uma ampliação do polígono 4.
e) Os polígonos 3, 4 e 5 são semelhantes.
Respostas: a) Verdadeira; b) Falsa; c) Verdadeira; d) Verdadeira; e) Verdadeira.
13. Em uma malha quadriculada, construa um polígono de sua escolha. Em seguida, resolva o que se pede.
a) Nessa mesma malha quadriculada, construa uma ampliação desse polígono na razão .
b) Ainda na mesma malha quadriculada, construa uma redução desse polígono na razão .
Respostas na seção Resoluções.
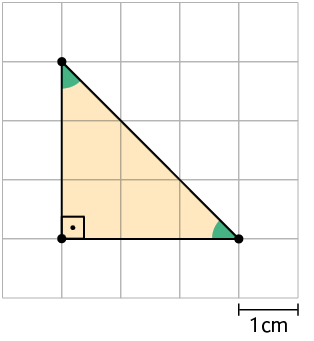
14. As
figuras A e B a
seguir são semelhantes.
Atenção!
Os triângulos A e B são equiláteros.
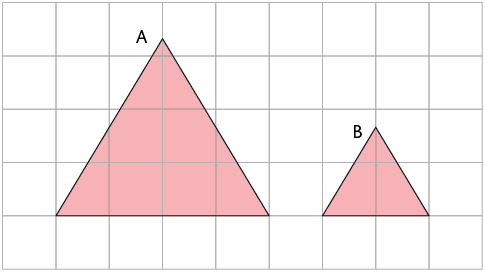
a) A figura B é uma redução ou uma ampliação da figura A?
b) Considerando o triângulo A como a figura original, utilize uma régua e determine a razão de redução utilizada para obter o triângulo B.
c) Se considerarmos o triângulo B como a figura original, qual seria a razão de ampliação para obter o triângulo A?
Respostas: a) Redução; b) ; c) .
Página 275
15. Em uma malha quadriculada, construa um plano cartesiano. Em seguida, construa o quadrilátero com as seguintes coordenadas dos vértices: e .
a) Construa uma redução desse quadrilátero de maneira que um dos vértices dessa redução tenha coordenadas .
b) Construa uma ampliação desse quadrilátero de maneira que um dos vértices dessa redução tenha coordenadas .
Respostas na seção Resoluções.
16. Vicente José de Oliveira Muniz, mais conhecido como "Vik Muniz", é um dos artistas plásticos brasileiros mais reconhecidos nacional e internacionalmente. Nascido em São Paulo (SP) em 1961, filho de uma telefonista e de um garçom, Muniz dá forma às suas criações utilizando materiais não convencionais, como lixo, sucata, poeira, terra, açúcar e chocolate. Ele compõe as imagens com esses materiais sobre uma superfície e depois as fotografa.
A imagem a seguir é uma redução de uma de suas obras.

A medida do comprimento de cada uma das dimensões da redução aplicada na página do livro corresponde a da obra original.
a) Quais são as medidas das dimensões aproximadas, em metros, da obra original?
Resposta: Medidas aproximadas: comprimento e largura, .
b) Escreva no caderno suposições de quais foram os materiais que o artista utilizou para compor essa obra.
Resposta pessoal.
c) Junte-se a um colega e façam uma pesquisa a respeito dos materiais que esse artista utilizou nessa obra e também em outras. Depois, compartilhe as informações obtidas com o restante da turma.
Resposta pessoal.
17. Construa
o polígono
no GeoGebra com a ferramenta Polígono.
Depois, faça o que se pede.
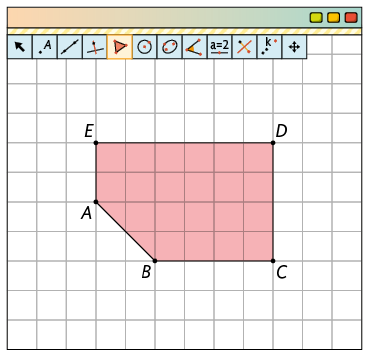
a) Ainda com a ferramenta Polígono, construa uma ampliação () desse polígono com o dobro das medidas dos comprimentos dos lados correspondentes.
Respostas na seção Resoluções.
b) Com a ferramenta Homotetia, construa uma redução () desse polígono, reduzindo pela metade as medidas dos comprimentos dos lados correspondentes.
Resposta na seção Resoluções.
c) Com a ferramenta Mover, clique e arraste um dos vértices do polígono . Qual polígono ainda continua semelhante? Por quê?
Resposta: Apenas o polígono continua semelhante ao polígono inicial, pois ele foi construído com uma ferramenta própria do GeoGebra para ampliação e redução.
Página 276
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. No quadro, a figura localizada na posição se encaixa na figura localizada na posição e forma um quadrado.
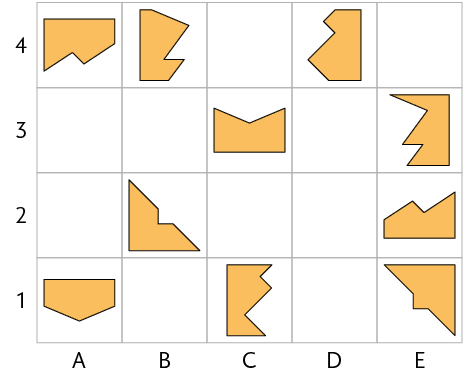
a) Escreva a posição dos outros pares de figuras que se encaixam e formam quadrados.
Resposta: e ; e ; e ; e .
b) Suponham que 2 novas figuras fossem colocadas no quadro de modo que, ao encaixá-las, formassem um quadrado. Quais poderiam ser as posições dessas figuras no quadro?
Sugestões de resposta: e ; e ; e .
2. Analise o plano cartesiano.

a) Qual ponto está na coordenada:
?
?
?
Respostas: Coordenada : ponto A; Coordenada : ponto D; Coordenada : ponto F.
b) Quais são as coordenadas dos pontos:
B?
C?
E?
Respostas: Ponto B: ; Ponto C: ; Ponto E: .
3. Analise o seguinte polígono no plano cartesiano.
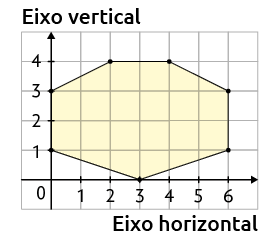
Quais são as coordenadas dos vértices desse polígono?
Resposta: e .
4. Maria
desenhou um quadrado em um plano cartesiano. Sabendo que 3 dos vértices desse quadrado têm coordenadas em , e , determine a
coordenada do vértice que falta.
Resposta: .