Página 119
UNIDADE
6
Cálculo algébrico

Agora vamos estudar...
- sequências;
- expressões algébricas;
- igualdades;
- fórmulas;
- equações.
Página 120
Expressões algébricas
Uma livraria está com promoção na venda de livros. Verifique como é possível calcular quantos reais seriam gastos na compra de 3 ou 5 livros.

3 livros
5 livros
Portanto, seriam gastos R$ 38,70 na compra de 3 livros e R$ 64,50 na compra de 5 livros.
Para obter o preço a ser pago, foi multiplicado o valor unitário de cada livro pela quantidade de livros a ser comprada. Ao indicar por x a quantidade de livros a ser comprada, pode-se escrever a seguinte expressão algébrica para obter o preço total de cada compra.
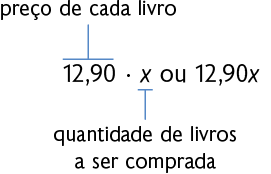
Atenção!
Em uma multiplicação de dois fatores em que ao menos um deles é uma letra, normalmente não se utiliza o sinal de multiplicação ( ou ).
Assim, para saber quantos reais uma pessoa vai pagar pela compra de 8 livros, por exemplo, basta substituir x por 8 e, então, efetuar o cálculo.
Logo, uma pessoa vai pagar R$ 103,20 na compra de 8 livros.
Nesse caso, foi calculado o valor numérico da expressão , quando .
As expressões nas quais aparecem letras e números são chamadas expressões algébricas.
Atenção!
O uso de letras para indicar variáveis teve início com o matemático e filósofo francês René Descartes (1596-1650). Ele também foi o responsável pela notação de potências, como e .
A seguir, alguns exemplos de expressões algébricas.
Nessas expressões, as letras são chamadas variáveis.
Questão 1. Considerando que uma pessoa aproveite a promoção de livros, calcule em seu caderno quantos reais ela vai pagar pela compra de:
a) 7 livros.
Resposta: R$ 90,30.
b) 10 livros.
Resposta: R$ 129,00.
c) 17 livros.
Resposta: R$ 219,30.
Questão 2. Nessa mesma livraria, há uma promoção de jogos de videogame. Sabendo que nessa promoção cada jogo custa R$ 123,90, escreva em seu caderno uma expressão algébrica para obter o preço total a ser pago pela compra de x jogos.
Resposta: .
Questão 3. Utilizando a expressão que você escreveu na questão 2, calcule a quantia paga na compra de 5 e na compra de 8 jogos e registre em seu caderno.
Resposta: 5 jogos: R$ 619,50; 8 jogos: R$ 991,20.
Página 121
Simplificação de expressões algébricas
A professora Marcela propôs a seguinte atividade aos estudantes.

A seguir, apresentamos duas maneiras para simplificar a expressão algébrica do item a.
Utilizando figuras
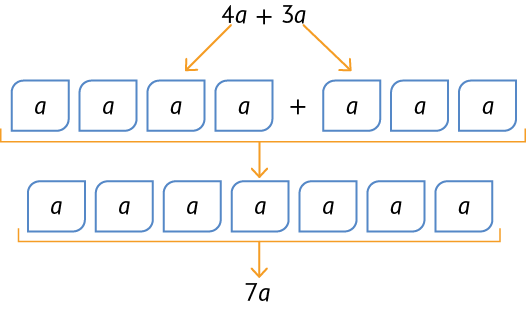
Utilizando a propriedade distributiva da multiplicação em relação à adição

Portanto, .
Questão 4. Em seu caderno, simplifique as demais expressões algébricas propostas pela professora Marcela.
Respostas: b) ; c) ; d) ; e) ; f) ; g) ; h) .
Questão 5. Calcule em seu caderno o valor numérico da expressão
a) do item c, quando .
b) do item d, quando .
c) do item e, quando .
d) do item g, quando .
Agora, confira como simplificar a expressão .
Respostas: a) 10; b) 12; c) 36; d) 11,5.
Página 122
Atividades
Faça as atividades no caderno.
1. Sabendo que n é um número natural, escreva em seu caderno uma expressão algébrica para cada item.
a) 25% desse número.
b) 8 unidades a mais do que esse número.
c) O antecessor desse número.
d) A quarta parte desse número.
e) O sucessor desse número.
f) A décima parte desse número.
g) O quíntuplo desse número.
Respostas: a) ou ou ; b) ; c) ; d) ou ou ou ; e) ; f) ; g) .
2. Os triângulos que formam a sequência a seguir foram representados com palitos. A cada novo triângulo foi acrescentado 1 palito em cada lado do triângulo anterior.
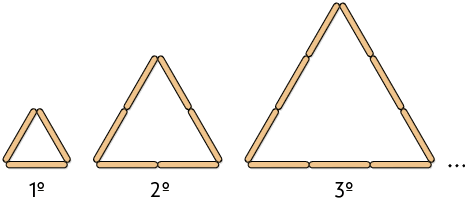
a) Com base na imagem, determine a quantidade de palitos utilizados para representar o 4º e o 5º triângulos dessa sequência.
Resposta: 12 e 15 palitos, respectivamente.
b) Escreva uma expressão algébrica que expresse a quantidade de palitos necessários para representar um triângulo em uma posição qualquer da sequência. Para isso, denomine p o número natural que representa a posição do triângulo.
Resposta: .
c) Efetue os cálculos e descubra quantos palitos são necessários para representar o:
Respostas: 27 palitos; 63 palitos.
- 9º triângulo.
- 21º triângulo.
3. Escreva no caderno os três próximos termos de cada sequência.
a)
b)
c)
Respostas nas orientações ao professor.
4. Substitua as letras de cada sequência da atividade anterior por um número natural menor do que 10 e escreva no caderno a sequência numérica formada.
Respostas nas orientações ao professor.
5. Para vender as roupas de sua loja, Judite acrescenta 28% ao preço de custo.
a) Escreva no caderno uma expressão algébrica em que se possa calcular o preço de venda de qualquer peça de roupa da loja.
Resposta nas orientações ao professor.
b) Por quantos reais Judite vai vender uma peça de roupa cujo preço de custo é:
- R$ 32,00?
- R$ 25,75?
- R$ 20,00?
- R$ 23,50?
Respostas: R$ 40,96; R$ 32,96; R$ 25,60; R$ 30,08.
6. Junte-se a um colega e analisem a quantidade de círculos em cada posição da sequência.

a) Escreva uma expressão algébrica que possibilite determinar a quantidade de círculos em uma posição qualquer dessa sequência.
Sugestão de resposta: , em que n é o número natural que representa a posição da figura na sequência.
b) Quantos círculos há na 35ª posição dessa sequência? E na 52ª posição?
Sugestão de respostas: 1.225 círculos; 2.704 círculos.
Página 123
7. Leia o diálogo de Daniele e Henrique.

a) Represente com expressões algébricas as falas de Daniele e Henrique.
Resposta: Indicando por x o número pensado por Daniele, obtemos: . Indicando por a o número pensado por Henrique, obtemos: .
b) Determine os resultados obtidos por Daniele e Henrique, sabendo que ela pensou no número 3 e ele pensou no número 8.
Resposta: Daniele: 7; Henrique: 6.
8. Para descobrir a quantia que Alberto, Carla, Gilberto e Heloisa têm, analise as informações a seguir, sabendo que Lúcio tem d reais.
- Alberto tem R$ 20,00 a mais do que Lúcio.
- Carla tem R$ 7,00 a menos do que Alberto.
- Gilberto tem o dobro da quantia de Carla.
- Heloísa tem a metade da quantia de Gilberto.
a) Represente no caderno a quantia de cada pessoa utilizando a variável d.
Resposta: Lúcio: d; Alberto: ; Carla: ou ; Gilberto: ou ; Heloísa: ou .
b) Sabendo que Lúcio tem R$ 21,00, quantos reais têm as demais pessoas?
Resposta: Alberto: R$ 41,00; Carla: R$ 34,00; Gilberto: R$ 68,00; Heloísa: R$ 34,00.
9. Em uma padaria, de leite custa y reais. Com base no preço de de leite, podemos escrever uma expressão algébrica para representar os preços de outros produtos dessa padaria.
Meia dúzia de pães custa R$ 1,00 a mais do que de leite.
Uma minipizza custa R$ 0,50 a menos do que de leite.
Uma caixinha de suco custa o dobro de meia dúzia de pães.
Um pão de queijo custa metade de uma minipizza.
Agora, escreva no caderno outras expressões algébricas para representar o preço de cada produto a seguir dessa padaria.
Atenção!
Utilize essas expressões algébricas para representar os preços dos demais produtos.
a) Um sonho custa R$ 0,65 a mais do que um pão de queijo.
b) Um pedaço de torta custa R$ 1,85 a menos do que uma caixinha de suco.
c) Uma fatia de bolo custa o dobro de um pedaço de torta.
d) Um biscoito custa a terça parte de uma caixinha de suco.
Sugestões de respostas: a) Um sonho: ou ; b) Um pedaço de torta: ou ; c) Uma fatia de bolo: ou ; d) Um biscoito: ou .
Página 124
10. Associe as expressões algébricas aos seus respectivos itens equivalentes, escrevendo a letra e o número correspondentes.
a)
b)
c)
1)
2)
3)
Resposta: a-3; b-1; c-2.
11. A seguir estão representados um número natural, seu antecessor e seu sucessor.
-
y
a) Escreva em seu caderno as representações em ordem crescente.
b) Adicione esses 3 números e, em seguida, simplifique a expressão algébrica obtida.
Respostas: a) , , ; b) .
12. Examine como Jussara obteve e simplificou a expressão algébrica que representa a medida do perímetro do polígono.
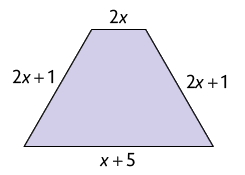
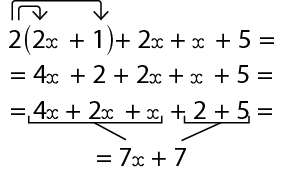
Agora, determine a expressão algébrica que representa a medida do perímetro de cada figura. Em seguida, simplifique a expressão obtida.

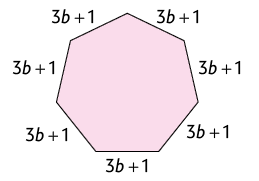
Respostas: A. ; B. .
13. Simplifique as expressões algébricas.
a)
b)
c)
d)
e)
Atenção!
é equivalente a .
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
14. Escreva uma expressão algébrica que, ao ser simplificada, seja equivalente a:
a)
b)
c)
d)
Sugestão de respostas: a) ; b) ; c) ; d) .
15. Leia a seguir o diálogo de Camila e Raí.

Atenção!
Dizemos que é equivalente a .
Agora, escreva no seu caderno uma expressão algébrica para representar a fala de Camila e Raí. Em seguida, simplifique as expressões.
Resposta: Camila: ; Raí: .
Página 125
Fórmulas
Para saber a possível frequência cardíaca máxima de uma pessoa adulta quando se exercita, os fisiologistas✚ utilizam a fórmula a seguir.
Nessa fórmula, B indica a quantidade de batimentos por minuto (bpm), enquanto i indica a idade em anos.
- Fisiologista:
- profissional que estuda as diversas funções dos organismos vivos, como a circulação, a nutrição, a respiração e o crescimento.↰
Para determinar a frequência cardíaca máxima que uma pessoa pode atingir ao exercitar-se, deve-se substituir a letra i na fórmula pela idade em anos da pessoa. Analise os cálculos realizados para uma pessoa com 18 anos de idade.
Assim, quando uma pessoa com 18 anos se exercita, ela pode ter uma frequência cardíaca máxima de .
As fórmulas são sentenças matemáticas que mostram, de maneira resumida, quais cálculos devem ser realizados para chegar a determinado resultado. Nas fórmulas, as letras, ou seja, as variáveis, representam números.
Atenção!
Na fórmula , estudada nesta página, B e i são as variáveis.
Questão 6. Em seu caderno, determine a frequência cardíaca máxima que uma pessoa pode atingir ao exercitar-se, caso ela tenha:
a) 25 anos.
b) 30 anos.
c) 45 anos.
d) 67 anos.
Respostas: a) ; b) ; c) ; d) .
Página 126
Instrumentos e softwares
Fórmulas na planilha eletrônica
As planilhas eletrônicas, como o Calc, são muito úteis e ajudam as pessoas a agilizar cálculos envolvendo fórmulas. Com base na fórmula apresentada na página 125 e no Calc, podemos obter a possível frequência cardíaca máxima de uma pessoa adulta quando ela se exercita da seguinte maneira.
1º. Digite "Idade em anos (i)" em A1 e "Batimentos cardíacos por minuto (B)" em B1. Em seguida, preencha três valores sequenciais na coluna da variável i, considerando que a variável representa a idade de uma pessoa adulta.

2º. Selecione esses valores clicando em A2, e com o botão pressionado arraste até A4. Clique na Alça de preenchimento automático, mantendo o botão pressionado, e arraste-a até a linha desejada, podendo ser até a linha A10. Desse modo, os demais valores da sequência serão inseridos automaticamente.
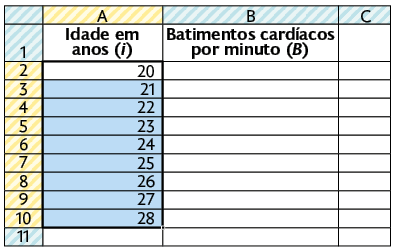
3º. Como , digite a fórmula na célula B2 e pressione Enter. A frequência cardíaca máxima de uma pessoa com 20 anos ao exercitar-se será exibida nessa célula.
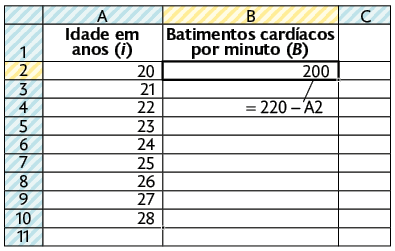
4º. Novamente, clique na Alça de preenchimento automático e arraste-a até a linha B10. Com isso, o valor correspondente da variável B é obtido de maneira automática para cada valor correspondente da variável i.
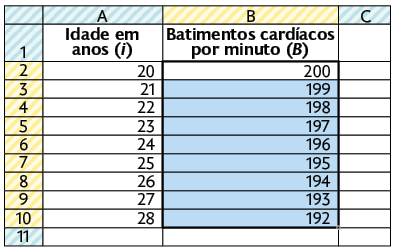
Professor, professora: Sugira aos estudantes que alterem algum valor de i para verificarem que o valor correspondente de B é atualizado automaticamente.
Página 127
Atividades
Faça as atividades no caderno.
16. Em certa loja, quando os produtos são vendidos em 3 prestações iguais, há um acréscimo de 15% sobre o preço de etiqueta. O valor de cada prestação corresponde ao preço do produto com acréscimo, dividido em três partes iguais.
a) Com base nessas informações, qual das fórmulas a seguir fornece o valor de cada prestação?
Atenção!
Na fórmula correta, p representa o valor de cada prestação e x representa o preço de etiqueta do produto.
A.
B.
C.
D.
E.
b) Sabendo que nessa loja o preço de etiqueta de determinado produto é R$ 132,00, calcule o valor de cada prestação quando o produto é vendido em 3 prestações iguais.
Respostas: a) Alternativa C; b) R$ 50,60.
17. O lucro mensal de uma fábrica de calçados é dado pela fórmula , em que y é o lucro em reais, e x é a quantidade de pares de calçados produzidos no mês.
Qual é o lucro mensal dessa fábrica quando ela produz 488 pares de calçados?
Resposta: R$ 8.540,00.
18. A milha
terrestre é uma unidade de medida de comprimento utilizada na Inglaterra e nos
Estados Unidos. Dada uma medida em milhas, para encontrar a medida equivalente
em metros, utiliza-se a fórmula , em que x é
a medida da distância em milhas terrestres, e y
é a medida da distância equivalente em metros. Com o auxílio do Calc, escreva as
seguintes medidas em metros.
a) 0 milha.
b) 1 milha.
c) 2 milhas.
d) 1.000 milhas.
Respostas: a) ; b) ; c) ; d) .
19. Amauri
desenvolveu uma fórmula em uma planilha eletrônica que multiplica por 7 o número de entrada e
subtrai 6 unidades do resultado
dessa multiplicação, obtendo, assim, o número de saída.

a) Escreva no caderno a fórmula utilizada por Amauri na planilha eletrônica. Para isso, use a letra N para representar o número de entrada e R para o número de saída.
b) Com base nessa fórmula, calcule com o Calc o valor de R para os seguintes números de entrada.
-
4
-
10
-
5,8
-
6,2
Respostas: a) ; b) 4: 22; 10: 64; 5,8: 34,6; 6,2: 37,4.
Página 128
Sequências
Uma sequência é uma lista ordenada de objetos que podem ser letras, números, palavras, figuras etc. Os objetos que compõem a sequência são chamados termos da sequência.
Confira um exemplo a seguir em que é representada uma sequência listando seus termos separados por vírgula.
.
Pode-se também denotar uma sequência escrevendo seus termos entre parênteses e separados por vírgula.
Atenção!
Ao trabalhar com sequências, a ordem dos termos é de suma importância, pois, por exemplo, e representam sequências diferentes.
Na sequência apresentada, 4 é o primeiro termo, 6 é o segundo, 8 é o terceiro, e assim por diante. Os termos das sequências podem ser representados por uma letra e um índice. Por exemplo:
: primeiro termo.
: segundo termo.
: terceiro termo.
: quarto termo.
: n-ésimo termo (n é natural maior do que zero).
Verifique outros exemplos de sequências.
A.
B.
Atenção!
As na sequência B indicam que ela continua infinitamente.
Questão 7. Qual é o primeiro termo da
sequência A? E o sexto termo da sequência
B?
Respostas: Amarelo; 11.
Em certos casos, podemos descrever uma sequência por meio de uma lei de formação. Por exemplo, considere a sequência cuja lei de formação é , para todo . Para obter os seus respectivos termos, deve-se substituir os valores de n na lei de formação. Nesse caso, obtemos a seguinte sequência:
Questão 8. Represente em seu caderno a sequência cuja lei de formação é , para todo .
Resposta: .

Página 129
A resposta é negativa para a pergunta da página anterior. Não há como garantir qual será o próximo termo de uma sequência conhecendo apenas alguns de seus termos.
Por exemplo, considere a sequência . Podemos supor que essa seja a sequência dos números ímpares maiores do que 2 em ordem crescente e, nesse caso, o próximo termo seria 9. Porém, existem infinitas sequências cujos primeiros termos são 3, 5 e 7, como é o caso da sequência dos números primos ímpares maiores do que 2 em ordem crescente – nesse caso, o próximo termo seria 11.
Sequências definidas por recorrência
Em algumas situações, é possível indicar uma sequência utilizando uma expressão que possibilite calcular um termo da sequência em função dos termos anteriores. Essa expressão é chamada relação de recorrência.
Por exemplo, considere uma sequência em que e que satisfaça a relação para todo . Nesse caso, temos:
Portanto, obtemos a seguinte sequência:
A ideia de recorrência (recursividade) não está presente apenas na Matemática, mas também nas Artes e na Literatura, como no poema "Velocidade", de Ronaldo Azeredo, produzido em 1957 e publicado em 1958. As imagens a seguir foram elaboradas, com base nesse poema, por dois estudantes da professora Adélia. Em uma delas a palavra VELOCIDADE foi trocada por MATEMÁTICA e na outra por INSPIRAÇÃO.

Marcos

Paula
Perceba que, nas imagens elaboradas por Marcos e Paula, de baixo para cima, a partir da segunda linha, a próxima é igual à anterior, porém com a última letra excluída e um M ou I, respectivamente, acrescido à esquerda.
Questão 9. Junte-se a um
colega e
pesquisem outros poemas e obras de arte em que seja possível identificar a
ideia de recorrência. Depois, apresentem seus resultados aos colegas.
Resposta pessoal.
Página 130
Atividades
Faça as atividades no caderno.
20. Escreva em seu caderno a sequência definida por:
a) , para todo , em que .
Resposta: .
b) , para todo .
Resposta: .
c) , para todo , em que .
Resposta: .
d) , para todo .
Resposta: .
e) , para todo , em que .
Resposta: .
f) , para todo , em que .
Resposta: .
Entre as sequências definidas anteriormente, quais foram descritas por meio de uma lei de formação?
Resposta: As sequências dos itens a, b, d e f.
21. Considere a sequência definida por , para todo , em que .
a) Escreva os 5 primeiros termos dessa sequência.
Resposta: 4, 5, 7, 11 e 19.
b) A sequência foi definida por recorrência ou por meio de uma lei de formação?
Resposta: Recorrência.
c) Se o primeiro termo fosse 3, qual seria a sequência obtida?
Resposta: .
22. A professora de Paulo apresentou aos estudantes a seguinte sequência:
Entre as expressões a seguir, quais podem descrever a sequência apresentada pela professora?
a) , para todo .
b) , para todo .
c) , para todo , em que .
d) , para todo , em que .
e) , para todo , em que .
Resposta: Expressões dos itens b e d.
O que podemos concluir em relação às expressões indicadas por você?
Resposta pessoal. Espera-se que os estudantes respondam que, apesar de duas definições aparentemente diferentes, elas representam a mesma sequência.
23. Determine o 38º termo da sequência definida por:
a) , em que .
b) , em que .
Respostas: a) ; b) .
24. Considerando a sequência dos números ímpares em ordem crescente , responda às questões.
a) A sequência é finita ou infinita?
b) Qual é a lei de formação dessa sequência?
c) Qual é o 100º termo dessa sequência?
Respostas: a) Infinita; b) , para todo ; c) 199.
25. Defina cada uma das sequências por meio de uma lei de formação ou por recorrência.
a)
Sugestões de resposta: , para todo ; , para todo , com .
b)
Sugestões de resposta: , para todo ; , para todo , com .
Página 131
26. Analise a sequência de figuras representadas com palitos de fósforo.

a) Quantos palitos de fósforo são necessários para representar a 2ª figura dessa sequência? E a 4ª figura?
Respostas: 5 palitos para representar a 2ª figura e 9 palitos para a 4ª figura.
b) Escreva no caderno uma expressão que represente a quantidade de palitos necessárias para uma figura em posição qualquer da sequência.
Sugestão de resposta: , para todo , em que n é o número natural que representa a posição da figura na sequência.
c) Quantos palitos de fósforo são necessários para representar a 9ª figura da sequência? E a 25ª figura?
Sugestão de respostas: 19 palitos para a 9ª figura e 51 palitos para a 25ª figura.
27. Com um programa de computador, Antônio construiu a seguinte sequência de retângulos.
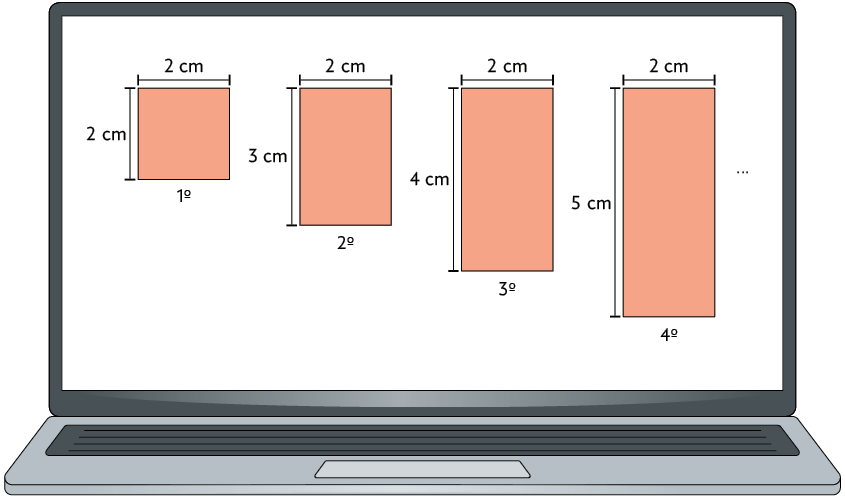
a) Com base nessa sequência, qual é a medida da área do 2º retângulo? E do 4º retângulo?
Respostas: para o 2º retângulo e para o 4º retângulo.
b) Escreva uma expressão que represente a medida da área, em centímetros quadrados, de um retângulo em uma posição qualquer da sequência.
Sugestão de resposta: , para todo , em que n é o número natural que representa a posição do retângulo na sequência.
c) Quanto mede a área do 525º retângulo dessa sequência?
Sugestão de resposta: .
28. A professora de Conceição e de Jorge solicitou aos estudantes que escrevessem a lei de formação da sequência dos números pares em ordem crescente. A seguir estão apresentadas as leis de formação por Conceição e Jorge.
- Conceição: , para .
- Jorge: , para .
Ao analisar a resposta deles, quem escreveu a lei de formação corretamente? Justifique sua resposta.
Resposta: Ambos escreveram a lei de formação corretamente, pois as expressões escritas por Conceição e Jorge são equivalentes.
Página 132
Igualdades
Tobias e Teobaldo participam de um clube de leitura. Durante o ano de 2023, Tobias leu 2 livros por mês, enquanto Teobaldo leu 6 livros a cada bimestre.

Questão 10. Quais cálculos devem ser
efetuados para determinar a
quantidade de livros lidos por Tobias no ano de 2023? E para determinar a
quantidade de livros lidos por Teobaldo?
Resposta pessoal. Espera-se que os estudantes efetuem multiplicações para determinar as quantidades de livros lidos pelas personagens do problema.
Realizando os cálculos necessários, concluímos que, em 2023, Tobias e Teobaldo leram 24 livros cada um. Nesse caso, podemos escrever a seguinte igualdade.
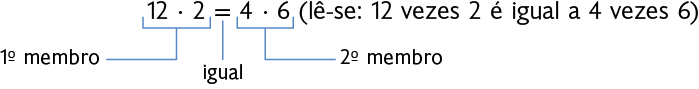
Só foi possível escrever essa igualdade pelo fato de as operações e apresentarem resultados iguais. A seguir, apresentamos outros exemplos de igualdades.
Atenção!
Em uma igualdade, o valor do 1º membro é igual ao do 2º membro.
Em anos anteriores, foram estudadas as seguintes propriedades de uma igualdade.
Propriedade 1: Ao adicionar ou subtrair um mesmo número em ambos os membros de uma igualdade, a relação de igualdade se mantém.
Propriedade 2: Ao multiplicar ou dividir ambos os membros de uma igualdade por um mesmo número positivo, a relação de igualdade se mantém.
A propriedade 2 pode ser estendida para números negativos, ou seja, ao multiplicar ou dividir ambos os membros de uma igualdade por um mesmo número diferente de zero (positivo ou negativo), a relação de igualdade se mantém. A seguir, apresentamos dois exemplos.
Questão 11. Escreva em seu caderno duas igualdades. Depois, compartilhe com um colega para verificar se essas igualdades são verdadeiras.
Resposta pessoal.
Página 133
Equações
Marília e Rodrigo estão brincando de desafios matemáticos. O desafio que Marília propôs está indicado a seguir.

Para responder à pergunta de Marília, podemos escrever uma equação.
Equação é uma sentença matemática expressa por uma igualdade em que há pelo menos uma letra, chamada incógnita, a qual representa um número desconhecido.
Em uma equação, cada lado em relação ao sinal de igual é chamado membro.
A seguir, apresentamos um exemplo de equação com a indicação de seus elementos.
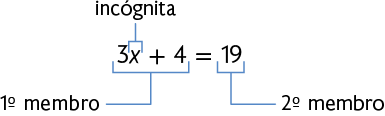
Atenção!
Fique atento! A variável pode assumir diversos valores, enquanto a incógnita tem um valor fixo.
Resolver uma equação é determinar o valor da incógnita, ou seja, obter sua solução.
Agora, vamos denominar x o número que Marília pensou para, então, escrever a seguinte equação.
Para resolvê-la, ou seja, para determinar o valor da incógnita x, procedemos da seguinte maneira.

Portanto, o número em que Marília pensou é 7.
Página 134
Na vez de Rodrigo, ele propôs o seguinte desafio.

Para responder à pergunta de Rodrigo, podemos também escrever uma equação. Nesse caso, o número desconhecido será indicado por n. Com isso, obtemos a seguinte equação.
Para resolvê-la, procedemos da seguinte maneira.

Portanto, o número em que Rodrigo pensou é 13.
Para verificar se a solução obtida está correta, podemos substituir a incógnita da equação pelo valor obtido. Assim, é possível verificar se as equações resolvidas neste tópico estão corretas.
Substituindo x por 7 em , obtemos:

Substituindo n por 13 em , obtemos:

Como a relação de igualdade se mantém em ambas as equações, as resoluções estão corretas.
Página 135
Atividades
Faça as atividades no caderno.
29. Entre as sentenças a seguir, quais são equações?
a)
b)
c)
d)
e)
f)
Resposta: Alternativas a, c e d.
30. Resolva as equações em seu caderno.
a)
b)
c)
d)
e)
f)
Respostas na seção Respostas e na seção Resoluções.
31. Ao triplicar a quantia que Leonardo tem em reais e subtrair R$ 18,00, ele obterá a quantia de R$ 15,60. Em reais, qual é a quantia que Leonardo tem?
Resposta: R$ 11,20.
32. Podemos resolver mentalmente as equações e da seguinte maneira.
Interpretamos essa equação assim:
Qual é o número que adicionado a 8 resulta em 12?
É o número 4, pois . Portanto, .
Interpretamos essa equação assim:
Qual é o número que, ao ser multiplicado por 2, resulta em 14?
É o número 7, pois . Portanto, .
Com base na informação apresentada, resolva mentalmente as seguintes equações.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
33. A figura a seguir representa um terreno retangular. Com base nas indicações, determine a medida do comprimento do terreno em metros.

Resposta: ; Medida do comprimento: .
34. Analise os elementos a seguir.
-
5
-
n
-
3
-
15
-
12
-
9
a) Com base nesses elementos, Silas montou a seguinte equação.
-
3
-
n
-
12
-
15
Qual é o valor de n?
Resposta: .
b) Junte-se a um colega e, com os elementos apresentados anteriomente, escrevam uma equação cujo valor de n seja:
- 7.
- maior do que 12.
- menor do que 7.
- maior do que 7 e menor do que 13.
Sugestão de respostas: ; ; ; .
35. Leia o que Jéssica está dizendo e determine a medida da massa corporal dela.

Resposta: .
Página 136
36. Antes de resolver as equações e , Marcos fez uma simplificação.

Termine de resolver as equações no caderno e obtenha os valores de x e y.
Resposta: ; .
37. Simplifique cada equação e obtenha sua solução.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
38. Leia o problema apresentado a seguir.
Márcia tem certa quantia em reais. Nivaldo tem o dobro da quantia de Márcia. Sabendo que juntos eles têm R$ 105,00, quantos reais Márcia tem? E Nivaldo?
a) Entre as equações a seguir, qual permite obter a solução desse problema?
A.
B.
C.
D.
b) Resolva a equação escolhida no item a e determine a resposta do problema.
Respostas: a) Alternativa C; b) ; Márcia: R$ 35,00; Nivaldo: R$ 70,00.
39. Um número p mais seu sucessor é igual a 79. Represente em seu caderno essa situação usando uma equação para, depois, resolver.
Resposta: ; .
40. Simone, Jaqueline e Mauro são primos. Os números que representam suas idades são consecutivos. Sabendo que a soma das idades dos três é 39, qual é a idade de cada um deles?
Resposta: Jaqueline: 14 anos; Simone: 13 anos; Mauro: 12 anos.
Atenção!
Jaqueline é a mais velha e Mauro é o mais novo.
41. Nos prismas e nas pirâmides, a quantidade de vértices (V) mais a quantidade de faces (F) é igual à quantidade de arestas (A) mais 2. Podemos representar essa relação pela seguinte fórmula.
Em certo prisma, a quantidade de vértices é 4 unidades a mais do que a quantidade de faces. Sabendo que esse prisma tem 18 arestas, responda às questões.
a) Quantas faces tem esse prisma? E quantos vértices?
b) Qual é o nome desse prisma?
Respostas: a) 8 faces; 12 vértices; b) Prisma de base hexagonal.
42. Escreva o enunciado de um problema cuja solução seja dada pela equação a seguir.
Depois, compartilhe o problema escrito com um colega para que resolva e, então, verifique se a resposta obtida está correta.
Resposta pessoal.
Página 137
Estudando mais equações
A balança representada a seguir está em equilíbrio, ou seja, a massa dos objetos que estão em um prato tem medida igual à massa dos objetos que estão no outro.
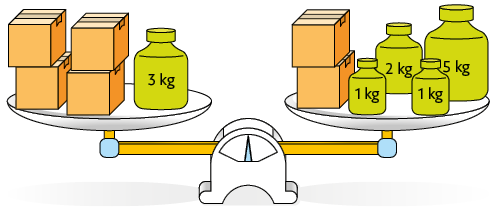
Em uma balança desse tipo, podemos acrescentar ou retirar objetos com medidas de massa iguais nos dois pratos sem que ela perca o equilíbrio.
Sabendo que as caixas nessa balança têm a mesma medida de massa, qual é a medida da massa de cada caixa?
Para responder a essa pergunta, vamos indicar a medida da massa de cada caixa por x e escrever uma equação.
Feito isso, é momento de resolver essa equação.
1º. Inicialmente, é necessário retirar de cada prato da balança. Na equação, são subtraídas 3 unidades de cada membro.
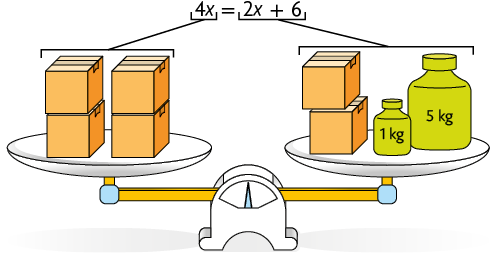
2º. Em seguida, deve-se retirar 2 caixas de cada prato da balança. Na equação, são subtraídos de cada membro.
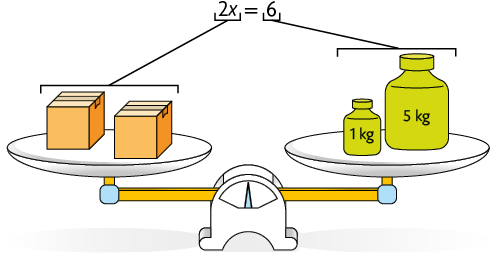
Na balança do 2º passo, 2 caixas juntas correspondem a . Assim, para obter a medida da massa de uma caixa, deve-se dividir por 2. Na equação, deve-se dividir cada membro por 2.
Portanto, a massa de cada caixa mede .
Página 138
Atividades
Faça as atividades no caderno.
43. Nas balanças em equilíbrio representadas a seguir, caixas de mesma cor têm medidas de massa iguais.
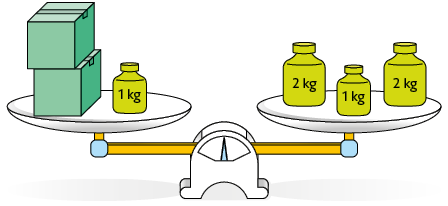
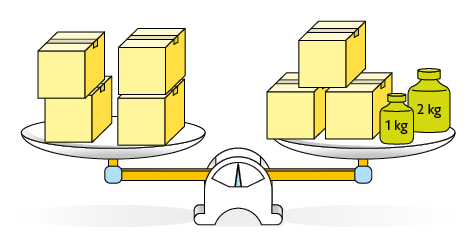
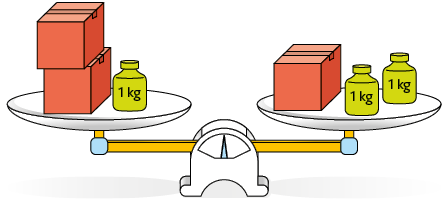
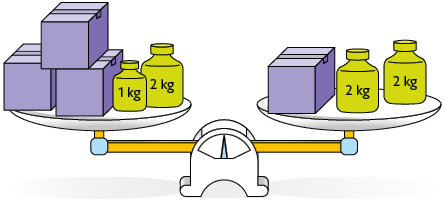
a) Associe cada balança à respectiva equação representada a seguir. Para isso, escreva o par de letras correspondentes.
E.
F.
G.
H.
b) Resolva as equações e determine a medida da massa de cada caixa.
Respostas: a) C-F; B-E; D-G; A-H; b) Caixa verde: ; caixa amarela: ; caixa vermelha: ; caixa roxa: .
44. Analise a representação da balança em equilíbrio. Sabendo que as caixas têm a mesma medida de massa, escreva e resolva no caderno uma equação que permita calcular a medida da massa de cada caixa.
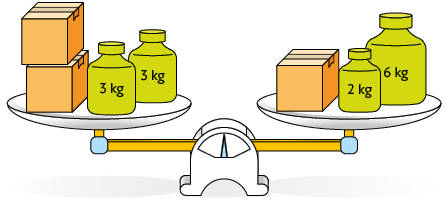
Resposta: ; ; .
45. A balança representada a seguir não está em equilíbrio. Para equilibrá-la, nessa situação, deve-se colocar 5 latas de achocolatado no prato da esquerda e 1 lata no prato da direita.
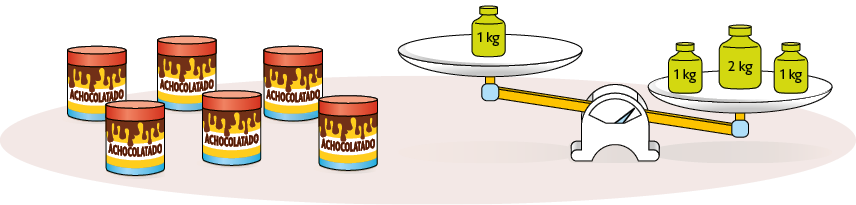
Sabendo que todas as latas de achocolatado têm massas com mesma medida, qual é a medida da massa de cada lata em quilogramas?
Resposta: .
Página 139
46. Resolva no caderno as equações a seguir.
a)
b)
c)
d)
e)
f)
46. Respostas: a) ; b) ; c) ; d) ; e) ; f) .
47. Associe cada problema à equação que permite resolvê-lo escrevendo a letra e o número correspondentes. Depois, escreva em seu caderno e resolva as equações para, então, obter a resposta de cada um deles.
A.Daqui a 9 anos Josiane vai completar 27 anos. Quantos anos Josiane tem hoje?
B. A quantia em reais que tenho mais R$ 2,00 multiplicada por 3 é igual a R$ 144,00. Quantos reais tenho?
C. Ao multiplicar por 2 a diferença entre a quantidade de canetas que Nair tem e 3 unidades, obtêm-se 6 canetas. Quantas canetas Nair tem?
D. O triplo da quantidade de peixes de meu aquário menos 3 peixes é igual a 2 vezes a quantidade de peixes do aquário mais 1 peixe. Quantos peixes tem meu aquário?
1.
2.
3.
4.
Respostas: A-3, B-1, C-2, D-4; A. 18 anos; B. R$ 46,00; C. 6 canetas; D. 5 peixes.
48. Uma prestadora de serviços telefônicos cobra R$ 24,90 pelo plano de ligações locais, com direito a 200 minutos por mês, além de um valor fixo por minuto excedente. Sabendo que em um mês Renato usou 453 minutos e pagou R$ 45,14, quanto ele pagou por minuto excedente?
Resposta: R$ 0,08.
49. Com base na fala de Marisa e Andrei, escreva no caderno uma equação para cada fala e, em seguida, resolva essas equações.


Resposta: Marisa: ; ; ; Andrei: ; ; 31 figurinhas.
50. Escreva no caderno uma equação e determine a medida de cada ângulo interno do triângulo a seguir.
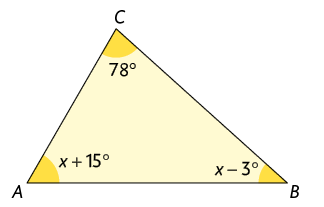
Atenção!
A soma das medidas dos ângulos internos de um triângulo é .
Resposta: ; ; ; .
Página 140
51. Júlia e Isadora estão disputando um jogo de perguntas e respostas. Nesse jogo, para cada resposta certa, ganham-se 4 pontos, e, para cada resposta errada, perdem-se 2 pontos. Em cada rodada são feitas 15 perguntas.
A seguir está indicada a quantidade de respostas certas e erradas de Júlia e Isadora em 2 rodadas.
|
Jogadora |
Acertou |
Errou |
|---|---|---|
|
Júlia |
8 |
7 |
|
Isadora |
6 |
9 |
|
Jogadora |
Acertou |
Errou |
|---|---|---|
|
Júlia |
5 |
10 |
|
Isadora |
7 |
8 |
a) Quantos pontos Júlia e Isadora fizeram na 1ª rodada?
b) Quantos pontos Júlia e Isadora fizeram na 2ª rodada?
c) Entre as expressões algébricas a seguir, qual permite obter a quantidade de pontos de um jogador em uma rodada, sabendo que x representa a quantidade de respostas certas?
I)
II)
III)
IV)
d) Em certa rodada, Júlia obteve 24 pontos e Isadora, 36 pontos. Quantos acertos cada uma delas teve nessa rodada?
Respostas: a) Júlia: 18 pontos; Isadora: 6 pontos; b) Júlia: 0 ponto; Isadora: 12 pontos; c) II; d) Júlia: 9 acertos; Isadora: 11 acertos.
52. Na sexta-feira, uma sorveteria vendeu y sorvetes. No sábado, vendeu 15 sorvetes a mais do que havia vendido na sexta-feira e, no domingo, o dobro da quantidade de sorvetes que havia vendido no sábado. Sabendo que essa sorveteria vendeu 273 sorvetes nesses 3 dias, determine a quantidade de sorvetes vendidos em cada dia.
Resposta: Sexta-feira: 57 sorvetes; sábado: 72 sorvetes; domingo: 144 sorvetes.
53. A medida do perímetro do retângulo A é igual ao dobro da medida do perímetro do quadrado B.


Qual é a medida da área de cada figura em metros quadrados?
Resposta: Retângulo: ; quadrado: .
54. Vanderlei e 4 amigos alugaram um veículo para uma viagem e decidiram dividir igualmente a quantia do aluguel. No dia da viagem, 2 pessoas não puderam ir. Por esse motivo, cada uma das pessoas restantes pagou R$ 75,00 a mais do que o combinado inicialmente.
a) Quantos reais cada pessoa pagaria inicialmente?
b) Por quantos reais o veículo foi alugado?
Atenção!
Ao escrever a equação, considere que x corresponde ao pagamento combinado para cada um inicialmente e corresponde ao pagamento efetivo de cada um no final da situação.
Respostas: a) R$ 112,50; b) R$ 562,50.
Página 141
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Usando x como variável, escreva em uma folha de papel avulsa uma expressão algébrica que represente três oitavos de um número mais 180.
Resposta: .
2. Roberto comprou 2 caixinhas de leite e 1 pacote de café e pagou com uma cédula de R$ 50,00. Indicando por p e c o preço da caixinha de leite e do pacote de café, respectivamente, escreva uma expressão algébrica que represente a quantia que Roberto deve receber de troco.
Resposta: ou .
3. As expressões algébricas , e representam números ímpares consecutivos, sendo n um número natural maior do que ou igual a 1.
a) Em uma folha de papel avulsa, escreva esses números em ordem decrescente.
b) Adicione esses números e simplifique a expressão algébrica obtida.
Respostas: a) ; ; ; b) .
4. Qual é a medida do comprimento do lado de um triângulo equilátero cuja medida do perímetro é igual à medida do perímetro do polígono a seguir?
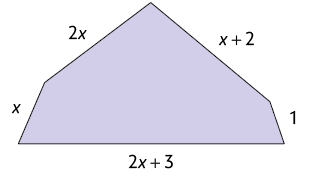
Resposta: .
5. Na área
da saúde são utilizados alguns índices internacionais para avaliar a obesidade
de uma pessoa. Dois índices muito comuns são: o Índice de Massa Corporal (IMC) e o Índice de Adiposidade Corporal (IAC).
Para determinar o IMC (i) de uma pessoa, podemos utilizar a fórmula , em que m e h indicam, respectivamente, a medida da massa, em quilogramas, e da altura, em metros, de uma pessoa.
Analise as categorias de avaliação consideradas pelo IMC a seguir. Dependendo da categoria em que a pessoa se encontra, outros testes e outros exames podem ser necessários.
|
Categoria |
Valor do IMC |
|---|---|
|
Abaixo do peso |
abaixo de 18,5 |
|
Peso normal |
de 18,5 a 24,9 |
|
Sobrepeso |
de 25,0 a 29,9 |
|
Obesidade de grau I |
de 30,0 a 34,9 |
|
Obesidade de grau II |
de 35,0 a 39,9 |
|
Obesidade de grau III |
acima de 40,0 |
Fonte: CALCULADORA de IMC. Associação Brasileira para o Estudo da Obesidade e Síndrome Metabólica (Abeso). Disponível em: https://oeds.link/2X6Oh1. Acesso em: 16 fev. 2022.
Com uma calculadora e aproximando os resultados a números com uma casa decimal, determine o Índice de Massa Corporal (IMC) com as medidas indicadas a seguir para, depois, classificar os resultados obtidos de acordo com as categorias apresentadas.
a) e
b) e
c) e
d) e
Respostas: a) 21,7; peso normal; b) 18,2; abaixo do peso; c) 22,4; peso normal; d) 27,7; sobrepeso.
Página 142
6. A escala Fahrenheit é a escala de temperatura mais utilizada nos países de língua inglesa. Para converter uma medida de temperatura F em graus Fahrenheit () em uma medida de temperatura C em graus Celsius (), utiliza-se a seguinte fórmula:
Transforme em graus Celsius as seguintes medidas dadas em graus Fahrenheit:
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
7. Rafael disse a Vânia: "Pense em um número. Triplique o número em que você pensou. Adicione 6 ao resultado e divida o novo resultado por 3. Quanto deu?". Vânia respondeu: "11". E, logo na sequência, Rafael revelou o número em que Vânia tinha pensado. Qual era esse número?
Resposta: 9.
8. Uma mãe tem 33 anos e sua filha, 14 anos. Daqui a quantos anos a mãe terá o dobro da idade da filha?
Resposta: Daqui a 5 anos.
9. Marina foi ao supermercado e comprou 5 pacotes de açúcar, 4 caixinhas de leite e 4 garrafas de óleo, totalizando R$ 88,97. Sabendo que um pacote de açúcar custou R$ 7,49 e uma caixinha de leite custou R$ 3,99 quanto Marina pagou:
a) pelos pacotes de açúcar?
b) pelas caixinhas de leite?
c) pelas garrafas de óleo?
d) em cada garrafa de óleo?
Respostas: a) R$ 37,45; b) R$ 15,96; c) R$ 35,56; d) R$ 8,89.
10. Escreva em uma folha de papel avulsa a sequência definida por , com . Essa sequência foi definida por meio de uma lei de formação ou de uma recorrência?
Respostas: ; lei de formação.
11. Verifique o triângulo.

Sabendo que o perímetro desse triângulo mede , determine a medida do comprimento de cada um de seus lados.
Resposta: , e .
12. O volume de um tijolo em formato de paralelepípedo reto retângulo mede . Sabendo que duas de suas dimensões medem e , determine a medida da outra dimensão desse tijolo.
Resposta: .
13. Cíntia,
Débora e Solange colecionam canetas. Solange tem 4
canetas a mais do que Débora, e Cíntia tem 3 canetas a menos do que Solange.
Sabendo que juntas elas têm 161 canetas, quantas canetas cada uma delas tem?
Resposta: Solange: 56; Débora: 52; Cíntia: 53.
14. Em uma partida de basquetebol, um time acertou uma quantidade x de arremessos que vale 1 ponto. Valendo 2 pontos, acertou o dobro dessa quantidade mais 2 arremessos. E valendo 3 pontos, acertou 10 arremessos a menos do que o de 2 pontos. Sabendo que ao todo foram 54 arremessos que pontuaram, quantos pontos o time fez nessa partida?
Resposta: 112 pontos.