Página 13
UNIDADE
1
Potenciação e radiciação

Agora vamos estudar...
- potenciação;
- radiciação;
- potência com expoente fracionário.
Página 14
Potenciação
Potência com expoente natural
Renata trabalha em uma fábrica de remédios. Ela armazena a produção em caixas, que são organizadas em pequenos lotes, como mostrado na imagem.

Para determinar quantas caixas de remédios são organizadas em cada lote, podemos efetuar uma multiplicação de fatores iguais, que pode ser escrita como potenciação.

A potência é lida da seguinte maneira: três elevado à terceira potência ou três elevado ao cubo.
Portanto, cada lote tem 27 caixas de remédio.
Denomina-se potência de base a e expoente b, em que b é um número natural maior do que 1, o número , que corresponde ao produto de b fatores a.
Caso ou , definimos: e , com .
Uma potência é positiva quando sua base é um número inteiro positivo.
Analise alguns exemplos de potências cuja base é um número inteiro positivo.
a)
b)
c)
Quando a base de uma potência for um número inteiro negativo, ela será:
- positiva, se o expoente for par;
- negativa, se o expoente for ímpar.
Analise alguns exemplos de potências cuja base é um número inteiro negativo.
a)
b)
c)
Página 15
Potência com expoente negativo
Agora, vamos estudar um pouco mais sobre potências com expoente inteiro, especificamente nos casos em que o expoente é um número inteiro negativo.
Um número diferente de zero elevado a um expoente negativo é igual ao inverso desse número elevado ao oposto do expoente.
Sendo a (base) um número diferente de zero e n (expoente) um número natural, temos:
ou
Atenção!
Lembre-se de que o inverso de a é , sendo a um número diferente de zero.
Analise mais alguns exemplos.
Considere a sequência apresentada.
Vamos escrever os termos dessa sequência como potência de base 2.
- 1º termo:
- 2º termo:
- 3º termo:
- 4º termo:
- 5º termo:
- 6º termo:
- 7º termo:
- 8º termo:
Questão 1. Agora, escreva em seu caderno os termos da sequência apresentada a seguir como potências de base .
Página 16
Instrumentos e softwares
Calculando potências com expoente negativo
Usando uma calculadora científica, vamos calcular potências com expoentes negativos seguindo alguns procedimentos, como o cálculo de no exemplo a seguir.
1º. Registre o
número 2. Em seguida, pressione a tecla .
2º. Digite as
teclas .
3º. Por fim,
pressione ,
para obter o número decimal como resultado.
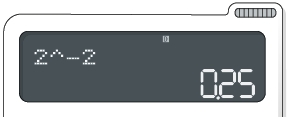
4º. Para obter
o resultado na forma
de fração, basta digitar na sequência a tecla .
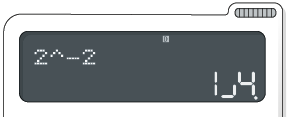
Para cálculos de potências com base e expoente negativos, como , procedemos da seguinte maneira:
1º. Pressione
as teclas ,
nesta ordem.
2º. Em seguida,
digite .
3º. Por fim,
pressione a tecla ,
para obter o número decimal como resultado.
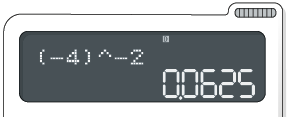
4º. Para obter
o resultado na forma
de fração, basta digitar na sequência a tecla .

Agora, verifique como podemos calcular o valor de .
1º. Pressione
as teclas ,
nesta sequência.
2º. Em seguida,
digite .
3º. Para obter
o resultado, pressione a tecla .

Portanto, o resultado é . Para obtê-lo na forma
fracionária, basta digitar as teclas e
,
nesta ordem. No fim, obteremos .
Página 17
Atividades
Faça as atividades no caderno.
1. No caderno, escreva com algarismos a potência apresentada por extenso em cada item. Depois, calcule o valor de cada uma.
a) Quatro elevado ao quadrado.
b) Dez elevado ao cubo.
c) Seis elevado à quarta potência.
d) Três elevado ao cubo.
e) Cinco elevado ao quadrado.
f) Dois elevado à quarta potência.
2. Calcule as potências a seguir em seu caderno.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
n)
o)
p)
3. No caderno, escreva a potência que representa a quantidade de cubinhos em cada pilha. Em seguida calcule-as.



4. As respostas que você escreveu para os itens A, B e C, da atividade anterior, formam uma sequência de potências de mesmo expoente. No caderno, escreva os próximos quatro termos dessa sequência e calcule quantos cubinhos terá a pilha correspondente a cada um deles.
5. Utilizando
uma calculadora científica, calcule as potências a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
6. Resolva as potências a seguir da maneira que preferir.
a)
b)
c)
d)
Atenção!
O inverso de é 3 e o inverso de é .
7. Sabendo que e , efetue os cálculos.
a)
b)
c)
d)
e)
8. Copie os itens no caderno e substitua cada pelo símbolo (igual), (maior do que) ou (menor do que).
a)
b)
c)
d)
e)
f)
9. Analise os itens a seguir e, no caderno, relacione as potências que têm o mesmo valor. Para isso, escreva a letra e o número correspondentes.
A.
B.
C.
D.
1.
2.
3.
4.
10. No caderno, elabore um problema que envolva potência. Em seguida, troque com um colega para que ele o resolva.
Página 18
Propriedades das potências
Neste tópico, vamos estudar as propriedades decorrentes da definição de potências, que podem auxiliar nos cálculos. Considere m e n números inteiros.
1ª propriedade
Um produto de potências de mesma base pode ser transformado em uma única potência mantendo a base e adicionando os expoentes. Exemplos:

Com isso, temos .

Desse modo, temos .
De modo geral, , com se ou .
2ª propriedade
Um quociente de potências de mesma base pode ser transformado em uma única potência mantendo a base e subtraindo os expoentes. Exemplo:

Assim, .
De modo geral, , com .
3ª propriedade
A potência de um produto pode ser transformada em um produto de potências elevando cada número ao expoente nela indicado. Exemplo:
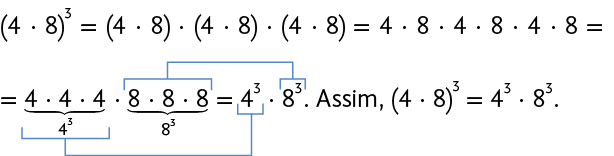
De modo geral, , com se .
4ª propriedade
A potência de um quociente pode ser transformada em um quociente de potências elevando cada número ao expoente nela indicado. Exemplo:

Assim, .
De modo geral, , com se e .
Página 19
5ª propriedade
A potência de uma potência pode ser transformada em uma única potência mantendo a base dela e multiplicando seus expoentes. Confira o exemplo:
, assim, .
De modo geral, , com se ou .
Agora, verifique dois casos.
No primeiro caso, o está elevado ao cubo.
No segundo caso, a base 2 está elevada a , ou seja, elevada a 8.
Note que as potências e são diferentes e têm resultados diferentes.
Potências de base 10
Analise alguns casos de potências de base 10.
Nas potências de base 10 em que os expoentes são números inteiros positivos, a quantidade de zeros após o algarismo 1 é igual ao valor do expoente.
Nas potências de base 10 em que os expoentes são números inteiros negativos, a quantidade de algarismos à direita da vírgula é igual ao oposto do valor do expoente.
De modo geral, em uma potência de base 10 com expoente positivo, a quantidade de zeros no resultado após o algarismo 1 é igual ao valor do expoente. Já no caso de uma potência de base 10 com expoente negativo, a quantidade de algarismos à direita da vírgula é igual ao oposto do valor do expoente.
Página 20
Notação científica
É comum alguns profissionais trabalharem com números de muitos algarismos e que, geralmente, correspondem a uma medida muito grande ou muito pequena. Para simplificar a escrita deles, pode ser usada a notação científica, que consiste em representar um número usando uma potência de base 10.
Nessa notação, os números são escritos da seguinte maneira:
a: número maior ou igual a 1 e menor do que 10;
n: número inteiro.
Analise alguns números escritos em notação científica.
A medida da temperatura aproximada no núcleo do Sol é .

Representação com elementos não proporcionais entre si. Cores-fantasia.
O comprimento da bactéria Mycobacterium tuberculosis mede .
Imagem obtida por microscópio e ampliada aproximadamente 570 vezes. Colorizada em computador.
Atividades
Faça as atividades no caderno.
11. Utilizando as propriedades das potências, simplifique os cálculos e obtenha os resultados.
a)
b)
c)
d)
e)
f)
g)
h)
12. No caderno, efetue os cálculos indicados nos itens.
a) O produto entre e .
b) O quociente de por .
c) O quadrado da metade de .
d) A metade do quadrado de .
e) O dobro do cubo de 4.
f) O cubo do quadrado de 2.
Página 21
13. No esquema apresentado, cada letra representa uma potência de base 2.
A
B
C
D
E
Sabendo que o produto dos números de cada linha, coluna e diagonal é , descubra quais são essas potências.
14. Resolva no caderno as expressões numéricas a seguir.
a)
b)
c)
d)
e)
f)
Atenção!
Utilize as propriedades das potências para facilitar os cálculos.
15. No caderno, elabore um problema que envolva as propriedades das potências. Depois disso, troque com um colega, para que o resolva.
16. Transforme os produtos e os quocientes a seguir em uma única potência.
a)
b)
c)
d)
e)
f)
g)
h)
17. O produto , com , equivale a:
A. 1
B.
C.
D.
18. Considerando , simplifique a expressão .
19. Escreva em seu caderno cada expressão na forma de uma única potência.
a)
b)
c)
d)
e)
f)
20. Calcule mentalmente o resultado de:
a)
b)
c)
d)
e)
f)
g)
h)
i)
21. A tabela a seguir apresenta a população aproximada dos estados da Região Sul do Brasil em 2021.
|
Estado |
População aproximada |
|---|---|
|
Paraná |
11.597.000 |
|
Santa Catarina |
7.338.000 |
|
Rio Grande do Sul |
11.466.000 |
Fonte de pesquisa: IBGE. Cidades e Estados. Disponível em: https://oeds.link/ny433l. Acesso em: 28 mar. 2022.
No caderno, calcule a população aproximada da Região Sul em 2021 e, depois, registre-a usando notação científica.
22. No caderno, escreva os números em destaque usando notação científica.
a) A massa da Lua mede aproximadamente .
b) Alguns vírus têm espessura aproximada de .
c) Em de sangue de um homem há cerca de 5.400.000 glóbulos vermelhos, enquanto na mesma quantidade de sangue de uma mulher há cerca de 4.800.000.
d) No vácuo, a luz viaja a uma velocidade de .
Página 22
Raízes
Cristiane está construindo em sua casa um jardim com o formato de um quadrado, cuja medida da área é igual a . Qual será a medida nesse jardim?
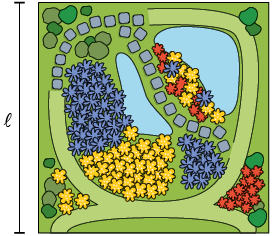
Para resolver essa questão, utilizamos a fórmula a seguir e calculamos a medida da área do quadrado.
A: medida da área;
: medida do comprimento do lado.
Substituindo A por 49 na fórmula, temos:
Para obter a medida do quadrado, precisamos determinar um número positivo que, multiplicado por si mesmo (ou seja, elevado ao quadrado), resulte em 49, isto é, devemos calcular a raiz quadrada de 49.
Na situação apresentada, o número procurado só pode ser 7, ou seja, 7 é a raiz quadrada de 49, que indicamos por:
, pois .
Lemos da seguinte maneira: raiz quadrada de 49.
Portanto, o comprimento do lado do jardim vai medir .
Atenção!
Geralmente, o índice 2 da raiz quadrada é omitido. Desse modo, indicamos simplesmente por .
A operação utilizada na situação apresentada é chamada radiciação, que é a inversa da potenciação. Na radiciação, podemos destacar os seguintes elementos:
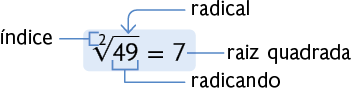
A raiz quadrada de um número positivo a é um número também positivo que, ao ser multiplicado por si mesmo, resulta em a.
Na situação apresentada, temos dois números que, elevados ao quadrado, resultam em 49, ou seja, e . No entanto, como a raiz quadrada de 49 é um número único e positivo, temos que .
Atenção!
Obtemos a raiz quadrada somente de números positivos, pois nenhum número elevado ao quadrado resulta em um número negativo.
Analise alguns exemplos.
- , pois
- , pois
- , pois
Se a e b são números naturais, com , temos:
Página 23
Considere uma caixa em formato de cubo cujo volume mede . Qual é a medida do comprimento a da aresta dessa caixa?

Para responder a essa pergunta, podemos utilizar a fórmula da medida do volume do cubo.
V: medida do volume;
a: medida do comprimento da aresta.
Substituindo V por 64 na fórmula, obtemos:
Para obter a medida do comprimento da aresta a do cubo, precisamos determinar um número que, elevado ao cubo, resulte em 64, ou seja, é necessário determinar a raiz cúbica de 64, que indicamos por (lê-se: raiz cúbica de 64).
Nesse caso, o número procurado é 4, pois . Assim, .
Portanto, o comprimento da aresta da caixa mede .
A raiz cúbica de um número a qualquer é um número que, elevado ao cubo, resulta em a.
Analise os exemplos a seguir.
- , pois .
- , pois .
Cálculo da raiz exata de um número natural
É possível calcular a raiz quadrada de um número natural por tentativa. Acompanhe, por exemplo, o procedimento para calcular a raiz quadrada de 2.116.
Sabemos que é necessário obter o número que, elevado ao quadrado, seja igual a 2.116. Para determiná-lo, vamos escrever os quadrados das dezenas exatas de 10 a 50.
|
Número |
Quadrado do número |
|---|---|
|
10 |
100 |
|
20 |
400 |
|
30 |
900 |
|
40 |
1.600 |
|
50 |
2.500 |
Como 2.116 está entre 1.600 e 2.500, concluímos que sua raiz quadrada está entre 40 e 50, pois e .
Como a raiz quadrada de 2.116 é um número entre 40 e 50, vamos calcular o quadrado dos números naturais entre eles até obter 2.116 como resultado.
Portanto, por esses cálculos, concluímos que e, então, .
Questão 2. Junte-se a um colega e obtenham, por tentativa, a raiz quadrada exata de 5.184 e registrem no caderno.
Página 24
Outro modo de calcular a raiz quadrada de um número natural é fazer sua decomposição em fatores primos e, na sequência, simplificar o resultado da decomposição. Acompanhe, por exemplo, o cálculo da raiz quadrada do número 324.
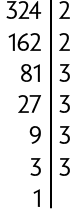
Assim, , pois .
Ainda usando a decomposição em fatores primos e simplificando o resultado da decomposição, podemos calcular .

Assim, , pois .
Questão 3. Junte-se a um colega e, no caderno, usem a decomposição em fatores primos para calcular novamente a raiz quadrada do número 5.184. Depois, verifiquem se o resultado obtido foi o mesmo da questão 2.
Cálculo da raiz aproximada de um número natural
Quando um número não é quadrado perfeito, ou seja, sua raiz quadrada não é um número natural, podemos calcular a raiz quadrada aproximada dele. Vamos obter, por exemplo, a raiz quadrada aproximada do número 11, com aproximação até os décimos, usando o procedimento a seguir.
1º. Verificamos entre quais números quadrados perfeitos o número 11 se encontra. Nesse caso, como ele está entre 9 e 16, sua raiz quadrada está entre 3 e 4.
2º. Em seguida, calculamos o quadrado de alguns números entre 3 e 4, nesse caso com uma casa decimal.
Resultados menores do que 11.
Resultados maiores do que 11.
Pelos valores obtidos, . Como está mais próximo de 11, temos:
Atenção!
O símbolo é usado para indicar aproximação.
Lê-se: raiz quadrada de 11 é aproximadamente 3,3.
Página 25
Continuando, vamos calcular a raiz quadrada aproximada de 11 com aproximação até os centésimos. Calculamos, então, o quadrado de alguns números entre 3,3 e 3,4, com duas casas decimais.
Resultado menor do que 11.
Resultados maiores do que 11.
Conforme os resultados obtidos, está mais próximo de 11. Sendo assim, temos:
Por esse procedimento, sucessivamente, o cálculo da raiz quadrada aproximada de um número natural também pode ser feito com três, quatro ou mais casas decimais.
Potências com expoente fracionário
Estudamos, até o momento, potências com expoentes de números inteiros positivos e negativos. Agora, vamos calcular potências com expoentes fracionários. Usando a 5ª propriedade apresentada na página 19, é possível verificar, por exemplo, que:
, pois
Essa propriedade também é válida em potências cujo expoente é fracionário, como indicado no exemplo a seguir.
, pois
Tais potências podem ser escritas por meio de um radical, assim como radicais podem ser escritos na forma de potência com expoente fracionário. Analise os exemplos a seguir.
De modo geral, sendo a um número inteiro positivo, n e m números naturais, com n maior do que 1, temos:
Atenção!
Ao representarmos uma potência com expoente fracionário por meio de um radical, note que o denominador do expoente da potência corresponde ao índice do radical e o numerador do expoente da potência, ao expoente do radicando.
As propriedades das potências também são válidas para aquelas com expoentes fracionários, sendo as restrições referentes à base e ao expoente as mesmas. Verifique alguns exemplos.
Página 26
Atividades
Faça as atividades no caderno.
23. Efetue os cálculos no caderno.
a)
b)
c)
d)
e)
f)
24. Escreva no caderno a medida do comprimento do lado de cada quadrado a seguir, conforme a medida da área A indicada em cada um deles.
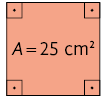
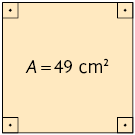
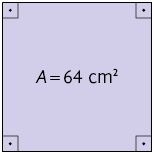
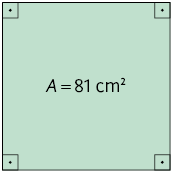
25. Em cada item está indicada a medida do volume de um cubo. Efetue os cálculos no caderno e obtenha a medida do comprimento da aresta de cada um deles.
a)
b)
c)
d)
e)
f)
26. Lauro é marceneiro e vai construir o tampo de uma mesa cujo formato é quadrado. Para esse trabalho, a medida da área do tampo deveria ser entre e . Entre os itens a seguir, qual está indicando uma possível medida do comprimento de um dos lados do tampo que ele vai construir?
a)
b)
c)
d)
27. Para cada item, determine entre quais números está o resultado da raiz.
a)
16 e 17
17 e 18
18 e 19
b)
27 e 28
28 e 29
30 e 31
28. Por meio da decomposição em fatores primos, determine em seu caderno a raiz cúbica dos números a seguir.
a) 4.096
b) 39.304
c) 15.625
d) 4.913
e) 64.000
f) 8.000
g) 59.319
h) 46.656
i) 125.000
29. Rogério calculou da seguinte maneira:
Usando o mesmo procedimento que Rogério, determine o resultado dos cálculos a seguir.
a)
b)
c)
d)
Página 27
30. Calcule a raiz quadrada aproximada dos números a seguir até os décimos.
a)
b)
c)
d)
e)
31. Calcule a raiz quadrada aproximada dos números a seguir até os centésimos.
a)
b)
c)
d)
e)
32. Lúcia obteve o número inteiro mais próximo de da seguinte maneira:

De maneira semelhante ao raciocínio de Lúcia, obtenha o número inteiro mais próximo dos radicais indicados nos itens a seguir.
a)
b)
c)
d)
33. Entre quais números inteiros está o valor de:
a) ?
b) ?
c) ?
d) ?
34. Represente no caderno as raízes a seguir usando potências com expoente fracionário.
a)
b)
c)
d)
35. No caderno, relacione as potências com expoente fracionário com as respectivas raízes. Para isso, escreva o número e a letra correspondentes.
1.
2.
3.
4.
5.
6.
7.
8.
A.
B.
C.
D.
E.
F.
G.
H.
36. Em seu caderno, escreva cada item na forma de uma única potência. Em seguida, escreva na forma de radical a potência obtida.
a)
b)
c)
d)
e)
f)
g)
h)
37. Em seu caderno, elabore um problema que envolva radiciação. Em seguida, troque com um colega, para que o resolva.
Página 28
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Responda às questões a seguir em uma folha de papel avulsa.
a) Qual é o valor da potência de base 7 e expoente 3?
b) Qual é o expoente da potência em que a base é 6 e o resultado é 216?
c) Qual é a base da potência em que o expoente é 5 e o resultado é 32?
2. Transforme os números decimais em frações e, depois, calcule o valor de cada potência.
a)
b)
c)
d)
e)
f)
3. Simplifique cada expressão utilizando as propriedades das potências.
a)
b)
c)
d)
e)
f)
g)
h)
4. Em cada item, calcule o valor de y, de modo que as igualdades sejam verdadeiras.
a)
b)
c)
d)
e)
f)
g)
5. O valor de é:
A.
B.
C.
D.
6. No caderno, calcule o que se pede em cada item.
a) O produto da raiz quadrada de 49 pela raiz quadrada de 64.
b) A raiz quadrada de 3.136.
c) O produto da raiz cúbica de 125 pela raiz cúbica de 216.
d) A raiz cúbica de 27.000.
e) O produto da raiz quadrada de 16 pela raiz cúbica de 27.
f) A raiz cúbica de 1.331.
7. Efetue os cálculos e determine a raiz quadrada aproximada até a casa dos centésimos.
a)
b)
c)
d)
e)
f)
8. Escreva, em uma folha de papel avulsa, os números naturais mais próximos da raiz apresentada em cada um dos itens a seguir.
a)
b)
c)
d)
9. Represente, em uma folha avulsa, os números a seguir como potência de base 2 e expoente fracionário.
a)
b)
c)
d)