Página 75
UNIDADE
5
Estatística, contagem e probabilidade

Agora vamos estudar...
- variáveis estatísticas;
- distribuição de frequência;
- intervalos de classe;
- tabelas e gráficos;
- medidas de tendência central;
- amplitude;
- pesquisa estatística;
- contagem;
- probabilidade.
Página 76
Variáveis quantitativas e variáveis qualitativas
Na Estatística, as informações obtidas por meio de pesquisas são geralmente apresentadas em tabelas e gráficos, com números que caracterizam determinado conjunto de dados.
Nas pesquisas, cada elemento analisado é chamado variável estatística ou variável.
Considere a situação a seguir.
Uma loja realizou uma pesquisa para obter algumas informações a respeito de seus clientes e, com os resultados obtidos, elaborou a tabela a seguir.
|
Clientes |
Tipo sanguíneo |
Sexo |
Nível de escolaridade |
Idade (em anos) |
Quantidade de irmãos/irmãs |
Medida da altura |
|---|---|---|---|---|---|---|
|
A |
A |
Masculino |
Ensino Fundamental |
35 |
1 |
1,60 |
|
B |
AB |
Feminino |
Ensino Superior |
28 |
0 |
1,65 |
|
C |
B |
Feminino |
Ensino Médio |
30 |
2 |
1,80 |
|
D |
O |
Feminino |
Ensino Fundamental |
29 |
3 |
1,72 |
|
E |
A |
Masculino |
Ensino Superior |
28 |
2 |
1,79 |
|
F |
B |
Feminino |
Ensino Superior |
37 |
4 |
1,58 |
|
G |
A |
Masculino |
Ensino Superior |
38 |
1 |
1,67 |
Fonte de pesquisa: anotações da gerência da loja.
As variáveis podem ser classificadas como variáveis quantitativas e variáveis qualitativas.
As variáveis quantitativas são aquelas cujos valores podem ser obtidos por meio de contagem ou mensuração. Na situação apresentada, as variáveis "quantidade de irmãos/irmãs", "idade" e "medida da altura" são quantitativas. Elas podem ser classificadas em discretas ou contínuas.
As variáveis quantitativas discretas assumem valores inteiros positivos, obtidos por meio de contagem, como as variáveis "quantidade de irmãos/irmãs" e "idade (em anos)". As variáveis quantitativas contínuas são aquelas que assumem qualquer valor em um intervalo de variação, envolvendo uma mensuração, como a variável "medida de altura".
As variáveis qualitativas são aquelas que descrevem uma qualidade ou um atributo e podem ser classificadas em nominal ou ordinal. As variáveis qualitativas nominais não apresentam ordenação, como as variáveis "sexo" e "tipo sanguíneo". As variáveis qualitativas ordinais são as que apresentam certa ordenação, como a variável "nível de escolaridade".
Página 77
Distribuição de frequência
Considere a tabela a seguir, que apresenta a quantidade de funcionários que trabalha em uma empresa. Na 2ª coluna desta tabela é apresentada a quantidade de funcionários que trabalha em cada setor da empresa. Cada uma dessas quantidades corresponde à frequência absoluta ou frequência ().
|
Setor |
Quantidade de funcionários |
|---|---|
|
Produção |
48 |
|
Informática |
8 |
|
Manutenção geral |
6 |
|
Limpeza |
6 |
|
Administrativo |
12 |
|
Total |
80 |
Fonte de pesquisa: registro da secretaria da empresa.
Para visualizar a representação de cada frequência absoluta em relação ao todo, podemos calcular a frequência relativa (), que, em geral, é dada em porcentagem e pode ser determinada pela relação , em que indica a frequência absoluta total ou a quantidade total de ocorrência.
Para a situação apresentada, temos:
- setor de produção: , ou seja, 60%.
- setor de informática: , ou seja, 10%.
- setor de manutenção geral: , ou seja, 7,5%.
- setor de limpeza: , ou seja, 7,5%.
- setor administrativo: , ou seja, 15%.
A tabela a seguir apresenta a frequência e a frequência relativa da quantidade de funcionários por setor.
|
Setor |
Frequência |
Frequência relativa |
|---|---|---|
|
Produção |
48 |
60% |
|
Informática |
8 |
10% |
|
Manutenção geral |
6 |
7,5% |
|
Limpeza |
6 |
7,5% |
|
Administrativo |
12 |
15% |
|
Total |
80 |
100% |
Fonte de pesquisa: registro da secretaria da empresa.
Página 78
Podemos também incluir na tabela anterior a frequência acumulada e a frequência acumulada relativa . A primeira é dada pela soma das frequências absolutas até determinado valor, e a segunda, pela soma das frequências relativas até determinado valor.
Acompanhe a seguir como podemos determinar essas frequências.
Setor de produção
Setor de informática
Setor de manutenção geral
Setor de limpeza
Setor administrativo
Note, na tabela a seguir, a frequência acumulada e a frequência acumulada relativa.
|
Setor |
Frequência |
Frequência relativa |
Frequência acumulada |
Frequência acumulada relativa |
|---|---|---|---|---|
|
Produção |
48 |
60% |
48 |
60% |
|
Informática |
8 |
10% |
56 |
70% |
|
Manutenção geral |
6 |
7,5% |
62 |
77,5% |
|
Limpeza |
6 |
7,5% |
68 |
85% |
|
Administrativo |
12 |
15% |
80 |
100% |
|
Total |
80 |
100% |
Fonte de pesquisa: registro da secretaria da empresa.
Analisando a tabela de distribuição de frequência apresentada, podemos verificar, pela frequência acumulada e pela frequência acumulada relativa, que 56 funcionários ou 70% do total de funcionários trabalham no setor de produção ou de informática.
Atividades
Faça as atividades no caderno.
1. No caderno, classifique as variáveis a seguir em quantitativa discreta, quantitativa contínua, qualitativa nominal ou qualitativa ordinal.
a) Quantidade de veículos que circulam por dia em uma avenida.
b) Esporte preferido dos estudantes do 8º ano.
c) Medida da massa.
d) Estágio de uma doença.
e) Número de livros em uma biblioteca.
f) Tipo sanguíneo.
g) Salário dos funcionários de uma empresa.
h) Classe social.
Página 79
2. Verifique no gráfico de colunas a seguir, a produção brasileira, em tonelada, de algumas frutas cítricas em 2020.
Produção brasileira de algumas frutas cítricas em 2020
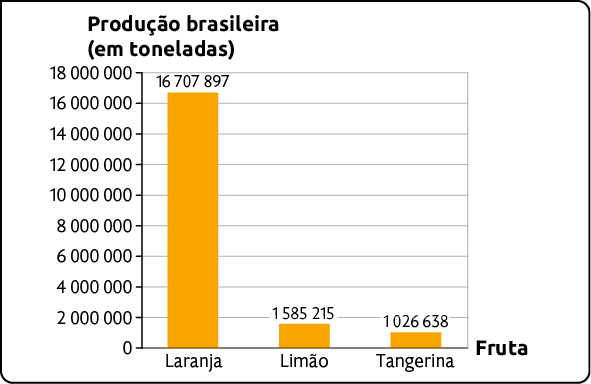
Fonte de pesquisa: IBGE. Produção agrícola municipal. Disponível em: https://oeds.link/k3UxIu.
Acesso em: 26 abr. 2022.
Escreva no caderno o nome das variáveis presentes no gráfico. Em seguida, classifique-as em quantitativa ou qualitativa.
3. No ano de 2023, uma montadora de automóveis realizou uma pesquisa para identificar a cor de veículo preferida dos clientes. Nessa pesquisa, cada cliente votou uma única vez. Analise no quadro os resultados da pesquisa.
|
Cor |
Quantidade de respostas |
|---|---|
|
Branco |
56 |
|
Preto |
96 |
|
Prata |
120 |
|
Vermelho |
24 |
|
Cinza |
104 |
a) Quantos clientes foram entrevistados?
b) Construa no caderno uma tabela de distribuição de frequência indicando a frequência absoluta e a frequência relativa para cada cor indicada no quadro.
c) Qual é a cor com menor preferência?
4. Considere as notas dos estudantes em uma prova de Matemática.
- 8,0
- 7,0
- 7,0
- 9,0
- 10,0
- 4,0
- 6,0
- 8,0
- 2,0
- 10,0
- 6,0
- 7,0
- 7,0
- 5,0
- 5,0
- 9,0
- 2,0
- 6,0
- 8,0
- 8,0
- 4,0
- 2,0
- 7,0
- 5,0
- 6,0
- 7,0
- 6,0
- 7,0
- 5,0
- 5,0
- 5,0
- 7,0
- 7,0
- 4,0
- 4,0
- 6,0
- 5,0
- 6,0
- 7,0
- 6,0
a) Quantos estudantes obtiveram nota maior do que 7?
b) Qual foi a menor e a maior nota obtida?
c) Utilizando os dados apresentados, construa no caderno uma tabela de distribuição de frequência contendo as frequências absoluta, relativa, acumulada e acumulada relativa para cada uma das notas.
Página 80
Intervalos de classe
A gerência de uma loja realizou uma pesquisa para saber a faixa etária de seus funcionários. Cada um dos valores apresentados no quadro a seguir corresponde à idade de cada um dos funcionários.
- 28
- 35
- 32
- 29
- 38
- 26
- 32
- 35
- 42
- 45
- 30
- 32
- 34
- 40
- 29
- 37
- 43
- 48
- 50
- 46
- 26
- 36
- 41
- 52
- 46
- 38
- 48
- 36
- 38
- 41
- 27
- 38
- 55
- 58
- 60
- 44
- 46
- 36
- 38
- 39
- 58
- 57
- 42
- 34
- 37
- 41
- 62
- 64
- 45
- 58
Questão 1. Escreva no caderno a quantidade de funcionários que participaram da pesquisa.
Podemos organizar os dados em ordem crescente ou decrescente. Essa organização é chamada rol.
- 26
- 26
- 27
- 28
- 29
- 29
- 30
- 32
- 32
- 32
- 34
- 34
- 35
- 35
- 36
- 36
- 36
- 37
- 37
- 38
- 38
- 38
- 38
- 38
- 39
- 40
- 41
- 41
- 41
- 42
- 42
- 43
- 44
- 45
- 45
- 46
- 46
- 46
- 48
- 48
- 50
- 52
- 55
- 57
- 58
- 58
- 58
- 60
- 62
- 64
Os dados também podem ser organizados em uma tabela de distribuição de frequências em que a variável é "faixa etária dos funcionários". Como há muitos valores diferentes e não há tantos valores repetidos, é conveniente agrupar esses dados em um intervalos de classe.
Note como podemos determinar esses intervalos.
Primeiro, calculamos a diferença entre o maior e o menor valor do rol, chamada amplitude total.
Depois, escolhemos de maneira conveniente um valor igual ou maior do que a amplitude total. Neste caso, escolhemos o valor 40. Também devemos escolher a quantidade de intervalos, que neste caso será 8. Com isso, calculamos o quociente entre esses dois valores escolhidos para obter a amplitude do intervalo.
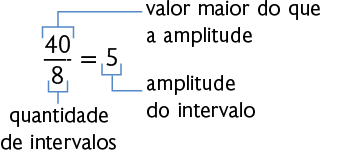
Em seguida, definimos os intervalos de classe a partir do menor valor.
Atenção!
A notação indica que o valor da esquerda pertence ao intervalo e o da direita não.
Por exemplo, em , o número 26 pertence ao intervalo, mas o 31 não.
Página 81
Agora, construímos a tabela de distribuição de frequências utilizando os intervalos de classes.
Ao analisarmos a organização dos dados em rol, verificamos que existem 7 valores iguais ou maiores do que 26 e menores do que 31. Logo, a frequência correspondente à classe é igual a 7. Procedendo da mesma maneira, obtemos as frequências das demais classes.
|
Faixa etária |
Frequência |
Frequência relativa |
Frequência acumulada |
Frequência acumulada relativa |
|---|---|---|---|---|
|
7 |
14% |
7 |
14% |
|
|
7 |
14% |
14 |
28% |
|
|
12 |
24% |
26 |
52% |
|
|
9 |
18% |
35 |
70% |
|
|
6 |
12% |
41 |
82% |
|
|
2 |
4% |
43 |
86% |
|
|
5 |
10% |
48 |
96% |
|
|
2 |
4% |
50 |
100% |
Fonte de pesquisa: anotações da gerência da loja.
Questão 2. Em seu caderno, determine a frequência e a frequência relativa de funcionários na faixa etária de .
Podemos representar os dados da tabela de distribuição de frequências agrupados em intervalos de classes em um histograma. Esse tipo de gráfico representa a frequência por meio de colunas justapostas.
O histograma a seguir representa a frequência relativa da faixa etária dos funcionários da loja.
Faixa etária dos funcionários em abril de 2024
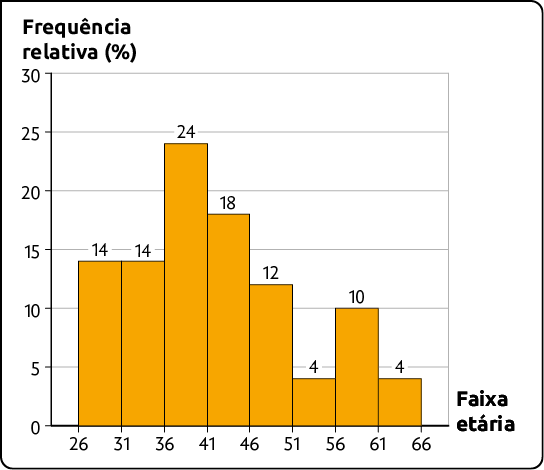
Fonte de pesquisa: anotações da gerência da loja.
Página 82
Atividades
Faça as atividades no caderno.
5. Em relação à faixa etária dos funcionários citada anteriormente, responda às questões a seguir.
a) Quantos têm menos do que 41 anos?
b) Qual é o percentual de funcionários com idade na faixa etária de 46 a 50 anos?
c) Qual faixa etária tem maior número de funcionários?
6. O departamento financeiro de uma empresa organizou a quantidade de funcionários por faixa salarial. Verifique os resultados na tabela a seguir.
|
Faixa salarial |
Frequência |
|---|---|
|
18 |
|
|
15 |
|
|
9 |
|
|
5 |
|
|
3 |
|
|
Total |
50 |
Fonte de pesquisa: departamento financeiro da empresa.
a) Quantas pessoas ganham menos de 7 salários mínimos?
b) De acordo com a tabela, determine a amplitude de cada intervalo de classe.
c) Copie a tabela no caderno e inclua as frequências relativa, acumulada e acumulada relativa.
7. A professora de Biologia realizou uma pesquisa para determinar a medida da massa, em quilograma, dos estudantes do 3º ano. Verifique no quadro a seguir os resultados dessa pesquisa.
- 65
- 83,5
- 63,5
- 67,2
- 82
- 69,8
- 57
- 66
- 60
- 60
- 71,7
- 59
- 73
- 74,4
- 62
- 79
- 58
- 64
- 67
- 68
- 64,5
- 66
- 68
- 71
a) No caderno, distribua os dados em 3 intervalos, de maneira que o primeiro seja . Em seguida, construa uma tabela de distribuição de frequência, indicando as frequências absoluta, relativa, acumulada e acumulada relativa.
b) Qual classe tem maior frequência?
Página 83
8. Um agente de saúde de um município realizou uma pesquisa por amostragem para determinar o Índice de Massa Corporal (IMC) dos habitantes do bairro em que ele trabalha. Verifique os resultados na tabela.
|
IMC |
Frequência |
|---|---|
|
3 |
|
|
25 |
|
|
7 |
|
|
4 |
|
|
1 |
|
|
Total |
40 |
Fonte de pesquisa: registros do agente de saúde.
a) Foi pesquisado o IMC de quantas pessoas?
b) A maior frequência ocorreu em qual intervalo de classe?
c) É possível determinar precisamente o IMC de cada uma das pessoas que participaram da pesquisa? Justifique sua resposta.
d) Junte-se a um colega e realizem uma pesquisa a respeito do IMC. Depois, calculem o IMC de cada um de vocês.
9. A equipe de organização de um campeonato de futebol realizou um levantamento para identificar a faixa etária dos atletas inscritos. Os resultados estão apresentados no histograma.
Faixa etária dos atletas inscritos em 2024
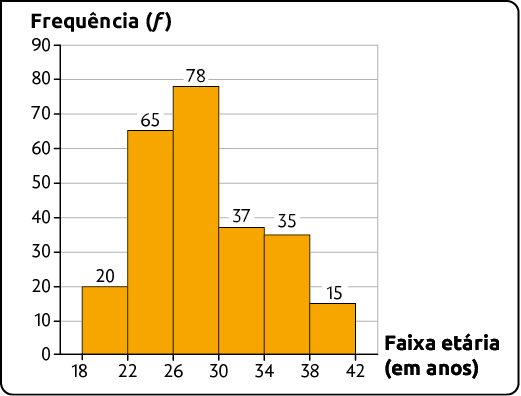
Fonte de pesquisa: registros da equipe de organização.
a) Determine a amplitude de cada intervalo de classe utilizado nesse histograma.
b) Em que intervalo ocorreu a maior frequência?
c) Qual é a porcentagem de atletas com menos de 22 anos inscritos nesse campeonato?
10. O professor de Educação Física fez um levantamento para saber a medida de tempo que cada estudante levou para realizar uma atividade física e registrou os resultados no histograma a seguir.
Medida de duração do intervalo de tempo gasto na realização da atividade em 2024
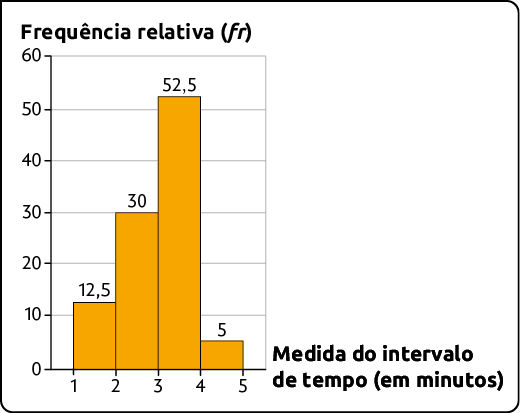
Fonte de pesquisa: registros do professor de Educação Física.
a) Quantos por cento dos estudantes gastaram pelo menos 3 minutos para realizar a atividade física?
b) Qual é a amplitude de cada intervalo de classe utilizado na construção desse histograma?
c) Sabendo que nessa turma há 40 estudantes, quantos deles gastaram menos de 2 minutos para realizar a atividade física?
Página 84
Medidas de tendência central
Neste tópico estudaremos a média aritmética, a moda e a medida, que são medidas de tendência central. Além disso, estudaremos a amplitude total, que é uma medida de dispersão.
Média aritmética
Verifique as medidas das alturas, em centímetros, das jogadoras de handebol do time da escola de Manuela.
- 176
- 173
- 179
- 174
- 182
- 184
- 175
- 176
- 173
- 178
- 174
- 174
- 183
- 174
- 185
- 188

Podemos, por exemplo, determinar a média aritmética das medidas das alturas das jogadoras adicionando as medidas da altura de cada jogadora e dividindo o resultado obtido pela quantidade de jogadoras.
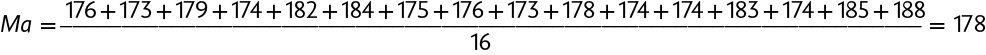
Assim, a média da medida das alturas das jogadoras é .
Média aritmética (Ma) ou média é a soma dos valores atribuídos à variável dividida pela quantidade de valores adicionados.
Moda e mediana
Podemos verificar que a medida de altura das jogadoras que ocorre com maior frequência é . Esse valor é chamado moda.
A moda (Mo) é o valor que ocorre com maior frequência, isto é, que se repete mais vezes em um conjunto de valores. Quando ocorrerem duas modas, o conjunto de valores é chamado bimodal; três modas, chamado trimodal; quatro modas, quadrimodal, e assim por diante. Caso um conjunto de valores não apresente moda, dizemos que o conjunto é amodal.
Página 85
Como esse conjunto tem uma quantidade par de valores (16), a mediana corresponde à média aritmética entre os dois valores centrais.
Assim, para determinar a mediana, primeiro organizamos todo o conjunto de valores em ordem crescente ou decrescente. Nesse caso, organizamos em ordem crescente as medidas das alturas das jogadoras.
Atenção!
Quando o conjunto tem uma quantidade ímpar de valores, a mediana corresponde ao valor central.
Portanto, a mediana das medidas das alturas das jogadoras de handebol é .
A mediana (Md) é o valor central de um conjunto com uma quantidade ímpar de valores que estejam organizados em ordem crescente ou decrescente. Caso o conjunto tenha uma quantidade par de valores, a mediana é dada pela média aritmética dos dois valores centrais.
Amplitude total
Para analisar a dispersão (variação) dos valores de um conjunto, calculamos a amplitude total. Essa medida auxilia na compreensão da distribuição dos valores de um conjunto em torno das medidas de tendência central.
Para calcular a amplitude total, subtraímos o menor do maior valor do conjunto de valores. No caso das medidas das alturas das jogadoras de handebol da escola em que Manuela estuda (Time A) temos:
Portanto, a amplitude total das medidas das alturas das jogadoras é .
Agora, vamos comparar a amplitude desse conjunto de valores com o conjunto das medidas das alturas do time de handebol da escola em que Marta estuda (Time B). Nesse time, a jogadora mais baixa tem e a mais alta, . Desse modo, a amplitude total é , pois:
Como a amplitude das medidas de altura do time B é menor do que a do time A, concluímos que as medidas de altura das jogadoras do time B apresentam menor dispersão, ou seja, estão mais próximas das medidas de tendência central (média, moda e mediana) do que as medidas de altura das jogadoras do time A.
Quanto maior a amplitude total, mais afastados os valores do conjunto estarão uns dos outros e das medidas de tendência central. Quanto menor a amplitude, mais próximos os valores do conjunto estarão uns dos outros e, consequentemente, mais próximos das medidas de tendência central.
A amplitude total de um conjunto de valores é calculada fazendo a diferença entre o maior e o menor valor.
Página 86
Atividades
Faça as atividades no caderno.
11. Verifique a parte destacada da fatura de água da casa de Suely.
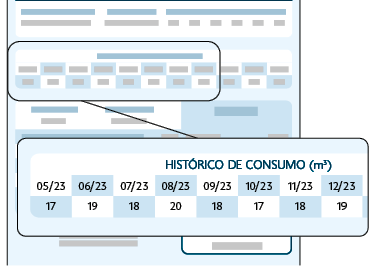
a) Qual foi o consumo médio mensal de água, em metros cúbicos, na casa de Suely no período de maio a dezembro de 2023?
b) Em quais meses o consumo de água ficou abaixo da média?
12. Analise no quadro as notas da prova de História dos estudantes do 8º ano da escola Crescer.
- 7,0
- 9,0
- 10,0
- 8,0
- 6,5
- 6,0
- 8,0
- 7,0
- 9,0
- 10,0
- 9,0
- 8,0
- 8,0
- 7,0
- 6,0
- 8,5
- 5,0
- 4,0
- 10,0
- 9,0
- 7,0
- 7,5
- 6,0
- 8,0
- 6,0
- 9,5
- 5,0
- 8,0
- 7,0
- 6,0
a) Calcule no caderno a mediana, a moda e a média dessas notas.
b) Determine a amplitude total das notas dos estudantes.
13. A tabela a seguir mostra as três primeiras notas dos candidatos em um processo de seleção para uma vaga de emprego. Nessa seleção, a nota máxima em cada etapa é 10.
|
Nome do candidato |
Etapas |
|||
|---|---|---|---|---|
|
Prova escrita |
Prova prática |
Entrevista |
Currículo |
|
|
Cecília |
8,8 |
8,0 |
8,6 |
|
|
Júlio |
7,4 |
8,4 |
9,2 |
|
|
Mariana |
8,7 |
8,8 |
9,1 |
|
|
Roberto |
8,4 |
8,4 |
9,0 |
|
Fonte de pesquisa: Departamento de Recursos Humanos.
a) Se todos os candidatos obtiverem nota 9,0 no currículo, qual será a média final de cada um deles? Quem ficará em 1º lugar?
b) Qual é a maior média possível que Júlio poderá obter ao final das quatro etapas?
14. No quadro a seguir aparece a medida da altura, em centímetro, dos quatro tenistas mais bem ranqueados de alguns países.
|
Brasil |
Espanha |
Estados Unidos |
França |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
183 |
185 |
183 |
185 |
185 |
185 |
188 |
183 |
196 |
211 |
208 |
188 |
193 |
188 |
196 |
183 |
Fonte de pesquisa: ATP. Disponível em: https://oeds.link/2oK8bN. Acesso em: 29 abr. 2022.
a) Calcule no caderno a média, a moda e a mediana da medida da altura dos tenistas para cada país.
b) A medida da altura de qual país apresenta menor amplitude total?
Página 87
15. (Enem-2011) Uma equipe de especialistas do centro meteorológico de uma cidade mediu a temperatura do ambiente, sempre no mesmo horário, durante 15 dias intercalados, a partir do primeiro dia de um mês. Esse tipo de procedimento é frequente, uma vez que os dados coletados servem de referência para estudos e verificação de tendências climáticas ao longo dos meses e anos. As medições ocorridas nesse período estão indicadas no quadro.
|
Dia do mês |
Temperatura (em ) |
|---|---|
|
1 |
15,5 |
|
3 |
14 |
|
5 |
13,5 |
|
7 |
18 |
|
9 |
19,5 |
|
11 |
20 |
|
13 |
13,5 |
|
15 |
13,5 |
|
17 |
18 |
|
19 |
20 |
|
21 |
18,5 |
|
23 |
13,5 |
|
25 |
21,5 |
|
27 |
20 |
|
29 |
16 |
Em relação à temperatura, os valores da média, mediana e moda são, respectivamente, iguais a
a) , e .
b) , e .
c) , e .
d) , e .
e) , e .
16. A tabela mostra os investimentos realizados ao longo de três anos consecutivos por quatro empresas do setor de telefonia, buscando melhorar a qualidade dos serviços oferecidos aos clientes.
|
Empresa |
Investimento total anual (em milhões de reais) |
||
|---|---|---|---|
|
2021 |
2022 |
2023 |
|
|
A |
82 |
95 |
120 |
|
B |
92 |
110 |
104 |
|
C |
93 |
101 |
109 |
|
D |
84 |
116 |
100 |
Fonte de pesquisa: setor financeiro das empresas.
Calcule no caderno a média de investimento anual das quatro empresas nesse período. Qual empresa mais investiu, em média, de 2021 a 2023?
17. Analise o gráfico a seguir.
Índice da Bolsa de Valores de São Paulo (Ibovespa) no final dos anos 2000 a 2008
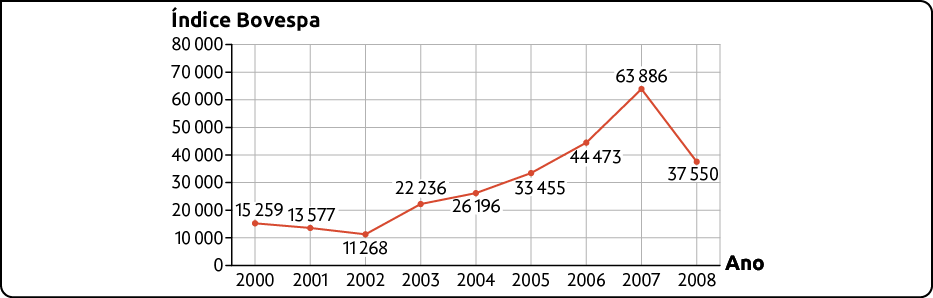
Fonte de pesquisa: B3 Investimentos. Disponível em: https://oeds.link/2SkwkA. Acesso em: 11 jul. 2022.
Considerando o menor e o maior valor assumido por esse índice no período apresentado, determine o aumento percentual aproximado em relação ao menor valor.
Página 88
Tabelas e gráficos
As tabelas e os gráficos estão presentes no cotidiano e podem ser observados, por exemplo, nas embalagens de produtos alimentícios que apresentam as tabelas nutricionais e em algumas notícias transmitidas pelos diversos meios de comunicação, como televisão, jornais impressos, revistas e internet.
A apresentação de informações em tabelas e gráficos tem o intuito de facilitar a compreensão e a interpretação dos dados.
Tabelas
Nas tabelas, as informações são apresentadas em linhas e colunas, o que permite uma rápida leitura e interpretação dos dados.
Toda tabela deve apresentar título, utilizado para expor a informação principal, e fonte de pesquisa, que mostra a origem dos dados e a data em que foram publicados ou acessados.
Considere a tabela apresentada a seguir.
|
Região |
Quantidade de pessoas vacinadas |
|---|---|
|
Norte |
13.328.566 |
|
Nordeste |
46.126.421 |
|
Centro-Oeste |
13.574.238 |
|
Sudeste |
78.571.071 |
|
Sul |
26.465.178 |
Fonte de pesquisa: BRASIL. Ministério da Saúde. Vacinômetro - COVID-19. Disponível em: https://oeds.link/7FZ8v9. Acesso em: 7 abr. 2022.
De acordo com os dados apresentados na tabela, podemos concluir que:
- a Região Norte teve a menor quantidade de pessoas vacinadas com a 1ª dose ou a dose única, seguida da Região Centro-Oeste, que também teve uma quantidade menor comparada às demais regiões;
- a maior quantidade de pessoas vacinadas com a 1ª dose ou dose única ocorreu na Região Sudeste do país.
Questão 3. No caderno, escreva o título e a fonte de pesquisa dessa tabela.
Página 89
A tabela de dupla entrada é utilizada para apresentar dois ou mais tipos de informações a respeito do mesmo assunto.
|
Ano |
Rede pública |
Rede particular |
|---|---|---|
|
2020 |
204.174 |
107.448 |
|
2019 |
251.374 |
998.702 |
|
2018 |
259.302 |
1.004.986 |
|
2017 |
251.793 |
947..976 |
|
2016 |
246.875 |
922.574 |
Fonte de pesquisa: INSTITUTO Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Sinopse estatística da educação superior. Disponível em: https://oeds.link/HXWy8u. Acesso em: 9 abr. 2022.
Gráficos
Existem diversos tipos de gráficos, cada um com características específicas, que se adéquam melhor para representar tipos diferentes de conjuntos de dados obtidos por meio de pesquisas.
Assim como nas tabelas, os gráficos devem ter título e fonte de pesquisa.
Gráfico de colunas
Os gráficos de colunas geralmente são utilizados para realizar comparações entre os dados obtidos. Nesses gráficos, aplicam-se retângulos para representar as colunas (verticais ou horizontais) as quais têm as mesmas medidas de largura e o mesmo espaçamento entre elas. A medida de altura – no caso das colunas horizontais – ou a medida do comprimento – no caso das colunas verticais – de cada retângulo deve ser proporcional ao valor que ele representa.
Quantidade de doses da vacina contra a COVID-19 aplicadas, por tipo, no Brasil até 7 de abril de 2022
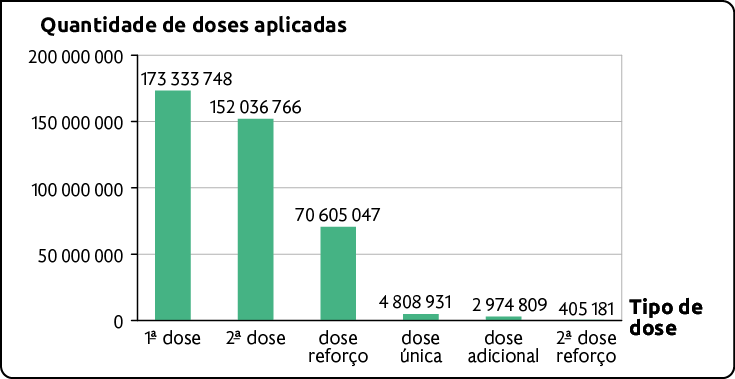
Fonte de pesquisa: BRASIL. Ministério da Saúde. Vacinômetro – COVID-19. Disponível em: https://oeds.link/7FZ8v9. Acesso em: 7 abr. 2022.
Analisando o gráfico, percebemos que a quantidade de doses de reforço aplicadas até abril de 2022 corresponde a aproximadamente metade da quantidade de segundas doses aplicadas.
Questão 4. Escreva no caderno os títulos do eixo horizontal e do eixo vertical do gráfico.
Página 90
Nos gráficos de colunas múltiplas ou agrupadas também são utilizados retângulos para representar as colunas. Porém, eles são agrupados mostrando os vários valores e as diversas informações de uma mesma categoria.
Quantidade de atletas homens e mulheres participantes nos Jogos Olímpicos de 2004 a 2020
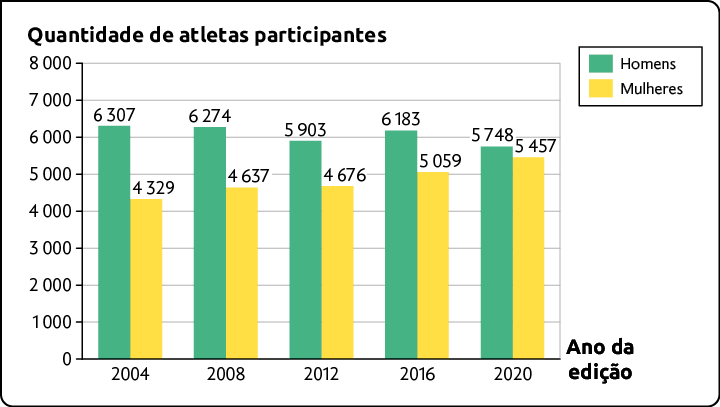
Fonte de pesquisa: INTERNATIONAL Olympic Committee. Disponível em: https://oeds.link/tmqHVz. Acesso em: 4 abr. 2022.
Analisando o gráfico, podemos perceber, por exemplo, que, em 2004, a diferença entre a quantidade de atletas homens e mulheres participantes dos Jogos foi maior do que em 2020.
Gráfico de linhas
O gráfico de linhas facilita a visualização do comportamento dos dados pesquisados em certo período de tempo. Nesse tipo de gráfico, são demarcados pontos que representam os dados da pesquisa, ligados por linhas que indicam uma tendência de crescimento, decrescimento ou a constância dos dados entre dois resultados consecutivos no intervalo analisado.
Medida da área desmatada da floresta Amazônica – 2012 a 2021
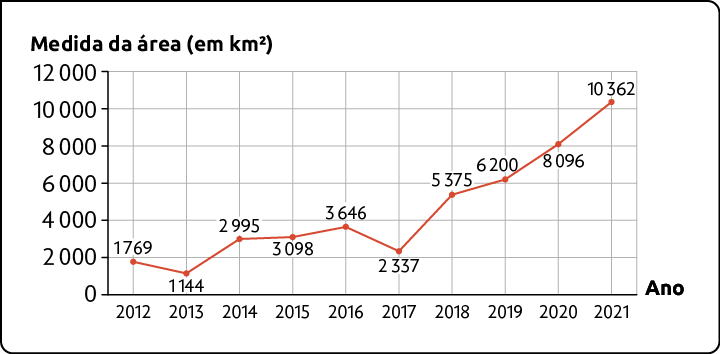
Fonte de pesquisa: INSTITUTO do homem e meio ambiente da Amazônia (Imazon). Disponível em: https://oeds.link/KU6cRM. Acesso em: 9 abr. 2022.
Examinando o gráfico, concluímos que 2013 foi o ano em que houve a menor medida de área desmatada da floresta Amazônica.
Página 91
Gráfico de setores
O gráfico de setores, também conhecido como gráfico de pizza, é adequado para comparar os dados coletados em relação ao universo pesquisado. Assim, cada setor representa partes de um todo, em que os dados geralmente são representados em porcentagem.
Cada setor do gráfico deve ser proporcional à parte dos dados que ele representa, considerando que o total corresponde a 100%.
Porcentagens do eleitorado brasileiro por faixa etária em dezembro de 2021
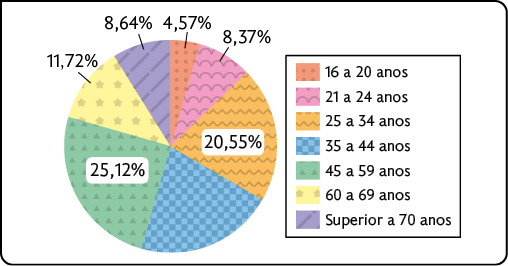
Fonte de pesquisa: BRASIL. Tribunal Superior Eleitoral. Disponível em: https://oeds.link/k2Q6wg. Acesso em: 11 abr. 2022.
Pictograma
É comum encontrarmos, em livros, revistas e jornais, gráficos em que as informações de uma pesquisa são representadas por meio de desenhos, figuras, fotos ou demais recursos visuais. A essa representação chamamos pictograma ou gráfico pictórico.
Nos pictogramas, as dimensões ou a quantidade de desenhos ou figuras que representam cada dado é proporcional ao valor desse dado.
Consumo anual aproximado de sorvetes, por pessoa, de alguns países em 2019 (em litro)
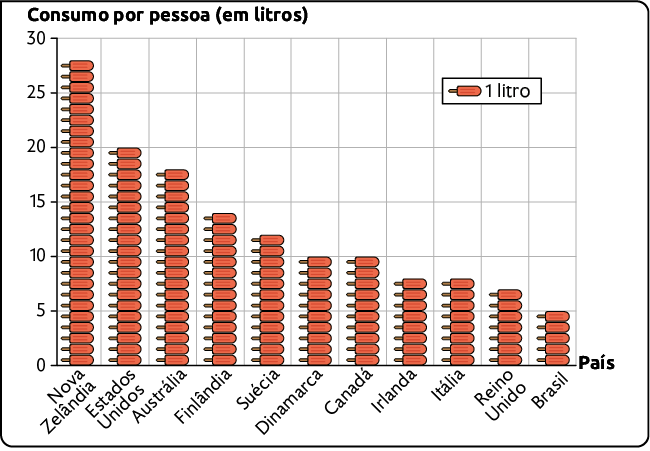
Fonte de pesquisa: WORLD Atlas. Disponível em: https://oeds.link/mRmSi4. Acesso em: 5 abr. 2022.
Com base nos dados apresentados no pictograma, a Dinamarca e o Canadá apresentaram o mesmo consumo aproximado de litros de sorvete por pessoa em 2019.
Página 92
Pirâmide etária
As pirâmides etárias são utilizadas para representar uma população, cuja distribuição está disposta em faixas etárias e separada por sexo. Esse tipo de gráfico geralmente é organizado de maneira que na base estejam indicadas as faixas etárias dos mais jovens e no topo as faixas etárias dos mais idosos.
Pirâmide etária da população do estado de Minas Gerais em 2010
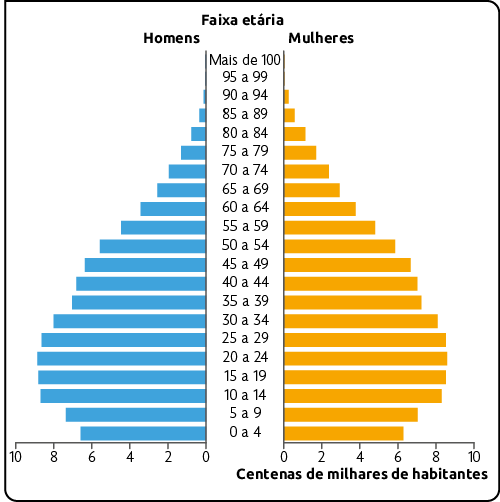
Fonte de pesquisa: IBGE. Cidades. Disponível em: https://oeds.link/tBNrMD. Acesso em: 9 abr. 2022.
Analisando esta pirâmide etária, podemos concluir que, em 2010, no estado de Minas Gerais, a quantidade de mulheres na faixa etária entre 90 e 94 anos é maior do que a quantidade de homens na mesma faixa etária da população.
Atividades
Faça as atividades no caderno.
18. A tabela a seguir mostra algumas informações sobre a quantidade de quilocalorias () obtidas no consumo de alguns alimentos.
|
Alimento |
Quantidade de |
|---|---|
|
Leite integral em pó |
497 |
|
Iogurte natural |
51 |
|
Pão francês |
300 |
|
Ovo de galinha inteiro frito |
240 |
|
Achocolatado em pó |
401 |
|
Amendoim torrado salgado |
606 |
|
Lentilha cozida |
93 |
Fonte de pesquisa: TABELA brasileira de Composição de Alimentos (TACO). Disponível em: https://oeds.link/E3x0qE. Acesso em: 25 fev. 2022.
a) Qual dos alimentos apresentados na tabela é o mais calórico?
b) Quantas calorias uma pessoa vai ingerir se, no café da manhã, comer 100 gramas de pão francês, 100 gramas de iogurte natural e beber 1 copo de leite integral preparado com 100 gramas de leite integral em pó?
c) Qual alimento é o mais calórico: 100 gramas de lentilha cozida ou 100 gramas de iogurte natural?
d) Em sua opinião, qual é a consequência de ingerir mais calorias do que se gasta durante o dia? O que podemos fazer para equilibrar o gasto calórico com a quantidade de calorias ingeridas por dia?
e) Junte-se a um colega e pesquisem as consequências para a saúde de consumir diariamente menos calorias do que precisamos e as consequências de consumir mais calorias do que gastamos. Em seguida, façam um cartaz com os resultados da pesquisa e exponham para os colegas.
Página 93
19. Exemplifique no caderno uma situação adequada para o tipo de gráfico indicado em cada item.
a) Gráfico de colunas.
b) Gráfico de colunas agrupadas.
c) Gráfico de linhas.
d) Gráfico de setores.
20. Exemplifique no caderno o tipo de gráfico mais adequado para a situação indicada em cada item.
a) Quantidade de habitantes do Brasil por região geográfica.
b) Taxa de inflação ao longo de 1 ano.
c) Resultado de uma eleição presidencial.
21. Analise os gráficos em cada item e em seguida escreva no caderno os erros que eles apresentam.
A.Taxa de desocupação nas grandes regiões do Brasil no 4º trimestre de 2021
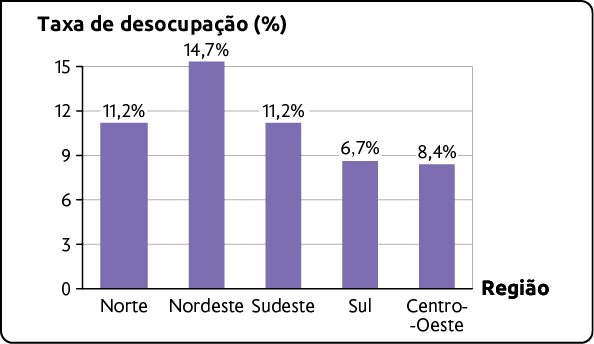
Fonte de pesquisa: IBGE. Disponível em: https://oeds.link/tTOqno. Acesso em: 29 abr. 2022.
B.Percentual de uso dos principais modais de transporte no Brasil em 2024
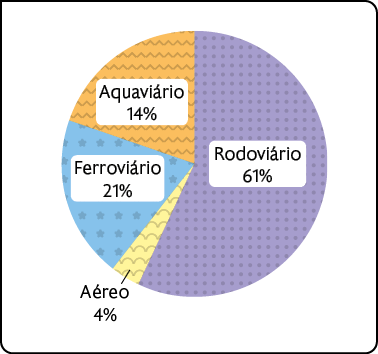
C.Produção brasileira de uva de 2018 a 2020
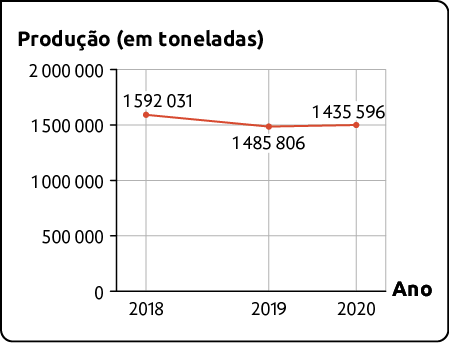
Fonte de pesquisa: IBGE. Disponível em: https://oeds.link/k3UxIu. Acesso em: 29 abr. 2022.
Página 94
22. Em um ambiente de cultura, um cientista iniciou o cultivo de bactérias das espécies I e II. Analise o gráfico a seguir, que apresenta as quantidades de bactérias de cada espécie, em função do dia, durante a primeira semana do mês de janeiro de 2023.
Bactérias das espécies I e II - primeira semana do mês de janeiro de 2023
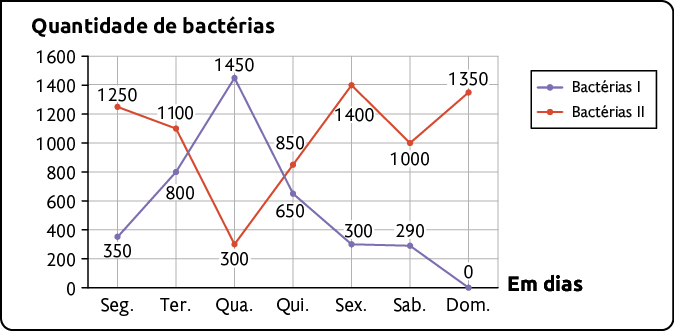
Fonte de pesquisa: registros do cientista.
Em que dia dessa semana a quantidade de bactérias foi máxima?
a) Terça-feira.
b) Quarta-feira.
c) Quinta-feira.
d) Sexta-feira.
e) Domingo.
23. No Brasil, o acesso à educação é um direito da criança e do adolescente. Durante a pandemia de COVID-19, muitos estudantes perderam o vínculo com a educação em razão da suspensão das aulas presenciais e da falta de infraestrutura, como a dificuldade de acesso a tecnologias. Analise o gráfico de setores a seguir.
Porcentagem de crianças e adolescentes, por faixa etária,
sem
acesso à educação ao final de 2020
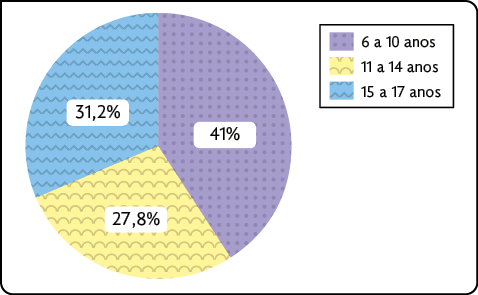
Fonte de pesquisa: AGÊNCIA Brasil. Disponível em: https://oeds.link/LpNWDX. Acesso em: 19 abr. 2022.
a) Qual faixa etária teve a maior porcentagem de estudantes sem acesso à educação?
b) Qual é a diferença das porcentagens de estudantes sem acesso à educação entre as faixas etárias de 15 a 17 anos e de 11 a 14 anos?
c) Em sua opinião, é importante assegurar o direito à educação para crianças e adolescentes? Justifique sua resposta.
d) Faça uma pesquisa sobre as consequências da falta do acesso à educação para crianças e adolescentes. Em seguida, registre no caderno os dados de sua pesquisa e converse com o professor e os colegas sobre o assunto.
e) Após sua pesquisa, você mudou de opinião sobre a importância de assegurar o direito à educação para crianças e adolescentes?
Página 95
24. Em 2020, houve aumento significativo no número de candidatos indígenas eleitos para os cargos de prefeitos e vereadores em relação ao pleito de 2016.
Esses resultados foram comemorados por Joenia Wapichana, única representante indígena eleita para a Câmara dos Deputados na eleição de 2018 e a primeira mulher indígena eleita para ocupar uma vaga no Parlamento.
Fonte de pesquisa: CRESCE número de prefeitos e vereadores indígenas. Câmara dos Deputados, 20 nov. 2020. Disponível em: https://oeds.link/GatGdf. Acesso em: 29 abr. 2022.
Joenia pertence à etnia Wapichana, povo indígena que, no território brasileiro, vive em Roraima, em uma região conhecida como Serra da Lua, localizada entre os rios Branco e Tacutu. Também há aldeias da etnia Wapichana na Guiana e na Venezuela. Estimava-se que em 2014 a população Wapichana era de 9.441 indivíduos em território brasileiro.
A língua nativa dos Wapichana pertence à família Aruak (ou Arawak), conjunto de línguas ameríndias, ou seja, dos povos indígenas que ocupam o continente americano. Os Arawak são uma etnia que tem sua língua com o mesmo nome. O termo "Arawakan" designa de maneira mais geral a língua Arawak, falada na Venezuela, na Guiana, no Suriname e na Guiana Francesa. Também se utiliza o termo "Maipuran" para designar a família da língua Arawak.
O meio de subsistência desses povos é baseado na agricultura tradicional, em que as famílias normalmente têm os próprios roçados. Entre os produtos produzidos, encontram-se milho, feijão e, principalmente, mandioca.
Fonte de pesquisa: POVOS indígenas do Brasil. Disponível em: https://oeds.link/EmliQt. Acesso em: 29 abr. 2022.
O gráfico a seguir mostra os dados sobre a quantidade de candidatos indígenas eleitos por região na eleição de 2020.
Quantidade de candidatos indígenas eleitos por região na eleição de 2020
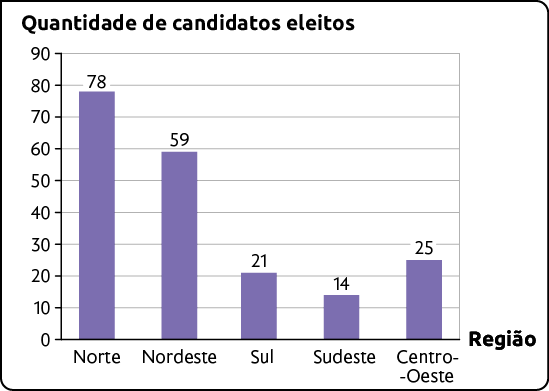
Fonte de pesquisa: BRASIL. Agência de Notícias da Câmara dos Deputados. Disponível em: https://oeds.link/GatGdf. Acesso em: 29 abr. 2022.
a) Escreva no caderno o nome da primeira mulher brasileira indígena eleita para a Câmara dos Deputados. Qual estado brasileiro ela representa?
b) Qual era a população da etnia Wapichana residente no Brasil em 2014? Quais países, além do Brasil, os povos Wapichana habitam?
c) Qual região do Brasil elegeu o maior número de candidatos indígenas na eleição de 2020?
Página 96
Construindo gráficos
Gráfico de colunas
A direção de um curso preparatório para vestibular realizou uma pesquisa com os estudantes para saber qual área de conhecimento eles preferem cursar na universidade. O resultado da pesquisa foi organizado em uma tabela.
|
Área de conhecimento |
Quantidade de estudantes |
|---|---|
|
Ciências Humanas e Sociais |
35 |
|
Ciências Biológicas e Saúde |
53 |
|
Engenharias e Ciências Exatas |
58 |
|
Ciências Agrárias |
34 |
|
Total |
180 |
Fonte de pesquisa: anotações da direção do curso.
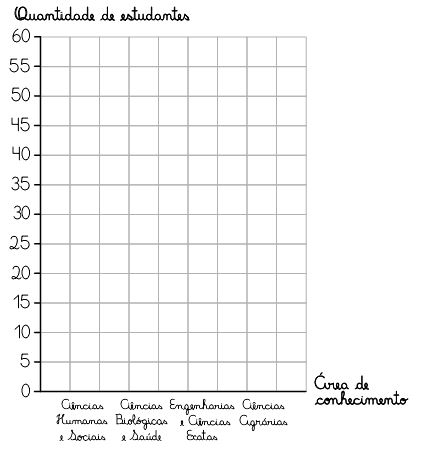
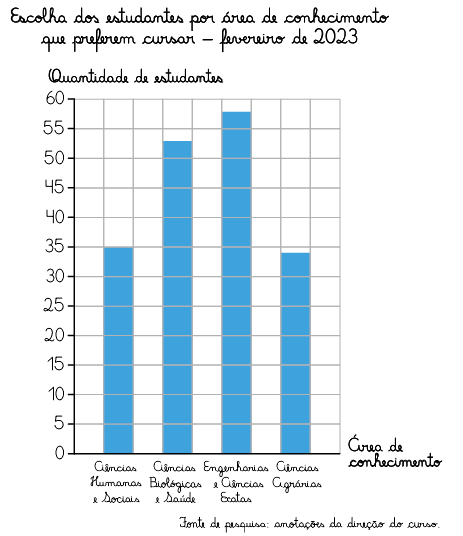
Com os dados apresentados na tabela, vamos construir um gráfico de colunas.
Para construir esse gráfico, em uma malha quadriculada, inicialmente traçamos dois eixos perpendiculares: um horizontal, para representar as áreas de conhecimento, e outro vertical, para representar a quantidade de estudantes. No eixo horizontal, indicamos os nomes das áreas de conhecimentos, e no eixo vertical, marcamos a escala escolhida, que no caso consideramos para cada 5 estudantes.
Em seguida, construímos as colunas relacionadas a cada área de conhecimento, de mesma medida de largura e com a medida da altura proporcional à quantidade de estudantes correspondentes a cada área de conhecimento, de acordo com a escala escolhida. Por fim, escrevemos o título e a fonte de pesquisa do gráfico.
Página 97
Gráfico de setores
Um filme de ação, um de comédia, um de drama e um de terror estavam em cartaz em um cinema. A tabela a seguir mostra, em porcentagem, o público de cada filme em um mesmo dia.
|
Gênero do filme |
Porcentagem |
|---|---|
|
Ação |
44% |
|
Terror |
32% |
|
Comédia |
16% |
|
Drama |
8% |
Fonte de pesquisa: anotações da bilheteria do cinema.
Com os dados da tabela, vamos construir um gráfico de setores. Para isso, inicialmente, calculamos a medida do ângulo central, em graus, correspondente a cada setor do gráfico que representa um gênero do filme. O círculo tem e corresponde ao percentual total de público desse cinema em 25 de março de 2024, ou seja, 100%. Assim, cada setor do círculo representará o percentual de público de cada gênero.
Ação
|
Porcentagem |
Medida do ângulo (em graus) |
|---|---|
|
100 |
360 |
|
44 |
x |
Comédia
|
Porcentagem |
Medida do ângulo (em graus) |
|---|---|
|
100 |
360 |
|
16 |
z |
Terror
|
Porcentagem |
Medida do ângulo (em graus) |
|---|---|
|
100 |
360 |
|
32 |
y |
Drama
|
Porcentagem |
Medida do ângulo (em graus) |
|---|---|
|
100 |
360 |
|
8 |
w |
Atenção!
Ao final de cada cálculo, foi realizada uma aproximação para uma medida inteira dos ângulos para facilitar a construção do gráfico.
Página 98
Para construir o gráfico de setores, traçamos uma circunferência utilizando um compasso e, com o auxílio de uma régua e de um transferidor, marcamos na circunferência a medida de cada ângulo central obtida anteriormente. Em seguida, construímos cada setor correspondente a essas medidas, cujo vértice é o centro da circunferência.
Depois, pintamos cada setor do gráfico com uma cor diferente e compomos a legenda conforme as cores escolhidas. Por fim, indicamos o título e a fonte de pesquisa do gráfico.
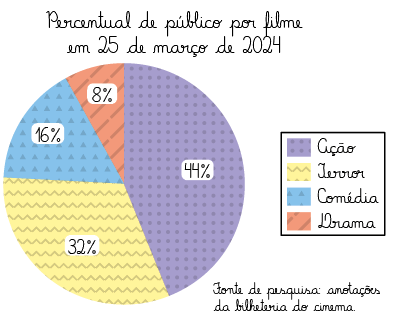
Gráfico de linhas
A fatura a seguir apresenta o consumo mensal de energia elétrica de uma residência em alguns meses de 2023.
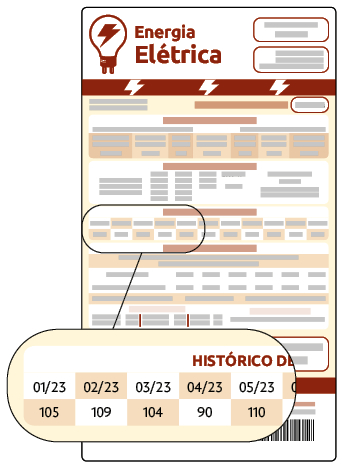
Vamos construir um gráfico de linhas para representar o consumo de energia elétrica em cada mês nessa residência.
Para construir o gráfico de linhas, inicialmente, traçamos dois eixos perpendiculares, em que o eixo horizontal representa os meses analisados e o eixo vertical representa o consumo mensal de energia elétrica (em ). Depois, traçamos algumas linhas, que servirão de referência para marcar os pontos.
No eixo horizontal indicamos os meses (jan., fev., mar., abr. e maio) e no eixo vertical marcamos a escala escolhida, no caso para cada .

Página 99
Em seguida, marcamos os pontos correspondentes ao consumo de energia elétrica de cada mês e, com o auxílio de uma régua, ligamos os pontos por segmentos de retas. Por fim, escrevemos o título e a fonte de pesquisa do gráfico.
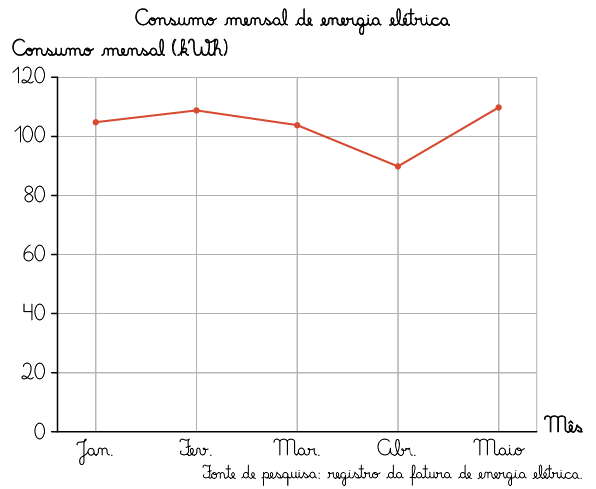
Atividades
Faça as atividades no caderno.
25. Verifique na tabela a seguir a taxa de mortalidade por 100 mil habitantes para a COVID-19 registrada até 30 de abril de 2022 por região e no Brasil.
|
Brasil e região |
Taxa de mortalidade por 100 mil habitantes |
|---|---|
|
Brasil |
315,7 |
|
Sul |
347,5 |
|
Centro-Oeste |
388,2 |
|
Norte |
271,7 |
|
Nordeste |
225,4 |
|
Sudeste |
359,1 |
Fonte de pesquisa: BRASIL. Ministério da Saúde. Coronavírus Brasil. Disponível em: https://oeds.link/mH7eJZ. Acesso em: 30 abr. 2022.
a) No caderno, construa um gráfico para representar os dados apresentados na tabela.
b) Que tipo de gráfico você construiu? Por que você escolheu esse tipo?
c) Qual região apresentou a maior taxa de mortalidade por 100 mil habitantes na data da pesquisa?
d) Quais regiões apresentaram taxa de mortalidade por 100 mil habitantes superior à taxa nacional?
26. Junte-se a um colega e construam no caderno um gráfico de setores para representar os dados da tabela a seguir.
|
Componente curricular |
Quantidade de estudantes |
|---|---|
|
Educação Física |
12 |
|
Ciências |
9 |
|
Língua Portuguesa |
8 |
|
Matemática |
6 |
|
Arte |
5 |
|
Outras |
2 |
Fonte de pesquisa: setor pedagógico da escola.
Página 100
27. Os planos de TV na modalidade streaming oferecem as opções pré-pago e pós-pago. Analise na tabela os preços cobrados por quatro empresas que oferecem esse serviço.
|
Empresa |
Preço da assinatura em reais por tipo de assinatura |
|
|---|---|---|
|
Pré-pago |
Pós-pago |
|
|
A |
35,00 |
25,90 |
|
B |
37,90 |
27,90 |
|
C |
17,90 |
8,99 |
|
D |
24,90 |
19,90 |
Fonte de pesquisa: catálogo de serviços de streaming.
a) Construa no caderno um gráfico de colunas agrupadas para representar os dados da tabela.
b) É possível representar esses dados em outro tipo de gráfico? Justifique sua resposta.
28. O Índice Nacional de Preços ao Consumidor Amplo (IPCA) é o principal índice oficial inflacionário brasileiro. Ele é calculado e divulgado mensalmente pelo Instituto Brasileiro de Geografia e Estatística (IBGE).
Analise na tabela o IPCA mensal do segundo semestre de 2021.
|
Mês |
IPCA (%) |
|---|---|
|
Julho |
0,96 |
|
Agosto |
0,87 |
|
Setembro |
1,16 |
|
Outubro |
1,25 |
|
Novembro |
0,95 |
|
Dezembro |
0,73 |
Fonte de pesquisa: IBGE. Disponível em: https://oeds.link/5tBdV1. Acesso em: 30 abr. 2022.
a) Em que mês do segundo semestre de 2021 o IPCA apresentou a maior taxa? Qual foi essa taxa?
b) Construa no caderno um gráfico de linhas para representar as informações da tabela.
c) Junte-se a um colega e realizem uma pesquisa sobre o IPCA identificando para que serve e como é calculado.
d) Pesquise o IPCA mensal ao longo de 2023 e registre os dados em uma tabela. Em seguida, construa no caderno um gráfico de linhas utilizando esses dados.
29. O Índice de Gini é utilizado para medir o grau de concentração de uma distribuição. Esse índice varia de 0, situação de perfeita igualdade, a 1, em que a desigualdade é máxima, ou seja, com a maior concentração possível.
Verifique na tabela o Índice de Gini referente ao Produto Interno Bruto (PIB) das grandes regiões brasileiras em 2019.
|
Grande região |
Índice de Gini |
|---|---|
|
Norte |
0,791372 |
|
Nordeste |
0,787295 |
|
Sudeste |
0,878735 |
|
Sul |
0,779467 |
|
Centro-Oeste |
0,835895 |
Fonte de pesquisa: IBGE. Disponível em: https://oeds.link/k3UxIu. Acesso em: 30 abr. 2022.
a) Construa no caderno um gráfico para representar os dados da tabela.
b) Com base na tabela e no gráfico que você construiu, elabore uma questão e troque com um colega. Em seguida, verifique se ele respondeu corretamente.
Página 101
Pesquisa estatística
As pesquisas estatísticas são realizadas com diversos objetivos, como verificar a durabilidade de um tipo de material ou conhecer a opinião de certo grupo de pessoas a respeito de um assunto, como as intenções de votos de um grupo de pessoas em certos candidatos durante o período eleitoral.
Um exemplo de pesquisa estatística é o Censo Demográfico realizado pelo IBGE, que tem como objetivo verificar as características da população brasileira relacionadas à educação, ao trabalho, à economia, à moradia etc.
Como o Censo envolve toda a população, dizemos que se trata de uma pesquisa censitária. No entanto, às vezes é inviável realizar uma pesquisa com toda a população em razão de algumas dificuldades, como medida do tempo, custo e acesso a todos os indivíduos. Nesses casos, escolhe-se uma amostra da população para realizar a pesquisa, que é denominada pesquisa amostral. A pesquisa amostral é realizada de maneira mais rápida e com menor custo, contudo ela tem uma margem de erro, pois não leva em consideração todos os indivíduos da população.

Em Estatística, chamamos população todo conjunto de elementos com pelo menos uma característica em comum. A amostra é uma parte selecionada da população, ou seja, um subconjunto não vazio de elementos da população com menor quantidade de elementos.
Atenção!
Uma população estatística não se refere necessariamente a um conjunto de pessoas. Nesse contexto, o termo população também pode fazer referência a um conjunto de objetos ou de informações, a exemplo das peças produzidas por uma máquina, de um grupo de animais de certa espécie, entre outros.
Ao realizar uma pesquisa amostral, é preciso definir uma amostra adequada e que esteja de acordo com os objetivos da pesquisa. A amostra deve ser representativa, de maneira que os resultados obtidos possam ser generalizados para a população.
A seguir, vamos estudar três tipos de amostragem: a amostragem aleatória, a amostragem sistemática e a amostragem estratificada.
Página 102
Exemplificaremos esses três tipos de amostragem. Para isso, considere uma pesquisa feita por uma empresa para saber a qualidade das calças fabricadas em cada lote. Nesse exemplo, a população é o conjunto de todas as calças fabricadas.
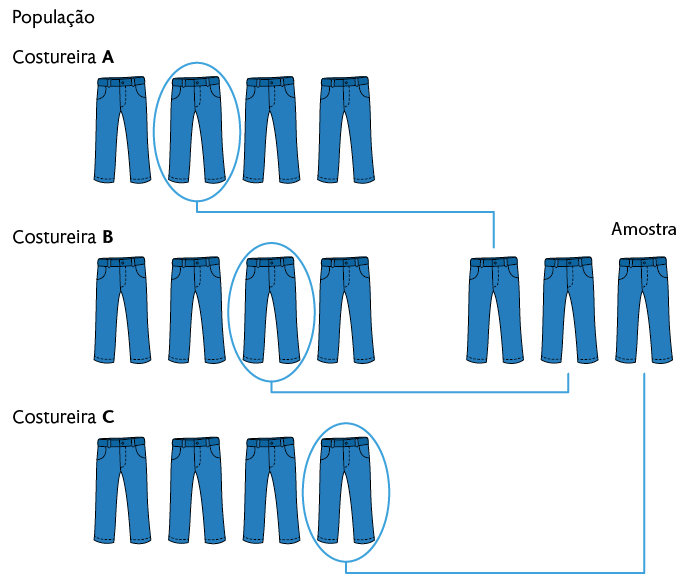
Amostragem aleatória: conhecida também como amostragem simples, é o tipo de amostragem em que é realizado um sorteio entre os elementos da população, garantindo a cada elemento a mesma probabilidade de pertencer à amostra. Na situação apresentada, pode-se colocar todas as calças produzidas em uma caixa fechada e retirar, aleatoriamente, algumas delas para compor a amostra.
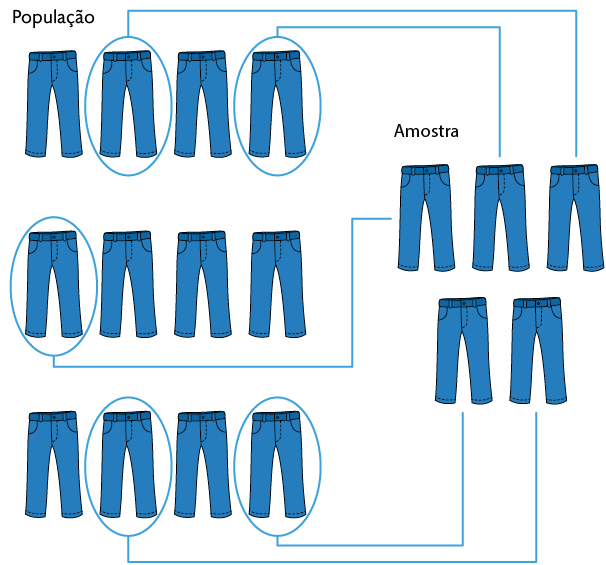
Amostragem sistemática: os elementos da população são organizados seguindo uma ordem predefinida e são escolhidos conforme um critério ou fator de repetição. Por exemplo, na ordem de produção das calças, escolher uma a cada três produzidas.
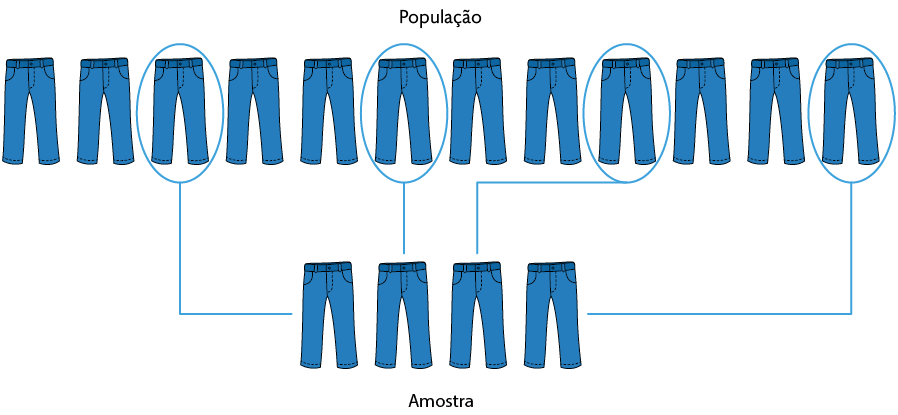
Página 103
Amostragem estratificada: nessa amostragem, a população é dividida em subgrupos ou estratos, conforme critérios estabelecidos pelo estudo. Em seguida, utiliza-se, em cada subgrupo, a amostragem aleatória ou a sistemática. Um exemplo é selecionar aleatoriamente calças produzidas por costureira ou lote.
Etapas de uma pesquisa estatística
Para realizar uma pesquisa estatística, é necessário seguir algumas etapas, com o intuito de prever os instrumentos e os recursos necessários, as dificuldades que podem ocorrer e as alternativas possíveis.
Verifique a seguir as etapas necessárias para a realização de uma pesquisa estatística.
1ª etapa – Planejamento
Nessa etapa, deve-se decidir o tipo de pesquisa que será realizada: pesquisa censitária ou pesquisa amostral. É preciso definir o tema da pesquisa, os instrumentos de coleta de dados, as variáveis, a população ou o tamanho da amostra, os critérios de escolha dos indivíduos da população ou da amostra, o local, a época e os materiais que serão utilizados.
2ª etapa – Coleta de dados
Essa etapa é o momento de execução da pesquisa e consiste na aplicação do instrumento de coleta de dados, que pode ser a aplicação de um questionário aos indivíduos que compõem a população ou amostra. Deve-se ficar atento às respostas dos entrevistados e anotá-las com atenção e cuidado para que nenhum dado seja perdido.
Página 104
3ª etapa – Organização
Essa etapa é o momento de organização dos dados coletados. Esses dados podem ser organizados em diversos recursos, como listas, tabelas e/ou gráficos. O pesquisador deverá avaliar o tipo de representação mais adequada, de acordo com a natureza dos dados coletados. Assim, deve-se avaliar todas as formas estudadas de representação de dados estatísticos, como as tabelas (simples, de dupla entrada e de distribuição) e os gráficos (de colunas, de linha, de setores, histogramas e pictogramas).
4ª etapa – Análise e interpretação dos dados
Nessa etapa, realizam-se a análise dos dados organizados na etapa anterior e a interpretação deles. Com isso, podemos calcular, por exemplo, os valores das medidas de tendência central (média aritmética, moda e mediana) e a amplitude total, os quais permitem visualizar como os dados estão distribuídos. Essa análise possibilita uma interpretação mais fidedigna dos dados.
5ª etapa – Divulgação
Essa é a última etapa de uma pesquisa estatística e consiste na divulgação dos dados e das informações obtidas após a realização da pesquisa. A divulgação pode ser feita em relatórios, cartazes ou por meio digital, como blogs, sites, TV e rádio. É importante assegurar que as pessoas interessadas tenham acesso aos resultados da pesquisa.
Atividades
Faça as atividades no caderno.
30. Em cada item, indique o tipo de pesquisa, censitária ou amostral, mais adequado para cada situação.
a) Uma empresa pretende analisar a qualidade dos produtos produzidos por ela.
b) O setor pedagógico da escola vai realizar uma pesquisa estatística para conhecer a área de conhecimento de interesse dos estudantes do 3º ano do Ensino Médio.
c) O município deseja saber a quantidade de pessoas que residem na área rural.
d) Um instituto vai realizar uma pesquisa de intenção de votos para o Senado Federal.
31. O setor de nutrição da escola aplicou o questionário a seguir para conhecer o sabor preferido de suco dos estudantes.

a) Essa pesquisa é censitária ou amostral?
b) Qual será a população entrevistada?
c) Quais dados serão obtidos?
Página 105
32. Uma unidade básica de saúde do bairro registrou a quantidade de atendimentos realizados ao longo de 5 dias de determinada semana.
|
Dia da semana |
Quantidade de atendimentos |
|---|---|
|
Segunda-feira |
68 |
|
Terça-feira |
59 |
|
Quarta-feira |
61 |
|
Quinta-feira |
66 |
|
Sexta-feira |
61 |
Fonte de pesquisa: secretária da unidade básica de saúde.
a) Calcule a média, a mediana, a moda e a amplitude total da quantidade de atendimentos.
b) Qual tipo de gráfico é mais adequado para representar esses dados?
c) Elabore um relatório e descreva os resultados dessa pesquisa, apresentando o tema e a representação dos dados em um gráfico. Explicite suas principais conclusões, levando em consideração as medidas de tendência central e a amplitude total dos dados.
33. Verifique no quadro a seguir a média do 1º bimestre de 2023 de Rafael por componente curricular.
|
Componente curricular |
Média do 1º bimestre |
|---|---|
|
Língua Portuguesa |
9,0 |
|
Matemática |
7,3 |
|
História |
8,2 |
|
Geografia |
7,4 |
|
Ciências |
6,0 |
|
Arte |
9,0 |
|
Língua Inglesa |
9,8 |
a) Qual foi a média geral do 1º bimestre de Rafael?
b) Calcule a mediana, a moda e a amplitude total das médias de Rafael.
c) Construa no caderno um gráfico de colunas com as informações apresentadas no quadro.
d) Elabore um relatório e descreva os resultados dessa pesquisa, apresentando o tema, a representação dos dados em um gráfico e suas principais conclusões, levando em consideração as medidas de tendência central e a amplitude total dos dados.
34. Junte-se a três colegas e realizem uma pesquisa estatística seguindo as etapas apresentadas anteriormente. Definam um tema de interesse, o tipo de amostragem e, ao final, elaborem um relatório para divulgar os resultados obtidos.
Como sugestão de temas, vocês podem pesquisar a quantidade de ruas não pavimentadas do bairro ou do município onde vivem, a quantidade de pessoas não alfabetizadas do bairro ou o índice de satisfação com a merenda escolar.
Na construção do relatório, indiquem o tema da pesquisa e utilizem gráficos e/ou tabelas para representar os dados. Para interpretá-los, façam uso das medidas de tendência central, da amplitude total e utilizem um meio de divulgação de fácil acesso, como cartazes, blogs, sites, entre outros.
Página 106
Possibilidades
Daniel foi a uma concessionária comprar um automóvel. Para determinado modelo, ele pode escolher entre três cores (preta, vermelha e prata) e dois kits de acessórios ( ou ). Quantas possibilidades diferentes ele tem para escolher esse modelo de automóvel nessa concessionária?
Para responder a essa questão, podemos representar todas as opções de escolha de Daniel construindo um diagrama, conhecido como diagrama de árvore ou árvore de possibilidades.

Outra maneira de representar todas essas possibilidades é em um quadro, chamado quadro de possibilidades.
|
Cor |
Kit de acessórios |
|
|---|---|---|
|
Preta |
Preta, |
Preta, |
|
Vermelha |
Vermelha, |
Vermelha, |
|
Prata |
Prata, |
Prata, |
Com base no diagrama e no quadro, podemos representar a quantidade de possibilidades pela multiplicação a seguir.
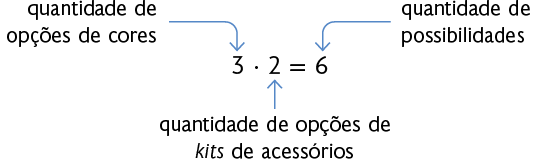
Assim, Daniel tem 6 possibilidades para escolher o automóvel.
Questão 5. Se em vez de 3 opções de cores fossem 4, determine no caderno a quantidade de possibilidades diferentes que Daniel teria para escolher o automóvel.
Chamamos possibilidades todos os resultados possíveis de ocorrer em determinada situação.
Na situação apresentada, calculamos a quantidade de possibilidades realizando uma multiplicação entre a quantidade de opções de cores e a quantidade de opções de kits de acessórios. Essa multiplicação é chamada princípio multiplicativo da contagem. Tal princípio é uma maneira de realizar adições de parcelas iguais e constitui uma ferramenta básica para resolver problemas de contagem sem precisar listar todos os elementos.
Página 107
Se há quantidades de opções para tomar a decisão , e uma vez realizado , há quantidades de opções para tomar a decisão , qualquer que tenha sido a primeira escolha, então há quantidades de opções para realizar as decisões e simultaneamente.
Agora, considere a situação a seguir.
Quantos números de três algarismos podem ser escritos de maneira que:
- o 1º algarismo seja 1, 2 ou 4?
- o 2º algarismo seja 3 ou 8?
- o 3º algarismo seja 6, 5 ou 9?
Temos 3 opções de escolha para o 1º algarismo, 2 opções para o 2º algarismo e 3 opções para o 3º algarismo. Assim, pelo princípio multiplicativo da contagem, obtemos:

Portanto, há 18 números que satisfazem às condições dadas.
Questão 6. No seu caderno, construa o diagrama de árvore para determinar os números que satisfaçam às condições dadas.
Atividades
Faça as atividades no caderno.
35. O time de basquetebol de uma escola precisa escolher as cores de seu uniforme, que será composto de 1 camiseta e 1 bermuda. As opções de cores de uniforme que esse time tem estão representadas a seguir.

a) Construa no caderno um diagrama de árvore e um quadro de possibilidades para representar essa situação.
b) De quantas maneiras diferentes esse time pode compor o uniforme?
36. Henrique foi a uma papelaria comprar 1 caderno e 1 lapiseira. Após olhar as opções, ficou em dúvida entre 3 cadernos e 4 lapiseiras. Quantas possibilidades Henrique tem para realizar sua compra?
37. De olhos vendados, Rogério vai retirar 2 bolas da caixa a seguir, que contém 1 bola verde, 2 bolas azuis, 2 bolas vermelhas e 3 bolas amarelas.

a) Se a primeira bola que Rogério retirar for verde, quantas possibilidades de cores ele terá ao retirar a segunda bola?
b) Construa no caderno um diagrama de árvore para indicar todas as possibilidades de cores que ele poderá obter ao retirar as duas bolas.
c) Quantas possibilidades de cores ele terá ao todo?
Página 108
38. Isadora foi comprar uma bicicleta. Ela poderia escolher entre 4 opções de cor, 3 de tamanho e 2 de banco.
a) De quantas maneiras diferentes Isadora pode compor a bicicleta, sabendo que ela deve escolher 1 opção de cor, 1 de tamanho e 1 de banco?
Podemos responder a essa atividade com a seguinte multiplicação. Copie no caderno e complete a expressão.
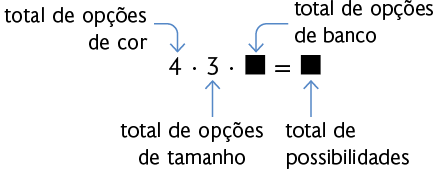
Atenção!
O resultado que você obteve do total de possibilidades pode ser verificado ao construir um diagrama de árvore ou um quadro de possibilidades.
b) Suponha que Isadora pudesse compor a bicicleta entre 5 opções de cor, 2 opções de tamanho e 4 opções de banco. Nesse caso, qual seria o total de possibilidades?
39. O quadro a seguir representa parte de um cardápio de um restaurante.
|
Prato principal |
Bebida |
Sobremesa |
|---|---|---|
|
Estrogonofe |
Suco de frutas |
Pudim |
|
Macarrão ao molho |
Fruta |
|
|
Bife parmegiana |
Água |
Gelatina |
|
Frango grelhado |
Bolo |
Quantos pedidos distintos podem ser formados por:
a) 1 prato principal e 1 bebida?
b) 1 prato principal, 1 bebida e 1 sobremesa?
40. Quantos
números diferentes de 4 ordens podem ser formados
utilizando todos os algarismos a seguir?
-
2
-
5
-
7
-
9
41. (OBM-2006)
Jade escreveu todos os números de 3 algarismos em
cartões amarelos, um por cartão, e escreveu todos os números de 4 algarismos em
cartões azuis, um por cartão. Os cartões são todos do mesmo tamanho.
a) Ao todo, quantos cartões foram utilizados? Lembre-se de que, por exemplo, 037 é um número de dois algarismos, bem como 0853 é um número de três algarismos.
b) Todos os cartões são então colocados numa mesma urna e embaralhados. Depois Jade retira os cartões, um a um, sem olhar o que está pegando. Quantos cartões Jade deverá retirar para ter certeza de que há dois cartões azuis entre os retirados?
42. Para montar um look, Marina precisa escolher 1 saia e 1 blusa. Sabendo que com as opções disponíveis ela pode montar, ao todo, 42 looks diferentes e que havia 6 opções de saia, quantas eram as opções de blusa?
43. Rafael foi a uma loja comprar um terno e um sapato para sua festa de formatura. O quadro a seguir apresenta os modelos e as cores disponíveis.
|
Modelos de terno disponíveis |
Cores de terno disponíveis |
Cores de sapato disponíveis |
|---|---|---|
|
tradicional slim |
cinza azul-marinho bege |
preto marrom |
Com base no quadro, elabore um problema e peça para um colega resolvê-lo. Depois, verifique se ele respondeu corretamente.
Página 109
Probabilidade
Joana está brincando de sortear bolinhas com os amigos. Cada um deles deve retirar, aleatoriamente, 1 bolinha de uma urna que contém bolinhas iguais, enumeradas de 1 a 20, e em seguida devolvê-la na urna. Ganha a brincadeira aquele que retirar a bolinha com o maior número. Joana já sorteou a bolinha com o número 12.

Qual é a probabilidade de um amigo de Joana sortear uma bolinha com número menor do que 12?
Desse experimento conhecemos o conjunto de todos os resultados possíveis, ou seja, o espaço amostral, que denotamos por (lê-se "ômega").
Se todos os resultados têm a mesma chance de ocorrer, a probabilidade (P) de um evento ocorrer é dada por:
Atenção!
Denominamos evento qualquer subconjunto do espaço amostral. No caso, o subconjunto é o evento de sortear um número menor do que 12.
Nessa situação, como há 11 bolinhas com números menores do que 12 de um total de 20 bolinhas, temos:
Portanto, a probabilidade de sortear uma bolinha com número menor do que 12 é 11 em 20, ou 55%.
A probabilidade de ocorrência de cada um dos elementos desse espaço amostral é .
Atenção!
Lembre-se de que chamamos elemento cada objeto de um conjunto.
Questão 7. Em seu caderno, determine a soma das probabilidades de todos os elementos desse espaço amostral.
A soma das probabilidades de todos os elementos do espaço amostral de um experimento é igual a 1.
Página 110
Considere outra situação.
Geraldo vai compor um número de dois algarismos com os números obtidos no lançamento de dois dados, um amarelo e outro azul, enumerados de 1 a 6. O número obtido no dado amarelo representa o algarismo da dezena, e o obtido no dado azul, o algarismo da unidade.
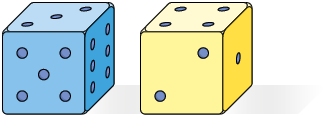
Ao lançar os dados, qual é a probabilidade de Geraldo compor um número par?
Para responder a essa pergunta, primeiro vamos construir um quadro de possibilidades para determinar o espaço amostral desse experimento.
|
Dado amarelo |
Dado azul |
|||||
|---|---|---|---|---|---|---|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
11 |
12 |
13 |
14 |
15 |
16 |
|
2 |
21 |
22 |
23 |
24 |
25 |
26 |
|
3 |
31 |
32 |
33 |
34 |
35 |
36 |
|
4 |
41 |
42 |
43 |
44 |
45 |
46 |
|
5 |
51 |
52 |
53 |
54 |
55 |
56 |
|
6 |
61 |
62 |
63 |
64 |
65 |
66 |
Desse modo, o espaço amostral é:
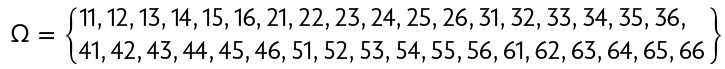
Assim, temos 36 resultados possíveis. Outra maneira de obter a quantidade de resultados possíveis é aplicando o princípio multiplicativo da contagem, efetuando .
Analisando o quadro de possibilidades, concluímos que a quantidade de resultados favoráveis para que Geraldo consiga formar um número par é 18. Portanto, a probabilidade de ele formar um número par ao lançar os dois dados é dada por:
Questão 8. Em seu caderno, determine a probabilidade de Geraldo formar um número cujo algarismo da dezena seja 3.
Atividades
Faça as atividades no caderno.
44. Em um saco, foram colocadas várias bolinhas iguais, sendo 24 vermelhas, 18 azuis, 15 verdes e 31 laranjas.

a) Quantas bolinhas foram colocadas no saco?
b) Ao retirar ao acaso uma bolinha desse saco, qual cor tem mais chance de ser retirada? Por quê?
c) Qual é a chance de retirar, ao acaso, uma bolinha azul? E uma bolinha verde?
Página 111
45. Flávio e Amanda recortaram alguns pedaços de cartolina e com eles confeccionaram fichas com os seguintes números.
-
192
-
205
-
180
-
152
-
136
-
117
-
72
-
241
-
51
-
190
-
30
-
85
-
147
-
67
-
108
Em seguida, eles misturaram as fichas e as colocaram com os números voltados para baixo.
Ao retirar uma das fichas ao acaso, qual é a probabilidade de o número:
a) terminar em zero?
b) ser par?
c) ser maior do que 100?
d) ser menor do que 125?
e) ser ímpar?
f) ser maior do que 77 e menor do que 151?
46. Flávia está participando de uma gincana na escola. Em uma das provas, ela deve estourar 2 balões com os olhos vendados. Dos 21 balões da prova, 5 valem 10 pontos, 8 valem 20 pontos, 2 valem 50 pontos e 6 valem 70 pontos.
a) Qual é a probabilidade de o 1º balão que Flávia estourar valer 20 pontos?
b) Qual é a probabilidade de o 1º balão que Flávia estourar valer mais do que 20 pontos?
c) Supondo que o 1º balão que Flávia estourou valha 10 pontos, qual é a probabilidade de o 2º balão valer 70 pontos?
47. (Obmep-2010) Carolina tem três cartões brancos numerados de 1 a 3 e três cartões pretos, também numerados de 1 a 3. Ela escolheu, ao acaso, um cartão branco e um preto. Qual é a probabilidade de a soma dos números dos cartões escolhidos ser par?
a)
b)
c)
d)
e)
48. Considere os números de três algarismos distintos, formados pelos algarismos 1, 2 e 3. Qual é a probabilidade de, ao sortearmos um desses números, ele ser:
a) par?
b) ímpar?
c) múltiplo de 4?
d) múltiplo de 12?
e) menor do que 320?
49. São lançados simultaneamente 1 dado e 1 moeda.
a) Construa no caderno um quadro de possibilidades que apresente o espaço amostral desse experimento.
b) Qual é a quantidade de resultados possíveis nesse lançamento?
c) Considerando esse lançamento, calcule no caderno a probabilidade de obter, nas faces voltadas para cima:
o número 1 e cara;
um número par e qualquer resultado para a moeda;
coroa e qualquer número para o dado;
um número ímpar e cara.
Página 112
50. Júlio tem um dado com formato de um tetraedro, numerado de 1 a 4, e um dado comum, numerado de 1 a 6. Ele lançou os dados simultaneamente e anotou o número da face do tetraedro voltada para baixo e o número da face do dado comum voltada para cima.

a) Escreva no caderno o espaço amostral desse lançamento.
b) Qual é a probabilidade de obter números pares em ambos os dados?
c) Qual é a probabilidade de obter números ímpares em ambos os dados?
d) Qual é a probabilidade de obter um número par e um número ímpar nesse lançamento?
e) Qual é a soma das probabilidades obtidas nos itens anteriores?
51. Em uma confecção foi verificado que, a cada 120 calças fabricadas, 5 apresentavam defeito na costura.
a) Ao retirar uma calça ao acaso de um lote de 120 calças, qual é a probabilidade de ela apresentar defeito na costura?
b) A probabilidade de retirar ao acaso uma calça de um lote de 240 calças e ela apresentar algum defeito é maior do que, menor do que ou igual a de ser retirada de um lote de 120 calças? Por quê?
52. Ana tem 5 cartões com as letras A, B, C, D e E.
a) Qual é a probabilidade de Ana sortear uma:
vogal?
consoante?
b) Calcule no caderno a soma das probabilidades do item anterior.
53. Nos itens a seguir, resolva o que se pede.
a) Escreva no caderno o espaço amostral de um sorteio em que serão considerados todos os divisores de 42.
b) Ao realizar um sorteio, calcule no caderno a probabilidade de obter cada um dos números do espaço amostral.
c) Qual é a soma das probabilidades obtidas no item anterior?
d) Ao sortear um desses números, calcule no caderno a probabilidade de ele ser:
par;
ímpar;
composto por 2 algarismos;
múltiplo de 6;
divisor de 11;
um número primo.
54. Na imagem a seguir, estão representadas as bolas do jogo de bilhar, sendo 15 bolas numeradas de 1 a 15 mais 1 bola branca sem numeração.

Com base nessa informação, elabore um problema e troque com o de um colega. Você resolverá o dele e ele vai resolver o seu. Depois, verifique se ele resolveu o problema corretamente.
Página 113
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. A professora de Educação Física mediu a altura, em centímetro, dos estudantes de sua turma e registrou as medidas em um quadro.
- 171
- 157
- 170
- 162
- 159
- 166
- 165
- 168
- 159
- 170
- 167
- 169
- 163
- 167
- 170
- 159
- 164
- 167
- 172
- 175
- 168
- 170
- 173
- 169
- 169
- 174
- 182
- 168
- 171
- 170
- 169
- 174
- 169
- 164
- 181
- 179
a) Construa, em uma folha de papel avulsa, uma tabela de frequência com 7 intervalos de classe, em que o primeiro seja , apresentando as frequências absoluta , relativa , acumulada e acumulada relativa para as medidas das alturas dos estudantes.
b) Qual é a porcentagem dos estudantes que têm medida de altura maior ou igual a ?
c) Qual é a porcentagem dos estudantes que têm altura medindo ou mais?
2. O quadro a seguir apresenta o salário, em reais, de 20 funcionários de uma empresa.
- 1.720,00
- 1.640,00
- 1.600,00
- 1.870,00
- 1.600,00
- 1.870,00
- 1.750,00
- 1.870,00
- 1.600,00
- 1.800,00
- 1.790,00
- 1.600,00
- 1.870,00
- 1.600,00
- 1.790,00
- 1.870,00
- 1.650,00
- 1.700,00
- 1.870,00
- 1.650,00
a) Determine a amplitude total dos salários desses funcionários.
b) Calcule em uma folha de papel avulsa a mediana, a moda e a média desses salários.
3. O boletim anual de Renata está representado na tabela.
|
Componente curricular |
Notas |
|||
|---|---|---|---|---|
|
1º bimestre |
2º bimestre |
3º bimestre |
4º bimestre |
|
|
Língua Portuguesa |
10 |
9,6 |
9,2 |
8,8 |
|
Língua Inglesa |
6,8 |
7 |
8,2 |
8 |
|
Matemática |
8,4 |
6,8 |
7,2 |
7,6 |
|
História |
8,2 |
8 |
9,6 |
7,8 |
|
Geografia |
7,5 |
6,5 |
7,7 |
8,3 |
|
Ciências |
6,0 |
5,5 |
7,0 |
6,7 |
|
Arte |
8,5 |
8,5 |
9 |
10 |
Fonte de pesquisa: secretaria da escola em 2023.
a) Calcule em uma folha de papel avulsa a média anual de Renata em cada componente curricular. Qual foi a média geral?
b) Determine a amplitude total das médias anuais de Renata, por componente curricular.
c) Calcule em uma folha de papel avulsa a mediana e a moda das médias, por componente curricular, obtidas por Renata.
Página 114
4. Escreva em uma folha de papel avulsa o tipo de gráfico mais adequado para a situação indicada em cada item.
a) Em uma partida de voleibol, registrou-se a quantidade de aces✚ de cada equipe.
- Ace:
- saque que o jogador oponente não consegue rebater.↰
b) Em certo município, registrou-se a medida de temperatura máxima diária durante o mês de janeiro.
5. Uma clínica médica realizou uma pesquisa para conhecer a satisfação dos pacientes durante o atendimento. Cada paciente escolheu apenas uma opção. O resultado está apresentado na tabela a seguir.
|
Qualidade do atendimento |
Quantidade de respostas |
|---|---|
|
Ruim |
45 |
|
Regular |
75 |
|
Bom |
120 |
|
Ótimo |
60 |
Fonte de pesquisa: setor de Recursos Humanos da clínica em 2023.
a) Quantos pacientes foram entrevistados?
b) Construa em uma folha de papel avulsa um gráfico de setores para representar os dados da tabela. Lembre-se de inserir no gráfico o título e a fonte de pesquisa.
c) Com base no gráfico, o resultado é favorável à clínica? Justifique a resposta no caderno.
6. Considerando o lançamento simultâneo de 2 dados de seis faces, resolva os itens.
a) Construa em uma folha de papel avulsa um quadro de possibilidades que apresente o espaço amostral desse experimento.
b) Quantas são as combinações possíveis nesse lançamento?
c) Em quantas dessas combinações as faces voltadas para cima de ambos os dados são números pares?
d) Em quantas dessas combinações as faces voltadas para cima de ambos os dados são números iguais?
e) Escreva todos os possíveis resultados considerando a adição entre os números nas faces voltadas para cima dos dados.
7. Uma urna contém bolas idênticas, sendo ao todo 35 bolas vermelhas, 24 azuis, 41 pretas e 20 amarelas.
a) Quantas bolas há na urna?
b) Ao retirar uma bola dessa urna ao acaso, qual é a probabilidade de ela não ser vermelha?
c) Qual é a probabilidade de retirar ao acaso uma bola azul?
d) Calcule em uma folha de papel avulsa a probabilidade de cada um dos elementos do espaço amostral. Qual é a soma dessas probabilidades?
8. Uma roleta tem 36 casas de mesma medida de área numeradas de 1 a 36. Sabendo que foi sorteado um número par, qual é a probabilidade de esse número ser o 18?