Estudando sequências

Estudamos em anos anteriores que uma sequência é uma lista de elementos ordenados, que podem ser números, figuras ou letras, por exemplo. Cada elemento da sequência chama-se termo.

Verifique a seguir, um exemplo de sequência de figuras formadas por pontos.

Podemos indicar a quantidade de pontos em cada figura pela seguinte sequência numérica: $\left(2,4,6,8,10,\dots \right)$. Nela, o primeiro termo é 2, o segundo termo é 4, o terceiro termo é 6, e assim sucessivamente.

Quando uma sequência tem uma lei de formação, ou seja, a obtenção de cada um de seus termos obedece a determinado padrão ou regra, podemos obter os próximos termos, escrevendo o termo geral dela. Por exemplo, a sequência apresentada pode ser definida por meio do termo geral $a_n=2n$ para $n>0$, que relaciona a quantidade de pontos em cada imagem com a posição que o termo ocupa.

Note também como podemos obter os termos dessa sequência por meio de um fluxograma.

As sequências podem ser finitas ou infinitas. Dizemos que uma sequência é finita quando é composta por determinada quantidade de termos, ou seja, quando há um último termo. Caso contrário, diz-se que ela é infinita. A sequência apresentada anteriormente é um exemplo de sequência infinita.

Agora, considere a sequência numérica $\left(2,5,8,11,\dots \right)$, em que:

Nela, o primeiro termo é igual a 2, e cada termo, do segundo em diante, é igual ao anterior mais 3. Podemos definir essa sequência da seguinte maneira:

Com isso, podemos calcular o quinto termo dessa sequência da seguinte maneira.

Portanto, $a_5=14$.

Quando definimos os termos de uma sequência em função dos termos anteriores a ele, dizemos que a sequência está definida por recorrência.

O fluxograma a seguir possibilita obter os termos da sequência $\left(\mathrm{2,}5,8,11,\dots \right)$.

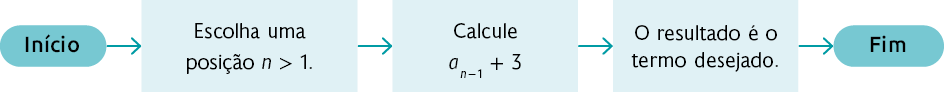
Acompanhe outros exemplos de sequências.

a) A sequência $\left(6,6,6,6,\dots \right)$, na qual os termos são todos iguais a 6, é um exemplo de sequência constante.

b) A sequência $\left(1,3,5,7,\dots \right)$ pode ser definida pelo termo geral $a_n=2n-1$, com $n\ge 1$. Essa é a sequência dos números ímpares positivos.

c) Se definirmos $a_1=6$ e $a_n=a_{n-1}+5$, para $n\ge 2$, obtemos uma sequência em que os seis primeiros termos são:

$a_1=6$

$a_2=6+5=11$

$a_3=11+5=16$

$a_4=16+5=21$

$a_5=21+5=26$

$a_6=26+5=31$

Questão 1. Em seu caderno, defina a sequência $\left(\mathrm{2,}4,6,8,10,\dots \right)$ por recorrência. Essa é a mesma sequência cujo termo geral foi apresentado na página anterior.

Questão 2. É possível definir a sequência constante do exemplo a por recorrência? Em caso afirmativo, apresente essa definição.

Atividades

Faça as atividades no caderno.

1. Escreva no caderno o termo geral de cada sequência.

a) $\left(3,6,9,12,15,\dots \right)$

b) $\left(13,25,37,49,\dots \right)$

c) $\left(0,3,6,9,12,\dots \right)$

d) $\left(2x,4x,6x,8x,\dots \right)$

e) $\left(x,x^2,x^3,x^4,\dots \right)$

f) $\left(\frac{1}{x},\frac{2}{x^2},\frac{3}{x^3},\frac{4}{x^4},\dots \right)$

2. Em cada item, é dado o termo geral, em que n é um número natural não nulo. Escreva em seu caderno os cinco primeiros termos das sequências.

a) $a_n=22n-7$

b) $a_n={\left(n-1\right)}^3$

c) $a_n=\frac{n^2}{3^n}$

d) $a_n=\frac{{\left(n-1\right)}^2+1}{n}$

3. Analise a sequência de bolinhas.

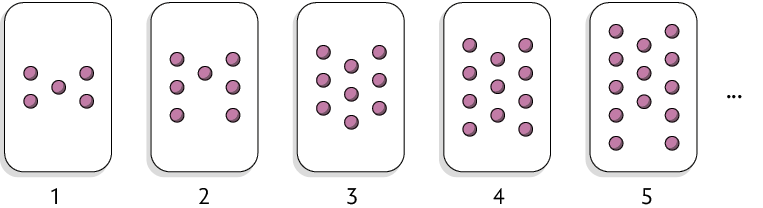
a) Quantas bolinhas terá a figura 6 dessa sequência?

b) Escreva a sequência que representa a quantidade de bolinhas na posição correspondente.

c) Qual dos itens apresenta o termo geral da sequência que você escreveu no item anterior?

I)$a_n=2n+3$, com $n>0$.

II)$a_n=2n-3$, com $n>0$.

III)$a_n=3-2n$, com $n>0$.

IV)$a_n=2+3n$, com $n>0$.

d) Determine a quantidade de bolinhas da figura 12 da sequência.

e) Defina a sequência que você escreveu no item b por recorrência.

4. Quais das sequências a seguir estão definidas por recorrência?

a) $a_n=n\cdot (n-1)$, com $n>0$.

b) $a_n=3n+n+1+2$, com $n>0$.

c) $a_n=2\cdot \left(a_{n-1}+3\right)$, com $a_1=0$ e $n>1$.

d) $a_n=a_{n-1}\cdot n-a_{n-1}$, com $a_1=10$ e $n>1$.

5. Milena escreveu uma sequência na qual um termo é obtido adicionando os dois termos imediatamente anteriores. Ela considerou $a_1=-2$ e $a_2=3$.

a) Escreva essa sequência até o 7º termo.

b) Essa sequência pode ser definida por um termo geral? Em caso afirmativo, escreva como obtê-la.

c) Essa sequência pode ser definida por recorrência? Em caso afirmativo, escreva como obtê-la.

6. Junte-se a um colega e analisem a sequência a seguir.

a) Construam um fluxograma por meio do qual seja possível obter um termo qualquer dessa sequência.

b) Usando o fluxograma que vocês construíram, determine os próximos 3 termos dessa sequência.

7. Analise as sequências.

Sequência 1

Sequência 2

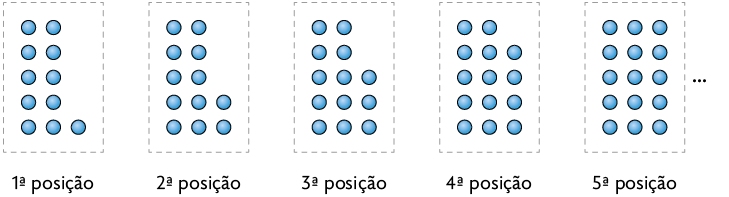
Sequência 3

a) Para cada uma das sequências, escreva uma fórmula que possibilite obter a quantidade de bolinhas que há em cada figura em função da posição ocupada na sequência.

b) Construa, para cada sequência, um fluxograma que possibilite determinar a quantidade de bolinhas em cada figura de acordo com sua posição.

8. Considere a sequência definida por $a_n=a_{n-1}\cdot n$, com $a_1=1$ e $n>1$.

a) Construa um fluxograma que possibilite obter os termos dessa sequência.

b) Usando o fluxograma feito no item anterior, escreva os seis primeiros termos dessa sequência.

9. Considere a sequência A, definida por $a_n=2n+5$, com $n>0$, e a sequência B, definida por $a_n=2\cdot a_{n-1}-1$, com $a_1=2$ e $n>1$.

a) Qual das sequências foi definida por recorrência?

b) Associe cada uma das sequências ao fluxograma que permite obter seus termos.

c) Escreva os 8 primeiros termos de cada uma dessas sequências.

10. Analise o que o professor Marcelo está dizendo.

a) Se os estudantes optaram por usar $a_1=10$, qual foi a sequência escrita?

b) Elabore um fluxograma para obter os termos dessa sequência.

c) Usando o fluxograma, escreva em seu caderno essa sequência após escolher um número natural maior do que 1 e diferente de 10 para ser o primeiro termo.

11. Quantos coelhos podem ser gerados de um par de coelhos em um ano, considerando que a cada mês ocorre a produção de um par de coelhos e que um par de coelhos começa a produzir coelhos quando completa dois meses.

Indicando a quantidade de pares de coelhos do mês n por $a_n$, obtemos:

$a_1=1$ (um par de coelhos jovem)

$a_2=1$ (um par de coelhos adulto, no período fértil)

$a_3=2$ (dois pares de coelhos: um adulto e um jovem)

$a_4=3$ (três pares de coelhos: dois adultos e um jovem)

$a_5=5$ (cinco pares de coelhos: três adultos e dois jovens)

$\dots$

Objeto digital

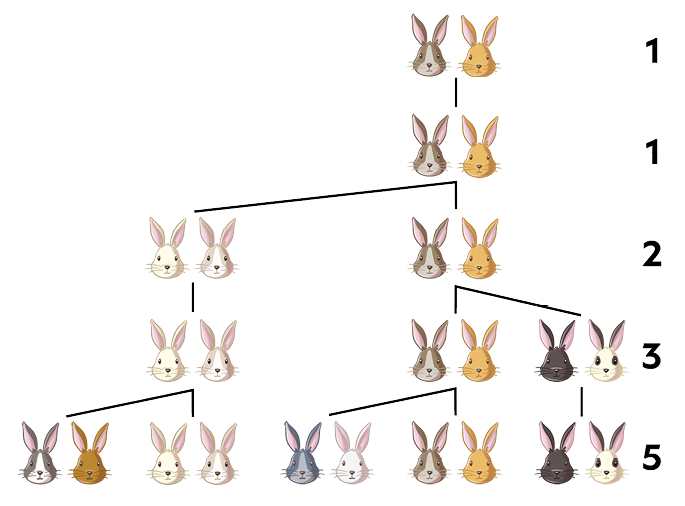
Se continuarmos esse processo, obtemos a seguinte sequência:

Essa sequência foi nomeada Sequência de Fibonacci, em homenagem ao matemático Leonardo de Pisa (1175-1250), também conhecido como Leonardo Fibonacci.

Nessa sequência, os dois primeiros termos são iguais a 1 e cada termo seguinte é obtido adicionando os dois termos anteriores.

a) Determine o 13º termo dessa sequência.

b) Junte-se a um colega e analisem como os termos dessa sequência são formados. Em seguida, definam-na por recorrência.

c) Faça uma pesquisa a respeito de Leonardo Fibonacci e as contribuições dele para a Matemática. Em seguida, monte um cartaz com imagens e informações e exponha sua produção para os colegas.