Página 243
UNIDADE
11
Medidas de área

Agora vamos estudar...
- medida da área do paralelogramo, do triângulo, do trapézio e do losango;
- medida da área do círculo;
- medida da área de setor e de coroa circulares.
Página 244
Medida da área do paralelogramo
Ideias relacionadas à medida de área já eram utilizadas há milhares de anos por vários povos antigos, como os egípcios.
Nesta unidade, estudaremos como as medidas das áreas de alguns polígonos podem ser calculadas.
No paralelogramo a seguir, cujo comprimento da base mede b e a altura mede h, vamos acompanhar os passos necessários para calcular a medida de sua área.
Primeiro, decompomos o paralelogramo em um triângulo e em um quadrilátero. Em seguida, fazemos uma recomposição, formando um retângulo.
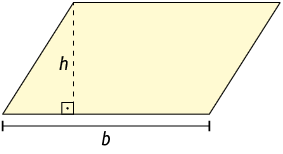
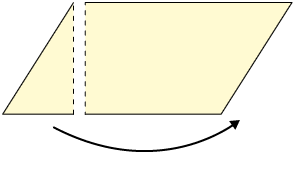
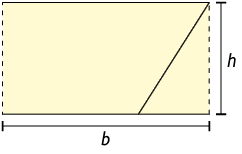
O comprimento da base do retângulo tem a mesma medida do comprimento da base do paralelogramo, assim como a altura desse retângulo tem a mesma medida da altura do paralelogramo.
Você já deve ter estudado que, para calcular a medida da área de um retângulo, multiplicamos a medida do comprimento da base pela medida da sua altura. Sendo assim, a medida da área do paralelogramo pode ser obtida do mesmo modo que a medida da área do retângulo.
Para calcular a medida da área de um paralelogramo, multiplicamos a medida do comprimento de sua base pela medida de sua altura.
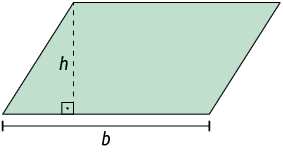
A: medida da área do paralelogramo
b: medida do comprimento da base
h: medida da altura
A seguir, calcularemos a medida da área do paralelogramo, utilizando a fórmula.
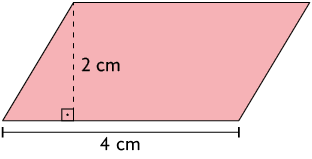
De acordo com as medidas indicadas, temos:
- medida do comprimento da base: ;
- medida da altura: .
Substituímos essas medidas na fórmula e efetuamos os cálculos:
Atenção!
Ao substituir as medidas na fórmula, elas devem estar na mesma unidade de medida.
Logo, a área desse paralelogramo mede .
Página 245
Atividades
Faça as atividades no caderno.
1. Em seu caderno, calcule a medida da área de cada um dos paralelogramos a seguir.

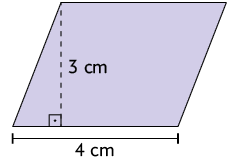
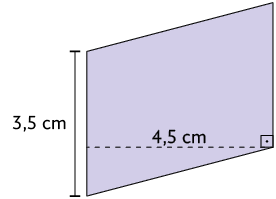
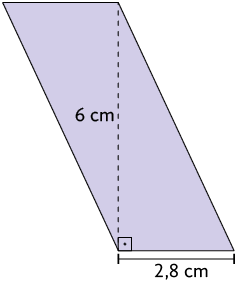
2. Qual é a medida da base, em centímetros, de um paralelogramo que tem de área e de altura?
3. Considere um paralelogramo cujo comprimento da base mede e cuja altura corresponde a 30% da medida do comprimento da base.
Calcule no caderno a medida da área desse paralelogramo, em centímetros quadrados.
4. Junte-se a um
colega e, usando transferidor, régua e
compasso, construam, no caderno de vocês, paralelogramos cujas informações são
dadas a seguir. Depois, determinem a medida da área A
de cada um deles.
A. Paralelogramo BCDE
é a altura
H é um ponto de
B. Paralelogramo FGHI
é a altura
J é um ponto de
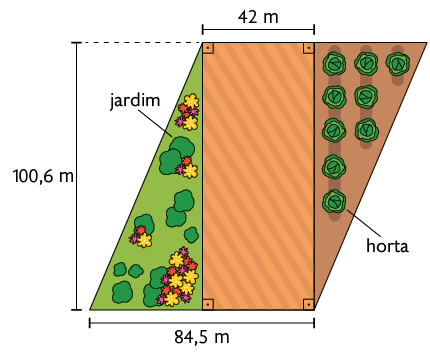
5. Cláudia comprou uma chácara cujo terreno tem o formato de um paralelogramo. Nesse terreno, ela deseja construir um jardim e uma horta, como representado na figura geométrica a seguir. No restante do terreno, Cláudia pretende construir uma casa. Calcule, no caderno, qual é a medida da área do terreno destinada à construção do jardim e da horta.
Página 246
Medida da área do triângulo
No triângulo representado a seguir, b é a medida do comprimento da base e h é a medida do comprimento da altura.
Para calcular a medida da área desse triângulo, consideramos um triângulo , congruente ao triângulo , e compomos um paralelogramo com os triângulos e .
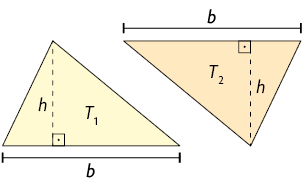
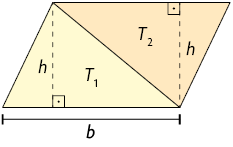
Os triângulos e compõem um paralelogramo com a mesma medida do comprimento da base e com a mesma medida de comprimento da altura do triângulo .
Assim, para obter a medida da área de cada triângulo, calculamos a medida da área do paralelogramo e dividimos por 2, pois os triângulos são congruentes.
Para calcular a medida da área de um triângulo, multiplicamos a medida do comprimento de sua base pela medida de comprimento de sua altura e dividimos o resultado por 2.
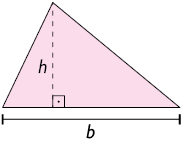
A: medida da área do triângulo
b: medida do comprimento da base
h: medida do comprimento da altura
Atenção!
A altura de um triângulo é um segmento que liga um vértice ao lado oposto (ou ao seu prolongamento), formando com ele um ângulo reto. Nesse caso, esse lado oposto é chamado base do triângulo. Um triângulo tem três alturas, cada uma relativa a determinado lado.
Vamos calcular a medida da área do triângulo a seguir utilizando a fórmula.
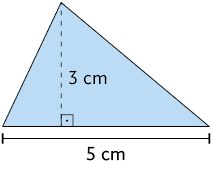
Conforme as medidas indicadas, temos:
- medida do comprimento da base: ;
- medida do comprimento da altura: .
Substituímos essas medidas na fórmula e efetuamos os cálculos:
Logo, a área desse triângulo mede .
Página 247
Atividades
Faça as atividades no caderno.
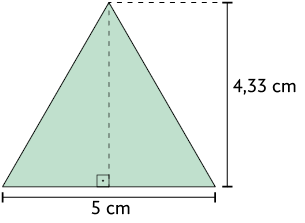
6. No caderno, calcule a medida da área de cada um dos triângulos a seguir.

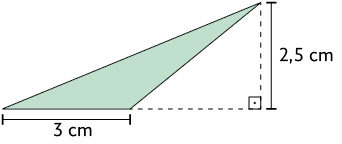
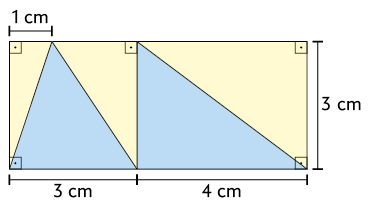
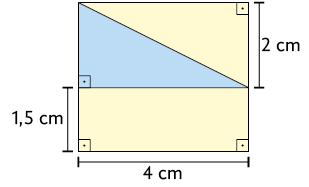
7. Em cada imagem a seguir, determine a medida da área da região colorida de amarelo e escreva as respostas em seu caderno.
8. Qual é a medida do comprimento da altura, em centímetros, de um triângulo cuja área mede e a base mede ?
9. O comprimento da base de um triângulo mede e o comprimento da altura mede x.
a) Escreva no caderno uma expressão algébrica que represente a medida da área desse triângulo.
b) Supondo que a área desse triângulo meça , qual é o valor de x?
10. A figura
geométrica a seguir é formada por 1 paralelogramo e 2
triângulos isósceles cujo comprimento da base mede x.
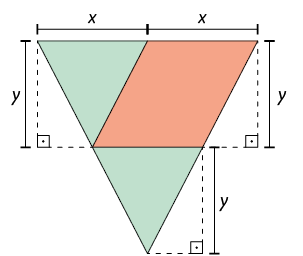
a) Escreva no caderno uma expressão algébrica que represente a medida da área total dessa figura geométrica.
b) Em seu caderno, calcule, em centímetro quadrado, a medida da área dessa figura geométrica, considerando e .
11. No triângulo isósceles a seguir, o comprimento dos lados congruentes mede e o comprimento da base mede .
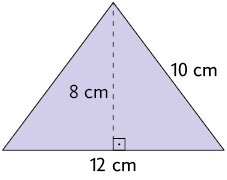
Utilizando essas informações, elabore um problema envolvendo medida de área e peça a um colega que o resolva. Depois, verifique se ele resolveu corretamente.
Página 248
12. Herão
foi um egípcio com formação
grega, que nasceu, viveu e morreu em Alexandria. Dedicou seus estudos às áreas
da Matemática, Física e Engenharia. Não se sabe ao certo a época exata em que ele viveu, mas estimativas de historiadores
indicam a segunda metade do século I d.C.
Dos trabalhos que Herão fez relacionados à Geometria, o mais importante é A métrica, em que se encontra a dedução da fórmula para calcular a medida da área de um triângulo em função das medidas do comprimento de seus três lados. Essa fórmula ganhou o nome de fórmula de Herão.

- a, b e c são as medidas do comprimento dos lados do triângulo, na mesma unidade de medida;
- p é a medida do semiperímetro do triângulo, ou seja, a metade da medida do seu perímetro .
Utilizando a fórmula de Herão, podemos calcular a medida da área do triângulo a seguir.

Logo, a área desse triângulo mede .
a) De maneira semelhante e com o auxílio de uma calculadora, determine a medida da área A de cada triângulo a seguir, utilizando a fórmula de Herão.
Atenção!
Se necessário, arredonde, para o centésimo mais próximo, os resultados obtidos em cada item.
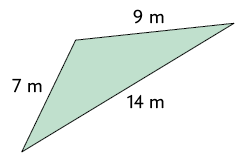



b) Realize uma pesquisa para obter o nome de outros trabalhos desenvolvidos por Herão de Alexandria. Depois, compartilhe-a com os colegas e o professor.
Atenção!
A pesquisa proposta nesta atividade pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Página 249
Medida da área do trapézio
No trapézio representado a seguir, B é a medida do comprimento da base maior, b é a medida do comprimento da base menor e h é a medida da altura.
Para calcular a medida da área desse trapézio, consideramos um trapézio , congruente ao trapézio , e compomos um paralelogramo com os trapézios e .
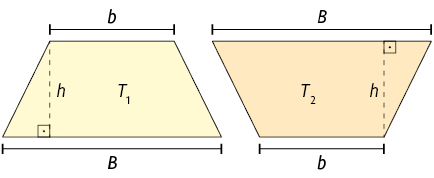
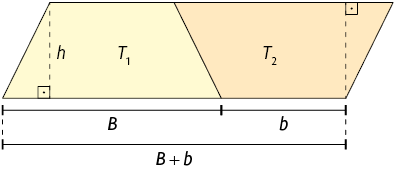
Os trapézios e compõem um paralelogramo cuja medida do comprimento da base é a soma das medidas do comprimento das bases maior com a menor dos trapézios, e cuja medida da altura é a mesma do trapézio .
Assim, basta calcular a medida da área do paralelogramo e dividi-la por 2 para obter a medida da área de cada trapézio, pois eles são congruentes.
Para calcular a medida da área de um trapézio, adicionamos a medida do comprimento de sua base maior com a medida do comprimento de sua base menor e multiplicamos a soma por sua medida da altura. Depois, dividimos o resultado por 2.
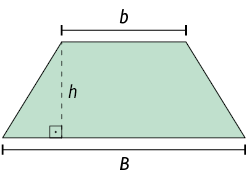
A: medida da área do trapézio
B: medida do comprimento da base maior
b: medida do comprimento da base menor
h: medida do comprimento da altura
Analise como podemos calcular a medida da área do trapézio a seguir, utilizando a fórmula.
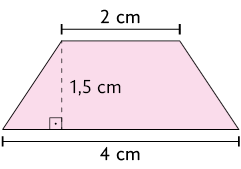
De acordo com as medidas indicadas, temos:
- medida de comprimento da base maior: ;
- medida de comprimento da base menor: ;
- medida de comprimento da altura: .
Substituímos essas medidas na fórmula e efetuamos os cálculos:
Logo, a área desse trapézio mede .
Página 250
É possível também calcular a medida da área do hexágono regular a seguir, decompondo-o em 2 trapézios congruentes.
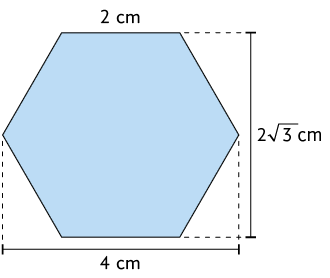
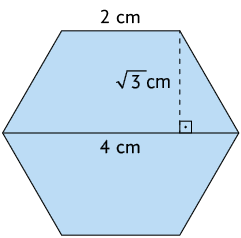
Calculamos a medida da área de um dos trapézios:
Atenção!
Para obter a medida da altura () de um dos trapézios, basta dividir a medida da altura do hexágono regular por 2, ou seja, .
Por último, multiplicamos o resultado por 2 para obter a medida da área do hexágono regular.
Portanto, a área desse hexágono regular mede .
Atividades
Faça as atividades no caderno.
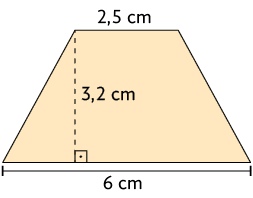
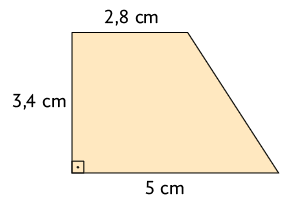
13. Calcule no caderno a medida da área de cada trapézio mostrado a seguir.
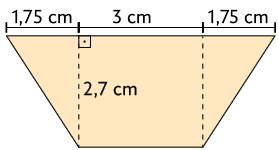
14. A área do trapézio representado a seguir mede .
a) Determine o valor de x.
b) Qual é a medida do comprimento da base maior desse trapézio?
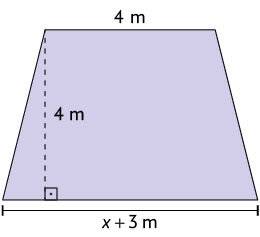
15. Considere um trapézio tal que:
a área meça ;
a altura meça ;
o comprimento da base maior meça .
Calcule no caderno a medida do comprimento da base menor desse trapézio.
Página 251
16. Determine a medida, em centímetros quadrados, da área de cada trapézio a seguir.
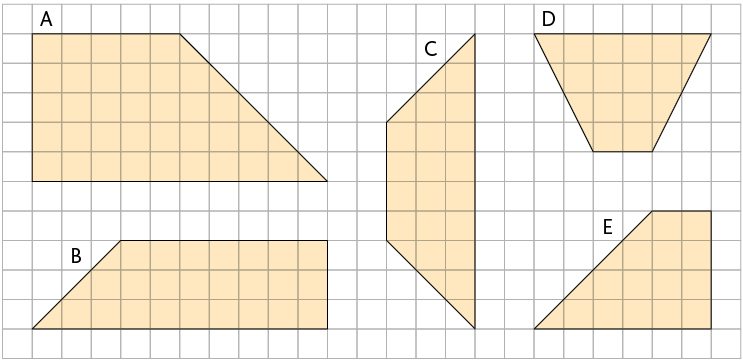
Atenção!
O
comprimento do lado de cada
![]() da
malha mede .
da
malha mede .
17. As medidas apresentadas nos quadros a seguir referem-se a trapézios. Efetue os cálculos no caderno e obtenha os valores de x, y e z.
A. Trapézio ABCD
Comprimento das bases: e
Altura:
Área:
B. Trapézio EFGH
Comprimento das bases: e
Altura:
Área:
C. Trapézio IJKL
Comprimento das bases: e
Altura:
Área:
18. A figura geométrica a seguir representa a vista superior do tampo de uma mesa.
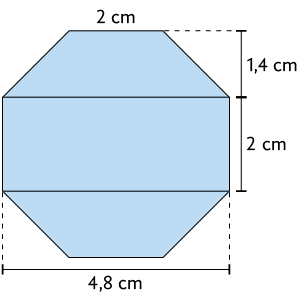
Sabendo que esse tampo é formado por 2 trapézios isósceles congruentes e por 1 retângulo, determine a medida da área de sua superfície.
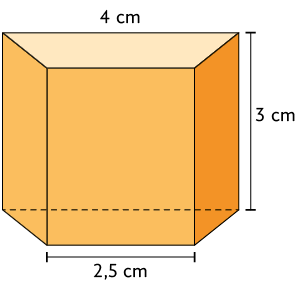
19. Determine a medida da área total da superfície do prisma reto representado a seguir, sabendo que suas bases são trapézios isósceles.

Página 252
Medida da área do losango
No losango a seguir, D é a medida do comprimento da diagonal maior e d é a medida do comprimento da diagonal menor.
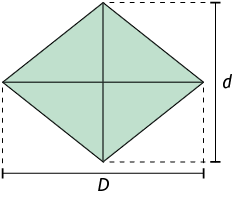
Para calcular a medida da área desse losango, traçamos um retângulo cuja medida do comprimento da base corresponde à medida do comprimento da diagonal maior do losango e cuja medida da altura corresponde à medida do comprimento da diagonal menor.
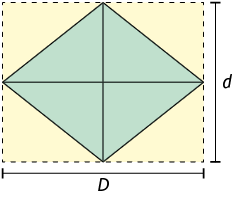
Esse retângulo é composto de 8 triângulos congruentes, e 4 desses triângulos formam o losango.
Assim, a medida da área do losango é a metade da medida da área desse retângulo.
Para calcular a medida da área de um losango, multiplicamos a medida do comprimento de sua diagonal maior pela medida do comprimento de sua diagonal menor e dividimos o resultado por 2.
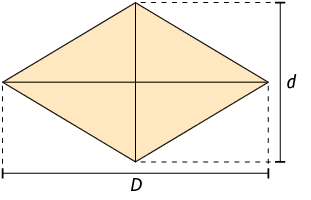
A: medida da área do losango
D: medida do comprimento da diagonal maior
d: medida do comprimento da diagonal menor
Acompanhe o cálculo da medida da área do losango a seguir, utilizando a fórmula.
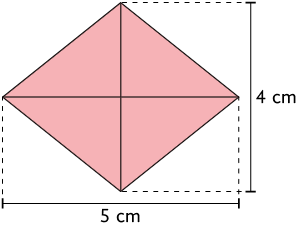
De acordo com as medidas indicadas, temos:
- medida do comprimento da diagonal maior: ;
- medida do comprimento da diagonal menor: .
Substituímos essas medidas na fórmula e efetuamos os cálculos:
Atenção!
Lembre-se de que, ao substituir as medidas na fórmula, elas devem estar na mesma unidade de medida.
Logo, a área desse losango mede .
testePágina 253
Atividades
Faça as atividades no caderno.
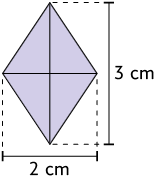
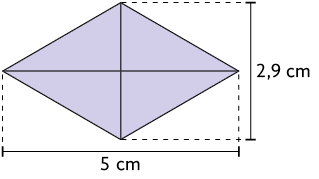
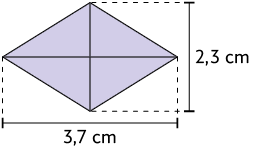
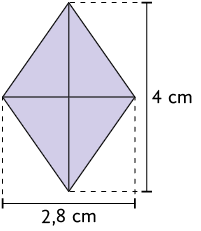
20. Calcule no caderno a medida da área dos seguintes losangos.
21. Sabendo que a área de um losango mede e o comprimento de sua diagonal menor mede , determine a medida do comprimento da diagonal maior.
22. Determine a medida do comprimento da diagonal menor de um losango que tenha de medida de área e cujo comprimento da diagonal maior meça .
23. A área do losango representado a seguir mede .
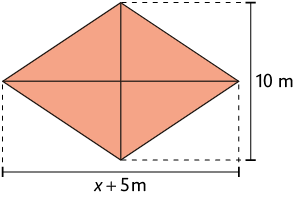
a) Em seu caderno, determine o valor de x.
b) Qual é a medida do comprimento da diagonal maior desse losango?
24. A figura geométrica a seguir é um prisma reto, cujas bases são losangos.
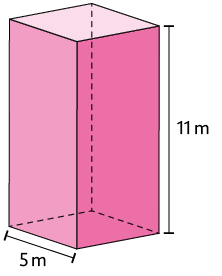
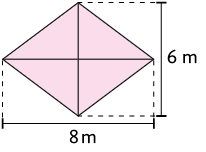
De acordo com as medidas indicadas, determine a medida da área total da superfície desse prisma.
25. Utilizando a imagem a seguir, elabore um problema envolvendo cálculo da medida de área.

Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Página 254
Medida da área do círculo
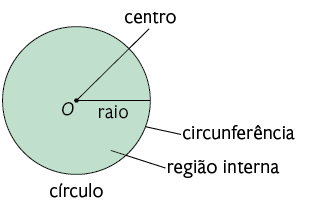
O círculo é a reunião da circunferência com todos os pontos que estão em sua região interna. Acompanhe os procedimentos para obter a fórmula que permite calcular a medida da área de um círculo.
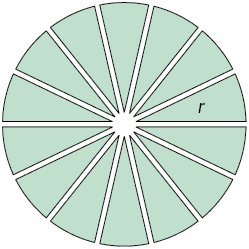
Inicialmente, decompomos o círculo em partes iguais. Por exemplo, na figura a seguir, o círculo de raio medindo r foi decomposto em 14 partes iguais.
Em seguida, organizamos essas partes, como mostra a imagem a seguir.
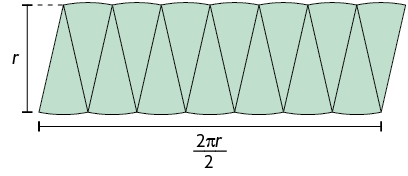
Organizando as partes do círculo dessa maneira, obtemos uma figura geométrica que lembra um paralelogramo, cuja medida do comprimento da base é aproximadamente metade da medida do comprimento da circunferência e cuja medida da altura é aproximadamente a medida do comprimento do raio do círculo.
Atenção!
Lembre-se de que a medida C do comprimento de uma circunferência de comprimento de raio medindo r é .
Quanto maior for a quantidade de partes em que o círculo é decomposto, menos "inclinado" é o lado do paralelogramo. Assim, aumentando significativamente a quantidade de partes, a figura geométrica obtida lembra um retângulo, cuja medida do comprimento da base é metade da medida do comprimento da circunferência e cuja medida da altura é a medida do comprimento do raio do círculo.
Para calcular a medida da área de um paralelogramo, multiplicamos a medida do comprimento de sua base (b) pela medida da sua altura (h). Nesse caso, temos e . Assim:
Como essa figura geométrica é formada por todas as partes do círculo, a medida da área do círculo é dada por:
Página 255
Agora, vamos calcular a medida aproximada da área do círculo a seguir, utilizando a fórmula e considerando .
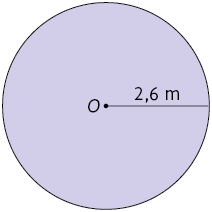
Portanto, a área desse círculo mede aproximadamente .
Arredondando esse valor ao centésimo mais próximo, obtemos .
Atividades
Faça as atividades no caderno.
26. Calcule no caderno a medida da área de cada círculo de centro O representado a seguir.
Atenção!
Para resolver as atividades desta unidade, utilize e, quando necessário, arredonde os resultados ao centésimo mais próximo do valor final.
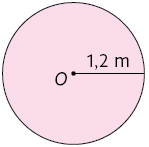
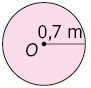
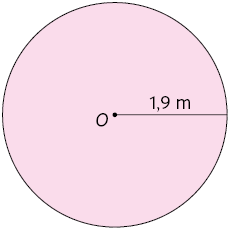
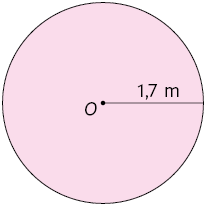
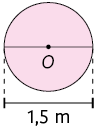
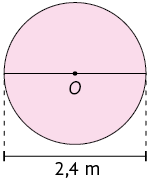
27. Calcule no caderno a medida da área do círculo cujo comprimento do raio mede .
28. Cada figura a seguir representa uma fração de um círculo de centro O. De acordo com a fração e a medida do comprimento do raio, determine, em seu caderno, a medida aproximada da área de cada uma dessas figuras.
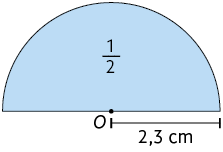
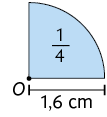
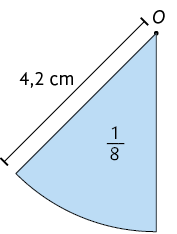
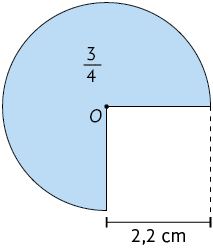
29. Determine a medida da área do círculo cujo comprimento da circunferência mede .
30. Qual é a medida do comprimento do raio do círculo cuja área mede ?
Página 256
31. No Papiro de Rhind, encontra-se uma aproximação para a medida da área de um círculo, que seria igual à de um quadrado com comprimento de lado medindo da medida do comprimento do diâmetro do círculo. Utilizando a fórmula da medida da área do círculo e o método utilizado no Papiro de Rhind, realize os cálculos e obtenha a medida da área de um círculo cujo comprimento do raio mede . Depois, verifique se os resultados obtidos são próximos entre si.
32. Para plantar hortaliças, Pedro separou uma região em seu sítio com formato de quadrado, cujo comprimento do lado mede .
Para facilitar a irrigação, ele separou uma região circular no interior da região quadrada, onde fará o plantio.
a) Qual deve ser a medida do comprimento do raio da região circular para que a medida de sua área seja máxima?
b) Calcule a medida dessa área.
33. A prefeitura de uma cidade vai construir uma praça em um terreno com formato retangular como representado na figura a seguir. A região com formato circular está reservada para a construção de um parque para as crianças.
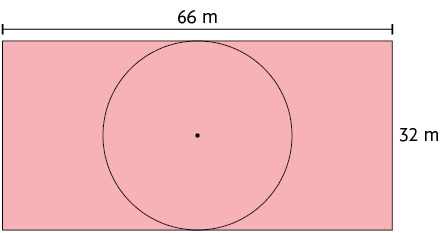
Calcule no caderno a medida da área aproximada do terreno que não está reservada para a construção do parque.
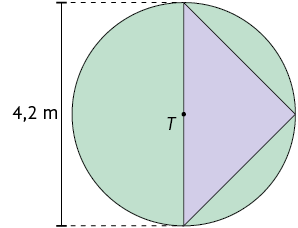
34. Calcule a medida da área da região verde em cada figura a seguir, sendo O, P, Q e T os centros dos círculos.
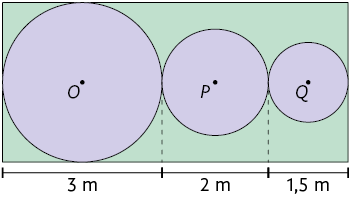
35. As imagens a seguir mostram uma lata com formato de cilindro reto e sua planificação.


De acordo com essas imagens, elabore um problema envolvendo medida de área e peça a um colega que o resolva. Depois, verifique se ele resolveu corretamente.
Página 257
Medida da área do setor circular
Setor circular é uma parte de um círculo determinada por um ângulo central qualquer. Por exemplo, a parte pintada em rosa no círculo a seguir é um setor circular, determinado pelo ângulo central de medida (lê-se: alfa).
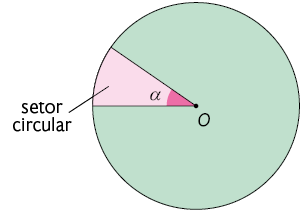
Atenção!
Nesse círculo, a parte verde também é um setor circular.
A medida da área de um setor circular é diretamente proporcional à medida do ângulo central que o determina.
Na imagem a seguir estão representados um círculo de centro O com comprimento de raio medindo e um setor circular determinado por um ângulo central de medida .
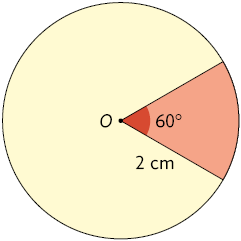
Para calcular a medida da área desse setor, inicialmente calculamos a medida da área do círculo, considerando .
Como a medida da área do setor circular é diretamente proporcional à medida do ângulo central que o determina, podemos escrever a seguinte proporção:
Medida da área
12,56
Medida do ângulo (graus)
360
60

Assim, a área desse setor circular mede aproximadamente .
Página 258
Agora, analise o círculo de centro O com comprimento de raio medindo r e o setor circular de ângulo central de medida .
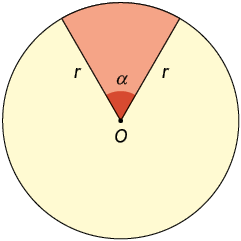
Sabemos que a medida da área total do círculo é e que um círculo completo corresponde a . Assim, podemos determinar a fórmula para calcular a medida da área desse setor circular.
Medida da área
Medida do ângulo (graus)
360
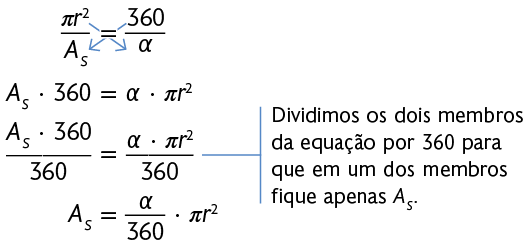
Assim, podemos calcular a medida da área do setor circular de medida pela seguinte fórmula.
A seguir, acompanhe os procedimentos de cálculo da medida da área do setor circular da página anterior, de medida , utilizando essa fórmula e considerando .
Portanto, a área do setor circular mede aproximadamente .
Página 259
Medida da área da coroa circular
A parte dourada em cada moeda a seguir lembra uma coroa circular.


Imagem com elementos não proporcionais entre si.
A região compreendida entre dois círculos concêntricos, de raios com medidas de comprimentos diferentes, é chamada coroa circular.
Por exemplo, na figura, a parte pintada de verde é uma coroa circular.
A medida da área de uma coroa circular é a diferença entre a medida da área do círculo maior e a medida da área do círculo menor.
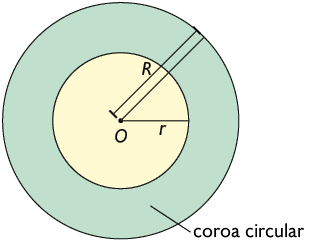
Atenção!
Analogamente ao conceito de circunferências concêntricas, círculos concêntricos são aqueles que têm o mesmo centro.
Acompanhe como podemos calcular a medida da área da coroa circular citada, sendo R a medida do comprimento do raio do círculo maior e r a medida do comprimento do raio do círculo menor.

Assim, para obtermos a medida da área de uma coroa circular, utilizamos a fórmula.
Por exemplo, vamos calcular a medida da área da coroa circular a seguir, indicada em verde, utilizando essa fórmula e considerando .
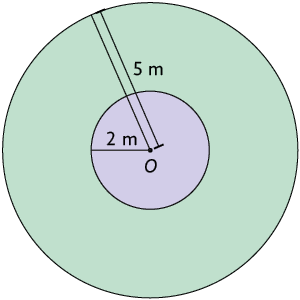
Logo, a área dessa coroa circular mede aproximadamente .
Página 260
Atividades
Faça as atividades no caderno.
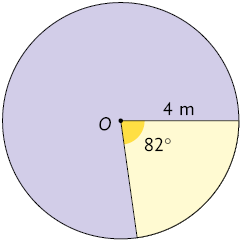
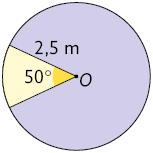
36. Calcule no caderno a medida da área aproximada do setor circular amarelo de centro O, em cada círculo a seguir.
37. A seguir é apresentada outra maneira de calcular a medida da área de um setor circular, considerando a fração do círculo que ele representa. Para isso, considere o setor circular verde representado.
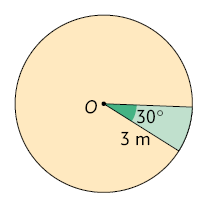
Esse setor é determinado por um ângulo central de medida em um círculo de centro O e comprimento de raio medindo .
Inicialmente, determinamos a razão entre a medida do ângulo central e do círculo: . Nesse caso, o setor circular é do círculo.
Depois, calculamos a medida da área total do círculo (A), considerando .
Por último, calculamos da medida da área total do círculo.
Portanto, a área do setor circular mede aproximadamente .
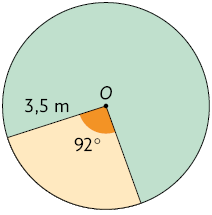
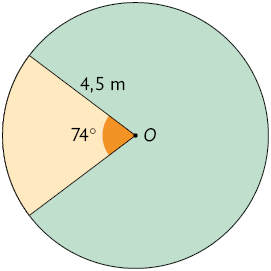
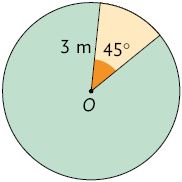
De maneira semelhante, calcule a medida da área aproximada de cada setor circular laranja, sendo O o centro de cada círculo.
Página 261
38. A figura geométrica a seguir representa um semicírculo.
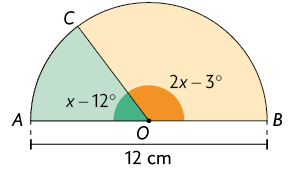
a) Quais são as medidas dos ângulos e ?
b) Qual é a medida da área aproximada do setor circular laranja? E do setor circular verde?
39. As figuras a seguir representam um cone e sua planificação.
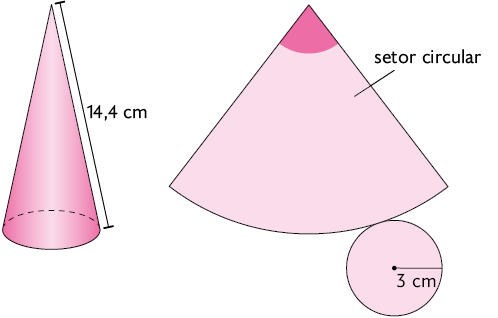
a) Com o auxílio do transferidor, meça o ângulo central da planificação desse cone.
b) Calcule no caderno a medida da área total da superfície do cone.
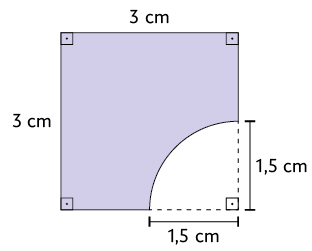
40. Em seu caderno, calcule a medida aproximada da área da figura a seguir.
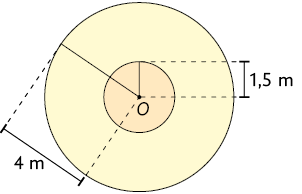
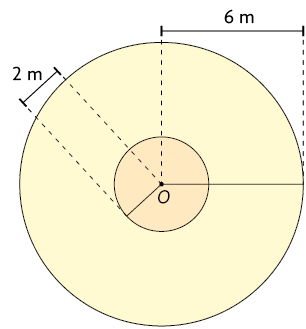
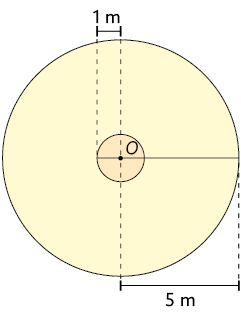
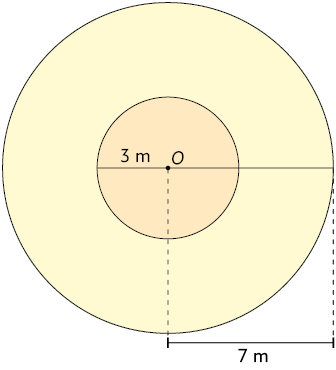
41. Considere as medidas indicadas e calcule no caderno a medida da área da coroa circular de cada item, sabendo que O é o centro dos círculos.
Página 262
42. Na figura a seguir estão representados 4 círculos concêntricos, de centro O.
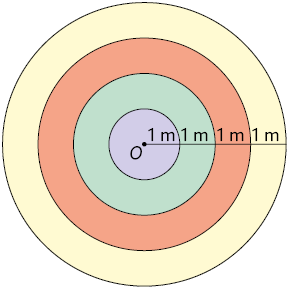
De acordo com as medidas indicadas, calcule no caderno a medida da área das coroas circulares pintadas de amarelo, vermelho e verde.
43. Janaína vai gravar as fotos digitais que estão em seu computador em 3 DVDs, que serão identificados por meio de etiquetas. Para isso, ela foi a uma papelaria e comprou uma folha com três etiquetas adesivas que serão destacadas e coladas.
A figura a seguir representa a folha com as etiquetas.
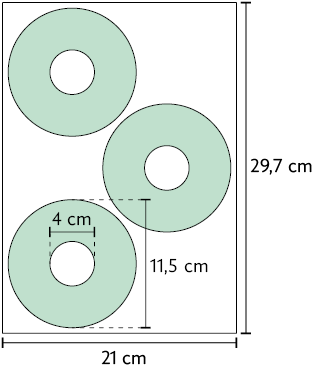
a) Qual é a medida da área da folha com as etiquetas?
b) Determine a medida da área aproximada de cada etiqueta.
c) Em relação à folha, qual medida da área não faz parte das etiquetas?
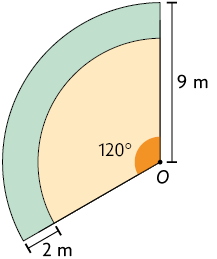
44. Calcule
no caderno a medida da área da região verde a seguir, formada por setores
circulares de centro O.
45. (Enem-2019) Em um condomínio, uma área pavimentada, que tem a forma de um círculo com diâmetro medindo , é cercada por grama. A administração do condomínio deseja ampliar essa área, mantendo seu formato circular, e aumentando, em , o diâmetro dessa região, mantendo o revestimento da parte já existente. O condomínio dispõe, em estoque, de material suficiente para pavimentar mais de área. O síndico do condomínio irá avaliar se esse material disponível será suficiente para pavimentar a região a ser ampliada.
Utilize 3 como aproximação para .
A conclusão correta a que o síndico deverá chegar, considerando a nova área a ser pavimentada, é a de que o material disponível em estoque
a) será suficiente, pois a área da nova região a ser pavimentada mede .
b) será suficiente, pois a área da nova região a ser pavimentada mede .
c) será suficiente, pois a área da nova região a ser pavimentada mede .
d) não será suficiente, pois a área da nova região a ser pavimentada mede .
e) não será suficiente, pois a área da nova região a ser pavimentada mede .
Página 263
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Um paralelogramo tem de medida de área e o comprimento de sua base mede . Qual é a medida da altura desse paralelogramo?
2. O triângulo, o retângulo e o trapézio representados a seguir foram obtidos a partir de quadrados com medidas de áreas iguais.
Quadrado
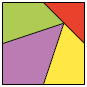


Figura obtida



Esses polígonos têm medidas de áreas iguais ou diferentes? Por quê?
3. Junte-se a um colega e calculem, em uma folha de papel avulsa, a medida da área de cada figura representada a seguir.
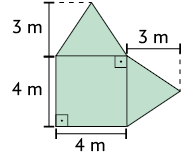
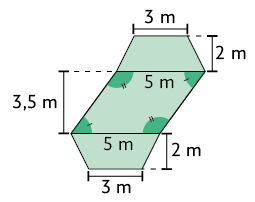
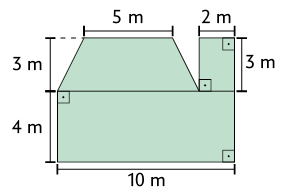
4. Determine o valor de x em cada polígono a seguir.
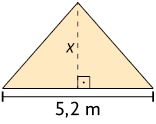
medida da área do triângulo:
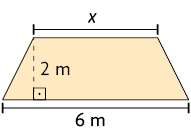
medida da área do trapézio:
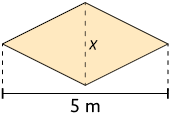
medida da área do losango:

medida da área do paralelogramo:
5. (Obmep-2006)
No retângulo a seguir, A, B e C são pontos
médios de seus lados e O é o ponto de
encontro de suas diagonais.
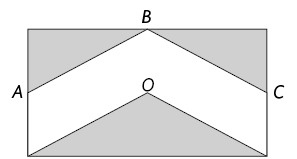
A área da região sombreada é
a) da área do retângulo.
b) da área do retângulo.
c) da área do retângulo.
d) da área do retângulo.
e) da área do retângulo.
Página 264
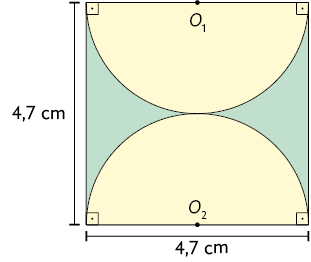
6. Calcule, em uma folha de papel avulsa, a medida da área da região verde em cada figura a seguir.
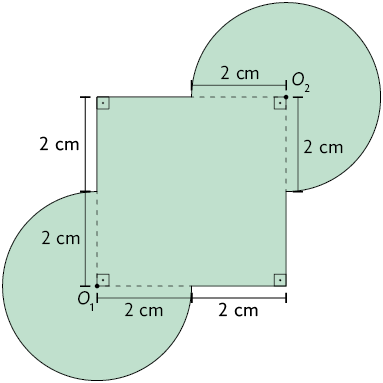
Atenção!
Na figura B, as partes amarelas são semicírculos.
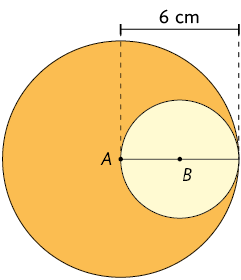
7. Na figura a seguir, a circunferência com centro B é tangente interna à circunferência de centro A. Qual é a medida da área da região laranja?
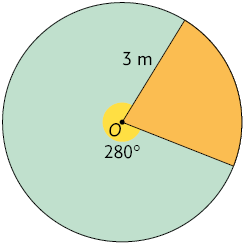
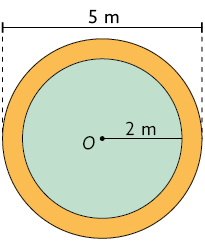
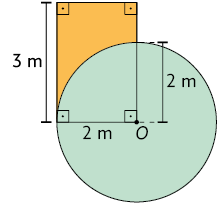
8. Calcule, em uma folha de papel avulsa, a medida da área da região laranja em cada figura a seguir, sendo O o centro de cada círculo.

9. Os círculos com centro A, B, C, D e E a seguir têm raio com mesma medida de comprimento.
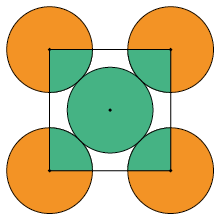
Sabendo que o círculo com centro E é tangente aos demais círculos, determine a razão entre a medida da área indicada em verde e a medida da área indicada em laranja.
a)
b)
c)
d)
e)