Página 131
UNIDADE
7
Estatística e probabilidade

Agora vamos estudar...
- gráficos;
- medidas de tendência central;
- medidas de dispersão;
- pesquisas amostrais;
- probabilidade.
Página 132
Gráficos
Os gráficos estão presentes em diversos meios de comunicação, como revistas, sites e jornais. Ao publicar, por exemplo, uma notícia que contenha um gráfico, o autor não escolhe o tipo dele aleatoriamente, pois há um tipo mais adequado para cada situação.
O gráfico de colunas, por exemplo, é mais adequado quando o objetivo é o de comparar os dados entre si.
Quantidade de candidatos a cargos políticos em 2022
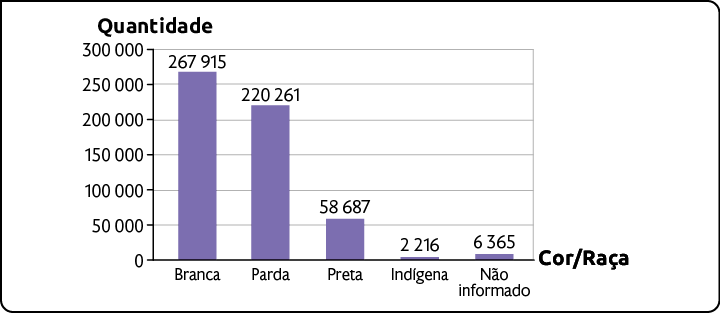
Fonte de pesquisa: ESTATÍSTICAS eleitorais. TSE. Disponível em: https://oeds.link/nq7m8f. Acesso em: 13 maio 2022.
Analisando o gráfico, podemos concluir que, em 2022, a maioria dos candidatos se autodeclarou da cor branca e a minoria, indígena.
Já o gráfico de linhas é mais adequado quando o objetivo é o de representar a evolução dos dados no decorrer de certo período de tempo.
Quantia disponível na conta bancária de Amarildo – 2022
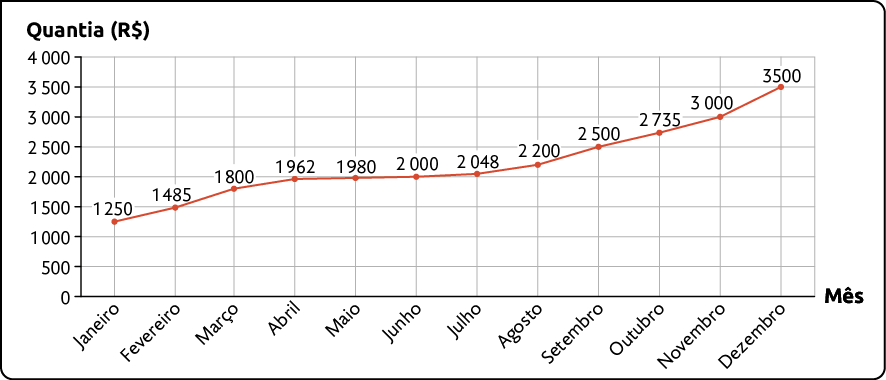
Fonte de pesquisa: extrato da conta bancária de Amarildo.
Analisando o gráfico, podemos concluir que a quantia disponível na conta de Amarildo aumentou ao longo do ano de 2022.
Página 133
O gráfico de setores, por sua vez, é mais adequado quando o objetivo é o de comparar os dados com o todo.
Analisando o gráfico, podemos concluir que, do total de consumidores, a maioria está muito satisfeito com o produto X.
Satisfação dos consumidores do produto X – 2022
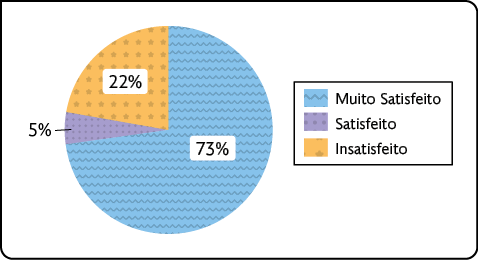
Fonte de pesquisa: fabricante do produto X.
Atividades
Faça as atividades no caderno.
1. O gráfico a seguir apresenta a quantidade de espécies ameaçadas de extinção, de acordo com o Ministério do Meio Ambiente.
Animais ameaçados de extinção – 2014
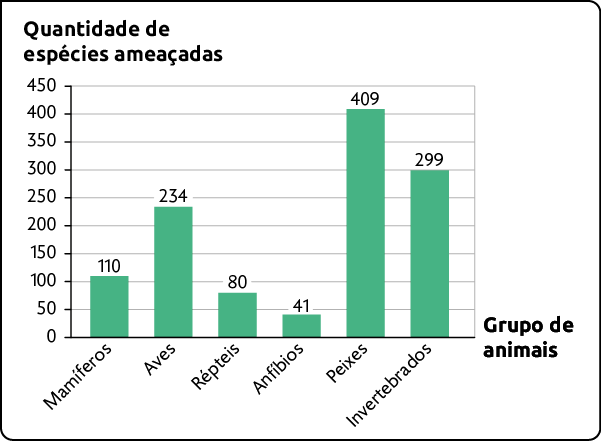
Fonte de pesquisa: SUMÁRIO executivo do livro vermelho da fauna brasileira ameaçada de extinção. Brasília, DF: ICMBio, 2016. p. 8. Disponível em: https://oeds.link/7IurZz. Acesso em: 26 maio 2022.
a) Qual dos grupos apresentados tem a maior quantidade de espécies ameaçadas de extinção? E a menor?
b) Em sua opinião, é importante preservar as espécies ameaçadas?
c) Agora, vamos fazer uma pesquisa! Com ela, espera-se que você responda às seguintes questões: quais motivos levam as espécies a serem ameaçadas de extinção? Qual é a importância de preservar essas espécies? Quais atitudes devem ser tomadas para preservar as espécies ameaçadas?
d) Após realizar a pesquisa, você mudou de opinião sobre a importância de preservar os animais ameaçados de extinção?
e) Escolha um animal ameaçado de extinção, junte-se a um colega da turma e faça um cartaz ou um vídeo incentivando sua preservação.
Respostas: a) Peixes; Anfíbios; b) Resposta pessoal; c) Resposta nas orientações ao professor; d) Resposta pessoal; e) Resposta pessoal.
Página 134
2. Um site que publica informações relacionadas à reciclagem realizou uma enquete com seus leitores. Depois que eles responderam à enquete, o resultado foi organizado em um gráfico de setores.
Porcentagem dos leitores do site que reciclam resíduos – novembro de 2023
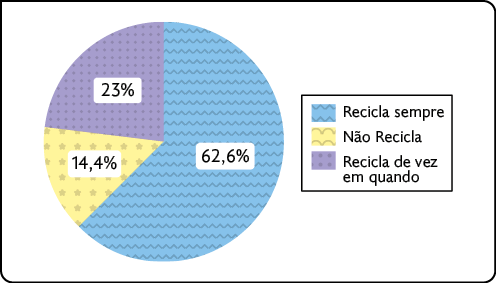
Fonte de pesquisa: organizadores do site.
a) Qual é a porcentagem de entrevistados que reciclam resíduos sempre? E quantos por cento reciclam de vez em quando?
b) Se o site recebeu 500 respostas, quantas pessoas:
I. reciclam sempre?
II. não reciclam?
III. reciclam de vez em quando?
Respostas: a) 62,6%; 23%; b) I - 313 pessoas; II - 72 pessoas; III - 115 pessoas.
3. Armando comprou algumas ações✚ de uma empresa. O gráfico de linhas a seguir apresenta o preço diário de uma dessas ações ao longo de determinada semana.
- Ação:
- Título que garante partes em uma sociedade aos proprietários ou aos investidores.↰
Preço da ação da empresa A – 1/5/22 a 7/5/22
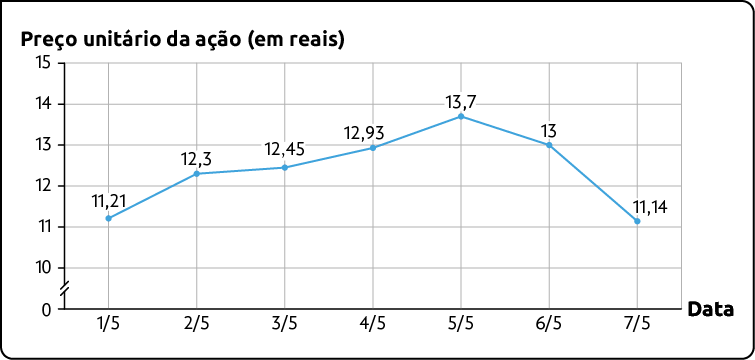
Fonte de pesquisa: Bolsa de Valores.
a) Em qual desses dias a ação teve o maior preço? E o menor?
b) De 2/5 a 4/5, o preço da ação aumentou ou diminuiu? Em quantos reais?
c) Qual foi a variação de preço da ação entre os dias 4/5 e 7/5?
Resposta: a) 5/5; 7/5; b) Aumentou; R$ 0,63; c) .
Página 135
4. Amanda precisa analisar o consumo de energia elétrica em sua casa nos últimos 6 meses de 2023. Para isso, ela vai utilizar um gráfico.
a) Qual dos gráficos apresentados é o mais adequado para o objetivo de Amanda? Justifique sua resposta.
Consumo de energia elétrica na casa de Amanda nos 6 últimos meses de 2023

Fonte de pesquisa: companhia de energia elétrica.
Consumo de energia elétrica na casa de Amanda nos 6 últimos meses de 2023
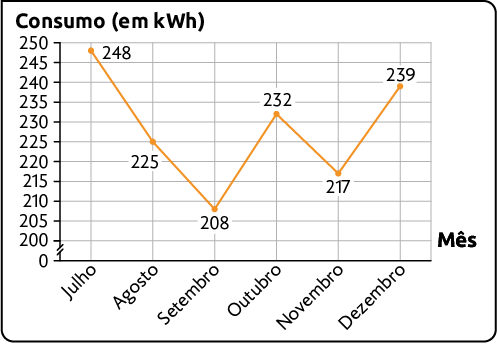
Fonte de pesquisa: companhia de energia elétrica.
b) De acordo com os gráficos do item a, responda às questões a seguir.
I . O consumo de energia na casa de Amanda aumentou ou diminuiu de novembro para dezembro de 2023?
II . Em qual desses meses ocorreu o maior consumo de energia elétrica?
Resposta: a) Sugestão de resposta: o gráfico de linhas, pois ele apresenta a evolução no consumo no período desejado por Amanda; b) I. Aumentou; II. Julho.
5. Analise as situações A, B e C apresentadas a seguir.
Situação A
Jairo trabalha em uma empresa de telefonia móvel. Para atender melhor a seus clientes, ele realizou uma pesquisa de satisfação. O quadro a seguir apresenta o resultado da pesquisa.
|
Nível de satisfação |
Muito satisfeito |
Satisfeito |
Insatisfeito |
|---|---|---|---|
|
Quantidade de clientes (%) |
30 |
15 |
55 |
Situação B
Ana vende perfumes e registrou, no quadro a seguir, o preço de venda de um de seus produtos durante 4 semanas.
|
Semana |
Preço do produto (R$) |
|---|---|
|
Primeira |
125 |
|
Segunda |
150 |
|
Terceira |
130 |
|
Quarta |
150 |
Situação C
Daniel vende camisetas. Ele registrou a quantidade e o tamanho dos produtos vendidos em 2 dias da semana no quadro a seguir.
|
Dia |
Sexta-feira |
Sábado |
||||
|---|---|---|---|---|---|---|
|
Tamanho |
P |
M |
G |
P |
M |
G |
|
Quantidade vendida |
15 |
36 |
20 |
21 |
40 |
18 |
Qual é o tipo de gráfico mais adequado para representar cada situação? Justifique sua resposta.
Sugestões de resposta: Situação A: gráfico de setores, pois permite a comparação dos dados com o todo; Situação B: gráfico de linhas, pois possibilita o acompanhamento da evolução do preço do produto; Situação C: gráfico de colunas, pois propicia a comparação dos dados entre si.
Página 136
Medidas de tendência central
No dia a dia, muitas vezes, encontramos informações que apresentam o conceito de média aritmética. Analise as situações apresentadas a seguir.
-
A Estação Meteorológica da cidade em que Afonso mora registrou, em 2022, a média de medida de temperatura de .
-
Em 2013, Joana poupou, em média, R$ 250,00 por mês.
-
O time para o qual Fabiana torce marcou, em média, 3 gols por jogo no último campeonato.
A média aritmética, ou simplesmente média, em geral, é utilizada com o objetivo de representar um conjunto de valores.
Para entendermos melhor o conceito de média, considere as medidas de massa, em quilogramas, dos jogadores de 2 times de futsal.
Time A
- 42,8
- 45,0
- 49,3
- 60,3
- 43,2
- 45,3
- 49,3
- 63,0
- 43,8
- 45,8
- 50,1
- 44,3
- 48,3
- 52,3
Time B
- 42,9
- 45,1
- 48,4
- 60,5
- 43,1
- 45,3
- 49,4
- 61,4
- 44,3
- 46,1
- 49,4
- 44,3
- 48,3
- 60,3
Para calcular a média aritmética (Ma) das medidas de massa dos jogadores do time A, adicionamos todas as medidas de massa e dividimos a soma pela quantidade de jogadores do time.
Assim, a massa média dos jogadores do time A mede, aproximadamente, .
A média aritmética de um conjunto de valores é o quociente entre a soma dos valores e a quantidade de valores do conjunto.
Questão 1. No caderno, calcule quanto mede a massa média dos jogadores do time B.
Resposta: .
Para obter a moda (Mo) de cada um desses conjuntos de valores, basta determinarmos os valores que ocorrem com maior frequência. Nesse caso, a moda das medidas de massa dos jogadores do time A é e do time B, e .
Atenção!
Note que o conjunto de valores referente à medida de massa dos jogadores do time B tem duas modas.
Página 137
A moda de um conjunto de valores é o valor que ocorre com maior frequência. Existem conjuntos com mais de uma moda ou nenhuma moda.
Para determinar a mediana (Md) de um conjunto de valores, devemos organizar os valores dele em ordem crescente ou decrescente (rol) e determinar o valor que ocupa a posição central. Vamos calcular, por exemplo, a mediana das medidas de massa dos jogadores do time A. Como a quantidade de valores do conjunto é um número par, calculamos a média aritmética dos dois valores centrais, ou seja:
Portanto, a mediana é .
Atenção!
Assim como a média aritmética, a moda e a mediana também são utilizadas para representar um conjunto de valores.
A mediana de um conjunto de valores, organizados em ordem crescente ou decrescente, é o valor que ocupa a posição central.
- Para
obter a posição da mediana em um conjunto com n
valores, em que n é ímpar,
efetuamos .
A mediana é o valor que ocupa essa posição.
- Para obter a mediana em um conjunto com quantidade par de valores, calculamos a média aritmética dos dois valores centrais.
Questão 2. Qual é a mediana das medidas de
massa dos jogadores do time B?
Resposta: .
Medidas de dispersão: amplitude
A amplitude de um conjunto possibilita analisar a dispersão dos valores do conjunto em torno de um valor central (média, moda e mediana). Para determinar a amplitude de um conjunto de valores, calculamos a diferença entre o maior e o menor valor do conjunto.
Vamos calcular, por exemplo, a amplitude dos conjuntos de valores referentes às medidas de massa dos jogadores dos times A e B apresentados na página anterior.
- Time A:
- Time B:
Como a amplitude das medidas de massa do time B é menor do que a do time A, concluímos que as medidas de massa dos jogadores do time B apresentam menor dispersão, ou seja, estão mais próximas entre si e das medidas de tendência central do que as medidas de massa dos jogadores do time A.
Página 138
Atividades
Faça as atividades no caderno.
6. Na internet, muitos sites mostram a quantidade de visitas em suas páginas. Considere um site que recebeu 1.825.145 visitas no período de 2.922 dias e calcule a média de visitas:
a) por dia no período.
b) por mês no período.
c) por ano no período.
Atenção!
Para efetuar os cálculos, considere 1 mês como um período com 30 dias e 1 ano como um período com 365 dias. Depois, arredonde os valores obtidos ao número inteiro mais próximo.
Respostas: a) Aproximadamente 625 visitas; b) Aproximadamente 18.739 visitas; c) Aproximadamente 227. 987 visitas.
7. No gráfico a seguir, além da quantidade de mel exportada mensalmente, está indicada a quantidade média do produto exportada em 2021.
Exportação de mel no Brasil de janeiro a dezembro de 2021
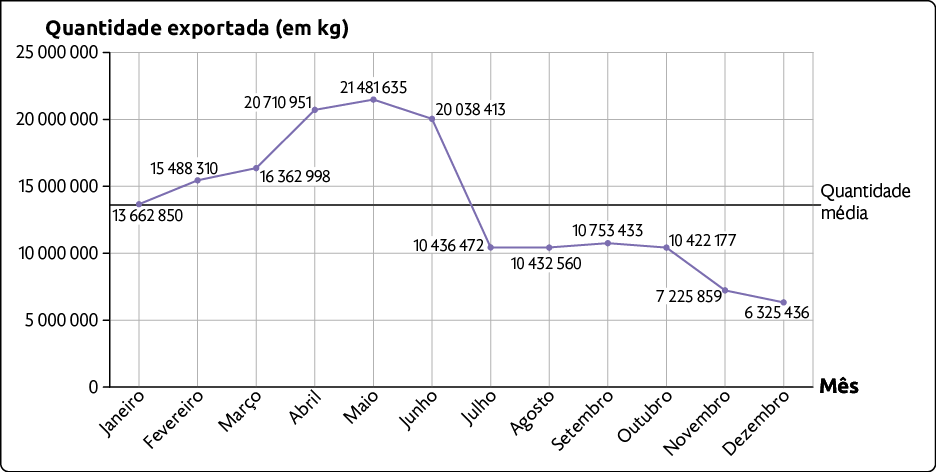
Fonte de pesquisa: EXPORTAÇÃO e importação geral. ComexVis. Disponível em: https://oeds.link/ZPVyxZ. Acesso em: 26 maio 2022.
a) Em qual mês foi exportada a maior quantidade de mel? E a menor?
b) No mês de janeiro, a exportação foi maior ou menor do que a de fevereiro? Qual é a diferença, em quilogramas, entre as quantidades exportadas nesses meses?
c) Nesse
ano, aproximadamente, quantos quilogramas de mel em média foram exportados no
Brasil por mês? Use uma calculadora para realizar o cálculo.
d) Nesse ano, em quais meses a quantidade de mel exportada ficou abaixo da quantidade média exportada?
e) Qual é a mediana dos valores apresentados no gráfico?
f) O que aconteceu com a exportação de mel entre os meses de setembro e dezembro de 2021? E de março a maio?
Respostas: a) Maio; Dezembro; b) Menor; ; c) ; d) Julho, agosto, setembro, outubro, novembro e dezembro; e) ; f) Diminuiu; Aumentou.
Página 139
8. Uma pesquisa realizada com moradores de 40 residências de certa avenida revelou a quantidade de pessoas que moram em cada uma delas. O pesquisador anotou os dados conforme a imagem a seguir.

a) Nessa avenida, há em média quantas pessoas morando em cada residência?
b) Esses valores apresentam uma moda? Caso a resposta seja positiva, escreva em seu caderno esse número e o que ele representa nessa situação.
c) Qual é a mediana desses valores?
Respostas: a) 4 pessoas; b) Sim. 6 pessoas. Esse número representa a quantidade de pessoas por residência que apresenta maior frequência no conjunto de dados; c) 5 pessoas.
9. Os quadros apresentam as notas obtidas pelos estudantes do 9º ano na última prova de Matemática.
9º ano A
- 10
- 9
- 8
- 5
- 4
- 3
- 5
- 9
- 2
- 10
- 5
- 9
- 10
- 5
- 3
- 9
- 10
- 7
- 8
- 3
- 3
- 10
- 10
- 10
- 9
- 8
- 7
9º ano B
- 5
- 9
- 10
- 10
- 10
- 10
- 10
- 6
- 3
- 2
- 1
- 4
- 4
- 3
- 1
- 1
- 2
- 3
- 9
- 9
- 10
- 10
- 1
- 5
- 5
- 4
- 3
a) Qual foi a nota média dos estudantes do 9º ano A? E do 9º ano B?
b) Qual é a moda das notas dos estudantes do 9º ano A? E do 9º ano B?
c) Qual turma apresentou a menor dispersão entre as notas? Justifique sua resposta.
Respostas: a) Aproximadamente 7,1; Aproximadamente 5,6; b) 10; 10; c) O 9º ano A apresentou menor dispersão, pois sua amplitude é menor.
10. Para determinar a ordem de largada em uma corrida de automóveis, cada competidor deve realizar 4 voltas na pista. Aquele que obtiver a menor média de medida de tempo por volta largará na 1ª posição, o que obtiver a 2ª menor média largará na 2ª posição e assim por diante. A seguir, estão representadas as medidas de tempo dos 5 pilotos que obtiveram as menores médias por volta.
|
Piloto |
Volta |
|||
|---|---|---|---|---|
|
1ª |
2ª |
3ª |
4ª |
|
|
A |
65 |
84 |
65 |
85 |
|
B |
84 |
79 |
81 |
72 |
|
C |
79 |
75 |
75 |
72 |
|
D |
70 |
79 |
72 |
86 |
|
E |
75 |
76 |
77 |
87 |
Fonte de pesquisa: organização da corrida.
a) Qual desses pilotos realizou a volta mais rápida?
Resposta: O piloto A.
b) Determine a média de medida de tempo por volta de cada piloto em segundos.
Resposta: Piloto A: ; Piloto B: ; Piloto C: ; Piloto D: ; Piloto E: .
c) Qual piloto largará na 1ª posição? E na 4ª posição?
Resposta: Piloto A; Piloto E.
d) Qual dos pilotos apresentou a maior regularidade entre as medidas de tempo de cada volta? Justifique sua resposta.
Resposta: O piloto C, pois ele apresentou a menor dispersão.
Página 140
11. Apesar de as mulheres terem conquistado vários direitos que antes lhes eram negados, em muitos países, ainda não há igualdade entre os sexos. No Brasil, por exemplo, a Constituição garante que homens e mulheres são iguais em direitos e obrigações, porém, pesquisas mostram que, em vários tipos de atividade, a renda das mulheres brasileiras ainda é menor do que a dos homens no exercício de uma mesma função.
Outro problema que assombra a sociedade brasileira é a violência contra a mulher, sobretudo a doméstica e familiar.

Fonte de pesquisa: SUPREMO TRIBUNAL DA JUSTIÇA. Twitter: @STJnoticias, Brasília, 24 jun. 2020. Disponível em: https://oeds.link/iVAmxP. Acesso em: 29 jun. 2022.
|
Local da agressão |
Sexo |
|
|---|---|---|
|
Homens |
Mulheres |
|
|
Própria residência |
14,5 |
39,5 |
|
Via pública ou outro local público |
19,3 |
9,7 |
|
Outros |
11,9 |
5,1 |
Fonte de pesquisa: TABELA 8066 - Pessoas de 18 anos ou mais de idade que sofreram violência física nos últimos 12 meses, por sexo e local da única ocorrência ou a mais grave. IBGE. Disponível em: https://oeds.link/Kb4pCl. Acesso em: 26 maio 2022.
a) De acordo com a tabela apresentada, responda às questões a seguir.
I. Qual é a moda dessa pesquisa para as mulheres?
II. Qual é a moda dessa pesquisa para os homens?
III. Converse com sua família sobre maneiras de combater a violência contra a mulher dentro e fora de casa. Compartilhe suas ideias com a turma e com o professor e anote em seu caderno as conclusões a que chegarem.
b) Reúnam-se em pequenos grupos e resolvam juntos os itens a seguir.
I. Calcule a porcentagem de meninos e de meninas da sua turma em relação ao total de estudantes. Em seguida, organize essas informações em um gráfico, aquele que melhor representar as informações obtidas.
II. Façam um levantamento de qual profissão cada menino e cada menina da turma pretende exercer no futuro. Em seu caderno, construam um gráfico para representar esses dados, separando-os por sexo. Nesse item, utilize o gráfico que julgar ser o mais adequado.
Respostas: a) I - Própria residência; II - Via pública ou outro local público; III - Resposta pessoal; b) I - Resposta pessoal. II - Resposta pessoal.
Página 141
Analisando tabelas e gráficos
As tabelas e os gráficos são utilizados para organizar e apresentar informações. Portanto, é muito importante saber analisá-los, pois podemos nos deparar com tabelas ou gráficos manipulados.
Muitas vezes, essas manipulações têm o objetivo de enganar o público, levando-os a interpretar as informações apresentadas de maneira errônea. Nesse tópico, verificaremos algumas possíveis manipulações, por meio da análise de algumas situações fictícias.
Exemplo 1. O gráfico a seguir foi divulgado em uma rede social do candidato a prefeito Marcos.
Intenção de voto para prefeito da cidade – 2024
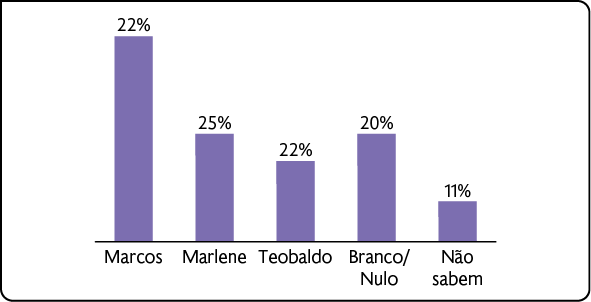
Fonte de pesquisa: instituto de pesquisa da cidade.
Ao analisarmos o gráfico publicado, percebemos que ele não apresenta escala, a medida da altura de algumas barras não está proporcional à porcentagem correspondente e, além disso, a barra correspondente ao candidato Marcos está muito mais alta do que as demais. Essa manipulação tem o objetivo de levar o eleitor a acreditar que ele tem mais intenções de votos do que os outros, o que não é verdade.
A seguir, apresentamos o gráfico correto, ou seja, sem manipulações.
Intenção de voto para prefeito da cidade – 2024
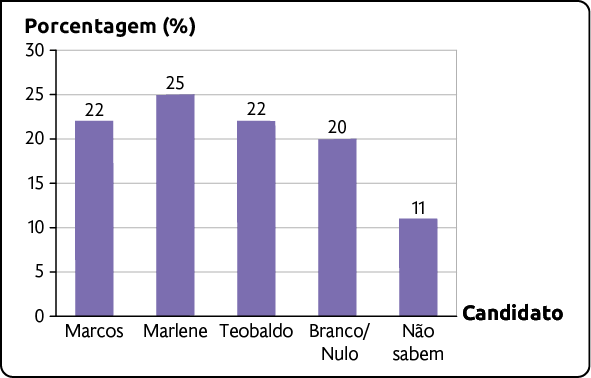
Fonte de pesquisa: instituto de pesquisa da cidade.
Página 142
Exemplo 2. O gráfico da esquerda foi publicado na rede social de um candidato à presidência de um país. Já o gráfico da direita foi publicado no portal do instituto de pesquisa do país.
Intenção de voto no candidato Alceu nas eleições presidenciais – 2027
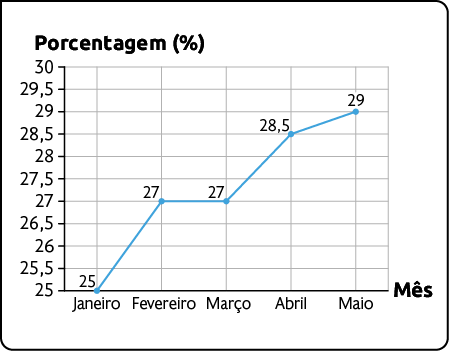
Fonte de pesquisa: instituto de pesquisa do país.
Intenção de voto no candidato Alceu nas eleições presidenciais – 2027
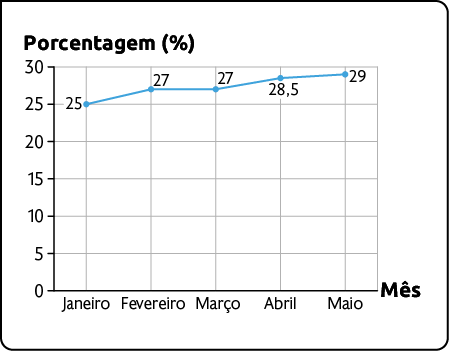
Fonte de pesquisa: instituto de pesquisa do país.
Ao analisar o gráfico da esquerda, percebemos que a escala se inicia em 25% e aumenta proporcionalmente a cada 0,5%. Nesse caso, o gráfico sugere que a intenção de voto no candidato Alceu aumentou rapidamente no período apresentado, o que não é demonstrado no gráfico da direita, em que a proporção de aumento é de 5%.
Exemplo 3. O gráfico da esquerda foi publicado no blog da marca A. Já o da direita foi publicado no portal do instituto de pesquisa do consumidor.
Marca preferida pelos consumidores – março de 2023
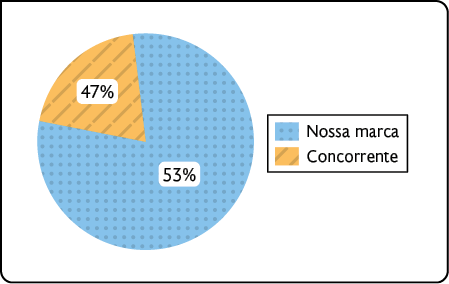
Fonte de pesquisa: instituto de pesquisa do consumidor.
Marca preferida pelos consumidores – março de 2023
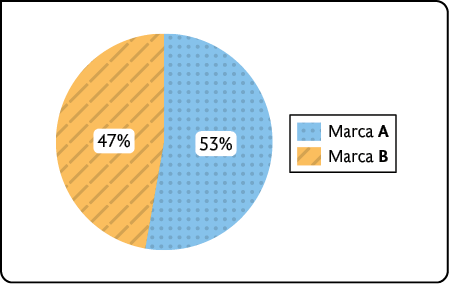
Fonte de pesquisa: instituto de pesquisa do consumidor.
Ao analisar o gráfico da esquerda, percebemos que os setores não estão proporcionais às porcentagens correspondentes.
Questão 3. Em sua opinião, qual foi a
intenção
da marca ao publicar esse gráfico em seu blog?
Resposta pessoal. Espera-se que os estudantes respondam que a intenção do gráfico é fazer parecer que a marca que publicou o gráfico é muito mais popular entre os consumidores.
Página 143
Atividades
Faça as atividades no caderno.
12. Quando há elementos faltantes em gráficos ou tabelas, a interpretação dos dados fica comprometida. Analise os gráficos e as tabelas apresentadas a seguir e identifique os elementos faltantes.
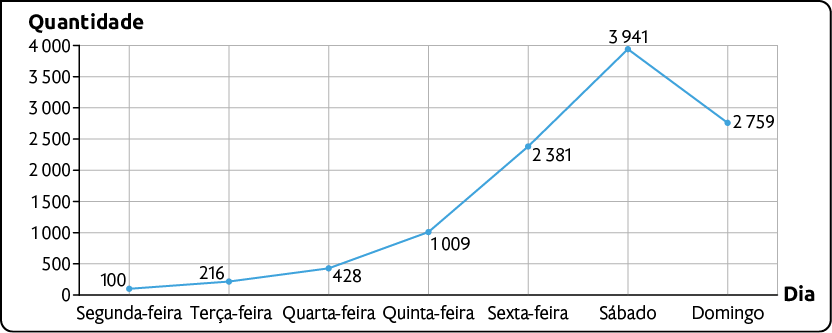
Quantidade de visualizações de um vídeo em 5 meses – 2023
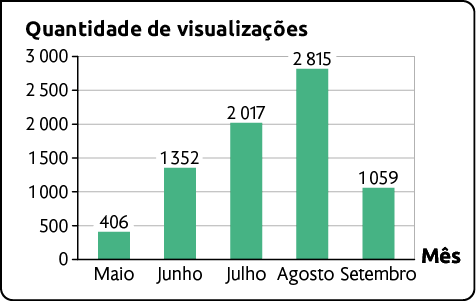
Conteúdo postado por Mariana em suas redes sociais – 2023
Fonte de pesquisa: assessoria das redes sociais de Mariana.
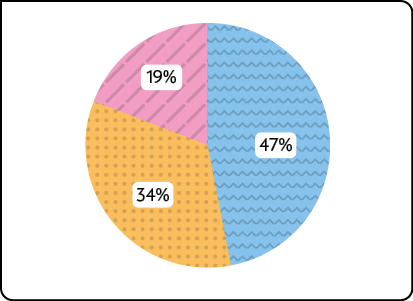
C. Quantidade de pessoas de uma cidade que compartilharam fake news
Fonte de pesquisa: instituto de pesquisa da cidade.
D.Quantidade de pontos de dois jogadores em uma partida de voleibol de 5 sets – 5 de janeiro de 2024

E.
|
Combustível |
Preço (R$) |
|---|---|
|
Gasolina comum |
4,99 |
|
Gasolina aditivada |
5,19 |
|
Etanol comum |
3,99 |
|
Diesel |
4,02 |
Fonte de pesquisa: administração do posto de combustível.
Resposta: A. Fonte de pesquisa; B. Legenda; C. Ano da pesquisa; D. Fonte de pesquisa; E. Data.
Página 144
13. Suponha que uma escola de idiomas tenha divulgado o seguinte gráfico em seu site.
Quantidade de turistas brasileiros e turistas que falam apenas inglês ou espanhol que visitaram a cidade nos anos de 2021 a 2023
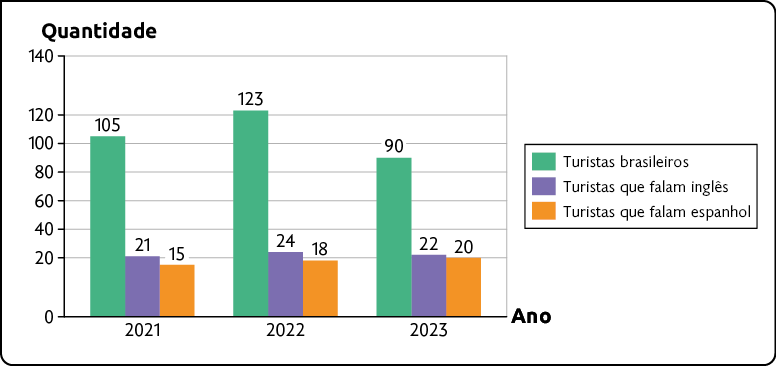
Fonte de pesquisa: informações do site da escola de línguas estrangeiras da cidade.
a) Esse gráfico foi manipulado. Qual alteração foi realizada para manipular a opinião do leitor?
Resposta: A escala do eixo vertical não está em proporção.
b) Em sua opinião, qual foi a intenção da escola de idiomas ao publicar esse gráfico em seu site?
Resposta pessoal. Espera-se que os estudantes respondam que o gráfico foi manipulado para parecer que a cidade recebe uma quantidade de turistas que falam inglês ou espanhol próxima à quantidade de turistas brasileiros.
14. O proprietário da loja Precinho Bom divulgou a tabela a seguir sobre a preferência de algumas pessoas entre a sua loja e de seus concorrentes.
|
Loja |
Percentual das pessoas que preferem |
||
|---|---|---|---|
|
comprar celulares |
comprar eletrodomésticos |
comprar móveis |
|
|
Precinho Bom |
65 |
48 |
53 |
|
Concorrente A |
15 |
18 |
22 |
|
Concorrente B |
20 |
34 |
25 |
a) O proprietário da loja não divulgou a fonte de pesquisa da tabela. Converse com seus colegas e escreva em seu caderno se a falta desse elemento pode ser uma maneira de manipular a tabela.
Resposta pessoal. Espera-se que os estudantes cheguem à conclusão de que a fonte de pesquisa é importante na análise dos resultados expostos na tabela.
b) Em sua opinião, por que o proprietário da loja não divulgou a fonte de pesquisa?
Resposta pessoal.
c) O proprietário da loja coletou as informações expostas na tabela em um grupo dos seus familiares em um aplicativo de mensagens instantâneas. Sabendo disso, a interpretação de quem lê a tabela pode mudar? Converse com seus colegas e seu professor.
Resposta pessoal. Espera-se que os estudantes concluam que as respostas foram dadas por pessoas que podem ser parciais e, nesse caso, seria necessário coletar informações com um grupo mais diverso.
Página 145
Pesquisas amostrais
Ao realizar uma pesquisa, nem sempre é possível entrevistar todas as pessoas que se pretende estudar (população). Nesses casos, realiza-se uma pesquisa amostral, na qual recorre-se a uma amostra✚.
- Amostra:
- parte representativa da população em dimensões reduzidas, porém, com as mesmas características.↰
Atenção!
As pesquisas em que todos os elementos da população são entrevistados são chamadas de pesquisas censitárias.


Acompanhe o exemplo a seguir.
A direção de uma empresa realizou uma pesquisa com 15 de seus 100 funcionários, a fim de determinar se eles gostavam do cardápio proposto no almoço.
Nessa pesquisa, os 15 funcionários entrevistados foram escolhidos aleatoriamente. Esse método utilizado é conhecido como amostragem probabilística (aleatória). Nele, todos os elementos da população têm a mesma probabilidade de serem incluídos na amostra.
Porém, outros métodos de amostragem poderiam ser utilizados nessa pesquisa, como a amostragem sistemática. Nesse tipo, a população deve ser ordenada para que os elementos sejam identificados pela posição, e a escolha dos elementos é feita de acordo com um critério ou fator de repetição. Para determinarmos as posições dos elementos da amostra, podemos realizar os passos apresentados a seguir.
1º. Calculamos a razão entre o número de elementos da população (N) e o número de elementos da amostra (n). Nessa etapa, consideramos apenas a parte inteira (R) da razão.
2º. Sorteamos um número (S) de 1 a R.
3º. A amostra será dada pelos elementos que ocupam as seguintes posições:
Página 146
Imagine que a direção da empresa apresentada anteriormente tenha utilizado a amostragem sistemática. Nesse caso, temos:
Logo, se o número sorteado for 1, a amostra será composta pelos elementos de posição 1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79 e 85.

Atividades
Faça as atividades no caderno.
15. Classifique as pesquisas apresentadas em amostral ou censitária.
a) A fim de avaliar o atendimento, um banco entrevistou 1.500 de seus 10.000 correntistas.
b) Uma escola pediu a todos os estudantes que respondessem a uma pesquisa sobre o material didático.
c) Uma empresa entrevistou 60 de seus 180 funcionários para conhecer as necessidades de melhorias no refeitório.
Resposta: a) Pesquisa amostral; b) Pesquisa censitária; c) Pesquisa amostral.
16. Na empresa em que Amanda trabalha, são produzidos diariamente 1.000 lotes com 150 peças cada. Com o objetivo de garantir a qualidade da produção, 500 peças são analisadas todos os dias. Em sua opinião, qual método de amostragem a empresa deveria utilizar na formação da amostra: amostragem probabilística ou amostragem sistemática?
Resposta pessoal.
17. Uma revista realizou uma pesquisa com seus assinantes para verificar qual é o gênero de publicação preferido por eles. Para isso, sortearam e entrevistaram 2.350 pessoas entre seus 18.345 assinantes. Qual método de amostragem essa revista utilizou nessa pesquisa?
Resposta: Amostragem probabilística.
18. Realize
uma pesquisa amostral envolvendo um tema da realidade social. Para isso, junte-se a
dois colegas e realize as seguintes etapas:
escolha do tema; planejamento; coleta de informações; organização; análise;
interpretação; divulgação.
Resposta pessoal.
Atenção!
Para divulgação, escreva um relatório que contenha gráficos e tabelas. Na construção deles, utilize planilhas eletrônicas. Além disso, destaque as medidas de tendência central e a amplitude do conjunto de informações coletadas.
Página 147
Probabilidade
Ao lançar um dado, é possível prever o resultado? A resposta é não, pois o lançamento de um dado é um exemplo de experimento aleatório.
Experimentos aleatórios são aqueles que, mesmo repetidos várias vezes sob as mesmas condições produzem resultados imprevisíveis.
Neste tópico, calcularemos a probabilidade de ocorrência de eventos independentes e de eventos dependentes. Antes disso, lembre-se de que a probabilidade de um evento X ocorrer é dada por:
Atenção!
Denominamos evento qualquer subconjunto do espaço amostral.
Eventos independentes
Dois eventos, A e B, de um mesmo espaço amostral são independentes quando a ocorrência de um não influencia a ocorrência do outro. Nesse caso, a probabilidade de eles ocorrerem simultaneamente é dada por:
Acompanhe a situação a seguir.
De uma caixa com 3 fichas iguais, identificadas com as letras O, Z e I, serão retiradas aleatoriamente 2 fichas com reposição, ou seja, após cada ficha ser sorteada, ela é devolvida à caixa. Qual é a probabilidade de obter uma vogal no primeiro sorteio e uma consoante no segundo?
Para solucionar esse problema, consideramos o evento A, "retirar a primeira ficha e a letra ser uma vogal"; o evento B, "retirar a segunda ficha e a letra ser uma consoante"; e, por fim, calculamos .
Ao retirar a primeira ficha, temos 2 vogais de um total de 3 letras. Nesse caso, a probabilidade de obter uma vogal na primeira retirada é:
Ao retirar a segunda ficha, temos 1 consoante de um total de 3 letras (lembre-se: a ficha obtida na primeira retirada foi devolvida). Nesse caso, a probabilidade de obter uma consoante na segunda retirada é:
Página 148
Logo:
Portanto, a probabilidade de obter uma vogal na primeira retirada e uma consoante na segunda é .
Eventos dependentes
Dois eventos, X e Y, de um mesmo espaço amostral são dependentes quando não são independentes. Nesse caso, a probabilidade de que eles ocorram simultaneamente é dada por:
, em que indica a probabilidade de Y, dado que X ocorreu.
Acompanhe a situação a seguir.
De uma caixa com 12 bolinhas iguais, identificadas com os números de 1 a 12, serão retiradas aleatoriamente 2 bolinhas sem reposição, ou seja, após cada bolinha ser sorteada, ela não é devolvida na caixa. Qual é a probabilidade de obter um número par no primeiro sorteio e um número ímpar no segundo?
Para solucionar esse problema, consideramos o evento C, "retirar a primeira bolinha e o número ser par"; o evento V, "retirar a segunda bolinha e o número ser ímpar"; e, por fim, calculamos .
Ao retirar a primeira bolinha, temos 6 números pares de um total de 12. Nesse caso, a probabilidade de obter um número par na primeira retirada é:
Ao retirar a segunda bolinha, temos 6 números ímpares de um total de 11 (lembre-se: a bolinha obtida na primeira retirada não foi devolvida). Nesse caso, a probabilidade de obter um número ímpar na segunda retirada é:
Desse modo, segue que:
Portanto, a probabilidade de obter um número par na primeira retirada e um número ímpar na segunda é .
Atenção!
Note que a ocorrência do evento C altera a quantidade de bolinhas na caixa e, consequentemente, influencia a ocorrência do evento V. Logo, os eventos C e V são dependentes.
Página 149
Atividades
Faça as atividades no caderno.
19. Bruno vai lançar uma moeda duas vezes.
a) Qual é a probabilidade de obter cara no primeiro lançamento?
b) No segundo lançamento, qual será a probabilidade de obter coroa?
c) Qual é a probabilidade de obter cara no primeiro lançamento e coroa no segundo?
Respostas: a) ; b) ; c) .
20. Em uma urna, foram colocadas as seguintes letras.
-
A
-
G
-
O
-
L
-
O
-
V
Ao retirar 3 letras aleatoriamente da urna, sem reposição, qual é a probabilidade de formar a palavra gol sorteando as letras nessa ordem?
Resposta: .
21. A roleta representada a seguir está dividida em partes iguais.
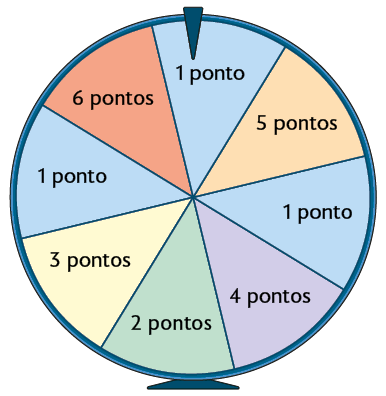
Essa roleta é utilizada em um jogo. Em dado momento, um jogador vai girá-la duas vezes. No primeiro giro, ele precisa obter 5 ou 6 pontos e, no segundo, 1 ou 2 pontos. Qual é a probabilidade de ele sortear os números de que precisa?
Resposta: .
22. Em uma prova, cada questão tem 5 alternativas, em que apenas 1 é correta. Márcia fez essa prova e, quando faltavam 3 questões, ela percebeu que não daria tempo de resolvê-las e que teria de responder-lhes aleatoriamente, sem ler os enunciados. Qual é a probabilidade de ela responder corretamente a essas questões da prova?
Resposta: .
23. Os naipes de um baralho são paus, copas, espadas e ouro. Em um jogo de baralho com 52 cartas, há 13 cartas de cada naipe. Amanda vai sortear 4 cartas desse baralho com reposição. Qual é a probabilidade dela sortear 4 cartas do mesmo naipe?
Resposta: .
24. A escola de Cauê está promovendo um jogo de bingo para arrecadar dinheiro para o laboratório de informática. Em cada rodada são sorteadas bolas numeradas de 1 a 75, sem reposição. Cauê comprou a cartela demonstrada a seguir.

Determine a probabilidade dos 4 primeiros números sorteados estarem na cartela de Cauê.
Resposta: .
Página 150
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
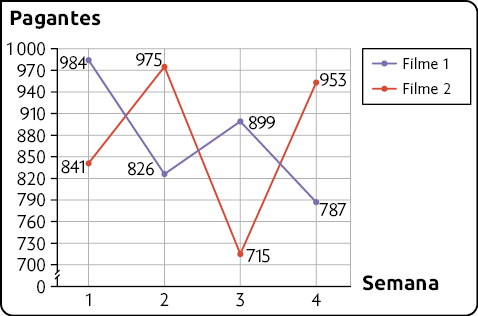
1. O dono de um cinema verificou e registrou a quantidade de pagantes durante 4 semanas em dois filmes. Os resultados estão expostos no gráfico a seguir.
Quantidade de pagantes em 4 semanas em dois filmes – julho de 2023
Fonte de pesquisa: administração do cinema.
a) Em qual semana houve mais pagantes? Quantos foram?
b) Qual filme teve mais pagantes?
Respostas: a) Semana 1; pagantes; b) Filme 1.
2. A seguir está apresentada a quantidade de irmãos dos estudantes de uma turma do 9º ano.
- 2
- 1
- 1
- 0
- 3
- 5
- 1
- 1
- 3
- 3
- 2
- 0
- 0
- 2
- 4
- 1
- 2
- 3
- 1
- 4
- 3
- 2
- 0
- 5
- 2
- 2
- 1
- 1
- 3
- 1
- 2
- 3
- 2
- 2
- 2
a) Qual é a quantidade de irmãos com maior frequência nessa turma?
b) Quantos estudantes têm menos de 4 irmãos?
c) Calcule a média, a moda e a mediana do conjunto de valores apresentado.
Respostas: a) 2; b) 31; c) Moda: 2; Média: 2; Mediana: 2.
3. A seguir, estão registradas as notas de Natália e sua irmã Bia nas 8 provas anuais de Matemática.
Notas de Natália
7,8
8,4
8,6
8,4
7,9
9,5
8,1
8,0
Notas de Bia
6,2
7,9
7,4
10,0
8,6
9,2
7,6
7,0
a) Qual é a média, a moda e a mediana das notas de Natália? E de sua irmã?
b) Qual das irmãs apresentou menor dispersão em suas notas de Matemática?
Respostas: a) Natália: média: aproximadamente 8,34; moda: 8,4; e mediana: 8,25. Bia: média: aproximadamente 7,99; não tem moda; mediana: 7,75; b) Natália.
4. Eduardo
colocou bolinhas brancas, vermelhas e pretas em uma urna, totalizando 25. Ele vai fazer três sorteios sem reposição.
Responda aos itens a e b,
considerando que:
- a probabilidade de tirar uma bolinha branca no 1º sorteio é .
- a probabilidade de retirar uma bolinha preta no 2º sorteio, sabendo que no 1º foi retirada uma bolinha branca, é .
a) Qual é a probabilidade de retirar uma bolinha vermelha no 3º sorteio, sabendo que no 1º e no 2º foram retiradas uma bolinha branca e uma preta, respectivamente?
b) Ao realizar esses sorteios, qual é a probabilidade de Eduardo obter três bolinhas pretas?
Respostas: a) ; b) .