Página 229
UNIDADE
11
Grandezas e medidas

Agora vamos estudar...
- medidas de comprimento;
- medidas em informática;
- medidas de volume;
- relação entre volume e capacidade.
Página 230
Medidas de comprimento
Medindo grandes comprimentos
Neste tópico, estudaremos algumas das unidades de medida de comprimento utilizadas para expressar medidas muito grandes, como a medida da distância média entre o Sol e alguns planetas do nosso Sistema Solar.
Questão 1. Você sabe quais são os planetas do nosso Sistema Solar? Escreva o nome de cada um deles em seu caderno.
Resposta: Espera-se que os estudantes conheçam os planetas do nosso Sistema Solar; Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno.
A seguir, é apresentada a medida da distância média aproximada entre alguns planetas e o Sol.
Representação com elementos não proporcionais entre si. Cores-fantasia.




Fonte de pesquisa: PLANETÁRIO UFSC. O Sistema Solar. Disponível em: https://oeds.link/rWdxPJ. Acesso em: 19 jul. 2022.
Essas medidas também podem ser expressas em notação científica. Acompanhe dois exemplos.
- Terra:
- Marte:
Atenção!
Lembre-se de que os números escritos em notação científica devem ter a forma . Sendo:
• a: um número maior ou igual a 1 e menor do que 10.
• n: um número inteiro.
Questão 2. Usando notação científica, escreva no caderno as medidas das distâncias médias aproximadas entre: Mercúrio e o Sol; Saturno e o Sol.
Resposta: Mercúrio: ; Saturno: .
Questão 3. Realize uma pesquisa e registre no caderno a medida, em quilômetros, da distância média aproximada entre o Sol e Vênus, Júpiter, Urano e Netuno.
Resposta: Vênus: ; Júpiter: ; Urano: ; Netuno: .
Página 231
Para medir grandes distâncias no Sistema Solar, também é usada pelos cientistas a chamada unidade astronômica, indicada por , que é a medida da distância média aproximada entre a Terra e o Sol, ou seja:
Acompanhe os procedimentos utilizados pelo professor Saulo para converter a medida aproximada da distância média entre Saturno e o Sol, expressa em quilômetros, em unidades astronômicas.

1.
2.
3.
Portanto, a medida da distância média aproximada entre Saturno e o Sol é .
Questão 4. Em seu caderno, escreva em unidade astronômica a medida da distância média aproximada, com duas casas decimais, entre Mercúrio e o Sol.
Resposta: .
Página 232
Outra unidade usada para medir a distância entre o Sol e as estrelas ou entre o Sol e as galáxias e a Terra é o ano-luz, indicada por , que é a medida da distância percorrida pela luz, no vácuo, em um ano, ou seja:
Analise o quadro a seguir, o qual apresenta a medida da distância aproximada entre a Terra e algumas estrelas em anos-luz.
|
Estrela |
Proxima Centauri |
Alpha Centauri |
|---|---|---|
|
Medida da distância da Terra (em AL) |
4,25 |
4,35 |
Fonte de pesquisa: NASA. Imagine the Universe. Disponível em: https://oeds.link/A5hs5S. Acesso em: 19 jul. 2022.
Atenção!
Com exceção do Sol, a estrela mais próxima da Terra visível a olho nu é a Proxima Centauri.
Agora, vamos escrever a medida (medida da distância aproximada entre a Terra e a Proxima Centauri) em quilômetros. Para isso, fazemos:
Questão 5. Em seu caderno, escreva, em quilômetros, a medida da distância aproximada entre a Terra e a Alpha Centauri.
Resposta: Aproximadamente .
Atividades
Faça as atividades no caderno.
1. Escreva no caderno as medidas a seguir em notação científica.
a) Medida aproximada da velocidade da luz: .
b) Medida aproximada da distância média do planeta-anão Éris ao Sol: .
c) Medida aproximada do diâmetro equatorial do planeta Júpiter: .
d) Medida aproximada do diâmetro equatorial do Sol: .
Respostas: a) ; b) ; c) ; d) .
2. Copie as sentenças a seguir no caderno substituindo cada pelo número adequado.
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
Página 233
3. A galáxia do Bode, ou M81, recebeu esse nome em referência ao astrônomo Johann Elert Bode, por tê-la descoberto em 1774. Assim como a Via Láctea, essa é uma galáxia espiral, pois sua estrutura tem o formato da curva espiral. Seu diâmetro mede aproximadamente 36.000 anos-luz e a medida da sua distância até a Terra é cerca de 12 milhões de anos-luz.
a) Qual é a medida aproximada, em quilômetros, do diâmetro da galáxia do Bode? E em unidades astronômicas? Escreva essas medidas em notação científica.
b) Qual é a medida aproximada, em unidades astronômicas, da distância entre a galáxia do Bode e a Terra? Escreva essa medida em notação científica.
Respostas: a) ; ; b) .
4. Plutão compõe o grupo dos planetas anões, que inclui Ceres, Haumea, Makemake e Éris. Eles são assim definidos por não serem os astros dominantes em suas órbitas. Plutão já foi considerado um planeta, mas em 2006 foi rebaixado a essa categoria, pois em sua órbita há outros objetos de tamanhos semelhantes ao dele. Sabendo que sua distância média até o Sol mede aproximadamente , e seu diâmetro equatorial mede aproximadamente , faça o que se pede.
a) Calcule no caderno a medida da distância aproximada, em quilômetros, de Plutão até o Sol.
b) Escreva a medida do diâmetro equatorial de Plutão em metros.
c) Escreva no caderno as medidas obtidas nos itens a e b em notação científica.
Respostas: a) ; b) ; c) ; .
5. Eclipse lunar é um fenômeno que bloqueia, total ou parcialmente, a chegada da luz solar até a superfície lunar. Ele acontece quando a Terra fica entre o Sol e a Lua, estando os três alinhados. Analisando a imagem a seguir, elabore um problema envolvendo notação científica, unidades astronômicas e anos-luz. Depois, dê para um colega responder. Por fim, verifique se ele respondeu corretamente.
Representação com elementos não proporcionais entre si. Cores-fantasia.
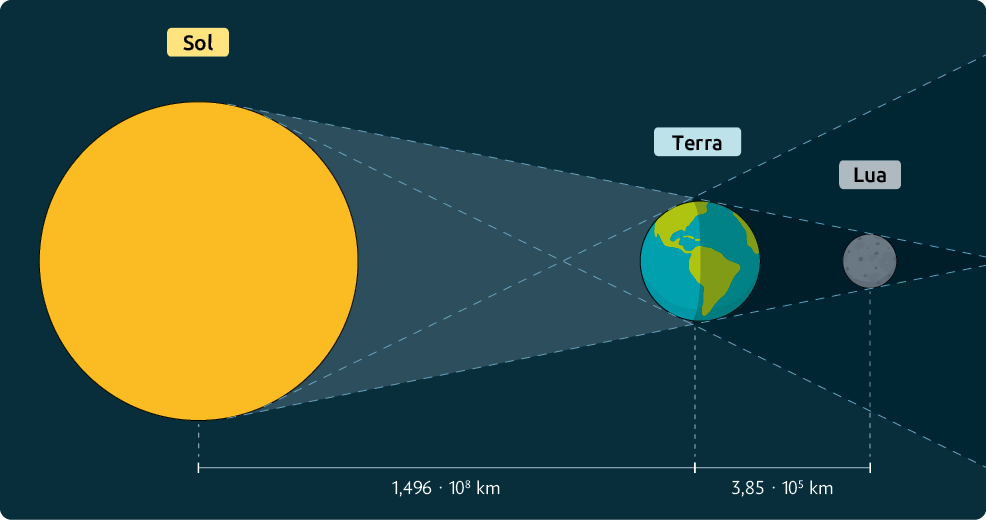
Resposta pessoal.
Página 234
Medindo pequenos comprimentos
No tópico anterior, estudamos algumas situações envolvendo medidas de comprimento muito grandes. Agora, vamos estudar situações envolvendo medidas de comprimento muito pequenas, como a medida do diâmetro de células, vírus, bactérias, protozoários, entre outros seres microscópicos, que são visíveis somente com a utilização de equipamentos que ampliem sua imagem, como os microscópios.
A função dos microscópios atuais não é só ampliar a imagem, mas também aumentar o poder de resolução do olho humano, permitindo observar estruturas muito menores do que as células.
Analise as seguintes informações.
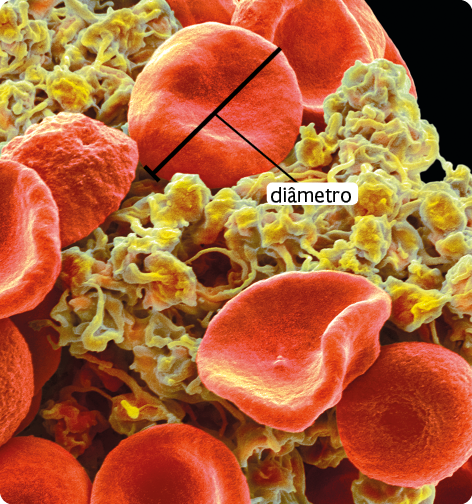
Representação com elementos não proporcionais entre si. Cores-fantasia.
O diâmetro de uma célula eritrócito mede .
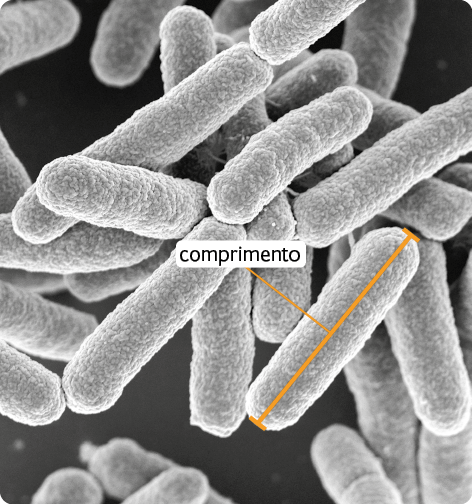
O comprimento de uma bactéria Escherichia coli mede .
Essas medidas também podem ser expressas usando a notação científica. Acompanhe o exemplo a seguir.
Célula eritrócito: .
Questão 6. Usando notação científica, escreva no caderno a medida do comprimento da bactéria Escherichia coli.
Resposta: .
Página 235
Também podemos expressar essas medidas utilizando uma unidade de medida chamada micrômetro (), que é um submúltiplo do metro. Na indicação , o símbolo , que lemos "mi", é uma letra minúscula do alfabeto grego.
Acompanhe os procedimentos utilizados pela professora Jussara para converter a medida do diâmetro da célula eritrócito, expressa em metros, em micrômetros.

1.
2.
3.
Portanto, o diâmetro da célula eritrócito mede .
Questão 7. Em seu caderno, escreva, em micrômetros, a medida do comprimento da bactéria Escherichia coli.
Resposta: .
Página 236
Atividades
Faça as atividades no caderno.
6. Escreva no caderno as medidas a seguir em notação científica.
a) .
b) .
c) .
d) .
Respostas: a) ; b) ; c) ; d) .
7. Copie as sentenças no caderno substituindo cada pelo número adequado.
a) .
b) .
c) .
d) .
e) .
f) .
Respostas: a) ; b) ; c) ou ; d) ; e) ; f) .
8. Microscópios permitem ampliar a imagem de objetos muito pequenos, como o diâmetro de uma célula, que na maioria dos casos é impossível de ser vista a olho nu. Em geral, existem basicamente dois tipos de microscópios: o óptico e o eletrônico. O primeiro é capaz de ampliar a imagem de um objeto em até vezes, enquanto o segundo, em até vezes.
Entre as células que não podem ser vistas a olho nu, encontram-se os basófilos, os quais estão relacionados à defesa do organismo. O diâmetro dessas células mede entre e . Já as plaquetas são fragmentos de certas células, cujo diâmetro mede entre e . Considere que o diâmetro de uma célula basófilo mede e o de uma plaqueta mede .
a) Qual é a medida, em metros, do diâmetro da imagem dessa célula quando observada com um telescópio óptico, se a ampliação for a máxima possível?
b) Qual é a medida do diâmetro, em micrômetros, dessa plaqueta, quando observada com um telescópio eletrônico, se a ampliação for a máxima possível?
Respostas: a) ; b) .
9. A bactéria Helicobacter pylori, conhecida como H. pylori, é a principal causadora da gastrite, doença que provoca inflamação no revestimento do estômago. Essa bactéria tem forma curva ou espiralar, cujo diâmetro mede de a e cujo comprimento mede de a . Ela tem ainda de 4 a 6 flagelos, cujo comprimento de cada um mede aproximadamente , os quais facilitam sua mobilidade e penetração na mucosa do estômago, assegurando sua sobrevivência no corpo humano.
Cores-fantasia.
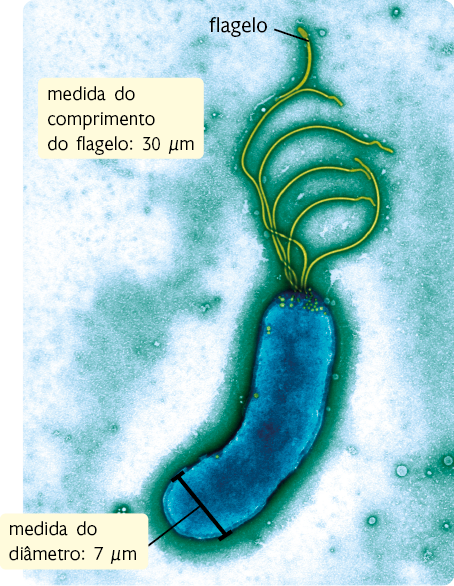
Com base nessas informações, elabore um problema e entregue-o para um colega resolver. Depois, verifique se ele respondeu corretamente.
Resposta pessoal.
Página 237
Medidas de informática
Armazenamento de dados
Os primeiros computadores surgiram na década de 1940 e eram muito grandes.
Com a evolução da tecnologia, eles foram ficando cada vez menores e mais eficientes, até chegar aos que conhecemos atualmente.

Ao utilizarmos um computador, é importante saber, por exemplo, a medida de sua capacidade de armazenamento de dados, que é uma tecnologia que possibilita guardar arquivos e informações com o auxílio de um dispositivo, como um HD✚ de computador, um cartão de memória e o pen drive. Para medir essa capacidade, são utilizadas as unidades de medida de informática.
- HD:
- iniciais de hard disk, termo em inglês para disco rígido. Consiste em um equipamento de computador que armazena diferentes arquivos e programas.↰
Entre essas unidades, estão os bites e os baites (). Um bite é a menor unidade de informação que um computador consegue entender. Ele pode ser um 0 (zero) ou um 1. Esse sistema de numeração com dois algarismos é chamado sistema binário.
Para um computador armazenar os dados em sistema binário, os bites são agrupados em conjuntos de 8 bites, formando assim 1 baite.
Página 238
Assim, 1 baite é um conjunto de 8 bites que forma um único caractere✚ guardado na memória do computador. A letra a, por exemplo, ocupa o espaço de 1 baite no computador. Quando o computador nos mostra a letra a como a conhecemos, em sua memória essa letra ficará arquivada como um conjunto de 8 bites (no caso, 01000001 bites).
- caractere:
- qualquer letra, algarismo, sinal gráfico ou matemático, espaço em branco etc. que pode ser digitado ou introduzido em um computador por outro dispositivo.↰
Outros exemplos de unidades de medida de informática são o quilobaite, o megabaite, o gigabaite e o terabaite.
|
Unidade de medida |
Quantidade de caracteres (em baite) |
Medida do espaço ocupado na memória do computador |
|---|---|---|
|
1 baite () |
1 |
8 bites |
|
1 quilobaite () |
1.024 |
|
|
1 megabaite () |
||
|
1 gigabaite () |
||
|
1 terabaite () |

Ao analisar o quadro, percebemos que 1 quilobaite equivale a 1.024 baites e, portanto, tem capacidade de armazenar 1.024 caracteres. Analogamente, 1 megabaite equivale a 1.024 quilobaites, que equivalem a 1.048.576 baites, e assim por diante.
Podemos fazer conversões entre essas unidades de medida utilizando o seguinte esquema.
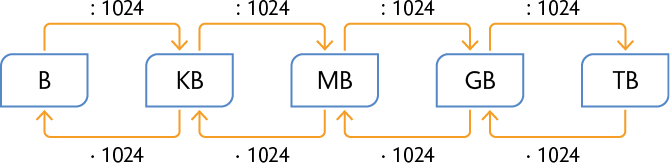
Questão 8. Em seu caderno, escreva um algoritmo que possibilite converter megabaite em quilobaite.
Resposta na seção Resoluções.
Página 239
Instrumentos e softwares
Convertendo medidas em megabaite para medidas em baite, quilobaite, gigabaite e terabaite no Calc
Com uma calculadora comum ou com o aplicativo calculadora do smartphone, podemos realizar conversões entre unidades de medida de informática. Porém, essas conversões também podem ser realizadas utilizando a planilha eletrônica Calc. Nesta seção, vamos escrever fórmulas que permitam converter medidas de megabaite em baite, quilobaite, gigabaite e terabaite. Para isso, siga as orientações do professor e os passos apresentados.
1º. Nas células A1, B1, C1, D1 e E1, escreva "Medida em ", "Medida em ", "Medida em ", "Medida em " e "Medida em ", respectivamente.
2º. Na célula:
- A2 digite , para converter a medida expressa em megabaites em baites;
- B2 digite , para converter a medida expressa em megabaites em quilobaites;
- D2 digite , para converter a medida expressa em megabaites em gigabaites;
- E2 digite , para converter a medida expressa em megabaites em terabaites.

Atenção!
No Calc, os símbolos , e indicam, respectivamente, multiplicação, "elevado a" e divisão.
Ao digitarmos em C2 a medida em megabaites, será exibida nas células A2, B2, D2 e E2 essa medida em baites, quilobaites, gigabaites e terabaites, respectivamente.
Para exemplificar, usaremos a medida . Ao digitarmos 10.240 na célula C2, obtemos:

Portanto .
Página 240
Capacidade de processamento de dados
Uma das características que diferencia os vários modelos de produtos tecnológicos presentes no dia a dia é sua Central Processing Unit (CPU – "Unidade Central de Processamento", em português), também conhecida como processador. Quanto maior a capacidade de processamento da CPU, mais rapidamente as instruções serão executadas.

A capacidade de processamento da CPU é geralmente medida em mega-hertz () ou em giga-hertz (), que são múltiplos do hertz (). Essas unidades indicam a quantidade de ciclos por segundo que o componente eletrônico consegue processar.
Analise, no quadro a seguir, a quantidade de ciclos correspondente a cada uma dessas unidades de medida.
|
Medida |
Ciclos por segundo |
|---|---|
|
1 hertz () |
1 |
|
1 mega-hertz () |
1.000.000 |
|
1 giga-hertz () |
1.000.000.000 |
Atenção!
Na maioria das CPUs da atualidade, a frequência é medida em giga-hertz.
De acordo com as correspondências apresentadas no quadro, podemos escrever as seguintes equivalências.
Página 241
Atividades
Faça as atividades no caderno.
10. Copie as sentenças a seguir no caderno substituindo cada pelo número adequado.
a) .
b) .
c) .
d) .
Respostas: a) ; b) ; c) ; d) .
11. Calcule em seu caderno a quantidade de ciclos por segundo que uma CPU consegue processar, sabendo que ela tem uma capacidade de:
a) .
b) .
c) .
d) .
Respostas: a) 25; b) 1.500.000; c) 250.000.000; d) 75.
12. Leia as informações referentes ao computador representado e responda às questões a seguir.
de memória RAM ✚
HD de

- RAM:
- iniciais de random access memory, termo em inglês para memória de acesso aleatório. É uma memória temporária que permite a leitura e a gravação das informações quando requeridas. ↰
a) Qual é a medida de capacidade de processamento desse desktop? Expresse essa medida em hertz.
b) Qual é a medida da capacidade de armazenamento de dados do HD?
c) Qual é a medida da capacidade de armazenamento da memória RAM?
Respostas: a) ; ; b) ; c) .
13. Em cada item, indique a unidade de medida mais adequada (, , ou ) para representar a medida:
a) da capacidade de armazenamento do HD de um computador de mesa.
b) do arquivo de uma foto.
c) da memória interna de um tablet.
d) do arquivo de um vídeo curto.
Respostas: a) ; b) ; c) ; d) .
14. Cada informação a seguir corresponde à configuração básica de um computador.
A.CPU de – de memória RAM – HD de .
B.CPU de – Monitor LED – de memória RAM – HD de .
C.CPU de – Monitor LED – de memória RAM – HD de .
a) Qual desses computadores tem maior medida de capacidade de armazenamento de dados no HD? E na memória RAM?
Respostas: C; B.
b) O HD do computador A tem quantos gigabaites de medida de capacidade a menos do que o do computador B?
Resposta: .
c) O computador B tem quantos gigabaites de memória RAM a mais do que o computador C?
Resposta: .
d) Se você fosse adquirir um computador, quais seriam as características mais importantes, na sua opinião, no momento da compra? Por quê?
Resposta pessoal.
Página 242
15. O armazenamento em nuvem é uma tecnologia que permite armazenar e acessar dados em servidores, por meio da internet. Há várias empresas que oferecem esse serviço, com diferentes medidas de capacidade de armazenamento.
Marina pretende aderir a um plano de armazenamento em nuvem para sua empresa. Para isso, ela realizou uma pesquisa nas principais empresas e obteve os seguintes pacotes de serviços.
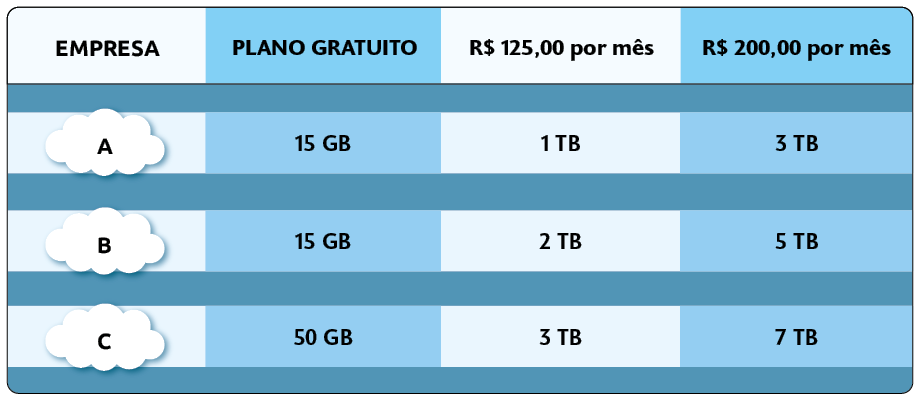
a) Considerando que, na empresa de Marina, há 50 funcionários, que geram de dados mensalmente cada um, e que esses dados devem ficar armazenados durante 1 ano, qual dos planos é o mais vantajoso para ela?
Resposta: Plano de da empresa B.
b) Você acha importante o desenvolvimento de tecnologias para armazenamento de dados? Justifique sua resposta.
Resposta pessoal.
c) Faça uma pesquisa sobre a importância das tecnologias de armazenamento e os benefícios do armazenamento em nuvem. Em seguida, converse com seus colegas e professor expondo as informações obtidas.
Atenção!
A pesquisa proposta no item c da atividade 15 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Resposta pessoal.
d) Após sua pesquisa, você mudou de ideia sobre a importância das tecnologias de armazenamento? Justifique sua resposta.
Resposta pessoal.
16. As câmeras fotográficas digitais têm um dispositivo eletrônico que armazena as fotos no cartão de memória. A câmera fotográfica digital de Márcia tem um cartão de memória com medida de capacidade igual a . Ela tirou algumas fotos que ocuparam da memória. Sabendo que cada foto tirada por ela tem, em média, , quantas fotos ela tirou? E quantas fotos como essas ela ainda pode tirar?
Resposta: 253 fotos; 387 fotos.
Página 243
17. Com
auxílio do Calc,
escreva:
a) em baites.
b) em gigabaites.
c) em gigabaites.
d) em quilobaites.
e) em baites.
f) em terabaites.
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
18. Os dados apresentados na forma de textos, imagens, sons e vídeos em um computador também podem ser armazenados em CDs, DVDs, cartões de memória etc. Embora os dois primeiros sejam tecnologias mais antigas, não deixaram de ser utilizados.
A seguir, estão apresentados alguns dispositivos físicos de armazenamento de dados.
Imagens não proporcionais entre si.

Medida da capacidade:

Medida da capacidade: .

Medida da capacidade: .

Medida da capacidade: .
a) Entre os dispositivos apresentados, qual tem a maior medida de capacidade de armazenamento de dados?
b) Quantos megabaites de informação é possível armazenar em 15 CDs? Esse valor é equivalente a quantos gigabaites?
c) Quantos CDs são necessários para armazenar a mesma quantidade de informações que é possível armazenar em um DVD?
d) É possível armazenar no máximo quantos megabaites no cartão de memória apresentado? E no DVD?
Respostas: a) HD portátil; b) ; aproximadamente ; c) 7 CDs; d) ; .
19. Giovana quer fazer o backup das informações que estão em seu computador para um sistema de armazenamento em nuvem, isto é, copiar seus arquivos com a finalidade de poder recuperá-los posteriormente, caso ocorra algum problema com o arquivo original. Sabendo que ela tem de dados e que no sistema de nuvem que ela vai utilizar não há arquivos, ou seja, ela terá toda a capacidade disponível, responda às questões.
a) O sistema de armazenamento que Giovana utiliza oferece grátis. Para realizar esse backup, ela precisará fazer um upgrade em seu plano? Justifique sua resposta.
b) Para que seu irmão também armazene arquivos na nuvem, Giovana fez um upgrade de seu plano. Agora, a operadora lhe oferece . Após realizar o backup de suas informações, quantos gigabaites sobrarão para o irmão de Giovana usar?
Respostas: a) Será necessário realizar um upgrade no plano, pois é maior do que ; b) Aproximadamente .
Página 244
Taxa de transferência de dados
A seguir é apresentado o cartaz de uma propaganda de certa operadora que oferece planos de internet.

Nesse cartaz, as informações "10 mega", "50 mega" e "75 mega" são maneiras de indicar a taxa de transferência de dados dos planos de internet. O plano "50 mega", por exemplo, indica que, em condições favoráveis, são transmitidos no máximo 50 megabites por segundo nessa conexão.
Atenção!
A expressão "50 megabites por segundo" também pode ser indicada por ou .

Ao contratar um plano de internet de , por exemplo, é incorreto imaginar que um arquivo de será baixado em apenas 1 segundo. Esse tipo de pensamento ocorre por ser mais comum o uso da unidade megabaite () no dia a dia.
Questão 9. O cartaz de propaganda
apresenta todas as informações
necessárias sobre o serviço? Em sua opinião,
qual é a importância de conhecer a taxa de transferência de dados ao se deparar
com o anúncio de uma propaganda semelhante à apresentada?
Resposta: Não. Espera-se que os estudantes percebam que a medida indicada no anúncio não corresponde a uma taxa de transferência de dados, assim como não contribui para distinguir megabites de megabaite.
Página 245
Afinal, quantos megabaites ou quilobaites podem ser transferidos, no máximo, em uma conexão de ?
Como 1 baite equivale a um conjunto de 8 bites, segue que 1 megabaite equivale a 8 megabites. Assim, para determinar quantos megabaites ou quilobaites podem ser transferidos por segundo, nessa conexão, fazemos:
Portanto, em uma conexão de , é possível transferir, no máximo, por segundo ( ou ) ou por segundo ( ou ).
Agora, vamos determinar qual é a medida do tempo mínimo necessário para fazer o download de um arquivo de em uma conexão de , por exemplo. Para isso, procedemos da seguinte maneira:
1º. Convertemos gigabaites em megabaites. Como , temos:
2º. Como equivale a , temos:
3º. Como , temos:
Portanto, são necessários, no mínimo, aproximadamente para transferir um arquivo de em uma conexão de .
Também podemos calcular quantos megabaites podem ser transferidos em nessa mesma conexão. Para isso, procedemos da seguinte maneira:
1º. Convertemos minutos em segundos. Como , temos:
2º. Como equivale a , temos:
Portanto, em , é possível transferir, no máximo, em uma conexão de .
Página 246
Além do megabite por segundo, existem outras unidades de medida de taxa de transferência de dados, e as mais usadas são quilobites por segundo ( ou ), gigabites por segundo ( ou ) e terabites por segundo ( ou ). Analise no quadro a seguir a equivalência entre algumas dessas unidades de medida.
|
Unidade de medida |
Taxa de transferência equivalente |
|---|---|
|
1.024 bites por segundo |
|
Podemos fazer conversões entre essas unidades de medida utilizando o seguinte esquema.
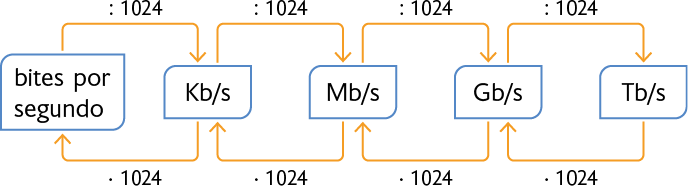
Acompanhe alguns exemplos.
Atividades
Faça as atividades no caderno.
20. Em um plano de internet de , o provedor promete uma taxa de upload de até 50% da taxa de transferência máxima. Nessas condições, faça os cálculos no caderno e determine:
a) a medida do tempo mínimo, em minutos, necessária para fazer o upload de um arquivo de .
b) o percentual máximo baixado de um arquivo de , 3 minutos após o início do download.
Respostas: a) Aproximadamente 41 minutos; b) aproximadamente 9,1%.
21. Para facilitar o acesso a seus arquivos, que juntos somam , Lucas fez o upload deles em um serviço de armazenamento em nuvem, a uma taxa de transferência de . Dias depois, ele precisou acessar uma parte desses arquivos, que tinha , e fez seu download a uma taxa de transferência medindo . Calcule no caderno as medidas do tempo, em horas, minutos e segundos, que Lucas levou para fazer esse upload e esse download.
Respostas: ; .
Página 247
22. O gráfico a seguir apresenta a taxa média diária de download fornecida pela rede móvel contratada por Juliana nos sete primeiros dias do mês de agosto de 2023.
Taxa média de download da rede móvel de Juliana nos sete primeiros dias do mês de agosto de 2023
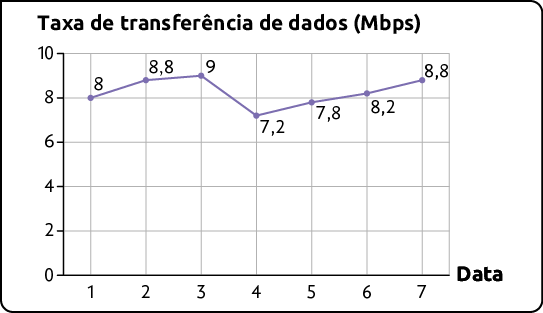
Fonte de pesquisa: registro do celular de Juliana.
a) No dia 2 desse mês, Juliana baixou um vídeo de e, no dia 4, ela baixou outro vídeo, de . Em qual desses dias foi necessária uma medida de tempo menor para concluir o download?
b) Sabendo que Juliana fez o download de um vídeo de no dia 3, qual foi, em minutos e segundos, a medida de tempo mínima necessária para concluí-lo?
Respostas: a) Dia 2; b) .
23. A tabela a seguir apresenta a taxa média de download e de upload disponibilizada por três empresas de telefonia móvel no primeiro semestre de 2023 na velocidade .
|
Empresa |
Taxa de transferência de dados |
|
|---|---|---|
|
Download () |
Upload () |
|
|
A |
13 |
2,34 |
|
B |
24 |
4,8 |
|
C |
14 |
3,5 |
Fonte de pesquisa: empresas A, B e C.
Qual das alternativas apresentadas a seguir é verdadeira?
a) Na empresa A, a taxa máxima de upload corresponde a 72% da taxa máxima de download.
b) A empresa B é a que apresenta a melhor taxa máxima de upload relativa à taxa máxima de download.
c) Na empresa C, a taxa máxima de upload é menor do que 25% da taxa máxima de upload.
d) A taxa máxima de upload da empresa B é igual a 20% da taxa máxima de download.
e) A taxa máxima de download na empresa C é igual a 350% da taxa máxima de download.
Resposta: Alternativa d.
Página 248
Medidas de volume
Você já deve ter estudado assuntos relacionados a volume e capacidade. Também deve ter aprendido a calcular a medida do volume do paralelepípedo reto retângulo e do cubo. Neste tópico, vamos retomar esses assuntos e aprofundar o estudo com o cálculo da medida do volume de prismas e de cilindros.

Acompanhe a seguir algumas informações sobre as Cataratas do Iguaçu, localizadas em Foz do Iguaçu (PR).

Essa vazão de por segundo significa que, a cada segundo, flui um volume de água cuja medida é .
Questão 10. Você acha que essa é uma grande
quantidade de água?
Resposta pessoal.
Atenção!
Para responder a essa pergunta, imagine uma caixa cúbica cuja medida do volume é . A medida do comprimento da aresta dessa caixa seria de aproximadamente .
Página 249
No caso relacionado às Cataratas do Iguaçu, constatamos uma situação envolvendo volume. Assim como podemos medir a massa de uma fruta, o comprimento de um fio e a área de um campo de futebol, também é possível medir o volume de um objeto tridimensional.
A unidade de medida de volume do Sistema Internacional (SI) é o metro cúbico ().
Um metro cúbico é igual à medida do volume de um cubo cujo comprimento das arestas mede .

Além do metro cúbico, as outras unidades de medida de volume mais utilizadas são o centímetro cúbico () e o decímetro cúbico ().
-
Um centímetro cúbico é igual à medida do volume de um cubo cujo comprimento das arestas mede .
-
Um decímetro cúbico é igual à medida do volume de um cubo cujo comprimento das arestas mede .
Analise as pilhas construídas por André, com cubos cujo comprimento das arestas mede .
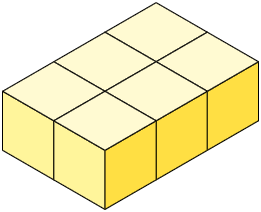
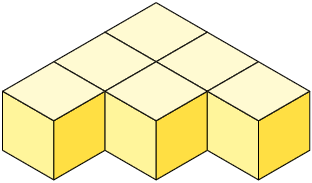
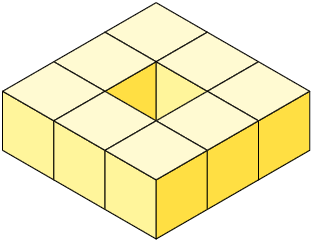
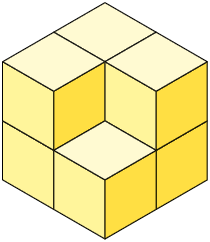
A pilha A, por exemplo, é formada por 6 cubos cujo comprimento das arestas mede , ou seja, por 6 cubos cujo volume mede . Desse modo, o volume dessa pilha mede .
Questão 11. Qual é a
medida do volume, em centímetros cúbicos, da:
a) pilha B.
b) pilha C.
c) pilha D.
Respostas: a) ; b) ; c) .
Página 250
Atividades
Faça as atividades no caderno.
Atenção!
Não há cubos escondidos atrás dos empilhamentos das atividades 24 e 25.
24. Determine a medida do volume de cada empilhamento a seguir, sabendo que eles são formados por cubos cuja medida do comprimento da aresta é .

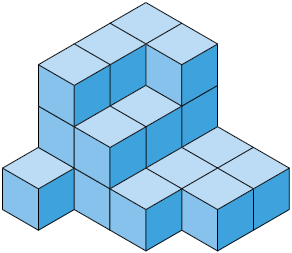
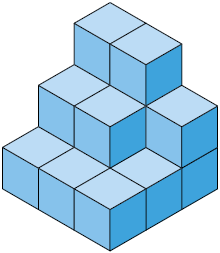
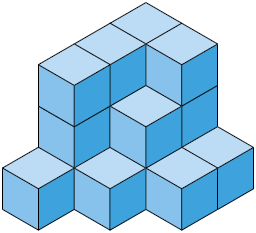
Respostas: A. ; B. ; C. ; D. .
25. As figuras A, B, C e D representam empilhamentos de cubos cujo comprimento de aresta mede .
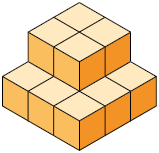
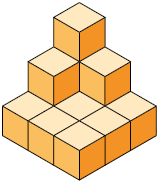
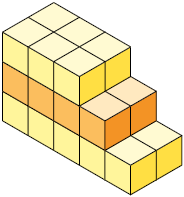
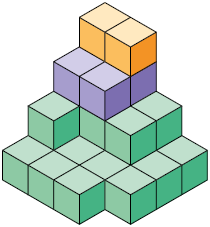
a) Qual desses empilhamentos tem o volume medindo ?
Resposta: C.
b) Quantos cubos iguais aos utilizados precisam ser retirados ou acrescentados nos outros empilhamentos para que eles fiquem com volume medindo ?
Resposta: A: acrescentar 11 cubos; B: acrescentar 11 cubos; D: retirar 4 cubos.
Página 251
Medida do volume do paralelepípedo reto retângulo e do cubo
Analise o paralelepípedo reto retângulo (imagem A) e sua decomposição em cubos (imagem B), em que o volume de cada um deles mede .
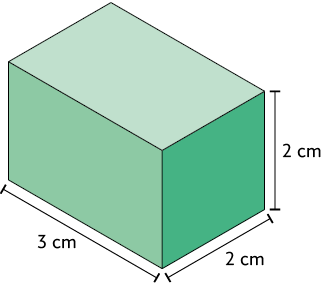
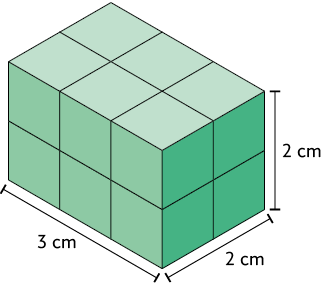
Podemos determinar a medida do volume desse paralelepípedo multiplicando a quantidade de cubos em cada camada pela quantidade de camadas.


Atenção!
Esse resultado equivale à medida do volume de 12 cubos, com cada um.
Portanto, a medida do volume desse paralelepípedo reto retângulo é .
Considere um paralelepípedo reto retângulo cujas dimensões medem c, e h. A medida do volume V desse paralelepípedo é igual à medida da área da base multiplicada pela medida da altura.
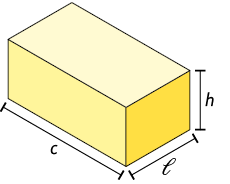
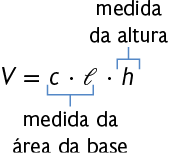
No caso apresentado, mostramos que a fórmula do volume do paralelepípedo reto retângulo é verdadeira quando a, b e c são números inteiros. Entretanto, essa fórmula também é válida quando as medidas não são números inteiros.
O cubo também é um paralelepípedo reto retângulo, cujas medidas das dimensões são iguais. Assim, a medida do volume V de um cubo em que o comprimento da aresta mede a é .
Página 252
Medida do volume de um prisma
Na imagem a seguir estão representadas duas folhas de papel de espessura de mesma medida, como se estivessem apoiadas sobre uma superfície plana. Uma delas tem o formato de um retângulo, e a outra, de um hexágono, ambas com a mesma medida de área.

Ao empilharmos certa quantidade das folhas de papel do formato retangular e empilharmos essa mesma quantidade de folhas de formato hexagonal, obteremos duas pilhas de papéis com formatos que lembram figuras geométricas espaciais, sendo um paralelepípedo reto retângulo e um prisma de base hexagonal. Logo, essas figuras geométricas espaciais têm a mesma medida de volume. Como ambas as folhas têm a mesma medida de espessura e a mesma medida de área, as pilhas têm a mesma medida de altura e bases com áreas de mesma medida.
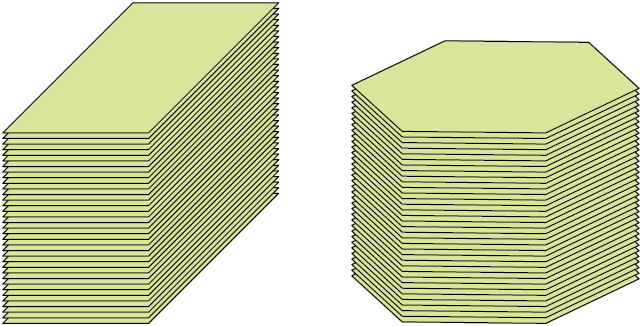
Como esses empilhamentos têm a mesma medida de volume, podemos obter a medida do volume do prisma de base hexagonal da mesma maneira que a medida do volume de um paralelepípedo reto retângulo, isto é, multiplicando a medida da área da base pela medida da altura.
Considere um prisma cuja medida da área da base é e da altura é h. A medida do volume V desse prisma é:
Essa relação é baseada no chamado princípio de Cavalieri, em homenagem ao matemático Bonaventura Cavalieri (1598-1647). O princípio de Cavalieri pode ser enunciado conforme apresentado na página seguinte.
Página 253
Princípio de Cavalieri: Sejam e figuras geométricas espaciais. Se qualquer plano horizontal secciona e segundo figuras planas com mesma medida de área, então a medida do volume de é igual à medida de volume de .
Questão 12. Junte-se
a um colega e realizem uma pesquisa sobre a
vida de Bonaventura Cavalieri. Depois, compartilhem
com a turma os resultados que vocês obtiveram.
Atenção!
A pesquisa proposta na questão 12 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Resposta nas orientações ao professor.
Agora, acompanhe como podemos calcular a medida do volume do prisma a seguir.
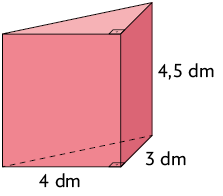
Inicialmente, calculamos a medida da área da base () do prisma, que é um triângulo retângulo.
Em seguida, calculamos a medida do volume.
Portanto, o volume desse prisma mede .
Atividades
Faça as atividades no caderno.
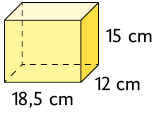
26. Calcule no caderno a medida do volume do prisma indicado em cada item.
a) Paralelepípedo reto retângulo.
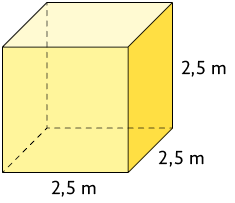
b) Cubo.
c) Prisma de base triangular.
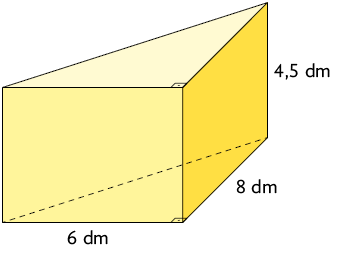
Respostas: a) ; b) ; c) .
27. Utilizando
uma calculadora, determine a medida do comprimento da aresta de um cubo cujo
volume mede:
a) .
b) .
c) .
d) .
Respostas: a) ; b) ; c) ; d) .
Página 254
28. O empilhamento a seguir é formado por cubos cujo comprimento da aresta mede .

Sabendo que não há cubos escondidos atrás do empilhamento, responda às questões.
a) Qual é a medida do volume desse empilhamento?
b) Quantos decímetros cúbicos faltam para que esse empilhamento tenha a mesma medida de volume de um paralelepípedo cujas dimensões medem , e ?
Respostas: a) 85 cubos ou ; b) .
29. Na
figura está representado um objeto feito de madeira que pode ser dividido em 6 cubos em que o volume
de cada um deles mede .

Qual é a quantidade máxima de objetos iguais a esse que podem ser colocados dentro de uma caixa como a representada a seguir?
Atenção!
Dois desses objeto podem se encaixar formando um paralelepípedo reto retângulo.
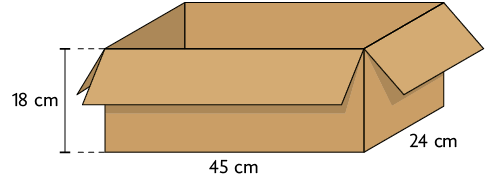
Resposta: 120 objetos.
30. Efetue os cálculos no caderno e determine a medida do volume do objeto a seguir.
Atenção!
Este objeto pode ser decomposto em paralelepípedos retos retângulos e cubos.
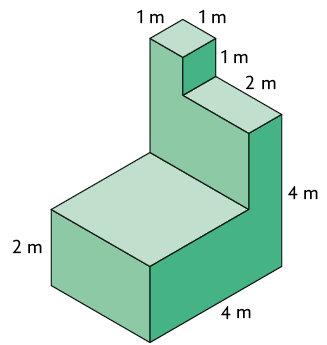
Resposta: .
31. De acordo com as medidas indicadas nas figuras geométricas espaciais a seguir, determine a medida do volume de cada uma delas.
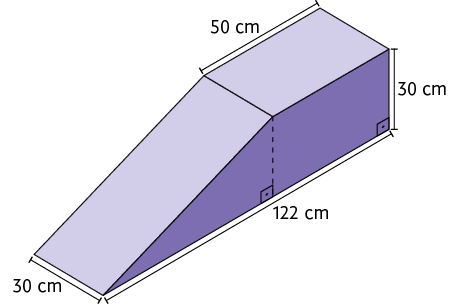
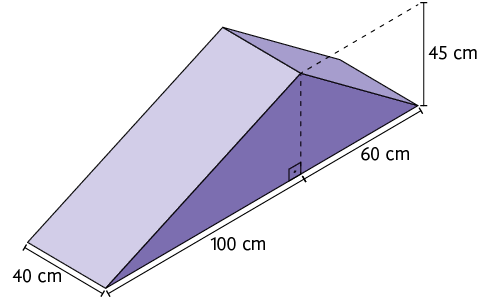
Respostas: A. ; B. .
Página 255
32. Os recipientes A e B estão com certa quantidade de água.


a) Desconsiderando a medida da espessura do vidro e sabendo que equivale a , quantos mililitros de água há em cada recipiente?
b) Para um experimento, despejou-se a água do recipiente A no recipiente B até enchê-lo. Qual é a medida do volume de água que sobrou no recipiente A? Qual é a medida da altura atingida pela água que sobrou no recipiente A?
Respostas: a) A: ; B: ; b) ; .
33. Elabore um problema envolvendo o recipiente representado a seguir.

Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Resposta pessoal.
34. Qual é a
medida do volume mínimo de concreto necessário para transformar a escada
representada em uma rampa, como mostra a figura?
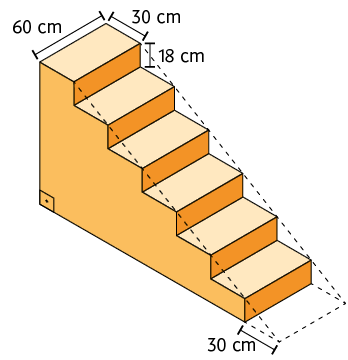
Resposta: .
35. (Enem-2015) Uma fábrica de sorvetes utiliza
embalagens plásticas no formato de paralelepípedo retangular reto.
Internamente, a embalagem tem
de altura e base de
por .
No processo de confecção do sorvete, uma mistura é colocada na embalagem no
estado líquido e, quando levada ao congelador, tem seu volume aumentado em 25%,
ficando com consistência cremosa.
Inicialmente é colocada na embalagem uma mistura sabor chocolate com volume de , e, após essa mistura ficar cremosa, será adicionada uma mistura sabor morango, de modo que, ao final do processo de congelamento, a embalagem fique completamente preenchida com sorvete, sem transbordar.
O volume máximo, em , da mistura sabor morango que deverá ser colocado na embalagem é
a) 450.
b) 500.
c) 600.
d) 750.
e) 1.000.
Resposta: Alternativa c.
Página 256
Medida do volume do cilindro
Partindo da mesma ideia do princípio de Cavalieri, assunto estudado anteriormente, vamos calcular a medida do volume de um cilindro. Para isso, considere duas folhas de papel do mesmo tipo e de espessura de mesma medida, como se estivessem apoiadas sobre uma superfície plana, uma com o formato de retângulo e a outra com o formato de círculo, ambas com a mesma medida de área.

Ao empilharmos a mesma quantidade dessas folhas de papel em formato de retângulos e de círculos, obtemos duas pilhas com a mesma medida de volume, cujos formatos lembram figuras geométricas espaciais, sendo um paralelepípedo reto retângulo e um cilindro.
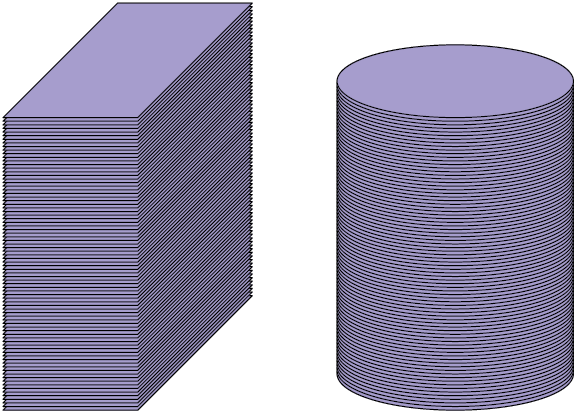
Como esses empilhamentos têm a mesma medida de volume, podemos obter a medida do volume do cilindro da mesma maneira que a medida do volume do paralelepípedo reto retângulo, isto é, multiplicando a medida da área da base pela medida da altura.
Considere um cilindro cuja medida da área da base é e da altura é h. A medida do volume V desse cilindro é dada por:
Como a base do cilindro é um círculo, a medida da área da base é dada por , em que r é a medida do comprimento do raio da base do cilindro. Portanto, a medida do volume do cilindro é dada por:
Página 257
Acompanhe, por exemplo, como calcular a medida do volume do cilindro a seguir utilizando essa fórmula e considerando .

Portanto, o volume desse cilindro mede aproximadamente .
Atividades
Faça as atividades no caderno.
Atenção!
Durante a realização das atividades desse tópico, considere .
36. O empilhamento a seguir é formado por três cilindros.
Efetue os cálculos no caderno e determine a medida do volume desse empilhamento.
Resposta: Aproximadamente .
37. As medidas de capacidade são usadas, em geral, para indicar a quantidade de líquido ou gás que pode ser colocado em um recipiente, isto é, a capacidade de um recipiente é igual a seu volume interno. Uma unidade de medida de capacidade muito utilizada o litro (), o qual não faz parte das unidades do SI, porém é aceito e usado no cotidiano.
Um submúltiplo do litro, que também é muito utilizado no cotidiano, é o mililitro ().
Podemos relacionar as unidades de medida de volume e de capacidade. Por exemplo, um recipiente cujo volume interno mede tem medida de capacidade igual a , isto é, .
Qual é a medida da capacidade aproximada de um recipiente de forma cilíndrica, em litros, cujo raio interno da base mede e a altura, ?
Resposta: Aproximadamente .
38. Uma fábrica produz peças de ferro. Na figura está representada uma peça na forma de paralelepípedo reto retângulo produzida por essa fábrica. No centro da peça há uma abertura de forma cilíndrica, cujo diâmetro mede .
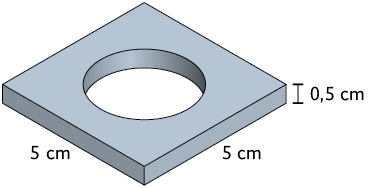
Qual é a medida do volume aproximado dessa peça, em centímetros cúbicos?
Resposta: Aproximadamente .
Página 258
39. Um objeto foi colocado em um recipiente cilíndrico, conforme apresentado a seguir. Na imagem, estão indicadas medidas internas do recipiente.

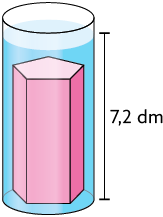
a) Qual é a medida da capacidade aproximada do recipiente, em litros?
b) Aproximadamente quantos litros de água há no recipiente?
c) Qual é a medida do volume do objeto que foi colocado no recipiente, em decímetros cúbicos?
Respostas: a) Aproximadamente ; b) Aproximadamente ; c) Aproximadamente .
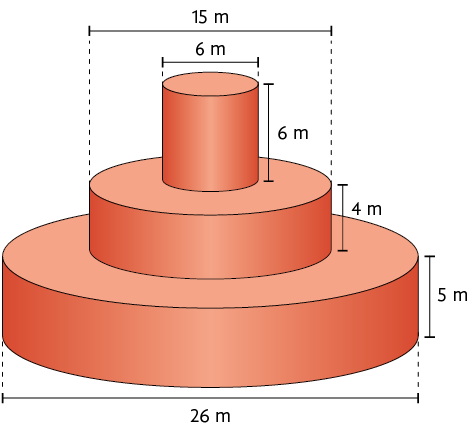
40. Elabore um problema envolvendo o reservatório representado a seguir, cujo formato é cilíndrico.
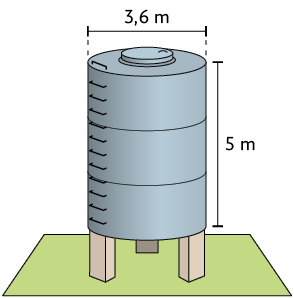
Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Resposta pessoal.
41. Uma caixa-d'água de formato cúbico, cujo comprimento das arestas mede , estava completamente cheia. Sabendo que foram retirados de água dessa caixa, quantos centímetros o nível da água baixou?
Resposta: .
42. Lucas tem a jarra a seguir, de formato cilíndrico. Ele vai despejar o líquido dela nos 2 recipientes A e B, que têm formato de um cilindro e de um paralelepípedo reto retângulo.
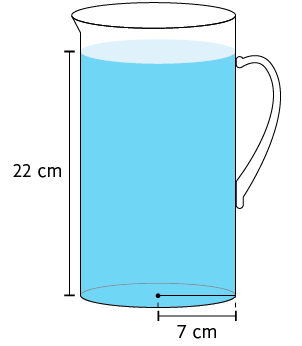


Sabendo que as medidas indicadas são internas, calcule no caderno a medida da capacidade de cada recipiente, em mililitros, e verifique se o líquido da jarra será suficiente para encher todos eles. Se não for, calcule quantos mililitros vão faltar.
Respostas: Recipiente A: aproximadamente ; recipiente B: ; o líquido será suficiente.
43. Em um recipiente com formato cilíndrico, podem ser colocados, no máximo, de água. Sabendo que o diâmetro interno da base desse recipiente mede , calcule no caderno a medida da altura interna aproximada desse recipiente.
Resposta: Aproximadamente .
Página 259
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. A estrela de Barnard está entre as mais próximas da Terra, com medida de distância média de aproximadamente 5,98 anos-luz, ou seja, a luz emitida por essa estrela viaja 5,98 anos até ser vista por um observador na superfície da Terra. Em uma folha de papel avulsa, escreva, em quilômetros e em unidades astronômicas, a medida da distância média entre a estrela de Barnard e a superfície terrestre.
Respostas: Aproximadamente ; Aproximadamente .
2. A estrela Sirius é a mais brilhante do céu noturno visível a olho nu e pode ser vista de qualquer ponto da superfície terrestre. É a principal estrela da constelação Cão Maior e tem como vizinha mais próxima a estrela Prócion. A medida de distância média aproximada entre elas é . Escreva em uma folha de papel avulsa essa medida em anos-luz.
Resposta: Aproximadamente .
3. A medida da espessura de cada flagelo da bactéria H. pylori mede aproximadamente . Em uma folha de papel avulsa, escreva essa medida em:
micrômetro.
centímetro.
Respostas: ; .
4. O HD-DVD é um disco semelhante a um DVD com capacidade de armazenamento maior e que permite a gravação de conteúdo de alta definição.
a) Quantos DVDs de são necessários para armazenar a mesma quantidade de informações que é possível armazenar em um HD-DVD de ?
b) Quantos CDs de são necessários para armazenar a mesma quantidade de informações que o HD-DVD de ?
Respostas: a) 4 DVDs; b) 22 CDs.
5. A diferença entre as frequências de processamento de dados entre dois smartphones é . Sabendo que o processador de um deles é , determine a medida do processador do outro smartphone.
Resposta: ou .
6. Rogério levou 2 minutos e meio para baixar um arquivo em seu computador. Sabendo que a taxa de transferência de dados da sua rede é , determine a quantidade máxima de dados desse arquivo em .
Resposta: .
7. Qual é a medida de tempo mínima necessária, em minutos, para transferir um arquivo de em uma conexão de ?
Resposta: 256 minutos.
8. A peça roxa de formato cilíndrico foi colocada no interior do recipiente transparente, também de formato cilíndrico, representado a seguir. Depois, o recipiente foi cheio completamente com água.
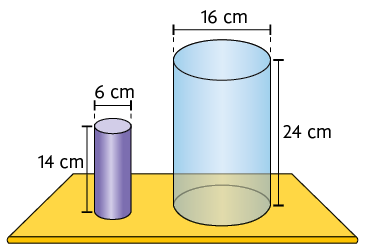
Sabendo que no recipiente estão indicadas suas medidas internas, determine quantos centímetros cúbicos de água foram colocados nele.
Resposta: Aproximadamente .
Página 260
9. A peça a seguir é composta por um prisma cuja base é um hexágono regular e um cilindro. Partindo dessa peça, será construído um parafuso sextavado. Calcule em uma folha de papel avulsa a medida do volume dela.
Atenção!
Um hexágono regular pode ser decomposto em seis triângulos equiláteros congruentes. Utilize .
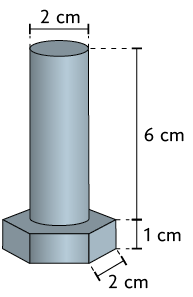

Resposta: .
10. Em certo paralelepípedo reto retângulo, foi feito um furo com formato cilíndrico, como mostra a imagem.
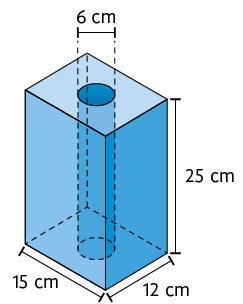
De acordo com as medidas indicadas, determine a medida do volume da peça obtida.
Resposta: Aproximadamente .
11. Calcule em uma folha de papel avulsa a medida da capacidade de processamento, em ciclos por segundo, dos processadores dos smartphones indicados na atividade 5 da página anterior.
Resposta: Processador de – por segundo; processador de – por segundo; ou processador de – por segundo; processador de – por segundo.
12. Calcule em uma folha de papel avulsa a medida do volume da figura geométrica a seguir.
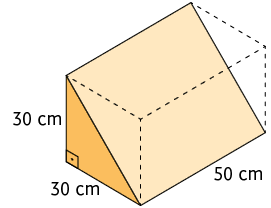
Resposta: .
13. Na fabricação de certa peça, uma marcenaria utiliza paralelepípedos retos retângulos de madeira como o representado a seguir.

Após torneá-la e dar acabamento, a peça obtida fica com a seguinte forma:
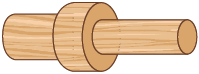
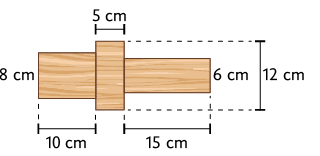
Quantos centímetros cúbicos de madeira foram retirados do paralelepípedo até obter essa peça?
Resposta: Aproximadamente .