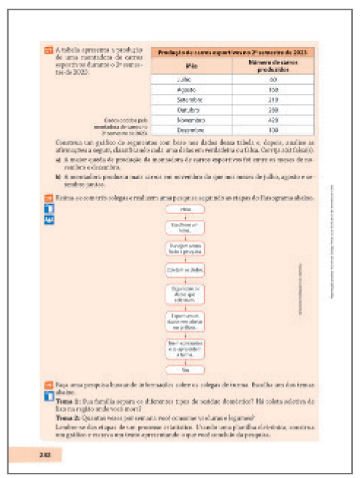
Apresentação
Professor, esta Coleção tem como objetivo principal servir de apoio didático para suas aulas. No Manual do Professor, você encontra algumas reflexões sobre o processo de ensino e de aprendizagem da Matemática nos Anos Finais do Ensino Fundamental.
Observe que falamos “de ensino e de aprendizagem”, separadamente, pois entendemos que são processos que se articulam, mas são distintos: processo de ensino mais processo de aprendizagem. Na escola, buscamos sempre que ambos andem juntos, complementem-se, e esse pressuposto guia a organização desta Coleção. Lembramos você, professor, que a escolha do livro didático deve ser feita sempre com base no conhecimento de sua realidade escolar. E, já que escolheu trabalhar com esta Coleção, queremos ajudá-lo a atingir seus objetivos didáticos, valorizando a autonomia pedagógica na organização e gestão de suas aulas.
Partimos do pressuposto que o professor é o grande mediador na relação entre os estudantes e a Matemática escolar: ele planeja, organiza, elabora as situações de aprendizagem e faz a gestão do trabalho, sempre buscando que seus estudantes adquiram conhecimentos para serem aplicados em situações presentes e futuras, tanto no âmbito escolar como na vida fóra dos muros da escola.
Esta Coleção atende aos requisitos da Base Nacional Comum Curricular (Bê êne cê cê), abrangendo o desenvolvimento das competências e habilidades tanto nos conteúdos quanto nas atividades e seções complementares. A Coleção também traz à tona aspectos relacionados à interdisciplinaridade, aos temas contemporâneos transversais (tê cê tês), à utilização da história da Matemática, ao uso significativo das tecnologias digitais no ensino desta disciplina, ao pensamento computacional, entre outros.
Organizamos este Manual do Professor em duas partes:
• Na primeira parte (Orientações gerais), há considerações em relação à Bê êne cê cê e ao modo como as competências e habilidades previstas neste documento são desenvolvidas na Coleção. São apresentadas também reflexões acerca da interdisciplinaridade, dos temas contemporâneos transversais, do uso de tecnologias digitais, do pensamento computacional, de avaliações e das características dos estudantes dos Anos Finais do Ensino Fundamental com orientações de como ajudá-los a desenvolver as capacidades de criticar, criar, propor, argumentar e inferir. Há também sugestões de avaliações formativas relacionadas aos capítulos do Livro do Estudante, uma sugestão de avaliação de preparação para exames de larga escala, resoluções e comentários de todas as atividades propostas no Livro do Estudante e sugestões de leitura, sites e vídeos.
• Na segunda parte (Orientações), disposta em formato de u, há a reprodução comentada das páginas do Livro do Estudante. Nela, também são apresentadas as competências e habilidades da Bê êne cê cê desenvolvidas em cada tópico ou seção, os objetivos traçados com a justificativa da pertinência de cada um e, também, sugestões de como diagnosticar os conhecimentos previamente adquiridos pelos estudantes e de como conduzir as aulas iniciais com base nesses diagnósticos. Além disso, estão presentes nestas Orientações sugestões de atividades interdisciplinares, de combate ao bullying e que auxiliam na promoção da saúde mental dos estudantes.
De modo geral, as orientações e sugestões deste Manual do Professor buscam auxiliar o desenvolvimento de conhecimentos e práticas pedagógicas que contribuam de maneira significativa para uma formação mais integral, humana e crítica do estudante e do professor. Queremos que os estudantes pensem matematicamente, resolvam problemas diversos e concluam essa etapa da Educação Básica preparados para continuar seus estudos.
Sumário
- ORIENTAÇÕES GERAIS
- A BNCC E O ENSINO DE MATEMÁTICA V
A BNCC E A COLEÇÃO X
- As competências gerais e específicas de Matemática na Coleção X
- As habilidades da BNCC na Coleção XV
- Exemplos concretos de trabalho com competências gerais, competências específicas e habilidades da BNCC na Coleção XVI
- INTERDISCIPLINARIDADE XXII
TEMAS CONTEMPORÂNEOS TRANSVERSAIS (TCTs) XXIII
- Os TCTs na Coleção XXIV
- AS TECNOLOGIAS DIGITAIS E O ENSINO DE MATEMÁTICA XXV
- PENSAMENTO COMPUTACIONAL XXVI SUGESTÕES DE CRONOGRAMAS XXVII
- ORIENTAÇÕES PARA AVALIAÇÃO XXVII
- Sugestões de avaliação formativa XXIX
- Sugestão de avaliação para a preparação para exames de larga escala XLII
- RESOLUÇÕES E COMENTÁRIOS DAS ATIVIDADES XLVIII
- CONHEÇA COMO SÃO FEITAS AS ORIENTAÇÕES NA REPRODUÇÃO COMENTADA DAS PÁGINAS DO LIVRO DO ESTUDANTE CIX
- REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS CXI
- A BNCC E O ENSINO DE MATEMÁTICA V
A BNCC E A COLEÇÃO X
- UNIDADE 1 25
- Capítulo 1 ‒ Números inteiros 26
- Capítulo 2 ‒ Múltiplos e divisores 55
- Capítulo 3 ‒ Retas e ângulos 66
- Capítulo 4 ‒ Frações 105
- Capítulo 5 ‒ Números racionais 117
- Capítulo 6 ‒ Linguagem algébrica e regularidades 141
- Capítulo 7 ‒ Porcentagem e juro simples 171
- Capítulo 8 ‒ Proporcionalidade 184
- Capítulo 9 ‒ Transformações geométricas 202
Orientações gerais
A BNCC E O ENSINO DE MATEMÁTICA
A Bê êne cê cê é um documento do Ministério da Educação (Méqui) que define as aprendizagens essenciais que todos os estudantes devem desenvolver ao longo da Educação Básica. Tais aprendizagens são organizadas com base em competências e habilidades que direcionam a formação integral de todos os estudantes em suas variadas dimensões (intelectual, afetiva, ética, física, sociopolítica etcétera).
Prevista nos principais documentos que regulam a educação do país, como a Constituição (1988), a Lei de Diretrizes e Bases da Educação Nacional (élê dê bê ê ênê 9.394/1996) e o Plano Nacional de Educação (2014), sua aprovação e a implementação visam garantir uma educação de qualidade e mais igualitária a todos os estudantes brasileiros.
Na Bê êne cê cê, a Matemática é considerada uma área do conhecimento essencial para que estudantes resolvam problemas, investiguem, estabeleçam conjecturas, troquem ideias e desenvolvam projetos em que possam aplicar os conceitos e procedimentos estudados de maneira crítica e significativa. Nesse sentido, é importante que as competências gerais e as competências específicas da área sejam mobilizadas por meio de atividades frequentes e intencionais. Colocar estudantes diante de situações que os convidem a usar a Matemática para desenvolver suas capacidades intelectuais, bem como as habilidades de observação, exploração, análise e reflexão, favorece a formação integral em suas variadas dimensões. Dessa fórma, a Bê êne cê cê é trabalhada de fórma efetiva.
Na Bê êne cê cê, o ensino e a aprendizagem da área são organizados em cinco Unidades temáticas que se correlacionam: Números, Álgebra, Geometria, Grandezas e medidas e Probabilidade e estatística. Observe o esquema a seguir.
|
UNIDADES TEMÁTICAS |
NÚMEROS |
|---|---|
|
ÁLGEBRA |
|
|
GEOMETRIA |
|
|
GRANDEZAS E MEDIDAS |
|
|
PROBABILIDADE E ESTATÍSTICA |
Para desenvolver o que se espera em cada unidade temática, a Bê êne cê cê prevê um conjunto de objetos de conhecimento e habilidades relacionadas. É o trabalho com estes objetos e habilidades que vai assegurar o desenvolvimento das competências específicas de Matemática que, por sua vez, promoverão o desenvolvimento das competências gerais, conforme mostra o esquema a seguir.
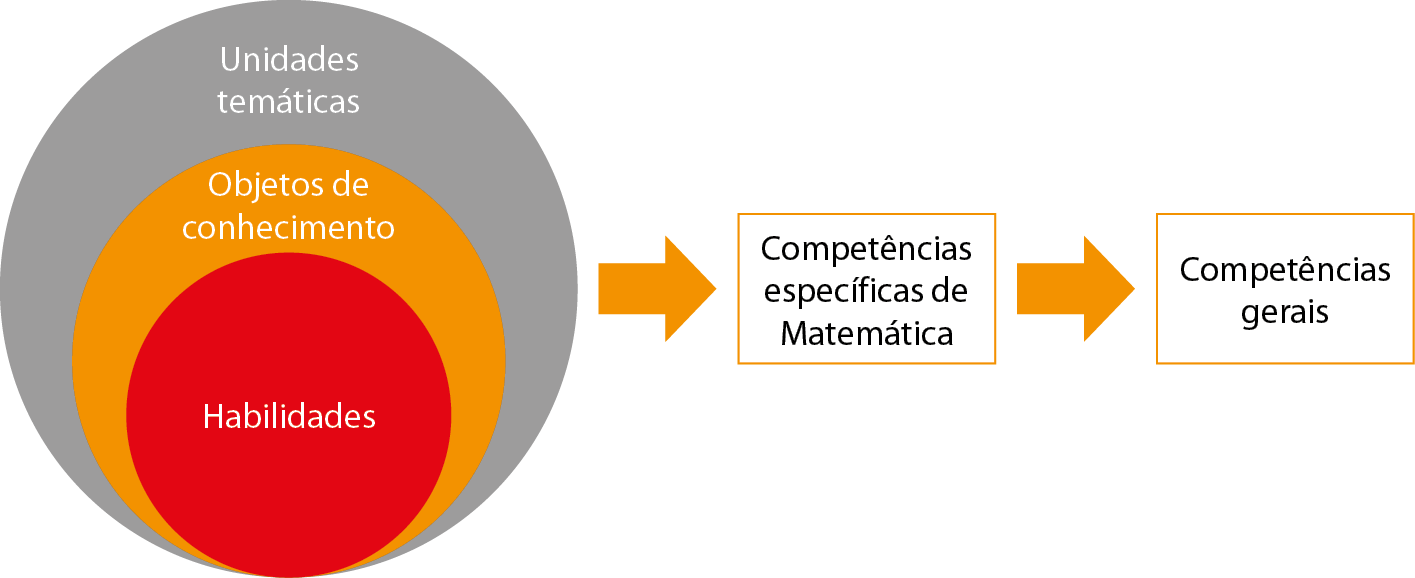
A seguir, vamos nos debruçar sobre as competências gerais, as competências específicas de Matemática e as habilidades do 7º ano.
Competências gerais
A Bê êne cê cê elenca um conjunto de dez competências gerais que devem ser desenvolvidas de fórma integrada aos componentes curriculares, ao longo de toda a Educação Básica. Define-se competência como um atributo que permite mobilizar conhecimentos, habilidades, atitudes e valores para resolver demandas complexas da vida cotidiana, permitindo o pleno exercício da cidadania. Esse direcionamento está ligado aos princípios éticos, estéticos e políticos das Diretrizes Curriculares Nacionais da Educação Básica (dê cê êne) e da Lei de Diretrizes e Bases da Educação Nacional (éle dê bê).
Reproduzimos a seguir o texto das competências gerais, segundo a Bê êne cê cê.
COMPETÊNCIAS GERAIS DA EDUCAÇÃO BÁSICA
|
Competência geral 1 |
Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva. |
|---|---|
|
Competência geral 2 |
Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas. |
|
Competência geral 3 |
Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural. |
|
Competência geral 4 |
Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo. |
|
Competência geral 5 |
Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva. |
|
Competência geral 6 |
Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade. |
|
Competência geral 7 |
Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta. |
|
Competência geral 8 |
Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo- se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas. |
|
Competência geral 9 |
Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza. |
|
Competência geral 10 |
Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários. |
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, Distrito Federal: Méqui, 2018. página 9-10. Disponível em: https://oeds.link/pKEA59. Acesso em: 19 julho 2022.
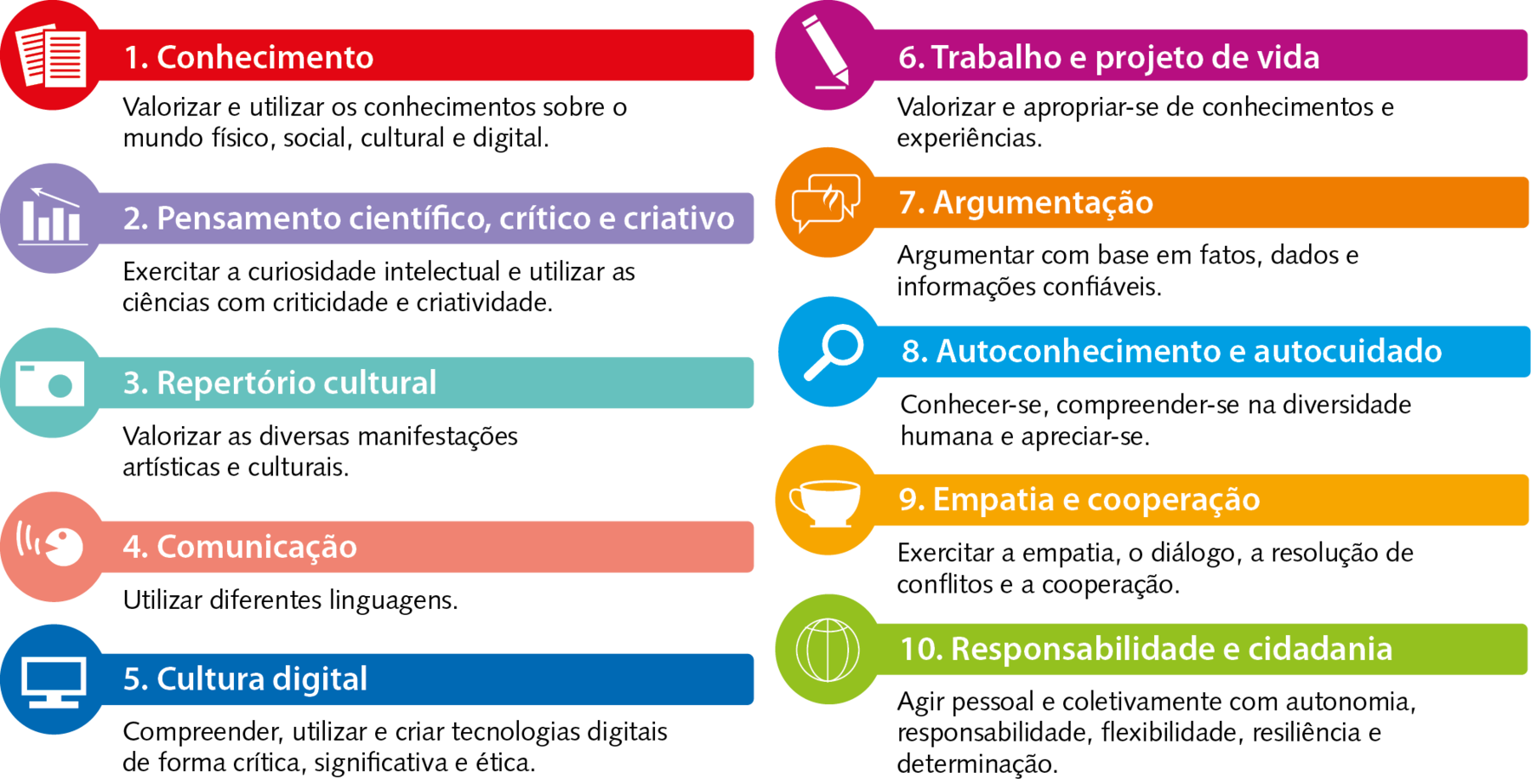
Podemos sintetizar as 10 competências gerais da Bê êne cê cê, por meio do seguinte esquema:
Competências específicas de Matemática
A Bê êne cê cê estabelece também as competências específicas para cada componente curricular. Em articulação com as competências gerais da Educação Básica descritas na Bê êne cê cê, a Matemática deve garantir aos estudantes o desenvolvimento das seguintes competências específicas.
|
Competência específica 1 |
Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho. |
|---|---|
|
Competência específica 2 |
Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo. |
|
Competência específica 3 |
Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções. |
|
Competência específica 4 |
Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes. |
|
Competência específica 5 |
Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados. |
|
Competência específica 6 |
Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados). |
|
Competência específica 7 |
Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza. |
|
Competência específica 8 |
Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles. |
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, Distrito Federal: Méqui, 2018. página 267. https://oeds.link/pKEA59. Acesso em: 19 julho 2022.
Habilidades
As habilidades presentes na Bê êne cê cê dizem respeito às aprendizagens essenciais que devem ser garantidas aos estudantes nos diferentes contextos escolares. O desenvolvimento delas visa promover a igualdade educacional, levando em consideração as particularidades do meio no qual cada escola está inserida.
O quadro a seguir relaciona cada unidade temática com seus objetos de conhecimento e as habilidades essenciais de Matemática a serem desenvolvidas no 7º ano, segundo a Bê êne cê cê.
|
Unidades temáticas |
Objetos de conhecimento |
Habilidades |
|---|---|---|
|
Números |
Múltiplos e divisores de um número natural |
(EF07MA01) Resolver e elaborar problemas com números naturais, envolvendo as noções de divisor e de múltiplo, podendo incluir máximo divisor comum ou mínimo múltiplo comum, por meio de estratégias diversas, sem a aplicação de algoritmos. |
|
Cálculo de porcentagens e de acréscimos e decréscimos simples |
(EF07MA02) Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros. |
|
|
Números inteiros: usos, história, ordenação, associação com pontos da reta numérica e operações |
(EF07MA03) Comparar e ordenar números inteiros em diferentes contextos, incluindo o histórico, associá-los a pontos da reta numérica e utilizá-los em situações que envolvam adição e subtração. |
|
|
(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros. |
||
|
Fração e seus significados: como parte de inteiros, resultado da divisão, razão e operador |
(EF07MA05) Resolver um mesmo problema utilizando diferentes algoritmos. |
|
|
(EF07MA06) Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmos procedimentos. |
||
|
(EF07MA07) Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas. |
||
|
(EF07MA08) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador. |
||
|
(EF07MA09) Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza. |
||
|
Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações |
(EF07MA10) Comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica. |
|
|
(EF07MA11) Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias. |
||
|
(EF07MA12) Resolver e elaborar problemas que envolvam as operações com números racionais. |
||
|
Álgebra |
Linguagem algébrica: variável e incógnita |
(EF07MA13) Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas, diferenciando-a da ideia de incógnita. |
|
(EF07MA14) Classificar sequências em recursivas e não recursivas, reconhecendo que o conceito de recursão está presente não apenas na matemática, mas também nas artes e na literatura. |
||
|
(EF07MA15) Utilizar a simbologia algébrica para expressar regularidades encontradas em sequências numéricas. |
||
|
Equivalência de expressões algébricas: identificação da regularidade de uma sequência numérica |
(EF07MA16) Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes. |
|
|
Problemas envolvendo grandezas diretamente proporcionais e grandezas inversamente proporcionais |
(EF07MA17) Resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas. |
|
|
Equações polinomiais do 1º grau |
(EF07MA18) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à forma ax + b = c, fazendo uso das propriedades da igualdade. |
|
Unidades temáticas |
Objetos de conhecimento |
Habilidades |
|---|---|---|
|
Geometria |
Transformações geométricas de polígonos no plano cartesiano: multiplicação das coordenadas por um número inteiro e obtenção de simétricos em relação aos eixos e à origem |
(EF07MA19) Realizar transformações de polígonos representados no plano cartesiano, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro. |
|
(EF07MA20) Reconhecer e representar, no plano cartesiano, o simétrico de figuras em relação aos eixos e à origem. |
||
|
Simetrias de translação, rotação e reflexão |
(EF07MA21) Reconhecer e construir figuras obtidas por simetrias de translação, rotação e reflexão, usando instrumentos de desenho ou softwares de geometria dinâmica e vincular esse estudo a representações planas de obras de arte, elementos arquitetônicos, entre outros. |
|
|
A circunferência como lugar geométrico |
(EF07MA22) Construir circunferências, utilizando compasso, reconhecê-las como lugar geométrico e utilizá-las para fazer composições artísticas e resolver problemas que envolvam objetos equidistantes. |
|
|
Relações entre os ângulos formados por retas paralelas intersectadas por uma transversal |
(EF07MA23) Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal, com e sem uso de softwares de geometria dinâmica. |
|
|
Triângulos: construção, condição de existência e soma das medidas dos ângulos internos |
(EF07MA24) Construir triângulos, usando régua e compasso, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma das medidas dos ângulos internos de um triângulo é 180°. |
|
|
(EF07MA25) Reconhecer a rigidez geométrica dos triângulos e suas aplicações, como na construção de estruturas arquitetônicas (telhados, estruturas metálicas e outras) ou nas artes plásticas. |
||
|
(EF07MA26) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um triângulo qualquer, conhecidas as medidas dos três lados. |
||
|
Polígonos regulares: quadrado e triângulo equilátero |
(EF07MA27) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos. |
|
|
(EF07MA28) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular (como quadrado e triângulo equilátero), conhecida a medida de seu lado. |
||
|
Grandezas e medidas |
Problemas envolvendo medições |
(EF07MA29) Resolver e elaborar problemas que envolvam medidas de grandezas inseridos em contextos oriundos de situações cotidianas ou de outras áreas do conhecimento, reconhecendo que toda medida empírica é aproximada. |
|
Cálculo de volume de blocos retangulares, utilizando unidades de medida convencionais mais usuais |
(EF07MA30) Resolver e elaborar problemas de cálculo de medida do volume de blocos retangulares, envolvendo as unidades usuais (metro cúbico, decímetro cúbico e centímetro cúbico). |
|
|
Equivalência de área de figuras planas: cálculo de áreas de figuras que podem ser decompostas por outras, cujas áreas podem ser facilmente determinadas como triângulos e quadriláteros |
(EF07MA31) Estabelecer expressões de cálculo de área de triângulos e de quadriláteros. |
|
|
(EF07MA32) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas. |
||
|
Medida do comprimento da circunferência |
(EF07MA33) Estabelecer o número como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica. |
|
|
Probabilidade e estatística |
Experimentos aleatórios: espaço amostral e estimativa de probabilidade por meio de frequência de ocorrências |
(EF07MA34) Planejar e realizar experimentos aleatórios ou simulações que envolvem cálculo de probabilidades ou estimativas por meio de frequência de ocorrências. |
|
Estatística: média e amplitude de um conjunto de dados |
(EF07MA35) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados. |
|
|
Pesquisa amostral e pesquisa censitária |
(EF07MA36) Planejar e realizar pesquisa envolvendo tema da realidade social, identificando a necessidade de ser censitária ou de usar amostra, e interpretar os dados para comunicá-los por meio de relatório escrito, tabelas e gráficos, com o apoio de planilhas eletrônicas. |
|
|
Gráficos de setores: interpretação, pertinência e construção para representar conjunto de dados |
(EF07MA37) Interpretar e analisar dados apresentados em gráfico de setores divulgados pela mídia e compreender quando é possível ou conveniente sua utilização. |
BRASIL. Ministério da Educação. Base Nacional Comum Curricular: Educação é a Base. Brasília, Distrito Federal: Méqui, 2018. página 307-311. Disponível em: https://oeds.link/pKEA59. Acesso em: 22 maio 2022.
A Bê êne cê cê E A COLEÇÃO
Esta Coleção é organizada em quatro volumes. Cada volume está dividido em quatro Unidades compostas de dois ou mais capítulos. Os volumes e os capítulos foram estruturados de modo a favorecer o desenvolvimento das competências gerais e específicas bem como das habilidades propostas para a Matemática, indicadas na Bê êne cê cê.
As competências gerais e específicas de Matemática na Coleção
Ao longo da Coleção, o desenvolvimento das competências gerais e específicas de Matemática é proporcionado de diferentes maneiras, por meio de textos teóricos, atividades, seções especiais, boxes etcétera A seguir, oferecemos informações detalhadas sobre as seções e os boxes da Coleção e, também, sobre como as competências gerais e específicas podem ter o seu desenvolvimento favorecido na proposta de cada um.
Seção Revisão dos conteúdos de anos anteriores
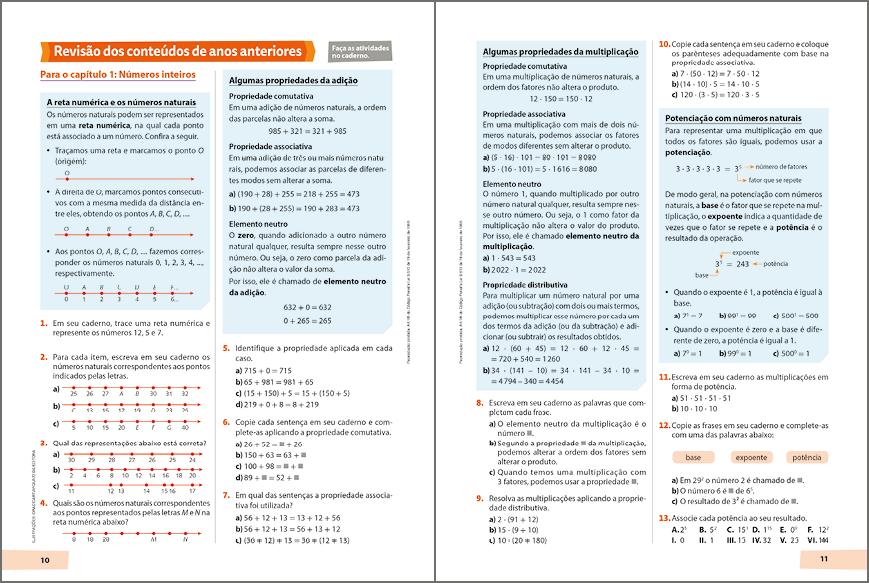
Presente no início de cada volume, esta seção traz resumos seguidos de atividades dos principais conceitos e procedimentos estudados em anos anteriores. A seção é estruturada para cada um dos capítulos do Livro do Estudante a fim de que o professor explore seu conteúdo antes de iniciar o trabalho com cada capítulo. No entanto, caso o professor julgue oportuno, o conteúdo da seção também pode ser todo trabalhado no início do ano letivo. É importante enfatizar que o professor pode e deve se sentir à vontade para adaptar o conteúdo da seção à realidade e às necessidades da turma e da escola.
Competências gerais: a seção traz atividades que exploram diferentes linguagens (competência geral 4). Algumas delas incentivam a argumentação e o diálogo e oferecem aos estudantes a oportunidade de exercitar a empatia (competências gerais 7 e 9).
Competências específicas: algumas atividades propostas desenvolvem o raciocínio lógico e o espírito de investigação (competência específica 2). Outras permitem aos estudantes relacionar conceitos de diferentes unidades temáticas (competência específica 3), utilizar processos e ferramentas matemáticas para modelar e resolver problemas (competência específica 5) e empregar distintos registros e linguagens (competência específica 6). Além disso, são propostas atividades que estimulam a interação dos estudantes com seus pares e que os colocam diante de situações em que devem investigar, organizar, representar e comunicar informações (competências específicas 4 e 8).
Abertura de Unidade e seção É hora de extrapolar

A abertura de Unidade apresenta a lista de capítulos que a integram, além de uma cena acompanhada de algumas questões que têm por objetivo instigar a curiosidade dos estudantes para os assuntos que serão estudados na Unidade. A cena e as questões estão relacionadas com o conteúdo da seção É hora de extrapolar, que fecha a Unidade. As questões não precisam ser respondidas em um primeiro momento, pois elas serão retomadas ao final da Unidade para que os estudantes reflitam sobre o que aprenderam.
Competências gerais: as aberturas de Unidade estimulam a curiosidade, a reflexão e o diálogo entre os estudantes (competências gerais 2 e 9). Alguns dos contextos trazidos possibilitam a valorização da diversidade de saberes e vivências (competência geral 6), a argumentação com base em fatos, dados e informações confiáveis (competência geral 7) e levam os estudantes a refletir e cuidar da sua saúde física e emocional (competência geral 8).
Competências específicas: as situações e questões trazidas nas aberturas evidenciam como a Matemática e as outras áreas do conhecimento se integram (competência específica 3) e oferecem aos estudantes a oportunidade de fazer observações de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais (competência específica 4). As questões também fazem com que os estudantes enfrentem situações-problema em múltiplos contextos (competências específicas 2 e 6) e utilizem ferramentas matemáticas para resolvê-las (competência específica 5), bem como promovem a interação deles com os colegas (competência específica 8).
Ao final de cada Unidade, é proposta a seção É hora de extrapolar. Nela, os estudantes são convidados a realizar um trabalho colaborativo, como um pequeno projeto explorando a pesquisa, a comunicação e a elaboração de um produto final (embalagens, cartazes, obras de arte e revistas), que será compartilhado com a turma ou com a comunidade escolar. Com a finalidade de organizar o trabalho, a seção é dividida em etapas, as quais promovem:
• entendimento do contexto e dos objetivos do trabalho a ser realizado;
• pesquisa individual ou coletiva;
• elaboração, em grupo, do produto proposto;
• apresentação e exposição do produto;
• reflexão sobre a atuação do grupo e síntese do trabalho.
É nesta seção, ainda, que são retomadas as questões feitas na abertura de Unidade correspondente.
As etapas de pesquisa e elaboração do produto podem ser feitas extraclasse. Será necessário que o professor oriente-os com relação ao prazo, aos materiais e a outros aspectos necessários à realização do trabalho.
É recomendável trabalhar a seção depois de estudar os capítulos, mas, se o professor preferir trabalhar as etapas da seção à medida que os capítulos forem estudados, deverá atentar para os conhecimentos prévios necessários.
Competências gerais: os trabalhos propostos na seção possibilitam aos estudantes investigar, refletir, analisar criticamente, imaginar e criar (competência geral 2). Em algumas seções eles terão a oportunidade de explorar obras de arte e pesquisar sobre diferentes manifestações culturais (competência geral 3). Na seção, os estudantes também utilizam distintas linguagens para elaborar o produto final ou expô-lo (competência geral 4); podem recorrer à internet para pesquisar ou disseminar informações (competência geral 5); argumentam com base em fatos, dados e informações confiáveis (competência geral 7) e exercitam a empatia e o diálogo (competência geral 9).
Competências específicas: a seção desperta o espírito investigativo, a capacidade de argumentar e traz à tona a relação entre os diferentes campos da Matemática e também da Matemática com outras áreas do conhecimento, (competências específicas 2 e 3). Para concretizar alguns trabalhos, os estudantes deverão utilizar processos e ferramentas matemáticas e enfrentar situações-problema em múltiplos contextos (competências específicas 5 e 6). Algumas das propostas abordam assuntos de urgência social e dão aos estudantes a oportunidade de discuti-las (competências específicas 7 e 8).
Seção Trocando ideias
A seção Trocando ideias “abre” cada um dos capítulos e traz à tona temas do cotidiano que visam despertar o interesse dos estudantes para o que será estudado no capítulo e também busca, por meio de questões, identificar os conhecimentos prévios deles. A ideia é que as questões sejam discutidas coletivamente.

Competências gerais: os contextos e as questões propostos na seção despertam a curiosidade dos estudantes (competência geral 2), permitem a eles valorizar diferentes manifestações artísticas e culturais (competência geral 3) e, em alguns casos, mobilizam diferentes linguagens (competência geral 4). Há também propostas que proporcionam aos estudantes argumentarem com base em dados e informações confiáveis (competência geral 7) e refletem sobre situações relacionadas à saúde física e emocional (competência geral 8). Além disso, incentiva o diálogo (competência geral 9).
Competências específicas: a seção tem como objetivos promover a interação entre os estudantes (competência específica 8), despertar a capacidade de argumentar (competência específica 2) e trazer à tona a relação entre os campos da Matemática e também entre a Matemática e outras áreas (competências específicas 3). Os estudantes também analisam aspectos quantitativos e qualitativos do cotidiano (competência específica 4) e utilizam ferramentas matemáticas para responder a alguma questão proposta (competência específica 5). A mobilização de diferentes registros e linguagens é exigência de algumas propostas que exploram, por exemplo, a leitura e a interpretação de gráficos e fluxogramas (competência específica 6).
Seção Lendo e aprendendo
A seção Lendo e aprendendo aparece no decorrer das Unidades e traz textos de jornais, revistas ou da internet que abordam temas atuais e de urgência social. O objetivo da seção é desenvolver a compreensão leitora por meio do desenvolvimento de vocabulário, fluência em leitura oral, compreensão de textos e produção de escrita. Além disso, a seção leva os estudantes a refletir sobre os temas tratados e discuti-los.

Competências gerais: os estudantes lidam com diferentes manifestações artísticas (competência geral 3), valorizam a diversidade de saberes e vivências culturais (competência geral 6), argumentam com base em fatos, dados e informações confiáveis (competência geral 5) e exercitam a empatia, o diálogo e a cooperação (competência geral 9).
Competências específicas: a seção contribui para que os estudantes compreendam as relações entre conceitos dos diferentes campos da Matemática e de outras áreas do conhecimento (competência específica 3) e para que discutam diferentes questões com seus pares (competência específica 8).
Seção Tecnologias digitais em foco
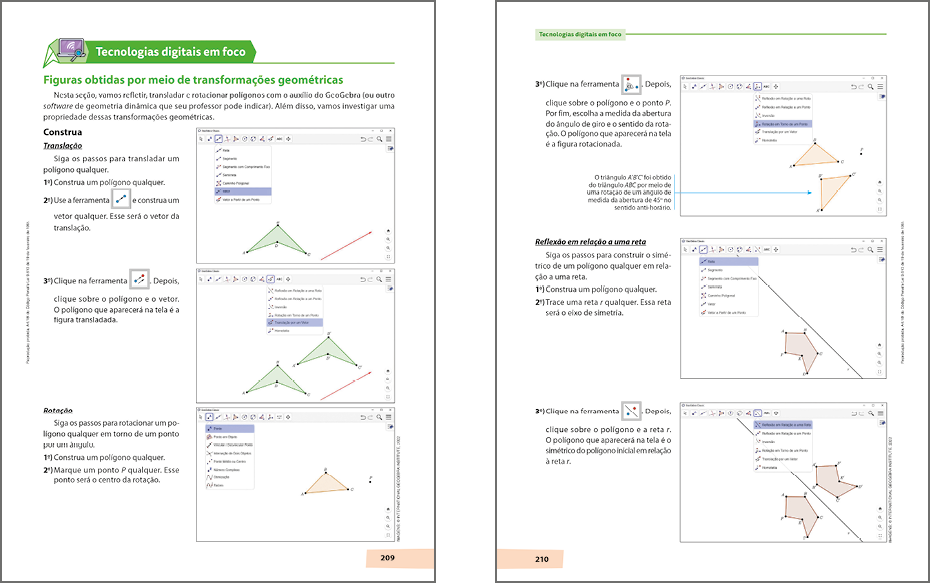
A seção Tecnologias digitais em foco aparece no decorrer de alguns capítulos e explora conteúdos de Matemática por meio de tecnologias digitais, como softwares de Geometria dinâmica, planilhas eletrônicas, calculadoras etcétera A seção é, em geral, dividida em duas etapas denominadas Construa e Explore. Em Construa, são apresentados passos para que os estudantes construam, por exemplo, figuras geométricas. Em Explore, eles utilizam as ferramentas do software, para investigar e testar hipóteses a respeito de alguma característica ou propriedade da figura que construíram.
Competências gerais: o uso de tecnologias digitais exercita a curiosidade intelectual dos estudantes e os coloca diante de situações em que devem investigar, refletir e analisar (competências gerais 2 e 5). A seção também permite que os estudantes exercitem a empatia e o diálogo (competência geral 9).
Competências específicas: a seção ajuda os estudantes a desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de argumentar (competência específica 2). Ainda por meio desta seção, os estudantes utilizam as tecnologias digitais para resolver problemas e validar resultados (competência específica 5) e lidam com diferentes registros e linguagens (competência específica 6). A interação dos estudantes com seus pares ocorre principalmente nas tarefas propostas na etapa Explore (competência específica 8).
Seção Resolvendo em equipe
Alguns capítulos apresentam esta seção que destaca as etapas que encaminham a resolução de problemas, as quais devem ser analisadas e discutidas com os estudantes. O trabalho em equipe é muito importante sob diversos pontos de vista: permite ao estudante aprender com os colegas, explicitar conhecimentos e dúvidas, facilitando a ação do professor, e validar o raciocínio construído por meio do diálogo com os colegas. Além disso, saber trabalhar em equipe é uma competência exigida nas mais diversas profissões.

Competências gerais: a seção contribui para que os estudantes resolvam problemas (competência geral 2), utilizem diferentes linguagens (competência geral 4), argumentem com base em dados e informações confiáveis (competência geral 7) e exercitem a empatia (competência geral 9). É preciso, ainda, que diante da pluralidade de ideias, os estudantes sejam flexíveis (competência geral 10).
Competências específicas: os problemas a serem resolvidos desenvolvem o raciocínio lógico (competência específica 2), alguns envolvem conceitos e procedimentos de diferentes campos da Matemática (competência específica 3) e outros precisam de processo e ferramentas matemáticas para serem solucionados (competência específica 5). Os contextos dos problemas são diversos e envolvem diferentes registros (competência específica 6). Além disso, o encaminhamento proposto incentiva os estudantes a compartilhar suas estratégias e conclusões (competência específica 2).
Seção Revisão dos conteúdos deste capítulo
Presente no final de cada capítulo, esta seção traz resumos seguidos de atividades dos principais conceitos e procedimentos estudados no capítulo. As revisões e atividades podem ser exploradas aos poucos, conforme se avança no estudo do capítulo, ou podem ser trabalhadas ao final com o objetivo de verificar o que os estudantes aprenderam e as principais dificuldades que ainda enfrentam.
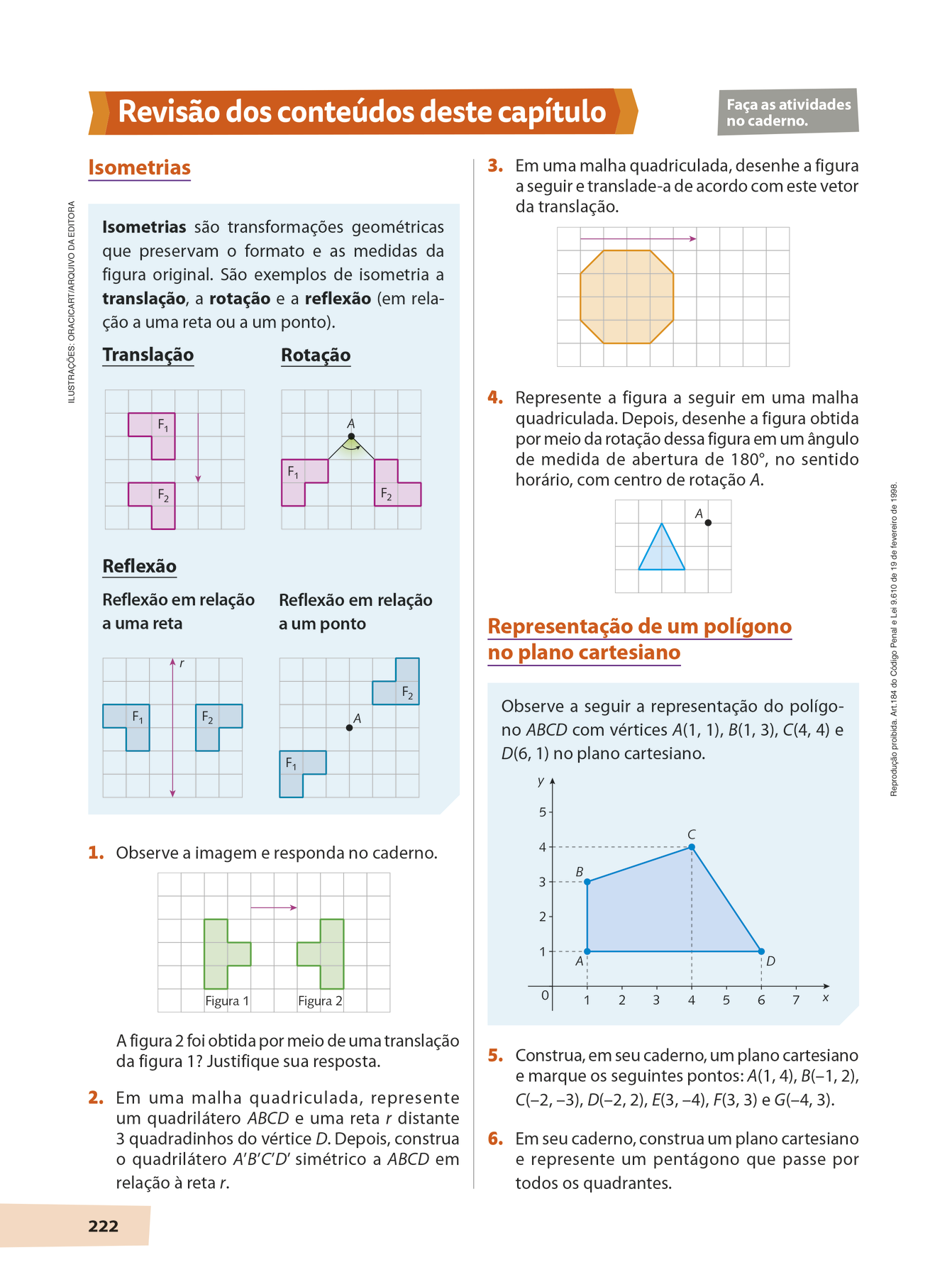
Competências gerais: a seção traz atividades que exploram diferentes linguagens (competência geral 4). Algumas delas incentivam a argumentação e o diálogo e oferecem aos estudantes a oportunidade de exercitar a empatia (competências gerais 7 e 9).
Competências específicas: na seção, são propostas atividades que desenvolvem o raciocínio lógico e o espírito de investigação (competência específica 2), outras que demandam a utilização de processos e ferramentas matemáticas para modelar e resolver problemas (competência específica 5) e ainda outras que fazem com que os estudantes mobilizem diferentes registros e linguagens (competência específica 6).
Seção Teste seus conhecimentos

Presente no final de cada volume, esta seção propõe questões de múltipla escolha com o objetivo de avaliar os conhecimentos adquiridos pelos estudantes no decorrer do ano letivo e prepará-los para a realização de exames de larga escala.
Competências gerais: algumas questões da seção possibilitam aos estudantes refletir e analisar (competência geral 2) e outras utilizam diferentes registros (competência geral 4). São propostas ainda questões em que os estudantes devem avaliar dados e informações confiáveis (competência geral 7).
Competências específicas: questões que estimulam o raciocínio lógico (competência específica 2) e que envolvem conceitos e procedimentos dos diferentes campos da Matemática (competência específica 3) estão presentes nesta seção. Além disso, são propostos problemas cuja solução se dá via utilização de processos e ferramentas matemáticas e também problemas envolvendo diferentes registros (competências específicas 5 e 6).
Boxe Veja que interessante
Boxe que complementa e enriquece o conteúdo estudado. Ao final, é proposta uma atividade para o estudante.

Competências gerais: o boxe traz temas diversos relacionados ao mundo físico, social, cultural e digital (competência geral 1), exercita a curiosidade dos estudantes por meio de atividades sobre esses temas (competência geral 2) e, em algumas propostas, os estudantes têm a oportunidade de apreciar manifestações artísticas e culturais (competência geral 3). O boxe possibilita, ainda, em alguns momentos a valorização da diversidade de saberes (competência geral 6) e coloca os estudantes diante de situações em que devem argumentar com base em informações confiáveis (competência geral 7). Algumas atividades solicitam aos estudantes que dialoguem com os colegas, e isso permite que desenvolvam a empatia e a capacidade de agirem com flexibilidade (competências gerais 9 e 10).
Competências específicas: alguns textos desse boxe possibilitam aos estudantes reconhecer como a Matemática contribui para solucionar problemas (competências específicas 1 e 2). Outros trazem à tona a relação da Matemática com as demais áreas do conhecimento (competência específica 3), e a atividade promove a interação entre os estudantes (competência específica 8).
Boxe Um pouco de história
Boxe que traz textos relacionados à história da Matemática para contextualizar alguns assuntos. Ao final, é proposta uma atividade para o estudante.

Competências gerais: é inerente à proposta desse boxe a valorização e utilização dos conhecimentos historicamente construídos (competência geral 1). A curiosidade, a investigação e a resolução de problemas são incentivados por meio das atividades propostas (competência geral 2). Os estudantes têm ainda a oportunidade de argumentar e dialogar com base em fatos e informações confiáveis a respeito da história da Matemática (competências gerais 7 e 10).
Competências específicas: os textos e as atividades propostos no boxe têm por objetivo levar os estudantes a reconhecer a Matemática como uma ciência viva que é resultado das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos (competência específica 1). A capacidade de argumentar (competência específica 2), de relacionar os campos da Matemática (competência específica 3), de lidar com diferentes registros e linguagens (competência específica 6) e de escultar os colegas com atenção e empatia (competência específica 8) são capacidades que podem ser desenvolvidas por meio das propostas desse boxe.
O quadro a seguir mostra as competências gerais e específicas de Matemática desenvolvidas em cada capítulo do volume 9 desta Coleção.
|
Capítulos |
Competências gerais |
Competências específicas |
|---|---|---|
|
1 ‒ Números inteiros |
2, 4, 9 e 10. |
2, 3, 5 e 8. |
|
2 ‒ Múltiplos e divisores |
2, 4, 9 e 10. |
2, 5 e 8. |
|
3 ‒ Retas e ângulos |
2, 3, 4, 5, 7 e 9. |
2, 3, 4, 5, 7 e 8. |
|
4 ‒ Frações |
2, 3, 4 e 9. |
2, 5, 6 e 8. |
|
5 ‒ Números racionais |
7 e 9. |
7 e 8. |
|
6 ‒ Linguagem algébrica e regularidades |
1, 2, 4, 5, 9 e 10. |
2, 4, 5, 7 e 8. |
|
7 ‒ Porcentagem e juro simples |
2, 4, 9 e 10. |
2, 3, 5 e 8. |
|
8 ‒ Proporcionalidade |
9. |
8. |
|
9 ‒ Transformações geométricas |
1, 2, 3, 4, 5, 6, 7, 8, 9 e 10. |
2, 3, 5, 7 e 8. |
|
10 ‒ Grandezas e medidas |
2, 3, 4, 9 e 10. |
2, 3, 5 e 8. |
|
11 ‒ Figuras geométricas planas |
3, 5 e 9. |
1, 4 e 8. |
|
12 ‒ Probabilidade e estatística |
2, 3, 4, 7, 8, 9 e 10. |
2, 3, 4, 5, 6, 7 e 8. |
As habilidades da Bê êne cê cê na Coleção
A Matemática trabalhada nos Anos Finais do Ensino Fundamental não tem um fim em si mesma; além de aprofundar e sistematizar as aprendizagens anteriores dos estudantes, abre as portas para novas aprendizagens, considerando as diversas áreas do conhecimento, contribuindo para o desenvolvimento intelectual do estudante.
Nesta Coleção, a seleção dos conteúdos foi feita nessa perspectiva, e as abordagens propostas pressupõem o desenvolvimento de atitudes relacionadas à formação cidadã do estudante. Escolhemos abordar conceitos e procedimentos (seleção e abordagem) tanto para aprofundar e retomar os conhecimentos prévios dos estudantes quanto para iniciar a aquisição de novos conhecimentos a serem consolidados em anos posteriores de escolaridade.
O professor pode acrescentar atividades, questionamentos, de modo a atender as especificidades de seus estudantes: o livro didático não pode ser uma amarra para o professor, mas, sim, um facilitador de seu trabalho.
O quadro a seguir apresenta uma visão geral do modo como as habilidades do 7º ano foram desenvolvidas em cada Unidade, capítulo a capítulo.
|
Unidades |
Capítulos |
Habilidades |
|---|---|---|
|
1 |
1 ‒ Números inteiros |
EF07MA03, EF07MA04 e EF07MA06. |
|
2 ‒ Múltiplos e divisores |
EF07MA01. |
|
|
3 ‒ Retas e ângulos |
EF07MA23 e EF07MA24. |
|
|
2 |
4 ‒ Frações |
EF07MA05, EF07MA06, EF07MA07, EF07MA08 e EF07MA09. |
|
5 ‒ Números racionais |
EF07MA06, EF07MA10, EF07MA11 e EF07MA12. |
|
|
6 ‒ Linguagem algébrica e regularidades |
EF07MA13, EF07MA14, EF07MA15, EF07MA16 e EF07MA18. |
|
|
3 |
7 ‒ Porcentagem e juro simples |
EF07MA02 e EF07MA06. |
|
8 ‒ Proporcionalidade |
EF07MA09, EF07MA13 e EF07MA17. |
|
|
9 ‒ Transformações geométricas |
EF07MA19, EF07MA20 e EF07MA21. |
|
|
4 |
10 ‒ Grandezas e medidas |
EF07MA29, EF07MA30, EF07MA31 e EF07MA32. |
|
11 ‒ Figuras geométricas planas |
EF07MA22, EF07MA24, EF07MA25, EF07MA26, EF07MA27, EF07MA28 e EF07MA33. |
|
|
12 ‒ Probabilidade e estatística |
EF07MA02, EF07MA34, EF07MA35, EF07MA36 e EF07MA37. |
Exemplos concretos de trabalho com competências gerais, competências específicas e habilidades da Bê êne cê cê na Coleção
Uma das finalidades do trabalho com as habilidades é assegurar o desenvolvimento das competências específicas de Matemática que, por sua vez, podem promover o desenvolvimento de competências gerais.
O quadro a seguir mostra, por meio de exemplos concretos da Coleção, a diferença de se trabalhar com competências gerais, específicas e habilidades.
|
Página 282 do capítulo 12 do volume 6 |
Página 155 do capítulo 6 do volume 7 |
|---|---|
|
Nas atividades 18 e 19 da página 282, os estudantes vão realizar uma pesquisa estatística, o que permite o desenvolvimento da habilidade EF06MA33. Ambas as propostas envolvem o uso de tecnologias digitais para a organização dos dados coletados o que favorece o desenvolvimento da competência específica 5. Além disso, as pesquisas podem estar relacionadas à questões de urgência social e para serem realizadas é necessário que os estudantes interajam com seus pares, o que pressupõe o desenvolvimento das competências específicas 7 e 8. Por meio destas competências específicas desenvolvem-se as competências gerais 7, 9 e 10, que versam sobre argumentação, exercício da empatia e agir com flexibilidade e resiliência.
|
No tópico Resolução de problemas são apresentados exemplos de problemas que podem ser resolvidos por meio de equações do 1º grau com uma incógnita. Também são propostos problemas para os estudantes resolverem e isso favorece o desenvolvimento da habilidade EF07MA18. Esses problemas permitem aos estudantes mobilizar conceitos e procedimentos de diferentes campos da Matemática, o que favorece o desenvolvimento da competência específica 3. A competência específica 5 também tem o seu desenvolvimento favorecido porque os problemas propostos são modelados e resolvidos por meio de equações. Já a variedade de problemas propostos é o que contribui para o desenvolvimento da competência específica 6. Essas competências específicas, por sua vez, contribuem para que as competências gerais 2 e 4 tenham o seu desenvolvimento favorecido, uma vez que estão relacionadas à resolução de problemas e ao uso de diferentes linguagens, respectivamente.
|
|
Página 77 do capítulo 4 do volume 8 |
Página 29 do capítulo 1 do volume 9 |
|
O estudo das composições de transformações geométricas desenvolve a habilidade EF08MA18. Por meio desse estudo, os estudantes têm a oportunidade de verificar como Matemática e Arte se relacionam, contribuindo para que a competência específica 3 tenha o seu desenvolvimento favorecido. É por meio dessa competência que se desenvolvem as competências gerais 1, 2, 3, 4 e 6.
|
Ao trabalhar a representação dos números em notação científica, desenvolve-se a habilidade EF09MA04. O trabalho com essa habilidade possibilita aos estudantes reconhecer como esse conceito é empregado para expressar números muito grandes ou muito pequenos em diversas áreas como Astronomia e Química, o que contribui para o desenvolvimento da competência específica 3 de Matemática, que, por sua vez, contribui para o desenvolvimento das competências gerais 4 e 7.
|
OS ESTUDANTES NOS ANOS FINAIS DO ENSINO FUNDAMENTAL
O estudante que se encontra nos Anos Finais do Ensino Fundamental está inserido na transição entre a infância e a adolescência, período marcado por intensas e profundas mudanças nos aspectos físico, psicológico, social e emocional. Ele é um sujeito “em desenvolvimento, com singularidades e formações identitárias e culturais próprias, que demandam práticas escolares diferenciadas, capazes de contemplar suas necessidades e diferentes modos de inserção social” (BRASIL, 2018, página 60).
Por isso, é preciso compreendê-lo, e para tanto é necessário aprender a ouvi-lo por meio da comunicação afetiva, em um movimento de aproximação, trocando experiências, vivências e histórias, em um ressignificar do processo de ensino e de aprendizagem.
É importante também estar atento às interações que eles estabelecem com os grupos sociais dos quais fazem parte, o que permite entender seus modos de agir e suas necessidades.
Assim, o ambiente escolar precisa refletir o clima de diálogo, do saber ouvir, da empatia e da boa convivência, combatendo toda fórma de violência, como a prática do bullying, comportamento intencional e agressivo na fórma de insultos, xingamentos, apelidos, ameaças, difamação, isolamento e exclusão social. Enfim, fazer do ambiente escolar um espaço inclusivo em todos os sentidos, pensando na formação do estudante como um sujeito ativo, protagonista do seu processo de aprendizagem e agente de transformação da sociedade.
A fim de garantir que isso aconteça diante da heterogeneidade das turmas, o professor precisa estar atento a tais necessidades, revendo sua prática e refletindo sobre as estratégias utilizadas.
Uma das formas de se trabalhar com grupos grandes de fórma mais eficaz é pensar nas tarefas matemáticas propostas. A professora Jo Boaler, autora do livro Mentalidades Matemáticas, propõe o uso das tarefas abertas, pois permite a participação de toda a turma. Segundo ela, toda tarefa pode ser transformada numa tarefa aberta desde que se pergunte aos estudantes “sobre suas diferentes maneiras de ver e resolver questões matemáticas e encorajando a discussão dos diversos modos de ver os problemas” (2018, página 83). Outro ponto é oferecer distintas opções de tarefa com diferentes níveis e áreas da matemática envolvidos, as quais são escolhidas pelo estudante, e não pelo professor. É uma mudança de ponto de vista, o que possibilitará ao estudante escolher suas próprias rotas de aprendizagem, “encontrando conteúdo individualizado, acompanhado por oportunidades para o trabalho em grupo e colaboração” (2018, página 104).
Esta mesma autora também sugere o uso das estratégias equitativas com o objetivo de tornar a Matemática mais inclusiva. Como fórma de melhorar o desempenho coletivo, ela propõe que se ofereçam conteúdos matemáticos de alto nível a todos os estudantes, e não somente àqueles que sempre tiram as melhores notas. Isso está imbricado à outra ideia que precisa ser mudada: a de que somente alguns podem ter êxito na Matemática. Por isso, oportunizar a todos o pensar profundamente a Matemática. Isso implica, por sua vez, trazer experiências práticas, um currículo baseado em projetos e com aplicabilidade na vida real, além de trabalhar colaborativamente, fato que precisa ser ensinado. Trabalhar em grupo é fundamental para um bom desempenho matemático. E por último, é preciso rever a ideia do dever de casa. Para a autora, é necessário mudar a natureza das tarefas, fazendo “perguntas que os incentivem a pensar na Matemática da aula e focar as ideias fundamentais” que são importantes para a aprendizagem (2018, página 94).
Isso tudo dialoga com outra proposta de trabalho, conectada com as atuais necessidades das diferentes turmas de estudante: as metodologias ativas, que, segundo José Moran (2019, página 7), são “alternativas pedagógicas que colocam o foco do processo de ensino e de aprendizagem nos aprendizes, envolvendo-os na aquisição do conhecimento por descoberta, por investigação ou resolução de problemas numa visão de escola como comunidade de aprendizagem (onde há participação de todos os agentes educativos, professores, gestores, familiares e comunidade de entorno e digital)”.
São exemplos de metodologias ativas a aprendizagem baseada em problemas, aprendizagem baseada em projetos e a sala de aula invertida.
• Aprendizagem baseada em problemas: é uma metodologia organizada por temas em torno de problemas e não de disciplinas. Nela os estudantes combinam teoria e prática para solucionar problemas.
• Aprendizagem baseada em projetos: é uma metodologia em que os estudantes se envolvem para resolver um problema ou desenvolver um projeto que tenha relação com a sua vida fóra da sala de aula. Nesta metodologia, eles lidam com questões interdisciplinares e trabalham em equipe.
• Sala de aula invertida: o estudante se apropria do conteúdo previamente, e a aula torna-se o lugar de aprendizagem ativa, onde há perguntas, discussões e atividades práticas. O professor pode explorar as dificuldades dos estudantes em vez de expor o conteúdo da disciplina.
Em todas elas, os recursos tecnológicos podem ou não estar presentes. Quando presentes, o seu uso pode auxiliar o desenvolvimento da autonomia, empatia, protagonismo, responsabilidade, participação e cooperação.
Nesse contexto, é importante também levar em consideração elementos da cultura juvenil (funk, hip-hop, grafite, tatuagem, esportes, entre outros) e os comportamentos construídos por eles nos diferentes contextos sociais e culturais dos quais participam. Ao fazer isso, o processo de construção de conhecimento é enriquecido. Uma das formas de se trabalhar as culturas juvenis com os estudantes é por meio da aprendizagem baseada em projetos que, nesta Coleção, são sugeridos principalmente na seção É hora de extrapolar. Outras possibilidades são as discussões em sala de aula e os fóruns promovidos pela escola. Essa inserção da cultura juvenil ressignifica o espaço escolar, intensifica o processo de reflexão e crítica e promove a aprendizagem.
Assim, é possível vislumbrar possibilidades de aprendizagem para toda a turma, aguçando o olhar inclusivo do professor, que, ao acolher as dificuldades, busca meios para atendê-las, sem deixar de lado os diferentes níveis de conhecimento que habitam a sala de aula.
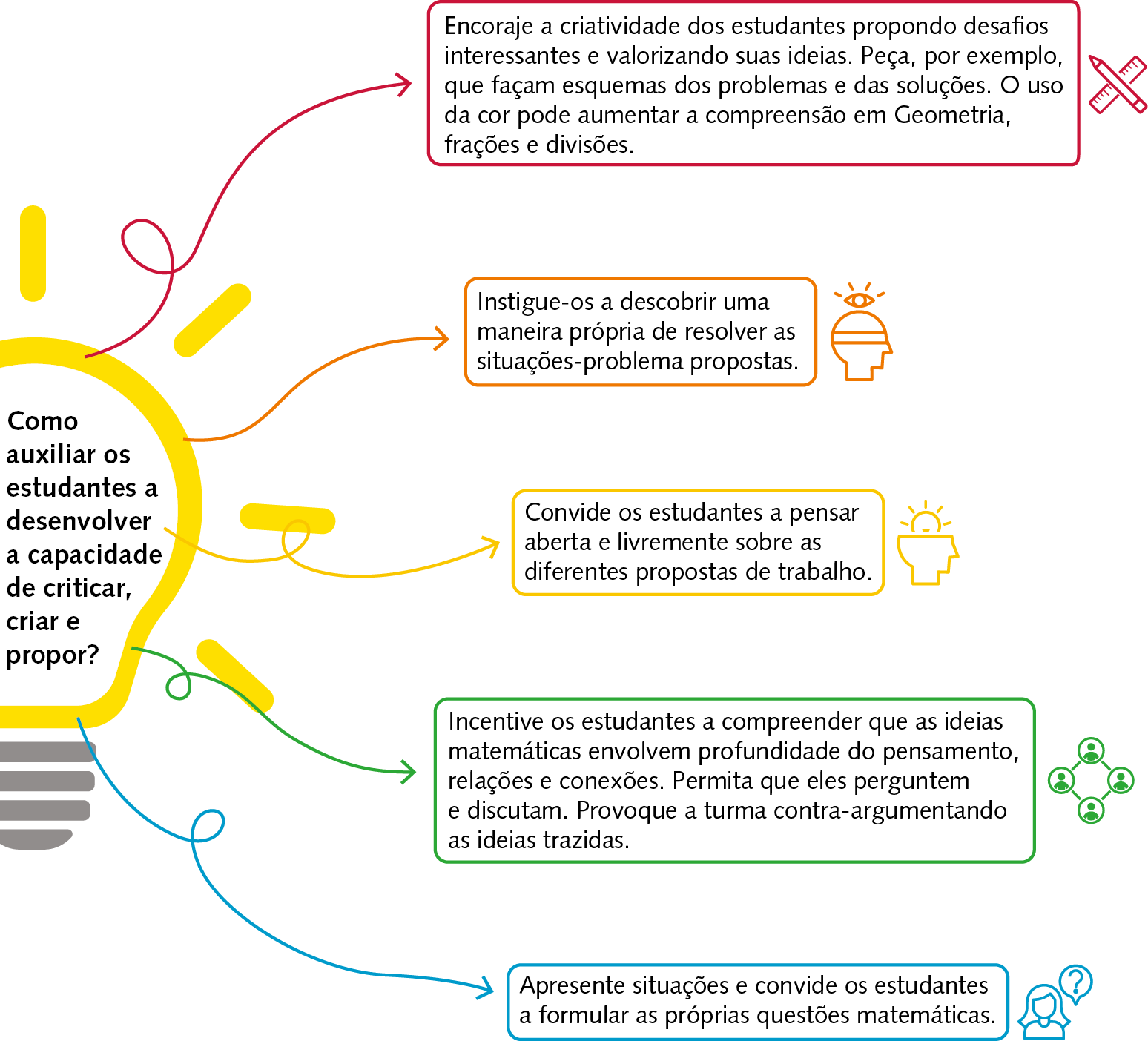
Capacidade de criticar, criar e propor
A criatividade e o pensamento crítico vêm ganhando cada vez mais espaço nas pautas de discussões sobre o que precisamos desenvolver nos estudantes. A criatividade tem relação com o potencial do ser humano para enfrentar o novo e seguir avançando na ciência, na tecnologia, na comunicação, na arte e em outras áreas do conhecimento. Pode ser compreendida também como a elaboração de ideias, processos e ou ou produtos que apresentem algum grau de ineditismo, mesmo que seja para a própria pessoa. O pensamento crítico, por sua vez, é a competência de a pessoa se posicionar de modo racional e analítico diante de diferentes situações cotidianas.
A Matemática é uma área do conhecimento com potencial para desenvolver as capacidades de criticar, criar e propor, na medida em que coloca os estudantes diante de situações em que devem resolver problemas, generalizar propriedades, analisar dados, construir figuras etcétera Para resolver um problema, por exemplo, o estudante precisa, primeiro, entender o enunciado e analisá-lo de maneira crítica. Depois, precisa imaginar como vai solucioná-lo. Em seguida, deve colocar em prática as ideias e, por fim, testar e refletir sobre o que fez.
O infográfico a seguir traz algumas orientações de como ajudar os estudantes a produzir análises críticas, criativas e propositivas:
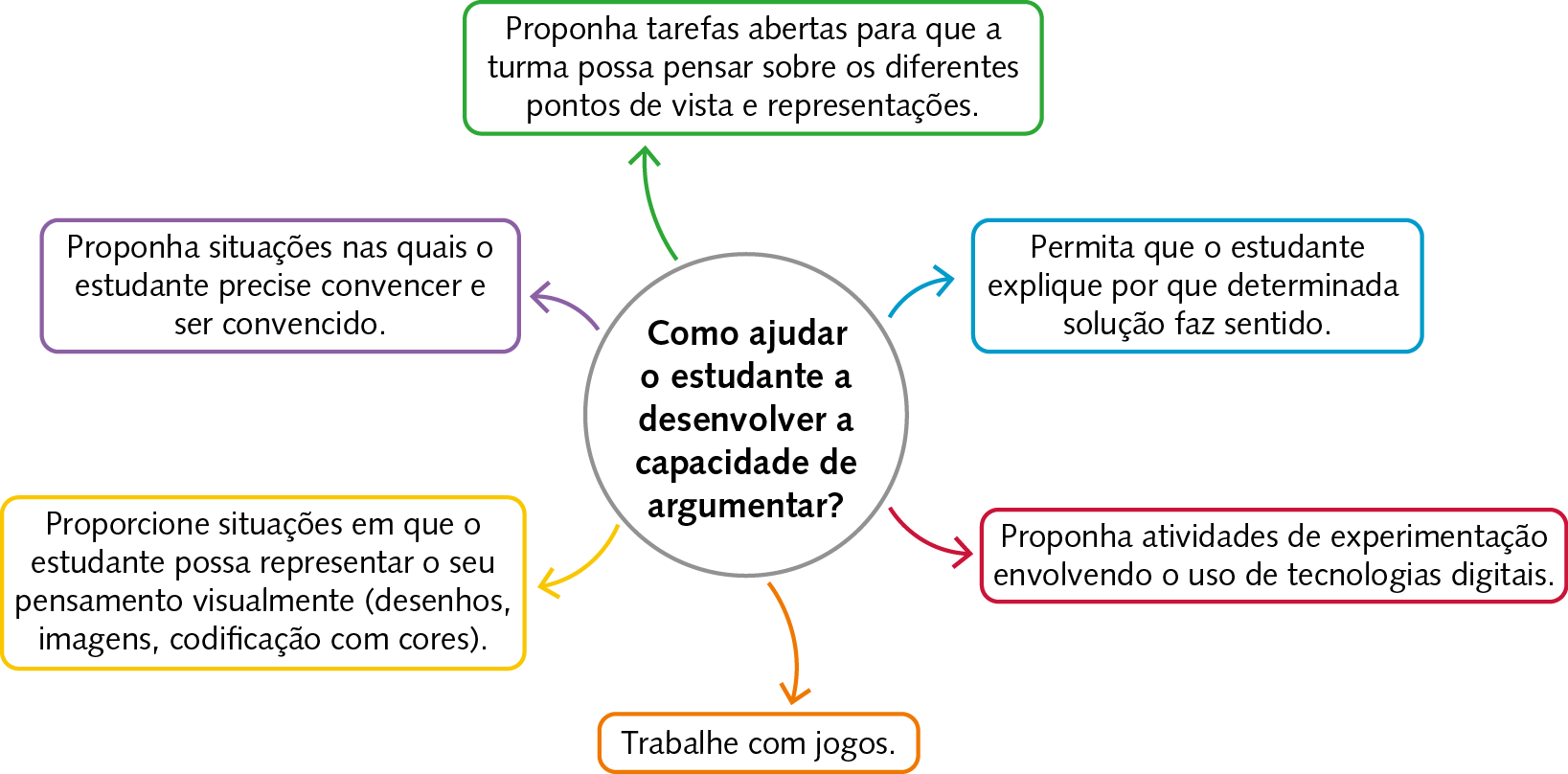
Capacidade de argumentar
A aprendizagem em Matemática muitas vezes é um processo dialógico, ou seja, pressupõe o desenvolvimento da capacidade de argumentar. Na Bê êne cê cê, essa capacidade está prevista nas competências específicas 2 e 4 de Matemática e na competência geral 7 e tem relação com a capacidade do indivíduo de explicar sua fórma de pensar verbalmente ou por escrito.
Em Matemática, os estudantes são incentivados a argumentar quando são colocados diante de situações em que devem resolver problemas, demonstrar propriedades, realizar experimentações, validar ou generalizar resultados, analisar erros, ler e interpretar dados representados em tabelas e/ou gráficos, construir figuras utilizando instrumentos de desenhos etcétera
O esquema a seguir traz algumas sugestões de como auxiliar os estudantes a desenvolver a capacidade de argumentar.
Capacidade de inferir
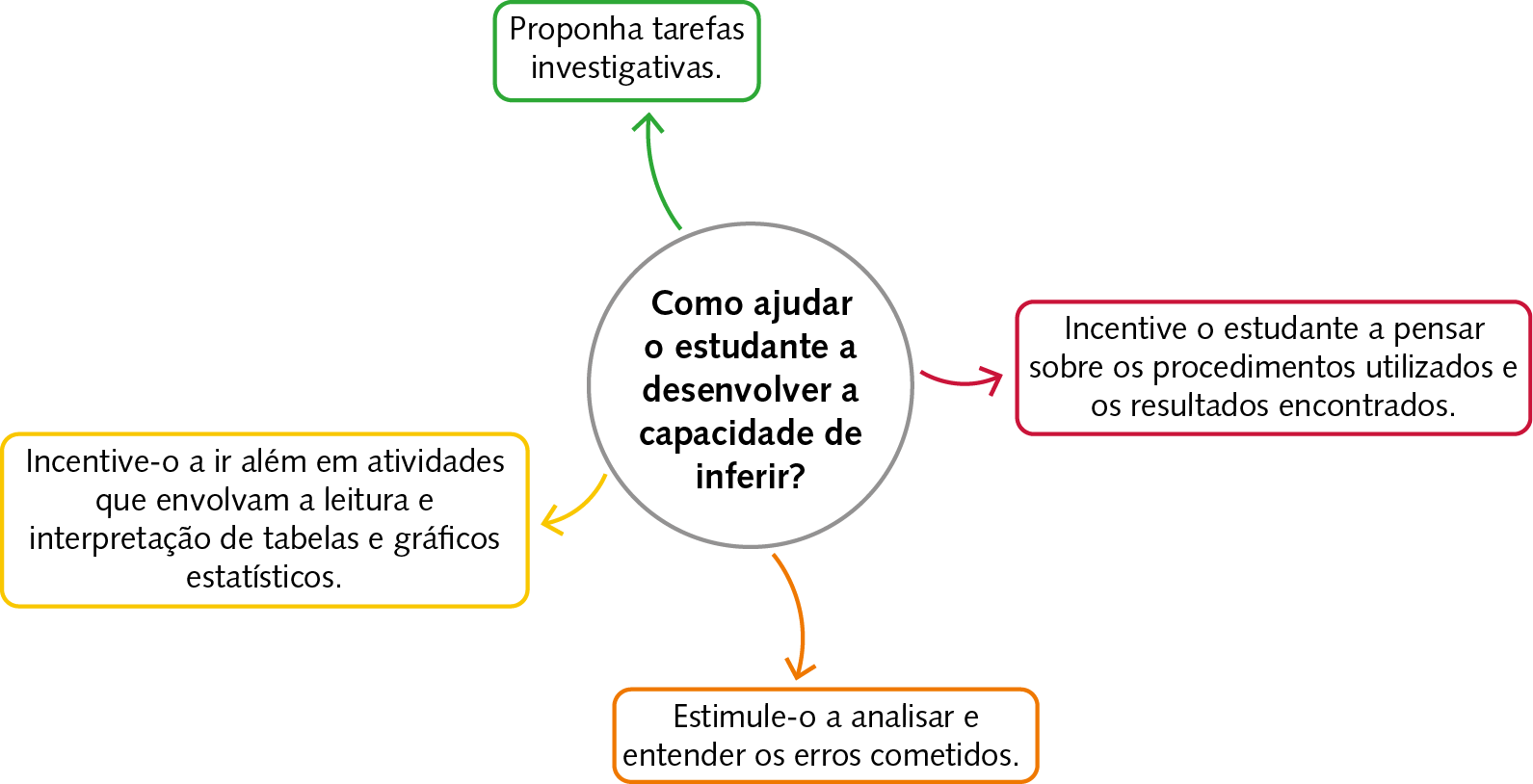
Inferir é tirar conclusões com base em uma ou mais proposições utilizando o raciocínio lógico. Essa é uma habilidade essencial que pode propiciar aprendizagens significativas não só na Matemática, como em outras áreas do conhecimento.
Em Matemática, os estudantes podem inferir informações embasadas em dados estatísticos representados em tabelas e ou ou gráficos. Também podem analisar sequências numéricas e inferir a regra de formação delas ou, ainda, inferir quando realizam tarefas investigativas.
O esquema a seguir traz algumas sugestões de como contribuir para que os estudantes desenvolvam a capacidade de inferir.
A INCLUSÃO DOS ESTUDANTES COM DEFICIÊNCIA
A Lei Brasileira de Inclusão de Pessoa com Deficiência instituiu o Estatuto da Pessoa com Deficiência (Lei 13.146/2015), garantindo, entre outros aspectos, o acesso à educação, e assegurando a inclusão escolar em todos os níveis e modalidades de ensino de acordo com os interesses e as necessidades de aprendizagem de cada um.
Com base nas premissas da lei, uma escola inclusiva é aquela que acolhe e inclui a todos sem discriminação, respeitando as diferenças e dificuldades, acreditando que todos podem aprender e que o processo de aprendizagem de cada pessoa é único, daí ser necessário adequar as estratégias e as condições para que todos possam aprender e desenvolver seu potencial.
As diferentes deficiências (visual, auditiva, intelectual, física, múltiplas) devem ser trabalhadas na sua especificidade para que possa ser garantida a aprendizagem de cada um. As altas habilidades ou superdotação também precisam de um olhar pontual.
Nesse sentido, são grandes os desafios enfrentados pela escola como um todo e pela equipe escolar em particular. Em muitos casos, faz-se necessário a existência de equipe multidisciplinar para orientar as possibilidades de trabalho de acordo com uma necessidade específica. Além, é claro, do investimento na formação continuada do professor e de todos que vão trabalhar com determinado tipo de deficiência ou dificuldade a fim de criar uma rede de apoio, aprimorando os conhecimentos, flexibilizando os materiais e as intervenções com estes e os demais alunos.
Outro ponto a ser destacado refere-se à existência de um projeto pedagógico inclusivo, ou seja, que contenha ações que viabilizem a aquisição de materiais necessários ao atendimento de todas as diferenças bem como a flexibilização do currículo para acolher a realidade de cada um.
A contribuição do professor de Matemática
Cada professor dentro da sua especificidade e com a ajuda da equipe encontrará os melhores meios para adequar as propostas a fim de promover o desenvolvimento da aprendizagem de todos. Contudo, disponibilizar momentos de trocas entre os membros da equipe escolar permitirá aumentar as estratégias e os materiais que possam contribuir para as dificuldades referentes à inclusão.
O professor precisa estar atento ao tipo da deficiência para planejar seu trabalho e fazer as adequações necessárias. Em se tratando de deficiência auditiva, é possível o uso da Língua Brasileira de Sinais (Libras), instituída pela Lei 10.436/2002, a qual é uma combinação do movimento das mãos e de pontos no corpo e no espaço em que os sinais são feitos.

Os algarismos também são representados por sinais. Como são menos, é mais fácil memorizá-los, e você poderá utilizá-los para as explicações:

O ideal seria que todo estudante com deficiência auditiva tivesse um intérprete de Libras que pudesse traduzir as aulas. Outra possibilidade para incluir estes estudantes, é a utilização de vídeos relativos aos conteúdos que contenham intérprete de Libras.
Quando se trata de deficiência visual, pode-se utilizar o Braille: sistema de sinalização ou de comunicação tátil. Este sistema possibilita escrever as atividades e complementar as explicações. Para tanto, é necessário o uso da máquina de escrever Braille. Vale lembrar que outros meios podem ser utilizados pelas pessoas com deficiência visual, como caracteres ampliados, linguagem escrita e oral, dispositivos multimídia, sistemas auditivos e os meios de voz digitalizados.
No que se refere às deficiências intelectuais, é preciso adequar as propostas tendo em vista a idade e as necessidades de cada estudante. O uso de materiais manipulativos é uma estratégia que contribui bastante nesses casos. Neles estão inclusos tampinhas, ábaco, colar de contas, material dourado para a contagem e a construção da ideia de número, canudos, linhas, palitos, massinha para a Geometria Espacial; geoplano, entre outros.
Jogos de tabuleiro, quebra-cabeças e jogos de memória são também ferramentas que possibilitam o trabalho de diferentes conteúdos matemáticos e podem ser adequados aos diferentes graus de dificuldades da turma. As propostas precisam conter desafios possíveis de serem executados, aumentando, posteriormente, as regras, os números de participantes e, até mesmo, o grau de complexidade.
Também, há muitos softwares e programas que podem ser utilizados e que tornam ainda mais significativo o processo de ensino e de aprendizagem quando se trata da inclusão.
Além disso, o uso das metodologias ativas pode ser bastante inclusivo, uma vez que poderá fortalecer o protagonismo dos estudantes por meio de “desafios, atividades e jogos colaborativos; uso de tecnologias; realização de projetos; aprendizado através de problemas e situações reais (informação contextualizada); e a sala de aula invertida” (PAVÃO, A. C. O.; PAVÃO, S. M. O., 2021, página 30). Cabe a cada professor adequar as propostas de acordo com a realidade de sua turma.
A inclusão é um direito. É importante acolher os estudantes com deficiência e dar a eles todas as condições necessárias para que se sintam motivados a desenvolver o seu potencial.
O PROFESSOR E SEU LOCAL DE FALA
Uma das missões do professor é criar ambientes que acolham os estudantes e forneçam uma boa experiência de aprendizado. Nesse contexto, a interação professor/estudantes é fundamental, pois possibilita compreender como vivem, suas necessidades, seus anseios, seu projeto de vida e o que pode motivá-los para ter uma aprendizagem significativa. Por meio dessa interação, é possível explorar problemas reais e buscar as informações de maneira coletiva, reconhecendo que os próprios estudantes podem ser a fonte de conhecimento. É importante encorajar a troca e a construção entre eles e se envolver nas discussões e nos trabalhos.
Esta relação com os estudantes também é uma fórma de criar, valorizar e manter uma cultura de paz dentro das salas de aula e, consequentemente, na comunidade escolar como um todo. De acordo com as orientações da Organização das Nações Unidas para a Educação, a Ciência e a Cultura (Unesco), para promover a cultura de paz nas escolas é preciso construir, no dia a dia, um ambiente pacífico e conciliador. Nesse âmbito, o professor pode desempenhar papel fundamental criando um ambiente de confiança, colocando-se à disposição para ouvir os estudantes e fornecendo condições para que tenham uma conduta respeitosa entre si na sala de aula e além dos muros da escola.
Trabalhar de fórma colaborativa com outros professores da escola e também com os demais profissionais da comunidade escolar como secretários, inspetores, merendeiras etcétera (caso estes tenham interesse) permite criar uma comunidade de aprendizagem que pode ser propícia para a concepção e execução de projetos que respondam às demandas do desenvolvimento humano integral e podem trazer retorno para a própria comunidade ao redor da escola.
INTERDISCIPLINARIDADE
Partindo do pressuposto que o conhecimento não é compartimentado, é necessário investir numa visão interdisciplinar da sua concepção a fim de garantir sua construção de uma fórma global. A interdisciplinaridade, tão discutida desde o século passado, é quando dois ou mais componentes curriculares se relacionam para aprofundar o conhecimento, integrando os saberes e superando essa visão fragmentada.
Podemos dizer que é uma fórma de encontrar conexões entre as áreas do conhecimento para o estudo de um tema de interesse, objetivando responder aos questionamentos por ele gerados. Esse processo dá significação e significado à aprendizagem, permitindo ao estudante estabelecer também ligações com conceitos já estudados e com o seu cotidiano. O que reforça a ideia de que interdisciplinaridade e aprendizagem significativa caminham imbricadas entre si.
Quando um estudante se defronta com um problema, o conhecimento adquirido previamente acerca da situação apresentada não se limita à abordagem unicamente disciplinar, mas ultrapassa-a. Maingain e Dufour (2002) observam que o conhecimento é global, pautado em multidimensão, que não necessariamente se restringem aos componentes curriculares; entretanto, um campo disciplinar oferece as sistematizações necessárias. A combinação das multidimensões e das sistematizações constrói representações de uma situação particular, sendo, portanto, compreendida como uma perspectiva interdisciplinar. Em outras palavras, pensar a interdisciplinaridade na Educação Básica significa estabelecer relação entre as diferentes áreas do conhecimento para além da mera justaposição, mas aquém de uma fusão e, consequentemente, da desintegração do saber disciplinar.
Assim, nesta Coleção, são favorecidas situações de aprendizagem que, para além dos limites de cada componente curricular, incentivam a participação social, a cooperação e a tomada de decisão.
Tudo isso corrobora com a visão interdisciplinar e estabelece um diálogo com a Bê êne cê cê e as competências gerais de aprendizagem, uma vez que permite, também, compreender a realidade, investigar, levantar hipóteses, defender ideias, respeitar a si e ao outro, contextualizando a aprendizagem com as necessidades e os interesses do estudante e favorecendo a tomada de decisões pautadas na ética.
Dessa maneira, o professor, que é pesquisador de sua prática, buscará os melhores caminhos para planejar boas estratégias e exercitar a interdisciplinaridade.
Um deles é o uso das metodologias ativas, como a aprendizagem baseada em projetos. A seção É hora de extrapolar, por exemplo, oferece oportunidades para que sejam desenvolvidos projetos que envolvam temáticas com potencial de mobilizar conhecimentos de diferentes áreas.
Vale ressaltar que, utilizando a ótica de escuta e observação, também é possível elaborar sequências de atividades envolvendo temas de interesse dos estudantes, sem constituir um projeto, mas com o foco interdisciplinar.
Atitudes interdisciplinares
Para que a interdisciplinaridade seja colocada em prática, é necessário que a escola invista na formação continuada de todos os segmentos, de fórma a promover o estudo das necessidades prementes da turma e das novas estratégias para serem colocadas em prática. Aprofundar o conhecimento do professor nas metodologias ativas, por exemplo, permite a prática interdisciplinar.
Criar momentos de interações e trocas entre as equipes gestoras e os professores abre espaço para a discussão das diferentes ideias e da própria prática, por meio de experiências exitosas que permitirão ressignificá-la. Além disso, investir nas reflexões sobre a gestão do tempo em sala de aula é uma fórma de buscar organizar as atividades.
Planejar as sequências do que será trabalhado seja em conjunto com outros professores, seja consigo mesmo é fundamental, bem como garantir momentos para replanejar o que não está dando certo ou que precisa de ajustes.
Outro ponto é trabalhar a pesquisa, aspecto que requer bastante atenção, uma vez que este é um procedimento que precisa ser ensinado e retomado constantemente. Aprender a pesquisar ajuda a investigar as hipóteses e encontrar as soluções.
O uso da gamificação é também uma fórma de promover a interdisciplinaridade. A gamificação consiste em utilizar elementos de jogos e técnicas de design de jogos em contextos diferentes. Em atividades ou propostas gamificadas, espera-se que os estudantes se engajem na resolução de problemas ou na superação de desafios, que aceitem as regras do jogo, que concordem em jogar com pessoas diferentes e que aceitem feedback corretivo para alcançar o resultado desejado. Em resumo, a gamificação não é transformar qualquer atividade em um game, mas, sim, aprender a partir dos games, ou seja, aproveitar elementos dos games que podem melhorar uma experiência de aprendizagem sem ignorar o mundo real.
O trabalho interdisciplinar só é efetivo se for desenvolvido por uma equipe comprometida. Além disso, os professores, mediadores do trabalho interdisciplinar, devem se preocupar mais com o processo do que com o produto. Para auxiliar nesse processo, esta Coleção sugere possibilidades de trabalhos interdisciplinares ao longo das Orientações, mas é importante ressaltar que compete a cada escola e a cada equipe de profissionais definir o projeto que será desenvolvido de acordo com a sua realidade. Nesse sentido, cabe a reflexão e a discussão coletiva para que se realize um trabalho interdisciplinar consistente e coerente com as propostas da escola e que seja enriquecedor para o estudante.
TEMAS CONTEMPORÂNEOS TRANSVERSAIS (tê cê tês)
Em 1996, os Parâmetros Curriculares Nacionais (pê cê ênes) traziam os temas transversais, os quais contemplavam temáticas relacionadas à vida cotidiana e à vida das pessoas. Não eram novas disciplinas curriculares, mas sim áreas do conhecimento que perpassavam os campos disciplinares. Em outras palavras, buscavam inserir questões sociais como objeto de aprendizagem.
Com a Bê êne cê cê, tais conceitos foram ampliados, e os temas contemporâneos transversais foram introduzidos, objetivando explicitar a ligação entre os diferentes componentes curriculares e as situações vivenciadas pelo estudante no cotidiano. Essas situações podem ser relacionadas aos problemas do mundo atual que afligem os estudantes, afetando a vida humana em escala local, regional e global.
Os tê cê tês estão distribuídos em seis macroáreas temáticas: Cidadania e Civismo, Ciência e Tecnologia, Economia, Meio Ambiente, Multiculturalismo e Saúde, englobando 15 temas contemporâneos.
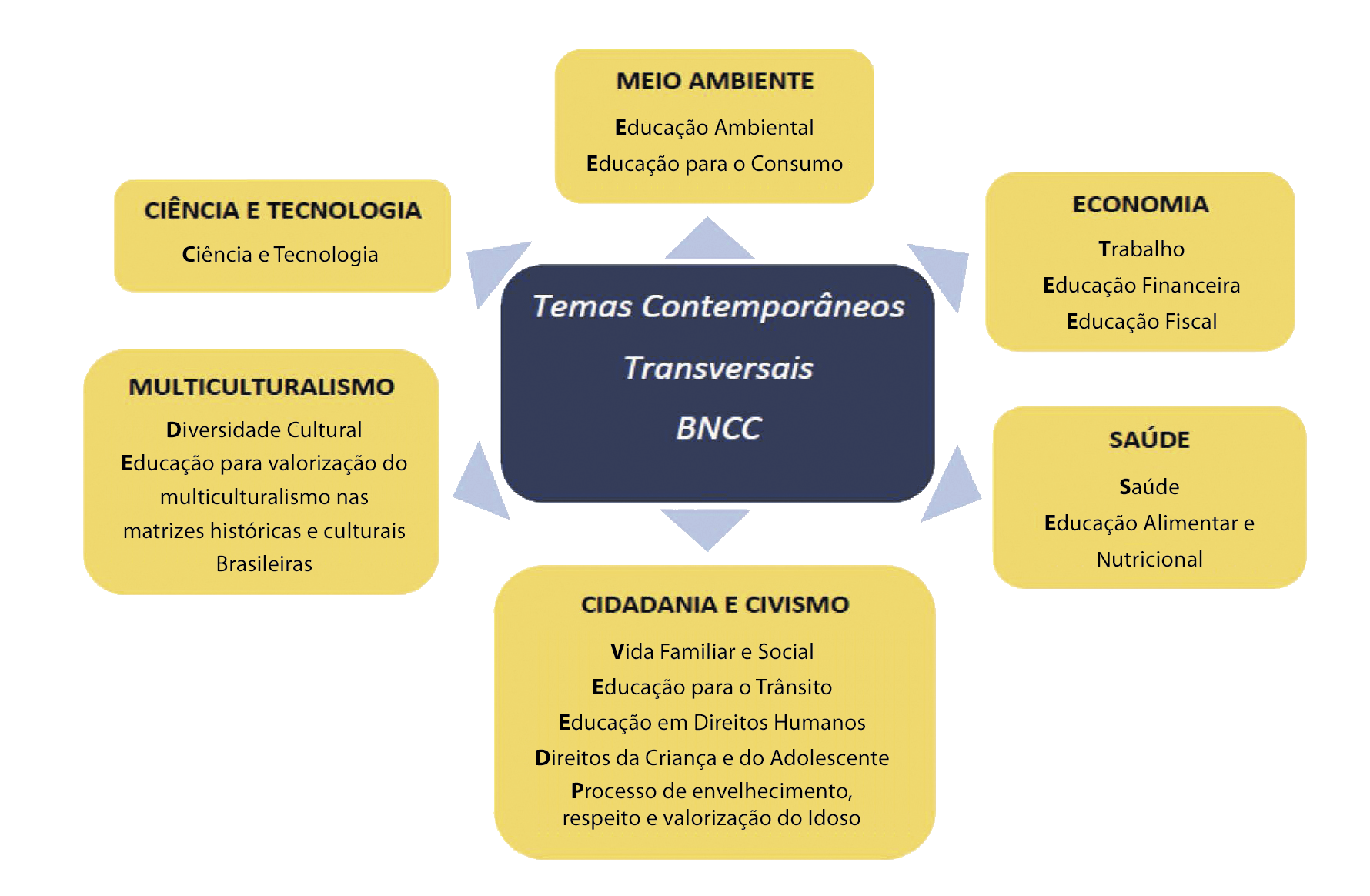
Para que o trabalho aconteça em sala de aula, é imprescindível refletir sobre o que estamos ensinando e o que os estudantes precisam aprender no que se refere a estas temáticas, mapeando quais tê cê tês poderão ser trabalhados atendendo a tais necessidades. Analisar como esses temas podem perpassar a área de conhecimento a partir do conteúdo a ser trabalhado é outro aspecto importante. Por exemplo, ao trabalhar porcentagem em Matemática é possível discutir o consumo e o consumismo (o que realmente necessitamos obter e o que compramos desnecessariamente), bem como a distribuição da renda e o trabalho.
Para isto a leitura e a pesquisa são fundamentais juntamente com as trocas estabelecidas a partir do trabalho em grupo, a socialização das ideias e a sistematização de discussões.
Os tê cê tês na Coleção
Os tê cê tês são abordados em diferentes momentos da Coleção: seções, boxes e atividades diversas. Nesse trabalho, os estudantes são incentivados a refletir, defender suas opiniões e a pesquisar sobre diferentes assuntos. O trabalho muitas vezes dialoga com as competências específicas e gerais da Bê êne cê cê.
Na Coleção, utilizam-se ícones para identificar a possibilidade de trabalho com os tê cê tês.
Ícones que indicam o trabalho com os Temas Contemporâneos Transversais

Cada um destes ícones se relaciona com uma das macroáreas temáticas conforme mostra o quadro a seguir.
|
Macroáreas temáticas |
Meio ambiente |
Economia |
Saúde |
Cidadania e civismo |
Multiculturalismo |
Ciência e tecnologia |
|---|---|---|---|---|---|---|
|
Ícones da Coleção |
|
|
|
|
|
|
O quadro a seguir apresenta um panorama da distribuição do trabalho com os temas contemporâneos transversais ao longo dos capítulos do volume 7.
|
|
|
|
|
|
|
|---|---|---|---|---|---|
|
Capítulos 1, 5, 7, 10 e 12. |
Capítulos 5 e 7. |
Capítulos 1, 5, 7 e 12. |
Capítulos 3, 5 e 8. |
Capítulos 3 e 9. |
Capítulo 7. |
Além dos momentos sinalizados no Livro do Estudante, outros são sugeridos nas Orientações presentes neste Manual do Professor, podendo enriquecer ainda mais as atividades propostas.
A UTILIZAÇÃO DA HISTÓRIA DA MATEMÁTICA
A abordagem de episódios da história da Matemática permite aos estudantes a percepção de que a Matemática não é uma ciência pronta e acabada. Ela se desenvolveu ao longo do tempo e continua se desenvolvendo. Textos breves que trazem informações sobre fatos e pessoas ligadas ao seu desenvolvimento permitem ao professor promover discussões e sugerir pesquisas aos estudantes, com o objetivo de promover a compreensão do desenvolvimento histórico de diferentes conceitos e, consequentemente, ampliar os horizontes da aprendizagem matemática.
No estudo de conteúdos da Geometria, por exemplo, o trabalho com pesquisas que permitam conhecer elementos sobre sua história, os locais onde a Geometria se desenvolveu, as características sociais e geográficas desses locais pode contribuir para a compreensão do contexto no qual o objeto matemático em estudo se desenvolveu.
A aprendizagem matemática tem, assim, como ferramenta didática disponível a história da Matemática, junto à resolução de problemas e à modelagem. Nesta Coleção, o boxe Um pouco de história busca trazer informações que podem servir de ponto de partida para a complementação e o aprofundamento dos conteúdos abordados.
AS TECNOLOGIAS DIGITAIS E O ENSINO DE MATEMÁTICA
Atualmente, tanto a computação como as tecnologias digitais de informação e comunicação (tê dê i cê) estão presentes na sociedade, moldando a comunicação, o meio de transporte, as relações interpessoais e influenciando a vida das pessoas. A ciência e a tecnologia evoluem rapidamente, e essa constante transformação reflete diretamente no funcionamento da sociedade e, consequentemente, no mundo do trabalho e da educação.
A prontidão para a atuação profissional compreende o conhecimento de diversas tecnologias e linguagens, e a escola é um dos ambientes mais propícios para a construção de tal conhecimento. Não cabe ao Ensino Fundamental o preparo de mão de obra especializada. No entanto, em uma época em que as tecnologias digitais estão mais acessíveis, haja vista a quantidade de telefones celulares no Brasil, a escola não pode ficar alheia a essa realidade, deixando de instrumentalizar os estudantes para o uso dessas tecnologias, especialmente para que conheçam os bons e os maus usos delas e que saibam se prevenir.
No que diz respeito à utilização das tecnologias digitais no ensino de Matemática, deseja-se que este uso possibilite a expansão das oportunidades de aquisição de conhecimento – por exemplo, a calculadora e os softwares para a aprendizagem da Matemática devem favorecer, entre outras coisas, a busca por novas estratégias para a resolução de problemas ou o desenvolvimento do raciocínio lógico. Sobre esse assunto, discorre Aguiar (2008, página 64):
A utilização e a exploração de aplicativos e ou ou softwares computacionais em Matemática podem desafiar o estudante a pensar sobre o que está sendo feito e, ao mesmo tempo, levá-lo a articular os significados e as conjecturas sobre os meios utilizados e os resultados obtidos, conduzindo-o a uma mudança de paradigma com relação ao estudo, na qual as propriedades matemáticas, as técnicas, as ideias e as heurísticas passem a ser objeto de estudo.
É importante que o uso do computador na escola não se limite apenas à função do uso dos editores de texto ou de slides; os estudantes devem aprender a utilizá-lo como uma ampliação das faculdades cognitivas e capacidades humanas. A sociedade contemporânea demanda um grande conhecimento tecnológico, não apenas em relação ao uso das tecnologias de maneira eficaz, mas também referente à elaboração de soluções para problemas cotidianos simples ou complexos de qualquer natureza.
Nesta Coleção, o uso de tecnologias digitais é incentivado por meio da seção Tecnologias digitais em foco e também por meio de atividades identificadas pelo ícone Calculadora e softwares:

Calculadora e softwares
A intenção é colocar os estudantes diante de situações em que devem resolver problemas, experimentar, formular hipóteses e argumentar. As propostas podem envolver estratégias como o uso de calculadoras, planilhas eletrônicas e softwares de Geometria dinâmica como o GeoGebra. Nesse contexto, espera-se criar um ambiente favorável para que eles se sintam motivados a aprender cada vez mais e de maneira significativa os conteúdos da disciplina.
PENSAMENTO COMPUTACIONAL
A expressão “pensamento computacional” surgiu em 2006, no artigo Computational Thinking, da pesquisadora Jeanéte Uingue. Nele, Uín relaciona o termo à resolução de problemas de maneira sistemática, decompondo um problema complexo em subproblemas e automatizando a solução, de fórma que pudesse ser executada por uma máquina.
O pensamento computacional se apoia em quatro pilares. São eles:
• Decomposição: consiste em quebrar um problema em partes menores (subproblemas) ou etapas, de maneira que a resolução de cada uma das partes ou etapas resulte na resolução do problema inicial. Dessa maneira, um problema ou uma situação complexa podem ser resolvidos aos poucos, com estratégias e abordagens diversas.
• Reconhecimento de padrões: ocorre ao se perceber similaridade da situação enfrentada com outra previamente resolvida, o que permite o reaproveitamento de uma estratégia conhecida. Esse reconhecimento de padrões pode se dar entre instâncias distintas de um problema ou dentro dele mesmo, quando há repetições de etapas ou padrões em sua resolução.
• Abstração: no contexto do pensamento computacional, significa filtrar as informações e os dados relevantes à resolução, eliminando dados desnecessários. Permite-se, assim, uma modelagem do problema mais limpa e eficaz.
• Algoritmo: a aplicação dos pilares anteriores pode facilitar o surgimento de um algoritmo, que é uma generalização da resolução e permite resolver toda uma família de problemas similares. Um algoritmo pode ser definido como uma sequência finita de passos cuja finalidade é resolver um problema ou executar uma tarefa.
É importante salientar que, dependendo do problema, nem todos os pilares serão necessários e estarão presentes. Além disso, para desenvolver o pensamento computacional e trabalhar com ele em sala de aula, apesar de a intenção ser a implementação computacional de uma solução, não é necessário um computador.
O pensamento computacional na Coleção
A Bê êne cê cê considera que a aprendizagem de Álgebra contribui para o desenvolvimento do pensamento computacional dos estudantes, uma vez que precisam mobilizar diferentes linguagens para traduzir situações-problema. Além disso, o documento destaca que:
Associado ao pensamento computacional, cumpre salientar a importância dos algoritmos e de seus fluxogramas, que podem ser objetos de estudo nas aulas de Matemática. Um algoritmo é uma sequência finita de procedimentos que permite resolver um determinado problema. Assim, o algoritmo é a decomposição de um procedimento complexo em suas partes mais simples, relacionando-as e ordenando-as, e pode ser representado graficamente por um fluxograma. A linguagem algorítmica tem pontos em comum com a linguagem algébrica, sobretudo em relação ao conceito de variável. Outra habilidade relativa à álgebra que mantém estreita relação com o pensamento computacional é a identificação de padrões para se estabelecer generalizações, propriedades e algoritmos (BRASIL, 2018, página 271).
Nesta Coleção, são propostas diferentes atividades envolvendo construção, leitura e interpretação de fluxogramas. Essas atividades favorecem o desenvolvimento da competência especifica 6 de Matemática e da competência geral 4 da Bê êne cê cê e são identificadas pelo ícone Pensamento computacional.

Pensamento computacional
Na Coleção, os fluxogramas também são utilizados na sistematização de alguns conteúdos.
De modo geral, o pensamento computacional também está presente, na Coleção, por meio da aplicação de algoritmos e procedimentos (algoritmos das operações, métodos para determinar o mmc ou mdc de números naturais, aplicação da fórmula resolutiva de equações do 2º grau etcétera), reconhecimento de padrões em sequências numéricas ou de figuras e, também, quando se propõe a elaboração e ou ou resolução de problemas.
SUGESTÕES DE CRONOGRAMAS
O quadro a seguir oferece ao professor possibilidades de trabalho com os capítulos do volume 6 da Coleção durante o ano letivo. O professor pode e deve se sentir à vontade para adaptar as sugestões aqui indicadas de acordo com a realidade e as necessidades da turma e da escola, uma vez que a aprendizagem depende da combinação de muitos fatores e, por conseguinte, os métodos e as estratégias que se mostram eficientes com um grupo de estudantes podem não ter o mesmo resultado com outro.
O arranjo desse quadro possibilita ao professor a previsão de uma organização bimestral, trimestral ou semestral.
|
Capítulos do volume 7 |
Bimestres |
Trimestres |
Semestres |
|
|---|---|---|---|---|
|
UNIDADE 1 |
Capítulo 1 ‒ Números inteiros |
1º bimestre |
1º trimestre |
1º semestre |
|
Capítulo 2 ‒ Múltiplos e divisores |
||||
|
Capítulo 3 ‒ Retas e ângulos |
||||
|
UNIDADE 2 |
Capítulo 4 ‒ Frações |
2º bimestre |
||
|
Capítulo 5 ‒ Números racionais |
2º trimestre |
|||
|
Capítulo 6 ‒ Linguagem algébrica e regularidades |
||||
|
UNIDADE 3 |
Capítulo 7 ‒ Porcentagem e juro simples |
3º bimestre |
2º semestre |
|
|
Capítulo 8 ‒ Proporcionalidade |
||||
|
Capítulo 9 ‒ Transformações geométricas |
3º trimestre |
|||
|
UNIDADE 4 |
Capítulo 10 ‒ Grandezas e medidas |
4º bimestre |
||
|
Capítulo 11 ‒ Figuras geométricas planas |
||||
|
Capítulo 12 ‒ Probabilidade e estatística |
ORIENTAÇÕES PARA AVALIAÇÃO
Avaliar é algo complexo e muito discutido entre as equipes escolares, principalmente quando almeja-se uma avaliação focada na evolução e no desenvolvimento das aprendizagens dos estudantes. Para isso, é necessário ir além da simples demonstração dos resultados, trazendo o “percurso, os obstáculos e os novos caminhos a serem percorridos para o alcance dos objetivos ainda não atingidos”.
A Bê êne cê cê vem propor uma ressignificação da avaliação, uma vez que há uma progressão na aquisição das habilidades, o que implica buscar mecanismos que mostrem o desenvolvimento do estudante no processo de ensino e de aprendizagem, no que se refere à aquisição ou não de tais habilidades.
Para isso é preciso refletir sobre o que avaliar e como fazê-lo. O professor precisa ter claro o que espera que cada turma aprenda em cada situação didática planejada. Necessita planejar intervenções que levem em consideração as orientações nacionais, mas também as necessidades de cada turma e cada estudante em particular.
É importante que as avaliações sejam aplicadas de fórma contínua ao longo do processo educativo. A análise dos dados obtidos ao longo desse caminhar permitirá ao professor reorientar o processo de ensino e de aprendizagem. Ao estudante, fornecerá elementos para reforçar e incentivar a aprendizagem, tornando-se, assim, parte ativa do seu processo de aprendizagem.
Vários são os instrumentos que permitem ao professor obter as informações necessárias para o melhor planejamento, assim como atender à necessidade de quantificação da aprendizagem: atribuir uma nota ou um conceito. Destaca-se a importância da utilização de vários instrumentos simultaneamente, de fórma a melhorar as oportunidades para que o estudante mostre efetivamente o que aprendeu (ou o que não aprendeu e precisa ser retomado pelo professor). Por exemplo: provas, relatórios, autoavaliação, trabalhos em equipe, participação em discussões orais, abertura para expor dúvidas e, especialmente, a possibilidade de discutir seus erros, compreender por que errou e corrigi-los.
Cabe ao professor, com base no conhecimento que tem de suas turmas, escolher os instrumentos mais adequados aos objetivos fixados em seu plano de ensino. Algumas dessas medidas são subjetivas, mas os critérios utilizados devem ser explicitados aos estudantes.
Entretanto, independentemente do instrumento escolhido, é necessário registrar os resultados obtidos por meio de pautas de observação, registros escritos ou audiovisuais e portfólios, a fim de acompanhar o desenvolvimento de cada um. A seguir, apresentamos uma sugestão de quadro que você pode utilizar para avaliar algumas capacidades desenvolvidas pelos estudantes ao longo do ano letivo.

|
Nome: _____ |
|||
|
Turma: _____ |
Data: ___/___/___ |
||
|
Capacidade avaliada |
Desempenho individual |
||
|---|---|---|---|
|
Plenamente satisfatório |
Satisfatório |
Insatisfatório |
|
|
Elaborar e resolver problemas. |
|||
|
Compreender conceitos e procedimentos. |
|||
|
Realizar cálculos mentais. |
|||
|
Mobilizar diferentes linguagens e registros. |
|||
|
Compreender textos publicados em diferentes mídias. |
|||
|
Mobilizar conhecimentos de diferentes unidades temáticas. |
|||
|
Realizar investigações utilizando tecnologias digitais. |
|||
|
Criticar, criar e propor. |
|||
|
Argumentar. |
|||
|
Inferir. |
|||
|
Construir, ler e interpretar tabelas e gráficos estatísticos. |
|||
|
Trabalhar em equipe. |
|||
O professor pode e deve se sentir à vontade para definir o critério que vai utilizar durante o preenchimento do quadro e até mesmo pode mudar as capacidades avaliadas, de acordo com a realidade da sua turma ou da escola em que trabalha. Também podem ser feitas versões similares do mesmo quadro, levando em consideração as habilidades e competências da Bê êne cê cê.
Outro ponto é a necessidade de não limitar a avaliação aos aspectos cognitivos, uma vez que a formação do estudante deve ser a mais completa: aspectos comportamentais, atitudinais, também, devem ser considerados. Lembramos que um objetivo a ser fixado é o de uma educação democrática, inclusiva, e a avaliação tem papel fundamental nesse processo.
Na Coleção, as atividades da seção Revisão de conteúdos de anos anteriores podem compor avaliações diagnósticas e as atividades da seção Revisão dos conteúdos deste capítulo, por sua vez, podem servir para que sejam elaboradas avaliações formativas.
Propomos a seguir sugestões de avaliações de caráter formativo abre parêntesesuma relacionada a cada capítulo do Livro do Estudantefecha parênteses e uma sugestão de avaliação de preparação para exames de larga escala.
Sugestões de avaliação formativa
Para o capítulo 1: Números inteiros
|
Questões |
Objetivos |
|---|---|
|
1 |
Comparar números na reta numérica. |
|
2 |
Resolver situação-problema com adição e subtração de números inteiros. |
|
3 |
Resolver situação-problema com subtração de números inteiros. |
|
4 |
Calcular multiplicação com números inteiros. |
|
5 |
Calcular divisão com números inteiros. |
|
6 |
Calcular potenciação e raiz quadrada com números inteiros. |
1. Observe a reta numérica a seguir e classifique as afirmações em verdadeiras ou falsas.
a) O oposto do número correspondente ao ponto B é o número correspondente ao ponto a.
b) O módulo do número correspondente ao ponto D é positivo.
c) O número correspondente ao ponto C é maior do que o número correspondente ao ponto D.
d) Os números correspondentes aos pontos dêêa são simétricos.
2. Tiago pegou R$ 80,00oitenta reais emprestados de José na semana passada. Nesta semana precisou pedir outro empréstimo de R$ 120,00cento e vinte reais a José. Tiago conseguiu pagar R$ 50,00cinquenta reais. A dívida dele ficou em:
a) R$ 10,00dez reais.
b) R$ 90,00noventa reais.
c) R$ 150,00cento e cinquenta reais.
d) R$ 250,00duzentos e cinquenta reais.
3. Maísa realizou uma viagem de avião para um país muito frio. Quando ela embarcou, no Brasil a medida de temperatura era 20 graus Célsius. No país de destino, quando ela desembarcou, a medida de temperatura era menos8 graus Célsius. A diferença dessas medidas de temperaturas foi de:
a) menos28 graus Célsius
b) menos12 graus Célsius
c) 12 graus Célsius
d) 28 graus Célsius
4. Observe os cálculos feitos por quatro estudantes e identifique o que está errado. Depois, refaça-o corretamente.
Maiara: (−18fecha parênteses ⋅ (−6fecha parênteses = +108
Carlos: (−7fecha parênteses ⋅ abre colchete abre parêntese+3fecha parênteses + (−5fecha parêntese fecha colchete = menos26
Agnaldo: (−10fecha parênteses ⋅ [(−6fecha parênteses menos (−8fecha parêntese fecha colchete = menos20
Elis: (−12fecha parênteses ⋅ abre parênteses+10fecha parênteses ⋅ (−5fecha parênteses = +600
5. Elaine escolheu um número e o dividiu por menos 4, obtendo quociente 15 e resto 0. Qual foi o número que Elaine escolheu? E se ela tivesse escolhido o oposto desse número, qual seria o quociente obtido?
6. Analise cada item e classifique-o como verdadeiro ou falso.
a) abre parênteses+8)⁰ = 1 e (−8)⁰ = menos1.
b) menos10elevado a 4 = −(10 ⋅ 10 ⋅ 10 ⋅ 10fecha parênteses = menos.10000.
c)
Menos raiz quadrada de 324, é igual a menos 18.d)
Raiz quadrada de menos 196 é igual a menos 14.Respostas
1. a. Verdadeira; b. Verdadeira; c. Falsa; d. Falsa
2. alternativa c
3. alternativa d
4. A multiplicação errada é a de Carlos. O correto é abre parênteses−7fecha parênteses ⋅ abre colchete abre parêntese+3fecha parênteses + (−5fecha parêntese fecha colchete = 14.
5. Elaine escolheu menos60. Caso ela tivesse escolhido 60, o quociente seria menos15.
6. a. Falso; b. Verdadeiro; c. Verdadeiro; d. Falso
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero três. Os estudantes precisam observar a posição dos pontos ei, B, C e D na reta numérica e lembrar a definição de módulo, oposto e simétrico de um número inteiro. É possível que alguns deles considerem que os pontos dêêa representam números simétricos apenas por estarem à mesma distância do ponto que corresponde ao número menos3. Em caso de dificuldades, oriente-os a, primeiro, determinar os números que correspondem aos pontos a, B, C e D e, depois, avaliar as afirmações. Se achar pertinente retome os conceitos explorados na questão com a turma.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero quatro. Essa questão apresenta o contexto de empréstimo. Os estudantes precisam perceber que a dívida de Tiago é calculada ao adicionar os valores dos empréstimos e subtrair o valor pago. Oriente-os a fazer um esquema da situação. Isso poderá ajudá-los a saber quais valores devem ser adicionados e subtraídos.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero quatro. Essa questão envolve comparação de medidas de temperatura. Para resolvê-la, os estudantes precisam perceber que uma medida de temperatura é positiva, enquanto a outra é negativa. Para calcular a diferença eles podem fazer 20 graus Célsius menos (−8 graus Célsiusfecha parênteses = 20 graus Célsius + 8 graus Célsius = 28 graus Célsius. Caso tenham dificuldades para realizar esse cálculo, oriente-os a utilizar a reta numérica como apoio.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero quatro. Os estudantes precisam analisar os cálculos realizados e identificar o que está errado. Espera-se que percebam que Carlos não fez o cálculo corretamente. Você pode pedir a eles que façam os mesmos cálculos no caderno e comparem o resultado obtido com o de Maiara, o de Carlos, o de Agnaldo e o de Elis. Dessa fórma, poderão perceber mais facilmente qual deles errou e identificar o possível erro.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero quatro. Essa questão apresenta uma situação envolvendo divisão exata com números inteiros. Os estudantes precisam recordar a relação fundamental da divisão para descobrir o dividendo que Elaine escolheu. Além disso, para a segunda pergunta, precisam perceber a relação entre os sinais do dividendo, divisor e quociente. Em caso de dificuldades, pode-se recordar divisão exata.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero quatro. Em cada item dessa questão, os estudantes devem analisar cálculos de potências e raízes envolvendo números inteiros. No item a, espera-se que percebam que todo número elevado a zero é igual a zero, portanto, é falso que (−8)⁰ = menos1. Já no item d, espera-se que eles recordem a definição de raiz quadrada e percebam que a raiz quadrada de um número inteiro negativo não é um número inteiro, pois o quadrado de um número inteiro nunca é negativo.
Para o capítulo 2: Múltiplos e divisores
|
Questões |
Objetivos |
|---|---|
|
1 |
Identificar múltiplos e divisores. |
|
2 |
Identificar múltiplos de um número inteiro. |
|
3 |
Identificar divisores de um número inteiro. |
|
4 |
Identificar mdc e mmc de números. |
|
5 |
Resolver situação-problema envolvendo mdc de números. |
|
6 |
Resolver situação-problema envolvendo mmc de números. |
1. Leia cada afirmação e classifique-a em verdadeira ou falsa.
a) 5 é divisível por 250.
b) 3 é múltiplo de 30.
c) 10 é divisor de 100.
d) 40 é múltiplo de 2.
2. Dos números a seguir, qual não é múltiplo de 16?
a) menos96
b) menos60
c) 48
d) 128
3. Após estudar divisores de números inteiros, quatro estudantes fizeram as seguintes afirmações.
Antônio: O número 1 é divisor de qualquer número inteiro.
Beatriz: Os divisores de 5 são menos5, menos1, 0, 1 e 5.
Samara: Os divisores de 4 são menos4, menos2, menos1, 1, 2 e 4.
Reinaldo: O número 1 tem apenas dois divisores.
Qual deles disse algo errado? Explique o porquê.
4. Observe a decomposição dos seguintes números:
24 = 2elevado a 3 ⋅ 3
60 = 2elevado a 2 ⋅ 3 ⋅ 5
O resultado de 2elevado a 3 ⋅ 3 ⋅ 5 é o:
a) máximo divisor comum de 24 e 60.
b) mínimo divisor comum de 24 e 60.
c) máximo múltiplo comum de 24 e 60.
d) mínimo múltiplo comum de 24 e 60.
5. Na escola em que Victor estuda, o 7º ano ei tem 32 estudantes, o 7º ano B tem 28 estudantes e o 7º ano C tem 24 estudantes. Será realizada uma atividade com as três turmas de modo que os estudantes de cada turma sejam divididos em grupos de mesma quantidade e com a maior quantidade de estudantes possível. Quantos grupos serão formados?
a) 4
b) 21
c) 42
d) 84
6. Daniel tem um pequeno ateliê em que trabalham três máquinas. Ele costuma fazer manutenção preventiva delas com frequência. A manutenção da mais nova ele faz de 16 em 16 dias e a da mais velha, de 4 em 4 dias. Para a máquina do meio, a manutenção ocorre de 8 em 8 dias. Se ele fez a manutenção das três máquinas hoje, daqui a quantos dias isso vai ocorrer novamente?
a) 4 dias.
b) 8 dias.
c) 16 dias.
d) 32 dias.
Respostas
1. a. Falsa; b. Falsa; c. Verdadeira; d. Verdadeira
2. alternativa b
3. Beatriz disse algo errado, pois ela incluiu o 0 na lista de divisores de 5.
4. alternativa d
5. alternativa b
6. alternativa c
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero um. Essa questão explora os conceitos de múltiplos e divisores de números naturais. Eles podem cometer equívocos na interpretação de cada termo. Caso isso ocorra, convém retomar cada um desses conceitos com eles.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero um. Os estudantes precisam identificar o número que é múltiplo de 16, ou seja, o número que é obtido multiplicando-se 16 por outro número inteiro. Outra maneira de interpretar esse enunciado é identificar o número divisível por 16. Você pode orientar os estudantes a dividir cada um dos números por 16 e verificar se a divisão é ou não exata ou incentivá-los a fazer cálculos mentais.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero um. Os estudantes precisam analisar cada afirmação para identificar a falsa. Espera-se que eles recordem que o 0 é múltiplo de qualquer número inteiro, porém não é divisor de nenhum número inteiro, já que não existe divisão por 0. Proponha aos estudantes que façam divisões ou multiplicações caso tenham dificuldades em reconhecer se um número é divisor de outro.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero um. Essa questão apresenta a decomposição de dois números em fatores primos e um produto. Os estudantes precisam comparar esse produto com as decomposições para perceber que se trata do mínimo múltiplo comum de 24 e 60. Eles podem cometer equívocos na interpretação desse produto. Caso isso ocorra, pode-se retomar o conceito de ême dê cê e ême ême cê. Para ampliar a questão, pode-se pedir-lhes que determinem o mdc de 24 e 60, ou seja, 2elevado a 2 ⋅ 3 = 12.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero um. Essa questão apresenta uma situação que envolve o máximo divisor comum entre as quantidades de estudantes das três turmas do 7º ano. Os estudantes precisam compreender que a questão envolve grupos de estudantes de cada turma, mas com a mesma e maior quantidade, portanto, é necessário calcular o máximo divisor comum de 32, 28 e 24. Com isso, vão descobrir que cada grupo terá 4 estudantes. Ao calcular abre parênteses32 dividido por 4fecha parênteses + abre parênteses28 dividido por 4fecha parênteses + abre parênteses24 dividido por 4fecha parênteses, descobrem a quantidade de grupos. Eles podem se equivocar na interpretação do problema ou do resultado. Em caso de dificuldades, convém propor-lhes situações similares a essa.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero um. Essa questão apresenta uma situação que envolve o mínimo múltiplo comum de três números. Espera-se que os estudantes percebam que a manutenção de cada máquina ocorre nos múltiplos de 4, 8 e 16, conforme o enunciado. Assim, ao calcular o mínimo múltiplo comum desses números, vão descobrir em quantos dias a manutenção ocorrerá novamente. Em caso de dificuldades, resolva com eles problemas similares.
Para o capítulo 3: Retas e ângulos
|
Questões |
Objetivos |
|---|---|
|
1 |
Reconhecer a posição relativa de retas e semirretas. |
|
2 |
Resolver problemas envolvendo medidas de abertura de ângulos. |
|
3 |
Resolver problemas envolvendo medidas de abertura de ângulos. |
|
4 |
Efetuar operações com medidas de abertura de ângulos. |
|
5 |
Aplicar a propriedade de que dois ângulos opostos pelo vértice são congruentes. |
|
6 |
Reconhecer relações entre as medidas de abertura de ângulos formados por duas retas paralelas cortadas por uma transversal. |
1. Observe a posição das retas e semirretas representadas a seguir e classifique cada afirmação em verdadeira ou falsa.
a) s e r são semirretas concorrentes.
b) têêu são semirretas paralelas.
c) têêu são retas paralelas.
d) s e r são retas paralelas.
2. Inês representou um ângulo de meia-volta em uma folha de papel. Depois, traçou um segmento de reta que intercepta e é perpendicular às semirretas que formam o ângulo representado. Com isso, ela vai obter quatro ângulos cuja abertura mede:
a) 45graus
b) 90graus
c) 180graus
d) 360graus
3. Rubi representou um pentágono regular e, utilizando um transferidor, obteve a medida da abertura do ângulo interno. Sabendo disso, percebeu que a medida da abertura do ângulo externo
Ângulo CDF.é:
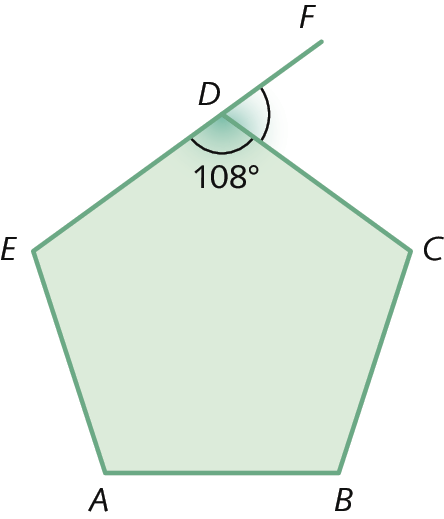
a) 45graus
b) 72graus
c) 90graus
d) 108graus
4. Jonas representou um ângulo cuja abertura tem medida igual a 18graus 32minutos. Mateus representou um ângulo cuja abertura tem medida 56minutos maior do que o de Jonas. Laís representou um ângulo com abertura cuja medida é o triplo da medida da abertura do ângulo representado por Jonas. Mônica representou um ângulo que tem metade da medida da abertura do ângulo representado por Jonas. Com base nessas informações, calcule a medida da abertura de cada ângulo representado.
5. Considere as duas retas a seguir e a medida da abertura do ângulo indicado para determinar a medida da abertura dos ângulos
Ângulo AED.,
Ângulo DEB.e
Ângulo BEC..
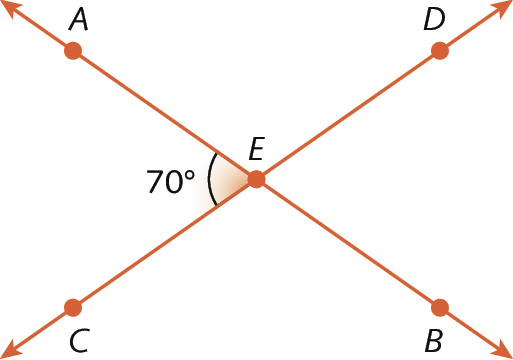
6. A figura a seguir apresenta duas retas paralelas cortadas por uma transversal e as indicações dos ângulos. Com base nela, classifique cada afirmação em verdadeira ou falsa.
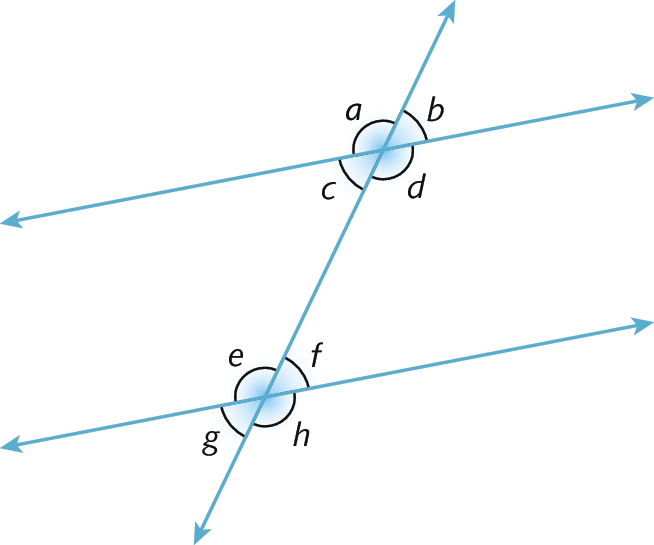
a) Os ângulos aêdê são correspondentes.
b) Os ângulos dêêê são colaterais internos.
c) Os ângulos aêgê são colaterais externos.
d) Os ângulos aêagá são alternos externos.
Respostas
1. a. Verdadeira; b. Falsa; c. Verdadeira; d. Falsa
2. alternativa b
3. alternativa b
4. Mateus: 19graus 28minutos; Laís: 55graus 36minutos; Mônica: 9graus 16minutos.
5.
Medida do ângulo AED é igual a 110 graus.;
Medida do ângulo DEB é igual a 70 graus.;
Medida do ângulo BEC é igual a 110 graus..
6. a. Falsa; b. Falsa; c. Verdadeira; d. Verdadeira
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois três. Os estudantes precisam avaliar afirmações sobre a posição relativa de retas e semirretas representadas na questão. Verifique se conseguem distinguir os dois conceitos e se utilizam o vocabulário adequado. Caso alguns estudantes tenham dificuldades, retome o estudo da posição relativa entre retas e estenda esse estudo para as semirretas.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois três. Os estudantes precisam recordar que a abertura de um ângulo de meia-volta mede 180graus. Assim, ao traçar um segmento de reta que intercepta as semirretas que formam esse ângulo e é perpendicular a elas, obtém-se quatro ângulos retos. Oriente-os a fazer um esboço da situação.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois três. Espera-se que os estudantes reconheçam que o ângulo externo é adjacente e suplementar ao ângulo interno correspondente, ou seja, a soma das medidas de suas aberturas é igual a 180graus. Assim, basta fazer 180graus ‒ 108graus para descobrir a medida da abertura de
ângulo CDF. Recorde os conceitos de ângulo adjacente e suplementar caso ache pertinente.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois três. Essa questão apresenta a medida da abertura de um ângulo inicial e operações realizadas com essa medida. Oriente-os a realizar a questão em 3 etapas, a primeira correspondendo ao cálculo da medida da abertura do ângulo representado por Mateus, a segunda ao cálculo da medida da abertura do ângulo representado por Laís e, a última, correspondendo ao cálculo da medida da abertura do ângulo representado por Mônica. Você pode incentivá-los a fazer os cálculos mentalmente. Deixe-os à vontade para empregar a estratégia que julgarem mais conveniente. Depois reserve um momento para que possam compartilhá-la. Isso não só amplia o repertório de cálculo deles, como pode auxiliar os estudantes que apresentaram dificuldades.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois três. Os estudantes precisam recordar a relação entre as medidas de abertura de ângulos opostos pelo vértice para determinar as medidas de abertura dos ângulos do enunciado. Recorde os conceitos de ângulos opostos pelo vértice e de ângulos congruentes, caso ache necessário.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois três. Essa questão apresenta duas retas paralelas cortadas por uma transversal e os estudantes precisam avaliar afirmações a respeitos dos ângulos formados. Essa questão mobiliza os conceitos de ângulos alternos internos, alternos externos, colaterais internos, colaterais externos e correspondentes. Em caso de dificuldades, pode-se retomar esses conceitos e apresentar exemplos.
Para o capítulo 4: Frações
|
Questões |
Objetivos |
|---|---|
|
1 |
Aplicar a ideia de fração como parte de um inteiro. |
|
2 |
Aplicar a ideia de fração como quociente. |
|
3 |
Aplicar a ideia de fração como razão. |
|
4 |
Aplicar a ideia de fração como operador. |
|
5 |
Aplicar a ideia de fração como parte de um inteiro e operador. |
1. O celular de Maciel fica com 100% de bateria quando totalmente carregado. Atualmente descarregou 75%. Que fração da bateria ainda resta para o celular?
a)
Fração. 1 sobre 4.b)
Fração. 3 sobre 4.c)
Fração. 4 sobre 3.d)
Fração. 4 sobre 1.2. Renata convidou Marcelo, Tiago e Luiza para um lanche da tarde em casa. Entre outras comidas, ela preparou 12 bolinhos de arroz para distribuir igualmente aos participantes do lanche. Sobre essa situação, avalie cada afirmação e classifique-a como verdadeira ou falsa.
a) Se tivesse um convidado a mais e a quantidade de bolinhos se mantivesse, cada convidado receberia menos bolinhos.
b) A fração que representa a distribuição dos bolinhos é
Fração. 12 sobre 3..
c) A fração que representa a distribuição dos bolinhos é
Fração. 4 sobre 12..
d) Cada participante do lanche recebeu 3 bolinhos de arroz.
3. Um sorteio será realizado entre as turmas do 7º ano da escola em que Fabrício estuda. A turma do 7º ano a tem 30 estudantes, a do 7º ano B tem 32 estudantes e a do 7º ano C tem 30 estudantes. Acompanhe o que três estudantes disseram sobre isso.
Fabrício: A probabilidade de sortear alguém do 7º ano a é
Fração. 30 sobre 92..
Elisa: A probabilidade de sortear alguém do 7º ano a é
15 sobre 46.
Josué: A probabilidade de sortear alguém do 7º ano B é maior do que a probabilidade de sortear alguém do 7º ano a. Quem fez uma afirmação correta?
4. Um processo seletivo para vagas de emprego vai ser realizado em duas etapas. Da primeira para a segunda, serão selecionados
dois terçosdos candidatos que foram inscritos. Sabendo que na primeira etapa há duzentas e treze pessoas, quantas vão para a segunda etapa?
a) setenta e uma pessoas.
b) 106 pessoas.
c) cento e quarenta e duas pessoas.
d) 160 pessoas.
5. Em uma pesquisa realizada na turma de Henrique, com 40 estudantes, descobriu-se que 15% dos estudantes não possuem irmãos, 25% possuem apenas um irmão, 35% possuem dois irmãos e o restante possui mais do que dois irmãos. Sobre essa situação, avalie cada afirmação e classifique-a como verdadeira ou falsa.
a) 10 estudantes não possuem irmãos.
b) 14 estudantes possuem mais do que dois irmãos.
c) 10 estudantes possuem apenas um irmão.
d) 14 estudantes possuem dois irmãos.
Respostas
1. alternativa a
2. a. Verdadeira; b. Falsa; c. Falsa; d. Verdadeira
3. Os três estudantes fizeram uma afirmação correta.
4. alternativa c
5. a. Falsa; b. Falsa; c. Verdadeira; d. Verdadeira
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero oito. Espera-se que os estudantes percebam que ainda restam 25% de bateria e que
25 por cento é igual a 25 sobre 100, que é igual à 1 quarto..
Eles podem cometer equívocos por não entenderem a situação-problema ou por não compreenderem o conceito de porcentagem. Observe as dificuldades apresentadas e ajude-os a superá-las.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero oito. Os estudantes precisam avaliar cada afirmação a respeito de uma situação que envolve a ideia de fração como quociente. Eles podem cometer equívocos, por exemplo, ao não considerar Renata na distribuição. Isso pode ocorrer por falta de atenção na leitura do enunciado ou não compreensão da ideia de fração como quociente. Em caso de dificuldades, oriente-os a fazer um esquema da situação descrita.
A questão 3 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah zero oito e ê éfe zero sete ême ah zero nove. Essa questão apresenta uma situação que envolve o conceito de probabilidade e, consequentemente, a ideia de fração como razão. Os estudantes precisam avaliar o que cada um disse com base nas informações fornecidas no enunciado. Espera-se que eles percebam que as afirmações de Fabrício e Elisa são equivalentes, uma vez que
30 sobre 92 é igual a 15 sobre 46. Além disso, ambas as afirmações são corretas, pois o número de estudantes do 7º ano ei é 30 e o número total de estudantes das turmas de 7º ano é 92; portanto, a probabilidade de alguém dessa turma ser sorteado é de 30 em 92 ou
30 sobre 92. A afirmação de Josué também é correta, pois
32 sobre 92 é maior que 30 sobre 92, e
32 sobre 92é a probabilidade de alguém do 7º ano B ser sorteado.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero oito. Essa questão apresenta uma situação em que os estudantes precisam calcular a fração de uma quantidade, ou seja, aplicar a ideia de operador. Espera-se que eles calculem
dois terços vezes 213. Acompanhe-os na realização desse cálculo.
A questão 5 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah zero cinco, ê éfe zero sete ême ah zero seis e ê éfe zero sete ême ah zero oito. Nessa questão os estudantes mobilizam o conceito de porcentagem e as ideias de parte de um inteiro e operador das frações. Caso tenham dificuldades, oriente-os a representar graficamente a situação.
Para o capítulo 5: Números racionais
|
Questões |
Objetivos |
|---|---|
|
1 |
Reconhecer as diferentes representações de números racionais. |
|
2 |
Localizar números racionais na reta numérica. |
|
3 |
Comparar números racionais. |
|
4 |
Resolver situação-problema envolvendo adição e subtração com números racionais. |
|
5 |
Analisar situação-problema envolvendo multiplicação e divisão com números racionais. |
|
6 |
Calcular o valor de expressão numérica envolvendo números racionais. |
1. Leia cada afirmação sobre números racionais e classifique-a como verdadeira ou falsa.
a) 0,35 pode ser escrito na fórma de
Fração. 7 sobre 20..
b)
Fração. O numerador é raiz quadrada de 2 e o denominador é 4.é um número racional, pois está escrito em fórma de fração.
c) 0,3333reticências não é um número racional, pois é uma dízima periódica.
d) Entre dois números racionais sempre há um número racional.
2. Fernando vai representar uma reta numérica e localizar o ponto correspondente ao número
Fração. 8 sobre 251.. Esse ponto deve estar localizado entre os pontos correspondentes aos números:
a) 0,01 e 0,02.
b) 0,02 e 0,03.
c) 0,03 e 0,04.
d) 0,04 e 0,05.
3. Copie no caderno cada sentença a seguir e substitua

por um dos sinais: <, > ou =.
a)
Módulo de menos 2 sobre 15
0,1
b) 2,567

2,657
c)
Menos 125 sobre 8,
menos12,287
d)
Fração. 12 sobre 24.
0,500
4. O saldo da conta corrente de Fátima era menosR$ 520,00quinhentos e vinte reais. Ontem, ela depositou um valor de modo que a dívida diminuiu pela metade. Hoje, ela depositou R$ 310,00trezentos e dez reais. O saldo atual da conta corrente de Fátima é:
a) menosR$ 210,00duzentos e dez reais
b) menosR$ 50,00cinquenta reais
c) R$ 50,00cinquenta reais
d) R$ 210,00duzentos e dez reais
5. Para realizar seu trabalho de artesão, Albuquerque precisa comprar quatro pedaços de fio que medem 12,5 métros. Na loja a que ele vai, o metro de fio custa R$ 6,50seis reais e cinquenta centavos. Sobre essa situação, classifique as afirmações a seguir em verdadeiras ou falsas.
a) Para essa compra, ele vai gastar R$ 81,25oitenta e um reais e vinte e cinco centavos.
b) Se ele parcelar a compra em duas vezes sem juro, vai pagar R$ 160,00cento e sessenta reais por parcela.
c) Se ele dividir 12,5 métros de fio em pedaços menores de 1,6 métro, vai obter 20 pedaços.
d) Se ele comprasse seis pedaços de 12,5 métros nessa loja, pagaria menos de R$ 500,00quinhentos reais.
6. Calcule o valor da expressão numérica a seguir e expresse-o na fórma de fração irredutível.
Sentença matemática. Abre parênteses, fração de numerador raiz quadrada de 121 e denominador 5, fecha parênteses, elevado a 2, mais, raiz quadrada de 0 vírgula zero 4, menos 2 vezes, abre parênteses, fração 1 sobre 2, fecha parênteses, elevado a 3, dividido por fração 1 sobre 4.
Respostas
1. a. Verdadeira; b. Falsa; c. Falsa; d. Verdadeira
2. alternativa c
3. a. >; b. <; c. <; d. =
4. alternativa c
5. a. Falsa; b. Falsa; c. Verdadeira; d. Verdadeira
6.
Fração. 101 sobre 25.Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um zero. Essa questão explora as diferentes representações de números racionais e o reconhecimento de que, entre quaisquer dois números racionais, sempre existe outro numero racional. Explore com eles o porquê de as afirmações dos itens b e c serem falsas. Espera-se que eles percebam que o número em questão do item b não é racional, pois
Raiz quadrada de 2.não é um número inteiro. Já, no caso do item c, espera-se que eles argumentem que a dízima periódica 0,333reticências pode ser representada pela fração
Fração. 1 sobre 3.e, portanto, é um número racional.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um zero. Para realizar essa questão os estudantes podem representar o número
Fração. 8 sobre 251.na fórma decimal e, depois, encontrar a localização aproximada do ponto correspondente a esse número na reta numérica. Para encontrar a representação na fórma decimal eles podem dividir o numerador pelo denominador ou perceber que, multiplicando o numerador e o denominador por 4, vão encontrar a fração equivalente
32 sobre 1004, que é aproximadamente igual a 0,032. Portanto, o ponto correspondente a esse número está localizado entre os pontos correspondentes a 0,03 e 0,04.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um zero. Os estudantes precisam analisar cada sentença para comparar os números e utilizar os sinais que representam as noções de maior que, menor que ou igual a para expressar a comparação. Eles podem utilizar diferentes estratégias. Oriente-os a representar ambos os números na fórma de fração ou na fórma decimal ou a utilizar a reta numérica como auxílio se apresentarem dificuldades.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um dois.Espera-se que os estudantes percebam que para saber o saldo atual da conta de Fátima precisam calcular as entradas de dinheiro na conta, cujo saldo era ‒R$ 520,00quinhentos e vinte reais. Assim, devem considerar que, primeiramente, entraram +R$ 260,00duzentos e sessenta reais e, depois, +R$ 310,00trezentos e dez reais. Eles podem cometer equívocos na interpretação do enunciado ou nos cálculos. Em caso de dificuldades, pode-se retomar adição e subtração com números racionais.
A questão 5 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah um ume ê éfe zero sete ême ah um dois. Os estudantes precisam analisar cada afirmação para verificar se é verdadeira ou falsa com base na medida do comprimento de fio, no preço de cada pedaço de 12,5 métros e na quantidade de pedaços de 12,5 métros que serão comprados. Espera-se que percebam que o valor da compra é R$ 325,00trezentos e vinte e cinco reais, pois: 4
vezes12,5
vezes6,50 = 325. Assim, ao parcelar a compra em duas vezes sem juro, Albuquerque vai pagar duas parcelas de R$ 162,50cento e sessenta e dois reais e cinquenta centavos, pois R$ 325,00trezentos e vinte e cinco reais : 2 = R$ 162,50cento e sessenta e dois reais e cinquenta centavos. Os estudantes podem cometer equívocos ao interpretar o enunciado ou calcular as multiplicações e divisões. Nesse caso, convém recordar essas operações com números racionais.
A questão 6 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah um um e ê éfe zero sete ême ah um dois. Os estudantes precisam calcular o valor da expressão numérica dada envolvendo potenciação e raiz quadrada de números racionais, lembrando da ordem em que se resolvem as operações. Alerte-os para a importância de realizar todas as passagens e fazer os cálculos de maneira organizada.
Para o capítulo 6: Linguagem algébrica e regularidades
|
Questões |
Objetivos |
|---|---|
|
1 |
Utilizar expressão algébrica para representar situação. |
|
2 |
Calcular o valor numérico de expressões algébricas. |
|
3 |
Calcular adição de termos algébricos. |
|
4 |
Analisar equação do 1º grau com uma incógnita. |
|
5 |
Resolver situação-problema com equação. |
|
6 |
Calcular o termo de uma sequência numérica. |
|
7 |
Reconhecer uma sequência numérica recursiva e determinar seus termos. |
1. Luís e Mônica foram ao mercado e compraram três unidades de um produto que custa a reais, duas unidades de um produto que custa b reais e uma unidade de um produto que custa c reais. Eles pagaram a compra com uma cédula de 100 reais e dividiram o troco igualmente entre eles. A expressão algébrica que pode representar essa situação é:
a)
100 menos, fração com numerador 3a mais 2b mais c e denominador 2b)
Fração com numerador abre parênteses, 3a mais 2b mais c, fecha parênteses, menos 100, e denominador 2c)
Fração com numerador abre parênteses, 3a mais 2b mais c, fecha parênteses, e denominador 2, tudo isso menos 100.d)
Fração com numerador 100 menos, abre parênteses, 3a mais 2b mais c, fecha parênteses, e denominador 2.2. Analise cada expressão algébrica a seguir e indique aquelas cujo valor numérico é 10 para x = 2 e y = menos2.
a)
y vezes fração 5 sobre x, tudo isso mais 15b)
20x menos fração 10y sobre 2c) xy + 14
d) menos xy + 14
3. Moacir calculou a seguinte adição de termos algébrico, mas cometeu um erro. Identifique esse erro.
Sentença matemática. 2a, mais 3 vezes a elevado a 2, menos 1 sobre 2, vezes a elevado a 2, vezes b, mais 1 sobre 2, vezes a elevado a 2, mais 1 sobre 2, vezes a, vezes b elevado a 2, igual, 2a, mais 7 sobre 2, vezes a elevado a 2.
4. Considere a equação
Fração 2x sobre 5, mais 1, igual, menos xe classifique cada afirmação em verdadeira ou falsa.
a) Essa equação tem duas incógnitas: x e menosx.
b) O segundo membro dessa equação é menosx.
c) A raiz dessa equação é
Fração. Menos 7 sobre 5..
d) Essa equação não tem solução no conjunto dos números inteiros.
5. Leia a seguinte situação. Depois, copie-a em seu caderno completando os espaços.
Para a aula de Arte, Mariana recortou uma folha retangular, cujo perímetro mede 55 centímetros, de modo que a medida do comprimento fosse igual ao quádruplo da medida da largura.
Se x é a medida da largura, então

é a medida do comprimento da folha. Assim, a equação que representa a medida do perímetro é

. Resolvendo essa equação, descobrimos que a largura mede

centímetros e o comprimento mede

centímetros.
6. Calcule o 5º termo da sequência cuja lei de formação é
Sentença matemática. a com índice n, igual, 2n, menos 1 sobre 2, n elevado a 2., em que n é um inteiro positivo.
7. A soma dos quatro primeiros termos da sequência dada pela lei de formação recursiva á₁ = 0, án + 1 = 2án + 5 é:
a) 13
b) 55
c) 75
d) 130
Respostas
1. alternativa d
2. alternativas a e c
3. Moacir calculou
Sentença matemática. menos 1 sobre 2, vezes a elevado a 2, vezes b, mais 1 sobre 2, vezes a, vezes b elevado a 2, igual, 0., porém os termos não são semelhantes.
4. a. Falsa; b. Verdadeira; c. Falsa; d. Verdadeira
5. 4x; 4x + 4x + x + x = 55; 5,5; 22
6. menos2,5
7. alternativa b
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um três. Os estudantes precisam perceber que o troco será dividido igualmente entre Luís e Mônica; portanto, será dividido por 2. Assim, precisam calcular a diferença entre 100 reais e o valor, em real, gasto na compra de 3a + 2b + c. Caso optem por qualquer outra alternativa que não seja a d, explore o significado das expressões representadas nelas com base no contexto apresentado.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um três. Para resolver essa questão, os estudantes podem calcular o valor numérico das expressões algébricas de cada item para x = 2 e y = menos2. Eles podem se equivocar ao substituir o valor das variáveis ou ao realizar os cálculos.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um três. Os estudantes precisam analisar o que há de errado na adição de termos algébricos que foi apresentada. Espera-se que eles recordem que podem somar e subtrair apenas termos semelhantes. Em caso de dificuldades, convém retomar adição de termos semelhantes, destacando a parte literal e a parte numérica.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um oito. Os estudantes precisam analisar a informação de cada item para avaliar se é verdadeira ou falsa. Espera-se que eles percebam que a equação dada é do 1º grau com uma incógnita (x). Espera-se que eles concluam que a raiz dessa equação é
Fração. Menos 5 sobre 7.. Caso tenham obtido outro valor, oriente-os a substituir a incógnita pelo valor encontrado e verificar se obtêm uma sentença verdadeira. No item d, espera-se que eles percebam que, se U =

, então S = ∅, uma vez que
Fração. Menos 5 sobre 7.não é um número inteiro.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um oito. Os estudantes precisam analisar os dados da situação para descobrir a equação que representa a medida do perímetro da folha. Com isso, podem calcular as medidas de comprimento e de largura dela. Oriente-os a fazer um esboço da situação.
A questão 6 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah um quatro, ê éfe zero sete ême ah um cinco e ê éfe zero sete ême ah um seis. Essa questão apresenta a lei de formação de uma sequência e pede aos estudantes que calculem o 5º termo. Espera-se que eles recordem que basta substituir n por 5 para determinar o termo desejado. Caso tenham dificuldades, mostre-lhes como calcular o primeiro ou o segundo termo dessa sequência.
A questão 7 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah um quatro, ê éfe zero sete ême ah um cinco e ê éfe zero sete ême ah um seis. Essa questão apresenta a lei de formação de uma sequência recursiva, em que os estudantes precisam calcular os quatro primeiros termos e, depois, adicioná-los. Espera-se que eles percebam que os primeiros termos dessa sequência são 0, 5, 15, 35, 75, reticências Eles podem cometer equívocos ao não considerar o 0 como um termo ou que a soma é dada pelo quinto termo. Em caso de dificuldades, convém retomar exemplos de lei de formação recursiva.
Para o capítulo 7: Porcentagem e juro simples
|
Questões |
Objetivos |
|---|---|
|
1 |
Calcular porcentagem de um valor. |
|
2 |
Calcular o valor total com base em uma porcentagem. |
|
3 |
Calcular taxa percentual. |
|
4 |
Calcular acréscimo percentual. |
|
5 |
Calcular descontos. |
|
6 |
Analisar situação com juro simples. |
1. Ana e Ricardo moram juntos e guardam uma porcentagem do salário mensalmente. Ana recebe R$ 3.450,00três mil quatrocentos e cinquenta reais e Ricardo recebe R$ 2.950,00dois mil novecentos e cinquenta reais. Sabendo que cada um deles guarda 5% do salário, quantos reais conseguem juntar mensalmente?
a) R$ 295,00duzentos e noventa e cinco reais
b) R$ 320,00trezentos e vinte reais
c) R$ 345,00trezentos e quarenta e cinco reais
d) R$ 475,00quatrocentos e setenta e cinco reais
2. Jussara realizou uma compra há alguns meses e fez um parcelamento. Ela já pagou 35% do valor inicial, o que equivale a R$ 857,50oitocentos e cinquenta e sete reais e cinquenta centavos. Sobre essa situação, classifique cada afirmação em verdadeira ou falsa.
a) Ainda falta Jussara pagar 70% da compra.
b) Jussara precisa pagar R$ 1.574,50mil quinhentos e setenta e quatro reais e cinquenta centavos para quitar a dívida.
c) A compra de Jussara custou R$ 2.450,00dois mil quatrocentos e cinquenta reais.
d) Quando Jussara tiver pagado 50% da compra, terá quitado R$ 1.225,00mil duzentos e vinte e cinco reais.
3. Um município com 58.420 pessoas fez uma campanha de vacinação contra a gripe. Até o momento 37.973 pessoas se vacinaram. A Secretaria de Saúde resolveu avaliar a taxa percentual de vacinados: se estiver abaixo de 70%, intensificará a campanha para que as pessoas faltantes se vacinem. Analise a taxa percentual e justifique se a Secretaria de Saúde terá que agir ou não.
4. A prefeitura da cidade em que Josefa mora vai ampliar a avenida principal da cidade. Atualmente, essa avenida tem 12 quilômetros de extensão. A previsão é de que a via seja ampliada em 9%, passando a ter:
a) 13 quilômetros de extensão.
b) 13,08 quilômetros de extensão.
c) 22 quilômetros de extensão.
d) 22,8 quilômetros de extensão.
5. Breno precisa comprar determinado produto. Ele pesquisou em dois sites e descobriu que, no site ei, o produto custa R$ 85,00oitenta e cinco reais, mas tem desconto de 6% se for comprado hoje; no site B, custa R$ 82,00oitenta e dois reais e o desconto será de 2% se comprado hoje. Em qual site ele deve comprar para pagar menos?
6. Valéria emprestou R$ 2.500,00dois mil quinhentos reais a Guilherme e combinou que ele devolveria esse valor acrescido de juro simples com taxa de 1,5% ao mês após 3 meses. Sobre essa situação, classifique cada afirmação como verdadeira ou falsa.
a) O juro que Guilherme terá que pagar será de R$ 1.125,00mil cento e vinte e cinco reais ao final dos 3 meses.
b) Valéria precisa receber R$ 2.612,50dois mil seiscentos e doze reais e cinquenta centavos de Guilherme ao final dos 3 meses.
c) O capital dessa situação é R$ 2.500,00dois mil quinhentos reais.
d) A taxa de juro paga nos 3 meses é de 3%.
Respostas
1. alternativa b
2. a. Falsa; b. Falsa; c. Verdadeira; d. Verdadeira
3. A Secretaria de Saúde terá que agir, pois a taxa percentual de vacinados é 65%.
4. alternativa b
5. Site A.
6. a. Falsa; b. Verdadeira; c. Verdadeira; d. Falsa
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero dois. Nessa questão, espera-se que os estudantes compreendam que Ana e Ricardo possuem salários diferentes, porém a porcentagem do salário que guardam é a mesma. Assim, podem calcular 5% de cada salário e, depois, adicionar os valores ou podem adicionar os salários e calcular 5% da soma obtida. Incentive-os a determinar as porcentagens mentalmente.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero dois. Essa questão traz uma situação de parcelamento em que são dados a porcentagem do que foi pago e o valor equivalente. Incentive os estudantes a justificar o porquê de cada afirmação ser verdadeira ou falsa.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero dois. Essa questão traz um contexto de campanha de vacinação, momento oportuno para conversar com os estudantes sobre a importância de manter as vacinas em dia. Espera-se que os estudantes percebam que a taxa percentual de vacinados é um parâmetro adotado nesse município para tomar decisões. Espera-se que eles concluam que foram vacinados 65% da população, pois .37973 : .58420 = 0,65. Portanto, a Secretaria de Saúde intensificará a companha.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero dois. Os estudantes precisam calcular o acréscimo de 9% na extensão de uma avenida que tem 12 quilômetros de extensão. Eles podem calcular 12 quilômetros + 0,09 ⋅ 12 quilômetros ou calcular 1,09 ⋅ 12 quilômetros. Caso não obtenham a resposta correta, incentive-os a verificar se a resposta obtida atende as condições do problema.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero dois. O contexto da questão se refere a uma pesquisa de preços de um produto em dois sites diferentes da internet. Os estudantes precisam calcular quanto Breno vai pagar pelo produto se comprar no site ei e no site B. Espera-se que eles percebam que no site ei o produto custa R$ 79,90setenta e nove reais e noventa centavos e no site B o mesmo produto sai por R$ 80,36oitenta reais e trinta e seis centavos. Eles podem cometer equívocos ao calcular as porcentagens. Nesse caso, convém retomar o cálculo de descontos percentuais.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah zero dois. Essa questão explora o conceito de juro simples. Espera-se que os estudantes percebam que precisam calcular o juro ao final dos 3 meses e adicioná-lo ao capital para saber o montante. Eles podem cometer equívocos durante os cálculos ao considerar, por exemplo, 1,5% como 15%. Em caso de dificuldades, pode-se retomar o conceito de juro simples.
Para o capítulo 8: Proporcionalidade
|
Questões |
Objetivos |
|---|---|
|
1 |
Aplicar o conceito de razão. |
|
2 |
Aplicar a propriedade fundamental das proporções. |
|
3 |
Resolver problemas que envolvam grandezas direta ou inversamente proporcionais. |
|
4 |
Resolver problemas que envolvam grandezas direta ou inversamente proporcionais. |
1. Regina representou um quadrado cujo lado mede 5 centímetros de comprimento. Depois, calculou a medida do perímetro dele. A razão entre a medida do comprimento do lado e a medida do perímetro desse quadrado é:
a)
Fração. 1 sobre 5b)
Fração. 1 sobre 4c)
Fração. 1 sobre 2.d) 1
2. Aplique a propriedade fundamental das proporções para verificar se as razões
12 sobre 18e
6 sobre 4formam uma proporção.
3. Itamar está organizando uma festa de aniversário. Ele pretende comprar 36 copos com medida de capacidade igual a 250 mililitros para distribuir todo o suco. Outra possibilidade, sem desperdício, é comprar copos com medida de capacidade igual a 600 mililitros. Nesse caso, Itamar precisa comprar:
a) 6 copos.
b) 10 copos.
c) 15 copos.
d) 36 copos.
4. Leandro trabalha fazendo manutenção em gráficas. Em sua última visita, constatou que cinco máquinas, trabalhando no mesmo ritmo e no mesmo intervalo de tempo, conseguiam produzir .6000 impressões. Como uma das máquinas estava quebrada, a produção de folhas, no mesmo período, passou a ser de:
a) uma.duzentas impressões.
b) duas.quatrocentas impressões.
c) 3.seiscentas impressões.
d) 4.oitocentas impressões.
Respostas
1. alternativa b
2. Não formam, pois 12 ⋅ 4 ≠ 18 ⋅ 6
3. alternativa c
4. alternativa d
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um sete. Nessa questão, os estudantes devem primeiro determinar a medida do perímetro do quadrado. Para isso devem calcular 4 ⋅ 5 centímetros. Depois, devem calcular a razão entre a medida do comprimento do lado e a medida do perímetro:
Retome os conceitos de perímetro e razão, caso ache necessário.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um sete. Essa questão apresenta duas razões para que os estudantes verifiquem se elas formam uma proporção. Ao aplicar a propriedade fundamental das proporções (o produto dos extremos é igual ao produto dos meios), os estudantes vão perceber que não se trata de uma proporção. Convém verificar se eles percebem que seria uma proporção no caso de a segunda razão ser
Fração. 4 sobre 6. Recorde os termos de uma proporção caso perceba que essa é uma dificuldade dos estudantes.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um sete. Essa questão apresenta uma situação comum envolvendo a organização de uma festa. Os estudantes precisam compreender que há duas opções de copos para Itamar e ele vai servir a mesma quantidade de suco, independentemente do copo escolhido. Logo, se aumenta a medida da capacidade de cada copo, a quantidade de copos diminui, ou seja, a medida da capacidade dos copos e a quantidade de copos são inversamente proporcionais. Espera-se que eles concluam que Itamar tem .9000 mililitros ou 6 litros de suco para servir, pois 36 ⋅ 250 mililitros = .9000 mililitros. Para distribuir essa quantidade de suco em copos de 600 mL serão necessários 15 copos, pois:
.9000 mililitros : 600 mililitros = 15
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um sete. Para resolver essa questão, os estudantes devem considerar que, se 5 máquinas produzem .6000 impressões, quatro máquinas produzem 4.800 impressões, pois cada máquina produz uma.duzentas impressões e uma delas está quebrada. É importante que eles percebam que o número de impressões e o número de máquinas são diretamente proporcionais.
Para o capítulo 9: Transformações geométricas
|
Questões |
Objetivos |
|---|---|
|
1 |
Construir o polígono obtido por simetria de translação. |
|
2 |
Reconhecer simetria de rotação e identificar a medida da abertura do ângulo de rotação. |
|
3 |
Reconhecer que a reflexão em relação a um ponto é equivalente a uma rotação em torno desse mesmo ponto com ângulo de medida de abertura igual a 180°. |
|
4 |
Analisar um polígono e seu simétrico representados no plano cartesiano. |
|
5 |
Analisar um polígono e sua ampliação representados no plano cartesiano. |
1. Copie o polígono a seguir em uma folha de papel quadriculado. Depois, translade-o de acordo com o vetor da translação.
2. Amanda vai desenhar uma flor de seis pétalas, inspirada na imagem a seguir, utilizando rotação. Qual é a medida da abertura do ângulo destacado na imagem?

a) 45graus
b) 60graus
c) 72graus
d) 90graus
3. Mateus construiu uma figura geométrica plana em uma malha quadriculada e marcou um ponto P fóra dessa figura. Depois, ele refletiu essa figura em relação ao ponto P. Mateus poderia obter o mesmo resultado ao fazer:
a) uma translação com direção e sentido de um vértice da figura ao ponto P.
b) uma rotação com centro em P e ângulo de medida de abertura igual a 90graus.
c) uma rotação com centro em P e ângulo de medida de abertura igual a 180graus.
d) uma reflexão em relação a uma reta que passasse por P.
4. Observe os polígonos representados no plano cartesiano a seguir e classifique cada afirmação como verdadeira ou falsa.
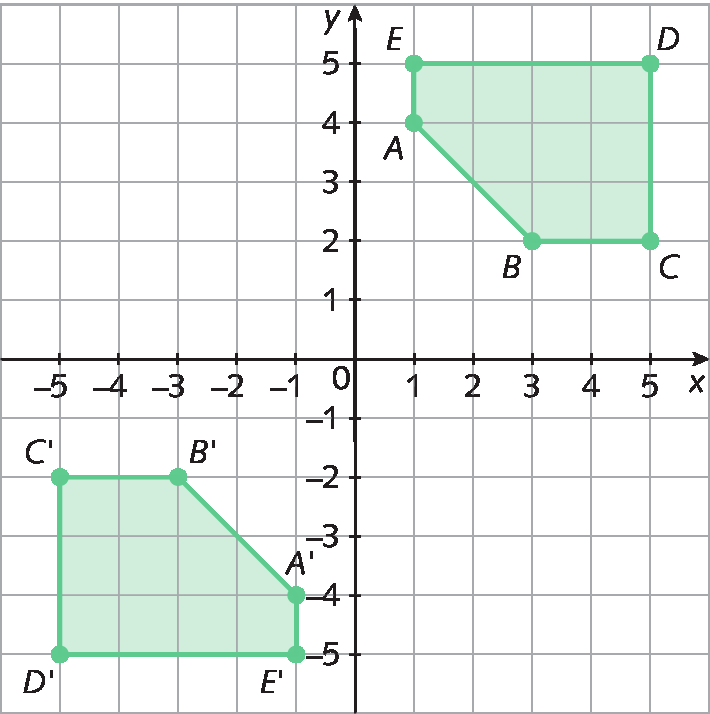
a) O polígono á linha bê linha cê linha dê linha é linha é simétrico ao polígono á bê cê dê é em relação ao eixo x.
b) O simétrico do polígono á bê cê dê é em relação ao eixo y estará no 2º quadrante.
c) As coordenadas dos vértices do polígono á bê cê dê é são positivas e as coordenadas dos vértices do polígono á linha bê linha cê linha dê linha é linha são negativas.
d) O polígono á linha bê linha cê linha dê linha é linha está no 4º quadrante.
5. Carlos representou no plano cartesiano um polígono cujos vértices são aabre parênteses1, menos2fecha parênteses, Babre parênteses5, menos2fecha parênteses, Cabre parênteses6, menos4fecha parênteses e Dabre parênteses1, menos4fecha parênteses. Ele planeja ampliar esse polígono de modo a mantê-lo no 4º quadrante do plano cartesiano, aumentando a medida de comprimento de cada um de seus lados em 2,5 vezes. Quais serão as coordenadas dos vértices do polígono ampliado?
Respostas
1.
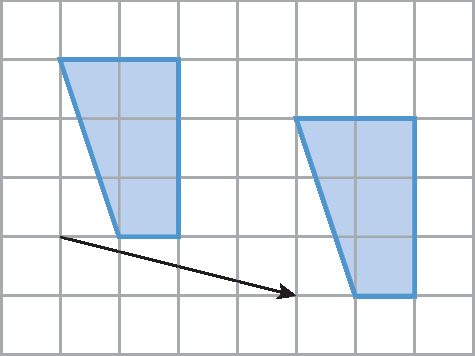
2. alternativa b
3. alternativa c
4. a. Falsa; b. Verdadeira; c. Verdadeira; d. Falsa
5. á linhaabre parênteses2,5; menos5fecha parênteses, bê linhaabre parênteses12,5; menos5fecha parênteses, cê linhaabre parênteses15; menos10fecha parênteses e dê linhaabre parênteses2,5; menos10fecha parênteses.
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois um. Os estudantes precisam analisar a direção, o sentido e a medida do comprimento do vetor para poder transladar o polígono. Espera-se que percebam que cada vértice do polígono deve ser transladado um quadradinho para baixo e quatro quadradinhos para a direita. Caso não tenham representado o polígono corretamente, oriente-os a investigar as razões pelas quais cometeram o equívoco. Oriente-os, por exemplo, a verificar se os polígonos são congruentes e se todos os vértices foram transladados da mesma fórma.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois um. Essa questão apresenta uma figura que será tomada como referência para a construção de uma flor de seis pétalas simétrica por rotação. Os estudantes precisam perceber que ao dividir 360graus por 6 encontram a medida da abertura do ângulo destacado na imagem, que é igual a 60graus. Amplie a questão e proponha aos estudantes que construam essa flor.
A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois um. Espera-se que os estudantes reconheçam que a reflexão em relação a um ponto é equivalente a uma rotação em torno desse mesmo ponto com ângulo de medida de abertura igual a 180graus. Caso tenham dificuldades, oriente-os a esboçar a situação descrita em cada alternativa da questão.
A questão 4 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah um nove e ê éfe zero sete ême ah dois zero. Essa questão apresenta um polígono representado no 1º quadrante do plano cartesiano e seu simétrico em relação à origem. Espera-se que os estudantes percebam que o polígono simétrico está localizado no 3º quadrante e possui coordenadas negativas, enquanto as coordenadas do polígono inicial são positivas. Caso optem pelos itens a ou b, oriente-os a representar o simétrico do polígono á bê cê dê é em relação ao eixo x e ao eixo y, respectivamente. Se optarem pelo item d, retome a nomeação dos quadrantes do plano cartesiano.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah um nove. Oriente os estudantes a representar o polígono a bê cê dê. Espera-se que percebam que esse quadrilátero é um trapézio. Além disso, eles devem perceber que, ao ampliar a medida de comprimento de cada um dos lados em 2,5 vezes, mantendo-o no 4º quadrante, as coordenadas dos vértices do polígono devem ser multiplicadas por 2,5. Após obterem as coordenadas do polígono ampliada, incentive-os a representá-lo no plano cartesiano.
Para o capítulo 10: Grandezas e medidas
|
Questões |
Objetivos |
|---|---|
|
1 |
Resolver problema envolvendo medidas de capacidade. |
|
2 |
Resolver problema envolvendo a medida da área de paralelogramos. |
|
3 |
Expressar medida de área do quadrado e do triângulo. |
|
4 |
Calcular a medida de área do trapézio. |
|
5 |
Calcular a medida de área do losango. |
|
6 |
Resolver problema envolvendo o cálculo da medida de paralelepípedos reto-retângulos. |
1. Marcelo estava preparando uma receita de bolo, porém não tinha um copo medidor para separar a quantidade exata de leite da receita. Para isso, ele utilizou um copo em que ele sabia que cabiam 150 mililitros. A receita indicava 750 mililitros de leite; portanto, Marcelo deve encher o copo:
a) 3 vezes.
b) 4 vezes.
c) 5 vezes.
d) 6 vezes.
2. Elaine tem um quadro retangular na parede cujos lados apresentam estas medidas de comprimento: 30 centímetros por 18 centímetros. Ela pretende trocar esse quadro por algum que também se pareça com um paralelogramo e que tenha a mesma medida de área. O quadro que ela encontrou tem 27 centímetros de medida de comprimento de altura; portanto, a medida de comprimento da base dele é:
a) 18 centímetros.
b) 20 centímetros.
c) 27 centímetros.
d) 30 centímetros.
3. Considere o quadrado a seguir, cujo lado apresenta a medida de comprimento x e cujo ponto E é o centro dele.
Analise cada afirmação e classifique-a como verdadeira ou falsa.
a) A medida de área do quadrado a bê cê dê pode ser expressa por 2x.
b) A medida de área do triângulo ABC pode ser expressa por
Fração. O numerador é x elevado ao quadrado e o denominador é 2..
c) Os triângulos á bê cê e á cê dê tem mesma medida de área.
d) A medida de área do triângulo AEB pode ser expressa por
Fração. O numerador é x elevado ao quadrado e o denominador é 2..
4. Marco representou o contorno de um trapézio. A medida do comprimento da base maior desse trapézio é 6 centímetros, a da base menor é 3 centímetros e a da altura é 2 centímetros. Ele vai pintar 40% do interior dessa figura de verde e o restante de lilás. Determine a medida da área que será pintada de cada cor.
5. Vânia construiu uma pipa que se parece com um losango utilizando varetas. Ela vai colar papel de seda sobre as varetas. Observe o esquema que ela fez antes de construir a pipa.
Qual será a medida de área ocupada por uma camada de papel de seda?
6. Rute tem um recipiente em formato de cubo com arestas cujo comprimento mede 2 decímetros e outro recipiente em formato de paralelepípedo reto-retângulo que mede 10 centímetros de largura, 60 centímetros de comprimento e 20 centímetros de altura. Sobre essa situação, analise cada afirmação e classifique-a como verdadeira ou falsa.
a) É possível despejar 8 litros de água no recipiente em formato cúbico.
b) Não é possível transferir toda a água que cabe no recipiente em formato cúbico para o recipiente em formato de paralelepípedo reto-retângulo.
c) Não é possível transferir toda a água que cabe no recipiente em formato de paralelepípedo reto-retângulo para o recipiente em formato cúbico.
d) A medida do volume do recipiente em formato de paralelepípedo reto-retângulo é .6000 centímetros cúbicos.
Respostas
1. alternativa c
2. alternativa b
3. a. Falsa; b. Verdadeira; c. Verdadeira; d. Falsa
4. Medida da área verde: 3,6 centímetros quadrados; Medida da área lilás: 5,4 centímetros quadrados.
5. 378 centímetros quadrados
6. a. Verdadeira; b. Falsa; c. Verdadeira; d. Falsa
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois nove. Nessa questão, espera-se que os estudantes percebam que precisam calcular 750 mililitros : 150 mililitros para determinar quantas vezes Marcelo deve encher o copo. É importante que eles também reconheçam 150 mililitros e 750 mililitros como medidas de capacidade.
A questão 2 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah três um e ê éfe zero sete ême ah três dois. Nessa questão convém chamar a atenção dos estudantes para o fato de que o retângulo é um paralelogramo em que todos os ângulos internos são retos. Uma informação importante é a de que o quadro que irá substituir o anterior tem formato de paralelogramo e mesma medida de área. A medida da área do quadro que será substituído é igual a 540 centímetros quadrados, pois 18 centímetros ⋅ 30 centímetros = 540 centímetros quadrados. O quadro que Elaine encontrou tem essa medida de área e 27 centímetros de medida de altura; portanto, a medida de comprimento desse quadro é igual a 20 centímetros, pois 540 centímetros quadrados : 27 centímetros = 20 centímetros. O estudantes podem ter dificuldades para interpretar a situação-problema. Caso isso ocorra, oriente-os a separar os dados fornecidos do quadro antigo e do quadro novo.
A questão 3 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah três um e ê éfe zero sete ême ah três dois. Essa questão explora a decomposição do quadrado em triângulos retângulos, o cálculo da medida da área de quadros e triângulos e a utilização da linguagem algébrica. Oriente os estudantes a representar os triângulos á bê cê, á cê dê e AEB mencionados nos itens b, c e d.
A questão 4 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah três um e ê éfe zero sete ême ah três dois. Os estudantes precisam calcular a medida da área do trapézio com base nas medidas apresentadas no enunciado. Utilizando a expressão estudada, vão descobrir que o trapézio de Marco tem 9 centímetros quadrados de medida de área. Aplicando as porcentagens indicadas (40% para verde e 60% para lilás), conseguem calcular a medida da área pintada de cada cor. Em caso de dificuldades, convém retomar o cálculo da área do trapézio.
A questão 5 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah três um e ê éfe zero sete ême ah três dois. Essa questão explora a medida da área de um losango. Espera-se que eles reconheçam que 42 centímetros corresponde à medida do comprimento da diagonal maior e 18 centímetros, à medida do comprimento da diagonal menor.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três zero. Essa questão apresenta dois recipientes para que os estudantes calculem a medida do volume de cada um deles e analisem as afirmações. Espera-se que percebam que a medida do volume do recipiente cúbico é 8 decímetros cúbicos, pois (2 decímetros)³ = 8 decímetros cúbicos, e a medida do volume do recipiente em formato de paralelepípedo reto-retângulo é 12 decímetros cúbicos, pois 1 decímetro ⋅ 6 decímetros ⋅ 2 decímetros = 12 decímetros cúbicos. A comparação é feita na mesma unidade de medida; portanto, é necessário que os estudantes fiquem atentos a essa informação. Assim, lembrando que 1 decímetro cúbico = 1 litro, podem perceber que todo o conteúdo do recipiente em formato cúbico cabe no outro recipiente, porém o contrário não é verdade. Em caso de dificuldades, convém retomar o cálculo da medida do volume do cubo e do paralelepípedo reto-retângulo e a relação entre decímetro cúbico e litro.
Para o capítulo 11: Figuras geométricas planas
|
Questões |
Objetivos |
|---|---|
|
1 |
Comparar medidas de comprimento do raio, do diâmetro e do perímetro de uma circunferência e de um círculo. |
|
2 |
Calcular a medida do perímetro aproximado de circunferência. |
|
3 |
Calcular a soma das medidas de abertura dos ângulos internos de um polígono regular. |
|
4 |
Calcular as medidas de abertura dos ângulos internos e externos de um polígono regular. |
|
5 |
Construir um triângulo conhecendo as medidas de abertura de dois ângulos e a medida de comprimento do lado compreendido entre eles. |
|
6 |
Resolver problema envolvendo a desigualdade triangular. |
1. Renato representou um círculo cujo raio tem comprimento com medida igual a 8 centímetros e uma circunferência cujo diâmetro apresenta comprimento com medida igual a 10 centímetros. Sobre essa situação, avalie cada afirmação e classifique-a como verdadeira ou falsa.
a) A medida do comprimento do diâmetro do círculo é menor do que a medida do comprimento do diâmetro da circunferência.
b) A medida do perímetro do círculo é maior do que a medida do perímetro da circunferência.
c) Ao dividir a medida do perímetro da circunferência pela medida do comprimento do diâmetro dela, chega-se próximo de 3,14.
d) Ao dividir a medida do diâmetro do círculo pela medida do comprimento dele, chega-se próximo de 3,14.
2. Vanda representou uma circunferência em que o comprimento do raio mede 12 centímetros. A medida do perímetro aproximado dessa circunferência é:
a) 24 centímetros.
b) 37,68 centímetros.
c) 75,36 centímetros.
d) 113,04 centímetros.
3. Vítor trabalha com usinagem de peças metálicas. Para que a máquina execute o corte corretamente, ele precisa indicar o número de lados da peça que terá formato de polígono regular e a soma as medidas de abertura dos ângulos internos. Para usinar uma peça que tenha 8 lados com 15 centímetros de medida de comprimento de lado cada, Vítor precisa digitar qual soma das medidas de abertura dos ângulos internos?
a) 360graus
b) .1080graus
c) .1440graus
d) .2160graus
4. A parte interna do recipiente a seguir se parece com um polígono regular.

Sobre o polígono regular utilizado, complete as informações:
Número de lados:

Soma das medidas de abertura dos ângulos internos:

Medida de abertura de cada ângulo interno:

Medida de abertura de cada ângulo externo:

5. Em seu caderno, construa um triângulo á bê cê em que A bê = 15 centímetros e que tenha ângulos adjacentes a esse lado medindo 30graus e 60graus. Depois, descreva o passo a passo que você utilizou.
6. Maria quer encomendar um quadro triangular. Para isso, ela indicou para o marceneiro as seguintes opções de medidas de comprimento para os lados do quadro:
ei: 4 centímetros, 5 centímetros e 6 centímetros.
B: 5 centímetros, 8 centímetros e 12 centímetros.
C: 8 centímetros, 14 centímetros e 15 centímetros.
D: 9 centímetros, 15 centímetros e 26 centímetros.
Ao observar as medidas, o marceneiro indicou que uma das opções não poderia ser feita. Que opção é essa?
Respostas
1. a. Falsa; b. Verdadeira; c. Verdadeira; d. Falsa
2. alternativa c
3. alternativa b
4. 12; .1800graus; 150graus; 30graus
5. Os estudantes podem traçar uma reta suporte e marcar um segmento de reta de 15 centímetros com extremidades em aêbê. Depois, podem construir um ângulo de medida de abertura igual a 30graus com vértice em A e um ângulo de medida de abertura igual a 60graus com vértice em B. Ao marcar o ponto C, de intersecção das semirretas dos ângulos traçados, e pintar o interior da figura, obtém-se o triângulo á bê cê.
6. D
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três três. Essa questão apresenta duas figuras geométricas planas (círculo e circunferência), a medida do comprimento do raio de uma e a medida do comprimento do diâmetro da outra. Oriente-os a representar as duas figuras antes de avaliar as afirmações.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três três. Para resolver essa questão os estudantes devem recordar que a medida do perímetro da circunferência é calculado multiplicando a medida do comprimento do diâmetro por π. Assim, como o a medida do comprimento do diâmetro da circunferência é igual a 24 centímetros, temos:
C ≃ (24 centímetros) ⋅ π ≃75,36 centímetros
A questão 3 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah dois sete e ê éfe zero sete ême ah dois oito. Essa questão explora propriedades dos polígonos regulares e a soma das medidas de abertura dos seus ângulos internos. Espera-se que os estudantes recordem que um polígono regular de 8 lados pode ser decomposto em 6 triângulos; como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, basta multiplicar 6 por 180graus para calcular a soma das medidas de abertura dos ângulos internos de um octógono regular. Caso tenham optado pelo item a, os estudantes consideraram a soma das medidas de abertura dos ângulos internos de um quadrilátero. Se optaram pelo item c, os estudantes multiplicaram 8 por 180graus. Já se concluíram que o item d é o correto, os estudantes multiplicaram 6 por 360graus. Em caso de dificuldades, retome a determinação da soma das medidas de abertura dos ângulos internos de um polígono regular.
A questão 4 auxilia no desenvolvimento das habilidades ê éfe zero sete ême ah dois sete e ê éfe zero sete ême ah dois oito. Os estudantes precisam observar a parte interna do prato da imagem e reconhecer que ela se parece com um polígono regular de 12 lados. Com isso podem calcular a soma (S) das medidas das aberturas dos ângulos internos:
S = (12 − 2) ⋅ 180graus = 10 ⋅ 180graus = .1800graus
Com base na soma obtida anteriormente, calcula-se a medida da abertura de cada ângulo interno:
.1800graus: 12 = 150graus
Assim, cada ângulo interno tem medida de abertura igual a 150graus.
Como cada ângulo externo do polígono regular é suplementar ao seu ângulo interno correspondente, cada ângulo externo tem medida de abertura igual a 30graus.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois cinco. Essa questão propõe aos estudantes que construam um triângulo tendo a medida do comprimento de um lado e a medida de abertura de dois ângulos adjacentes. Espera-se que eles recordem que podem fazer essa construção utilizando régua e compasso ou transferidor. Alerte-os para que tomem cuidado ao manusear o compasso. Em caso de dificuldades, convém recordar a construção de outros triângulos a partir de elementos dados.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah dois cinco. Essa questão explora a desigualdade triangular. Os estudantes precisam analisar as medidas de comprimento de cada opção para verificar se a medida de comprimento de qualquer lado é menor do que a soma das medidas de comprimento dos outros dois lados. Caso isso não ocorra, é impossível construir o triângulo. Em caso de dificuldades, convém retomar a desigualdade triangular e propor a construção de triângulos utilizando softwares de geometria dinâmica.
Para o capítulo 12: Probabilidade e estatística
|
Questões |
Objetivos |
|---|---|
|
1 |
Calcular e comparar probabilidades. |
|
2 |
Calcular e comparar probabilidades. |
|
3 |
Reconhecer uma pesquisa amostral. |
|
4 |
Determinar a medida de abertura dos ângulos dos setores de um gráfico. |
|
5 |
Calcular média aritmética simples. |
|
6 |
Calcular média ponderada. |
1. Para a realização de um sorteio, Fabrício vai colocar as fichas mostradas a seguir, que têm medidas de massa iguais e as mesmas medidas de comprimento de raio e espessura, em uma caixa. Em seguida, vai fechar a caixa e balançá-la, misturando as fichas. Depois, vai colocar a mão dentro da caixa e retirar uma ficha, sem olhar. A cor de ficha que tem a maior probabilidade de ser sorteada é:

a) amarela.
b) azul.
c) verde.
d) vermelha.
2. A escola em que Mônica estuda tem uma turma para cada um dos anos finais do Ensino Fundamental. O 6º ano tem 32 estudantes, o 7º ano tem 32 estudantes, o 8º ano tem 30 estudantes e o 9º ano tem 34 estudantes. Será realizado um sorteio entre todos os estudantes. Sobre essa situação, classifique cada afirmação como verdadeira ou falsa.
a) A probabilidade de sortear um estudante do 8º ano é maior do que a de sortear um estudante do 6º ano.
b) A probabilidade de sortear um estudante do 6º ano é igual à probabilidade de sortear um estudante do 7º ano.
c) A probabilidade de sortear um estudante do 9º ano é
17 sobre 64.
d) A probabilidade de sortear um estudante do 8º ano é aproximadamente 47%.
3. Caio vai realizar uma pesquisa com as turmas dos anos finais do Ensino Fundamental para descobrir a frequência com que realizam atividade física. Na escola em que ele estuda há 10 turmas para cada ano, e ele resolveu entrevistar metade da quantidade de estudantes de cada turma. Qual é o tipo de pesquisa que Caio vai realizar?
a) Pesquisa amostral.
b) Pesquisa censitária.
c) Pesquisa informativa.
d) Pesquisa pontual.
4. A escola em que Marina estuda entrevistou os .1000 estudantes matriculados para saber o tema de uma palestra que será realizada no início do ano. O gráfico a seguir foi construído com base nas respostas dadas, em que cada estudante escolheu apenas uma opção.
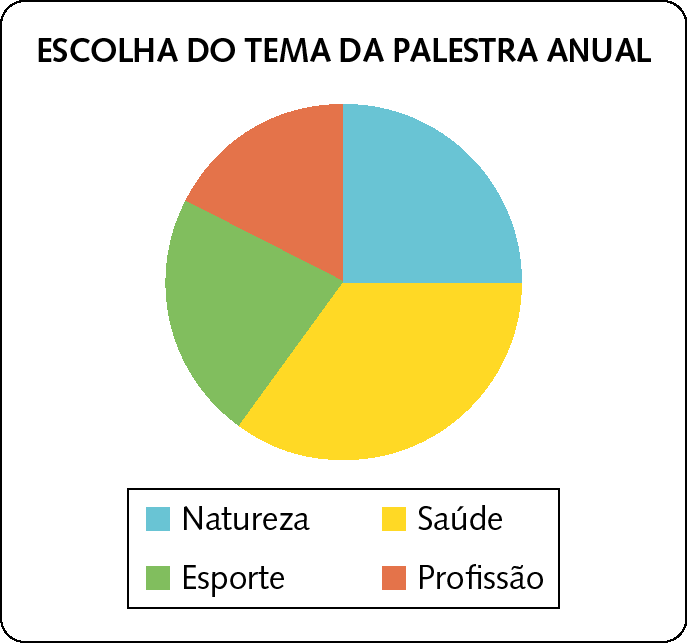
Determine a medida da abertura do ângulo de cada setor do gráfico, sabendo que 250 estudantes votaram em Natureza, 350 votaram em Saúde, 225 votaram em Esporte e 275 votaram em Profissão.
5. Na etapa final de um concurso a uma vaga de emprego, foi realizada uma prova com notas de 0 a 10. Acompanhe as notas dos quatro concorrentes que tiveram amplitude 2,5:
Samuel: 6,5
Moacir: 7
Carla: 8
Isabela: 5,5
Vai passar para a próxima fase quem estiver acima da nota média dos quatro concorrentes. Determine quem vai para a próxima fase.
6. Para saber a satisfação do atendimento em um posto de saúde, a administração pediu às pessoas atendidas que dessem uma nota de 0 a 4, sendo 0 a pior nota e 4 a melhor. Observe o resultado das notas dadas ontem.
|
Quantidade de pessoas |
Nota |
|---|---|
|
6 |
0 |
|
12 |
1 |
|
24 |
2 |
|
30 |
3 |
|
12 |
4 |
Dados obtidos pela administração do posto de saúde na última semana de 2023.
Qual foi a nota média que esse posto recebeu ontem?
a) 2
b) 2,4
c) 2,5
d) 3
Respostas
1. alternativa d
2. a) Falsa;
b) Verdadeira;
c) Verdadeira;
d) Falsa
3. alternativa a
4. Natureza: 90graus;
Saúde: 126graus;
Esporte: 81graus;
Profissão: 63graus.
5. Carla e Moacir.
6. alternativa b
Comentários da avaliação
A questão 1 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três quatro. Essa questão apresenta um contexto envolvendo sorteio para que os estudantes analisem a cor da ficha que tem a maior probabilidade de ser sorteada. Espera-se que eles percebam que se trata de um evento aleatório e, como as fichas têm as mesmas características físicas, aquela que tem maior probabilidade de ser sorteada é a que aparece em maior quantidade. Você pode ampliar a proposta da questão e solicitar a eles que determinem a probabilidade de cada cor de ficha ser sorteada.
A questão 2 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três quatro. Os estudantes precisam analisar cada afirmação para verificar as probabilidades mencionadas. Oriente-os a organizar os dados fornecidos na questão em um quadro e calcular as probabilidades de um estudante de cada ano ser sorteado:
Probabilidade de sortear um estudante do 6º ano:
32 sobre 128ou
1 sobre 4Probabilidade de sortear um estudante do 7º ano:
32 sobre 128ou
1 sobre 4Probabilidade de sortear um estudante do 8º ano:
30 sobre 128ou
15 sobre 64Probabilidade de sortear um estudante do 9º ano:
34 sobre 128ou
17 sobre 64A questão 3 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três seis. Essa questão apresenta um exemplo de pesquisa para que os estudantes analisem se é amostral ou censitária. Espera-se que eles percebam que a entrevista que Caio vai realizar não vai abranger todos os estudantes, porém vai abranger todas as turmas, sendo coletada uma amostra de cada turma. É um momento propício para retomar a diferença entre pesquisa amostral e censitária, além de discutir sobre a escolha de cada pesquisa, no que diz respeito a tempo, custo e análise de dados.
A questão 4 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três sete. Os estudantes precisam observar o gráfico apresentado e os dados da pesquisa realizada. Sabendo a quantidade de estudantes e a quantidade de votos que cada tema recebeu, eles podem calcular a medida da abertura do ângulo correspondente a cada setor. Oriente-os a primeiro determinar a porcentagem correspondente a cada tema. Depois, eles vão utilizar essas porcentagens para determinar a medida da abertura do ângulo de cada setor do gráfico, tomando o ângulo de medida de abertura igual a 360º como referência.
A questão 5 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três cinco. Os estudantes precisam calcular a média aritmética das quatro notas e compará-la com a nota de cada concorrente. Ao calcular a nota média, eles chegam a 6,75. Portanto, quem teve nota superior a essa vai para a próxima fase. Os estudantes podem cometer equívoco ao calcular a nota média ou ao compará-la com a nota individual dos candidatos. Em caso de dificuldades, convém retomar o cálculo da média aritmética simples.
A questão 6 auxilia no desenvolvimento da habilidade ê éfe zero sete ême ah três cinco. Essa questão apresenta notas dadas pelas pessoas que foram atendidas em um posto de saúde fictício para que os estudantes calculem a nota média. Espera-se que os estudantes percebam que, nessa situação, convém calcular a média aritmética ponderada. Os estudantes podem cometer equívocos ao não considerar as pessoas que deram nota 0, por exemplo. Em caso de dificuldades, convém retomar o cálculo da média ponderada.
Sugestão de avaliação para a preparação para exames de larga escala
|
Questões |
Objetivos |
|---|---|
|
1 |
Resolver problemas que envolvam adição e subtração com números inteiros. |
|
2 |
Resolver problemas com números naturais envolvendo as noções de divisor e de múltiplo. |
|
3 |
Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal. |
|
4 |
Comparar e ordenar frações associadas à ideia de partes de inteiros. |
|
5 |
Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias. |
|
6 |
Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas. |
|
7 |
Resolver problemas que envolvam porcentagens e juro simples. |
|
8 |
Resolver problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas. |
|
9 |
Reconhecer figuras obtidas por simetrias de translação, rotação e reflexão, usando instrumentos de desenho. |
|
10 |
Resolver problemas de cálculo da medida de volume de blocos retangulares envolvendo as unidades padrão. |
|
11 |
Reconhecer a condição de existência do triângulo quanto à medida do comprimento dos lados e verificar que a soma das medidas de abertura dos ângulos internos de um triângulo é 180°. |
|
12 |
Calcular probabilidades. |
1. Marcela imprimiu um demonstrativo de sua conta bancária com as movimentações feitas em um dia. Analise o demonstrativo da conta de Marcela e assinale a alternativa correta.
a) O saldo atual da conta corrente de Marcela é negativo.
b) Antes do depósito bancário de R$ 120,00cento e vinte reais, o saldo da conta de Marcela estava negativo.
c) Após o pagamento do cartão de crédito, o saldo da conta ficou negativo.
d) Para Marcela ficar com um saldo de R$ 450,00quatrocentos e cinquenta reais, ela deve fazer um depósito de R$ 250,00duzentos e cinquenta reais.
2. Carolina e Bruno fizeram uma charada para que cada um descobrisse a idade do outro. Veja o que eles disseram:
Carolina: “A minha idade corresponde a um número formado por dois algarismos; é um número menor que 20, múltiplo de 6 e divisor de 96”.
Bruno: “A minha idade está entre 10 e 25 anos; é um número divisível por 7 e divisor de 112”.
As idades de Carolina e Bruno são, respectivamente:
a) 16 e 14 anos.
b) 12 e 14 anos.
c) 12 e 16 anos.
d) 18 e 21 anos.
3. Observe a figura a seguir.
Sabendo que r // s e observando os ângulos destacados, assinale a alternativa correta.
a) A medida da abertura do ângulo
aé 120graus.
b) Os ângulos
ce
bsão congruentes.
c) b + c é igual a 180graus.
d) Os ângulos
be
csão opostos pelo vértice.
4. Ângela, Cristiane e Emike participaram de uma campanha de plantio de árvores nativas. Em uma das etapas da campanha, as três amigas deviam plantar árvores nativas em uma área como a representada na figura a seguir.
Ângela plantou árvores em uma parte que corresponde a
1 sobre 3da medida dessa área, Cristiane plantou árvores em uma parte que corresponde a
Fração. 4 sobre 9.da medida dessa área, e Emike plantou árvores no restante da área. Quem conseguiu plantar árvores na maior parte da área?
a) Ângela.
b) Cristiane.
c) Emike.
d) Todas plantaram árvores em partes iguais.
5. Ao sair em viagem, Jaqueline parou no posto 1 e gastou R$ 196,80cento e noventa e seis reais e oitenta centavos para completar o tanque de combustível de seu automóvel. Nesse posto, o preço do litro de gasolina era R$ 4,10quatro reais e dez centavos. Ao voltar para casa, Jaqueline reabasteceu o carro no posto 2 com
3 quartosdo que havia abastecido ao iniciar a viagem.
Se ela gastou R$ 143,64cento e quarenta e três reais e sessenta e quatro centavos no posto 2, podemos afirmar que:
a) o preço do litro de gasolina no posto 1 é menor que no posto 2.
b) o preço do litro de gasolina no posto 2 é R$ 4,02quatro reais e dois centavos.
c) ela abasteceu seu carro com 42 litros de gasolina no posto 1.
d) ela abasteceu seu carro com 36 litros de gasolina no posto 2.
6. Jonas é entregador de pizza. Ele recebe o salário mensal de R$ 1.250,00mil duzentos e cinquenta reais mais R$ 2,00dois reais por entrega.
Se x indica número de entregas, que expressão algébrica pode representar o salário mensal de Jonas?
a) 2x menos .1250
b) .1250 menos 2x
c) .1250 + 2x
d) .1250x ‒ 2
7. Pedro aplicou R$ 3.200,00três mil duzentos reais em um fundo de investimento a uma taxa de juro simples de 4% ao mês.
De acordo com essas informações, assinale a afirmação correta.
a) Após 3 meses, o juro recebido por Pedro será de R$ 768,00setecentos e sessenta e oito reais.
b) Pedro terá seu capital dobrado após dois anos.
c) Após 6 meses, o montante será de R$ 3.968,00três mil novecentos e sessenta e oito reais.
d) Esse investimento corresponde a uma taxa de juro de 44% ao ano.
8. Uma fábrica de brindes, funcionando com capacidade máxima, produz, por período, a seguinte quantidade de chaveiros personalizados.
|
Medida do tempo (minutos) |
Quantidade de chaveiros |
|---|---|
|
25 |
250 |
|
50 |
500 |
|
75 |
750 |
|
100 |
1.000 |
Nesse ritmo de produção, quantas horas serão necessárias para produzir .8250 chaveiros personalizados?
a) 825
b) 137,5
c) 13,75
d) 82,5
9. Observe a figura 1 e o ponto óh a seguir.
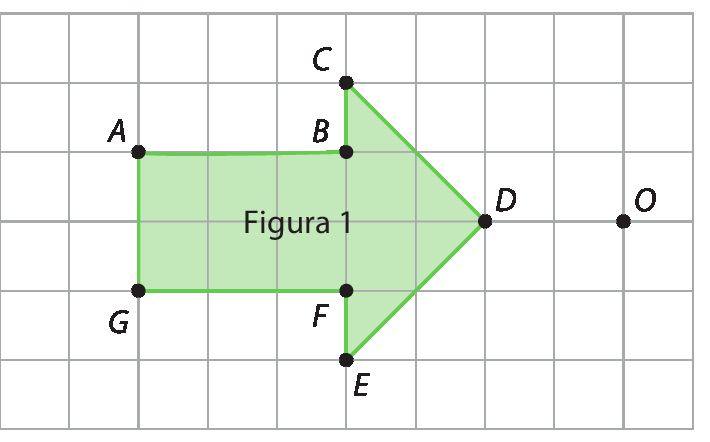
Assinale a alternativa que apresenta uma rotação de 90graus no sentido horário da figura 1 em relação ao ponto óh.
a)
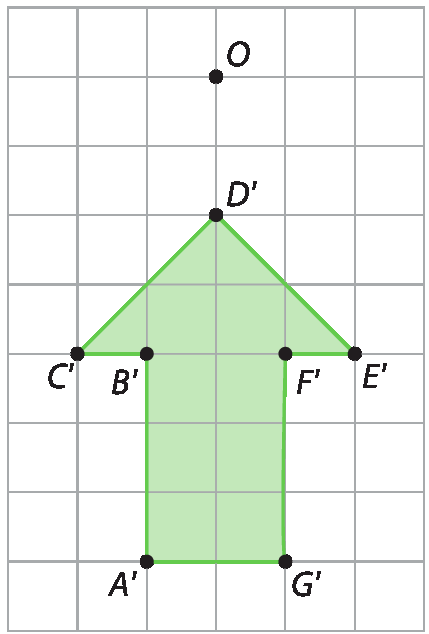
b)
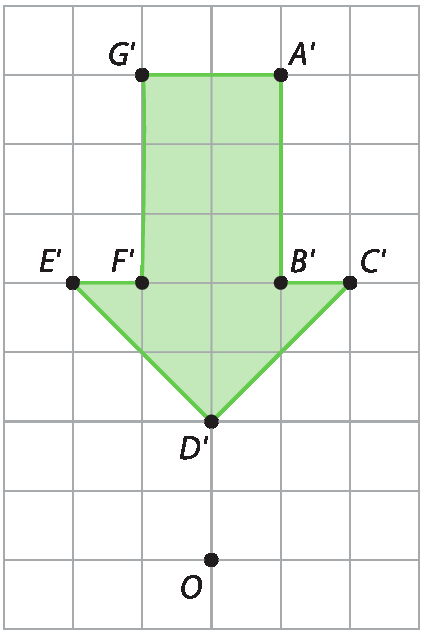
c)
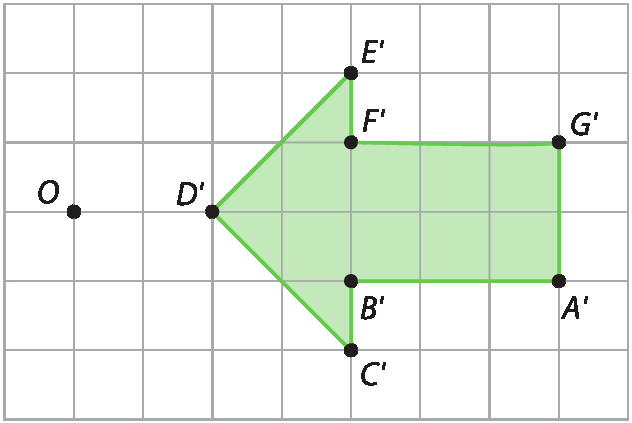
d)
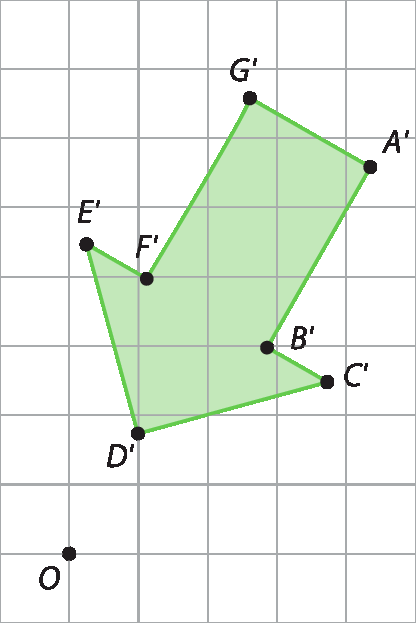
10. Rodrigo trabalha em uma marcenaria, e, para atender o pedido de um cliente, ele fez uma peça com formato de cubo usando um pedaço de madeira maciça. Nessa peça, Rodrigo escavou 4 buracos para encaixar perfeitamente quatro peças cúbicas menores. Observe a peça vista de cima.

Sabendo que cada aresta dessa peça tem medida de comprimento 30 centímetros e que em cada buraco deve ser encaixada uma peça cúbica com arestas de medida de comprimento 12 centímetros, qual é a medida do volume aproximado de madeira da peça final em decímetro cúbico?
a) 27 decímetros cúbicos
b) 25,27 decímetros cúbicos
c) 20,09 decímetros cúbicos
d) 6,9 decímetros cúbicos
11. Observe o triângulo representado a seguir.
Agora, indique qual das afirmações a seguir é verdadeira.
a) Observando a figura, podemos concluir que a + b = 90graus.
b) Os ângulos
ae
csão ângulos complementares.
c) É possível que as medidas de comprimento dos lados desse triângulo sejam 18 centímetros, 10 centímetros e 7 centímetros.
d) Podemos afirmar que b = 180graus menos a.
12. Em um período de quatro meses, uma fábrica de botões fez um levantamento do número de botões defeituosos em certa quantidade de botões testados. A cada mês, a gerente de produção aumentava o número de botões testados. Observe no quadro a seguir os resultados obtidos.
|
Quantidade de botões testados |
Quantidade de botões com defeito |
|
|---|---|---|
|
1º mês |
1.200 |
47 |
|
2º mês |
1.600 |
65 |
|
3º mês |
2.200 |
87 |
|
4º mês |
3.600 |
148 |
Observando os resultados obtidos, estima-se que a probabilidade de um botão testado ser defeituoso é de aproximadamente:
a) 2%
b) 4%
c) 6%
d) 9%
Respostas
1. alternativa b
2. alternativa b
3. alternativa c
4. alternativa b
5. alternativa d
6. alternativa c
7. alternativa c
8. alternativa c
9. alternativa b
10. alternativa c
11. alternativa a
12. alternativa b
Comentários da avaliação
Na questão 1, caso o estudante assinale a alternativa a, é possível que ele tenha cometido algum equívoco ao realizar os cálculos. Acompanhe a resolução junto dele e saliente que, para saber o saldo atual da conta, ele deve considerar o saldo anterior, subtrair os valores negativos e adicionar os valores positivos; caso o estudante assinale a alternativa c, verifique se ele compreendeu que deve considerar as movimentações bancárias somente até o momento do pagamento do cartão de crédito. Saliente que, nesse caso, devem-se subtrair do saldo anterior os valores referentes ao pagamento da conta de água, da conta de luz e do cartão de crédito para verificar o saldo disponível.
Após realizar os cálculos considerando as movimentações apresentadas no demonstrativo, o estudante deve concluir que o saldo da conta de Marcela é R$ 110,00cento e dez reais. Então, para que o saldo seja R$ 450,0quatrocentos e cinquenta reais0zero reais, Marcela deve depositar R$ 340,00trezentos e quarenta reais; portanto, a alternativa d está incorreta. Verifique se o estudante percebeu que é necessário calcular a diferença entre R$ 450,0quatrocentos e cinquenta reais0zero reais e o saldo atual para saber quanto Marcela deve depositar.
Na questão 2, caso o estudante indique a alternativa a, é possível que ele não tenha considerado que a idade de Carolina deve corresponder a um número que é múltiplo de 6, pois somente essa condição não é atendida pelos números desse item; caso o estudante indique a alternativa c, é possível que ele não tenha considerado que a idade de Bruno deve corresponder a um número que é divisível por 7, pois somente essa condição não é atendida pelos números desse item; caso o estudante indique a alternativa d, é possível que ele não tenha considerado que a idade de Carolina deve corresponder a um número que é divisor de 96 e a idade de Bruno deve corresponder a um número que é divisor de 112, pois essas condições não são atendidas pelos números desse item.
Na questão 3, caso o estudante assinale a alternativa a, analise a figura com ele e mostre que 75graus + a = 180graus; portanto, a = 105graus. Se julgar necessário, retome o estudo sobre ângulos suplementares; caso o estudante assinale a alternativa b, mostre que a medida de abertura do ângulo
ce o ângulo de medida de abertura 75graus são correspondentes; portanto, a medida de abertura do ângulo
ctambém é 75graus. Assim, os ângulos
be
cnão podem ser congruentes, pois são suplementares e a reta t não é perpendicular à reta s; caso o estudante assinale a alternativa d, relembre o conceito de ângulos opostos pelo vértice. Se julgar necessário, destaque o ângulo correspondente ao ângulo
ae mostre ao estudante que esse ângulo e o ângulo
bsão opostos pelo vértice.
Na questão 4, caso ocorra erro, verifique se o estudante percebeu que, para resolver esse problema, é preciso comparar as frações correspondentes à medida de área que cada amiga plantou. Desse modo, é necessário descobrir que fração da medida de área corresponde ao que Emike plantou. Se julgar necessário, mostre ao estudante que ele pode usar a figura como referência, marcando as partes que foram plantadas por Ângela e Cristiane para verificar as partes que sobraram e foram plantadas por Emike.
Para comparar as frações, o estudante pode usar diferentes estratégias, como a de calcular frações equivalentes ou registrar com cores diferentes na figura as partes plantadas por cada uma das amigas.
Na questão 5, caso o estudante assinale a alternativa a, verifique se ele calculou corretamente o preço do litro da gasolina no posto 2 para fazer a comparação. Caso o estudante não tenha calculado corretamente o preço do litro da gasolina no posto 2, acompanhe a resolução para identificar possíveis equívocos; caso o estudante assinale a alternativa b, é possível que ele não tenha clareza sobre como resolver o problema ou esteja cometendo equívocos nos cálculos. Nesse caso, saliente que, para calcular o valor do litro da gasolina no posto 2, é necessário calcular quantos litros foram utilizados para abastecer o veículo e, depois, dividir o valor pago pela quantidade de litros; caso o estudante assinale a alternativa c, é provável que ele tenha cometido equívocos ao fazer a divisão de 196,80 por 4,10. Nesse caso, retome com o estudante o algoritmo da divisão com números decimais.
Na questão 6, caso ocorra erro, releia o enunciado com o estudante para esclarecer a que se refere cada valor apresentado. Saliente que o salário fixo de R$ 1.250,00mil duzentos e cinquenta reais é pago independentemente da quantidade de entregas feitas por Jonas; portanto, esse valor não se altera. Verifique se o estudante percebeu que Jonas recebe R$ 2,00dois reais por entrega feita; portanto, o salário de Jonas aumenta de acordo com a quantidade x de entregas. Se julgar necessário, monte um quadro com o estudante para que ele perceba o valor do salário de Jonas a cada entrega e, a partir disso, chegue à expressão que generaliza o cálculo do salário.
Na questão 7, caso o estudante assinale a alternativa a, solicite a ele que calcule o valor que é acrescido ao investimento de Pedro por mês, ou seja, 4% de R$ 3.200,00três mil duzentos reais. Depois, peça-lhe que multiplique esse valor por 3, que é a quantidade de meses a que a afirmação se refere. Espera-se que, ao fazer esses cálculos, o estudante perceba que o juro recebido por Pedro em 3 meses será de R$ 384,00trezentos e oitenta e quatro reais. Portanto, a alternativa a está incorreta.
Depois de ter feito os cálculos para analisar a alternativa a, espera-se que o estudante perceba que o valor acrescido ao investimento de Pedro por mês é R$ 128,00cento e vinte e oito reais. Assim, caso assinale a alternativa b, verifique se ele fez os cálculos corretamente e se percebeu que é necessário converter os 2 anos em meses para calcular o valor do juro recebido por Pedro. Mostre-lhe que: 128 ⋅ 24 = .3072; portanto, o capital de Pedro não será dobrado, e a afirmação da alternativa b está incorreta.
Caso o estudante assinale a alternativa d, verifique se ele converteu 1 ano em 12 meses e multiplicou o juro mensal por 12. Caso ele tenha compreendido o que era necessário fazer e mesmo assim assinalado essa alternativa, é possível que ele tenha cometido algum equívoco nos cálculos. Nesse caso, mostre ao estudante que 0,04 ⋅ 12 = 0,48, ou seja, a taxa de juro anual corresponde a 48%, e a afirmação da alternativa d também está incorreta.
Caso o estudante cometa algum erro na questão 8, verifique se o estudante percebeu que o tempo e a quantidade de chaveiros produzidos são grandezas diretamente proporcionais, pois variam sempre preservando a mesma razão entre elas.
Caso o estudante cometa algum erro na questão 9, retome com ele a definição de sentido horário e, depois, analise as figuras apresentadas em cada alternativa. Verifique se o estudante percebeu que, na alternativa a, a figura sofreu uma rotação de 90graus no sentido anti-horário ou de 270graus no sentido horário; na alternativa c, a figura sofreu uma rotação de 180graus em ambos os sentidos, e, na alternativa d, a figura sofreu uma rotação de 240graus no sentido anti-horário ou de 120graus no sentido horário. Se julgar oportuno, solicite ao estudante que confirme as medidas das rotações realizadas usando um transferidor.
Na questão 10, caso o estudante tenha assinalado a alternativa a, é provável que ele tenha apenas calculado a medida do volume da peça sem desconsiderar os vãos que foram entalhados; se o estudante assinalou a alternativa b, pode ser que ele tenha calculado a medida do volume da peça e também a medida do volume correspondente a um dos vãos que foram entalhados, mas não tenha considerado os quatro vãos; se o estudante assinalou a alternativa d, é possível que ele tenha calculado a medida do volume correspondente aos quatro vãos, mas não tenha prosseguido com os cálculos.
Em caso de erro, releia a questão com o estudante e saliente que é necessário subtrair a medida do volume que corresponde aos quatro vãos do volume da peça cúbica.
Na questão 11, caso ocorra erro, retome com o estudante a condição de existência do triângulo quanto às medidas de comprimento dos lados e a soma das medidas da abertura dos ângulos internos de um triângulo.
Comente com o estudante que ângulos complementares são aqueles em que a soma das medidas de abertura é igual a 90graus.
Assim, não é possível que os ângulos
ae
csejam complementares, pois a medida de abertura do ângulo
cé 90graus. Portanto, a segunda afirmação é falsa.
Explique que a terceira afirmação é falsa porque, em qualquer triângulo, a medida de comprimento de um lado deve ser menor que a soma das medidas de comprimento dos outros dois lados.
Na questão 12, caso o estudante assinale uma alternativa errada, é possível que ele não tenha clareza sobre como proceder para resolver o problema. Nesse caso, explique que, considerando a quantidade de botões testados e a quantidade de botões que apresentaram defeito, é possível estimar a probabilidade de um botão novo apresentar algum tipo de defeito. Analise com o estudante a porcentagem de botões com defeito em relação aos botões testados e verifique se ele percebeu que, nos 4 meses, cêrca de 4% dos botões testados apresentaram defeito.
SUGESTÕES PARA PESQUISA OU CONSULTA PARA O PROFESSOR
Sugestões de livros
BOALER, J. Mentalidades matemáticas: estimulando o potencial dos estudantes por meio da matemática criativa, das mensagens inspiradoras e do ensino inovador. Tradução de: Daniel Bueno. Porto Alegre: Penso, 2018.
O livro aponta por que a Matemática é vista como vilã pelas pessoas. Por meio de pesquisas, mostra aos professores e pais como ajudar os estudantes a transformar as experiências negativas com a Matemática em mentalidades de crescimento. Aborda ainda a questão do erro como uma fórma de crescimento e traz atividades práticas que podem ser aplicadas dentro e fóra da sala de aula.
BOALER, J.; MUNSON, J.; Willian, C. Mentalidades matemáticas na sala de aula: ensino fundamental. Porto Alegre: Penso, 2019.
Este livro traz atividades práticas e desafiadoras – alinhadas à Bê êne cê cê – que permitem ao professor engajar seus estudantes a partir de uma nova concepção de Matemática, mais aberta e criativa e que promove o protagonismo dos estudantes.
Bréquiman C P Desenvolvimento do pensamento computacional através de atividades desplugadas na educação básica. Tese de Doutorado. Programa de Pós-Graduação em Informática na Educação do Centro Interdisciplinar de Novas Tecnologias na Educação da Universidade Federal do Rio Grande do Sul. Porto Alegre: u éfe érre gê ésse, 2017.
Essa pesquisa teve como objetivo verificar a possibilidade de desenvolver o pensamento computacional na Educação Básica utilizando exclusivamente atividades desplugadas (sem o uso de computadores). Nesse trabalho encontram-se diferentes sugestões de atividades que podem ser realizadas em sala de aula sem o uso do computador.
NACARATO, A. M.; CUSTÓDIO, I. A. (organizador). O desenvolvimento do pensamento algébrico na educação básica [livro eletrônico]: compartilhando propostas de sala de aula com o professor que ensina (ensinará) matemática. Brasília: Sociedade Brasileira de Educação Matemática, 2018.
A obra compartilha propostas de sala de aula relacionadas ao Pensamento Algébrico que vão da Educação Infantil ao Fundamental dois. Traz tarefas elaboradas e colocadas em prática, bem como os resultados obtidos com esse trabalho nas diferentes turmas pelos integrantes do Grucomat (Grupo Colaborativo de Matemática). O link de acesso para a obra está disponível em: https://oeds.link/aAkXIRpdf.
PONTE, J. P. et al. Investigações matemáticas na sala de aula. quarta ediçãoBelo Horizonte: Autêntica, 2019.
O livro mostra como práticas de investigação desenvolvidas por matemáticos podem ser usadas na sala de aula e as vantagens e as dificuldades de se trabalhar nessa perspectiva.
TORRES, J. D. S. Jogos de Matemática e de Raciocínio Lógico. segunda edição Petrópolis: Vozes, 2013.
O livro apresenta uma coletânea de jogos de matemática e raciocínio lógico, que podem ser propostos em qualquer momento do ano letivo. São propostos jogos com números, jogos com xadrez e dominó, sofismas e diferentes tipos de enigma.
Sugestões de sites
• Sociedade Brasileira de Educação Matemática (SBEM):
https://oeds.link/lb9F2Z
Acesso em: 5 junho 2022.
Disponibiliza informações sobre eventos regionais, nacionais e internacionais na área de educação matemática.
• Educação Matemática e Tecnologia Informática (Edumatec):
https://oeds.link/9hnp7K
Acesso em: 5 junho 2022.
O site oferece softwares, atividades, artigos e links de interesse para o professor de Matemática.
• Laboratório de Ensino de Matemática (LEM):
https://oeds.link/4YrYcrp.br/line/lem1.html
Acesso em: 5 junho 2022.
Site do Laboratório de Ensino de Matemática, objetiva difundir o ensino de Matemática por meio do computador, trazendo softwares educacionais, apostilas e informações nessa área.
• Plataforma Laplace
https://oeds.link/RvGtfc
Acesso em: 5 junho 2022.
A plataforma traz questões com resoluções completas, jogos, resumos teóricos e videoaulas por assunto ou habilidade. O professor pode ainda gerar provas digitais e simulados dos principais vestibulares com correção automática.
• Plataforma Youcubed:
https://oeds.link/QDTlNL
Acesso em: 5 junho 2022.
A plataforma foi desenvolvida pela Universidade de sténfordi, pelas professoras Jo Boaler e Cathy Willians. Foi traduzido pelo Instituto Sidarta e Itaú Social. Traz conteúdos como atividades, jogos, aplicativos e videoaulas para ensinar Matemática de fórma criativa. É baseado nas ideias do livro Mentalidades matemáticas, de Jo Boaler.
• Rede Mentalidades Matemáticas (Rede ême ême):
https://oeds.link/FDvIim
Acesso em: 19 julho 2022.
O site é uma criação do Instituto Sidarta em parceria com o Centro de Pesquisas Youcubed, da Universidade de sténfordi, com o suporte do Itaú Social. Traz informações, recursos, cursos, artigos científicos e atividades variadas para a aplicação das ideias das mentalidades matemáticas, propagadas pela professora Jo Boaler.
• Site oficial da família e dos admiradores do matemático Malba Tahan:
https://oeds.link/SOhmBi
Acesso em: 19 julho 2022.
O site traz teses, dissertações, artigos e relatos referentes a esse matemático que esteve à frente do seu tempo, propondo uma Matemática com significado. Possui desafios matemáticos.
• Nova Escola:
https://oeds.link/oJstGh
Acesso em: 8 agosto 2022.
Disponibiliza diversos recursos digitais gratuitos que poderão ajudá-lo na inclusão de estudantes com deficiência.
Sugestões de vídeos
• Coleção Matemática Multimídia, da Universidade de Campinas (Unicamp):
https://oeds.link/Lmtg7Pp.br/
Acesso em: 5 junho 2022.
O site traz diversos vídeos com conteúdos de Matemática voltados para o Ensino Médio. Alguns desses conteúdos podem ser trabalhados com estudantes dos Anos Finais do Ensino Fundamental e são acompanhados de um “Guia do Professor”. Além dos vídeos, no site é possível encontrar experimentos, softwares e áudios.