Sumário

Conheça a estrutura da coleção

Livro do estudante

Esta coleção é composta de quatro volumes destinados aos Anos Finais do Ensino Fundamental. Os volumes estão organizados em unidades e em tópicos com títulos e subtítulos, considerando as competências e as habilidades da BNCC estabelecidas para cada ano.

Além desses elementos, esta coleção apresenta a seguinte estrutura.

O que eu já sei?

Seção presente no início de cada volume com atividades que têm como objetivo propor uma avaliação diagnóstica dos estudantes, permitindo verificar os conhecimentos prévios deles referentes aos conteúdos que são pré-requisitos daqueles que serão abordados no volume. Algumas atividades propostas nessa seção também podem colaborar com a preparação do estudante para exames de larga escala, pois elas têm formato semelhante ao de questões abordadas nesse tipo de exame, como as provas do Sistema de Avaliação da Educação Básica (Saeb), aplicadas aos estudantes do 9º ano.

Páginas de abertura das unidades

Além de delimitar graficamente cada unidade, a página de abertura tem a função de introduzir, de maneira informal, o conteúdo a ser trabalhado. Nessa página, a foto apresentada tem como objetivo proporcionar um estímulo visual relacionado a alguns dos conteúdos que serão trabalhados. Além disso, o boxe Agora vamos estudar... apresenta os conteúdos estudados na unidade, elencados por tópicos. Antes de iniciar o trabalho com os tópicos da unidade, instigue os estudantes a analisar a foto e conjecturar exemplos de conexões entre ela e os conteúdos. Se necessário, faça perguntas que direcionem o olhar dos estudantes para os aspectos desejados.

Desenvolvimento dos conteúdos

Em cada unidade, os conteúdos são apresentados por meio de textos expositivos ou de situações-problema que abordam temas próximos à realidade dos estudantes.

Os conteúdos referentes aos eixos de conteúdos da Matemática são distribuídos de forma alternada e articulada em cada volume. Contudo, cabe ao professor trabalhar os conteúdos na ordem que considerar mais conveniente, conforme suas necessidades em sala de aula.

Instrumentos e softwares

Nessa seção, apresentamos orientações para o uso da calculadora comum e da científica, do software de Geometria dinâmica e das planilhas eletrônicas, além de instrumentos como régua, esquadro e compasso.

Atividades

Na seção Atividades, são apresentadas atividades com características variadas que incentivarão os estudantes a refletir, a relacionar diferentes conteúdos e a ampliar conceitos desenvolvidos nos tópicos, além de desenvolver as competências e habilidades da BNCC.

Atenção!

Boxe com informações complementares para auxiliar os estudantes na compreensão dos conteúdos e na resolução de algumas atividades.

Vocabulário

Apresenta o significado de termos destacados no texto que os estudantes desconheçam ou não compreendam totalmente.

O que eu estudei?

Seção presente ao final de cada unidade com atividades em diferentes formatos, inclusive com características dos exames de larga escala, que têm como objetivo fazer uma avaliação formativa dos estudantes, permitindo-lhes que verifiquem suas aprendizagens e retomem conteúdos trabalhados sempre que for necessário.

O que eu aprendi?

Seção presente ao final de cada volume com atividades que têm como objetivo propor aos estudantes uma avaliação de resultado (ou somativa), permitindo-lhes que consolidem as aprendizagens acumuladas no ano letivo. Algumas atividades com características de exame de larga escala também são propostas nessa seção.

Destaques em atividades e questões

Certas atividades e questões que, por apresentarem estruturas diferenciadas, têm alguns termos em destaque. Confira a seguir algumas informações a respeito de cada um deles.

Cálculo mental

Atividades ou questões que envolvem cálculo mental, desenvolvendo nos estudantes a agilidade para realizar cálculos e verificar os resultados por meio de diferentes estratégias. O termo que indica que a atividade ou a questão envolve cálculo mental é destacado no enunciado. Por exemplo: “Efetue os cálculos mentalmente.”.

Elaboração de problemas

Atividades em que os estudantes deverão elaborar problemas ou questões. O termo que indica que a atividade envolve elaboração de problemas é destacado no enunciado. Por exemplo: “De acordo com os preços apresentados, elabore um problema envolvendo adição.”.

Estimativa

Atividades ou questões em que é preciso fazer estimativas. O termo que indica que a atividade ou a questão envolve estimativa é destacado no enunciado. Por exemplo: “Estime o resultado das subtrações.”.

Em duplas e em grupo

Atividades ou questões elaboradas com o objetivo de incentivar os estudantes a trabalhar com os colegas, bem como a debater as principais ideias matemáticas abordadas, incentivando também o respeito às diferentes opiniões. O termo que indica a necessidade de se juntar aos colegas é destacado no enunciado. Por exemplo: “Junte-se a um colega e resolvam os problemas”.

Algumas atividades são destacadas com ícones. Confira a seguir algumas informações a respeito de cada um deles.

Desafio

Indica que a atividade ou a questão tem caráter desafiador, favorecendo o desenvolvimento de estratégias próprias de resolução.

Instrumentos e softwares

Indica que, para resolver a atividade ou a questão, os estudantes precisarão utilizar alguns dos recursos mencionados na seção Instrumentos e softwares, aplicando os conhecimentos adquiridos.

Atividade oral

Atividade oral: indica que a atividade ou a questão deve ser respondida oralmente.

Para a realização de algumas atividades ou questões, são necessários materiais que não acompanham o livro didático (calculadora, régua, compasso, tesoura etc.). Nesses casos, o professor deve solicitar previamente aos estudantes que os levem para a sala de aula. Em algumas situações, eles devem ser incentivados a compartilhá-los com os colegas. O professor ou a escola, na medida do possível, pode providenciar esses materiais.

Projeto em ação

O desenvolvimento dessa seção permite à turma toda que se envolva em uma atividade prática dividida em etapas de planejamento, execução e divulgação para alcançar determinado objetivo. As atividades possibilitam aos estudantes que atuem de modo ativo na resolução de problemas locais ou na reflexão acerca de questões mais amplas, que influenciam a vida de muitas pessoas. Com relação às demais atividades da coleção, a proposta dessa seção demanda um tempo maior de planejamento e realização, mas, apesar de estar localizada no final do volume, não deve ser, necessariamente, a última seção trabalhada. Além disso, as atividades propostas nessa seção estabelecem relações com outros componentes curriculares e exercitam habilidades desenvolvidas em outros momentos do volume. Neste Manual do professor, há orientações para auxiliá-lo na condução de todo o processo.

Sugestões complementares

A fim de enriquecer o trabalho em sala de aula, são apresentadas, nessa seção, sugestões de livros, filmes, sites, vídeos e podcasts, de modo a incentivar o gosto pela leitura e pela busca por informações em outras fontes além do livro didático.

Respostas

Seção que apresenta respostas das atividades, organizadas por unidade.

Referências bibliográficas comentadas

Essa seção apresenta, ao final de cada volume, as referências bibliográficas que foram usadas na elaboração do livro, com um breve comentário sobre cada uma delas.

Siglas

Essa seção apresenta o significado das siglas apresentadas ao longo do volume.

Manual do professor

Este manual é dividido em duas partes. A primeira apresenta orientações gerais acerca dos aspectos teórico-metodológicos que fundamentam a coleção, a estrutura e a organização do livro do estudante e do manual do professor, além das resoluções das atividades e das questões apresentadas no livro do estudante.

A segunda parte, chamada orientações ao professor, apresenta a reprodução reduzida do livro do estudante com respostas a questões e atividades e algumas orientações pontuais. As respostas que não constam na reprodução do livro do estudante podem ser localizadas nas laterais e nos rodapés dessa parte do manual, no gabarito do livro do estudante e/ou nas resoluções das atividades. Ainda nas laterais e nos rodapés, há orientações específicas para enriquecer e complementar o trabalho com as páginas. Em alguns momentos, para deixar mais evidente o sentido de leitura, na lateral e rodapé de algumas páginas ímpares é utilizado o seguinte recurso visual: .

A estrutura do manual está descrita a seguir.

Seções O que eu já sei?, O que eu estudei? e O que eu aprendi?

Apresentam os objetivos das atividades dessas seções, destacando os conteúdos e as habilidades que se pretende avaliar durante o aprendizado dos estudantes, as orientações de estratégias de remediação para as possíveis dificuldades e como trabalhar as defasagens, além das respostas das atividades.

Páginas de abertura das unidades

Elenca possíveis orientações de como instigar os estudantes a estabelecer relações entre a foto apresentada e o conteúdo que será estudado.

Respostas

As respostas das atividades são apresentadas, preferencialmente, na seção Respostas, na reprodução do livro do estudante. Porém, em alguns casos específicos, em atividades abertas ou que não cabem na seção, como as que contêm imagens, quadros, tabelas ou esquemas, elas aparecem apenas nas orientações ao professor ou na seção Resoluções.

Metodologias ativas

Apresenta as orientações específicas para atividades que envolvem metodologias ativas, podendo remeter às orientações gerais de cada metodologia ativa que estão nas orientações gerais deste Manual do professor.

Objetivos da unidade

Na primeira página após a abertura da unidade, apresentamos os objetivos que evidenciam o que se espera alcançar no trabalho com a respectiva unidade.

Justificativas

Após os objetivos da unidade, são contempladas as justificativas dos principais objetivos propostos apresentando a importância deles para a formação dos estudantes.

Um texto a mais

Apresenta textos complementares que auxiliam o trabalho com a página ou contribuem para a formação do professor. O trabalho com esse recurso também tem o intuito de proporcionar ao professor a possibilidade de conduzir o conteúdo de maneira alternada e/ou ampliar os próprios conhecimentos a respeito do tema abordado.

Atividade a mais

Sempre que possível, são apresentadas propostas de atividades complementares que envolvem o conteúdo desenvolvido na unidade. Em meio a essas atividades, também é possível reconhecer dinâmicas que proporcionem aos estudantes o exercício de convívio em sociedade, o reconhecimento e o respeito às diferenças, a discussão, a reflexão e o combate a qualquer tipo de violência e a promoção da saúde mental, além de trabalhar de maneira interdisciplinar com outros componentes curriculares.

Sugestão de avaliação

Indica momentos e estratégias para auxiliar o professor no processo de avaliação da aprendizagem dos estudantes. Tais propostas são condizentes com as características desta obra e têm o intuito tanto de preparar a turma para exames quanto de verificar o andamento deles em contexto formativo. As informações obtidas pelo professor por meio desse boxe contribuem para que ele reavalie seu planejamento e o modifique se necessário.

Algo a mais

Apresenta sugestões de livros, artigos, filmes, vídeos, sites, entre outras mídias que contribuem para a formação do professor.

Comentários da seção Projeto em ação

Apresenta os objetivos metodológicos do trabalho com os projetos e as orientações relacionadas ao desenvolvimento e à divulgação dessas atividades, destacando as relações interdisciplinares envolvidas, assim como as habilidades e as competências da BNCC trabalhadas. Além disso, esses comentários apresentam ao professor as respostas às questões e as sugestões relacionadas ao envolvimento da comunidade escolar e extraescolar.

Outras orientações específicas ao professor

Além das orientações e dos comentários apresentados nos boxes indicados anteriormente, nas orientações ao professor são organizados os tópicos que apresentam comentários, curiosidades, sugestões e informações complementares para o trabalho com as páginas de teoria, atividades, questões e seções.

Nesses comentários, sempre que possível, são evidenciados os códigos das habilidades e das competências gerais e específicas, além dos temas contemporâneos transversais da BNCC que foram trabalhados na página, destacando as relações entre esses itens e o desenvolvimento dos conteúdos. Além disso, são apresentadas, nesses comentários, orientações claras para trabalhar a empatia e a cooperação e desenvolver o pensamento crítico, o pluralismo de ideias e a análise criativa e propositiva, além da capacidade de argumentar e fazer inferências sobre o conteúdo, aspectos essenciais na formação de cidadãos críticos e atuantes na sociedade. Outro aspecto que será evidenciado nesses comentários é o desenvolvimento do pensamento computacional. Sempre que uma atividade ou seção possibilitar esse trabalho, ele estará destacado nas orientações.

Em atividades que envolvem o trabalho com gêneros textuais, o professor encontra orientações sobre como desenvolver nos estudantes a leitura inferencial e a prática de argumentação.

A fim de valorizar e incentivar a autonomia do professor, os comentários das orientações ao professor apresentam diferentes maneiras de abordar determinados conteúdos ao iniciar uma aula, destacando contextualizações e situações-problema. Essa estratégia, além de aumentar o interesse dos estudantes pelo assunto, contribui para aproximar os conteúdos trabalhados ao cotidiano deles. Além disso, sempre que necessário, o professor é orientado a providenciar materiais e recursos ou realizar reservas de locais ou de equipamentos antes de iniciar determinadas atividades.

Em atividades práticas que envolvem o manuseio de diferentes materiais e ferramentas ou a visita a locais fora da escola, o professor conta ainda com orientações específicas sobre os cuidados que devem ser tomados a fim de manter a integridade de todos os envolvidos no processo educacional.

Em atividades e abordagens que possibilitam uma articulação com outros componentes curriculares, os comentários das orientações ao professor explicitam essas articulações e trazem sugestões de diferentes estratégias para obter o melhor proveito delas, em conjunto com o professor dos outros componentes curriculares envolvidos.

Fundamentação e orientações gerais

A BNCC e os Anos Finais do Ensino Fundamental

A Base Nacional Comum Curricular (BNCC) é um dos documentos norteadores da Educação Básica, homologada para a Educação Infantil e o Ensino Fundamental, em 2017, e, em 2018, para o Ensino Médio. A BNCC foi criada como um documento de referência que estabelece as competências gerais e específicas e as habilidades que os estudantes devem desenvolver em cada segmento da Educação Básica ao longo dos anos letivos. Embora a BNCC tenha caráter norteador para todas as instituições de Ensino Básico no Brasil, sabe-se que as instituições de ensino têm realidades distintas, o que demanda a elaboração de currículos adequados ao projeto político pedagógico de cada uma.

Com relação aos Anos Finais do Ensino Fundamental, é importante compreender que a BNCC propõe que os componentes curriculares retomem e ressignifiquem as aprendizagens dos Anos Iniciais do Ensino Fundamental, objetivando o aprofundamento e a ampliação do repertório de aprendizagens dos estudantes, além de fortalecer a autonomia deles com estratégias de ensino que lhes permitam interagir de maneira crítica com as diferentes fontes de informação e conhecimentos.

Para atender a essas necessidades, a BNCC dos Anos Finais do Ensino Fundamental propõe um conjunto de habilidades para cada componente curricular. As habilidades propostas estão relacionadas a objetos de conhecimento compreendidos em conteúdos, conceitos e processos, que se articulam com foco no desenvolvimento das ideias fundamentais de cada componente curricular. Desse modo, a descrição das habilidades é baseada em processos cognitivos, objetos de conhecimento e contextos específicos que fazem parte do meio em que devem se desenvolver, considerando também a faixa etária dos estudantes.

Os volumes desta coleção foram organizados tendo como um dos objetivos contemplar as competências gerais e específicas e as habilidades da BNCC com suas respectivas relações com os objetos de conhecimento. Essas relações podem ser percebidas na organização dos objetivos de aprendizagem e respectivos conteúdos, nas abordagens apresentadas, nas questões no decorrer do desenvolvimento dos conteúdos, nas atividades e em outros momentos dos volumes, como na seção Projeto em ação. No Manual do professor, destacamos os momentos em que o livro do estudante proporciona o desenvolvimento das competências gerais e específicas e as habilidades, de modo que o livro didático seja uma ferramenta segura e de apoio ao professor no processo de ensino e de aprendizagem.

Competências gerais da Educação Básica

Com base nos princípios éticos, políticos e estéticos preconizados pelas Diretrizes Curriculares Nacionais, a BNCC apresenta dez competências gerais que consolidam os direitos de aprendizagem e desenvolvimento, com foco na formação integral dos estudantes nos âmbitos físico, cognitivo, emocional e social. O trabalho com essas competências perpassa todos os componentes curriculares e está intrinsicamente ligado ao desenvolvimento de atitudes e valores fundamentais para a formação cidadã dos estudantes, além de contribuir para a construção de conhecimentos e para o desenvolvimento das habilidades de cada componente curricular.

Confira a seguir as dez competências gerais da Educação Básica.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 9-10. Disponível em: https://oeds.link/pKEA59 Acesso em: 19 maio 2022.

Competências gerais da Educação Básica

1. 1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
2. 2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
3. 3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.
4. 4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
5. 5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. 6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
7. 7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbitos local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
8. 8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.
9. 9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
10. 10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 9-10. Disponível em: https://oeds.link/pKEA59 Acesso em: 19 maio 2022.

Competências específicas de Matemática para o Ensino Fundamental

A BNCC estabelece, além das competências gerais, as competências específicas para cada componente curricular. Essas competências determinam o trabalho com habilidades, conceitos e noções que orientam a prática docente e que estão relacionados às unidades temáticas e aos objetos de conhecimento, promovendo também o desenvolvimento cognitivo dos estudantes.

De acordo com a BNCC, no decorrer do Ensino Fundamental, os estudantes devem desenvolver as seguintes competências específicas de Matemática.

Competências específicas de Matemática para o Ensino Fundamental

1. 1.Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
2. 2.Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. 3.Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. 4.Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. 5.Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
6. 6.Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
7. 7.Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. 8.Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 267. Disponível em: https://oeds.link/pKEA59 Acesso em: 19 maio 2022.

No processo de desenvolvimento das competências gerais, é preciso que os estudantes desenvolvam os princípios das competências específicas de cada área do conhecimento, que é assegurado por meio do trabalho com as habilidades de cada componente curricular.

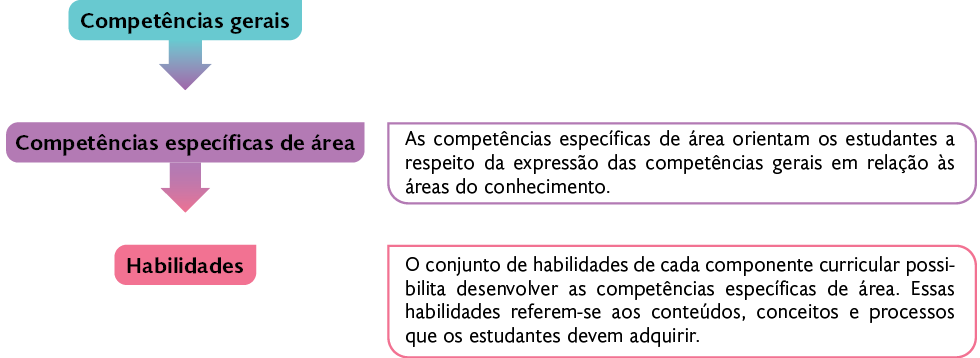
Esta coleção foi elaborada buscando contemplar habilidades e competências específicas relacionadas à Matemática, a fim de fornecer aos estudantes subsídios para desenvolverem as competências gerais propostas na BNCC. Tais relações estão presentes nas abordagens dos conteúdos, em textos, seções e atividades. Confira um exemplo de como é feita essa orientação nos volumes da coleção.

Ao elaborar e resolver problemas envolvendo adições com números inteiros na atividade 45, os estudantes têm a oportunidade de desenvolver a habilidade EF07MA04. Nesse caso, por eles enfrentarem situações-problema, incluindo situações imaginadas, expressando suas respostas e sintetizando conclusões, desenvolvem aspectos da Competência específica de Matemática 6 e, por exercitarem a curiosidade intelectual, a empatia, o diálogo, a cooperação e a resolução de conflitos, trabalham aspectos das Competências gerais 2 e 9.

Ao final das orientações gerais deste Manual do professor, há o Quadro de conteúdos deste volume que apresenta as relações entre as habilidades e/ou competências e os conteúdos da área, explicitando como esses elementos são desenvolvidos.

Temas contemporâneos transversais e a formação cidadã

Os temas contemporâneos transversais propõem a inserção de temas nos conteúdos curriculares e nas práticas pedagógicas que auxiliam na contextualização de modo transversal e integrador, favorecendo aos estudantes conhecimentos que contribuem para sua formação cidadã.

Esses temas devem ser considerados por todos os componentes curriculares, devendo ser trabalhados de modo transversal e integrador, ampliando a compreensão dos estudantes com relação a temas sociais, proporcionando o desenvolvimento do pensamento crítico-reflexivo e contribuindo para sua formação cidadã, para a democracia e para a inserção no mundo do trabalho.

Os temas contemporâneos transversais da BNCC visam cumprir a legislação que assegura a Educação Básica. Entre os documentos que guiam o trabalho com esses temas, podemos destacar: as Diretrizes Curriculares Nacionais para a Educação Básica (DCN), além de leis e decretos, como o Estatuto da Criança e do Adolescente (Lei n. 8.069/1990), a Lei de Educação Ambiental (Lei n. 9.795/1999, Parecer CNE/CP n. 14/2012 e Resolução CNE/CP n. 2/2012), o Código de Trânsito Brasileiro (Lei n. 9.503/1997), o Estatuto do Idoso (Lei n. 10.741/2003), as Diretrizes Nacionais para a Educação em Direitos Humanos (Decreto n. 7.037/2009, Parecer CNE/CP n. 8/2012 e Resolução CNE/CP n. 1/2012), as leis que instituem a obrigatoriedade do ensino de história e cultura afro-brasileira e indígena (Leis n. 10.639/2003 e 11.645/2008, Parecer CNE/CP n. 3/2004 e Resolução CNE/CP n. 1/2004), o Programa Nacional de Alimentação Escolar – PNAE (Lei n. 11.947/2009) e as Diretrizes Curriculares Nacionais para o Ensino Fundamental de nove anos (Parecer CNE/CEB n. 11/2010 e Resolução CNE/CEB n. 7/2010).

A organização dos temas contemporâneos transversais na BNCC acontece por meio de seis macroáreas temáticas, que visam dar subsídios aos estudantes para um melhor entendimento da sociedade em que vivem. As macroáreas que a BNCC aborda se organizam da seguinte maneira.

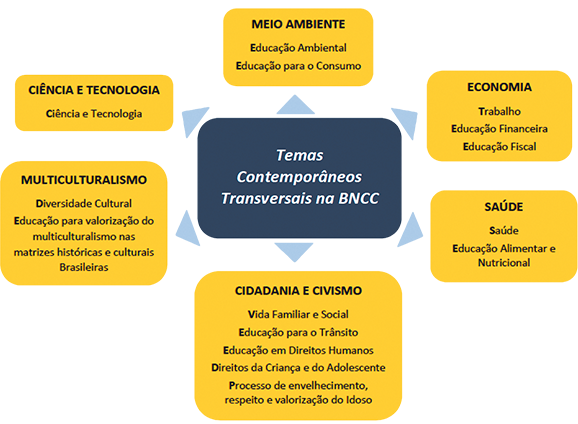
BRASIL. Ministério da Educação. Temas contemporâneos transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília: MEC, 2019. p. 13. Disponível em: https://oeds.link/Mp6RcA Acesso em: 18 maio 2022.

A seguir, apresentamos uma breve descrição acerca dos temas contemporâneos transversais.

Temas contemporâneos transversais

Temas contemporâneos transversais

Nesta coleção, os temas contemporâneos transversais são abordados por meio de atividades contextualizadas envolvendo assuntos relacionados a eles, como Educação em direitos humanos, Ciência e tecnologia, Diversidade cultural, Educação ambiental e Educação financeira. Nessas atividades, além do desenvolvimento do assunto matemático, os estudantes são levados a realizar pesquisas, a expor e defender suas opiniões e a identificar fake news.

Nos comentários página a página do manual, orientamos o professor no trabalho com essas atividades a fim de aprimorar a abordagem dos temas, inclusive, em alguns casos, propondo outras tarefas, como conversar com um profissional ou membro da comunidade em que ele vive. Além disso, sempre que possível, explicamos como a abordagem dos temas contemporâneos transversais explora o desenvolvimento das competências gerais, em especial a Competência geral 9.

Proposta teórico-metodológica do componente curricular de Matemática

Objetivos da obra

Esta coleção de Matemática – destinada a estudantes dos Anos Finais do Ensino Fundamental – tem por objetivo promover o processo de ensino e de aprendizagem de Matemática por meio de uma linguagem de fácil compreensão, buscando ampliar, assim, o interesse dos estudantes por essa área do conhecimento.

A coleção contempla as cinco unidades temáticas propostas pela BNCC: Números, Álgebra, Geometria, Grandezas e medidas e Probabilidade e estatística. Os conteúdos são retomados em vários momentos da coleção, ampliados e articulados entre si. Sempre que possível, os conteúdos são abordados por meio de situações contextualizadas e próximas à realidade do estudante. Procura-se também associar os conteúdos a outros componentes curriculares, como História, Geografia, Ciências, Língua Portuguesa e Arte.

No decorrer dos volumes, também são propostas situações que tratam de temas contemporâneos transversais, favorecendo o debate em sala de aula e a formação de opinião. Além disso, o conhecimento prévio dos estudantes é valorizado e tomado como ponto de partida para a construção de novos conhecimentos.

As atividades e os textos propostos no livro do estudante incentivam a curiosidade e o espírito de investigação, o desenvolvimento da capacidade de resolver problemas recorrendo à modelagem matemática, ao raciocínio lógico-matemático (indução, dedução, abdução ou raciocínio por analogia), à dedução de algumas propriedades e à verificação de conjecturas.

O ensino de Matemática do 6º ao 9º ano

Na etapa da vida que corresponde ao Ensino Fundamental, o estatuto de cidadão vai se definindo gradativamente conforme o educando vai [...] assumindo a condição de um sujeito de direitos. As crianças, quase sempre, percebem o sentido das transformações corporais e culturais, afetivo-emocionais, sociais, pelas quais passam. Tais transformações requerem-lhes reformulação da autoimagem, a que se associa o desenvolvimento cognitivo. Junto a isso, buscam referências para a formação de valores próprios, novas estratégias para lidar com as diferentes exigências que lhes são impostas.

BRASIL. Ministério da Educação. Diretrizes Curriculares Nacionais da Educação Básica. Brasília: MEC: SEB: DICEI, 2013. p. 37.

Todos os dias, as pessoas estão envolvidas em situações nas quais é necessário contar, adicionar, subtrair, multiplicar, dividir, medir, comparar etc. Por isso, o conhecimento matemático constitui uma ferramenta de vasta aplicabilidade e deve ser explorado de forma ampla no Ensino Fundamental, desenvolvendo nos estudantes a estruturação do pensamento, a agilização do raciocínio dedutivo e a capacidade de resolver problemas, além de possibilitar o apoio à construção de conhecimentos em outras áreas do conhecimento.

Além disso, na atual sociedade, a interpretação crítica de informações e sua utilização de modo adequado tornam-se cada vez mais necessárias. Partindo desse princípio, o cidadão deve ser capaz de interpretar e transformar sua realidade, de desenvolver estratégias pessoais e de utilizar recursos tecnológicos para resolver situações-problema, bem como trabalhar de maneira coletiva e cooperativa, entre outras capacidades.

O conhecimento matemático aliado ao saber cotidiano tem a função de contribuir para a formação de cidadãos capazes de compreender e se comunicar na sociedade. Isso porque está relacionado a várias outras áreas, como Ciências da Natureza e Ciências Sociais, e porque está presente nas artes, como em composições musicais e em coreografias, e nos esportes.

Conhecer os objetivos gerais para o Ensino Fundamental de Matemática é essencial para que sejam obtidos bons resultados no processo de ensino e de aprendizagem. Apresentamos a seguir alguns objetivos do ensino de Matemática para os Anos Finais do Ensino Fundamental.

• Identificar os conhecimentos matemáticos como meios de compreensão e transformação da realidade.
• Perceber o caráter intelectual característico da Matemática como meio que incentiva a curiosidade, o interesse, o espírito investigativo e o desenvolvimento da capacidade para resolver problemas.
• Realizar observações empíricas do mundo real com o objetivo de estabelecer relação com conteúdos matemáticos estudados e, com base neles, fazer induções e conjecturas.
• Selecionar, organizar e produzir informações significativas com o objetivo de interpretá-las e avaliá-las criticamente.
• Formular e resolver situações-problema a fim de desenvolver formas de raciocínio e processos utilizando conceitos e procedimentos matemáticos, além de instrumentos tecnológicos disponíveis.
• Comunicar-se em linguagem matemática usando linguagem simbólica.
• Estabelecer relações entre o conhecimento matemático e o conhecimento de outras áreas do conhecimento.
• Ter segurança na própria capacidade de construção do conhecimento matemático.
• Deduzir algumas propriedades matemáticas e verificar conjecturas.

A resolução de problemas

As situações-problema estão presentes em todos os volumes desta coleção e apresentam diferentes objetivos, tais como:

• abordar conteúdos e conceitos;
• apresentar diferentes estratégias de resolução;
• promover a troca de ideias entre os estudantes por meio de questões abertas;
• resgatar o conhecimento prévio dos estudantes sobre determinado conteúdo;
• aplicar técnicas e conceitos trabalhados anteriormente.

Nas orientações educacionais para o ensino de Matemática, a resolução de problemas tem conquistado um papel de destaque em razão dos benefícios que pode oferecer ao processo de ensino e de aprendizagem desse componente curricular.

Nela, defende-se a proposta de que conceitos, ideias e métodos matemáticos devem ser abordados por meio de situações-problema que levem os estudantes a desenvolver suas estratégias de resolução. Em resumo, uma situação-problema é o ponto de partida da atividade matemática.

[...]

Um dos maiores motivos para o estudo da Matemática na escola é desenvolver a habilidade de resolver problemas. Essa habilidade é importante não apenas para a aprendizagem matemática da criança, mas também para o desenvolvimento de suas potencialidades em termos de inteligência e cognição. Por isso, acreditamos que a resolução de problemas deva estar presente no ensino de matemática, em todas séries escolares, não só pela sua importância como forma de desenvolver várias habilidades, mas especialmente por possibilitar ao aluno a alegria de vencer obstáculos criados por sua própria curiosidade, vivenciando, assim, o que significa fazer matemática.

Para uma criança, assim como para um adulto, um problema é toda situação que ela enfrenta e não encontra solução imediata que lhe permita ligar os dados de partida ao objetivo a atingir. A noção de problema comporta a ideia de novidade, de algo nunca feito, de algo ainda não compreendido.

Dessa forma, a primeira característica da abordagem de resolução de problemas que propomos é considerar como problema toda situação que permita algum questionamento ou investigação.

SMOLE, Kátia Stocco; DINIZ, Maria Ignez; CÂNDIDO, Patrícia (org.). Resolução de problemas. Porto Alegre: Artmed, 2000. p. 13. (Coleção Matemática de 0 a 6).

Ao se engajar nesse processo, os estudantes poderão:

[...] identificar e selecionar informações relevantes, buscar padrões, relações e generalizações; formular planos e procedimentos, integrar e empregar conceitos e habilidades aprendidos previamente; e estender seu conhecimento a novas situações. [...]

HOUSE, Peggy A. Aventurando-se pelos caminhos da resolução de problemas. In: KRULIK, Stephen; REYS, Robert E. (org.). A resolução de problemas na matemática escolar. São Paulo: Atual, 1997. p. 234.

Isso pode contribuir para que eles deixem de ser apenas espectadores e se tornem agentes no processo de aprendizagem da Matemática.

Alguns pesquisadores afirmam que a principal razão e a real justificativa para ensinar Matemática são sua utilidade e a capacitação que ela desenvolve no estudante para resolver problemas, os quais devem exigir do estudante uma interpretação do enunciado, uma reflexão sobre os dados envolvidos e uma definição de sua estratégia de resolução. Nessa concepção, o educando terá a oportunidade de desenvolver o espírito crítico, o raciocínio lógico e o modo de pensar matemático, bem como perceber que a Matemática pode ajudar na resolução de problemas comuns do dia a dia.

Com a resolução de problemas, tem-se a oportunidade de tornar os estudantes em cidadãos com capacidade de desenvolver as próprias estratégias de resolução nas mais diversas situações.

[...] Na perspectiva de uma sociedade muito flexível nas demandas trabalhistas e culturais de seus cidadãos e, ao mesmo tempo, muito competitiva, não basta proporcionar conhecimentos “empacotados”, fechados em si mesmos. Ao contrário, é preciso tornar os alunos pessoas capazes de enfrentar situações e contextos variáveis, que exijam deles a aprendizagem de novos conhecimentos e habilidades. [...]

POZO, Juan Ignacio (org.). A solução de problemas: aprender a resolver, resolver para aprender. Tradução: Beatriz Afonso Neves. Porto Alegre: Artmed, 1998. p. 9.

Para que o trabalho com a resolução de problemas possa ser viabilizado, é necessário que o professor promova situações em sala de aula que possibilitem aos estudantes vivenciar experiências nas quais ela esteja presente. Nesta coleção, as situações-problema são apresentadas com o propósito de desenvolver no estudante habilidades que lhe permitam enfrentar situações em contextos variáveis, no âmbito escolar ou não. Nessa proposta, as atividades visam motivar os estudantes a resgatar conhecimentos prévios, desenvolver estratégias próprias de resolução e verbalizar seu raciocínio por meio da oralidade e de registros escritos.

A prática docente

Atualmente, a interação dos estudantes com a tecnologia incorporou mudanças de comportamento em sala de aula, e essa “geração digital” passou a exigir do professor a mesma alteração. Eles esperam, por exemplo, que o professor utilize essa tecnologia em suas aulas. Com isso, seu papel, mesmo sendo essencial, passa a ser redimensionado significativamente.

Assim como a sociedade, a comunidade escolar e mais especificamente o estudante têm passado por mudanças, por uma transição de metodologias de ensino. O estudante passa a ter participação ativa no processo de ensino e de aprendizagem, ou seja, torna-se protagonista da construção de seu conhecimento. Nesse sentido, o professor torna-se um mediador e um avaliador de processos, ou seja, aquele que ajuda a fornecer as informações necessárias para que o estudante tenha condições de construir seu conhecimento, reestruturando o processo quando necessário. Para Santaló:

a missão dos educadores é preparar as novas gerações para o mundo em que terão que viver. Isto quer dizer proporcionar- lhes o ensino necessário para que adquiram as destrezas e habilidades que vão necessitar para seu desempenho, com comodidade e eficiência, no seio da sociedade que enfrentarão ao concluir sua escolaridade.

[...]

SANTALÓ, Luis Antônio. Matemática para não matemáticos. In: PARRA, Cecilia; SAIZ, Irma (org.). Didática da matemática: reflexões psicopedagógicas. Porto Alegre: Artes Médicas, 1996. p. 11.

Sendo assim, o professor deve assumir os papéis descritos a seguir.

• Provedor: aquele que torna os conceitos e os conteúdos matemáticos passíveis de serem aprendidos pelos estudantes, fornecendo informações necessárias que eles ainda não têm condições de obter sozinhos. Para isso, o professor deverá ter um sólido conhecimento dos conteúdos que serão trabalhados.
• Orientador: aquele que conduz e organiza o trabalho em sala de aula, buscando desenvolver a autonomia dos estudantes.
• Incentivador: aquele que motiva continuamente os estudantes, incentivando-os a refletir, investigar, levantar questões e trocar ideias com os colegas.

Diante disso, é importante que o professor conheça as condições socioculturais, as expectativas e as competências cognitivas dos estudantes. Assim, terá condições de selecionar situações-problema relacionadas ao cotidiano de sua turma. É relevante também o trabalho de determinado conteúdo em diversos contextos, a fim de que eles desenvolvam a capacidade de generalização.

Além disso, o professor precisa ter conhecimento das mudanças que ocorrem dentro e fora da escola. Nesse aspecto, a formação do professor é fundamental, não se resumindo apenas à graduação ou à especialização, mas à formação continuada, a fim de acompanhar o desenvolvimento de estudos e os progressos que ocorrem no âmbito educacional. Não basta, por exemplo, que um professor de Matemática saiba o conteúdo da área; é necessário que ele conheça psicologia, pedagogia, linguagem, sexualidade, infância, adolescência, sonho, afeto, vida etc.

Para se informar a respeito das mudanças que ocorrem fora da escola, o professor precisa estar atento às constantes transformações e evoluções sociais, para, dessa maneira, verificar se seu trabalho contribui para a construção do conhecimento do estudante enquanto cidadão. De acordo com Brousseau:

o professor é uma espécie de ator. Atua segundo um texto escrito em outro contexto e segundo determinada tradição. Podemos imaginá-lo como um ator da Commedia dell’arte: improvisa na hora, em função de um argumento ou uma trama.

[...]

BROUSSEAU, Guy. Os diferentes papéis do professor. In: PARRA, Cecilia; SAIZ, Irma (org.). Didática da matemática: reflexões psicopedagógicas. Porto Alegre: Artes Médicas, 1996. p. 71.

Planejamento

Como parte da prática docente, o planejamento tem o intuito de auxiliar o professor a se organizar quanto ao conteúdo curricular que precisa trabalhar e às situações cotidianas de uma sala de aula numerosa. Trata-se de uma estratégia de organização para elencar os objetivos que pretende alcançar; as habilidades e competências que se pretende desenvolver; os conteúdos que necessita preparar; a maneira como o ensino pode ser conduzido; além da verificação dos materiais que utilizará visando ao êxito nas aulas.

Embora tenha a intenção de programar o andamento diário ou semanal dos conteúdos e das práticas, o planejamento deve ser pensado e produzido de maneira flexível, permitindo alterações no decorrer do percurso, pois eventualidades podem ocorrer e a necessidade de uma nova condução do ensino deve ser proposta visando à aprendizagem dos estudantes.

O planejamento pode ser considerado um roteiro norteador, construído de acordo com experiências de falhas e acertos do docente no dia a dia. Ele se torna um instrumento de grande utilidade, principalmente quando o professor já conhece seus estudantes e os ritmos do processo de aprendizado que eles apresentam.

Avaliação

Um aspecto importante do processo de ensino e de aprendizagem é a avaliação. Nesse sentido, partimos do pressuposto de que avaliar consiste em algo essencial a todas as atividades humanas e, consequentemente, a toda proposta educacional.

A avaliação não pode ser pensada como algo isolado, estanque, mas como parte do processo de ensino e de aprendizagem, vinculada a um projeto pedagógico coerente com relação às suas finalidades. Pensar na ação avaliativa consiste em refletir sobre todos os elementos que compõem o processo de ensino de aprendizagem, ou seja, enxergá-la como parte de um todo.

Vista por essa ótica, como parte de um projeto pedagógico, a avaliação passa a ser uma forma de verificação da eficácia do método didático-pedagógico do professor. Com base nos resultados das avaliações, o professor tem como refletir se os elementos de sua prática estão adequados aos objetivos que pretende atingir e se favorecem a aprendizagem dos estudantes, de modo que possa reorientar sua prática pedagógica quando necessário.

Outro papel importante do processo avaliativo diz respeito aos estudantes. É preciso dar a eles a oportunidade de verificar suas dificuldades e necessidades na construção do conhecimento. E, por meio da avaliação, eles poderão tomar consciência dos conteúdos que já aprenderam e também identificar se é necessária uma dedicação maior com relação a alguns assuntos.

A fim de que a avaliação possa contribuir para uma aprendizagem bem-sucedida por parte dos estudantes, é necessário que ela:

[...] deixe de ser utilizada como recurso de autoridade, que decide sobre os destinos do educando, e assuma o papel de auxiliar o crescimento.

[...]

LUCKESI, Cipriano Carlos. Avaliação da aprendizagem escolar: estudos e proposições. 18. ed. São Paulo: Cortez, 2006. p. 166.

Diante das considerações apresentadas anteriormente, o processo de avaliação deve ser contínuo e praticado diariamente no ambiente escolar. Uma avaliação contínua é uma maneira de o professor estar ciente das conquistas da turma e, desse modo, manter-se atento às falhas que podem ocorrer no processo de ensino e de aprendizagem da Matemática.

Avaliação é “movimento”, é ação e reflexão. Na medida em que as crianças realizam suas tarefas, efetivam muitas conquistas: refletem sobre suas hipóteses, discutem-nas com pais e colegas, justificam suas alternativas diferenciadas. Esses momentos ultrapassam o momento próprio da tarefa. E, portanto, não se esgotam nelas. As tarefas seguintes incluem e complementam dinamicamente as anteriores. A média de escores, na escola, e a concepção constativa do teste, se contradiz a esse dinamismo. Obstaculiza, provoca a estagnação, as arbitrariedades.

[...]

HOFFMANN, Jussara Maria Lerch. Avaliação: mito e desafio: uma perspectiva construtivista. Porto Alegre: Mediação, 2005. p. 52.

Para proporcionar um trabalho contínuo de avaliação dos estudantes, o professor pode utilizar diversos recursos, a fim de auxiliá-lo nesse processo. Apresentamos a seguir alguns deles.

• Registros orais, que permite ao professor compreender como os estudantes estão desenvolvendo o pensamento e que estratégia estão elaborando na resolução de uma situação matemática, a fim de acompanhar a evolução das ideias manifestadas por eles.
• Registros escritos, que se referem às anotações que os estudantes fazem ao realizar atividades.
• Registros pictóricos, por meio de desenhos, que permitem aos estudantes representar seu conhecimento durante a atividade.

Mediante a utilização de instrumentos que envolvam a produção escrita dos estudantes, o professor terá:

[...] valiosas informações sobre o modo como compreenderam e registraram suas ideias a respeito de uma situação apresentada. Tais informações fornecem rico material para o professor incorporar ao seu repertório no planejamento das aulas e para orientar suas escolhas didáticas, servindo como referência para conversar sobre matemática com o aluno.

[...]

BURIASCO, Regina Luzia Corio de; CYRINO, Márcia Cristina de Costa Trindade; SOARES, Maria Tereza C. Um estudo sobre a construção de um manual para correção das provas com questões abertas de matemática – AVA2002. In: VIII ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA,
2004, Recife. Anais... Recife: UFPE, 2004. p. 2.

Por meio de recursos que possibilitem a comunicação oral, professor e estudantes poderão trabalhar na negociação de significados sobre conceitos, ideias matemáticas relacionadas a eles e estratégias e procedimentos de resolução de problemas, visando auxiliar a turma no processo de aprendizagem da Matemática.

Organizar os trabalhos feitos pelos estudantes em pastas ou arquivos individuais é outra estratégia. Por meio desses arquivos, é possível verificar e identificar os registros e os acertos indicados por eles, além de problemas de aprendizagem, permitindo um acompanhamento da evolução de cada um.

Outra questão importante na avaliação é mantê-los sempre informados de suas competências. Atitudes como a valorização do esforço e comentários sobre a maneira como constroem e se apropriam dos conhecimentos incentivam e conscientizam os estudantes da própria aprendizagem.

Desse modo, a avaliação pode assumir diferentes formas para cumprir com diferentes objetivos.

• Avaliação diagnóstica: normalmente realizada antes de iniciar o trabalho com determinado conteúdo curricular. Tem o objetivo de sondar o que os estudantes sabem sobre determinado conteúdo e permite ao professor se basear nesses conhecimentos para planejar suas aulas.
• Avaliação formativa (ou de processo): comumente realizada no decorrer do desenvolvimento do conteúdo em estudo. Tem o objetivo de verificar se os estudantes estão acompanhando e compreendendo o conteúdo em estudo. Assim, é possível retomar o processo de ensino e de aprendizagem em tempo real, dar feedbacks à turma e rever estratégias de ensino.
• Avaliação somativa (ou de resultado): geralmente proposta ao final do trabalho com os conteúdos curriculares. Tem cunho classificatório, por meio de notas, por exemplo, com a intenção de verificar qual foi o aproveitamento obtido pelos estudantes. Com esse tipo de avaliação, é possível ter um panorama sobre as aprendizagens da turma e rever estratégias para suprir possíveis dificuldades dos estudantes.

No processo de avaliação dos estudantes, o livro didático precisa cumprir o papel importante de contribuir com questões de relevante significado. Por isso, esta coleção propõe ao professor oportunidades progressivas de verificar o rendimento da turma e analisar a prática pedagógica utilizada durante o desenvolvimento das unidades. Em cada volume, há a preocupação em oferecer subsídios suficientes para a avaliação acontecer de maneira contínua e coerente na sala de aula, como é o caso, por exemplo, das sugestões de atividades apresentadas nas seções O que eu já sei? (atividades que podem ser utilizadas como avaliação diagnóstica), O que eu estudei? (atividades que podem ser utilizadas como avaliação formativa) e O que eu aprendi? (atividades que podem ser utilizadas como avaliação somativa), além de outras propostas indicadas no boxe Sugestão de avaliação, presentes nas orientações ao professor deste manual ao redor das reproduções das páginas do livro do estudante.

Esta coleção tem o intuito de auxiliar o professor a preparar os estudantes para desafios futuros. Por esse motivo, apresenta atividades que possibilitam o preparo deles para exames de provas oficiais, como as aplicadas pelo Sistema de Avaliação da Educação Básica (Saeb), que visam mensurar a qualidade da aprendizagem. Por meio da linguagem ou da estrutura das atividades, os estudantes entrarão em contanto com exercícios avaliativos que se assemelham aos propostos pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep), não perdendo a intencionalidade de também servir como parâmetro diagnóstico ou formativo de uma avaliação.

Fichas de avaliação e autoavaliação

Para facilitar o trabalho do professor, ele pode fazer uso de fichas para avaliar o desempenho de cada estudante e, assim, elaborar um relatório individual de acompanhamento da aprendizagem.

A seguir, apresentamos o modelo de uma ficha utilizada para auxiliar no acompanhamento do desenvolvimento individual dos estudantes, com o objetivo de avaliar seus conhecimentos, habilidades, suas atitudes e seus valores.

Modelo de ficha de acompanhamento individual

Avaliação do desempenho individual dos conteúdos estudados

Acompanhamento de aprendizagem por objetivos e/ou habilidades	Não consegue executar	Executa com dificuldade	Executa com facilidade	Observações
Exemplo por objetivo: Identificar a relação entre raio e diâmetro de uma circunferência.
Exemplo por habilidade: (EF07MA33) Estabelecer o número $\pi$ como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica.

Avaliação do desenvolvimento de cada aluno dentro de sala de aula

Acompanhamento socioemocional	Desenvolvimento do estudante
	Sim	Às vezes	Não	Observações
Escuta com atenção a explicação dos conteúdos?
Questiona quando não compreende o conteúdo?
Faz uso correto da oralidade e/ou escrita para se expressar?
Desenvolve as atividades com autonomia?
Participa de maneira responsável das atividades propostas dentro e fora da sala de aula?
Coopera com os colegas quando seu auxílio é solicitado?
Demonstra ter empatia pelas pessoas de seu convívio?
Demonstra zelo pelos seus materiais e pelos espaços da escola?
Informações sobre o progresso nesse período letivo

O exercício de ensino e de aprendizagem não deve ser uma responsabilidade apenas do professor. Ele também deve ser compartilhado com os estudantes, para que eles identifiquem seus avanços e seus limites. Com isso, o professor terá melhores condições de avaliar sua metodologia de ensino. Uma das sugestões para esse processo é o uso de fichas de autoavaliação, por meio das quais eles são incentivados a refletir sobre o próprio desenvolvimento em sala de aula e no processo de aprendizagem.

A seguir, apresentamos um modelo de ficha de autoavaliação.

Ficha de autoavaliação

Nome:	Sim	Às vezes	Não
Tenho interesse em participar das atividades realizadas em sala de aula?
Compreendo os assuntos abordados pelo professor?
Falo com o professor sobre minhas dúvidas?
Expresso minhas opiniões durante os trabalhos em sala de aula?
Mantenho um bom relacionamento com meus colegas de turma?
Organizo meu material escolar?

Relações entre os componentes curriculares

Considerando as tendências atuais no âmbito da educação e em consonância com os princípios da BNCC, a interdisciplinaridade passou a ser frequentemente sugerida no trabalho escolar. De modo geral, ela tem sido entendida como uma maneira de articular duas ou mais áreas do conhecimento por meio da exploração de determinado assunto, visando à análise, à discussão e à compreensão de tal tema sob os diferentes pontos de vista apresentados em cada uma dessas áreas. Esse modo de trabalho pode auxiliar os estudantes na construção de conhecimentos em uma perspectiva múltipla, com a participação dos professores de outros componentes curriculares e de outras pessoas da comunidade escolar e da comunidade local.

Nesse sentido, o ensino da Matemática deve:

[...] engajar-se na crescente preocupação com a formação integral do aluno como cidadão da sociedade contemporânea onde cada vez mais é obrigado a tomar decisões políticas complexas. Introduz-se, assim, definitivamente, na agenda da Matemática escolar, o ensino voltado para a formação de cidadãos críticos e responsáveis.

[...]

TOMAZ, Vanessa Sena; DAVID, Maria Manuela Martins Soares. Interdisciplinaridade e aprendizagem da matemática em sala de aula. Belo Horizonte: Autêntica, 2008. p. 15. (Coleção Tendências em Educação Matemática).

Quando os componentes curriculares são usados para a compreensão dos detalhes de uma situação, os estudantes percebem sua natureza e utilidade. Além disso, o estabelecimento de uma relação entre o conhecimento prévio e o recém-adquirido, inclusive envolvendo outras áreas do conhecimento, permite a criação de conflitos cognitivos, demonstrando a necessidade de reorganização de conceitos e dando significado à aprendizagem. Nesse sentido, a Matemática permite um trabalho integrado, por exemplo, com Geografia, História, Ciências, Língua Portuguesa, Educação Física e Arte.

Para que o trabalho interdisciplinar seja bem estruturado e atinja os objetivos propostos em cada planejamento, é necessário atentar à realidade particular do grupo de estudantes envolvidos. Santomé fornece apontamentos importantes sobre o diagnóstico que antecede tal proposta.

[...]

A análise do contexto sociocultural oferece as chaves para o diagnóstico do nível cultural dos estudantes, do seu nível real de desenvolvimento, assim como das suas expectativas diante da instituição escolar, dos seus preconceitos, etc. Conhecer as respostas a essas interrogações é requisito essencial para que a proposta planejada possa se ligar diretamente a esses meninos e meninas reais, à sua autêntica vida cotidiana. Outro requisito prévio importante é conhecer e localizar os recursos que existem na comunidade, no meio natural e social, que possam sugerir a realização de tarefas concretas, bem como facilitar e enriquecer outras que podem ser desenvolvidas através da unidade didática.

[...]

SANTOMÉ, Jurjo Torres. Globalização e interdisciplinaridade: o currículo integrado. Porto Alegre: Artmed, 1998. p. 225-226.

Para que a aula seja realmente interdisciplinar, é preciso considerar os seguintes pontos.

• Realizar um bom planejamento, atendando às possíveis relações entre o conteúdo do respectivo componente curricular e o dos outros.
• Pesquisar e compreender o conteúdo trabalhado por outros componentes curriculares.
• Conversar com os professores de outros componentes curriculares e, quando possível, envolvê-los em um planejamento conjunto.
• Considerar a heterogeneidade dos estudantes da turma.
• Propor atividades de maneira contextualizada e que auxiliem os estudantes nessa visão interdisciplinar.

Outra forma de viabilizar o trabalho interdisciplinar na escola é por meio do desenvolvimento de projetos. Contudo, para que um projeto interdisciplinar seja bem-sucedido, é preciso garantir mais do que uma simples integração entre componentes curriculares. É necessário que haja também uma integração entre seus participantes, tanto professores quanto estudantes. Para Nogueira, essa integração:

[..] pretende atingir como complementaridade das diferentes disciplinas, já que demonstra aos alunos possíveis inter-relações nelas existentes.

[...]

NOGUEIRA, Nilbo Ribeiro. Interdisciplinaridade aplicada. São Paulo: Érica, 1998. p. 33.

Segundo o autor, outro fator importante para a execução de projetos interdisciplinares é a possibilidade de acesso à pesquisa. Com isso, espera-se que o estudante, ao perceber as relações existentes entre os componentes curriculares:

[...] motive-se a buscar novos conhecimentos sobre um tema, problema ou questão, pois agora o projeto apresenta perspectivas múltiplas, em que todas as disciplinas contribuem de uma certa forma, e, por consequência, ele poderá receber orientações e desafios para a pesquisa de vários professores em prol de um tema único.

[...]

NOGUEIRA, Nilbo Ribeiro. Interdisciplinaridade aplicada. São Paulo: Érica, 1998. p. 33.

Nesta coleção, o caráter interdisciplinar da Matemática é explorado por meio de atividades, apresentação de informações e contextos diversificados. Nas atividades, a Matemática atua como instrumento de apoio para a resolução de problemas, em geral, vinculados a situações envolvendo medições, cálculos e interpretação de informações relacionadas a várias atividades desenvolvidas por profissionais, bem como à análise e à interpretação de dados populacionais. Algumas dessas articulações estão dispostas nas orientações ao professor, com o intuito de contribuir com sugestões que reforçam essa integração dos conhecimentos. No livro do estudante, também é proposta a seção Projeto em ação, na qual a realização e a divulgação das atividades possibilitam estabelecer relações interdisciplinares.

O aprendizado em sala de aula

O ambiente escolar abrange uma diversidade de estudantes, os quais potencialmente buscam meios de lidar com situações na vida pessoal e na vida escolar. Eles têm se tornado cada vez mais protagonistas da própria aprendizagem, de sua prática social e da formação do seu futuro. Esse processo recebe grande influência dos espaços a que esses estudantes pertencem, onde vivem experiências, tiram dúvidas e, em seguida, obtêm o êxito daquilo que se espera por meio do conhecimento adquirido, e é na sala de aula que podemos utilizar diferentes estratégias para auxiliar no desenvolvimento do aprendizado.

O trabalho em grupo

Nas aulas de Matemática, os estudantes precisam expressar suas ideias mediante o uso da escrita ou do diálogo com o professor e os colegas. Ao interagir com os colegas durante a realização de algumas atividades, eles têm a oportunidade de desenvolver a capacidade de organizar o raciocínio e comunicá-lo, bem como de argumentar em favor dele e de ouvir seus colegas. Assim, eles são levados a ter atitudes de respeito mútuo, empatia, cooperação, senso crítico, entre outras.

Diversas pesquisas demonstraram que o aumento da oportunidade de discussão e de argumentação aprimora a capacidade de compreensão dos temas ensinados e os processos de raciocínio envolvidos. Desse modo, torna-se necessário que a interação entre os estudantes não seja deixada em segundo plano. Devem ser criados momentos para a comunicação, a reflexão, a argumentação e a troca de ideias entre eles.

O enfrentamento de diferentes ideias e opiniões faz com que os estudantes coordenem as próprias ideias, formando novas relações entre os assuntos. Além disso, os diálogos entre eles os incentivam a reconhecer a necessidade de obter novas informações, reorganizar e reconceituar as ideias já existentes.

Essa interação com os colegas, visando potencializar o desenvolvimento de tais atitudes – essenciais para a formação dos estudantes enquanto indivíduos –, pode ser propiciada pelo trabalho em grupo. O trabalho em pequenas equipes, por exemplo, favorece a interação entre seus integrantes. Com isso, eles têm mais possibilidades de expor ideias, argumentar sobre seus pontos de vista e discutir diferentes estratégias e soluções. Devido a esses fatores, o trabalho em pequenos grupos tem sido mais frequentemente sugerido nas aulas de Matemática, sendo uma prática pedagógica eficiente para trabalhar com turmas que tenham grande quantidade de estudantes e que também apresente ritmos diferentes de aprendizagem.

No entanto, é importante que o professor esteja atento para a forma de organização dos estudantes sugerida em determinada atividade, de modo a permitir que eles atinjam satisfatoriamente os respectivos objetivos estabelecidos.

Iniciar o trabalho em grupo desde a Educação Básica torna-se cada vez mais importante, visto que essa é uma competência valorizada em nossa sociedade, na qual:

[...] além de ter uma sólida formação, o indivíduo é desafiado a interagir em dinâmicas de grupos com pessoas detentoras de outras competências. [...]

PAIS, Luiz Carlos. Ensinar e aprender matemática. Belo Horizonte: Autêntica, 2006. p. 34.

Para que o trabalho em grupo apresente resultados satisfatórios, o professor deve planejar muito bem cada atividade, estar o tempo todo atento ao que acontece e auxiliar os grupos quando necessário. A seguir, são listadas algumas orientações que podem fazer parte do planejamento de uma atividade em grupo.

• Os grupos devem ser heterogêneos e, a cada novo trabalho, os integrantes do grupo devem ser variados.
• Os intervalos entre as realizações dos trabalhos em grupo devem ser avaliados para que as metas a serem atingidas no ano letivo não fiquem comprometidas.

• Devem ser propostas situações adequadas à faixa etária e ao nível de conhecimento dos estudantes.
• O professor deve verificar constantemente as dificuldades dos estudantes e fornecer as informações necessárias à realização da atividade proposta.

No livro do estudante, os trabalhos em dupla e em grupo são sugeridos na abordagem de alguns conteúdos e no desenvolvimento de determinadas atividades, sendo identificados por meio de um destaque em negrito no termo que indica a necessidade de se juntar aos colegas (por exemplo, “Junte-se a um colega e resolvam os problemas.”). Em algumas dessas atividades, é solicitado a eles que: comparem sua resolução com a de outros colegas, expliquem a alguém seu processo de resolução ou se juntem a um ou mais estudantes para a realização de certa tarefa.

Recursos tecnológicos

Vivemos em um cenário repleto de tecnologias. Os eletrodomésticos de nossa residência ficaram mais modernos e agregaram novas funções; a informatização do comércio permite maior agilidade nas transações comerciais; a consulta e a movimentação bancária também foram facilitadas com o uso da internet e de smartphones, especialmente com a elevação do nível de confiança dos usuários com relação a esse meio de comunicação. Diante dessa realidade, a escola deve exercer um papel fundamental na formação de cidadãos aptos a utilizar tais tecnologias.

Na escola, os recursos tecnológicos, como calculadoras e computadores, podem, quando devidamente empregados, desempenhar uma função importante no processo de ensino e de aprendizagem. No entanto, é necessário compreender que, para seu uso em práticas pedagógicas, tanto em sala de aula quanto fora dela, é importante o resultado desse uso, que deve convergir para uma produção colaborativa, na qual estudantes e professores sejam os agentes.

As calculadoras eletrônicas evoluíram de maneira significativa e, como consequência, houve a redução de custo para sua aquisição, o aumento de sua capacidade operacional e também sua incorporação a outros equipamentos, como relógios, computadores, tablets e smartphones.

Diante disso, não podemos ignorar a presença desse instrumento no cotidiano dos nossos estudantes, visto que é uma tecnologia simples, de fácil manuseio e que pode ser explorada pelo professor em sala de aula.

Ao integrar a calculadora em um processo de descoberta e investigação matemática, cuja situação-problema é o ponto de partida, criam-se condições para o surgimento de novos ambientes que resultarão em novas capacidades e atitudes dos estudantes com uma participação mais ativa e criativa na construção do conhecimento.

Uma maneira de usar a calculadora em sala de aula é explorar os conteúdos utilizando a capacidade operatória da calculadora, propondo atividades que exijam dos estudantes a elaboração de estratégias e a resolução de problemas mais complexos, bem como a tomada de decisões. Além disso, ela pode ser utilizada, em alguns casos, para substituir o cálculo manuscrito, que se apresenta muitas vezes em situações de urgência, ou com números que têm muitos algarismos, portanto, passíveis de erro. A BNCC também propõe que os estudantes utilizem calculadoras e planilhas eletrônicas desde os anos iniciais do Ensino Fundamental e, assim, sejam incentivados, nos anos finais, a interpretar e a elaborar algoritmos, desenvolvendo o pensamento computacional.

O uso da calculadora em sala de aula, portanto, não significa o fim do cálculo, e sim a possibilidade de discussões relacionadas aos processos, às regras, às estratégias e às fórmulas, em vez dos simples e, algumas vezes, trabalhosos cálculos com algoritmos.

É importante lembrar que a habilidade de cálculo e a memorização de fórmulas têm seu valor e não devem ser extinguidas das aulas. O que precisa ser enfatizado é que a Matemática pode ser estudada e ensinada com o auxílio de vários instrumentos, entre eles a calculadora e o computador. Assim, devemos nos preocupar em explorar conceitos, fórmulas e regras de maneira que possibilite aos estudantes compreender o que estão fazendo e usar seus conhecimentos em problemas que se aproximem da realidade.

A utilização de algum recurso tecnológico, como a calculadora, não torna mais fácil algum conteúdo, nem se almeja que os estudantes fiquem dependentes da máquina. O objetivo é dar oportunidade a eles de explorar seus recursos de maneira crítica e consciente, fazendo com que discutam os resultados obtidos, assim como as estratégias utilizadas.

Nesse sentido, ao planejar o uso da calculadora em sala de aula com o objetivo de haver uma contribuição para o aprendizado, deve-se ter noção de suas possibilidades e limitações e conhecer a familiaridade dos estudantes com a máquina. Além disso, é preciso que fiquem evidentes os motivos pelos quais a calculadora está sendo utilizada, além dos objetivos correspondentes.

Quando o professor se dispõe a usar uma calculadora científica, deve estar preparado para tirar dúvidas dos estudantes quanto a seu manuseio. Se não souber utilizá-la em determinada situação, deve admitir suas limitações e propor-se pesquisar tais funções para se atualizar.

Em vários momentos desta coleção, são apresentados exemplos e atividades que demandam a utilização de calculadora e computador. Na seção Instrumentos e softwares, há orientações para o uso das calculadoras comum e científica, softwares de geometria dinâmica e planilha eletrônica, além de instrumentos como régua, esquadro e compasso. Além dessa seção, indicamos, com um ícone, atividades que, para serem resolvidas, os estudantes precisarão utilizar alguns dos recursos mencionados na seção Instrumentos e softwares, aplicando conhecimentos adquiridos.

O computador, como apoio ao ensino e à aprendizagem, só faz sentido se for usado como gerador de conhecimento e ferramenta de comunicação, que amplia o currículo, impulsiona o desenvolvimento de competências e habilidades e promove a interação e a colaboração entre professores e estudantes.

A diversidade de seus recursos atende a diferentes metodologias e amplia os espaços educacionais, antes restritos ao ambiente presencial e aos meios impressos. Além disso, o computador pode tornar a aprendizagem mais interessante, criativa e efetiva, com situações didáticas que integram os recursos tecnológicos a outros recursos, como livros, jornais e revistas. Entre eles, destaca-se a internet como um dos mais utilizados na escola para pesquisa, publicação e comunicação.

Outra atividade que pode contribuir para o ensino da Matemática é o trabalho com softwares, que tem aumentado e alcançado diversas áreas. Por exemplo, existem softwares específicos para as mais diversas atividades, como planilhas eletrônicas, editores de texto, de imagem e de animação, bancos de dados, simuladores, entre outros.

O uso de alguns desses softwares pode trazer grandes contribuições para o ensino da Matemática. As planilhas eletrônicas, por exemplo, podem ser empregadas na verificação de resultados e regularidades, na organização de dados numéricos, na plotagem de gráficos etc., colaborando para o desenvolvimento do pensamento computacional. Existe também uma grande variedade de softwares matemáticos que podem ser utilizados nas aulas, como o Maple e o GeoGebra.

Por fim, cabe destacar que a inserção do computador nas escolas não veio substituir o professor no processo de ensino e de aprendizagem. Pelo contrário, ela possibilitou dinamizar a função do professor na elaboração, na condução e na avaliação do processo educacional.

Competência leitora

O ato de ler está relacionado à organização dos significados dos textos, à interpretação, à análise, à comparação e ao sentido que os textos trazem. A leitura está presente em diversos momentos de nossas vidas. As crianças buscam sentidos em placas e outras imagens, por exemplo, mesmo antes de serem alfabetizadas. Desse modo, fazer atividades que colaborem para o desenvolvimento da competência leitora dos estudantes também é responsabilidade de todos os componentes curriculares, e não somente de Língua Portuguesa, visto que um mesmo texto pode ser trabalhado de diversas maneiras, de acordo com os objetivos que se pretende alcançar.

A escola é um ambiente em que a prática leitora é aprimorada e o professor pode e deve ser o mediador desse processo, promovendo a interação dos estudantes com ferramentas necessárias para o desenvolvimento da competência leitora, auxiliando-os nessa prática e em entendê-la como algo essencial para a formação como cidadão, entre outras ações.

O professor pode aplicar em sala de aula, por exemplo, estratégias de leitura que viabilizem o trabalho com a competência leitora dos estudantes. A seguir, sugerimos algumas estratégias, baseadas na teoria de Isabel Solé (1998).

Antes da leitura do texto

Antes da leitura, é possível propor aos estudantes alguns questionamentos, de modo que:

• apresentem os conhecimentos prévios a respeito do tema e do gênero textual a ser lido;
• levantem hipóteses sobre quem é o autor, o suporte utilizado e quais são os objetivos do texto;
• antecipem o assunto ou a ideia principal do texto com base em títulos, subtítulos, ilustrações etc.;
• falem sobre suas expectativas com relação à estrutura do gênero.

Durante a leitura do texto

Durante a leitura, é possível propor aos estudantes certos questionamentos, de modo que:

• encontrem o tema ou a ideia principal do texto;
• façam inferências;
• pesquisem no dicionário palavras que não conheçam ou cujo sentido não saibam;
• construam o sentido global do texto;
• identifiquem e compreendam a posição do autor.

Após a leitura do texto

Após a leitura, é possível propor aos estudantes alguns questionamentos, de modo que:

• confrontem seus conhecimentos prévios e as hipóteses levantadas antes da leitura com o que o texto realmente apresenta, podendo confirmar ou refutar as expectativas manifestadas antes e durante a leitura;
• troquem ideias com os colegas a respeito do que foi lido, argumentando sobre suas opiniões e respeitando as opiniões diferentes das suas.

Estratégias como as sugeridas anteriormente podem colaborar para o desenvolvimento de habilidades, tais como: resgate de conhecimentos prévios, levantamento de hipóteses, localização de informações em um texto, compreensão da ideia central de um texto, leitura inferencial, confirmação ou retificação de hipóteses levantadas, argumentação, entre outras.

Ao fazer inferências, os estudantes atribuem coerência intencional aos significados, levando-os a perceber outras informações além das que leram e interpretaram, possibilitando a construção e/ou reconstrução de conhecimentos para si próprios e para os outros, por meio da interação, da comunicação e do diálogo com o texto. Ao propor a leitura inferencial, é preciso que eles sejam orientados a ler raciocinando e interpretando, de modo que compreendam as situações descritas em um texto e cheguem a determinadas conclusões. Desse modo, estratégias de leitura bem conduzidas podem auxiliar nesse processo.

A leitura também auxilia os estudantes a fortalecer sua capacidade de argumentação, habilidade que permite ao indivíduo se expressar, defender ideais e se posicionar, de maneira oral e escrita. Por meio da argumentação, é possível identificar e conhecer diferentes opiniões e argumentos a respeito de determinado assunto, permitindo analisá-lo de diferentes ângulos e utilizar informações confiáveis ao argumentar, de acordo com o posicionamento escolhido.

Nesta coleção, sempre que possível, em atividades que envolvem o trabalho com gêneros textuais, o professor encontra orientações sobre como incentivar os estudantes a desenvolver diferentes habilidades, entre elas a leitura inferencial e a argumentação.

Metodologias e estratégias ativas

O contexto educacional vem passando por grande e considerável evolução. O protagonismo, a participação, a opinião e a experiência dos estudantes têm sido tomados como ponto de partida no processo de ensino-aprendizagem, na intenção de auxiliá-los a alcançar o conhecimento de maneira concreta e significativa. A sala de aula costuma contemplar um grande número de estudantes que carregam consigo diferentes experiências de vida e diversas maneiras de agir e pensar o mundo. Trabalhar com as metodologias e estratégias ativas contribui para que o estudante seja protagonista no processo de aprendizado, possibilitando a construção do conhecimento de maneira prática, reflexiva e autônoma. Desenvolver estratégias como essas permitem um melhor desempenho tanto dos estudantes quanto do professor, enquanto mediador no contexto educacional.

[...] A ênfase na palavra ativa precisa sempre estar associada à aprendizagem reflexiva, para tornar visíveis os processos, os conhecimentos e as competências do que estamos aprendendo com cada atividade. Ensinar e aprender tornam-se fascinantes quando se convertem em processos de pesquisa constantes, de questionamento, de criação, de experimentação, de reflexão e de compartilhamento crescentes, em áreas de conhecimento mais amplas e em níveis cada vez mais profundos. A sala de aula pode ser um espaço privilegiado de cocriação, maker, de busca de soluções empreendedoras, em todos os níveis, onde estudantes e professores aprendam a partir de situações concretas, desafios, jogos, experiências, vivências, problemas, projetos, com os recursos que têm em mãos: materiais simples ou sofisticados, tecnologias básicas ou avançadas. O importante é estimular a criatividade de cada um, a percepção de que todos podem evoluir como pesquisadores, descobridores, realizadores; que conseguem assumir riscos, aprender com os colegas, descobrir seus potenciais. Assim, o aprender se torna uma aventura permanente, uma atitude constante, um progresso crescente.

[...]

MORAN, José. Metodologias ativas para uma aprendizagem mais profunda. In: BACICH, Lilian; MORAN, José. (org.). Metodologias ativas para uma educação inovadora: uma abordagem teórico-prática. Porto Alegre: Penso, 2018. p. 3.

Esta coleção propõe, em diversos momentos, o trabalho com diferentes estratégias e metodologias ativas, visando proporcionar condições de trabalho significativo com as competências gerais, específicas e habilidades da BNCC. A seguir, são apresentadas as descrições das estratégias de metodologias ativas que serão trabalhadas no decorrer dos volumes, proporcionando o desenvolvimento de atividades contextualizadas com os estudantes.

Gallery walk

Esta metodologia ativa tem sua dinâmica semelhante às exposições vistas em museus, pois consiste, como produto final, na exibição de trabalhos. O que a difere é o protagonismo dos estudantes ao trabalhar a argumentação no decorrer das apresentações dos cartazes construídos em equipe. A estratégia em questão, conhecida como caminhada na galeria, ocorre seguindo estes passos.

• Em sala de aula, o professor apresenta os temas, assuntos ou situações-problema que pretende colocar em foco na discussão. Se oportuno, tópicos podem ser elencados na lousa com o intuito de proporcionar uma melhor condução do trabalho.
• A turma deve ser organizada em duplas ou grupos, considerando as respectivas especificidades. Isso deve ser avaliado com base na quantidade de assuntos apresentados. O importante é considerar as tarefas que devem ser desempenhadas para que todos os integrantes participem no decorrer da atividade.
• O professor deve disponibilizar tempo para que os grupos tenham condições de fazer pesquisa de busca, aprofundamento, exemplificação e fundamentação dos estudos de maneira contextualizada.

• Cada grupo deve produzir cartazes que servirão de recurso para exposição e apresentação da pesquisa que fizeram. No dia previamente agendado e conforme a ordem preestabelecida com os estudantes, eles se prepararão para as exibições dos trabalhos.
• Os cartazes devem ser fixados em local de fácil acesso à turma (em sala de aula ou no pátio da escola). Assim, terão condições de apreciar os trabalhos dos colegas, fazer leitura e, em momento oportuno, fazer questionamentos aos responsáveis pelo cartaz.
• Para cada apresentação deve ser disponibilizado um tempo viável para a interação de todos. Terminadas as trocas de informação e argumentações entre os estudantes, faça outras inferências voltadas a sanar lacunas que, porventura, possam ter ficado.

Para concluir o trabalho com esta metodologia ativa, o professor deve convidar os estudantes para uma roda de conversa com a intenção de pedir opiniões sobre a atividade realizada. Neste momento, deve-se atentar aos pontos levantados pela turma avaliando o que precisa ser considerado e alterado em outros momentos semelhantes a este.

Think-pair-share

Esta metodologia, também conhecida como pensar-conversar-compartilhar, é realizada em três momentos, sendo o primeiro de maneira individual, o segundo em dupla e o terceiro em grupo maior, isto é, agregando todos os que estiverem presentes no dia da dinâmica. O professor tem condições de propô-la antes de iniciar o trabalho com um conteúdo novo, no decorrer da discussão sobre ele ou mesmo enquanto são feitas atividades do livro, por exemplo. Para compreender esta metodologia, verifique a seguir como ela ocorre.

É interessante combinar com a turma a medida do tempo disponível para as etapas que sucedem a questão lançada, no caso, para o registro no caderno, para o momento em duplas e, por fim, para as exposições dos estudantes a toda a turma. Para esta última etapa, é interessante acordar com eles como se manifestarão, possibilitando a todos que tenham seu momento de fala, de maneira organizada para que possam ser ouvidos e compreendidos. A argumentação é exercitada no decorrer desta metodologia, pois estarão constantemente em pronunciamento de suas falas com a intenção de convencer os colegas acerca das opiniões com as quais concordam ou discordam, apresentando seus pontos de vista.

Quick writing

Trata-se de uma metodologia ativa que proporciona um momento de desafio e de diversão com os estudantes. É desenvolvida com uma medida de tempo cronometrada, para registro de conhecimento prévio ou da compreensão de conteúdos trabalhados com a turma. Desse modo, esta estratégia, também conhecida como escrita rápida, pode ocorrer conforme orientações a seguir.

Esta metodologia desenvolve nos estudantes as habilidades de análise, síntese e registro objetivo sobre a compreensão de determinado conteúdo. Durante seu desenvolvimento, o professor tem o papel de mediador das discussões, lançando posicionamentos com o intuito de trabalhar com seus estudantes a argumentação, por exemplo.

Sorting strips

Esta estratégia, também conhecida como tiras de classificação, proporciona aos estudantes a oportunidade de organizar, em sala de aula, os conteúdos em estudo, por meio de classificações. Desse modo, enquanto planeja a aula, o professor deve pensar nas definições, nas características do assunto a ser tratado e transcrevê-las em tiras de papel para serem levadas para a sala de aula. A atividade deverá ser organizada em grupos. Sendo assim, a quantidade de cópias dessas tiras deve ser suficiente para que todos os grupos tenham esse material em mãos. Os passos a seguir descrevem como a atividade ocorre.

• O professor explica o conteúdo e faz questionamentos à turma sobre os assuntos em que se baseou para produzir as tiras de papel, verificando o que eles sabem e/ou
  o que estão compreendendo a esse respeito.

• A turma é organizada em grupos (por meio de sorteio, afinidade ou outro critério que desejar). Cada grupo recebe um envelope com as tiras referentes aos assuntos estudados.

• Os estudantes devem ler e interpretar as informações apresentadas nas tiras para classificarem-nas de acordo com os assuntos estudados. As classificações organizadas pelo grupo devem ser fixadas em papel kraft ou cartolina.

• Terminada a etapa anterior, todos os trabalhos devem ser apresentados e/ou discutidos, para que eles verifiquem os pontos em comum e os divergentes nas classificações feitas pelos grupos, atentando às justificativas para tal divisão.

Esta metodologia permite explorar diferentes temas e situações-problema, além de desenvolver a habilidade de argumentação e possibilitar trocas e/ou construções de conhecimentos entre os estudantes.

Peer instruction

Esta metodologia ativa, também conhecida como instrução por pares ou abordagem por pares, ocorre após o estudo de determinado conteúdo, possibilitando discorrer sobre ele de maneira clara, objetiva e sucinta. Em seguida, são disponibilizadas atividades e/ou testes, com o intuito de verificar como os estudantes se saem, percebendo se houve e como ocorreu a compreensão do conteúdo. Nesta metodologia ocorre uma categorização de rendimento da turma para nortear o professor, levando-o a decidir se vale passar para o próximo conteúdo ou se há necessidade de permanecer no mesmo por algum tempo. Assim, verifica-se a seguinte situação sobre a turma.

É importante que o professor conheça bem sua turma, pois há estudantes com ritmos de aprendizagens diferentes.

Design thinking

Esta metodologia também é conhecida como pensamento do design. Seu objetivo é desenvolver nas pessoas que a praticam principalmente a criatividade, a empatia e a colaboração, visto que partem de um problema do contexto em que vivem, buscando a melhor solução para resolvê-lo.

Nesta metodologia ativa, situações-problema serão propostas para que, em grupos, os estudantes interpretem e compreendam o desafio, projetem e registrem as possibilidades de solução, anotem e providenciem materiais necessários, montem um protótipo para teste e verifiquem se o problema pode ser solucionado com ele.

Em momento seguinte, na data marcada e no local elencado, cada grupo deve apresentar aos demais a solução a que chegou. Ao término da explanação deve ser estipulado determinado tempo para que os demais tenham condições de avaliar, opinar e concordar ou discordar da saída proposta pelo grupo para resolver o problema em questão.

Para cada apresentação, deve-se reservar tempo para a discussão, relato da experiência vivida no decorrer da atividade realizada e apontamentos sobre possíveis causas e efeitos favoráveis ou desfavoráveis dos protótipos apresentados.

O professor será o mediador durante as etapas do trabalho, deixando para os estudantes a prática de pesquisa, o manuseio e a construção do protótipo e a argumentação sobre a solução palpável.

Pensamento computacional

Diante de propostas criativas e inovadoras para a educação, a relação do ensino com a tecnologia vem sendo suprida e adaptada para uma aprendizagem em que estudantes, chamados de nativos digitais, aprimorem ainda mais seu domínio sob as novas tecnologias e aprendam a resolver problemas por meio delas e do pensamento computacional.

As tecnologias educacionais carregam consigo uma maneira dinâmica e atrativa de trabalhar os conteúdos de modo digital e tecnológico em sala de aula. A Sociedade Brasileira de Computação (SBC) propôs estratégias importantes para a formação dos estudantes com o ensino tecnológico, e as organizou em três eixos, considerando-os como conhecimentos básicos de computação. Entre esses eixos, encontra-se o do pensamento computacional. A SBC o define como: “capacidade de sistematizar, representar, analisar e resolver problemas.”.

Fonte de pesquisa: CENTRO de Inovação para a Educação Brasileira. Disponível em: https://oeds.link/YZ44mW Acesso em: 17 maio 2022.

O estudante desenvolve diferentes habilidades ao realizar atividades que exploram o pensamento computacional. A BNCC diz que o:

[...] pensamento computacional envolve as capacidades de compreender, analisar, definir, modelar, resolver, comparar e automatizar problemas e suas soluções, de forma metódica e sistemática, por meio do
desenvolvimento de algoritmos [...]

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 474. Disponível em: https://oeds.link/pKEA59 Acesso em: 08 jul. 2022.

Esse pensamento está organizado em quatro pilares. Conheça as características de cada um deles, a seguir.

• Abstração: classificar e filtrar as informações que são relevantes e que auxiliarão na resolução, descartando o que não é relevante.
• Decomposição: dividir, ordenar e analisar o problema em partes, ou em subproblemas, fragmentando-o para auxiliar em sua resolução.
• Reconhecimento de padrões: verificar e identificar o que gera o problema e os elementos que o estruturam, identificando características comuns entre os problemas e soluções.
• Algoritmo: definição e execução de estratégias para a resolução do problema, podendo ser entendido também como o desenvolvimento de um passo a passo para que o objetivo seja alcançado.

Ao trabalhar o pensamento computacional com estudantes dos Anos Finais do Ensino Fundamental, é importante ter alternativas adequadas e eficientes para desenvolvê-lo. Ao buscar solucionar um problema é possível utilizar ou não todos esses pilares. Essas formas de ação do pensamento computacional e de seus pilares são modos de explorar o raciocínio lógico e viabilizar aprendizagens, por meio da computação plugada ou desplugada.

Plugada: faz uso de ferramentas tecnológicas e digitais, como vídeo, computador, tablet, smartphone, softwares e hardwares.

Desplugada: não necessita de recursos tecnológicos, podendo ser aplicada em qualquer contexto educacional, como em jogos manuais, alinhados às metodologias ativas, em dinâmicas ou situação-problema do dia a dia e até mesmo em atividades de pesquisa.

Esta coleção sugere em determinados momentos, do Manual do professor, atividades plugadas e desplugadas de maneira contextualizada. Durante a realização das atividades, considere as diferentes características dos estudantes, para que eles possam desenvolver o pensamento computacional, de acordo com as capacidades e habilidades individuais.

Práticas de pesquisa

O desejo de obter ou produzir novas informações é construído por meio de uma inquietação, uma situação-problema, uma dúvida ou um tema a ser investigado. O desenvolvimento da pesquisa permite aos estudantes adquirir conhecimentos por meio da busca de informações para a produção de novos saberes, incentivando sua autonomia, argumentação, defesa de ideias, compreensão de diversas linguagens e a produção de diferentes discursos.

Nesta coleção, serão propostas diversas pesquisas relacionadas à história da Matemática, com o objetivo de promover a compreensão do desenvolvimento histórico de diferentes conceitos e de fatos da realidade, visando identificar e desmentir fake news. Uma possível prática de pesquisa que pode ser desempenhada pelos estudantes é a revisão bibliográfica. Essa prática tem como objetivo realizar um levantamento do que já foi escrito e debatido sobre determinado tema ou assunto. A busca pode ser feita em livros, artigos, jornais, sites e revistas.

Lima e Mioto defendem que:

[...] a pesquisa bibliográfica implica em um conjunto ordenado de procedimentos de busca por soluções, atento ao objeto de estudo, e que, por isso, não pode ser aleatório [...]

LIMA, Telma Cristiane Sasso de; MIOTO, Regina Célia Tamaso. Procedimentos metodológicos na construção do conhecimento científico: a pesquisa bibliográfica. Katálysis, Florianópolis, v. 10, n. esp., maio 2007. p. 38.

Podemos considerar, então, que a pesquisa de revisão bibliográfica revisa e interpreta em seu método a visão de outros autores a respeito de determinado assunto, por meio de estratégias de pesquisa histórica e sócio-histórica, gerando, assim, uma nova visão acerca do tema. A prática de revisão bibliográfica deve ser desenvolvida da seguinte maneira.

• Definir qual tema ou assunto será investigado.
• Buscar informações sobre o tema por meio de palavras-chave, autores, assuntos etc.
• Realizar a pesquisa em fontes importantes, significativas e variadas.
• Selecionar os textos relevantes, de acordo com o objetivo da pesquisa.
• Fazer a leitura atenta do material selecionado.
• Produzir uma síntese com base no material selecionado.

É importante orientar os estudantes a sempre pesquisar em fontes atuais e confiáveis, bem como a confrontar as informações obtidas.

O estudante dos Anos Finais do Ensino Fundamental

Os estudantes dos Anos Finais do Ensino Fundamental buscam por conhecimentos que os ajudarão a solucionar os desafios diários e também aqueles que poderão surgir no futuro. Para isso, eles precisam ter suporte social e emocional. Cabe, então, à educação auxiliar na formação e no processo de aprendizagem desse cidadão em todos os seus aspectos, como cita a BNCC:

[...]

Independentemente da duração da jornada escolar, o conceito de educação integral com o qual a BNCC está comprometida se refere à construção intencional de processos educativos que promovam aprendizagens sintonizadas com as necessidades, as possibilidades e os interesses dos estudantes e, também, com os desafios da sociedade contemporânea. Isso supõe considerar as diferentes infâncias e juventudes, as diversas culturas juvenis e seu potencial de criar novas formas de existir.

[...]

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 357. Disponível em: https://oeds.link/pKEA59 Acesso em: 19 maio 2022.

Portanto, preparar a juventude para a vida a partir do agora é imprescindível para seu desenvolvimento pessoal e em sociedade, promovendo uma independência responsável frente aos seus estudos, direitos e deveres, na sua representação social enquanto adolescente e em sua interioridade, com seus desejos, sonhos, anseios, sentimentos por meio do ensino-aprendizagem.

Cultura de paz e combate ao bullying

Saber ouvir e respeitar os outros é uma maneira de viver em sociedade de forma pacífica. Nesse sentido, a cultura de paz, de acordo com Von (2003)
envolvem as práticas de respeito aos valores, atitudes, tradições, comportamentos e modos de vida, que o indivíduo deve desenvolver em relação ao outro, pelos princípios de cada ser humano, ao direito à liberdade de expressão de cada um, direito de ir e vir e pelo respeito aos direitos do ser humano.

O compromisso pessoal que o cidadão firma quando se compromete a promover a cultura de paz é de responsabilidade com a humanidade em seus aspectos físicos, sociais e emocionais, com intuito de fomentar a responsabilidade social em respeitar cada pessoa, evidenciando o bom tratamento às pessoas sem discriminação, preconceito ou violência, prezando por atos generosos, defendendo a liberdade de expressão e diversidade cultural, além de promover a responsabilidade de conservação da natureza e contribuir com a comunidade em que se está envolvido.

Para que essas práticas respeitosas sejam difundidas por meio da educação, o professor deve trabalhá-las de maneira contextualizada e de forma direta ao combate de todo e qualquer tipo de violência e preconceito aos aspectos físicos, sociais, econômicos, psicológicos e sexuais, inclusive com o bullying, que é uma das violências mais presenciadas nas instituições escolares, causando constrangimento a quem o sofre, desfavorecendo o ambiente da sala de aula e da escola.

O diálogo é o principal meio de combate à violência na escola, por meio da reflexão sobre o indivíduo e o coletivo, na discussão de ideias, de temas sensíveis e de valores e atitudes. É também um meio de alerta para promover a cultura de paz e os valores éticos educacionais ligados a ela, como respeito, solidariedade, amor e responsabilidade. Tais temáticas são fundamentais atualmente, na busca por fomentar o aprendizado com um olhar mais igualitário, de inclusão, de troca de experiências e de valores, envolvendo os profissionais de educação e os estudantes, uma vez que a educação sem violência é proposta nesta coleção por meio de atividades que promovem valores, atitudes e ideais de paz.

Culturas juvenis

O olhar para a juventude é múltiplo e de contínua construção, pois a cada dia ela vem sendo compreendida de maneira expressiva por meio da transformação constante de sua realidade, que se adequa baseada nos gostos musicais, artísticos, tecnológicos, esportivos, profissionais, entre outros que envolvem essa heterogeneidade. A identidade dessa geração é moldada e vive em constante processo de mudança em relação aos gostos e experiências sociais, por meio de suas relações, fator que também a caracteriza. Essa modulação de identidade e preferências é algo que torna o jovem autônomo em seu modo de agir, de pensar seu presente e seu futuro, bem como de produzir a si mesmo.

Uma de suas principais produções envolve seu modo de ser e agir, de se vestir, comprar e consumir o que lhe agrada, com base em influências de um mundo globalizado cujo trânsito de informações é veloz. A tecnologia e outros recursos influenciadores são fontes que alimentam essas informações e incentivam as produções de estilos e expressões culturais da juventude, podendo ser influenciados pelas redes sociais, por influenciadores digitais, filmes, fotos, games, entretenimentos, entre outros recursos tecnológicos que se renovam a cada dia.

Esse momento de descoberta de coisas novas envolve os atos de participar, criar, interagir, dialogar e, principalmente, mudar. A juventude se constrói, reconstrói e planeja para si o que reconhece como tomada de consciência, atitude voltada a alcançar o que se almeja. Esse processo de projeção do futuro vem da necessidade de pensar a sua vida profissional e pessoal. Diante desse desafio, eles argumentam, criam projetos, pesquisam, interagem, descobrem inovações e vivem experiências que os faz pensar em seu crescimento.

Esta coleção propõe trabalhar com as culturas juvenis por meio de diversos temas e atividades explorados nos volumes. Ademais, é contemplado o trabalho com o protagonismo para a construção de projetos particulares, tirando dúvidas e incertezas quanto ao seu futuro pessoal e profissional, possibilitando a eles que o idealize com base naquilo de que gostam, no que pensam e no que expressam.

Habilidades da BNCC - Matemática 7º ano

Habilidades na BNCC - 7º ano

Unidades temáticas	Habilidades
Números	(EF07MA01) Resolver e elaborar problemas com números naturais, envolvendo as noções de divisor e de múltiplo, podendo incluir máximo divisor comum ou mínimo múltiplo comum, por meio de estratégias diversas, sem a aplicação de algoritmos. (EF07MA02) Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros. (EF07MA03) Comparar e ordenar números inteiros em diferentes contextos, incluindo o histórico, associá-los a pontos da reta numérica e utilizá-los em situações que envolvam adição e subtração. (EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros. (EF07MA05) Resolver um mesmo problema utilizando diferentes algoritmos. (EF07MA06) Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmos procedimentos. (EF07MA07) Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas. (EF07MA08) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador. (EF07MA09) Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração $2/3$ para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza. (EF07MA10) Comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica. (EF07MA11) Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias. (EF07MA12) Resolver e elaborar problemas que envolvam as operações com números racionais.
Álgebra	(EF07MA13) Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas, diferenciando-a da ideia de incógnita. (EF07MA14) Classificar sequências em recursivas e não recursivas, reconhecendo que o conceito de recursão está presente não apenas na matemática, mas também nas artes e na literatura. (EF07MA15) Utilizar a simbologia algébrica para expressar regularidades encontradas em sequências numéricas. (EF07MA16) Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes. (EF07MA17) Resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas. (EF07MA18) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à forma $\mathit{\text{ax}}+\mathit{\text{b}}=\mathit{\text{c}}$ , fazendo uso das propriedades da igualdade.
Geometria	(EF07MA19) Realizar transformações de polígonos representados no plano cartesiano, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro. (EF07MA20) Reconhecer e representar, no plano cartesiano, o simétrico de figuras em relação aos eixos e à origem.

Habilidades na BNCC - 7º ano

Unidades temáticas	Habilidades
Geometria	(EF07MA21) Reconhecer e construir figuras obtidas por simetrias de translação, rotação e reflexão, usando instrumentos de desenho ou softwares de geometria dinâmica e vincular esse estudo a representações planas de obras de arte, elementos arquitetônicos, entre outros. (EF07MA22) Construir circunferências, utilizando compasso, reconhecê-las como lugar geométrico e utilizá-las para fazer composições artísticas e resolver problemas que envolvam objetos equidistantes. (EF07MA23) Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal, com e sem uso de softwares de geometria dinâmica. (EF07MA24) Construir triângulos, usando régua e compasso, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma das medidas dos ângulos internos de um triângulo é $180°$. (EF07MA25) Reconhecer a rigidez geométrica dos triângulos e suas aplicações, como na construção de estruturas arquitetônicas (telhados, estruturas metálicas e outras) ou nas artes plásticas. (EF07MA26) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um triângulo qualquer, conhecidas as medidas dos três lados. (EF07MA27) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos. (EF07MA28) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular (como quadrado e triângulo equilátero), conhecida a medida de seu lado.
Grandezas e medidas	(EF07MA29) Resolver e elaborar problemas que envolvam medidas de grandezas inseridos em contextos oriundos de situações cotidianas ou de outras áreas do conhecimento, reconhecendo que toda medida empírica é aproximada. (EF07MA30) Resolver e elaborar problemas de cálculo de medida do volume de blocos retangulares, envolvendo as unidades usuais (metro cúbico, decímetro cúbico e centímetro cúbico). (EF07MA31) Estabelecer expressões de cálculo de área de triângulos e de quadriláteros. (EF07MA32) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas. (EF07MA33) Estabelecer o número $\mathit{\pi }$ como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica.
Probabilidade e estatística	(EF07MA34) Planejar e realizar experimentos aleatórios ou simulações que envolvem cálculo de probabilidades ou estimativas por meio de frequência de ocorrências. (EF07MA35) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados. (EF07MA36) Planejar e realizar pesquisa envolvendo tema da realidade social, identificando a necessidade de ser censitária ou de usar amostra, e interpretar os dados para comunicá-los por meio de relatório escrito, tabelas e gráficos, com o apoio de planilhas eletrônicas. (EF07MA37) Interpretar e analisar dados apresentados em gráfico de setores divulgados pela mídia e compreender quando é possível ou conveniente sua utilização.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2017. p. 300-305. Disponível em: https://oeds.link/pKEA59 Acesso em: 9 maio 2022.

Quadro de conteúdos do 7º ano

Este volume foi organizado com base na abordagem teórico-metodológica da coleção, que busca transmitir os conhecimentos deste componente curricular e oferecer subsídios para que os estudantes possam, de maneira cada vez mais autônoma, analisar, selecionar, organizar e questionar as informações que farão parte tanto de seu processo de aprendizagem quanto de sua formação cidadã. De acordo com essa proposta, consta a seguir um quadro com a organização dos principais conteúdos e conceitos trabalhados no volume, além dos objetos de conhecimento, das habilidades, das competências gerais e específicas e dos temas contemporâneos transversais. Esses elementos foram organizados com base no trabalho desenvolvido em cada unidade, permitindo uma progressão da aprendizagem de acordo com as necessidades reais da turma em sala de aula. As justificativas referentes aos objetivos de ensino encontram-se na primeira página após a abertura de cada unidade, na parte da reprodução do Livro do Estudante.

Unidade 1 • Múltiplos e divisores de um número

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Múltiplos de um número natural. Divisores de um número natural. Números primos. Decomposição em fatores primos. Máximo divisor comum. Mínimo múltiplo comum.	Múltiplos e divisores de um número natural.	EF07MA01	Competências específicas: 1, 2, 3, 4, 6, 7, 8. Competências gerais: 1, 2, 4, 7, 9.	Saúde

Unidade 2 • Os números inteiros

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Números inteiros. Números inteiros na reta numérica. Comparação entre números inteiros. Adição com números inteiros. Subtração com números inteiros. Multiplicação com números inteiros. Divisão com números inteiros. Potenciação com números inteiros.	Números inteiros: usos, história, ordenação, associação com pontos da reta numérica e operações.	EF07MA03 EF07MA04	Competências específicas: 1, 6. Competências gerais: 1, 2, 9.	Educação financeira

Unidade 3 • Frações

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Fração como parte de um todo. Fração como resultado da divisão. Fração como razão. Fração de uma quantidade. Frações equivalentes e simplificação de frações. Comparação de frações.	Fração e seus significados: como parte de inteiros, resultado da divisão, razão e operador.	EF07MA05 EF07MA06 EF07MA07 EF07MA08 EF07MA09	Competências específicas: 1, 5, 6, 8. Competências gerais: 1, 2, 5, 9.	Saúde Educação financeira

Unidade 4 • Os números racionais

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Números racionais. Números racionais na reta numérica. Módulo de um número racional. Oposto ou simétrico de um número racional. Comparação de números racionais.	Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações.	EF07MA10	Competências específicas: 6, 8. Competência geral: 9.

Unidade 5 • Operações com números racionais

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Adição e subtração de números racionais. Multiplicação e divisão de números racionais. Potenciação cuja base é um número racional.	Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operações.	EF07MA11 EF07MA12	Competências específicas: 3, 6. Competências gerais: 7, 9.	Educação fiscal

Unidade 6 • Cálculo algébrico

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Sequências. Expressões algébricas. Igualdades. Fórmulas. Equações.	Linguagem algébrica: variável e incógnita. Equivalência de expressões algébricas: identificação da regularidade de uma sequência numérica. Equações polinomiais do 1º grau.	EF07MA13 EF07MA14 EF07MA15 EF07MA16 EF07MA18	Competências específicas: 2, 3, 5, 6. Competências gerais: 2, 4, 8, 9.	Educação financeira Saúde

Unidade 7 • Figuras geométricas planas e ângulos

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Ângulos. Propriedades das retas paralelas cortadas por uma transversal. Polígonos. Triângulos. Circunferência.	A circunferência como lugar geométrico. Relações entre os ângulos formados por retas paralelas intersectadas por uma transversal. Triângulos: construção, condição de existência e soma das medidas dos ângulos internos. Polígonos regulares: quadrado e triângulo equilátero.	EF07MA22 EF07MA23 EF07MA24 EF07MA25 EF07MA26 EF07MA27 EF07MA28 EF07MA33	Competências específicas: 3, 6, 8. Competências gerais: 1, 3, 4, 5, 9.	Saúde Diversidade cultural

Unidade 8 • Grandezas e medidas

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Grandezas e suas respectivas medidas. Sistema Internacional de Unidades (SI). Medidas de área. Medidas de volume.	Problemas envolvendo medições. Cálculo de volume de blocos retangulares utilizando as unidades de medida convencionais mais usuais. Equivalência de área de figuras planas: cálculo de áreas de figuras que podem ser decompostas por outras cujas áreas podem ser facilmente determinadas como triângulos e quadriláteros.	EF07MA29 EF07MA30 EF07MA31 EF07MA32	Competências específicas: 6, 8. Competências gerais: 2, 6, 9.	Ciência e tecnologia

Unidade 9 • Proporção

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Grandezas diretamente e inversamente proporcionais. Regra de três e grandezas diretamente proporcionais. Regra de três e grandezas inversamente proporcionais.	Problemas envolvendo grandezas diretamente proporcionais e grandezas inversamente proporcionais.	EF07MA17	Competências específicas: 2, 6. Competências gerais: 1, 4, 8, 9.	Educação ambiental Alimentação e nutrição

Unidade 10 • Porcentagem

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Conceito de porcentagem. Relação entre fração e porcentagem. Uso e cálculo de porcentagem.	Cálculo de porcentagens e de acréscimos e decréscimos simples.	EF07MA02	Competências específicas: 3, 4, 6, 7. Competências gerais: 7, 9.	Educação financeira Educação ambiental

Unidade 11 • Estatística e probabilidade

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Tabelas e gráficos. Média aritmética e amplitude. Média ponderada. Pesquisa estatística. Probabilidade.	Experimentos aleatórios: espaço amostral e estimativa de probabilidade por meio de frequência de ocorrências. Estatística: média e amplitude de um conjunto de dados. •esquisa amostral e pesquisa censitária. Planejamento de pesquisa, coleta e organização de dados, construção de tabelas e gráficos e interpretação de informações. Gráficos de setores: interpretação, pertinência e construção para representar um conjunto de dados.	EF07MA34 EF07MA35 EF07MA36 EF07MA37	Competências específicas: 1, 2, 3, 4, 5, 6, 8. Competências gerais: 4, 7, 9, 10.	Educação para o consumo Educação ambiental

Unidade 12 • Transformações de figuras

Principais conteúdos e conceitos	Objetos de conhecimento	Habilidades	Competências	Temas contemporâneos transversais
Simetria axial. Transformação de reflexão. otação. Simetria de rotação. Transformação de translação. Plano cartesiano. Transformações no plano cartesiano.	Transformações geométricas de polígonos no plano cartesiano: multiplicação das coordenadas por um número inteiro e obtenção de simétricos em relação aos eixos e à origem. Simetrias de translação, rotação e reflexão.	EF07MA19 EF07MA20 EF07MA21	Competências específicas: 5, 8. Competências gerais: 3, 5, 9.	Diversidade cultural

Sugestões de cronograma

O cronograma a seguir sugere possibilidades de distribuição do conteúdo curricular deste volume durante o ano letivo. Todos os volumes são estruturados considerando a autonomia em sua prática pedagógica. Assim, torna-se possível analisar e verificar diferentes e melhores maneiras de conduzir os estudos junto aos estudantes, pois a sequência dos conteúdos pode ser organizada da maneira que julgar conveniente.

Sugestões de cronograma

Bimestral
1º bimestre	O que eu já sei? Unidade 1 – Múltiplos e divisores de um número Unidade 2 – Os números inteiros
2º bimestre	Unidade 3 – Frações Unidade 4 – Os números racionais Unidade 5 – Operações com números racionais Unidade 6 – Cálculo algébrico
3º bimestre	Unidade 7 – Figuras geométricas planas e ângulos Unidade 8 – Grandezas e medidas
4º bimestre	Unidade 9 – Proporção Unidade 10 – Porcentagem Unidade 11 – Estatística e probabilidade Unidade 12 – Transformações de figuras O que eu aprendi?
Trimestral
1º trimestre	O que eu já sei? Unidade 1 – Múltiplos e divisores de um número Unidade 2 – Os números inteiros Unidade 3 – Frações Unidade 4 – Os números racionais
2º trimestre	Unidade 5 – Operações com números racionais Unidade 6 – Cálculo algébrico Unidade 7 – Figuras geométricas planas e ângulos
3º trimestre	Unidade 8 – Grandezas e medidas Unidade 9 – Proporção Unidade 10 – Porcentagem Unidade 11 – Estatística e probabilidade Unidade 12 – Transformações de figuras O que eu aprendi?